2018年广州中考数学一模一次函数与反比例函数汇编
广东省广州市白云区2018届九年级数学下学期综合测试(一模)试题

(A)3+ = (B) — =
(C)— + =0 (D) - =
4.矩形ABCD的对角线AC、BD交于点O,以下结论不一定成立的是(*)
(A)∠BCD=90° (B)AC=BD (C)OA=OB (D)OC=CD
5。不等式组 的整数解有(*)
(A)4个 (B)3个 (C)2个 (D)1个
答:现在从A地到B地可比原来少走5.9km路程.………………………………8分
23.(本小题满分12分,分别为3、3、6分)
解:(1)由tan∠AOB= ,得 = ,……………………………………1分
∴OH=2BH,又B( , ),即 =2× = ,………………………2分
∴H点的坐标为H(0, );……………………………………………………3分
=2( +2)( -2)………………………………………………9分
18.(本小题满分9分)
证明:∵C是BD的中点,∴BC=CD(线段中点的 定义);……………2分
∵AB∥EC,∴∠B=∠ECD(两直线平行,同位角相等)。…………4分
在△ABC和△ECD中,……………………………………………………5分
∵ ,∴△ABC≌△ECD(AAS),……………………8分
14。从1至9这9个自然数中任取一个,是2的倍数或是3的倍数的概率是*.
15。若分式 的值为0,则 =*。
16。如图3,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为*(结果用根号表示).
三、解答题(本大题共9小题,满分102分.解答应写出文字说明、证明过程或演算步骤)
∴该区九年级学生大约有36000人视力不良;…………………………4分
【中考数学复习】一次函数与反比例函数知识
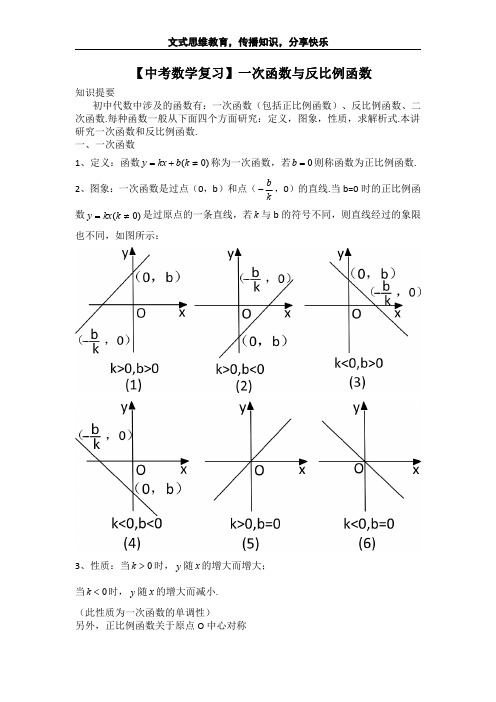
【中考数学复习】一次函数与反比例函数知识提要初中代数中涉及的函数有:一次函数(包括正比例函数)、反比例函数、二次函数.每种函数一般从下面四个方面研究:定义,图象,性质,求解析式.本讲研究一次函数和反比例函数.一、一次函数1、定义:函数)0(≠+=k b kx y 称为一次函数,若0=b 则称函数为正比例函数.2、图象:一次函数是过点(0,b )和点(kb -,0)的直线.当b=0时的正比例函数)0(≠=k kx y 是过原点的一条直线,若k 与b 的符号不同,则直线经过的象限也不同,如图所示:3、性质:当0>k 时,y 随x 的增大而增大;当0<k 时,y 随x 的增大而减小.(此性质为一次函数的单调性)另外,正比例函数关于原点O 中心对称4、求解析式:求一次函数的解析式,一般需要两个条件,求出表达式b kx y +=中的k 及b 的值,常用待定系数法来求一次函数.而正比例函数的解析式只需要一个条件.二、反比例函数1、定义:形如)0(≠=k x k y 形式称为反比例函数,定义域为0≠x 的所有实数.2、图象:反比例图象为双曲线,如图所示:3、性质:反比例函数x k y =在0>k 且0>x 时,函数值y 随x 的增大而减小;在0>k 且0<x 时,函数值y 随x 的增大而减小.即:当0>k 时,反比例函数x k y =分布在一、三象限,在每个象限内,y 随x 的增大而减小,如图(1)所示.当0<k 时,反比例函数xk y =分布在二、四象限,在每个象限内,y 随x 的增大而增大,如图(2)所示.反比例函数x k y =图象上的点关于原点O 成中心对称的.当0>k 时,函数的图象关于直线x y =成轴对称;当0<k 时,函数的图象关于直线x y -=成轴对称.4、求解析式:反比例函数的解析式,只需要一个条件,求出xk y =)0(≠k 中的k 即可.在解决有关一次函数及反比例函数的问题时,常运用数形结合及分类讨论的思想方法.待定系数法是研究函数表达式的基本方法,同时紧密结合图象寻求思路,是处理这类问题的重要方法.例1、已知正比例函数x y =和)0(>=a ax y 的图象与反比例函数xky =(k>0)的图象在第一象限内分别相交于A 、B 两点,过A 、B 作x 轴的垂线,垂足分别为C 、D ,设△AOC 和△BOD 的面积分别为1S 、2S ,则1S 与2S 的大小关系怎样?例2、两个反比例函数x y 3=,x y 6=在第一象限内的图象如图所示,点1P ,2P ,3P ,…2005P 在反比例函数x y 6=图象上,它们的横坐标分别是1x ,2x ,3x ,…2005x ,纵坐标分别是1,3,5,…,共2005个连续奇数,过点1P ,2P ,3P ,…2005P 分别作y 轴的平行线,与xy 3=的图象交点依次是)(111y x Q ,,)(222y x Q ,,)(333y x Q ,,…)(200520052005y x Q ,,则_________2005=y .例3、平面直角坐标系内有A (2,-1)、B (3,3)两点,点P 是y 轴上一动点,求P 到A 、B 距离之和最小时的坐标.例4、已知一次函数的图象经过点(2,2),它与两坐标轴所围成的三角形的面积等于1,求这个一次函数的解析式.例5、已知A (-2,0)、B (4,0),点P 在直线221+=x y 上,若△PAB 是直角三角形,求点P 的坐标.例6、已知两人连续6年对某县农村甲鱼养殖业的规模(产量)进行调查,提供两个方面的信息,如图所示,请根据图中提供的信息,求:(1)第2年全县生产甲鱼的只数及甲鱼池的个数;(2)到第6年,这个县的甲鱼养殖规模比第1年是扩大了还是缩小了,请说明理由.例7、如图,已知C 、D 是双曲线xm y =在第一象限内的分支上的两点,直线CD 分别交x 轴、y 轴于A 、B 两点,设C 、D 的坐标分别是(11y x ,)、(22y x ,),连接OC 、OD.(1)求证:111y m y OC y +<<;(2)若α=∠=∠AOD BOC ,31tan =α,10=OC ,求直线CD 的解析式.(3)在(2)的条件下,双曲线是否存在一点P ,使POD POC S S ∆∆=?若存在,求出P 点坐标;若不存在,请说明理由.例8、有一个附有进、出水管的容器,每单位时间进、出的水量都是一定的,设从某时刻开始5分钟内只进水不出水,在随后的15分钟内既进水又出水,得到时间x (分)与水量y (升)之间的关系如图所示,若20分钟后只放水不进水,求多长时间能将水放完?例9、为了预防流感,某学校对教室用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y (毫克)与时间x (分钟)成正比例,药物燃烧后,y 与x 成反比例(如图),观测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中提供的信息解答下列问题:(1)药物燃烧时,y 关于x 的函数关系式为__________,自变量x 的取值范围是___________;药物燃烧后y 关于x 的函数关系式为____________.(2)研究表明,当空气中的每立方米含药量低于1.6毫克时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回到教室.(3)研究表示,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?例10、某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台,且冰箱至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表所示:家电名称空调器彩电冰箱工时/个213141产值/千元432问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)练习1、已知0≠abc 并且p b a c a c b c b a =+=+=+而直线p px y +=一定通过()A 第一、二象限B 第二、三象限C 第三、四象限D 第一、四象限2、函数kx y =和)0(<=k x k y 在同一坐标系中的图象是()3、一次函数b kx y +=过点)(11y x ,和)(22y x ,,且0>k ,b<0,当210x x <<时,有()A 21y b y >>B 21y b y <<C b y y <<<210D 012<<<y b y 4、若点(-2,1y ),(1,2y ),(2,3y )在反比例函数x y 21=的图象上,则下列结论正确的是()A 123y y y >>B 312y y y >>C 132y y y >>D 321y y y >>5、反比例函数x k y =的图象是轴对称图形,它的一条对称轴是下列正比例函数图象中的()A kxy -=B x k y =C x k k y =D kxy =6、一个一次函数图象与直线49545+=x y 平行,与x 轴、y 轴的交点分别为A 、B ,并且过点(-1,-25),则在线段AB 上(包括端点A 、B ),横、纵坐标都是整数的点有()A 4个B 5个C 6个D 7个7、如图,正比例函数x y 3=的图象与反比例函数xk y =(0>k )的图象交于点A ,若取k 为1,2,3,…,20,对应的Rt △AOB 的面积分别为1S ,2S ,…20S ,则__________2021=+++S S S .8、不论k 为何值,解析式0)11()3()12(=--+--k y k x k 表示函数的图象都经过一定点,则这个定点是_________.9、如图所示,直线l 和双曲线x k y =(0>k )交于A 、B 两点,P 是线段AB 上的点(不与A 、B 重合),过点A 、B 、P 分别向x轴作垂线,垂足分别为C 、D 、E ,连接OA 、OB 、OP.设△AOC 的面积为1S ,△BOD 的面积为2S ,△POE 的面积为3S ,则321S S S 、、的大小关系是______________.10、甲、乙两车出发后再同一条公路行驶,行驶路程与时间的关系如图所示,那么可以知道:(1)出发行驶在前面的车是_________,此时两车相隔_________;(2)两车的速度分别为甲:___________千米/小时,乙:_________千米/小时,经过___________小时,快车追上慢车;(3)甲、乙两车均行驶600千米时各用的时间分别是:甲用_________小时,乙用__________小时.11、如图,函数221+-=x y 的图象交y 轴于M ,交x 轴于N ,MN 上两点A ,B 在x 轴上射影分别为11B A 、,若411>+OB OA ,则A OA 1∆的面积1S 与B OB 1∆的面积2S 的大小关系是_____________.12、已知非负数x 、y 、z 满足323=++z y x ,433=++z y x ,则z y x w 423+-=的最大值为_________,最小值为__________.13、在直角坐标系中,有四个点:A (-8,3),B (-4,5),C (0,n ),D (m ,0),当四边形ABCD 的周长最短时,求nm 的值.14、设直线1)1(=++y k kx (k 是自然数)与两坐标轴所围成的图形的面积为1S ,2S ,…,2000S .求200021S S S +++ 的值.15、如图(1),已知直线m x y +-=21与反比例函数xk y =的图象在第一象限内交于A 、B 两点(点A 在点B 的左侧),分别于x 、y 轴交于C 、D ,AE ⊥x 轴于E.(1)若OE·CE=12,求k 的值;(2)如图(2),作BF ⊥y 轴于F ,求证:EF ∥CD ;(3)在(1)(2)的条件下,5=EF ,52=AB ,P 是x 轴正半轴上一点,且△PAB 是以P 为直角顶点的等腰直角三角形,求P 点的坐标.(1)(2)16、已知直线62+-=-k y x 和143+=+k y x ,若它们的交点在第四象限内.(1)求k 的取值范围;(2)若k 为非负整数,点A 的坐标为(2,0),点P 在直线62+-=-k y x 上,求使△PAO 为等腰三角形的点P 的坐标.17、A 市、B 市和C 市分别有某种机器10台、10台和8台,现决定把这些机器支援给D 市18台,E 市10台.已知从A 市调运一台机器到D 市、E 市的运费分别为200元和800元,从B 市调运一台机器到D 市、E 市的运费分别为300元和700元,从C 市调运一台机器到D 市、E 市的运费分别为400元和500元.(1)设从A 市、B 市各调x 台到D 市,当28台机器全部调运完毕后,求总运费w (元)关于x (台)的函数式,并求w 的最大值和最小值;(2)设从A 市调x 台到D 市,从B 市调y 台到D 市,当28台机器全部调运完毕后,用x ,y 表示总运费w (元),并求w 的最大值和最小值.18、直线133+-=x y 与x 轴、y 轴分别交于点A 、B ,以线段AB 为直角边在第一象限内作等腰直角三角形ABC ,其中∠BAC=90°.如果第二象限内有一点P (a ,21),使△ABP 的面积和△ABC 的面积相等,求a 的值.文式思维教育,传播知识,分享快乐19、如图,在直角坐标系中,点1O 的坐标为(1,0),⊙1O 与x 轴交于原点O 和点A ,又点B 、C 的坐标分别为(-1,0),(0,b ),且30<<b ,直线l 是过B 、C 点的直线.(1)当点C 在线段OC 上移动时,过点1O 作l D O 直线⊥1,交l 于D ,若a S S CBO BOC=∆∆1,试求b a 与的函数关系式及a 的取值范围.20、某仓储系统有20条输入传送带、20条输出传送带.某日,控制室的电脑显示,每条输入传送带每小时进库的货物流量如图(a ),每条输出传送带每小时出库的货物流量如图(b ),而该日仓库中原有货物8吨,在0时至5时,仓库中货物存量变化情况如图(c ),则在0时至2时有多少条输入传送带在工作?在4至5时有多少条输入传送带和输出传送带在工作?。
2018年广州中考数学一模函数综合压轴题汇编参考答案
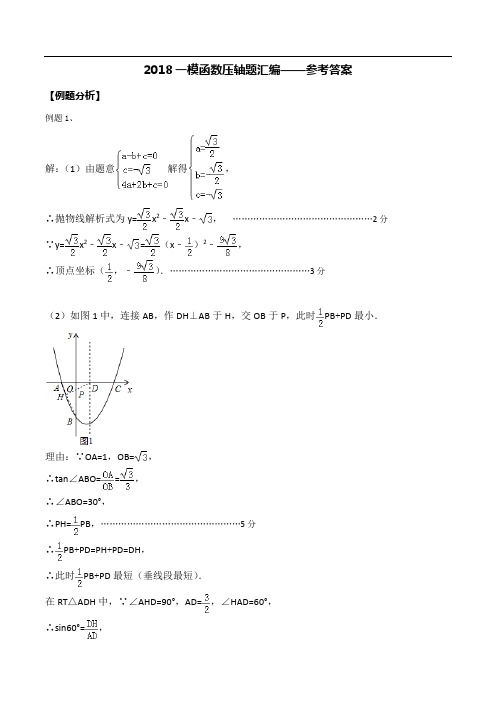
2018一模函数压轴题汇编——参考答案【例题分析】例题1、解:(1)由题意解得,∴抛物线解析式为y=x2﹣x﹣,…………………………………………2分∵y=x2﹣x﹣=(x﹣)2﹣,∴顶点坐标(,﹣).…………………………………………3分(2)如图1中,连接AB,作DH⊥AB于H,交OB于P,此时PB+PD最小.理由:∵OA=1,OB=,∴tan∠ABO==,∴∠ABO=30°,∴PH=PB,…………………………………………5分∴PB+PD=PH+PD=DH,∴此时PB+PD最短(垂线段最短).在RT△ADH中,∵∠AHD=90°,AD=,∠HAD=60°,∴sin60°=,∴DH=,∴PB+PD的最小值为.故答案为.…………………………………………7分(3)如图,RT△AOB中,∵tan∠ABO==,∴∠ABO=30°,…………………………………………8分作AB的中垂线与y轴交于点E,连接EA,则∠AEB=120°,以E为圆心,EB为半径作圆,与抛物线对称轴交于点F、G.则∠AFB=∠AGB=60°,从而线段FG上的点满足题意,∵EB==,∴OE=OB﹣EB=,…………………………………………10分∵F(,t),EF2=EB2,∴()2+(t+)2=()2,解得t=或,…………………………………………12分故F(,),G(,),∴t的取值范围≤t≤…………………………………………14分例题2、解:(1)根据题意得A(﹣4,0),C(0,2),∵抛物线y=﹣x2+bx+c经过A、C两点,∴,∴,∴y=﹣x2﹣x+2;…………………………………………3分(2)①如图,令y=0,∴﹣x2﹣x+2=0,∴x1=﹣4,x2=1,∴B(1,0),…………………………………………4分过D作DM⊥x轴于M,过B作BN⊥x轴交于AC于N,∴DM∥BN,∴△DME∽△BNE,∴==,…………………………………………5分设D(a,=﹣a2﹣a+2),∴M(a,a+2),∵B(1.0),∴N(1,),∴==(a+2)2+;…………………………………………7分∴当a=2时,的最大值是;…………………………………………8分②∵A(﹣4,0),B(1,0),C(0,2),∴AC=2,BC=,AB=5,∴AC2+BC2=AB2,∴△ABC是以∠ACB为直角的直角三角形,取AB的中点P,………………………9分∴P(﹣,0),∴PA=PC=PB=,∴∠CPO=2∠BAC,∴tan∠CPO=tan(2∠BAC)=,…………………………………………10分过D作x轴的平行线交y轴于R,交AC的延长线于G,情况一:如图,∴∠DCF=2∠BAC=∠DGC+∠CDG,∴∠CDG=∠BAC,∴tan∠CDG=tan∠BAC=,即,令D(a,﹣a2﹣a+2),∴DR=﹣a,RC=﹣a2﹣a,∴,∴a1=0(舍去),a2=﹣2,∴x D=﹣2,…………………………………………12分情况二,∴∠FDC=2∠BAC,∴tan∠FDC=,设FC=4k,∴DF=3k,DC=5k,∵tan∠DGC==,∴FG=6k,∴CG=2k,DG=3k,∴∴RC=k,RG=k,DR=3k﹣k=k,∴==,∴a1=0(舍去),a2=,点D的横坐标为﹣2或﹣.…………………………………………14分例题3、解:(1)A(0,4),B(4,0),C(-1,0) ……………………………3分(2) ①AQ AO AQ COQP CO QP AO ==或 2431x x x =-2134x x x =-或 解得134x =或7x =, 均在抛物线对称轴的右侧. ∴点P 的坐标为1351(,)-416或(7,24). …………………5分 (图1) ② Q (x ,4) ,P (x ,2-34x x ++) PQ =23x x -=PM ,△AEM ∽△MFP . 则有AM MPME PF=. ∵ME =OA =4,AM=AQ =x ,PM =PQ =23x x -,所以234x x xPF-=.得PF =4x -12,∴ OM =(4x -12)-x =3x -12. ………………7分 Rt △AOM 中,由勾股定理得222OM OA AM +=,∴222(312)4x x -+=,解得x 1=4,x 2=5.,均在抛物线对称轴的右侧. (图2) ∴点P 的坐标为(4,0)或(5,-6).………………………………9分例题4、解:(1)由题意得,⎧⎪⎨⎪⎩∴二次函数的解析式为y =(10)B ∴,,其顶点坐标为(-(2)由题意知,3AO =,OB 60CBA ∴∠=︒,又BM BN =,∴△MBN将BMN ∆沿MN 翻折后,2t B N BN '==,60B NM BMN '∠=∠=︒,//,B N MB '∴(13t B '∴-). …………………………5分若点B '=化简得:29t 9t=0-,t 0≠∴,此时,(10(0M N -,),,(3)由题意可得ABC ∆且30,60.BAC ABC ∠=︒∠=︒又分二种情况讨论:1),当P 在x 轴上时,过Q 作1PQ BQ x ⊥交轴于1P ,则1PBQ ABC ∆∆∽,此时1(10)P -,; 过Q 作2PQ x ⊥轴于2P ,则2QBP ABC ∆∆∽,此时21(0)2P,;P 在x 轴上其他位置时,三角形PQB ∆不为直角三角形,不可能与ABC ∆相似. ……………………………11分2),同理,当P 点在y 轴上时,设1PQ BQ y ⊥交轴于3P ,则3BPQ ABC ∆∆∽,此时3(03P,;过B 作4P B BQ ⊥交y 轴于4P ,但4,BP ACBQ BC≠则2QBP ABC ∆∆与不相似,P 在y 轴上其他位置时,三角形PQB ∆不为直角三角形,不可能与ABC ∆相似. ……………………………14分例题5、解: (1) 抛物线223(0)y ax ax a =-->的对称轴为:212x a-=-=. ………………………1分 a >0,抛物线开口向上,大致图象如图所示. ∴当1x ≥时,y 随x 增大而增大;由已知:当24x ≤≤时,函数有最大值5.∴当4x =时, 5y =, 16835,1a a a ∴--==得:. 223y x x ∴=-- ……………………………2分令0,x = 得3y =- ,令0,y = 得13x x =-=或,∴ 抛物线与y 轴交于0(,-3), 抛物线与x 轴交于-(1,0)、(3,0). ……………………………3分 (2)2223(1)4y x x x =--=--,其折叠得到的部分对应的解析式为:2(1)43)y x x =--+<<(-1,其顶点为1,4(). …………………4分图象与直线y n =恒有四个交点, ∴04n <<由2(1)4x n --+=,解得1x =(1),(1)B n C n ∴,BC =…………………………6分当以BC 为直径的圆与x 轴相切时,2BC n =.即:2n =,=24n n ∴=- ,得n =,04n <<,∴n =………………………8分 (另法:∵BC 直径,且⊙F 与x 轴相切,∴FC =y =n ,∵对称轴为直线x =1,∴F (1,n ),则C (1+n ,n ),又∵C 在2(1)43)y x x =--+<<(-1上, ∴2(11)4n n =-+-+,得12n -±=,04n <<,∴12n -+=(3)若关于m 的一元二次方程20040m y m k y -+-+= 恒有实数根,则须 200=)4(4)0y k y ∆---+≥( 恒成立, ……………………………10分即2004416k y y ≤-+恒成立,即202124y k -+≤()恒成立点00(,)P x y 是(2)中翻折得到的抛物线弧部分上任意一点,004y ∴<≤,∴ 20212344y -+<≤(), ( k 取 202124y -+()值之下限)…………………………13分∴ 实数k 的最大值为3. ……………………………14分例题6、解:(1)∵C (0,3).∴﹣9a=3,解得:a=﹣.令y=0得:ax 2﹣2 x ﹣9a=0, ∵a ≠0,∴x 2﹣2 x ﹣9=0,解得:x=﹣ 或x=3 . ∴点A 的坐标为(﹣ ,0),B (3 ,0).∴抛物线的对称轴为x= .……………………………3分 (2)∵OA= ,OC=3, ∴tan ∠CAO= , ∴∠CAO=60°.∵AE 为∠BAC 的平分线, ∴∠DAO=30°.∴DO=AO=1. ∴点D 的坐标为(0,1)……………………………5分设点P 的坐标为( ,a ).依据两点间的距离公式可知:AD 2=4,AP 2=12+a 2,DP 2=3+(a ﹣1)2. 当AD=PA 时,4=12+a 2,方程无解.当AD=DP 时,4=3+(a ﹣1)2,解得a=2或a=0,∴点P的坐标为(,2)或(,0).……………………………6分当AP=DP时,12+a2=3+(a﹣1)2,解得a=﹣4.∴点P的坐标为(,﹣4).综上所述,点P的坐标为(,2)或(,0)或(,﹣4).…………………………8分(3)设直线AC的解析式为y=mx+3,将点A的坐标代入得:﹣m+3=0,解得:m=,∴直线AC的解析式为y=x+3.设直线MN的解析式为y=kx+1.把y=0代入y=kx+1得:kx+1=0,解得:x=﹣,∴点N的坐标为(﹣,0).∴AN=﹣+=.……………………………10分将y=x+3与y=kx+1联立解得:x=.∴点M的横坐标为.……………………………12分过点M作MG⊥x轴,垂足为G.则AG=+.∵∠MAG=60°,∠AGM=90°,∴AM=2AG=+2=.∴+=+=+===.…………………14分例题7、解:(1)由题意,得点B的坐标为(4,–1).∵抛物线过点A(0,–1),B(4,–1)两点,∴21,1144.2c b c -=⎧⎪⎨-=-⨯++⎪⎩解得2,1.b c =⎧⎨=-⎩ ∴抛物线的函数表达式为:21212y x x =-+-. ……………………………3分(2)ⅰ)∵A 的坐标为(0,–1),C 的坐标为(4,3).∴直线AC 的解析式为:y =x –1.设平移前的抛物线的顶点为P 0,则由(1)可得P 0的坐标为(2,1),且P 0在直线AC 上. ∵点P 在直线AC 上滑动,∴可设P 的坐标为(m ,m -1),则平移后的抛物线的函数表达式为21()(1)2y x m m =--+-.解方程组21,1()(1).2y x y x m m =-⎧⎪⎨=--+-⎪⎩得{11,1,x m y m ==-{222,3.x m y m =-=- 即P (m ,m -1),Q (m -2,m -3).……………………………5分 过点P 作PE ∥x 轴,过点Q 作QE ∥y 轴,则 PE =m -(m -2)=2,QE =(m -1)-(m -3)=2. ∴PQ=AP 0.……………………………6分若△MPQ 为等腰直角三角形,则可分以下两种情况:①当PQ 为直角边时:M 到PQ 的距离为为22(即为PQ 的长). 由A (0,-1),B (4,-1),P 0(2,1)可知:△ABP 0为等腰直角三角形,且BP 0⊥AC ,BP 0=22.过点B 作直线l 1∥AC 交抛物线21212y x x =-+-于点M ,则M 为符合条件的点.∴可设直线l 1的解析式为:1y x b =+.又∵点B 的坐标为(4,–1),∴114b -=+.解得15b =-. ∴直线l 1的解析式为:5y x =-.解方程组25,12 1.2y x y x x =-⎧⎪⎨=-+-⎪⎩得:114,1,x y =⎧⎨=-⎩222,7.x y =-⎧⎨=-⎩ ∴1(4,1)M -,2(2,7)M --. ……………………………8分②当PQ 为斜边时:MP =MQ =2,可求得M 到PQ 的距离为为2.取AB 的中点F ,则点F 的坐标为(2,-1).由A(0,-1),F(2,-1),P 0(2,1)可知:△AFP 0为等腰直角三角形,且F 到AC 的距离为2.∴过点F 作直线l 2∥AC 交抛物线21212y x x =-+-于点M ,则M 为符合条件的点.∴可设直线l 2的解析式为:2y x b =+.又∵点F 的坐标为(2,–1),∴212b -=+.解得23b =-.∴直线l 2的解析式为:3y x =-. 解方程组23,12 1.2y x y x x =-⎧⎪⎨=-+-⎪⎩ 得:1112x y ⎧=⎪⎨=-⎪⎩2212x y ⎧=⎪⎨=-⎪⎩∴3(12M -,4(12M -.综上所述:所有符合条件的点M 的坐标为: 1(4,1)M -,2(2,7)M --,3(12M -,4(12M -.……………10分ⅱ) PQ NP BQ +存在最大值,理由如下: 由ⅰ)知PQ =22,当NP +BQ 取最小值时,PQ NP BQ+有最大值. 取点B 关于AC 的对称点B ′,易得B ′ 的坐标为(0,3),BQ = B ′Q .连接QF ,FN ,QB ′,易得FN PQ .∴四边形PQFN 为平行四边形.……………………………12分∴NP=FQ .∴NP +BQ =F Q + B ′P ≥F B ′当B ′,Q ,F 三点共线时,NP +BQ最小,最小值为. ∴PQ NP BQ +的最大值. …………………………14分例题8、解:(1)y =-223x +43x +2………………………………………………………2分[或y =-228(1)33x -+](2)△PAC的周长有最小值.……………………………………………………1分连结AC、BC,∵AC的长度一定,∴要使△PAC的周长最小,就是使PA+PC最小.∵点A关于对称轴x =1的对称点是B点,∴BC与对称轴的交点即为所求的点P(如图2).…………………………………2分设直线BC(用BC l 表示,其他直线可用相同方式表示)的表达为BC l :y =kx b +,则有302k b b +=⎧⎨=⎩,解得232k b ⎧=-⎪⎨⎪=⎩,∴BC l :y =-23x +2.……………………………3分 把x =1代入,得y =43, 即点P的坐标为P(1,43).…………………………………………………………4分 ∴△PAC的周长取得最小值,取得最小值时点P的坐标为P(1,43);作DE∥BC交x 轴于点E,DE交对称轴x =1于点Q(如图3).……………5分在Rt过点D作DF⊥y 轴于点F,交对称轴x =1于点N. ∵Rt △CDF∽Rt △CHO,∴CF CD CO CH=, ∴CF=CO CD CH ⋅=5,OF=CO-CF=2-5; 同样,FD CD OH CH =,FD=OH CD CH ⋅5, x y,…………………………6分. ∵DE∥BC,∴可设DE l (过点D、E的直线):y =-23x +1b ,把D点坐标代入其中,得-23⋅1b解得1b DE l :y =-23x 8分点E的纵坐标为0,代入其中,解得x =3-5,.∵点Q在对称轴x =1上,把x =1代入DE l 中,解得y =43∴Q(1,43.PQ=43-(43EH=3-5-1=2-5. S=S△PDE=S△PDQ+S△PEQ=12PQ·DN+12PQ·EH=12PQ(DN+EH)=12·15(1-5+2-5),化简得S=-225m 10分 可知S是关于m 的二次函数.S存在最大值.配方可得:S=-22(5m +12,由此可得,S取得最大值为12,…………12分取得最大值时m的值为:m14分例题9解:(1)∵将点A(﹣1,0)代入抛物线的解析式得:﹣1﹣b+3=0,解得:b=2,∴y=﹣x2+2x+3.………………………………………………1分∴抛物线的对称轴为直线x=1.令x=0得:y=3,则C(0,3).∵点B与点A、点D与点C分别关于该抛物线的对称轴对称,∴D(2,3),B(3,0).设直线AD的解析式为y=kx+b.∵将A(﹣1,0)、D(2,3)代入得:,解得:k=1,b=1,∴直线AD的解析式为y=x+1.…………………………………………………2分∴直线AD与x轴正方向的夹角为45°.………………………………………………3分(2)如图1所示:设E(m,﹣m2+2m+3),则F(﹣m2+2m+2,﹣m2+2m+3),EF=﹣m2+2m+2﹣m=﹣m2+m+2.∵∠EGF=90°,∠EFG=45°,∴△EFG为等腰直角三角形.…………………………………………………6分∴l=EF+FG+EG=EF+EF+EF=(1+)EF=(1+)(﹣m2+m+2)=﹣()m2+(+1)m+2+2.…………………………………………………7分(3)∵y=﹣x2+2x+3=﹣(x﹣1)2+4,∴M(1,4).…………………………………………………8分①AM为矩形的对角线时,如图2所示:∵由矩形的性质可知:N为AM的中点,A(﹣1,0),M(1,4),∴N(0,2).…………………………………………………10分∵由两点间的距离公式可知:MN==.∴NQ1=NQ2=,∴Q1(0,2+),Q2(0,2﹣).…………………………………………………11分②当AM为矩形的一边时,如图3所示:过Q3作Q3E⊥y轴,垂直为E,过Q4作Q4F⊥y轴,垂足为F.∵在△ANO中,AO=1,ON=2,∴tan∠ANO=,∴tan∠MNP4=,∴P4M MN=,NP4=MN=.…………………………………………………12分∴P4Q3=.∴P4E=P4Q3=1,EQ3=P4Q3=2.∵OE=OP4﹣P4E=4.5﹣1=3.5,∴Q3的坐标为(2,3.5).…………………………………………………13分∵点Q3与Q4关于点N对称,∴Q4(﹣2,).综上所述,点Q的坐标为(0,2+),或(0,2﹣)或(2,3.5)或(﹣2,).…………………………………………………14分例题10 解:(1)将(2,5)A -,(1,0)B -代入2y x bx c =++得42510b c b c -+=⎧⎨-+=⎩………………2分(每个各1分) 解得23b c =-⎧⎨=-⎩ ∴二次函数的解析式为223y x x =-- ………………3分 (2)将0y =代入223y x x =--得2230x x --=,解得121,3x x =-=∴点(3,0)C ……………………4分∵点P 直线AC 下方抛物线上的一动点,过点P 作PE x ⊥轴交AC 于点E ,如右图所示: 则1()2PAC C A S PE x x =-…………………5分 由(2,5)A -,(3,0)C 得直线AC 的解析式为:3y x =-+∴设2(,23)P x x x --,则点(,3)E x x -+ ………………………6分∴3(2)5C A x x -=--=22(3)(23)6E P PE y y x x x x x =-=-+---=-++……………………7分 ∴221155()(6)5152222PAC C A S PE x x x x x x =-=-++=-++ ……………………8分 ∵5125222()2b x a =-=-=-, 将12x =代入2551522PAC S x x =-++可得最大面积为1258PAC S =………………9分 (3)答:存在………………………10分1(1,8)Q ,2(1,2)Q -,3(1,6),Q 4(1,1)Q -………………………14分(注:每个坐标1分)【强化训练】1、解:(1)设抛物线为y=a(x﹣1)2+4,将点(2,3)代入得到a=﹣1 ∴抛物线解析式为y=﹣(x﹣1)2+4,∴y=﹣x2+2x+3.……………………………3分(2)如图1,令y=0,则﹣(x﹣1)2+4=0,∴x=﹣1或x=3,∴A(﹣1,0),B(3,0),∵C(0,3),M(1,4),∴直线CM的解析式为y=x+3,……………………………4分令y=0,则x+3=0,∴x=﹣3,∴D(﹣3,0),∵∠DEM=∠AEP=90°,∠DME=∠APE,∴△DEM∽△AEP,∴,……………………………6分∵A(﹣1,0),E(1,0),D(﹣3,0),M(1,4),∴DE=4,ME=4,AE=2,∴,∴PE=2,∴P(1,2)或(1,﹣2);……………………………8分(3)如图2,当点P在x轴上方时,连接BP,∵PE是抛物线的对称轴,∴∠APE=∠BPE,∵∠ANB=2∠APE,∴∠ANB=∠APB,∴点A,B,N,P四点共圆,……………………………9分∴设圆心F的坐标为(1,n),∴PF=AF=NF,∵A(﹣1,0),N(2,3),∴AF=,NF=,∴n2+4=1+(3﹣n)2,∴n=1,……………………………10分∴F(1,1),PF=AF=,∴PE=+1,∴P(1,+1),当点P在x轴下方时,由对称知,P'(1,﹣﹣1),……………………………12分即:点P的坐标为P(1,+1),或(1,﹣﹣1).……………………………14分2、解:(1)将点A、B坐标代入抛物线解析式,得:,解得,∴抛物线的解析式为:y=﹣x2+4x+5.……………………………3分(2)∵点P的横坐标为m,∴P(m,﹣m2+4m+5),E(m,﹣m+3),F(m,0).∴PE=|y P﹣y E|=|(﹣m2+4m+5)﹣(﹣m+3)|=|﹣m2+m+2|,EF=|y E﹣y F|=|(﹣m+3)﹣0|=|﹣m+3|.由题意,PE=5EF,即:|﹣m2+m+2|=5|﹣m+3|=|m+15| ……………………………5分(a)若﹣m2+m+2=m+15,整理得:2m2﹣17m+26=0,解得:m=2或m=;(b)若﹣m2+m+2=﹣(m+15),整理得:m2﹣m﹣17=0,解得:m=或m=.……………………………7分由题意,m的取值范围为:﹣1<m<5,故m=、m=这两个解均舍去.∴m=2或m=.……………………………8分(3)假设存在.作出示意图如下:∵点E、E′关于直线PC对称,∴∠1=∠2,CE=CE′,PE=PE′.∵PE平行于y轴,∴∠1=∠3,∴∠2=∠3,∴PE=CE,∴PE=CE=PE′=CE′,即四边形PECE′是菱形.……………………………10分由直线CD解析式y=﹣x+3,可得OD=4,OC=3,由勾股定理得CD=5.过点E作EM∥x轴,交y轴于点M,易得△CEM∽△CDO,∴,即,解得CE=|m|,∴PE=CE=|m|,又由(2)可知:PE=|﹣m2+m+2|∴|﹣m2+m+2|=|m|.……………………………12分①若﹣m2+m+2=m,整理得:2m2﹣7m﹣4=0,解得m=4或m=﹣;②若﹣m2+m+2=﹣m,整理得:m2﹣6m﹣2=0,解得m=3+或m=3﹣.由题意,m的取值范围为:﹣1<m<5,故m=3+这个解舍去.综上所述,存在满足条件的点P,可求得点P坐标为(﹣,),(4,5),(3﹣,2﹣3).……………………………14分3、解:⑴ 点C 的坐标为(0,2).点A 坐标为(-1,0). ……………………………3分⑵ AD=. ……………………………6分 ⑶ 要使,由于PQA=PDE ,所以只须∽,即须∽.……………………………8分○1 当0 <m<1时,点P 在x 轴下方,此时PQA 显然为钝角, 而PDE 显然为锐角,故此时不能有∽. ………………………10分○2 当1<m<2时, ,而此时1<m<2, 则应有,由此知>1. ……………………………12分 综上所述,当>1时,才存在实数m 使得∽, 从而有,此时;当0<1时, 不存在实数m 使得.……………………………14分4、解:(1)设抛物线解析式为y =a (x +1)(x -3),则有4=a (6+1)(6-3),解得a =421, 故抛物线解析式为y =421(x +1)(x -3),对称轴为x =-1+32=1,………………………2分 顶点坐标D (1,-1621).……………………3分(2) 设E (1,t ),则有DE =t +1621, t =421(x +1)(x -3)即421x 2-821x -47-t =0 …………4分 故丨x 1-x 2丨=(x 1-x 2)2=(x 1+x 2)2-4x 1x 2=16+21t ,即FG =16+21t ,由DE FG =157,解得DE =157FG , ∴t +1621=15716+21t ,解得 t =173,故E (1,173).……………………………6分 m 25DE PQ AQ CD ⋅=⋅∠∠PQA ∆CDE ∆PQA ∆PDE ∆∠∠PQA ∆CDE ∆a a m 1+=211<+<aa a a PQA ∆CDE ∆DE PQ AQ CD ⋅=⋅a a m 1+=≤a DE PQAQ CD ⋅=⋅如图,作∠ABC 的平分线与对称轴x =1的交点即为符合题意的H 点,记为H 1;在x 轴上取点R (-2,0),连接RC 交∠ABC 的平分线BH 1于Q ,则有RB =5;过点C 作CN ⊥x 轴交x 轴于点N在Rt △BCN 中,∵BC =RB ,BQ 平分∠ABC ,∴Q 为RC 中点∵R (-2,0),C (6,4)∴Q (2,2).∵B (3,0),∴过点B 、Q 两点的一次函数解析式为y =-2x +6当x =1时,y =4.故H 1(1,4)…………………………8分如图,过点B 作BH 2⊥BH 1交对称轴于点H 2,则点H 2符合题意,记对称轴于x 轴交于点T.∵BH 2⊥BH 1,∴∠H 1BH 2=90°即∠H 1BT +∠TBH 2=90°∵∠H 1BT +∠TH 1B =90°,∴∠TBH 2=∠TH 1B∵∠BTH 2=∠H 1TB =90°,∴Rt △BTH 2∽Rt △H 1TB∴BT H 1T =H 2T TB =即24=H 2T 2解得H 2T =1即H 2(1,-1)综上,H 1(1,4),H 2(1,-1).………………10分(3)存在定值λ=35,使得(CJ +λ·EJ )min =26. 理由如下: 如图,在对称轴上取点K (1,3),则EI =173-32=256,JI =4-32=52,IK =3-32=32故 EI JI =JI IK =53,∵∠JIE =∠KIJ ∴△IJE ∽△IKJ , ∴EJ KJ =IJ IK =53,即KJ =35EJ …………………………12分 从而CJ +35EJ =CJ +KJ ,当且仅当K 、J 、C 三点共线时, (CJ +λ·EJ )min =KC =26,即(CJ +λ·EJ )min =26故存在定值λ=35,使得(CJ +λ·EJ )min =26. ……………………………14分5、解:(1)∵直线l :y=x +m 经过点B (0,﹣1),∴m=﹣1, ……………………………1分∴直线l 的解析式为y=x ﹣1,∵直线l:y=x﹣1经过点C(4,n),∴n=×4﹣1=2……………………………2分(2)∵抛物线y=x2+bx+c经过点C(4,2)和点B(0,﹣1),∴,解得,……………………………5分∴抛物线的解析式为y=x2﹣x﹣1;……………………………7分(3)令y=0,则x﹣1=0,解得x=,∴点A的坐标为(,0),∴OA=,……………………………9分在Rt△OAB中,OB=1,∴AB===,∵DE∥y轴,∴∠ABO=∠DEF,……………………………11分在矩形DFEG中,EF=DE•cos∠DEF=DE•=DE,DF=DE•sin∠DEF=DE•=DE,∴p=2(DF+EF)=2(+)DE=DE,∵点D的横坐标为t(0<t<4),∴D(t,t2﹣t﹣1),E(t,t﹣1),∴DE=(t﹣1)﹣(t2﹣t﹣1)=﹣t2+2t,∴p=×(﹣t2+2t)=﹣t2+t,∵p=﹣(t﹣2)2+,且﹣<0,……………………………13分∴当t=2时,p有最大值;……………………………14分6、解:(1)设抛物线为y=a(x﹣4)2﹣1,∵抛物线经过点A(0,3),∴3=a(0﹣4)2﹣1,;∴抛物线为;……………………………3分(2)相交.证明:连接CE,则CE⊥BD,当时,x1=2,x2=6.A(0,3),B(2,0),C(6,0),对称轴x=4,∴OB=2,AB==,BC=4,∵AB⊥BD,∴∠OAB+∠OBA=90°,∠OBA+∠EBC=90°,∴△AOB∽△BEC,∴=,即=,解得CE=,∵>2,∴抛物线的对称轴l与⊙C相交.(7分)(3)如图,过点P作平行于y轴的直线交AC于点Q;可求出AC的解析式为;(8分)设P点的坐标为(m,),则Q点的坐标为(m,);∴PQ=﹣m+3﹣(m2﹣2m+3)=﹣m2+m.∵S△PAC=S△PAQ+S△PCQ=×(﹣m2+m)×6=﹣(m﹣3)2+;∴当m=3时,△PAC的面积最大为;…………………………13分此时,P点的坐标为(3,).…………………………14分【课后训练】1、解:(1)由题意得,,∴,∴抛物线的解析式y=﹣x2﹣2x+3;…………………………3分(2)如图2,∵抛物线的解析式y=﹣x2﹣x+3;∴B(﹣3,0),∵A(1,0),∴AB=4,…………………………………………4分在x轴上方抛物线的对称轴上,取一点M,使DM=AB=2,∴∠AMB=90°,M(﹣1,2),∴MA=2,………………………………………………………5分以点M为圆心,以MA为半径,作圆,与y轴正半轴相较于点N,即:∠ANB=45°,∴MN=MA=2,…………………………………………6分设点N(0,m)(m>0),∴=2,∴m=2+或m=2﹣(舍)即:当∠ANB=45°时,N(0,2+);…………………………………………8分(3)如图3,∵D(﹣1,0),C(0,3),∴直线CD的解析式为y=3x+3,过点D作DE⊥CD交y轴于E,∴直线DX的解析式为y=﹣x﹣,…………………………………………9分∴E(0,﹣),∵∠CDP=45°,∴DF是∠CDE的平分线,∴,…………………………………………10分设F(0,n),∵C(0,3),∴CF=3﹣n,EF=n+,∵D(﹣1,0),C(0,3),E(0,﹣),∴CD=,DE=,…………………………………………11分∴,∴n=,∴直线DF的解析式为y=x+①,…………………………………………12分∵抛物线的解析式y=﹣x2﹣2x+3②;联立①②得,,或(舍)∴点P的坐标(,).…………………………………………14分2、解:⑴ 令01=y ,得△=222)1(4484)12(4)2(-=+-=---t t t t t , ……………………1分∵t >1,∴△=2)1(4-t >0,…………………………………………2分∴无论t 取何值,方程0)12(22=-+-t tx x 总有两个不相等的实数根,∴无论t 取何值,抛物线1C 与x 轴总有两个交点.…………………………………………3分 ⑵解法一:解方程0)12(22=-+-t tx x 得,11=x ,122-=t x , …………………………………………4分 ∵t >1,∴112>-t .得A (1,0),B (12-t ,0),∵D (m ,n ),E (m +2,n ), ∴DE =AB =2,即2112=--t ,解得2=t . …………………………………………5分 ∴二次函数为1)2(34221--=+-=x x x y ,…………………………………………6分显然将抛物线1C 向上平移1个单位可得抛物线2C :22)2(-=x y ,………………………7分故1=n . …………………………………………8分 解法二:∵D (m ,n )在抛物线2C :22)(t x y -=上,∴2)(t m n -=,解得n t m ±=, …………………………………………5分 ∴D (n t -,n ),E (n t +,n ),∵DE =2,∴n t +-(n t -)=n 2=2, …………………………………………7分解得 1=n . …………………………………………8分⑶由⑵得抛物线2C :22)2(-=x y ,D (1,1),E (3,1),翻折后,顶点F (2,0)的对应点为F '(2,2), 如图,当直线b x y +-=21经过点D (1,1)时,记为1l , 此时23=b ,图形G 与1l 只有一个公共点;………………10分 当直线b x y +-=21经过点E (3,1)时,记为2l ,此时25=b ,图形G 与2l 有三个公共点; ………………………………………12分当3<b 时,由图象可知,只有当直线l :b x y +-=21位于1l 与2l 之间时,图形G 与直线l 有且只有两个公共点,∴符合题意的b 的取值范围是2523<<b .…………………………………………14分3、解:(1)∵抛物线y=﹣ x +2与y 轴交于点C , ∴C (0,2),令y=0,则0=﹣x +2, ∴x=﹣1或x=4,…………………………………………1分∵点A 在点B 的左侧,∴A (﹣1,0),B (4,0),∴OA=1,OB=4,OC=2,根据勾股定理得,AC= ,BC=2 ,∵AB=OA +OB=5,∴AC 2+BC 2=5+20=25=AB 2,∴△ABC 是直角三角形,…………………………………………2分∴AB 是Rt △ABC 的外接圆的直径,∴△ABC 的外接圆的圆心是线段AB 的中点,∴其坐标为(,0);…………………………………………3分(2)∵C(0,2)设直线BC的解析式为y=kx+2,∵B(4,0),∴4k+2=0,∴k=﹣,∴直线BC的解析式为y=﹣x+2,…………………………………………4分∵P是抛物线上一点,设点P(m,﹣m2+m+2)如图,过点P作PQ∥y轴交直线BC于点Q,∴Q(m,﹣m+2),…………………………………………5分①当点P在直线BC上方时,S△PBC=S△PQC+S△PBQ=S△ABC,∴[(﹣m2+m+2)﹣(﹣m+2)]×m﹣[(﹣m2+m+2)﹣(﹣m+2)](m﹣4)=×5×2∴m2﹣4m+5=0,∵△=(﹣4)2﹣4×1×5=﹣4<0,…………………………………………6分∴此方程没有实数根;∴当点P在直线BC上方时,S△PBC ≠S△ABC,②当点P在直线BC下方时,S△PBC=S△PQC﹣S△PBQ=S△ABC,∴[(﹣m+2)﹣(﹣m2+m+2)]×m﹣[(m+2)﹣(﹣m2+m+2)](m﹣4)=×5×2∴m2﹣4m﹣5=0,∴m=﹣1(舍)或m=5,∴P(5,﹣3)…………………………………………6分作PM⊥x轴于,交BC于Q,∴PM=3,MB=1,根据勾股定理得,BP=,AP=3,过点B作BN⊥AP于N,∴∠ANB=∠AMP=90°,∠BAN=∠PAM,∴△ABN∽△APM,∴,,∴BN=,…………………………………………7分在Rt△BPN中,PN==,∴BN=PN,∴∠APB=45°;…………………………………………8分(3)存在,如图2,∵抛物线y=﹣x+2的对称轴为x=,由(2)知,P(5,﹣3),BP=,设E(n,﹣n2+n+2),…………………………………………9分①当点E在抛物线对称轴右侧时,即:点E处时,EF=BP=,∴点E到对称轴的距离为EG=BM=1,∴n﹣=1,∴n=,∴E(,),易知,FG=PM=3,∴F(,);…………………………………………11分②当点E在抛物线对称轴左侧时,即:E'处时,E'F'=BP=,∴点E'到对称轴的距离为E'G'=BM=1,∴﹣n=1,∴n=,∴E'(,),易知,F'G'=PM=3,∴F'(,﹣).…………………………………………13分即:满足条件的点F的坐标为(,)或(,﹣).…………………………………14分4、解:(1)∵抛物线y=mx 2+(m +2)x +2过点(2,4), ∴m•22+2(m +2)+2=4,解得m=﹣,…………………………………1分∴抛物线解析式为y=﹣x 2+x +2,令y=0,则﹣x 2+x +2=0,整理得,x 2﹣5x ﹣6=0,解得x 1=﹣1,x 2=6,令x=0,则y=2,∴A (﹣1,0),B (6,0),C (0,2),…………………………………2分 ∴()721621=⨯+⨯=∆ABC S …………………………………3分(2)过点B 作BM ⊥CD 交CD 的延长线于M , 在Rt △DOC 中,∵OC=OD=2,∴∠CDO=∠BDM=45°,CD=2,在Rt △BMD 中,∵BD=6﹣2=4,∴DM=BM=4×=2,…………………………………5分在Rt△CMB中,tan∠BCM===,又∵tan∠ACO==,∴∠ACO=∠BCD;…………………………………7分(3)①由勾股定理得,BC==2,BE=DE时,点E的横坐标为6﹣×(6﹣2)=4,点E的纵坐标是×(6﹣2)×=,所以,点E1(4,);…………………………………8分BE=BD时,点E的横坐标为6﹣(6﹣2)×=6﹣,点E的纵坐标为(6﹣2)×=,所以,点E2(6﹣,),综上所述,点E1(4,)或E2(6﹣,)时,△BDE是等腰三角形;…………………………………10分②设P(x,﹣x2+x+2),过点P作x轴的垂线,垂足为F,交CD的延长线于点Q,则直线CD的解析式为y=﹣x+2,∴点Q(x,﹣x+2),S△CDP=S△CPQ﹣S△DPQ,=PQ•OF﹣PQ•DF,=PQ•OD,∵OD=2,=PQ=﹣x2+x+2﹣(﹣x+2)=﹣x2+x(0<x<6),…………………………………11分∴S△CDP∵S=﹣x2+x=﹣(x﹣4)2+,∴当x=4时,△CDP的面积最大,此时,﹣x2+x+2=﹣×42+×4+2=,∴点P(4,),…………………………………12分设直线PD的解析式为y=kx+b(k≠0),∴,解得,∴直线PD的解析式为y=x﹣,…………………………………13分直线BC的解析式为y=﹣x+2,联立,解得,所以,点E的坐标为(,).…………………………………14分5、解:(1)∵y=x2﹣x﹣,∴y=(x+1)(x﹣3).∴A(﹣1,0),B(3,0).…………………………………1分当x=4时,y=.∴E(4,).…………………………………2分设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得:,解得:k=,b=.∴直线AE的解析式为y=x+.…………………………………3分(2)设直线CE的解析式为y=mx﹣,将点E的坐标代入得:4m﹣=,解得:m=.∴直线CE的解析式为y=x﹣.过点P作PF∥y轴,交CE与点F.设点P的坐标为(x,x2﹣x﹣),则点F(x,x﹣),则FP=(x﹣)﹣(x2﹣x﹣)=x2+x.∴△EPC的面积=×(x2+x)×4=﹣x2+x.∴当x=2时,△EPC的面积最大.∴P(2,﹣).…………………………………5分如图2所示:作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.∵K是CB的中点,∴k(,﹣).∴tan∠KCP=.…………………………………6分∵OD=1,OC=,∴tan∠OCD=.∴∠ODD=∠KCP=30°.∴∠KCD=30°.∵k是BC的中点,∠OCB=60°,∴OC=CK.∴点O与点K关于CD对称.…………………………………7分∴点G与点O重合.∴点G(0,0).∵点H与点K关于CP对称,∴点H的坐标为(,﹣).…………………………………8分∴KM+MN+NK=MH+MN+GN.当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH.∴GH==3.∴KM+MN+NK的最小值为3.…………………………………10分(3)如图3所示:∵y′经过点D,y′的顶点为点F,∴点F(3,﹣).…………………………………11分∵点G为CE的中点,∴G(2,).∴FG==.…………………………………13分∴当FG=FQ时,点Q(3,),Q′(3,).当GF=GQ时,点F与点Q″关于y=对称,∴点Q″(3,2).当QG=QF时,设点Q1的坐标为(3,a).由两点间的距离公式可知:a+=,解得:a=﹣.∴点Q1的坐标为(3,﹣).…………………………………13分综上所述,点Q的坐标为(3,)或′(3,)或(3,2)或(3,﹣).…………………………………14分。
2018年广州中考数学一模一次函数与反比例函数汇编参考答案

2018一模一次函数与反比例汇编——参考答案【例题分析】例题1、选B.例题2、选D 例题3、 4 例题4、32 例题5、16 例题6、例7、解:(1)在矩形ABCD 中,BC =OA =3,AB =OC =4∵CE =a =2∴点E 的坐标为(2,4)把点E (2,4)代入y =k x得k =8 (2)DA =OA -OD =3-1=2,点E 的坐标为(a ,4)∵点E 、F 均在函数y =k x上 ∴k =4a ,点F (3,43a ) S 梯形ODEC =OC ×OD +CE 2=4×1+a 2=2+2a S △BEF =BE ×BF 2=12(3-a )(4-43a )=23a ²-4a +6 S △ADF =AD ×AF 2=12×2×43a =43a S △DEF =S 矩形OABC -S 梯形ODEC -S △BEF -S △ADF =23a ²+23a +4对称轴为a =12,开口向下,且14≤a ≤52∴当a =12时,S 最大=256;当a =52时,S 最小=32【强化训练】1、选B ;2、3;3、4、835、解:(1)把A (2,m )代入y = 6x得:m =3 ∴点A 坐标为(2,30)把B (n ,-2)代入y = 6x 得:6x= -2,n=-3 ∴点B 坐标为(-3,-2)把A (2,3),B (-3,-2)分别代入y =kx +b 得:⎩⎨⎧2k +b = 3-3k +b = -2 解得:⎩⎨⎧k =1b =1 ∴一次函数解析式为:y =x +1,m =3,n =-3(2)由图可知:当x <-3或0<x <2时,6x<kx +b ∴6x-kx <b 的解集是x <-3或0<x <2 6、解:(1)作BM ⊥x 轴于M ,作DN ⊥x 轴于N ,如图, ∵点A ,B 的坐标分别为(5,0),(2,6),∴BC=OM=2,BM=OC=6,AM=3,∵DN ∥BM ,∴△ADN ∽△ABM ,∴==,即==,∴DN=2,AN=1,∴ON=OA ﹣AN=4,∴D 点坐标为(4,2),把D (4,2)代入y=得k=2×4=8,∴反比例函数解析式为y=;(2)S 四边形ODBE =S 梯形OABC ﹣S △OCE ﹣S △OAD=×(2+5)×6﹣×|8|﹣×5×2=12.7、解:(1)将x=1代入直线y=4﹣x得,y=4﹣1=3,则A点坐标为(1,3),将A(1,3)代入y=(m>0,x>0)得,m=3,则反比例函数解析式为y=,组成方程组得,解得,y=1,x=3,则B点坐标为(3,1).当不等式4﹣x<时,0<x<1或x>3.(2)存在.点A、B在直线y=4﹣x上,则可设A(a,4﹣a),B(b,4﹣b).如右图所示,过点A作AM⊥x轴于点M,则AM=4﹣a,PM=1﹣a;过点B作BE⊥x轴于点E,则BE=4﹣b,PE=b﹣1.∵点P在以AB为直径的圆上,∴∠APB=90°(圆周角定理).易证Rt△AMP∽Rt△PEB,∴=,即,整理得:5(a+b)﹣2ab=17 ①∵点A、B在双曲线y=上,∴a(4﹣a)=m,b(4﹣b)=m,∴a2﹣4a+m=0,b2﹣4b+m=0,∴a、b是一元二次方程x2﹣4x+m=0的两个根,∴a+b=4,ab=m.代入①式得:5×4﹣2m=17,解得:m=.∴存在以AB为直径的圆经过点P(1,0),此时m=.【课后训练】1、选B2、选D3、解:4、解:(1)∵点A (6,2)在反比例函数y =k x的图象上 ∴6212k =⨯=,即反比例函数函数解析式为12y x =, 将B (-4,n )代入12y x =,得:1234n ==--, ∴43B --(,),把A (6,2),43B --(,)代入y =ax +b ,得:6243a b a b +=⎧⎨-+=-⎩,解得:121a b ⎧=⎪⎨⎪=-⎩ ∴一次函数解析式为112y x =-,反比例函数解析式为12y x =。
2018年广州中考数学一模计算题汇编参考答案

2018一模计算题汇编——参考答案一、一元一次方程1、(育才一模)解方程:()4321x x -=-解: 2234-=-x x3224+-=-x x 12=x21=x2、(广州中学一模)解方程:1615312=--+x x 解:-3x 3x - 2-1-65x -4x 61524 6)15(1226====+-+=--+x x x x )(得,等式两边同时二、解不等式/组1、(海珠区一模)解不等式组⎩⎨⎧≥--+1)1(2042x x x >解:解①得:2->x解②得:1≤x此不等式组的解集为:12-≤x <2、(二中一模)解不等式 2123+-x x >,并把它的解集在数轴上表示出来. 解:146+-x x >416+->x x 55>x 1>x解集1>x 在数轴上表示如下:3、(荔湾区一模)解不等式组⎩⎨⎧++≥7)2(251-3x x x <,并把解集在数轴上表示出来.解:解①得:2≥x解②得:3<x此不等式组的解集为:32<x ≤ 解集32<x ≤在数轴上表示如下:4、(汇景实验一模)解不等式:)1(35-≥+x x解: 335-≥+x x533---≥x x 82--≥x 4≤x5、(越秀八一一模)解不等式组 ⎩⎨⎧-≤-4)2(36-2x x x >.解:解①得:3->x解②得:1≤x此不等式组的解集为:13-≤x <6、(增城一模)解不等式组 ⎩⎨⎧≤-+0203x x >,并把它的解集在数轴上表示出来。
解:解①得:3->x解②得:2≤x此不等式组的解集为:23-≤x <解集23-≤x <在数轴上表示如下:7、(黄埔区一模)解不等式组 ⎩⎨⎧--+2453x43x x x <>.解:解①得:2->x解②得:3->x此不等式组的解集为:2->x三、二元一次方程组1、(番禺区一模)解方程组⎩⎨⎧=-=+1323y x y x解:由①得,y x -=3③③代入②得,13)3(2=--y y 即55-=-y 解得1=y把1=y 代入③得,2=x∴原方程组的解为⎩⎨⎧==12y x .2、(天河区九校)解方程组⎩⎨⎧=-=+112332y x y x解:①+②得, 144=x解得27=x 把27=x 代入①得,3227=+y即212-=y解得41-=y① ②∴原方程组的解为⎪⎪⎩⎪⎪⎨⎧==41-27y x .四、分解因式1、(白云区一模)分解因式:822-x解:原式()422-=x)2(22-+=x x )(五、一元二次方程1、(花都一模)解方程:0562=+-x x解:1,532234)3(95965621222==+±=±=-=-+-=+--=-x x x x x x x x x2、(广大附中一模)解方程:(1)22)1(3-=-x x x 解:32,1023010)23)(1(0253022332122===-=-=--=+-=+--x x x x x x x x x x x 或六、分式方程1、(省实一模)解方程:312-=x x解:6x 6x -2x 62 323===-=--⨯xx x x x x )(得,)(等式两边同时经检验,6=x 是原方程的解2、(一中一模)解方程:141-x 21x 12-=++x解:1x 33x 12-4x 2x 4221 4)1(21)1)(1(==+=+=++-=++-+-⨯x x x x x x )得,(等式两边同时 经检验,1=x 时01,012=-=-x x ,所以原方程无解。
2018年广州越秀区联考中考一模数学试题答案

…………1 分
∴ x1 = 1 + m , x2 = −m …………2 分 1 1 当 m = − 时, x1 = x2 , 当 m − 时, x1 x2 , 2 2 ∵ 抛物线的开口向上 ∴ 无论 m 取何值,抛物线与 x 轴必定有公共点 …………3 分
∴△AED∽△ABC
AM = 8 = 3.2 ………12 分 ∴ ED = 12 = 4.8 , 2 5 2 5
以 D、E、F、G 为顶点的四边形是矩形 ∴∠DEF=90° ∴ DF 是⊙O 的直径…………13 分 ∴ EF = DF 2 − DE 2 = 62 − 4.82 = 3.6 ∴平移的距离是 8 − 3.2 − 3.6 = 1.2 …………14 分 25.解:(1)解法 1:令 y = 0 得 x2 − x − m2 − m = 0 ∴ = b 2 − 4ac = 4m 2 + 4m + 1 ………1 分 ∴ = (2m + 1) 2 ………2 分 无论 m 取何值, = (2m + 1)2 0 ∴ 抛物线与 x 轴必定有公共点 …………3 分 解法 2:∵ y = x 2 − x − m2 − m 1 1 2 ) ) …………1 分 ∴ 抛物线的顶点坐标是 ( , (m 2 2 1 2 ) ≤0 无论 m 取何值, (m 2 ∴ 抛物线的顶点坐标在第四象限或 x 轴正半轴上…………2 分 ∵ 抛物线的开口向上 ∴ 抛物线与 x 轴必定有公共点 …………3 分 解法 3:令 y = 0 即 x 2 − x − m 2 − m = 0 根据公式法得: x =
∴ ∠AEB=∠EBC…………4 分 又 ∠ABE=∠EBC ∴ ∠AEB=∠ABE ∴ AB=AE= 2 ∴ DE= a = 6 − 2 …………5 分
2018年广州中考一模试卷-三中-初中数学
23.(本题满分 12 分)如图,直线 y=ax+1 与 z 轴.y 轴分别相交于 A.B 两点,与双曲线 y=kx(x>0)相交于点 P,PC⊥x 轴于点 C,且 PC=2,点 A 的坐标为(﹣2,0). (1)求双曲线的解析式. (2)若点 Q 为双曲线上点 P 右侧的一点,且 QH⊥x. 轴于 H,当以点 Q,C,H 为顶点的三角形于△AOB 相似时,求点 Q 的坐标.
第 24 题图
25.(本小题满分 14 份)如图,C 为∠AOB 的边 OA 上的一点,OC=6,N 为边 OB 上异于 点 O 的一动点,P 是线段.CN 上一点,过点 P 分别作 PQ//OA 交 OB 于点 Q,PM//OB 交 OA 子点 M. (1)判断四边形 OMPQ 的形状,并证明.’ (2)当点 N 在边 OB 上运动时,若四边形 OMPQ 始终保持为菱形. ① 问O1M-O1N的值是否发生变化?如果变化,求出其取值范围.如果不变,请说明理由. ② 设菱形 OMPQ 的面积为 S1,△NOC 的面积为 S2,求SS12的取值范围.
2018 年初三毕业班综合测试(一)
数学
第一部分选择题(共 30 分)
一.选择题(本大题共 10 小题,每小题 3 分,满分 30 分)
l.如果 a 与-3 互为倒数,那么 a 是( ).
A.﹣3
B.3
C.﹣31
D.31
2.如图,一个放置在水平桌面上的圆柱,它的主视图是( ).
第二题图
A
B
C
D
3.下列计算正确的是( ).
○1 ∠DCF=21∠BCD ○3 S△BEC=2S△CEF
○2 EF=CF ○4 ∠DFE=3∠AEF
第 16 题图
三.解答题(本大题共 9 小题,满分 102 分) 17.(本小题满分 9 分)先化简,再求值(x2x-x+1)÷x2x-2-2x1+1其中 x 的值从不 等式组﹣2x-x≤11<4 的整数解中选取. 18.(本小题满分 9 分)如图,在△ABC 中,AB=AC,D 是 BA 延长线上的一点,点 E 是 AC 的中点. (1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母 (保留作图痕迹,不写作法). ○1 作∠DAC 的平分线 AM. ○2 连结 BE 并延长交 AM 于点 F. (2)猜想与证明:试猜想 AF 与 BC 有怎样的位置关系
2017年广州中考数学一模一次函数与反比例函数汇编
2017年广州中考数学一模一次函数与反比例函数汇编例题分析例题1、(二中一模)如图,一次函数y ax b =+的图像分别与x 轴、y 轴的负半轴相交于A B 、,则下列结论一定正确的是( )A. 0a b ->B.0a b +>C.0b a ->D.0a b -->例题2、(白云一模)在反比例函数y =13mx-的图象上有两点A(1x ,1y ),B(2x ,2y ),当1x <0<2x 时,有1y <2y ,则m 的取值范围是 ( )A.m >0B.m <0C. m >13D. m <13例题3、(白云一模)如图,一条直线分别交x 轴、y 轴于A、B两点,交反比例函数y =mx(m ≠0)位于第二象限的一支于C 点,OA=OB=2. (1)m = ;(2)求直线所对应的一次函数的解析式;(3)根据(1)所填m 的值,直接写出分解因式2a +ma +7的结果.x例题4、(南沙一模)如图)0,4(-A ,)3,1(-B ,以OA 、OB 为边作□OACB ,经过A 点的一次函数b x k y +=1与反比例函数y =k 2x的图象交于点C .(1) 求一次函数b x k y +=1的解析式;(2)请根据图象直接写出在第二象限内,当xk b x k 21>+时,自变量x 的取值范围; (3)将□OACB 向上平移几个单位长度,使点A 落在反比例函数的图象上.例题5、(海珠一模)如图,在平面直角坐标系中,一次函数1+b y ax =(a ≠ 0)的图象与y 轴相交于点A ,与反比例函数2ky x=(c ≠0)的图象相交于点B (3,2)、C (-1,n ). (1)求一次函数和反比例函数的解析式;(2)根据图象,直接写出1y >2y 时x 的取值范围;(3)在y 轴上是否存在点P ,使△P AB 为直角三角形,如果存在,请求点P 的坐标,若不存在,请说明理由.例题6、(省实一模)已知双曲线kyx=与直线14y x=相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线kyx=上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线kyx=于点E,交BD于点C.(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.例题7、(二中一模)如图,点A是双曲线yx=在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边做等边ABC∆,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线kyx=上运动,则k的值是__________.强化训练1、(天河一模)已知一次函数y=(m-2)x+3的图象经过第一、二、四象限,则m 的取值范围是( ) A. m<0 B. m>0 C. m<2 D. m>22、(二中一模)甲、乙、丙三维同学分别正确指出了某一个函数的性质,甲:函数的图像经过第一象限;乙:函数的图像经过第三象限;丙:在每一个象限内,y 随x 的增大而减小。
中考数学专题复习《一次函数与反比例函数的综合》经典题型讲解
中考数学专题复习《一次函数与反比例函数的综合》经典题型讲解【经典母题】如图Z6-1是一个光学仪器上用的曲面横截面示意图,图中的曲线是一段反比例函数的图象,端点A的纵坐标为80,另一端点B的坐标为B(80,10).求这段图象的函数表达式和自变量的取值范围.【解析】利用待定系数法设出反比例函数的表达式后,代入点B的坐标即可求得反比例函数的表达式.解:设反比例函数的表达式为y=k x ,∵一个端点B的坐标为(80,10),∴k=80×10=800,∴反比例函数的表达式为y=800x.∵端点A的纵坐标为80,∴80=800x,x=10,∴点A的横坐标为10,∴自变量的取值范围为10≤x≤80.【思想方法】求反比例函数的表达式宜用待定系数法,设y=kx,把已知一点代入函数表达式求出k的值即可.【中考变形】1.已知正比例函数y=ax与反比例函数y=bx的图象有一个公共点A(1,2).(1)求这两个函数的表达式;图Z6-1(2)在图Z6-2中画出草图,根据图象写出正比例函数值大于反比例函数值时x 的取值范围.图Z6-2中考变形1答图解:(1)把A (1,2)代入y =ax ,得2=a , 即y =2x ;把A (1,2)代入y =b x ,得b =2,即y =2x ; (2)画草图如答图所示.由图象可知,当x >1或-1<x <0时,正比例函数值大于反比例函数值. 2.如图Z6-3,已知一次函数y =k 1x +b 与反比例函数y =k 2x 的图象交于第一象限内P ⎝ ⎛⎭⎪⎫12,8,Q (4,m )两点,与x 轴交于A 点.(1)分别求出这两个函数的表达式; (2)写出点P 关于原点的对称点P ′的坐标; (3)求∠P ′AO 的正弦值.图Z6-3【解析】①将P 点坐标代入反比例函数关系式,即可求出反比例函数表达式;将Q 点代入反比例函数关系式,即可求出m 的值;将P ,Q 两个点的坐标分别代入一次函数关系式,即可求出一次函数的表达式.②根据平面直角坐标系中,两点关于原点对称,则横、纵坐标互为相反数,可以直接写出点P ′的坐标;③过点P ′作P ′D ⊥x 轴,垂足为D ,可构造出′AD ,又∵点A 在一次函数的图象上,∴可求出点A 坐标,得到OA 长度,利用P ′ 点坐标,可以求出P ′D ,P ′A ,即可得到∠P ′AO 的正弦值. 解:(1)∵点P 在反比例函数的图象上,∴把点P ⎝ ⎛⎭⎪⎫12,8代入y =k 2x ,得k 2=4,∴反比例函数的表达式为y =4x ,∴Q 点坐标为(4,1).把P ⎝ ⎛⎭⎪⎫12,8,Q (4,1)分别代入y =k 1x +b 中,得⎩⎨⎧8=12k 1+b ,1=4k 1+b ,解得⎩⎪⎨⎪⎧k 1=-2,b =9.∴一次函数的表达式为y =-2x +9; (2)P ′⎝ ⎛⎭⎪⎫-12,-8;(3)如答图,过点P ′作P ′D ⊥x 轴,垂足为D . ∵P ′⎝ ⎛⎭⎪⎫-12,-8,中考变形2答图∴OD =12,P ′D =8.∵点A 在y =-2x +9的图象上,∴点A 坐标为⎝ ⎛⎭⎪⎫92,0,即OA =92,∴DA =5,∴P ′A =P ′D 2+DA 2=89. ∴sin ∠P ′AD =P ′D P ′A =889=88989.∴sin ∠P ′AO =88989.3.[2017·成都]如图Z6-4,在平面直角坐标系xOy 中,已知正比例函数y =12x与反比例函数y =kx 的图象交于A (a ,-2),B 两点. (1)求反比例函数表达式和点B 的坐标;(2)P 是第一象限内反比例函数图象上一点,过点P 作y 轴的平行线,交直线AB 于点C ,连结PO ,若△POC 的面积为3,求点P 的坐标.图Z6-4 中考变形3答图解:(1)∵点A (a ,-2)在正比例函数y =12x 图象上, ∴-2=12a ,∴a =-4, ∴点A 坐标为(-4,-2).又∵点A 在反比例函数y =kx 的图象上, ∴k =xy =-4×(-2)=8, ∴反比例函数的表达式为y =8x .∵A ,B 既在正比例函数图象上,又在反比例函数图象上, ∴A ,B 两点关于原点O 中心对称, ∴点B 的坐标为(4,2);(2)如答图,设点P 坐标为⎝ ⎛⎭⎪⎫a ,8a (a >0),∵PC ∥y 轴,点C 在直线y =12x 上,∴点C 的坐标为⎝ ⎛⎭⎪⎫a ,12a ,∴PC =⎪⎪⎪⎪⎪⎪12a -8a =⎪⎪⎪⎪⎪⎪a 2-162a , ∴S △POC =12PC ·a =12⎪⎪⎪⎪⎪⎪a 2-162a ·a =⎪⎪⎪⎪⎪⎪a 2-164=3, 当a 2-164=3时,解得a =28=27, ∴P ⎝⎛⎭⎪⎫27,477. 当a 2-164=-3时,解得a =2,∴P (2,4).综上所述,符合条件的点P 的坐标为⎝⎛⎭⎪⎫27,477,(2,4). 4.如图Z6-5,一次函数y =kx +b 与反比例函数y =mx 的图象交于A (1,4),B (4,n )两点.(1)求反比例函数的表达式; (2)求一次函数的表达式;(3)P 是x 轴上的一个动点,试确定点P 并求出它的坐标,使得P A +PB 最小.图Z6-5解:(1)∵点A (1,4)在函数y =mx 上, ∴m =xy =4,∴反比例函数的表达式为y =4x ; (2)把B (4,n )代入y =4x ,4=xy =4n ,得n =1, ∴B (4,1),∵直线y =kx +b 经过A ,B , ∴⎩⎪⎨⎪⎧4=k +b ,1=4k +b ,解得⎩⎪⎨⎪⎧k =-1,b =5, ∴一次函数的表达式为y =-x +5; (3)点B 关于x 轴的对称点为B ′(4,-1), 设直线AB ′的表达式为y =ax +q , ∴⎩⎪⎨⎪⎧4=a +q ,-1=4a +q ,解得⎩⎪⎨⎪⎧a =-53,q =173,∴直线AB ′的表达式为y =-53x +173, 令y =0,解得x =175,∴当点P 的坐标为⎝ ⎛⎭⎪⎫175,0时,P A +PB 最小.5.[2017·广安]如图Z6-6,一次函数y =kx +b 的图象与反比例函数y =mx 的图象在第一象限交于点A (4,2),与y 轴的负半轴交于点B ,图Z6-6且OB =6.(1)求函数y =mx 和y =kx +b 的表达式.(2)已知直线AB 与x 轴相交于点C .在第一象限内,求反比例函数y =mx 的图象上一点P ,使得S △POC =9.解:(1)∵点A (4,2)在反比例函数y =mx 的图象上, ∴m =4×2=8,∴反比例函数的表达式为y =8x . ∵点B 在y 轴的负半轴上,且OB =6, ∴点B 的坐标为(0,-6),把点A (4,2)和点B (0,-6)代入y =kx +b 中, 得⎩⎪⎨⎪⎧4k +b =2,b =-6,解得⎩⎪⎨⎪⎧k =2,b =-6. ∴一次函数的表达式为y =2x -6; (2)设点P 的坐标为⎝ ⎛⎭⎪⎫n ,8n (n >0).在直线y =2x -6上,当y =0时,x =3, ∴点C 的坐标为(3,0),即OC =3, ∴S △POC =12×3×8n =9,解得n =43. ∴点P 的坐标为⎝ ⎛⎭⎪⎫43,6.6.[2017·黄冈]如图Z6-7,一次函数y =-2x +1与反比例函数y =kx 的图象有两个交点A (-1,m )和B ,过点A 作AE ⊥x 轴,垂足为E ;过点B 作BD ⊥y 轴,垂足为D ,且点D 的坐标为(0,-2),连结DE . (1)求k 的值;(2)求四边形AEDB 的面积.图Z6-7 中考变形6答图解:(1)将点A (-1,m )代入一次函数y =-2x +1, 得-2×(-1)+1=m ,解得m =3.∴A 点的坐标为(-1,3).将A (-1,3)代入y =kx ,得k =(-1)×3=-3;(2)如答图,设直线AB 与y 轴相交于点M ,则点M 的坐标为(0,1), ∵D (0,-2),则点B 的纵坐标为-2,代入反比例函数,得DB =32, ∴MD =3.又∵A (-1,3),AE ∥y 轴, ∴E (-1,0),AE =3. ∴AE ∥MD ,AE =MD .∴四边形AEDM 为平行四边形. ∴S 四边形AEDB =S ▱AEDM +S △MDB =3×1+12×32×3=214.7.[2016·金华]如图Z6-8,直线y =33x -3与x ,y 轴分别交于点A ,B ,与反比例函数y =kx (k >0)的图象交于点C ,D ,过点A 作x 轴的垂线交该反比例函数图象于点E . (1)求点A 的坐标;(2)若AE =AC ,①求k 的值;②试判断点E 与点D 是否关于原点O 成中心对称?并说明理由.图Z6-8中考变形7答图解:(1)当y =0时,得0=33x -3,解得x =3. ∴点A 的坐标为(3,0);(2)①如答图,过点C 作CF ⊥x 轴于点F .设AE =AC =t ,点E 的坐标是(3,t ),则反比例函数y =k x 可表示为y =3tx . ∵直线y =33x -3交y 轴于点B , ∴B (0,-3).在Rt △AOB 中,tan ∠OAB =OB OA =33, ∴∠OAB =30°.在Rt △ACF 中,∠CAF =30°, ∴CF =12t ,AF =AC ·cos30°=32t ,∴点C 的坐标是⎝⎛⎭⎪⎫3+32t ,12t .∴⎝⎛⎭⎪⎫3+32t ×12t =3t ,解得t 1=0(舍去),t 2=2 3. ∴k =3t =6 3.②点E 的坐标为()3,23,设点D 的坐标是⎝ ⎛⎭⎪⎫x ,33x -3,∴x ⎝ ⎛⎭⎪⎫33x -3=63,解得x 1=6(舍去),x 2=-3, ∴点D 的坐标是()-3,-23, ∴点E 与点D 关于原点O 成中心对称. 【中考预测】如图Z6-9,一次函数y =kx +b (k ,b 为常数,k ≠0)的图象与x 轴,y 轴分别交于A ,B 两点,且与反比例函数y =nx (n 为常数且n ≠0)的图象在第二象限交于点C ,CD ⊥x 轴,垂足为D ,若OB =2OA =3OD =6. (1)求一次函数与反比例函数的表达式; (2)求两函数图象的另一个交点的坐标;(3)直接写出不等式kx +b ≤nx 的解集.图Z6-9解:(1)∵OB =2OA =3OD =6, ∴OB =6,OA =3,OD =2, ∵CD ⊥DA ,∴DC ∥OB , ∴OB DC =AO AD ,∴6DC =35, ∴DC =10,∴C (-2,10),B (0,6),A (3,0), 代入一次函数y =kx +b , 得⎩⎪⎨⎪⎧b =6,3k +b =0,解得⎩⎪⎨⎪⎧k =-2,b =6, ∴一次函数的表达式为y =-2x +6. ∵反比例函数y =nx 经过点C (-2,10), ∴n =-20,∴反比例函数的表达式为y =-20x ;(2)由⎩⎨⎧y =-2x +6,y =-20x ,解得⎩⎪⎨⎪⎧x =-2,y =10或⎩⎪⎨⎪⎧x =5,y =-4, ∴另一个交点坐标为(5,-4);(3)由图象可知kx +b ≤nx 的解集为-2≤x <0或x ≥5.。
【水印已去除】2018年广东省广州市白云区中考数学一模试卷
2018年广东省广州市白云区中考数学一模试卷一.选择题(本大题共10小题.有小题3分,满分30分,在每小题给出的四个选项中.只有一项是符合题目要求的)1.(3分)﹣2的绝对值是()A.﹣2B.2C.﹣D.2.(3分)下列说法正确的是()A.直线BA与直线AB是同一条直线B.延长直线ABC.射线BA与射线AB是同一条射线D.直线AB的长为2cm3.(3分)下列计算,正确的是()A.3+2ab=5ab B.5xy﹣y=5xC.﹣5m2n+5nm2=0D.x3﹣x=x24.(3分)矩形ABCD的对角线AC、BD交于点O,以下结论不一定成立的是()A.∠BCD=90°B.AC=BD C.OA=OB D.OC=CD 5.(3分)不等式组的整数解有()A.4个B.3个C.2个D.1个6.(3分)在Rt△ABC中,∠C=90°,sin A=,则AC:AB=()A.3:5B.3:4C.4:3D.4:57.(3分)下列说法错误的是()A.必然发生的事件发生的概率为1B.不可能发生的事件概率为0C.不确定事件发生的概率为0D.随机事件发生的概率介于0和1之间8.(3分)下列判断中,正确的是()A.各有一个角是67°的两个等腰三角形相似B.邻边之比为2:1的两个等腰三角形相似C.各有一个角是45°的两个等腰三角形相似D.邻边之比为2:3的两个等腰三角形相似9.(3分)若抛物线y=x2+px+8的顶点在x轴的正半轴上,那么p的值为()A.±4B.4C.﹣4D.010.(3分)如图,D、E、F分别为△ABC边AC、AB、BC上的点,∠A=∠1=∠C,DE =DF,下面的结论一定成立的是()A.AF=FC B.AE=DE C.AE+FC=AC D.AD+FC=AB二.填空题(本大题共6小题,每小题3分,满分18分)11.(3分)式子在实数范围内有意义,则x的取值范围是.12.(3分)如图,四边形ABCD中,若∠A+∠B=180°,则∠C+∠D=°.13.(3分)已知二元一次方程组的解是方程kx﹣8y﹣2k+4=0的解,则k的值为.14.(3分)从1至9这9个自然数中任取一个,是2的倍数或是3的倍数的概率是.15.(3分)若分式的值为0,则a=.16.(3分)如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为cm.三、解答题(本大题共9小题,满分102分.解答应智出文字说明、证明过程或演算步骤)17.(9分)分解因式:2x2﹣8.18.(9分)如图,C是线段BD的中点,AB∥EC,∠A=∠E.求证:AC=ED.19.(10分)我市某区为调查学生的视力变化情况,从全区九年级学生中抽取了部分学生,统计了每个人连续三年视力检查的结果,井将所得数据处理后,制成折线统计图(图①)和扇形统计图(图②)如下:解答下列问题:(1)该区共抽取了多少名九年级学生?(2)若该区共有9万名九年级学生,请你估计2018年该区视力不良(4.9以下)的该年级学生大约有多少人7(3)扇形统计图中B的圆心角度数为.20.(10分)如图,在平面直角坐标系中,一次函数y=kx+1的图象交y轴于点D,与反比例函数y=的图象在第一象限相交于点A,过点A分别作x轴、y轴的垂线,垂足分别为点B、C.(1)点D的坐标为;(2)当AB=4AC时,求k的值;(3)当四边形OBAC是正方形时,直接写出四边形ABCD与△ACD面积的比.21.(12分)如图,已知▱ABCD的周长是32cm,AB:BC=5:3,AE⊥BC,垂足为E,AF⊥CD,垂足为F,∠EAF=2∠C.(1)求∠C的度数;(2)已知DF的长是关于x的方程x2﹣ax﹣6=0的一个根,求该方程的另一个根.22.(12分)如图所示,A,B两地之间有一座山,原来从A地到B地需要经过C地,现在政府出资打通了一条山岭隧道,使从A地到B地可沿直线AB直接到达.已知BC=8km,∠A=45°,∠B=53°.(1)求点C到直线AB的距离;(2)求现在从A地到B地可比原来少走多少路程?(结果精确到0.1km.参考数据:≈1.41,sin53°≈0.80,cos53°≈0.60)23.(12分)如图,在平面直角坐标系中,点A坐标为(0,3),点B(,m)是以OA为直径的⊙M上的一点,且tan∠AOB=,BH⊥y轴,H为垂足,点C(,)(1)求H点的坐标;(2)求直线BC的解析式;(3)直线BC是否与⊙M相切?请说明理由.24.(14分)如图,AD是Rt△ABC斜边BC上的高.(1)尺规作图:作∠C的平分线,交AB于点E,交AD于点F(不写作法,必须保留作图痕迹,标上应有的字母);(2)在(1)的条件下,过F画BC的平行线交AC于点H,线段FH与线段CH的数量关系如何?请予以证明;(3)在(2)的条件下,连结DE、DH.求证:ED⊥HD.25.(14分)已知抛物线y=ax2+bx+c(a≠0)与x轴交于A.B两点,与y轴交于C点,其对称轴为x=1,且A(﹣1,0)、C(0,2).(1)直接写出该抛物线的解析式:(2)P是对称轴上一点,△P AC的周长存在最大值还是最小值?请求出取得最值(最大值或最小值)时点P的坐标;(3)设对称轴与x轴交于点H,点D为线段CH上的一动点(不与点C、H重合).点P是(2)中所求的点.过点D作DE∥PC交x轴于点E.连接PD、PE.若CD的长为m,△PDE的面积为S,求S与m之间的数关系式,试说明S是否存在最值.若存在,请求出最值,井写出S取得的最值及此时m的值;若不存在,请说明理由.2018年广东省广州市白云区中考数学一模试卷参考答案与试题解析一.选择题(本大题共10小题.有小题3分,满分30分,在每小题给出的四个选项中.只有一项是符合题目要求的)1.【解答】解:|﹣2|=2.故选:B.2.【解答】解:A.直线BA与直线AB是同一条直线,故本选项正确;B.延长线段AB,故本选项错误;C.射线BA与射线AB不是同一条射线,故本选项错误;D.线段AB的长为2cm,故本选项错误;故选:A.3.【解答】解:A、一个是数字,一个是字母,不是同类项,不能合并,错误;B、字母不同,不是同类项,不能合并,错误;C、正确;D、字母的指数不同,不是同类项,不能合并,错误.故选:C.4.【解答】解:∵四边形ABCD是矩形,∴∠BCD=90°,AC=BD,OA=OB=OC=OD,即选项A、B、C都正确,选项D不一定正确;故选:D.5.【解答】解:对一元一次不等式组求解可得:﹣1≤x<1.5.又由于x是整数,则x可取﹣1,0,1.故不等式组的整数解有3个.故选:B.6.【解答】解:如图所示:∵∠C=90°,sin A==,∴设BC=3x,则AB=5x,故AC=4x,故AC:AB=4:5.故选:D.7.【解答】解:A、必然发生的事件发生的概率为1,正确;B、不可能发生的事件概率为0,正确;C、不确定事件发生的概率>0并且<1,错误;D、随机事件发生的概率介于0和1之间,正确.故选:C.8.【解答】解:A,C没有指明角是顶角还是底角无法判定;D没有指明谁是底边谁是腰,所以不相似;B中因为边的比值为2:1,所以大的一定是腰,否则不能组成三角形,所以对应边都成比例,相似.故选:B.9.【解答】解:∵抛物线y=x2+px+8的顶点在x轴的正半轴上,∴p<0,且b2﹣4ac=p2﹣32=0,解得:p=﹣4.故选:C.10.【解答】解:∵∠A=∠1,∠CDE=∠1+∠CDF=∠A+∠AED,∴∠CDF=∠AED,在△ADE和△CFD中,,∴△ADE≌△CFD(AAS),∴AE=CD,AD=CF,∴AE+FC=CD+AD=AC,故选:C.二.填空题(本大题共6小题,每小题3分,满分18分)11.【解答】解:由题意可得:x﹣3≥0,解得:x≥3.故答案为:x≥3.12.【解答】解:∵∠A+∠B=180°,∴∠C+∠D=360°﹣180°=180°.故答案为:180.13.【解答】解:由方程组,得,∵二元一次方程组的解是方程kx﹣8y﹣2k+4=0的解,∴k×1﹣8×0﹣2k+4=0,解得,k=4,故答案为:4.14.【解答】解:P(2的倍数或是3的倍数)==.故本题答案为:.15.【解答】解:由题意,得|a|﹣3=0且(a+2)(a﹣3)≠0,解得a=﹣3,故答案为:﹣3.16.【解答】解:如图,圆心为A,设大正方形的边长为2x,圆的半径为R,∵正方形有两个顶点在半圆上,另外两个顶点在圆心两侧,∴AE=BC=x,CE=2x;∵小正方形的面积为16cm2,∴小正方形的边长EF=DF=4,由勾股定理得,R2=AE2+CE2=AF2+DF2,即x2+4x2=(x+4)2+42,解得,x=4,∴R=4cm,故答案为:4三、解答题(本大题共9小题,满分102分.解答应智出文字说明、证明过程或演算步骤)17.【解答】解:2x2﹣8=2(x2﹣4)=2(x+2)(x﹣2).18.【解答】解:∵C是线段BD的中点,∴BC=CD,∵AB∥EC,∴∠B=∠ECD,在△ABC与△ECD中,∴△ABC≌△ECD(AAS),∴AC=ED.19.【解答】解:(1)1200÷40%=3000(人),∴该区共抽取了3000名九年级学生;(2)90000×40%=36000(人),∴2018年该区视力不良(4.9以下)的该年级学生大约有36000人;(3)扇形统计图中B的圆心角度数为30%×360°=108°,故答案为:108°.20.【解答】解:(1)由于点D是一次函数y=kx+1的图象与y轴的交点,当x=0时,kx+1=1所以点D的坐标为(0,1);故答案为:(0,1);(2)设AC=x,则AB=4x,所以点A(x,4x)由于点A在反比例函数y=上,所以16=x•4x,整理,得x2=4,所以x=2或x=﹣2(舍去),所以点A(2,8),因为A在一次函数y=kx+1的图象上,所以8=2k+1,解得:k=3.5;(3)由于点A在反比例函数y=上,所以AB•AC=16∵四边形OBAC是正方形,∴OB=AB=AC=OC=4,∵OD=1,∴CD=3,∵S四边形ABDC==(3+4)×4=14S△ACD=AC•CD=×4×3=6∴则四边形ABDC与△ACD面积的比7:3.21.【解答】解:(1)∵AE⊥BC,AF⊥CD,∴∠AFD=∠AEB=90°,∴∠EAF+∠C=360°﹣90°﹣90°=180°.又∵∠EAF=2∠C,∴∠C=60°.(2)∵▱ABCD的周长是32cm,AB:BC=5:3,∴AB=10cm,BC=6cm.在Rt△ADF中,∠AFD=90°,AD=6cm,∠ADF=∠C=60°,∴∠DAF=30°,∴DF=AD=3cm.∵DF的长是关于x的方程x2﹣ax﹣6=0的一个根,∴方程的另一根为﹣6÷3=﹣2.22.【解答】解:(1)如图所示,作CD⊥AB于点D,由题意知,∠B=53°、∠A=45°、BC=8,则CD=BC sin B=8sin53°≈6.4;(2)∵BD=BC cos53°≈4.8,AD=CD=6.4,∴AB=AD+BD=11.2,又∵AC=CD≈9.0,∴AC+BC=9.0+8=17.0,则17.0﹣11.2=5.8(km),答:现在从A地到B地可比原来少走5.8km路程.23.【解答】解:(1)如图,连结OB,∵点B(,m),tan∠AOB=,∴OH=÷tan∠AOB=,∴H点的坐标为(0,);(2)∵H点的坐标为(0,),∴点B(,),∵点C(,),设直线BC的解析式为y=kx+b,则,解得.故直线BC的解析式为y=﹣x+4;(3)∵点A坐标为(0,3),∴点M坐标为(0,),∵点B(,),点C(,),∴BC==,BM==,CM=,∵()2+()2=()2,∴△BMC是直角三角形,∠MBC=90°,∴直线BC与⊙M相切.24.【解答】解:(1)如图所示:(2)结论:FH=HC.理由:∵FH∥BC,∴∠HFC=∠FCB,∵∠FCB=∠FCH,∴∠FCH=∠HFC,∴FH=HC.(3)∵AD是Rt△ABC斜边BC上的高,∴∠ADC=∠BAC=90°,∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,∴∠B=∠CAD,∵∠AEF=∠B+∠ECB,∠AFE=∠CAD+∠ACF,∠ACF=∠ECB,∴∠AEF=∠AFE,∴AE=AF,∵FH∥CD,∴=,∵AF=AE,CH=FH,∴=,∴=,∵∠BAD=∠DCH,∴△EAD∽△HCD,∴∠ADE=∠CDH,∴∠EDH=∠ADC=90°,∴ED⊥DH.25.【解答】解:(1)由题意抛物线交x轴于A(﹣1,0),B(3,0),∴可以假设抛物线的解析式为y=a(x+1)(x﹣3),把C(0,2)代入得到a=﹣,∴抛物线的解析式为y=﹣(x+1)(x﹣3),即y=﹣x2+x+2.(2)如图1中,连接BC甲对称轴于P,此时△P AC的周长最小.设直线BC的解析式为y=kx+b,∵C(0,2),B(3,0),∴,∴,∴直线BC的解析式为y=﹣x+2,∴P(1,).(3)如图2中,连接BD.作DF⊥AB于F.∵DE∥BC,∴S△PDE=S△BED,∵H(1,0),C(0,2),∴CH=,BH=2,∵=,∴=,∴BE=m,∵DF∥OC,∴=,∴=,∴DF=(﹣m),∴S=•BE•DF=﹣m2+m=﹣(m﹣)2+,∵﹣<0,∴m=时,s有最大值,最大值为,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018一模一次函数与反比例函数汇编
例题分析
例题1、(2018十六中一模)若点A (a ,b )在反比例函数y =2
x 的图像上,则代数式ab -4的值为( ).
A.0
B.-2
C.2
D.-6
例题2、(2018培正一模)如图,Rt △ABC 的顶点B 在反比例函数y =12
x 的图象上,AC 边在x 轴上,已知
∠ACB =90°,∠A =30°,BC =4,则图中阴影部分的面积是( ). A .12 B .4 3 C.12-3 3 D.12-32
3
例题2图
例题3图
例题3、(2018三中一模)如图所示,已知双曲线经过矩形OABC 边AB 的中点F ,交BC 于点E ,且四边形OEBF 的面积为4,则k =_________.
例题4、(2018十六中一模)如图,菱形OABC 的顶点C 的坐标为(3,4).顶点A 在x 轴的正半轴上.反比例函数y =k
x
(x >0)的图象经过顶点B ,则k 的值为_____________.
例题4图
例题5图
例题5、(2018四中、聚贤一模)如图,在矩形ABCD 中,AB =3,E 为AD 中点,AC 与BE 相交于点P ,点B 坐标为(2,2),反比例函数y =k
x (x >0)的图象经过点P ,C ,则k 的值为 .
例题6、(2018十六中一模)已知反比例函数y =a +4
x (a 为常数)的图象经过点B (-4,2).
(1)求a 的值;
(2)如图,过点B 作直线AB 与函数y =a +4
x
的图象交于点A ,与x 轴交于点C ,且
AB =3BC ,过点A 作直线AF ⊥AB ,交x 轴于点F ,求线段AF 的长.
例题7、(2018海珠区一模)如图,在矩形OABC 中,OA =3,OC =4,点E 是BC 上的一个动点,CE =a (14≤a ≤5
2),
过点E 的反比例函数y =k
x 的图像与AB 边交于点F .
(1)当a =2时求k 的值;
(2)若OD =1,设S 为△EFD 的面积,求S 的取值范围.
强化训练
1、(2018三中一模)下图是反比例函数y =k
x (k 为常数,k ≠0)的图像,则一次函数y =kx -k 的图像大
致是( ).
A
B
C
D
2、(2018番禺一模)直线y =x -2与x 轴、y 轴分别交于B 、C ,与反比例函数y =k
x (k >0)的图像在第一象
限交于点A ,连接OA ,若S △AOB ∶S △BOC =1∶2,则k 的值为 .
3、(2018广大附中一模)如图,正比例函数y 1=k 1x 和反比例函数y =k 2
x 的图象交于A (-1,2),
B (1,-2)两点,若y 1<y 2,则x 的取值范围是 .
2题图
3题图
4、(2018广雅一模)如图,A ,B 是双曲线y =k
x (x >0)上的两点,过A 作AC ⊥x 轴于点C ,交OB 于点D ,
且D 为OB 的中点,若△ABO 的面积为2,则k 的值为________.
5、(2018海珠区一模)如图,一次函数y =kx+b 与反比例函数y =6
x 图象交于点A (2,m )和B (n ,-2)
(1)求此一次函数的解析式及m 、n 的值; (2)结合图像不等式6
x -kx >b 的解集.
6、(2018广大附中一模)如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为
(5,0),(2,6),点D为AB上一点,且BD=2AD,双曲线y=k
x(k>0)经过点D,交BC于点E
.
(1)求双曲线的解析式.(2)求四边形ODBE的面积.
课后训练
1、(2018汇景一模).某公园要种植一块面积为500m 2的矩形草坪,草坪的长y (单位:m )与宽x (单位:m )的函数关系式为( ).
A.y =500x
B.y =500x
C.
500
x
D.y =250―x 2、(2018一中一模)二次函数y =ax 2+bx +c 的图象如图所示,则一次函数y =bx +b 2-4ac 与反比例函数y =
a +
b +c
x
在同一坐标系内的图象大致为( ).
A .
B .
C .
D .
3、(2018华侨一模)如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于第二、四象限内的 A,B 两点,与x 轴交于点C,与y 轴交于点D,点B 的坐标是(m,-4),连接AO,AO =5 sin ∠AOC =3
5
(1)反比例函数的解析式 (2)连接OB,求△AOB 的面积
4、(2018增城区一模)如图所示,一次函数y =ax +b 与反比例函数y =k
x 的图象交于A ,B 两点,点A 坐标
为(6,2),点B 坐标为(-4,n ),直线AB 交y 轴于点C ,过C 作y 轴的垂线,交反比例函数图象于点D ,连接OD ,BD .
(1)分别求出一次函数与反比例函数的解析式; (2)求四边形OCBD 的面积.
5、(2018育才一模)如图,在平面直角坐标系xOy 中,直线y =-x +3交y 轴于点A ,交反比例函数y =k x (x
<0)的图象于点D ,y =k
x (x <0)的图象过矩形OABC 的顶点B ,矩形OABC 的面积为4,连接OD
(1)求反比例函数的表达式; (2)求△AOD 的面积.
6、(2018白云区一模)如图,在平面直角坐标系中,一次函数y =kx +1的图象交y 轴于点D ,与反比例函数y =16
x 的图象在第一象限相交于点A .过点A 分别作x 轴、y 轴的垂线,垂足为点B ,C .
(1)点D 的坐标为____________; (2)当AB =4AC 时,求k 的值;
(3)当四边形OBAC 是正方形时,直接写出四边形ABOD 与△ACD 面积的比.
7、(2018省实一模)如图,直线 y =k 1x (x >0)与双曲线y =k 2
x (x >0)相交于点p (2,4),已知点A (4,
0),B (0,3),连接AB ,将Rt △AOB 沿OP 方向平移,使点O 移动到点P ,得到△A'PB'.过点A'作A'C ∥y 轴交双曲线于点C . (1)求k 1与k 2的值; (2)求直线PC 的表达式; (3)直接写出线段AB 扫过的面积.。
