缠论的区间套定理
缠61课
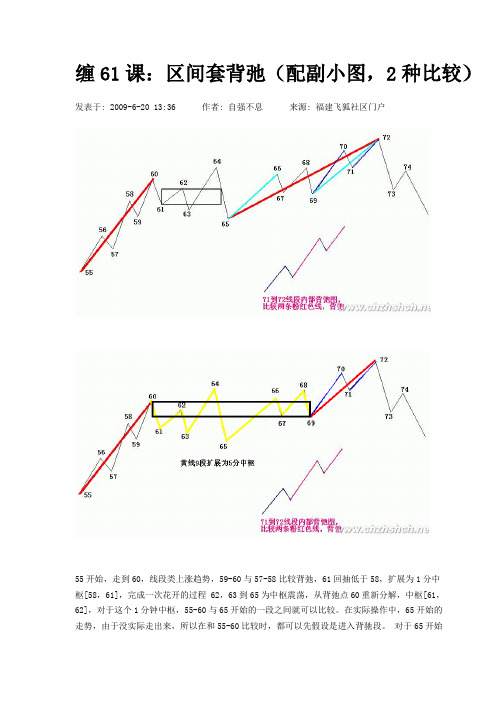
缠61课:区间套背弛(配副小图,2种比较)发表于: 2009-6-20 13:36 作者: 自强不息来源: 福建飞狐社区门户55开始,走到60,线段类上涨趋势,59-60与57-58比较背弛,61回抽低于58,扩展为1分中枢[58,61],完成一次花开的过程 62,63到65为中枢震荡,从背弛点60重新分解,中枢[61,62],对于这个1分钟中枢,55-60与65开始的一段之间就可以比较。
在实际操作中,65开始的走势,由于没实际走出来,所以在和55-60比较时,都可以先假设是进入背驰段。
对于65开始背驰段的内部走势,当下走到69时,并不构成任何背驰,因为背驰如果没有创新高,是不存在的。
由于69-70段与67-68段比并没有盘整背驰,所以70点并没有走的理由,除非你是按线段以下级别操作的。
而71点,构成对66-69这1分钟中枢的第三类买点。
按照本ID的理论,其后无非只有两种情况,中枢级别扩展或者走出新的中枢上移。
对后者,一个最基本的要求就是,从71点这第三类买点开始的向上段不能出现盘整背驰,而在实际中,不难发现,71点开始的走势力度明显比不上69-70段,而对于65-66段,69开始的走势力度也明显比不上,这从两者下面对应的MACD 红柱子面积之和可以辅助判断。
因此,65开始的走势是第一重背驰段,69开始的是第二重背驰段,也就是65开始背驰段的背驰段,而71开始的是第三重背驰段,也就是65开始背驰段的背驰段的背驰段,最后当下考察71开始的走势,从走势上红尖头以及MACD上红尖头可以当下知道,71的内部背驰也出现,也就是第四重的背驰段出现了。
由此可见,72点这个背驰点的精确定位,是由65开始背驰段的背驰段的背驰段的背驰段构成的,这就构成一个区间套的精确定位,这一切,都可以当下地进行。
对于实际的操作,72四重背驰点出现后,卖是唯一的选择,而区别只在于卖多少。
当然,如果是按5分钟级别以及以下级别操作的,当然就全卖了,因为后面至少会形成5分钟的中枢震荡,实际上,60-69就是一个5分钟中枢。
区间套定理证明确界定理

区间套定理证明确界定理
区间套定理证明确界定理(Interval-Completeness Theorem),也称全线性收敛定理,它是数学上重要的一个定理,被广泛应用于数学建模,模式识别,统计学,图形识别,最优化,信号处理等。
区间套定理证明确界定理表明(1)实线上函数在定义域上收敛为凸函数则其定义域是完全的;(2)实线上函数在定义域上收敛为半凸函数则其定义域仍然是完全的,但定义域缩小。
区间套定理的确界定理可以如下证明:
首先,根据公理,实线上的函数在定义域内收敛为凸函数。
这意味着,如果函数f(x)在[a,b]之间有定义,那么该函数f(x)必须满足以下3个条件:
(1)它的导数有限且存在;
(2)它的导数非负;
(3)其二阶导数存在并在[a,b]内一直保持正值或零值。
接下来,以函数f(x)为例,假设函数在定义域内收敛为凸函数,那么函数f(x)必须满足以上3个条件。
根据第3条条件,函数f(x)的二阶导数一定为正值或者零,故在定义域内[a,b],f(x)得函数值
y=f(x)由式子
y=f(x)=ax^2+bx+c
表示,根据前一条讨论,a,b,c均为正值,那么当x=a时,函数f(x)的值最小,也就是说定义域[a,b]为f(x)的完全确界。
最后,可以推出,在定义域上函数收敛为凸函数时,定义域即为完全确界,即区间套定理证明确界定理(Interval-Completeness Theorem)为真。
区间套定理证明

区间套定理证明一、区间套定理的基本概念区间套定理(Interval Division Theorem)是数学中一个关于区间分割的定理。
它指出,对于任意一个实数,都可以通过不断缩小区间的办法,找到一个区间,使得这个区间内的所有实数都满足给定的条件。
区间套定理在数学分析、数值计算等领域具有广泛的应用。
二、区间套定理的证明过程区间套定理的证明过程可以分为以下几个步骤:1.设区间A的左端点为a,右端点为b,区间长度为Δx。
2.假设存在一个实数c,位于区间A内,满足条件。
3.将区间A分割为两个子区间:左子区间(A1)的左端点为a,右端点为c;右子区间(A2)的左端点为c,右端点为b。
此时,Δx1为左子区间的长度,Δx2为右子区间的长度。
4.由于c满足条件,因此可以在左子区间A1中找到一个实数d,使得d 满足条件。
将左子区间A1继续分割为两个子区间:左子区间(A3)的左端点为a,右端点为d;右子区间(A4)的左端点为d,右端点为c。
此时,Δx3为左子区间的长度,Δx4为右子区间的长度。
5.重复步骤4,直到左子区间的长度Δxn趋近于0。
此时,得到的左子区间(An)即为所求的满足条件的区间。
三、区间套定理的应用实例1.求解方程根:对于一元二次方程ax+bx+c=0,可以通过区间套定理求解其根的位置。
首先确定方程的判别式Δ=b-4ac的符号,然后选取一个合适的区间(如[-1,1]),利用区间套定理逐步缩小区间,直到找到满足条件的根。
2.数值计算:在计算机科学中,区间套定理可用于求解非线性方程组、求解微分方程初值问题等。
通过不断缩小区间,可以提高计算精度。
四、结论与启示区间套定理告诉我们,只要我们找到一个合适的区间,就可以通过不断缩小区间的办法求解实数满足的条件。
在实际应用中,区间套定理为我们提供了一种有效的方法,帮助我们解决了许多数学问题。
缠论区间套定理图解

缠论区间套定理图解一、什么是缠论区间套定理缠论区间套定理是一种用于判断价格走势的技术分析方法,通过观察价格的高低点形成的区间套来预测价格的未来走势。
该定理认为,价格的波动是由多个不同周期的波浪组成的,而这些波浪形成了一种特殊的区间套结构,因此可以通过观察这种区间套来预测价格的未来走势,特别是趋势的转折点。
二、区间套的判断方法1.观察高低点观察价格走势中的高低点是判断区间套的首要步骤。
在上升趋势中,高点和低点是不断创新的,在下降趋势中则是不断创新的低点和不断创新的高点。
通过观察这些高低点的变化,可以确定价格的趋势方向和力度。
2.绘制趋势线在确定了高低点后,可以使用趋势线来判断价格的走势。
趋势线可以连接价格的高点或低点,形成上升或下降的趋势线。
通过观察趋势线的变化,可以确定价格走势的力度和趋势的转折点。
3.构建缠论区间套在观察趋势线的基础上,可以构建缠论区间套。
区间套分为两种类型:上升区间套和下降区间套。
上升区间套由上升的高点和低点组成,下降区间套由下降的低点和高点组成。
通过观察这些区间套的形成和变化,可以预测价格的未来走势。
三、区间套的应用案例1.上升区间套案例1.观察高低点:在一段时间内,价格的高点和低点不断上升。
2.绘制趋势线:通过连接高点和低点,可以绘制上升的趋势线。
3.构建区间套:根据上升的趋势线,可以构建上升区间套。
例如,连接第一个高点和低点,形成第一个上升区间套;连接第二个高点和低点,形成第二个上升区间套,以此类推。
4.预测走势:通过观察上升区间套的变化,可以预测价格的未来走势。
如果上升区间套开始收缩,说明价格有可能出现反转;如果上升区间套继续扩张,说明价格继续上涨的概率较大。
2.下降区间套案例1.观察高低点:在一段时间内,价格的低点和高点不断下降。
2.绘制趋势线:通过连接低点和高点,可以绘制下降的趋势线。
3.构建区间套:根据下降的趋势线,可以构建下降区间套。
例如,连接第一个低点和高点,形成第一个下降区间套;连接第二个低点和高点,形成第二个下降区间套,以此类推。
缠论----区间套

缠论----区间套一、基本概念区间套:就是根据背驰段从高级别向低级别逐级寻找背驰点(即买卖点)的方法。
精确大转折点寻找程序定理:某大级别的转折点,可以通过不同级别背驰段的逐级收缩范围而确定。
二、应用要点某大级别的转折点,先找到其背驰段,然后在次级别图里,找出相应背驰段在次级别里的背驰段,将该过程反复进行下去,直到最低级别,相应的转折点就在该级别背驰段确定的范围内。
三、分析理解区间套寻找背驰点的理论依据:低级别背驰是本级别背驰的必要条件而非充分条件,换句话说,就是只有在低级别发生背驰时,本级别才可能背驰。
所以,我们可以从低级别去发现本级别背驰的精确点,也就是说次级别的背驰决定了背驰点,我们说某个级别的走势背驰了,那么必须确定它以下所有级别都转折了,这是所有背驰的前提。
四、操作指导第一种情况最普遍。
其特点是时间和级别完全契合。
具体方法就是本级别进入背驰段后,到次级别去寻找背驰点,然后逐级找下去,直到所有的级别都在背驰段,最小的级别最终背驰。
这种方法要求使用者对本级别以下的所有级别都同时关注,就像一个魔方,只对一面是不够的,只有多个面都对好才有价值。
第二种情况是小转大。
本级别并未进入背驰段,由于小级别的突发情况,导致本级别背驰,这种情况是无法抓到第一买点的,只能在次级别回抽确认之后才能买到。
这种情况发生在空头/多头陷阱,在本级别一个猛烈的上或下,但随后就反转了。
第三种情况是反复背离。
注意是背离不是背驰,所谓的背了又背就是这种情况,就是本级别进入了背驰段,但次级别以下的力度很大,导致本级别迟迟无法背驰,在本级别上就显示背了又背。
但是只要没有打破背驰段,就要密切注意。
这种情况发生在筑顶/底的时期,反复地诱多或诱空,诱多时要快出,诱空时可以战略建仓。
区间套是精度逐级确定的方法。
区间套操作的终极意义是追踪节点。
从高到低一级级背驰下去,一直追踪到某一单成交为止。
这个概念就好比在某个区域搜索一个人,先去定哪个区,然后哪栋楼,然后哪间房,然后哪个座位。
缠论概念、定义、定理、定律、原理汇总

缠论概念、定义、定理、定律、原理汇总整理人:天_佑版权人:缠中说禅。
教你炒股票14:喝茅台的高潮程序!飞吻:短期均线略略走平后继续按原来趋势进行下去。
唇吻:短期均线靠近长期均线但不跌破或升破,然后按原来趋势继续下去。
湿吻:短期均线跌破或升破长期均线甚至出现反复缠绕,如胶似漆。
女上位:短期均线在长期均线之上。
男上位:短期均线在长期均线之下。
第一类买点:用比较形象的语言描述就是由男上位最后一吻后出现的背驰式下跌构成。
第二类买点:女上位第一吻后出现的下跌构成。
缠中说禅买点定律:大级别的第二类买点由次一级别相应走势的第一类买点构成(该定律是有专利的,发明权一定要明确,这一点必须明确,否则以后本ID不会再说任何定律了,该定律一定没有任何人发现过,其他本ID已发现的定律也一样,哪天本ID心情好再说几个,但前提是不能让本ID发现有盗版的,各位也应该和本ID一起监督)。
例如,周线上的第二类买点由日线上相应走势的第一类买点构成。
有了这个缠中说禅买点定律,所有的买点都可以归结到第一类买点。
缠中说禅短差程序就是:大级别买点介入的,在次级别第一类卖点出现时,可以先减仓,其后在次级别第一类买点出现时回补。
对于周线买点介入的,就应该利用日线的第一类卖点减仓,其后在第一类买点回补。
缠中说缠买点定律:大级别的第二类买点由次一级别相应走势的第一类买点构成。
如果资金量不特别巨大,就要熟练缠中说禅短差程序:大级别买点介入的,在次级别第一类卖点出现时,可以先减仓,其后在次级别第一类买点出现时回补。
这样才能提高资金的利用率。
注意,该定律和程序都要注意版权,任何人都可以用,也不收任何版权费,但这个版权必须要明确,否则本ID心情不好,就没兴趣再说任何定律、程序了。
严惩所有企图盗版去招摇撞骗的人。
各位要多看图,根据相应的资金量以及性格去定自己的操作级别,然后具体是熟练,否则就是纸上谈兵,毫无意义了。
教你炒股票15:没有趋势,没有背驰上涨:最近一个高点比前一高点高,且最近一个低点比前一低点高。
最新缠中说禅数学原理
缠中说禅数学原理一、为什么叫“缠中说禅”?1、以股市为基础。
缠者,价格重叠区间也,买卖双方阵地战之区域也;禅者,破解之道也。
以阵地战为中心,比较前后两段之力度大小,大者,留之,小者,去之。
2、以现实存在为基础。
缠者,人性之纠结,贪嗔疾慢疑也;禅者,觉悟、超脱者也。
以禅破缠,上善若水,尤如空筒,随波而走,方入空门。
3、缠中说禅的哲学路线安排。
由股市之解决之道,至论语之入世之道,至佛学之大至深大圆满境界。
以静坐、心经、佛号,引入大超脱之路。
然“理则顿悟,乘悟并销;事须渐除,依次第进”,有缘者得之,无缘者失之,而得并未得,失并未失,一颗明珠,总有粉碎虚空,照破山河之日。
二、“缠中说禅”股市技术理论成立的前提两个前提:价格充分有效和市场里的非完全绝对趋同交易。
三、“缠中说禅”股市技术简解1、以走势中枢为中间点的力度比较,尤如拔河,力大者,持有原仓位,力小者,反向操作。
2、把走势全部同级别分解,关注新的走势之形成,以前一走势段为中间点与再前一走势段比大小,大者,留之,小者,去之。
3、进行多重赋格性的同级别分解操作,尤如行船、尤如开车,以不同档位适应不同情况,则可一路欣赏风景矣。
4、其至高,则眼中有股,心中无股,当下于五浊纷缠之股市得大自在,亦于五浊纷缠之现世得大自在,即为“缠中说禅”。
四、《缠论》的本质分为两个部分:1.形态学。
走势中枢、走势类型、笔、线段之类的东西。
2.动力学。
任何涉及背驰的、走势中枢、走势的能量结构之类的东西。
3.两者的结合。
注:截止目前尚没有任何涉及成交量的分析或者说明,或许这也正是体现了价格包容一切市场信息的原则。
五、学习《缠论》的线路图分型-笔-线段-走势中枢-走势趋势-背驰-区间套-转折及其力度第一节自同构性结构一、基本概念自同构性结构:下节讲到的分型,在不同的级别上,如在1分钟级别、甚至是在年线上,结构是一样的,这就是自同构性结构。
同样,后面讲到走势中枢、走势类型、走势必完美的本质也是自同构性结构。
区间套定理证明
区间套定理证明1. 引言区间套定理是实分析中的一个重要定理,它在数学分析、拓扑学以及其他领域中有着广泛的应用。
本文将介绍区间套定理的定义、证明思路和具体证明过程。
2. 定义首先,我们来定义区间套。
定义1:区间套设给定一系列闭区间[a n,b n],其中n∈ℕ。
如果满足以下两个条件:1. 区间之间存在包含关系,即对于任意自然数n,都有a n+1≤a n且b n+1≥b n; 2. 区间长度逐渐趋于0,即lim n→∞(b n−a n)=0。
则称闭区间序列[a n,b n]为一个区间套。
3. 区间套定理接下来,我们将介绍区间套定理。
定理2:区间套定理如果存在一个闭区间套{[a n,b n]},满足上述定义,并且这个闭区间套的长度逐渐趋于0,则存在唯一的实数c,使得c∈[a n,b n]对于所有n∈ℕ成立。
简言之,区间套定理表明,在实数轴上的闭区间套中,存在一个实数c,它同时属于每一个闭区间[a n,b n]。
4. 证明思路我们将使用实数完备性公理来证明区间套定理。
实数完备性公理:如果对于任意的实数序列{a n}满足a1≤a2≤a3≤⋯≤a n,则存在一个实数L,使得L=lim n→∞a n。
我们将利用实数完备性公理来证明区间套定理。
首先,我们构造两个序列{a n}和{b n},使得a n是闭区间[a n,b n]的左端点,b n是闭区间[a n,b n]的右端点。
然后证明这两个序列分别满足单调有界条件,并利用实数完备性公理得出结论。
5. 证明过程步骤1:构造两个序列给定一个闭区间套{[a n,b n]},我们构造两个序列{a n}和{b n}: - 序列{a n}:每一项a n是闭区间[a n,b n]的左端点; - 序列{b n}:每一项b n是闭区间[a n,b n]的右端点。
步骤2:证明序列{a n}和{b n}满足单调有界条件由定义可知,对于任意自然数n,都有a n+1≤a n且b n+1≥b n。
5分钟讲清缠论
转,缠中说禅图解本文地址:[日内交易者] /daytrade-1976220-1-1/缠中说禅操盘流程图缠中说禅:买卖点图示1- 3类买、卖点图示11- 3类买、卖点图示2第3类买、卖点图示底背驰图例说明1底背驰图例说明2底背驰图例说明3底背驰图例说明4底背驰图例说明5 缠中说禅线段画分图例缠中说禅分型图例5分钟讲清缠论1、首先缠论不是玄学,是一门应用技术!!缠论揭示的操作方法是切实可行。
2、缠论的核心的:背驰、级别、中枢及买卖点。
其他的都是缠师为了说明缠论是科学而增加的说明!!3、缠论运用:背驰:由于背驰的存在,确保了买卖1、2点的必然被抓。
级别:由于级别之间存在演进规律,按照级别逐级研判,可以提高自己至少3个数量级的战斗能力。
中枢:中枢的大量存在和运动规律,给出了操作选择—震荡操作或者买卖3点把握。
走势终完美:给走势预测提供了最有力的保证。
4、总论:缠论是股市赢家操作秘诀的最精要注解。
按照他揭示的规律操作一定会有收获。
学习缠中说禅的五个层次(转)也谈谈学习缠中说禅(以及任何股票操作方法)进步的标志第一层次初学者目标:开始直接接触市场,阅读市场本身的信息;不再听其他人对于市场的间接意见。
已经可以运用分型、线段、中枢直接观察走势图第二层次晋级者能够正确分解不同级别的走势,正确判断背驰,正确处理中阴阶段,买卖点比较精确。
第三层次胜任者能够熟练运用理论,并同时配合资金管理,对政策、比价也有较深的理解。
级别、仓位、韵律配合基本到位,还需要一定的反应时间,反应虽机械,但一板一眼正确到位。
但此时还没有对自己本身的理解,尚无法掌握感觉因素,直觉还没有升起。
第四层次大师对自己内在的感觉较深,并能够与市场关联。
能清晰的感觉到自己与市场之间存在的沟通渠道,不再觉得自己处于市场之外,而是融入市场的大信息场之中。
可以轻易无中生有地取得所需要的信息,仓位轻重自如,并可以随时表达自己的感受,不机械,操作轻松自然。
第五层次仙家清楚的了解自己和市场的本质,并已将二者融为一体。
缠论中枢基础逻辑-终极推理-陈秋明
首先是同级别走势的分析。
也就是固定周期的,不涉及任何高级别低级别次级别之类的玩意,比如日线。
那么在日线的K线图中,走势形态只有三种:上涨、下跌、盘整。
注意,这是走势形态,也就是说你在图上看起来是下跌就是下跌,上涨就是上涨,不涉及中枢什么东西。
而这三种形态,无论是什么形态,都有结束的时候,而且当某一种形态走势结束后,只能跟着其他两种形态走势中的一种。
这样,日线级别K线图就可以看做是上涨、下跌、盘整的组合图形,这样就可以把整个走势图拆解了。
经过分析,这种组合,一共有12种,这12中组合里面,分为四种类型。
上涨、下跌、盘整,还有一种无法归类。
而进一步对无法归类的组合进行分析,发现在这种无法归类的组合前后,再增加其他走势,总能构成由上涨、下跌、盘整,其中两种组合形态的二次组合。
换言之,在日线K线图中,任意走势图,都可以拆解为由上涨、下跌、盘整三三组合构成的高一级别的上涨、下跌、盘整。
其中盘整根据走势结构特征,分为N型与U型两种。
因此可以得出结论:任何级别的任何走势图,都可以拆解为由本级别上涨、下跌、盘整走势形态的连接。
而同样根据上面的推论,在本级别中的任意上涨、下跌、盘整,都可以在次级别拆解出至少由三段完成的走势形态。
这样的推论可以不断的向次级别推演。
但由于最低级别是不可观察的,所以要确定操作级别,并同时根据操作级别定义最小级别。
在最小级别图中,将最小级别的上涨、下跌、盘整,根据以上的嵌套推论进行定义。
那么最基本的图形,比如上涨,就是几根没有三根K线重叠的K线向上+至少三根K线重叠+几根没有三根K线重叠的K线向上这样就可以把最低级别的走势类型确定,进而再向上推演,将操作级别的走势类型近乎精确的划分。
而由于任何级别的任意走势类型都必须至少由次级别三段连接而成,可以确定的是,这三段中,中间一段与前后两段的方向一定是不同的,否则三段就连成一段了。
而这种逆向的走势,会至少造成5日均线的走向变化,从而使5日均线至少接近10日均线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
缠论的区间套定理(2009-11-15 02:10:53)转载▼
缠论的区间套定理也就是缠中说禅精确大转折点寻找程序定理:某大级别的转折点,可以通过不同级别背驰段的逐级收缩范围而确定。
换言之,某大级别的转折点,先找到其背驰段,然后在次级别图里,找出相应背驰段在次级别里的背驰段,将该过程反复进行下去,直到最低级别,相应的转折点就在该级别背驰段确定的范围内。
如果这个最低级别是可以达到每笔成交的,理论上,大级别的转折点,可以精确到笔的背驰上,甚至就是唯一的一笔。
数学的区间套好理解也就是集合的包含,最后只剩一个无限小的数0达到一个极限,闭球套就更容易理解大球套小球最后的小球成为一个点,这个点应该是所有球都包括的。
缠论的区间套最后定位在走势结束的最低(高)的那一个价位上,这个价位逐级从最高级别(背驰发生的级别可能是日线也可能是30分钟等)到最低级别,逐步去找这个点,放大镜的倍数越来越大,越来越清晰的去定位。
当各个级别都走入背驰段发生共振很可能1分钟甚至更低级别的背驰导致大级别的背驰确认。
通过小级别来确认大级别的背驰,通过大级别背驰来找小级别的背驰,在大级别没有背驰发生的情况下,小级别的背驰不要轻举妄动很可能一个小的调整把背驰消灭继续原来的走势。
大级别背驰,小级别的一个微小的变化都可能引起大的情况,这个时候,小级别的背驰就要注意了。
