关于有出手高度的斜抛运动的最大射程分析
高中物理教学论文：斜抛运动的极值问题例析
斜抛运动的极值问题例析斜抛运动由于其速度的不确定性，使其在运动过程中派生出许多的极值问题，比如射程和运动的对称性是斜抛运动常见的问题。
而物体在不同平面的斜抛其特点不同，对应的极值也各不同，现就物体在几种平面上斜抛运动时的极值问题进行分类说明。
（一）在水平面上的斜抛运动的极值问题例题1：在水平地面上以速度v 抛出一小球，v 的方向与水平面的夹角为θ，试确定θ为多大时，小球的射程最远？解：建立如图一所示的坐标系，把小球的运动看作是竖直方向的竖直上抛运动和水平方向的匀速直线运动的合运动。
则两速度的分量为：v x ＝v sin θ v y ＝v cos θ 小球在空中运动的时间为：t ＝2v y /g ＝2v cos θ/g则小球的射程X ＝v x t ＝v sin θ·2v cos θ/g ＝v 2sin 2θ/g由上式可知：当θ＝45o 时，射程具有最大值。
最大射程为：X ＝v 2/g即要使物体以一定的速度在平面上有最大的射程的条件是：物体的抛射角为45o 。
（二）斜抛到上斜面的斜抛运动的极值问题例题2：如图二所示，倾角为θ的斜面光滑，自斜面上某处以速度v 沿与斜面夹角为Ф的方向向斜面上抛出一质点，设质点与斜面间的碰撞没有动能损失，斜面有足够长，要求质点最后仍能回到原出发点，Ф应满足什么条件？解析：整个运动过程中，质点的机械能守恒，显然，若质点能回到原出发点，则它沿斜面向上的运动和向下的运动应该是互相对称的，亦即质点沿斜面方向运动到其能达到的最高点后，它应沿“原路”返回。
这样，有两种情况都能满足这一要求。
一是质点最后一次与斜面相碰时，其速度方向刚好与斜面垂直，则其反弹起来的速度必与其碰前的速度大小相等而方向相反，这样，质点此后的运动将把其上升过程的运动“反演”一次，可回到原出发点。
二是质点最后一次与斜面相碰后，其反弹起来的速度恰沿竖直向上的方向，则质点弹起后作竖直上抛运动，当质点达到竖直上抛的顶点后，接着便会将此前的运动“反演”，也会回到原出发点。
求解斜上抛运动“射高”和“射程”的两个小妙招
高一使用2021年2月■潘慧斜上抛运动是一种复杂的曲线运动，往年高考中很少出现考查斜上抛运动相关计算的试题，而2020年高考山东卷中出现了涉及求解斜上抛运动“射高”和“射程”的试题，使得很多同学感觉不知从何入手。
下面介绍两个求解斜上抛运动“射高”和“射程”的小妙招，希望能够帮助同学们轻松化解这类难题。
一、正交分解求“射高”斜上抛运动的“射高”是指做斜上抛运动的物体在运动过程中距水平面或斜面的最大距离，因此建立以竖直方向或垂直于斜面方向为y轴的平面直角坐标系，将做斜上抛运动物体的初速度或加速度沿x轴和y轴正交分解，就可以利用“沿y轴方向的末速度为0”这个隐含条件求“射高”了。
1.正交分解初速度。
例1固定在水平地面上的迫击炮炮筒与水平方向成60°角，炮弹从炮口射出时的速因为射高隐含着“竖直方向上的末速度为0”这个条件，所以应建立以竖直方向为y轴的平面直角坐标系。
因为初速度不在坐标轴上，所以需要沿y轴方向分解初速度，从而分析得出沿y轴方向分运动的规律，最后运用运动学公式即可求得炮弹的射高。
2.正交分解初速度和加速度。
例2如图2所示，固定在倾角6—30°的斜面上的迫击炮炮筒与水平方向成30°角，炮弹从炮口射出时的速度是V0,若忽略空气阻力和炮筒的长度，已知重力加速度为g o求炮弹射出后距斜面的最大距离。
度是V0,若忽略空气阻力和炮筒的长度，已知重力加速度为g o求炮弹的射高。
建立如图3所示的平面直角坐标系，将炮弹的斜上抛运动建立如图1所示的平面直角坐标系，将炮弹的斜上抛运动分解为水平方向上的匀速直线运动和竖直方向上的竖直上抛运动。
将炮弹的初速度V0沿y轴方向分解得V y—V0sin60°。
设炮弹的射高为h,因为炮弹到达最高点时在竖直方向上的末速度为0,所以在竖直方向上根据运动学公式得0—V——gh。
联立以上二式解得h _3V=8g°图1分解为沿斜面方向的匀加速直线运动和垂直于斜面方向的匀减速直线运动。
(2021年整理)斜抛运动知识要点
(完整版)斜抛运动知识要点编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)斜抛运动知识要点）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)斜抛运动知识要点的全部内容。
(完整版）斜抛运动知识要点编辑整理:张嬗雒老师尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布到文库，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是我们任然希望（完整版）斜抛运动知识要点这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区，这将是我们进步的源泉,前进的动力。
本文可编辑可修改，如果觉得对您有帮助请下载收藏以便随时查阅，最后祝您生活愉快业绩进步,以下为〈(完整版)斜抛运动知识要点〉这篇文档的全部内容。
斜抛运动知识要点【知识要点】1.对概念的理解：根据斜抛运动的概念可知：斜抛运动应同时满足两个条件，一是物体的初速度V0不等于零,且方向斜向上；二是物体仅受到重力的作用，根据牛顿第二定律易知斜抛运动物体的加速度即为重力加速度g,方向竖直向下，它和平抛运动以及竖直方向上的抛体运动的加速度是一样的。
2.斜抛运动的简单处理法（运动的分解与合成法）前面学习平抛运动的时候我们为了处理问题的方便，知道把平抛运动看成水平方向上的匀速直线运动和竖直方向上自由落体运动的合运动，那么今天学习斜抛运动仍可使用前面学习的方法，巧妙的把斜抛运动看成水平方向上的匀速直线运动和竖直方向上的竖直上抛运动的合运动。
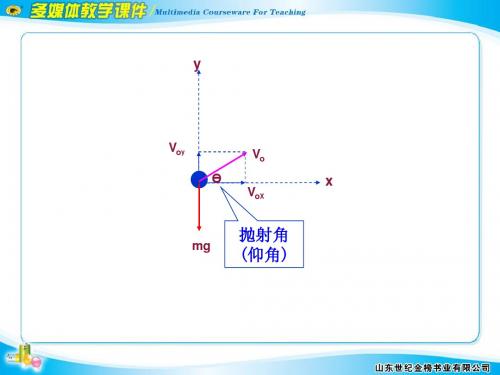
3.斜抛运动的规律如图1，物体以初速度v0斜向上抛出,其方向与水平方向的夹角θ角。
110. 高中物理中的斜抛运动如何分析？
110. 高中物理中的斜抛运动如何分析？关键信息1、斜抛运动的定义和特点定义：＿___________________________特点：＿___________________________2、斜抛运动的分解水平方向：＿___________________________竖直方向：＿___________________________3、斜抛运动的基本公式水平位移公式：＿___________________________竖直位移公式：＿___________________________速度公式：＿___________________________4、斜抛运动的射程和射高射程的影响因素：＿___________________________射高的影响因素：＿___________________________5、斜抛运动的实际应用体育项目中的应用：＿___________________________日常生活中的应用：＿___________________________1、斜抛运动的定义和特点11 定义斜抛运动是指将物体以一定的初速度沿与水平方向成一定角度抛出，物体仅在重力作用下所做的曲线运动。
12 特点斜抛运动具有以下特点：121 运动轨迹为抛物线。
122 加速度恒为重力加速度 g，方向竖直向下。
123 水平方向做匀速直线运动，竖直方向做匀变速直线运动（先竖直上抛，再竖直下抛）。
2、斜抛运动的分解21 水平方向水平方向不受力，速度大小不变，做匀速直线运动。
水平方向的速度分量为 Vx ＝V0 cosθ，其中 V0 为初速度，θ 为初速度与水平方向的夹角。
22 竖直方向竖直方向受重力作用，加速度为 g，做匀变速直线运动。
竖直方向的速度分量为 Vy ＝V0 sinθ gt。
3、斜抛运动的基本公式31 水平位移公式水平位移 X ＝V0 cosθ × t，其中 t 为运动时间。
斜抛运动最大射程问题分析
斜抛运动最大射程问题分析作者：刘尚昊来源：《科技资讯》2018年第25期摘要：本文着眼于讨论物体从一定高度被抛出后，其水平方向的最大射程与抛射角之间的关系，讨论了斜抛运动达到最大射程应满足的条件，并通过理论公式的证明和实际数据的测量，指出45°不再是能够得到最大射程的角度。
本文通过具体计算了实际铅球抛出的最大射程和抛射角，并且随机取数进行了实验，从而得出了二者之间的关系，为斜抛运动的实际应用提供了力学理论依据。
关键词：斜抛运动最大射程抛射角力学理论依据中图分类号：O313 文献标识码：A 文章编号：1672-3791（2018）09（a）-0233-021 分部求导法该分析方法需要经过两次的求导，通过判断导数的大小和倒数的解，判断能否取到最大的射程。
将该物体在空中进行斜抛运动的时间假设为t，则可以得到物体在坐标轴X和Y方向的运动方程，如下：X=v0tcosθ （1）Y=H+v0tsinθ-1/2gt2 （2）假设物体在经过时间T以后由斜抛运动落地，此时物体的坐标为x=R，y=0，此时上式（1）（2）则变为：R=v0Tcosθ （3）0=H+v0Tsinθ-1/2gT2 （4）将上式联立起来，即可得出水平射程的表达式：R={v0{sin2θ+[sin22θ+8gH/v02cos2θ]1/2}}/2g （5）当物体落地后，H=0时，可以将上式化简为：R=v02sin2θ/g （6）假设物体的最大射程为Rm，在求解最大射程时使用导数求极值的方法，分析最大射程和抛射角度θ之间的关系，在求解时引入无量纲参数定义为Z：Z=gH/v02在进行求导时，令R对θ的一阶导数R’=0，此时可以得到最后求解出结果为：cos2θ=z/（1+z）（7）然后对R进行二次求导，即可以推论出R的二阶导数是小于零的，因此可以得出R是能够取得最大值的。
因此得出：Rm=vo2（1+2z）1/2/g （8）T=vo2/g[2（1+z）]1/2 （9）θm=1/2arccos（z/1+z）（10）根据上式当中的化简结果可知，决定最大射程的影响因素不仅包括抛射角度θ，还有无量纲参数Z，因此影响最大射程的参数还有距离地面的高度H和物体运动的初速度v0。
1.5斜抛运动
Voy Ө
Vo VoX
x
mg
抛射角 (仰角)
三
斜抛运动的规律
射程与射高
射高：在斜抛运动中，物体能到达的最大高度 射程：物体从抛出点到落地点的水平距离
vo
Ө
射高H
射程X
射高
ymax
2 v0 sin 2 2g 2g
2 v0 y
射程
Байду номын сангаасxmax
2 2v0 sin v0 sin 2 v0 xt v0 cos t v0 cos g g
位移: y v 0y t gt 2 v 0sin θ t gt 2
2 2 2 v0 sin 2 2v sin cos v sin 2 射程： X 0 = 0 2g 2g g g 2 v0y
1 2
1 2
y max 3、射高：
课本23页第4题
vo
Ө
v0 当 45时，x , 射程x最大. g
2
弹道曲线
定义： 物体的初速度很大时(如射出的枪弹、炮弹 等)，空气阻力的影响是很大的，轨迹不再是 理论上的抛物线，这种实际的抛体运动曲线
通常称为弹道曲线。
1、斜抛运动分解为
水平方向： 匀速直线运动 竖直方向： 竖直上抛运动
2、斜抛运动的规律： 速度 :vx =v0x =v0cosθ 水平方向: 位移: x=voxt= v0tcosθ 竖直方向： 速度:vy=v0y-gt=v0sinθ -gt
运动学之斜抛物体在斜坡上的射程
射程公式可化为
S
v02[sin(2
g cos2
)
sin
]
y v0
当2θ - α = π/2时，即
π
42
射程最大。 θ α S O
P x
射程的最 大值为
SM
v02 (1 sin ) g cos2
v02
g(1 sin )
当θ1 + θ2 = 90°+ α时， 可得
S1
v02[sin(21 g cos2
下抛，S'趋于无穷大，表示物体无法落在悬崖侧面上。
如果物体竖直向下抛，物体就沿着悬崖的侧面向下运动。不 计摩擦，物体与悬崖的接触点都是射程，但不存在最大射程。
图例表示斜坡的仰角，仰角 越大，射角取值范围就越小。
每条曲线都 有一个极大 值，表示最 大射程。
所有射程曲线最后都交于一点(90,0)， 说明不管坡度为多少，物体竖直上抛 时，最后都落在原处，射程当然为零。
最大射程随 仰角的增加 而减小。
[讨论]
S 2v02 sin( ) cos v02[sin(2 ) sin ]
g cos2
g cos2
①在平地上斜抛物体时，α = 0，可得水平射程
S v02 sin 2 g
最大射程为
SM
v02 g
此时的射角为θ = π/4。
y v0 θα S
P
O
x
②当α = π/2时，山坡就变成峭壁，物体只能竖直上抛，沿 峭壁运动。不计摩擦，物体与峭壁的接触点都是射程。
最大射程为
SM
v02 2g
这正是竖直上抛的最大高度。
射程
S
2v02
sin( ) cos g cos2
高中物理研究斜抛运动-例题思考沪科版必修三
研究斜抛运动-例题思考1.斜抛运动有斜上抛运动和斜下抛运动两种，当斜上抛时，被抛物体所能达到的高度叫射高，抛出点与落点之间的水平距离叫射程.如下图：物体斜上抛的仰角为θ，抛出的初速度为v 0.我们先将v 0正交分解为水平分速度v 0x 和竖直分速度v 0y .根据数学关系可以得出：v 0x =v 0cos θv 0y =v 0sin θ假设把物体看作是可忽略空气影响的“理想抛体〞，那么根据运动分解的理论可知：斜上抛物体水平方向不受力，应做匀速直线运动，其速度为v 0x ＝v 0cos θ，其位移方程应为：x =v 0cos θ·t ①斜上抛物体竖直方向受向下的重力，与竖直向上的初速度v 0y ＝v 0sin θ的方向相反，应做竖直上抛运动，其位移方程应为：y =v 0sin θ·t －21gt 2② 由①式可以导出:t =θcos 0v x ③ 将③式代入②式，导出：y ＝tan θ·x －2220cos 2x v g θ④ 我们称导出的④式为“斜上抛物体运动的轨道方程〞.如果斜上抛物体是在水平面上进行的，那么它的抛出点和落地点应在同一水平面上(这实际上是日常最常见的斜上抛情况)，也就是说物体在竖直方向的起点到终点的位移y =0.因此我们将y ＝0代入前面导出的④式(即“轨道方程〞)，就可推导出最大水平位移x m (即“射程〞). x m =gv θ2sin 20,即“射程公式〞. 现在我们根据“射程公式〞讨论前面所提出的问题——当v 0不变时，以多大的仰角θ斜上抛出的物体射程最远？ 据射程公式： x m ＝gv θ2sin 20，可以看出g 是常量，假设v 0不变，那么决定x m 大小的因素就只有sin2θ的数值了.根据数学知识我们知道正弦的最大值为：sin90°＝1因此当sin2θ＝sin90°时，x m 值最大那么：2θ＝90°，所以θ＝45°.①即当抛物的初速度v 0不变时，以45°的仰角斜上抛出的物体射程最远.由此，能推导出斜上抛物体运动的“射高公式〞H ＝g v 2sin 220θ. ②推导出斜上抛物体运动的“飞行时间公式〞T ＝gv θsin 20. [例1] 如下图，从O 点发射一速度为v 0的子弹，竖直靶AC 与发射点的水平距离为d .如果子弹射至靶面时正好与靶面垂直.(1)求投射角θ多大？(2)证明AB 的高度为瞄准点AC 高度的一半.思路：这是斜抛运动通常的解题思路和方案.可以充分利用我们前面推导出的公式来直接求解.解析：(1)子弹射中靶子时与靶子垂直，说明子弹在B 点速度方向是水平的.因而B 点是轨迹的最高点，d 是射程的一半.即2d =gv θ2sin 20 解之得投射角θ=202arcsin 21v dg . (2)子弹射到B 点所经历的时间t =gv θsin 0 BC 是在时间t 内由于重力作用于子弹自由下落的距离，BC =21gt 2=21g (g v θsin 0)2=g v 2sin 220θ AB 是子弹做斜抛运动上升的最大高度(即射高)，AB =gv 2sin 220θ 所以BC =AB =21AC . 2.斜抛运动虽然是比较复杂的一种运动，但我们在处理时并不一定按照一种僵化的方案来分解.如果能巧妙地选择分运动，将会使分析解决问题变得简单.[例2] 子弹以初速度v 0、投射角α从枪口射出，刚好能掠过一高墙，如下图.假设测得枪口至高墙顶连线的仰角为θ，求子弹从发射到飞越墙顶的时间.思路：该题中子弹的斜抛运动可以按照常规分解为水平方向和竖直方向的运动来求解，但要麻烦一些，如果我们能把该斜抛运动看成沿v 0方向的匀速直线运动和自由落体运动的合成，就可简化运算，下面分别用两种方法来比较一下.解析：解法一：把斜抛运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动.设从发射到飞越墙顶的时间为t ，那么在水平方向和竖直方向上的分位移为x =v 0cos α·ty =v 0sin α·t －21gt 2 由题设条件知y =x ·tan θ故可解得t =gv )tan cos (sin 20θαα⋅-. 解法二：把斜抛运动分解为沿v 0方向的匀速直线运动和自由落体运动，如下图.由正弦定理，可得)90sin()sin(2102θθα+︒=-t v gt 解得t =θθαcos )sin(20g v - 由三角函数关系知道这两个答案是相等的.例题解析[例1] 如下图，打高尔夫球的人在发球处(该处比球洞所在处低15 m)击球，该球初速度为36 m/s ，方向与水平方向成30°角.问他会把球向球洞处打到多远?(忽略空气阻力)解析：小球初速度的水平分量和竖直分量分别是v 0x ＝v 0cos θ＝36cos30°＝31.2 m/s ，v 0y ＝v 0sin θ＝36sin30°＝18.0 m/s .由y ＝CD ，可得CD ＝v 0y t －21gt 2， 代入量，整理后可得t ＝2.40 s 或1.28 s其中t ＝1.28 s 是对应于B 点的解，表示了该球自由飞行至B 点处所需时间.因此在本例中，应选解t ＝2.40 s.在此飞行时间内，球的水平分速度不变，于是最后可得x =v 0x t =31.2×2.40 m=74.7 m.点评：该题考查实际问题中的斜抛运动.涉及到斜抛运动中的一个分运动——竖直上抛运动的时间能出现双解.这两个时间，一个是在上升过程中，一个在下落过程中.一般的斜抛运动考查的抛出点和落地点在同一水平面上，而该题的落地点与抛出点不在同一平面内，在时间的考查上也有新意.。
关于斜抛运动的最大射程
关于斜抛运动的最大射程关于抛出点和落地点在同一水平面上的斜抛运动的最大射程问题，已经被众多的读者所熟知，也就是：当抛出角为45°时，水平射程最大，为 gv X m 20。
但对抛出点和落地点不在同一水平面上的斜抛运动来说，抛出角满足什么条件时，水平射程最远？最远为多少？下面就以上两个问题与读者一起进行探讨。
如下图所示，设斜抛物体的初速度为0v ，抛出点与落地点的水平高度差为H ，令当斜抛运动的初速度与水平方向间的夹角为α时，水平射程X 最大。
对初速度0v 进行分解，然后由运动学规律不难可以得到以下两个式子：α消去①②中的α，得到 ③t V H gHt t g X 2202242221+-+-=整理③式得到 ④ggH ） （V t g H ggH ）（VX 222021222202]2[21][+---+=从④式不难可以看出，当t=22022g gtV + 时 X 最大，有222202H g gH ）（VXm-+=即gH V gV X m 2200+=⑤ 又因为物体在空中下落的过程中，遵守机械能守恒定律，故有gH V V t 220+= 所以有gV V X tm 0=⑥ 从①②式中可以得出 XHgt tg -=221α将22022g gHV t +=及gV V gH V g V X t 02002=+= 带入上式得 tV V gHV V tg 02002=+=α ⑦ 由以上推导，可以得出从距水平地面高为H 的小球以初速度V 0斜抛时：当初速度方向与水平方向间的夹角满足 α=arctg tV V 0时，小球的水平射程为最大，且最大射程为X m =gV V t0 （其中V t 为物体落地时的速度，大小为gH V V t 220+= ）另外，以上结论也可以由动量定理加以证明：当V 0和H 一定时，由机械能守恒定律得，物体落地时的速度必为定值gHV V t 220+=因为小球在空中运动时只受重力的作用，由动量守恒定律得：小球从抛出到落地这段时间内，速度由初速度0V 变化到t V ，速度的变化量△V 的方向一定在竖直向下的方向上，且满足上图的矢量关系（图中的为物体落地时的速度方向与水平方向间的夹角）设物体在空中的运动时间为t ，水平射程为X ，则由运动学知识及动量定理可得出下述两式：将②式中的t 带入①中得到又因为 而所以有 由③④⑤三式得因为0V 、t V 及g 均为定值，所以，当（α+β）=90°时，X 有最大值，且为gV V X tm 0=，而这一结论与上面的推导结论是完全一致的。
高一物理斜抛运动知识点
高一物理斜抛运动知识点斜抛运动是物理中非常重要的一个概念，它是指物体在某一初速度下以一定的角度斜向上或者斜向下运动的过程。
在高一物理课程中，斜抛运动是一个重要的知识点，理解斜抛运动的原理和规律对于解题和应用都至关重要。
一、斜抛运动的基本概念1. 速度与角度的关系斜抛运动中初速度的大小和发射角度的变化会直接影响物体的飞行轨迹。
当初速度越大且发射角度较高时，物体的飞行弧线会更高，射程也会更远。
而初速度较小和发射角度较低时，物体的飞行弧线会更低，射程也会较短。
2. 轨迹的形状斜抛运动的轨迹一般为抛物线形状。
这是因为物体在垂直方向上受到重力的作用，而在水平方向上不受重力的作用，导致物体呈抛物线形状运动。
这也是为什么我们在日常生活中投掷物体时，物体总是会呈现出一个曲线的轨迹。
3. 飞行时间和最大高度斜抛运动中，飞行时间不仅取决于物体的初速度和发射角度，还受到重力加速度的影响。
当初速度相同的情况下，发射角度越小，物体的飞行时间越短；发射角度越大，物体的飞行时间越长。
而最大高度则是在物体垂直上升过程中达到的高度，最大高度取决于物体的初速度和发射角度。
二、斜抛运动的公式与计算1. 水平方向的运动斜抛运动中，物体的水平运动速度始终保持恒定，与受力和时间无关。
因此，在水平方向上，物体的位移可以通过公式 S=Vx⋅t 来计算，其中 S 表示位移，Vx 表示水平方向的初速度，t 表示时间。
2. 垂直方向的运动在斜抛运动中，物体在垂直方向上受到重力的影响，因此垂直方向上的位移与时间有关。
对于物体的垂直位移，可以通过公式Sy=V0y⋅t－(1/2)⋅g⋅t²来计算，其中 Sy 表示垂直位移，V0y 表示物体的垂直初速度，t 表示时间，g 表示重力加速度。
3. 飞行时间与水平射程飞行时间是物体在斜抛运动中飞行的总时间，可以通过公式t=2⋅V0⋅sinθ/g来计算，其中 V0 表示初速度大小，θ 表示发射角度，g 表示重力加速度。
斜抛运动高中一年级学生如何计算斜抛物体的水平和垂直位移
斜抛运动高中一年级学生如何计算斜抛物体的水平和垂直位移斜抛运动是力学中的一个重要概念，也是高中物理课程中必学的内容之一。
对于一名高中一年级的学生来说，掌握如何计算斜抛物体的水平和垂直位移是非常关键的。
本文将介绍斜抛运动的基本概念以及计算水平和垂直位移的方法。
一、斜抛运动的基本概念斜抛运动是指物体在一个斜向上抛的情况下所进行的运动。
在斜抛运动中，物体同时具有初速度（即抛出物体的速度）和初向上抛的角度。
根据重力的作用，物体在抛出后会先上升到最高点，然后再下落到地面。
在斜抛运动中，我们通常会遇到以下几个重要的物理量：1. 初速度（Vo）：物体离开地面时的速度，可以是沿斜线方向的初速度（Vox）以及垂直向上的初速度（Voy）。
2. 角度（θ）：物体抛出时与水平方向之间的夹角。
3. 时间（t）：物体在空中运动的时间。
4. 加速度（g）：物体在地球上受到的重力加速度，取9.8 m/s²。
二、水平位移的计算方法水平位移是指物体在水平方向上运动的距离，也可以理解为物体在水平方向上的位移。
在斜抛运动中，水平位移可以通过物体的初速度和时间来计算。
水平位移的计算公式为：水平位移（dx）= 水平初速度（Vox） ×时间（t）其中，水平初速度（Vox）可以使用正弦函数来计算：水平初速度（Vox）= 初速度（Vo） ×正弦角度（θ）综合以上公式，我们可以得出计算水平位移的综合公式：水平位移（dx）= 初速度（Vo） ×正弦角度（θ） ×时间（t）三、垂直位移的计算方法垂直位移是指物体在垂直方向上运动的距离，也可以理解为物体在垂直方向上的位移。
在斜抛运动中，垂直位移可以通过物体的初速度、时间和加速度来计算。
垂直位移的计算公式为：垂直位移（dy）= 垂直初速度（Voy） ×时间（t） + 0.5 ×加速度（g） ×时间（t）²其中，垂直初速度（Voy）可以使用正弦函数来计算：垂直初速度（Voy）= 初速度（Vo） ×正弦角度（θ）综合以上公式，我们可以得出计算垂直位移的综合公式：垂直位移（dy）= 初速度（Vo） ×正弦角度（θ） ×时间（t） + 0.5 ×加速度（g） ×时间（t）²四、实例分析现假设一个物体以30°的角度抛出，初速度为20 m/s，求物体在水平和垂直方向上的位移。
高一物理必修二斜抛知识点
高一物理必修二斜抛知识点斜抛运动是高中物理中的重要知识点之一，它描述了一个物体在一定初速度的情况下，在重力的作用下沿一定角度抛出后的运动轨迹。
了解斜抛运动的基本概念、公式以及相关实验是理解高一物理必修二的重要前提。
下面将详细介绍斜抛运动的相关知识点。
一、斜抛运动的基本概念斜抛运动是指一个物体在给定的初速度和一定角度的情况下进行的运动。
这种运动既有水平分速度，也有垂直分速度。
当物体沿着一个斜向上的轨迹飞行时，它同时受到重力和空气阻力的作用。
二、斜抛运动的相关公式1. 水平速度分量（Vx）：沿着水平方向的物体速度。
2. 垂直速度分量（Vy）: 沿着垂直方向的物体速度。
3. 抛体达到最高点时的垂直速度（Vy_max）：最高点的速度为0，方向由正向转为负向。
4. 抛体飞行的时间（t_total）：抛体从起点抛出到落地所经过的时间。
5. 抛体达到最大高度的时间（t_top）：抛体从起点抛出到达最高点所经过的时间。
6. 抛体飞行的水平距离（R）：抛体从起点抛出后到达落点的水平距离。
三、斜抛运动的实验为了更好地理解斜抛运动，我们可以通过实验进行验证。
下面介绍两个常见的斜抛运动实验。
1. 斜抛实验一：测量斜抛物体达到最大高度的时间材料：一束光电门、一支小球和一个计时器。
操作步骤：a. 首先，将光电门放在一定高度的桌子上，并将接收器放在下方的固定支架上。
b. 将小球置于架子上的发射器上方，并用手指抛出小球，使其通过光电门。
c. 调整发射器和接收器的位置，使其对准光电门，当小球通过光电门时，计时器开始计时并记录时间。
d. 重复实验多次，取平均值，即可得到斜抛物体达到最大高度的时间。
2. 斜抛实验二：测量斜抛物体的飞行水平距离材料：一根水平放置的长木板、一支小球和一个测量尺。
操作步骤：a. 将木板平放在地面上。
b. 在木板的一端放置小球，并用手指推出。
c. 用测量尺测量小球从起点到落地的水平距离。
d. 重复实验多次，取平均值，即可得到斜抛物体的飞行水平距离。
斜抛运动公式总结
斜抛运动公式总结
斜抛运动是物理学中的一个重要概念，也是生活中常见的运动形式之一。
斜抛运动的公式可以帮助我们计算出物体在斜向抛出的情况下的速度、高度、时间等参数，为我们了解和掌握斜抛运动提供了帮助。
下面是斜抛运动公式的总结：
1. 斜抛运动初速度的分解式：$v_{0x}=v_0cosθ$，
$v_{0y}=v_0sinθ$。
2. 斜抛运动与水平运动的关系：$v_x=v_{0x}$，$a_x=0$，
$x=x_0+v_{0x}t$。
3. 斜抛运动与竖直运动的关系：$v_y=v_{0y}-gt$，$a_y=-g$，$y=y_0+v_{0y}t-frac{1}{2}gt^2$。
4. 斜抛运动的最高点：$t=frac{v_{0y}}{g}$，
$y_{max}=y_0+frac{v_{0y}^2}{2g}$。
5. 斜抛运动的落地点：$t=frac{2v_{0y}}{g}$，
$x_{max}=x_0+frac{v_0^2sin2θ}{g}$。
6. 斜抛运动的抛射时间：$t=frac{2v_0sinθ}{g}$。
7. 斜抛运动的最大射程：$R=frac{v_0^2sin2θ}{g}$。
通过掌握斜抛运动公式，我们可以更好地理解和应用斜抛运动的原理，进而为生活和学习中的相关问题提供科学的解答。
- 1 -。
用运动的合成法解斜抛运动的射程
用运动的合成法解斜抛运动的射程在高中阶段,学生所学的抛体运动主要是平抛运动,但有时又会涉及到一般的抛体运动,如斜抛运动,而斜抛运动的射程求解是难点。
其实,对斜抛运动问题,可以采用与研究平抛运动相同的方法,即把斜抛运动分解成两个较为简单的直线运动。
下面用运动的合成与分解两种不同的方法来讨论斜抛运动的射程。
先来看特殊情况:例1:不计空气阻力,在水平地面上将一物体以初速度v0,与水平面成夹角θ的角度抛出,求射程。
方法1:用分解的方法原理:将初速度v0分解,将斜抛运动看成竖直方向上的初速度为v0s inθ、加速度为g的匀减速直线运动和水平方向上速度为v0cosθ的匀速直线运动的合运动。
由对称性可知,从抛出到落地:竖直方向:-v0sinθ=v0sinθ-gt水平方向:x=v0tcosθ由以上两式可得射程:由上式可知,当θ=45°时,射程的最大值xm=方法2:用合成的方法原理:将斜抛运动看成初速度方向上的匀速直线运动和竖直方向上的自由落体运动的合运动。
如图,从抛出到落地,由正弦定理可知,在△OAB中有:①②由①、②式可得射程:x=从以上可以看出,对这种特殊的情况,不管是分解的方法还是合成的方法,都比较简单自然。
但对一般的情况,比如在斜面上向上抛或向下抛最后落在斜面上,采用合成的方法要简单得多。
下面,看一般的情况:例2:如图,一斜坡仰角是α,斜抛物体的初速度大小是v0,与水平面之间的夹角是θ且落在斜坡上,求其射程。
在这个问题中,若用分解的方法,由于抛物体最终落在斜坡上,整个运动轨迹不存在对称性,不好求解。
但用合成的方法却不存在这个问题。
原理还是将斜抛运动看成匀速直线运动OA和自由落体运动AB的合运动。
OA=v0t,AB= gt2,OB=x,由正弦定理,在△OAB中有:①②由①、②可得射程:x= [sin(2θ-α)+sinα]上式中只有sin(2θ- )一项随θ变化,当2θ-α= 时,此项有极值1,由此可见,当θ= + 时,x有极大值,xm= ,当=0时,即在水平地上斜抛,可得熟悉的结论:当θ= 时,x有极大值,xm=例3:如图,一斜坡仰角是-α,斜抛物体的初速度大小是v0,与水平面之间的夹角是θ且落在斜坡上,求其射程。
斜上抛物体最大射程讨论的一个结论
斜上抛物体最大射程讨论的一个结论作者：赵刚来源：《中学物理·高中》2012年第08期中学物理中对在离地高度为h、以初速度v0斜向上抛出的物体，应具有多大的抛射角α才能达到最大射程这一问题已经有了许多讨论，本文从讨论最大射程抛射角入手，发现其中一个公理.由于在理想状态下物体运动中只受重力作用，根据运动合成与分解的有关定理定律，我们可以将斜抛物体的运动视为初速度为v0与水平方向成α角的斜向上匀速直线运动和竖直方向自由落体运动的合成运动.如图1示，设物体由抛出点A至水平着地点B处飞行时间为t.匀速直线运动的位移大小为AC=v0t，其中C点为物体匀速直线运动的末位置.由图示几何关系可以得出：AC2=（CD—DB）2+OB2，由于AC=v0t、CD—DB=12gt2—h，且OB=s，所以有（v0t）2=（12gt2—h）2+s2，将该式展开整理后可得s2=—（12gt2—v20+hgg）2+（v20+ghg）2—h2（1）为使射程s达到最大，则（1）式等式右边必有由此式可求出斜抛物体达到最大射程所用时间t=2v20+2ghg（2）此时物体达到最大射程为s2max=（v20+ghg）2—h2=v40+2ghv20+g2h2—g2h2g2=v20（v20+2gh）g2，smax=v0gv20+2gh=OB=AD（3）由图知：最大射程对应抛射角应有如下三角关系tanα=CDAD=12gt2—hsmax（4）将（2）、（3）式代入（4）式，可得tanα=CDAD=12gt2—hsmax=v20+2gh2g—hv0gv20+2gh=11+2ghv20（5）讨论：（1）h=0时，tanα=1，α=45°，这是我们熟知的斜上抛物体最大射程抛射角.（2）h≠0时，物体着地点速度为v可以视为物体抛射初速度v0与物体做自由落体运动经时间t后的速度v′的合成.因为t=2v20+2ghg，故v′2=2v20+2gh=v20+v20+2gh（6）由机械能守恒定律考察斜上抛物体运动有如下关系v2—v20=2gh，即v2=v20+2gh（7）将（6）式代入（7）式可得v′2=v2+v20，即v与v0方向垂直.结论由上述讨论可知，斜抛物体若达到最大射程，则其抛射角与着地时速度与地面的夹角之和必为90°；亦即当二角之和为90°时，斜抛物体射程最大（也可以表述为当上抛物体初速度与末速度方向垂直时，射程最大.）________________________________________可推导出适用一切电路的公式E=U外+U内，按从一般的规律走向特殊的规律，若为纯电阻电路，则可推导出E=IR+Ir或I=ER+r.这样建立闭合电路欧姆定律的过程是符合学生的认知特点和规律的，更有利于学生建立起相关的概念和规律.。
关于有出手高度的斜抛运动的最大射程分析
关于斜抛运动的最大射程宁强县第一中学贾银锁（724400）关于抛出点和落地点在同一水平面上的斜抛运动的最大射程问题，已经被众多的读者所熟知，也就是：当抛出角为45°时，水平射程最大，为。
但对抛出点和落地点不在同一水平面上的斜抛运动来说，抛出角满足什么条件时，水平射程最远？最远为多少？下面就以上两个问题与读者一起进行探讨。
如下图所示，设斜抛物体的初速度为，抛出点与落地点的水平高度差为H，令当斜抛运动的初速度与水平方向间的夹角为α时，水平射程X最大。
对初速度进行分解，然后由运动学规律不难可以得到以下两个式子：α消去①②中的α，得到整理③式得到从④式不难可以看出，当t=时 X最大，有即⑤又因为物体在空中下落的过程中，遵守机械能守恒定律，故有所以有⑥从①②式中可以得出将及带入上式得⑦由以上推导，可以得出从距水平地面高为H的小球以初速度V斜抛时：当初速度方向与水平方向间的夹角满足α=arctg时，小球的水平射程为最大，且最大射程为Xm=（其中V为物体落地时的速度，大小为）另外，以上结论也可以由动量定理加以证明：当V和H一定时，由机械能守恒定律得，物体落地时的速度必为定值因为小球在空中运动时只受重力的作用，由动量守恒定律得：小球从抛出到落地这段时间内，速度由初速度变化到，速度的变化量△V的方向一定在竖直向下的方向上，且满足上图的矢量关系（图中的为物体落地时的速度方向与水平方向间的夹角）设物体在空中的运动时间为t，水平射程为X，则由运动学知识及动量定理可得出下述两式：将②式中的t带入①中得到又因为而所以有由③④⑤三式得因为、及g均为定值，所以，当（α+β）=90°时，X有最大值，且为，而这一结论与上面的推导结论是完全一致的。
在此，可以得到从高出水平地面H处以初速度V0斜抛出的物体，当满足V的方向与水平面间的夹角α=arctg时，水平射程最大为，并且正好初速度的方向与落地时的末初速度的方向垂直（）。
运动学之斜抛物体的水平射程和竖直射高
2
v0 g
2
可见：当两个射角 互余时，物体的水 平射程相同。
v 0 sin (1 8 0 2 2 )
2
v 0 sin 2 2
2
g
g
g
X2
{范例1.6} 斜抛物体的水平射程和竖直射高
物体斜抛的初速度为v0，不计空气阻力，求物体的水平射 程和竖直射高与射角的关系。求证：物体轨迹的最高点都 分布在一个椭圆上。 水平 最大 X v 轨道 y x ta n g x v sin 2 X 2 v c o s 射程 g g 射程 方程 射高的横坐标是射程的一半，将 Y v sin y 2g x = X/2代入轨道方程可得射高 v0y v0 x O θ 射程与射高的 ta n 4 Y 上式代入Y X v0x 的公式得 坐标关系为 化简可得X2 + (4Y)2 – 2XM(4Y) = 0， v X tan ( 4Y / X ) Y 2 g 1 tan 2 1 ( 4 Y / X ) 配方得X2 + (4Y - XM)2 = XM2，
2
2
2
0
0
2
2
M
0
22ຫໍສະໝຸດ 0222
0
M
2
2
可得
( X / 2)
2 2
(Y X M / 4 ) ( X M / 4)
2
2
1
( X M / 2)
X/2是射高的横坐标。
可见：最高点分布在半长 轴为XM/2、半短轴为XM/4、 中心为(0,XM/4)的椭圆上。
射程随射角的增加 先增后减，射高随 射角的增加而增加。
五节斜抛物体的运动
斜抛运动的分解 斜抛运动的规律
射程与射高 弹道曲线
什么是斜抛运动 :
将物体用一定的初速度沿斜上方抛出去，
仅在重力作用下物体所做的运动叫斜抛运动。
举例： 踢出的足球；投出的标枪；射出的炮弹
斜抛运动的分解
V0y=V0 sinθ
V0
θ
V0x=V0 cosθ
水平方向：V0x=V0 cosθ做匀速直线运动 竖直方向： V0y=V0 sinθ做竖直上抛运动
表达式
飞行时间：T=2V0y/g=2V0sinθ/g
y
射程:X= V0xT=V0Tcos θ
射高:Y=
V
2 0y
/2g
V0
YXx*影响射因素：V0、射角θ弹道曲线
1、以相同的初速率和抛射角射出的炮弹 在空气中飞行的轨迹，这种曲线叫做弹 道曲线。
2、物体速率与空气阻力影响的关系：速 率越小，空气阻力影响的程度就越小。
3、弹道曲线特点：不对称，升弧长而平伸， 降弧短而弯曲。
作业
1、以初速度V0=30m/s、射角θ=300
求：X、Y、T
2、以初速度V0=30m/s、射角θ=300
求：X、Y、T
3、P24 3、4
斜抛运动的规律
1、任一时刻的分速度 Vx= V0x=V0cosθ Vy= V0y+at =V0sinθ-gt
2、任一时刻位置公式： x= V0t cos θ y= Voyt+1/2at2
a=-g
射程与射高
1、射程：在斜抛运动中，从物体被抛出 的地点到落地点的水平距离。
2、射高：从抛出点的水平面到物体运动轨 迹最高点的高度。 3、飞行时间：从物体被抛出到落地所用的 时间。
数理结合,五种方法求解斜面上抛体最远距离
数理结合，五种方法求解斜面上抛体最远距离题：从倾角为θ的斜面上O 点，以初速度V 0 水平抛出一个小球，落至斜面B 点。
求：从抛出开始经多长时间小球离斜面的距离最大？最大距离是多大？解法一：设小球抛出t 秒后，当速度方向与斜面平行时，小球离斜面的距离达到最大，此时小球速度方向与初速度方向成θ角。
根据“平抛运动任意时刻末速度的反向延长线经过水平位移的中点”。
设图中M 点为末速度反向延长线与水平位移的交点，线段MN 的长即为所求的最远距离H 。
解：当末速度方向与斜面平行时，物体离斜面距离最大,tan y y v v gt v θ==可得：0tan v t g θ=因为平抛运动中任意时刻末速度的反向延长线经过水平位移的中点。
所以2x OM =由几何关系可知最远距离： 200sin tan sin =sin sin 222v t v xH MN OM gθθθθθ====解法二：利用斜抛思想求解，将物体初速度v 0、重力加速度g 都分解成沿着斜面和垂直斜面方向的两个分量。
在垂直斜面方向上，物体做的是以v 0y 为初速度、g y 为加速度的类竖直上抛运动。
物体上升到顶端的时间等于它从抛出至离斜面最远的运动时间。
可得:00sin tan t=cos oyy v v v g g gθθθ==物体在垂直于斜面方向“上升”的最大高度20000sin tan tan sin =222y v tv v v H g gθθθθ==解法三：以抛出点O 为坐标原点，建立图示水平竖直坐标系斜面直线方程为()tan h x x θ= 抛体轨迹方程为22220011()222x g h gt g x v v ===（下同） 抛物线上某点00(,)p x h 的导函数为该点处的切线斜率，当切线与斜面平行时，该点距斜面最远2'()22gh x x v =0020'()2tan 2gh x x v θ==200tan v x gθ=42220000220tan tan ()22v v g h h x v g gθθ===所以离斜面tan 0x h θ-=距离最远的点为22200tan tan (,)2v v p g gθθ利用点到直线距离公式可得：20tan sin 2v H gθθ==解法四：设抛物线上某点00(,)p x h 距斜面最远，其切线与斜面平行20'()22gh x x v = 002=h '()22gk x x v =切 200tan v x gθ=可得：000tan x v t v gθ==42220000220tan tan ()22v v g h h x v g gθθ===抛物线上点00(,)p x h 的切线方程为：00)h h k x x -=-切（22200tan tan tan ()2v v h x g gθθθ-=-xx222200tan tan tan 2v v h x g gθθθ-=-可得切线方程：220tan tan 02v x h gθθ--= 与斜面tan 0x hθ-=的距离为：20tan sin 2v H g θθ==解析五：抛物线上任意一点00(,)p x h 到直线tan 0x h θ-=的距离为：H ==H =0x =当点(p 020tan sin =2v H g θθ=以上解法，各有所长，解法一、二突出了物理过程的理解与应用，其余解法展示了学生扎实的数学基本功，体现了数学知识在物理学习上的应用，起到了相辅相成的作用。