4 多组分系统热力学
物理化学：第4章_多组分系统热力学_
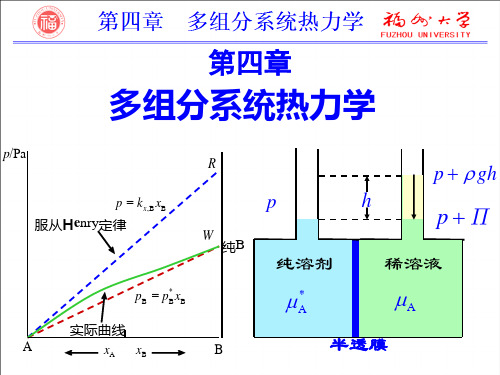
真实混合物：实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时，两组 分偏摩尔体积随之改变，且二者 变化相互关联。
组成接近某纯组分，其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分：
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面，由加和公式
，恒温恒压下求导：
比较两式，得
或
或
吉布斯-杜亥姆方程－－在一定温度压力下，当混合物
组成变化时，各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立，而是相 互依存的。
➢ 例：固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件：该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移， 直至物质迁移达平衡时为止，此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0：自发不可逆； =0：平衡、可逆
任一化学反应，假定系统已处于相平衡，
任一组分B在每个相中的化学势都相等： Bα B
B
B
整个系统中B组分物质的量的变化量： dnBα dnB
α
BdnB
B
化学平衡时
平衡条件：与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
hx04多组分系统热力学
VB def
V n B T , p,nC(CB)
U B def
U n B T , p,nC(CB)
H B def
H n B T , p,nC(CB)
SB def
S n B T , p,nC(CB)
AB def
A n B T , p,nC(CB)
GB def
G n B T , p,nC(CB)
上一内容 下一内容 回主目录
返回
2024/7/4
4.2.2 偏摩尔量的定义
(4) 偏摩尔量是两个广度性质X、nB之比，因此它是一强度性质，与体积的量无关。
上一内容 下一内容 回主目录
返回
2024/7/4
4.2.3 偏摩尔量的加和公式
已知
k X
dX
B=1
nB
T , p,nC(CB)
dnB
量和除B以外的其他组分不变时，热力学函数对B 物质的量求偏导。
上一内容 下一内容 回主目录
返回
2024/7/4
4.3.2 化学势的定义
把化学势的广义定义代入热力学函数的微分式：
dU TdS pdV BdnB B
dH TdS Vdp BdnB B
dA SdT pdV BdnB B
溶剂，含量少的称为溶质。
上一内容 下一内容 回主目录
返回
2024/7/4
4.1.2 多组分系统的组成表示法
1. B的物质的量浓度
cB def
nB V
溶质 B 的物质的量与溶液体积V 的比
值称为溶质 B 的物质的量浓度，或称为溶
质 B 的浓度.
物质的量浓度的单位 mol ×m-3
或
mol ×dm-3
南京大学物理化学(第五版)04章_多组分系统热力学
(
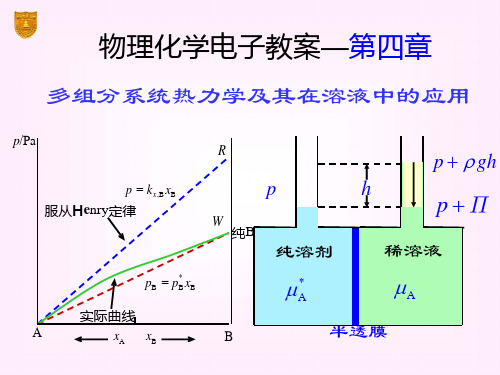
Gm p
)T
Vm
对多组分系统，把 Gm 换为 B ，则摩尔体积变为偏
摩尔体积 VB 。
化学势与温度的关系
(
B
T
)
p
,nB
,
nc
[ T
G ( ) ] T , p,nc p,nB ,nc nB
[ nB
G ( T ) p,nB ,nc ]T , p,nc
(S) [ nB ]T , p,nc
nk 0
dnk
k
n1Z1 n2 Z2 nk Zk nBZB B=1
偏摩尔量的加和公式
k
Z= nB ZB
B=1
这就是偏摩尔量的加和公式，说明系统的总 的容量性质等于各组分偏摩尔量的加和。
例如：系统只有两个组分，其物质的量和偏 摩尔体积分别为 n1,V1 和 n2 ,V2 ，则系统的总体积为：
（1）热力学能
设系统中有 1, 2,3, , k 个组分
所含的量分别为 n1, n2, , nk
U U (S,V , n1, n2, , nk )
化学势的定义
U U (S,V , n1, n2, , nk )
其全微分为
dU
U ( S )V ,nB dS
(
U V
)
S
,nB
dV
k U B1 ( nB )S ,V ,nc(cB) dnB
如果转移是在平衡条件下进行，则
dG 0 又
dnB dnB
所以 (B B )dnB 0
化学势在相平衡中的应用
(B B )dnB 0
因为 dnB 0 所以
B B
组分B在α，β两相中，达平衡的条件是该
大学物理化学--第四章
混合物（mixture）：对系统中的各组分采用同样 的标准态和研究方法，系统中的各组分是平等的。
溶液（solution）： 各组分区分为溶剂（solvent） 和溶质（solute ），并对二者采用不同的标准态和研 究方法；系统中的各组分是不平等的。
偏摩尔量
XB
(
X nB
)T
,
p
,
，下标必须是
nC
T
,
p。, nC
只有广度量才有偏摩尔量（质量除外）。
偏摩尔量是强度量。
偏摩尔量随温度、压力、组成（浓度）变化而变， 与系统的总量无关。
上一内容 下一内容 回主目录
返回
2020/8/23
§4.1 偏摩尔量
偏摩尔量的加和公式
X nB X B
B
它的含义是：在一定温度、压力下，一定组成混合
物理化学电子教案—第四章
多组分系统热力学
上一内容 下一内容 回主目录
返回
2020/8/23
第四章 多组分系统热力学
目录
§4.1 偏摩尔量 §4.2 化学势 §4.3 气体组分的化学势 §4.4 逸度及逸度因子 §4.5 拉乌尔定律和亨利定律 §4.6 理想液态混合物 §4.7 理想稀溶液
§4.8 活度及活度因子 §4.9 稀溶液的依数性
标准态 kb,B ( p p )
实际溶液 pB - bB 关系曲线
pB
O
b
上一内容 下一内容 回主目录
bB
返回
2020/8/23
4.7 理想稀溶液
理想稀溶液中溶质的化学势
B(溶 质)
0 B(溶 质)
物理化学 第四章 多组分系统热力学
Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B，C形成真实液态混合物： 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时，两组分的偏摩尔体积可用下法表示： 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线，此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB，VC。
B
系统中各广度量的偏摩尔量： 对于多组分系统中的组分B，有： 偏摩尔体积： VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能： UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓： HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵： SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数：AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数： GB=(ƽG/ƽnB)T,p,n
C
几点说明： (1)偏摩尔量为两个广度性质之比，所以为强度 性质； (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下，偏导数式的下标为T，p 时才是偏摩尔量； (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中，偏摩尔量不同； (4)若系统为单组分系统，则该组分的偏摩尔量 与该组分的摩尔量相等，即： XB=X*B，m
C
=VB (数学知识：二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势，用符号μB表示：
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质，其化学势等于它的摩尔吉布斯函 数。
第四章 多组分系统热力学及其在溶液中的应用
第四章 多组分系统热力学及其在溶液中的应用1.在298K 时，有0.10kg 质量分数为0.0947的硫酸H 2SO 4水溶液，试分别用（1）质量摩尔浓度B m ；（2）物质的量浓度和B c （3）摩尔分数B x 来表示硫酸的含量。
已知在该条件下，硫酸溶液的密度为331.060310kg m -⨯⋅ ，纯水的浓度为3997.1kg m -⋅ 。
解：质量摩尔浓度：()2410.19.47%/1009.47%0.1981.067mol H SO B n m W kg -⨯==-⨯=⋅水物质量浓度：()24331009.47%0.10.19.47%/98997.11.02310mol H SO B n c V m --⨯⨯===⨯g 水 摩尔分数：242420.0189H SO B H SO H On x n n ==+2、在K 298和大气压力下，含甲醇()B 的摩尔分数B x 为0.458的水溶液密度为30.8946kg dm -⋅，甲醇的偏摩尔体积313()39.80V CH OH cm mol -=⋅，试求该水溶液中水的摩尔体积2()V H O 。
解：3322CH OH CH OH H O H O V n V n V =+3322CH OH CH OHH O H OV n V V n -=以1mol 甲醇水溶液为基准，则330.45832(10.458)180.027290.894610m V dm ρ⨯+-⨯===⨯ ∴23310.027290.45839.801016.7210.458H OV cm mol ---⨯⨯==⋅-3.在298K 和大气压下，某酒窖中存在酒10.0m3，其中含乙醇的质量分数为0.96。
今欲加水调制含乙醇的质量分数为0.56的酒，试计算（1）应加入水的体积；（2）加水后，能得到含乙醇的质量分数为0.56的酒的体积已知该条件下，纯水的密度为3997.1kg m -⋅，水和乙醇的偏摩尔体积为()25C H OH ω()()6312/10V H O m mol --⋅()()63125/10V C H OH m mol --⋅0.96 14.61 58.0 0.5617.1156.58解：设加入水的物质的量为O H n 2'，根据题意，未加水时，2520.9610.96::9.3914618C H OH H O n n -== 2525221C H OHC H OH H O H O V n V n V =⋅+⋅ 即 661001.581061.1410522--⨯⨯+⨯⨯=OH H C O H n n解出：25167882C H OH n mol =217877H O n mol = 加入水后，25220.5610.56:():0.4984618C H OH H O H O n n n -'+== 20.5610.56167882:(17877):0.4984618H O n -'+==2'317887H On mol = 加入水的物质的体积为23331788718105.727()999.1H O V m -⨯⨯'== 2525222252'26'6()56.5810(17877)17.1110C H OH C H OH H O H OH OC H OH H OV n V n n V n n --=++=⨯⨯++⨯⨯329.4984495 5.76753115.266V m =+=4.在K 298和kPa 100下，甲醇)(B 的摩尔分数B x 为30.0的水溶液中，水)(A 和甲醇)(B 的偏摩尔体积分别为：132765.17)(-⋅=mol cm O H V ，133632.38)(-⋅=mol cm OH CH V 。
第四章、多组分系统热力学
第四章，多组分系统热力学一、选择题1. 在 298K 时，A 和 B 两种气体单独在某一溶剂中溶解，遵守亨利定律，亨利常数分别为 kA 和 KB，且知 KA>KB，则当 A 和 B 压力（平衡时的）相同时，在一定量的该溶剂中所溶解的关系为 ( ) B (A) A 的量大于 B 的量 (B) A 的量小于 B 的量(C) A 的量等于 B 的量 (D) A 的量与 B 的量无法比较2. 在 400K 时，液体 A 的蒸气压为 4×104Pa，液体 B 的蒸气压为 6×104Pa，两者组成理想液体混合物，平衡时，溶液中 A 的物质的量分数为 0.6，则气相中 B 的物质的量分数为： ( ) B(A) 0.60 (B) 0.50 (C) 0.40 (D) 0.313. 已知挥发性纯溶质 A 液体的蒸气压为 67 Pa，纯溶剂 B 的蒸气压为 26665Pa，该溶质在此溶剂的饱和溶液的物质的量分数为 0.02，则此饱和溶液（假设为理想液体混合物）的蒸气压为：( ) C(A) 600 Pa (B) 26198 Pa (C) 26133 Pa (D) 599 Pa4. 已知 373.2K 时，液体 A 的饱和蒸气压为 133.32 kPa，另一液体 B 可与 A构成理想液体混合物。
当 A 在溶液中的物质的量分数为 0.5 时，A 在气相中的物质量分数为 2/3 时，则在 373.2K时，液体 B 的饱和蒸气压应为： ( ) A(A) 66.66 kPa (B) 88.88 kPa (C) 133.32 kPa (D) 266.64 kPa5. 已知 373K 时液体 A 的饱和蒸气压为 133.24kPa,液体 B 的饱和蒸气压为66.62kPa。
设 A 和 B形成理想溶液,当 A 在溶液中的摩尔分数为 0.5 时,在气相中 A 的摩尔分数为： ( ) D(A) 1 (B) 1/2 (C) 1/3 (D) 2/36. 关于亨利系数,下列说法中正确的是： ( ) D(A) 其值与温度、浓度和压力有关(B) 其值与温度、溶剂性质和浓度有关(C) 其值与温度、溶质性质和浓度有关(D) 其值与温度、溶质和溶剂性质及浓度的标度有关7. 已知 373K 时，液体 A 的饱和蒸气压为 5×104 Pa，液体 B 的饱和蒸气压为 105Pa，A 和 B构成理想液体混合物，当 A 在溶液中的物质的量分数为 0.5时，气相中 B 的物质的量分数为：( ) A(A) 1/1.5 (B) 1/2 (C) 1/2.5 (D) 1/38.2molA物质和3molB物质在等温、等压下，混合形成理想液态混合物，该系统中A和B的偏摩尔体积分别为1.79×10-5m3×mol-1，2.15×10-5m3×mol-1，则混合物的总体积为：（） C(A)9.67×10-5m3 (B)9.85×10-5m3(C)1.003×10-4m3 (D)8.95×10-5m39.298K，标准压力下，苯和甲苯形成理想液态混合物。
物理化学第四版 第四章 多组分系统热力学2014.2
)
p,n
(
B
)
,V
(
G P
)T
,n(
B
)
k
dG SdT VdP BdnB
证毕
B 1
14
又 dA d(G PV ) dG pdV Vdp
将上式dG 代入，整理得：
k
dA sdT PdV BdnB ……..(3) B 1
同理可得出另二个热力学基本方程。
因 A=A(T,V,n1,n2…….nk)
B
B
B
........
n B
相平衡条件
有N 个组分，就有N 个这样的式子
19
例：在、 两相中均含有A和B两种物质，达到相平衡时，下列
各式正确的是（
）。
A、
A
B
B、
B
B
C、
A
B
D、
B
A
例：组分B从相扩散入相中，则以下说法正确的有（ A、总是从浓度低的相扩散入浓度高的相 B、平衡时两相浓度相等 C、总是从化学势高的相移向低化学势低的相
dA
(
A T
)V
,n
(
B
)
dT
( A V
)T ,n(B)
dV
k B 1
(
A n(B)
)T
,V
,n
(
c,c
B)
dnB
将式（4）和式（3）比较
B
A ( nB
)T ,V ,n(c,cB)
同样可得出
B
U ( nB
)S ,V ,n(c,cB)
H ( nB
)S ,P.n(c,cB)
…..(4)
15
例 2： 下列偏导数中那些是偏摩尔量?那些是化学势?
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
( p p* H 2 O ) 0.40 (105.4 7.33) 0.40kPa 39.23kPa
p N2 p p * H 2 O p H 2 (105.4 7.33 39.23) kPa 58.84kPa
M H 2 2.0158, x H2 pH2 k x,H2 M N 2 28.0134 mH2 / M H 2 m H 2O / M H 2O m H 2 / M H 2 m N 2 / M N 2 mH 2 / M H 2 m H 2O / M H 2O
* p甲苯 y苯
p p
* 苯
* 甲苯
y苯 p y苯
* 苯
38.7 0.3 0.142 ； x甲苯 1 x苯 0.858 100 38.7 0.3 100 0.3
4-6 在 18℃，气体的压力为 101.325kPa 下，1dm3 的水中能 溶解 O20.045g，能溶解 N20.02g。现 1dm3 将被 202.65kPa 空气饱 和了的水溶液加热沸腾，赶出所溶解 O2 的和 N2，并干燥之，求此 干燥气体在 101.325kPa、18℃下的体积及组成。设空气为理想 气体混合物，其组成（体积百分数）为： (O 解： M
x 2 d 2 RTdx2 x1 d 1 x 2 d 2
x 1 d 1 RTdx 2 RTd (1 x1 ) RTdx1
d1 RTdx1 / x1
1
1
d 1 RT d ln x1
x1 1
x1
1 1 RT ln x1 1 ( pg ) RT ln( p1* / p ) RT ln x1 1 1 ( pg ) RT ln( p1 / p )
p N 2 m H 2O M N2 k x, N M H 2O
2
4-9 试用吉布斯-杜亥姆方程证明在稀溶液中溶质服从亨利定 律，则溶剂服从拉乌尔定律。 证：p2=kx，2x2
d 2 RTdx2 / x2
2 x , 2 RT ln x 2
（恒温、恒压）
(恒温、恒压) 联立得： (恒温、恒压)
4-5
80℃时纯苯的蒸气压为 100kPa，纯甲苯的蒸气压为
38.7kPa。两液体可形成理想液态混合物。若有苯-甲苯的气-液 平衡混合物，80℃时气相中苯的摩尔分数 y 苯=0.300，求液相的 组成。 解： x
x苯
苯
py苯
* p苯
* * （ 1 x苯） p苯 x苯 p甲苯 y苯 * p苯
O2
2
) 21%， ( N 2 ) 79%。
31 .9988,
M N 2 28.0134
p O2 k c , O 2 c O2 k c , O 2 k c , O2 k c, N2 p O2 V 液 M O2 m O2 p N 2 V液 M N 2 mN2
4-3 在 25℃、1kg 水（A）溶解有醋酸（B） ，当醋酸的质量 摩尔浓度 bB 介于 0.16 和 2.5mol·kg-1 之间时，溶液的总体积 V/cm3=1002.935+51.832× （ bB/ mol·kg-1 ） +0.1394 （ bB/ mol·kg-1）2。 （1）把水（A）和醋酸的偏摩尔体积分别表示成 bB 的函数关系式； （2）求 bB =1.5 mol·kg-1 时水和醋酸的偏摩尔体 积。 解： （1）V
B
B
WB / M B 0.095 / 180 0.0104 WB / M B (1 WB ) / M B 0.095 / 180 0.905 10 3 mol dm 3 0.547mol dm 3 1 / 1.0365
B
0.095 / 180 10 3 mol kg 1 0.583mol kg 1 (1 0.095) / 1000
B
(V / n B ) T , p ,nC nB (V / b B ) T , p , n A 55.5 mol
={51.832+0.2788 bB/ mol·kg-1} cm3·mol-1
V VB n B V A n A V B bB / kg 1 V A VA V VB bB / kg 1 55.5mol 1000 mol 18.015 1002.935 0.1394(bB / mol kg 1 ) 2 cm 3 mol 1 55.5
cB cB ( nB M B / V ) ( cB M B ) cB cB MA MA
式中 ρ 为溶液的密度，单位为 kg·m-3；A 代表溶剂。 而物质 B 的质量摩尔浓度则是溶液中溶质 B 的物质的量除以 溶剂的质量即
bB nB mA
其单位为 mol·kg-1。在二组分溶液中溶质 B 的摩尔分数 xB 与质 量摩尔浓度 bB 的关系为
4-7
20℃下 HCl 溶于苯中达平衡，气相中 HCl 的分压为
101.325kPa 时，溶液中 HCl 的摩尔分数为 0.0425，已知 20℃时 苯的饱和蒸气压为 10.0kPa。若 20℃时 HCl 和苯蒸气总压为 101.325kPa，求 100g 苯中溶解多少 HCl。 解： k
x , HCl
m O2 V 液 M O2 101.325 1 31.9988 kPa dm 3 mol 1 72.05 10 3 kPa dm 3 mol 1 0.045 101.325 1 28.0134 kPa dm 3 mol 1 14.19 10 4 kPa dm 3 mol 1 0.02
比较上述两式可得
p1 p1* x1
4-10 A、B 两液体能形成理想液态混合物。已知在 t 时纯 A 的饱和蒸气压 p =400kPa，纯 B 的饱和蒸气压 p =120kPa。
* A * B
（1）在温度 t 下，于气缸中将组成为 y（A）=0.4 的 A、B 混
合气体恒温缓慢压缩， 求凝结出第一滴微细液滴时总压及该液滴 的组成（以摩尔分数表示）为多少？ （2）若将 A、B 两液体混合，并使此混合物在 100kPa、温度 t 下开始沸腾，求该液态混合物的组成及沸腾时饱和蒸气的组成 （摩尔分数）？ 解： （1） p
∴
mH 2 mN2
p H 2 m H 2O M H 2 k x , H M H 2O
2
39.23 100 2.0158 g 60.6g 7.24 10 6 18.015 58.84 100 28.0134 g 871g 10.5 10 6 18.015
MHCl=34.461， M 苯=78.113，W 苯=100g XHCl=（mHCl/ MHCl）/{（mHCl/ MHCl）+（m 苯/ M 苯）} 所以 4-8
mHCl 36.41 100 0.03847 1.867 g M苯 （1 x HCl） 78.113 （1 0.03847） M HCl m苯 x HCl
第四章
多组分系统热力学
4-1 由溶剂 A 与溶质 B 形成一定组成的溶液。此溶液中 B 的 浓度为 cB，质量摩尔浓度为 bB，此溶液的密度为 ρ。以 MA，MB 分别代表溶剂和溶质的摩尔质量， 若溶液的组成用 B 的摩尔分数 xB 表示时，试导出 xB 与 cB，xB 与 bB 之间的关系式。 解:对于 A， B 二组分溶液， 溶液中物质 B 的物质的量 nB 与溶 液的物质的量之比，称为物质 B 的摩尔分数，符号 xB 。即
所以
V nRT / p (n O2 n N 2 ) RT / p {(5.907 11.28) 10 4 8.314 291.15 / 101325}m 3 41.1cm 3 y O2 n O2 /( nO2 n N 2 ) 5.907 /(5.907 11.28) 0.344 y N 2 1 y O2 0.656
气压是 47.0kPa。二者可形成理想液态混合物，若混合物的组成 为质量百分数各 50%，求 60℃时此混合物的平衡蒸气组成，以摩
尔分数表示。 解：M 甲醇=32.042，M 乙醇=46.069
x甲醇 50 / 32.042 0.58979 ； 50 / 32.042 50 / 46.069
p HCl / x HCl (101 .325 / 0.0425)kPa 2384 kPa
* p p苯 p HCl p苯 （ 1 x HCl） k x，HCl x HCl
x HCl
* p p苯 * k x，HCl p苯
101.325 10.0 0.03847 2384 10.0
={18.0681-0.0025（bB/ mol·kg-1）2} cm3·mol-1 （ 2 ） VA= （ 18.0681-0.0025×0.152 ） cm3·mol-1=18.0625 cm3·mol-1 VB=（51.832+0.2788×0.15）cm3·mol-1=52.25 cm3·mol-1 4-4 60℃时甲醇的饱和蒸气压是 83.4kPa，乙醇的饱和蒸
xB nB / m A bB bB n B / m A n A / m A bB n A /(n A M A ) bB 1 / M A
4-2 D-果糖 C6H12O6（B）溶于水（A）中形成的某溶液，质量
分数 WB=0.095，此溶液在 20℃时的密度 ρ=1.0365Mg·m-3。求此 果糖溶液的（1）摩尔分数； （2）浓度； （3）质量摩尔浓度。 解： （1） x （2） c （3） b
* p甲醇 p甲醇 x甲醇 83 .4 0.58979 49 .19 kPa