西北工业大学《电磁场和电磁波》课后习题
《电磁场与电磁波》课后习题解答(第五章)

《电磁场与电磁波》课后习题解答(第五章)————————————————————————————————作者:————————————————————————————————日期:习题及参考答案5.1 一个点电荷 Q 与无穷大导体平面相距为d ,如果把它移动到无穷远处,需要作多少功?解:用镜像法计算。
导体面上的感应电荷的影响用镜像电荷来代替,镜像电荷的大小为-Q ,位于和原电荷对称的位置。
当电荷Q 离导体板的距离为x 时,电荷Q 受到的静电力为2)2(042x Q F επ-=静电力为引力,要将其移动到无穷远处,必须加一个和静电力相反的外力2)2(042x Q f επ=在移动过程中,外力f 所作的功为d Q d dx dx Q dx f 016220162επεπ=⎰∞⎰∞= 当用外力将电荷Q 移动到无穷远处时,同时也要将镜像电荷移动到无穷远处,所以,在整个过程中,外力作的总功为dq8/2επ。
也可以用静电能计算。
在移动以前,系统的静电能等于两个点电荷之间的相互作用能:d Q d Q Q d Q Q q q W 082)2(04)(21)2(042122211121επεπεπϕϕ-=-+-=+=移动点电荷Q 到无穷远处以后,系统的静电能为零。
因此,在这个过程中,外力作功等于系统静电能的增量,即外力作功为dq8/2επ。
5.2 一个点电荷放在直角导体内部(如图5-1),求出所有镜像电荷的位置和大小。
解:需要加三个镜像电荷代替 导体面上的感应电荷。
在(-a ,d )处,镜像电荷为-q ,在(错误!链接无效。
)处, 镜像电荷为q ,在(a ,-d )处,镜像电荷为-q 。
图5-1 5.3 证明:一个点电荷q 和一个带有电 荷Q 、半径为R 的导体球之间的作用力为]2)22(2[04R D DRq D D qR Q q F --+=επ其中D 是q 到球心的距离(D >R )。
证明:使用镜像法分析。
电磁场与电磁波课后习题与答案七章习题解答(2)

《电磁场与电磁波》习题解答 第七章 正弦电磁波7.1 求证在无界理想介质内沿任意方向e n (e n 为单位矢量)传播的平面波可写成j()e n r t m βω⋅-=e E E 。
解 E m 为常矢量。
在直角坐标中故 则 而 故可见,已知的()n j e r t m e βω⋅-=E E 满足波动方程 故E 表示沿e n 方向传播的平面波。
7.2 试证明:任何椭圆极化波均可分解为两个旋向相反的圆极化波。
解 表征沿+z 方向传播的椭圆极化波的电场可表示为 式中取显然,E 1和E 2分别表示沿+z 方向传播的左旋圆极化波和右旋圆极化波。
7.3 在自由空间中,已知电场3(,)10sin()V/my z t t z ωβ=-E e ,试求磁场强度(,)z t H 。
解 以余弦为基准,重新写出已知的电场表示式这是一个沿+z 方向传播的均匀平面波的电场,其初相角为90︒-。
与之相伴的磁场为 7.4 均匀平面波的磁场强度H 的振幅为1A/m 3π,以相位常数30rad/m 在空气中沿z -e 方向传播。
当t=0和z=0时,若H 的取向为y -e,试写出E 和H 的表示式,并求出波的频率和波长。
解 以余弦为基准,按题意先写出磁场表示式 与之相伴的电场为由rad/m β=30得波长λ和频率f 分别为 则磁场和电场分别为7.5 一个在空气中沿ye +方向传播的均匀平面波,其磁场强度的瞬时值表示式为(1)求β和在3ms t =时,z H =的位置;(2)写出E 的瞬时表示式。
解(1)781π10πrad /m rad /m 0.105rad /m 31030β==⨯==⨯在t =3ms 时,欲使H z =0,则要求 若取n =0,解得y =899992.m 。
考虑到波长260mπλβ==,故因此,t =3ms 时,H z =0的位置为(2)电场的瞬时表示式为7.6 在自由空间中,某一电磁波的波长为0.2m 。
当该电磁波进入某理想介质后,波长变为0.09m 。
电磁场和电磁波课后习题答案与解析__第四章习题解答
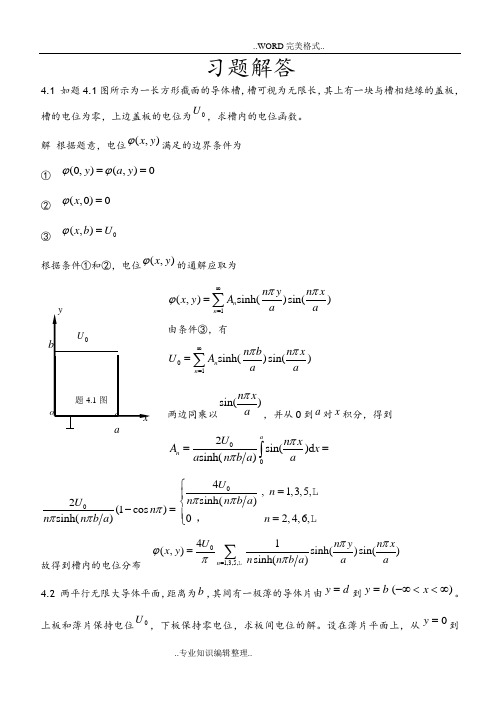
习题解答4.1 如题4.1图所示为一长方形截面的导体槽,槽可视为无限长,其上有一块与槽相绝缘的盖板,槽的电位为零,上边盖板的电位为U ,求槽内的电位函数。
解 根据题意,电位(,)x y ϕ满足的边界条件为① (0,)(,)0y a y ϕϕ== ② (,0)0x ϕ=③0(,)x b U ϕ=根据条件①和②,电位(,)x y ϕ的通解应取为1(,)sinh()sin()n n n y n xx y A a a ππϕ∞==∑由条件③,有01sinh()sin()n n n b n x U A a a ππ∞==∑两边同乘以sin()n x a π,并从0到a 对x 积分,得到002sin()d sinh()an U n xA x a n b a aππ==⎰02(1cos )sinh()U n n n b a πππ-=04,1,3,5,sinh()02,4,6,U n n n b a n ππ⎧=⎪⎨⎪=⎩,故得到槽内的电位分布1,3,5,41(,)s i n h ()s i n ()s i n h ()n U n yn xx y n n b a aa ππϕππ==∑4.2 两平行无限大导体平面,距离为b ,其间有一极薄的导体片由d y =到b y =)(∞<<-∞x 。
上板和薄片保持电位U ,下板保持零电位,求板间电位的解。
设在薄片平面上,从0=y 到d y =,电位线性变化,0(0,)y U y d ϕ=。
解 应用叠加原理,设板间的电位为(,)x y ϕ=12(,)(,)x y x y ϕϕ+其中,1(,)x y ϕ为不存在薄片的平行无限大导体平面间(电压为U )的电位,即10(,)x y U y b ϕ=;2(,)x y ϕ是两个电位为零的平行导体板间有导体薄片时的电位,其边界条件为: ①22(,0)(,)0x x b ϕϕ==②2(,)0()x y x ϕ=→∞③002100(0)(0,)(0,)(0,)()U U y y d by y y U U y y d y b d b ϕϕϕ⎧-≤≤⎪⎪=-=⎨⎪-≤≤⎪⎩根据条件①和②,可设2(,)x y ϕ的通解为 21(,)sin()en x bn n n y x y A b ππϕ∞-==∑由条件③有00100(0)sin()()n n U U y y d n y b A U U b y yd y b d b π∞=⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩∑两边同乘以sin()n yb π,并从0到b 对y 积分,得到0002211(1)sin()d ()sin()d dbn d U U y n y n y A y y y b b b b d b b ππ=-+-=⎰⎰022sin()()U b n d n d b ππ故得到(,)x y ϕ=0022121sin()sin()e n x bn U bU n d n y y b d n b b ππππ∞-=+∑ 4.3 求在上题的解中,除开0U y 一项外,其他所有项对电场总储能的贡献。
《电磁场和电磁波》课后习题解答(第一章)

第一章习题解答【习题Ll解】【习题L2解】【习题L3解】(1)要使ALR,则须散度A-B=O所以从Z∙5=T+3H8c=0可得:3b+8c=l即只要满足3b÷8c=l就可以使向量二和向量了垂直。
(2)要使4||月,则须旋度AxB=O所以从可得b=-3,c=-8【习题1・4解】A=I2以+9e y+6z,B=CIeX+be y,因为3JLA,所以应有A∙3=0g∣j(12久+9e y+e z^∙^ae x+Z?Gy)=12Q+9/?=0(I)又因为同=1;所以病存=1;(2)一4由⑴,⑵解得Q=±《,"=+W【习题1.5解】由矢量积运算规则4_B=A?C a x a2a3=(%Z-+(a3x-a x z)e y+(01y-a2x)e7xyz =8名+纥5+BZeZ取一线元:dl=e x dx+e y dy+e z dz则有dx_dy_dz则矢量线所满足的微分方程为丁二万一=Hιy xy"z或写成=常数)a2z-a3ya3x-a l za↑y-a2x求解上面三个微分方程:可以直接求解方程,也可以采用以下方法d(qx)="(/丁)二d(%z)a i a2z-a i a3ya2a3x-a l a2za l a3y-a2a i xxdx_ydy_ZdZx(a2z-a3y)y{a3x-a x z)z(a l y-a2x)由(1)(2)式可得d(a2y)=k(a2a3x-aλa2z)ydy=k(a3xy-a}yz)(4)对⑶⑷分别求和所以矢量线方程为【习题L6解】矢量场A=(αxz+x2)eχ+Sy+孙2)0+{z-z1-∖-cxz-2xyz)e z假设A是一个无源场,则应有divΛ=O即:divA=V•4=空L+空L+空■=O∂x∂y∂z因为A=axz+X2∕ξ=by+xy1A z=z-z1+cxz-2xyzx所以有divA=az+2x+b+2xy+l-2z+cχ-2xy=X(2+c)÷z(a-2)+b+l=0 得a=2,b=-1,c=-2【习题1.7解】设矢径r的方向与柱面垂直,并且矢径不到柱面的距离相等(r=a)f∙ds-[rds=a∖ds=a2πah所以,①=S JSJS【习题1.8解】φ=3X2y i A=X2yze v+3xy2e^而rot((∕A)=Vx(以)=×A÷V^×A又=巴?十3?+再等=6xye x+3jc2e y ox-oy∂z所以+9x3y2e v-lSx2y3e v+6x3y2ze z=3X2y2[(9X一X2)e x-9yeγ+4xze z]【习题1.9解】所以&CyCzrotA=VXA=———∂x∂y∂zA x A y A(-1+1)&+(4/Z-4xz)e、+(2y-2y)&=6由于场H的旋度处处等于0,所以矢量场A为无旋场。
西北工业大学《电磁场和电磁波》课后习题

或者 F , sin sin 六 解: 1)
cos sin 2 2
Sav
1 2 Em 100 2 m
w 2 10 7
Em 274.6 v
k1 w 0 0
15
E1 274.6 cos 2 10 7 t z a x v m 15 H1 0.728 cos 2 10 7 t z a y A m 15
2)
2 1 1 = 2 1 3
T
2 2 2 2 1 3 2 15
k2
j z ˆx E1 Em e jk1 z ax 91.5e 15 a
2 j z jk 2 z ˆx E2 TEm e a x 183e 15 a
R2 R3
2 2 2
2
v E1dr E2 dr
R1 R2
s 2 1 1 s 2 1 1 R1 R R R1 R R 3 0 2 0 3 1 2
C
Q 12 0 1 2 3 V R1 R2 R3
E E 1 E 2 j
I 0l e jkr 0 sin sin cos sin r 2
I 0l e jkr H j sin sin cos sin r 2
2) 方向性函数
F , sin sin cos sin 2
空间 P 点的电位:
( x, y , z )
其中:
q q q q , 4 0 r1 4 0 r2 4 0 r3 4 0 r4
r1 x 2 y 2 ( z d ) 2
2009B-2西北工业大学《电磁场和电磁波》课后习题

(1 分) (2 分) (2 分)
ˆ Er = −10e jkz ax 1 jkz ˆ Hr = e ay 12π
(3)总场
ˆ E = 20sin kz sin ωtax H=
(4)电流
20
η
ˆ cos kz cos ωta y(4 分)ˆ J = n × Hz =0
=
20
η
ˆ cos(109 t )ax
π
(2 分) (2 分)
(2)方向性函数:
cos( cos θ ) π 2 F (θ , ϕ ) = cos( sin θ cos ϕ ) sin θ 4
π
(2 分)
1 d 2φ = −k x2 2 X ( x) dx
变量分离得:
1 d 2φ 2 = −k y 2 Y ( y ) dy
2 k x2 + k y = 0
由边界条件得方程的解为: nπ nπ (4 分) φ = Cn sh[ ( x + a )]sin( y ) n = 1, 2, b b ∞ nπ nπ φ ( x, y ) = ∑ Cn sh[ ( x + a )]sin( y ) 则: (1 分) b b n =1 ∞ 2anπ nπ 3π φ ( a, y ) = ∑ Cn sh sin( y ) = 10 sin( y) 由 b b b n =1 得:
三解(10 分)(1)该区域无源,电位函数满足拉普拉斯方程 :
∂ 2φ ∂ 2φ + =0 ∂x 2 ∂y 2
其边界条件为:
(1 分)
φ =0 φ =0 φ =0
0 ≤ x < ∞, y = 0
(1 分)
0 ≤ x < ∞, y = b x = − a, 0 < y < b 3π φ = 10sin( y ) x = a, 0 < y < b b
西北工业大学《电磁场和电磁波》课后习题

y > 0, ε2 = 9 pF / m, µ2 = 4µ H / m, σ 2 = 0 。 在 区 域 I 内 , 一 极 化 方 向 为 aˆz ,
ω = 108 rad / s 的平面电磁波振幅为 500V/m,垂直投射到 y = 0 的边界面上,求:
v 1. 入射波 Ei ;
v 2. 反射系数 Γ 和反射波 Er ;
二、(15 分)球形电容器内外导体球之间填充介电常数为 3ε0 的介质,如图 1 所示。设内球上
面电荷密度为 ρs ,求:
1. 各区域的电位移矢量和电场强度; 2. 内外导体之间的电压; 3. 此电容器的电容。
三、(10 分)一点电荷 Q 位于两个半无限大接地导体平面形成的直角形区域内的 A 点(如图 2 所示),求区域内任一点 P 处的电位。
成 2004-2005 学年 第一学期
绩
开课学院 电子信息学院 课程 电磁场与电磁波 学时 考试日期 2004 年 12 月 16 日 考试时间 2 小时
54 开A
考试形式(闭 )( B )卷
考生班级
学号
姓名
[注: ε0
=
1 36π
×10−9
F
/
m
µ0 = 4π ×10−7 H / m ]
一、简答题(25 分)
教务处印制
第2页共2页
2. 命题教师和审题教师姓名应在试卷存档时填写。
教务处印制
第3页共2页
四、(10 分)一个金属槽如图 3 所示,侧面和底面的电位均为 0,顶盖与侧壁绝缘,其电位为
φ = sin(π x) ,求槽内电位分布。
教务处印制
第1页共2页
φ = sin(π x)
R1 R2
电磁场与电磁波课后习题及答案七章习题解答 (2)

《电磁场与电磁波》习题解答 第七章 正弦电磁波求证在无界理想介质内沿任意方向e n (e n 为单位矢量)传播的平面波可写成j()e n r t m βω⋅-=e E E 。
解 E m 为常矢量。
在直角坐标中故 则 而 故可见,已知的()n j e r t m e βω⋅-=E E 满足波动方程 故E 表示沿e n 方向传播的平面波。
试证明:任何椭圆极化波均可分解为两个旋向相反的圆极化波。
:解 表征沿+z 方向传播的椭圆极化波的电场可表示为式中取显然,E 1和E 2分别表示沿+z 方向传播的左旋圆极化波和右旋圆极化波。
在自由空间中,已知电场3(,)10sin()V/my z t t z ωβ=-E e ,试求磁场强度(,)z t H 。
解 以余弦为基准,重新写出已知的电场表示式这是一个沿+z 方向传播的均匀平面波的电场,其初相角为90︒-。
与之相伴的磁场为 均匀平面波的磁场强度H 的振幅为1A/m 3π,以相位常数30rad/m 在空气中沿z -e 方向传播。
当t=0和z=0时,若H 的取向为y -e,试写出E 和H 的表示式,并求出波的频率和波长。
解 以余弦为基准,按题意先写出磁场表示式 与之相伴的电场为由rad/m β=30得波长λ和频率f 分别为 '则磁场和电场分别为一个在空气中沿ye +方向传播的均匀平面波,其磁场强度的瞬时值表示式为(1)求β和在3ms t =时,z H =的位置;(2)写出E 的瞬时表示式。
解(1)781π10πrad /m rad /m 0.105rad /m 31030β==⨯==⨯在t =3ms 时,欲使H z =0,则要求 若取n =0,解得y =。
考虑到波长260mπλβ==,故因此,t =3ms 时,H z =0的位置为(2)电场的瞬时表示式为在自由空间中,某一电磁波的波长为0.2m 。
当该电磁波进入某理想介质后,波长变为0.09m 。
设1r μ=,试求理想介质的相对介电常数r ε以及在该介质中的波速。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、(10 分)一个金属槽如图 3 所示,侧面和底面的电位均为 0,顶盖与侧壁绝缘,其电位为
φ = sin(π x) ,求槽内电位分布。
教务处印制
第1页共2页
φ = sin(π x)
2. 磁场强度的瞬时值和复数形式;
六、( 15 分 ) 区 域 I : y < 0,ε1 = 10 pF / m, µ1 = 2.5µ H / m,σ1 = 0 ; 区 域 II :
y > 0, ε2 = 9 pF / m, µ2 = 4µ H / m, σ 2 = 0 。 在 区 域 I 内 , 一 极 化 方 向 为 aˆz ,
考生班级
学号
姓名
[注: ε0
=
1 36π
×10−9
F
/
m
µ0 = 4π ×10−7 H / m ]
一、简答题ቤተ መጻሕፍቲ ባይዱ25 分)
1. 请写出一般形式麦克斯韦方程组的微分形式。
2. 请写出两种理想介质分界面上电磁场的边界条件。
3. 什么是均匀平面波?
4. 请判断下列平面波的传播方向和极化类型:
v (1) E = aˆye− jkx
R1 R2
3ε 0
φ =0
φ =0
φ =0
图 1 第二题图
图 2 第三题图
图 3 第四题图
v 五、(10 分)在自由空间中传播的均匀平面波电场强度为 E = aˆx100 sin(2π ×106 t − kz) +
aˆy 200 cos(2π ×106 t − kz)V / m ,求:
1. 频率 f,相位常数 k,波长 λ ,相速 vp ;
ω = 108 rad / s 的平面电磁波振幅为 500V/m,垂直投射到 y = 0 的边界面上,求:
v 1. 入射波 Ei ;
v 2. 反射系数 Γ 和反射波 Er ;
v 3. 透射系数 Τ 和透射波 Et 。
七、(15 分)电偶极子长 10m,电流振幅为 1A,频率为 1MHz,求:
1. 电偶极子的远区辐射电场和方向性函数;
v
vv
2. 在垂直于电偶极子轴线方向上 (θ = 90°) 10m 处的 Sav 及 100km 处的 E和Sav 。
注:1. 命题纸上一般不留答题位置,试题请用小四、宋体打印且不出框。
教务处印制
第2页共2页
2. 命题教师和审题教师姓名应在试卷存档时填写。
教务处印制
第3页共2页
诚信保证
本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场
规则,诚实做人。
本人签字:
编号:
西北工业大学考试试题(卷)
成 2004-2005 学年 第一学期
绩
开课学院 电子信息学院 课程 电磁场与电磁波 学时 考试日期 2004 年 12 月 16 日 考试时间 2 小时
54 开A
考试形式(闭 )( B )卷
v (2) E = (aˆx + jaˆy )e jkz
5. 电偶极子的近区场和远区场的性质有何不同?
二、(15 分)球形电容器内外导体球之间填充介电常数为 3ε0 的介质,如图 1 所示。设内球上
面电荷密度为 ρs ,求:
1. 各区域的电位移矢量和电场强度; 2. 内外导体之间的电压; 3. 此电容器的电容。
