西工大理论力学模拟题选讲
西北工业大学理论力学习题答案(完整资料).doc

第1章:静力学的基本概念
第二章:平面基本力系
第三章:平面任意力系
第五章:空间基本力系
第六章:空间任意力系
第七章:重 心
第八章:点的运动
第九章:刚体的基本运动
第十章:点的复合运动
第十一章:刚体的平面运动第十 Nhomakorabea章:刚体的转动合成
第十四章:质点动力学基础
第十五章:质点的振动
第十七章:动能定理
第十八章:动量定理
第十九章:动量矩定理
第二十章:碰撞理论
第二十一章:达朗伯原理
第二十二章:虚位移原理
西北工业大学 2020年4月 理论力学大作业答案
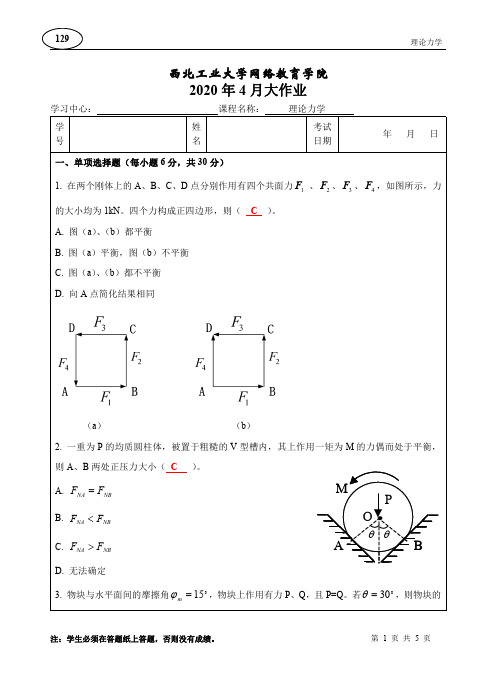
西北工业大学网络教育学院2020年4月大作业(a )(b )2.一重为P 的均质圆柱体,被置于粗糙的V 型槽内,其上作用一矩为则A 、B 两处正压力大小()。
A.NB NA F F =B.NB NA F F <C.NB NA F F >D.无法确定3.物块与水平面间的摩擦角15=,物块上作用有力状态为(A A.临界平衡状态B.静止(非临界平衡状态)C.滑动状态D.无法确定,它们的方向是(C C 121mL =3mL =48mL =4mL =解:该物体系为平行力系若取整体为研究对象,有三个未知量,不能解出,先取CD 为研究对象。
=∑cm 0412=⋅-+⨯D F M q ()kN M q F D 15241=+==∑yF02=+-D c F q F kNF q F D c 52=-=取AC 为研究对象=∑Bm02122=⋅-⨯-⋅-c A F q F ()kNF q F c A 15-=+-=0=∑yF02='--+c B A F q F F kNF B 40=综上,kN F A 15-=,kN F B 40=,kN F C 5=;kNF D 15=2.直径为cm d 8=的滚子在水平面上只滚动不滑动。
杆BC 一端与滚子铰接,另一端与滑块C 铰接,已知图示位置(杆BC 水平)滚子的角速度为s rad /10=ω,30=α,60=β,cm BC 30=,求BC 杆的角速度和滑块C 的速度。
(23分)∙AO αCBβω。
理论力学_西北工业大学中国大学mooc课后章节答案期末考试题库2023年

理论力学_西北工业大学中国大学mooc课后章节答案期末考试题库2023年1.SQL Server提供了3种数据库还原模型,它们是()。
答案:简单还原、完整还原、大容量日志还原2.已知两个关系:职工(职工号,职工名,性别,职务,工资)设备(设备号,职工号,设备名,数量)其中“职工号”和“设备号”分别为职工关系和设备关系的关键字,则两个关系的属性中,存在一个外部关键字为()。
答案:设备关系的“职工号”3.学生成绩表grade中有字段score,float类型,现在要把所有在55至60分之间的分数提高5分,以下SQL语句正确的是()。
答案:UPDATE grade SET score=score+5 WHERE score BETWEEN 55 AND 604.在为students数据库的student_info表录入数据时,常常需要一遍又一遍地输入“男”到学生“性别”列,以下()方法可以解决这个问题。
答案:创建一个DEFAULT约束(或默认值)5.设A、B两个数据表的记录数分别为3和5,对两个表执行交叉联接查询,查询结果中最多可获得()条记录。
答案:156.为了从数据源向数据集填充数据,应该调用()。
答案:DataAdapter.Fill方法7.在如下2个数据库的表中,若雇员信息表EMP的主键是雇员号,部门信息表DEPT的主键是部门号,部门号为EMP表的外键。
若执行所列出的操作,()操作要求能执行成功。
答案:从雇员信息表EMP中删除行('010','王宏达','01','1200')在雇员信息表EMP中插入行('102','赵敏','01','1500')将雇员信息表EMP中雇员号='010'的工资改为1600元8.假设有关系R和S,在下列的关系运算中,()运算要求:“R和S具有相同的元数,且它们的对应属性的数据类型也相同”。
西北工业大学0708(一)理论力学试题a答案

西北工业大学考试试题(卷)2007-2008学年第1 学期开课学院六院课程理论力学(上)学时40R2. 命题教师和审题教师姓名应在试卷存档时填写。
共5页第1页a CP N BN AyN AxP西北工业大学命题专用纸西北工业大学命题专用纸x’y’图中v E 为滑块E 的绝对速度,v ED 为E 相对于D 的相对速度,由速度合成定理 v E =v D +v ED 得,23243cos /vv v v D E =⨯==β,4212sin v v v v E ED =⨯=⋅=β可以得到D 点的法向加速度a Dn 和切向加速度a Dt 的方向和大小以及E 相对于D 的法向相对加速度a EDn 的方向和大小,各加速度的方向见图所示。
b v b b v b OD a OCOCDn 16333169sin 222222=⨯=⋅=⋅=γωω bv b b v b OD a OC OC D 833833sin 2222=⨯=⋅=⋅=γαατbv b v b vDE va EDEDEDn 16116sin 2//2222=⨯===β 假设E 相对于D 的法向相对加速度a EDt 的方向以及E 的绝对加速度a E 方向如图所示。
由加速速度合成定理 a E =a Dn +a Dt +a EDn +a EDt由于E 水平运动,所以在垂直方向上的加速度分量等于零ββττcos )(sin )(⋅-=⋅+ED D n D ED n a a a a解得 bv a E D t 2432=所以, bv a a a a a ED DnD EDnE 2437sin )(cos )(2=⋅-+⋅+=ββττ。
理论力学模拟考试题和答案解析

理论力学模拟试题及答案一、是非题(每题2分。
正确用√,错误用×,填入括号内。
)1、作用在一个物体上有三个力,当这三个力的作用线汇交于一点时,则此力系必然平衡。
()2、力对于一点的矩不因力沿其作用线移动而改变。
()3、在自然坐标系中,如果速度υ = 常数,则加速度α = 0。
()4、虚位移是偶想的,极微小的位移,它与时间,主动力以及运动的初始条件无关。
()5、设一质点的质量为m,其速度 与x轴的夹角为α,则其动量在x轴上的投影为mv x =mvcos a。
()二、选择题(每题3分。
请将答案的序号填入划线内。
)1、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化的结果是。
①主矢等于零,主矩不等于零;②主矢不等于零,主矩也不等于零;③主矢不等于零,主矩等于零;④主矢等于零,主矩也等于零。
2、重P的均质圆柱放在V型槽里,考虑摩擦柱上作用一力偶,其矩为M时(如图),圆柱处于极限平衡状态。
此时按触点处的法向反力N A与N B的关系为。
①N A = N B;②N A > N B;③N A < N B。
3、边长为L 的均质正方形平板,位于铅垂平面内并置于光滑水平面上,如图示,若给平板一微小扰动,使其从图示位置开始倾倒,平板在倾倒过程中,其质心C 点的运动轨迹是 。
①半径为L/2的圆弧; ②抛物线; ③椭圆曲线; ④铅垂直线。
4、在图示机构中,杆O 1 A //O 2 B ,杆O 2 C //O 3 D ,且O 1 A = 20cm ,O 2 C = 40cm ,CM = MD = 30cm ,若杆AO 1 以角速度 ω = 3 rad / s 匀速转动,则D 点的速度的大小为 cm/s ,M 点的加速度的大小为 cm/s 2。
① 60; ②120; ③150; ④360。
5、曲柄OA 以匀角速度转动,当系统运动到图示位置(OA//O 1 B 。
AB |OA )时,有A V B V ,A αB α,ωAB 0,εAB 0。
(NEW)西北工业大学《817理论力学》历年考研真题汇编

图8
第2部分 其他院校理论力学最新真题 2017年杭州电子科技大学813理论力学考研真题
2017年中山大学873理论力学考研真题
图4
3.图5所示平面机构中,AOC为直角曲杆,AO=a,
,
,曲柄 可绕过点 的定轴转动,带动滑块B在水平滑道内运
动。在图示瞬时,BD垂直于 ,
,该瞬时,若给曲杆AOC的
Байду номын сангаас
A端一虚位移 ,则滑块B的虚位移 为( ),方向为( )。
图5
三、平面支架由杆AB、CD及滑轮组成(图6)。B处是铰链连接,半径 r=20cm的滑轮上饶有不可伸长的细绳,绳的一端吊有重为Q=300N的
A. B. C.
D.
图1
2.原盘以匀角速度 绕定轴O转动(图2),动点M相对圆盘以匀速 沿圆盘直径运动。当动点M到达圆盘中心O位置时,动点M的科氏加速
度 是( )。
A.
B.
,方向垂直向上
C.
,方向垂直向下
D.
,方向垂直向右
图2 3.在某介质中,上抛一质量为m的小球,已知小球所受阻力R=-kv, 坐标选取如图3所示,则小球上升段和下降段的运动微分方程分别为 ( )和( )。
图11
2003年西北工业大学422理论力学考研真题
2004年西北工业大学422理论力学考研真题
2007年西北工业大学422理论力学考研真题 一、简答题(每小题14分,共56分) 1.三力作用在正方形板上,各力的大小、方向及位置如图1所示,试求 合力的大小、方向及位置。分别以O点和A点为简化中心,讨论选不同 的简化中心对结果是否有影响。
重物,另一端系在杆AB上的点E,并使EF段水平,杆、滑轮及绳重均不 计,试求两杆在B处的相互作用力。
理论力学(答案)西北工业大学
10.69kN
* 亦可用直接投 影法求 F3 y、F3 z。
10
第三节 力对点之矩、力对轴之矩 一、力对点之矩 1.平面力对点之矩 力对点之矩是力使刚体绕一点转动 效应之度量,简称力矩,为代数量。 力矩计算式:MO(F)=±Fd O:矩心;d:力臂,矩心至力作用
O(矩心) d (力臂) F
线的距离。
用合力矩定理, D M O Fn M O Ft M O Fr Ft 2 D Fn cosα 75.2 N m 2
14
D cosα 2
2.空间力对点之矩
空间力F与矩心O确定一平面,在此平 面内F对O点之矩即为空间力对点 之矩。 因为F在空间的方位是任意的 ,故空间 力对点之矩要用由矩心 O画出的定位矢量 M O ( F )表示。
正交分解。
6
推论2(三力平衡汇交定理) 刚体受同平面内互不平行三 力作用而平衡时,三力作用线必汇交于一点。
F2 A2 A1 F1 F2 A2 A2 F2
O
A2 F R1 A1 F1
A3 F3
=
F3
O A3
A1
F1
=
F3
O A3
=
F3
O A3
F R1 A1
4.作用与反作用定律 两物体间相互作用的一对力,等值、反向、共线,同时存在, 分别作用于两物体上。 5.刚化原理 变形体在某力系作用下处于平衡,如将此变形体刚化为刚体,
* 注意力矩的正负和单位 。
O
3m
F2
F
30°
A
1m
F1
13
例补1-3 作用于齿轮的啮合力Fn =1000N,齿轮节圆直径
D=0.16m,压力角(啮合力与齿轮节圆切线间的夹角)=20°。 求啮合力Fn对轮心O之矩。
理论力学模拟试题和答案
理论力学模拟试题和答案理论力学模拟试题(一) 单项选择题(每题2分,共4分) 1. 物块重P,与水面的摩擦角o,其上作用一力Q,且已知P=Q,方向如图,则物块的状态为( )。
A 静止(非临界平衡)状态B 临界平衡状态C 滑动状态第1题图第2题图2. 图(a)、(b)为两种结构,则( )。
A 图(a)为静不定的,图(b)为为静定的B 图(a)、(b)均为静不定的C图(a)、(b)均为静定的D图(a)为静不定的,图(b)为为静定的(二) 填空题(每题3分,共12分)1. 沿边长为的正方形各边分别作用有F1,F2,F3,F4,且F1=F2=F3=F4=4kN,该力系向B点简化的结果为:主矢大小为,主矩大小为MB=____________ 向D点简化的结果是什么?____________。
F3DCF4AF2F1B第1题图第2题图2. 图示滚轮,已知R,r,,作用于B点的力F,求力F对A点之矩MA=____________。
3. 平面力系向O点简化,主矢与主矩合力大小及作用线位置,并画在图上。
,MO,求理论力学(MOO第3题图第4题图4. 机构如图,O1A与O2B均位于铅直位置,已知,,2,则杆O1A的角速度,C点的速度。
1(三) 简单计算题(每小题8分,共24分)1. 梁的尺寸及荷载如图,求A、B2. 丁字杆ABC的A端固定,尺寸及荷载如图。
求A端支座反力。
3. 在图示机构中,已知,,O1A杆的角速度角加速度理论力学(五) 2,2,求三角板C点的加速度,并画出其方向。
(四) 图示结构的尺寸及载荷如图所示,q=10kN/m,q0=20kN/m。
求A、C处约束反力。
(五)l=2m,求支座A、D、E处的约束反力。
(六) 复合梁的制成、荷载及尺寸如图所示,杆重不计。
已知q=20kN/m,l=2m,求1、2杆的 3五理论力学(AⅠ)期终试题解答01级土木(80学时类)用(一) 单项选择题1. A2. B (二) 填空题1. 0 ;2.;3. 合力FR4.,合力作用线位置(通过O1)4.5rads ;9ms(三) 简单计算1. 取梁为研究对象,其受力图如图所示。
西北工业大学级《力学》期末考试试卷(西北工业大学级《力学》期末考试标准答案及评分标准可在文
诚信保证
本人知晓我校考场规则和违纪处分条例的有关规定,保证遵守考场规则,诚实做人。
本人签字:
编号:
西北工业大学期末考试试题(卷)
2008~2009学年第一学期
开课学院理学院课程力学学时60
考试日期2009年1月12日考试时间2小时考试形式(闭)(A)卷
班级学号姓名
重要提示:
1.本试卷分为“单选题”、“填空题”和计算题三部分,总分为100分;2.在答题卡上答题,最后把试卷和答题卡一并交回;
3.答题卡分为两张,答题卡(1)为机读卡,答题卡(2)为书写卡;4.机读卡中数字用钢笔填写,涂点用2B铅笔填涂。
填空题答案栏每格填1位数字,小数点单独占1格,左对齐填写,按要求取位,4舍5入进位;5.题中所涉重力加速度g一律取9.8 m/s2计算;
6.草稿纸不再另发,将试题的背面作为草稿纸,
一、单选题(共30分,每小题3分,在答题卡(1)上完成)
1.对于惯性参考系,下列那项叙述是正确的?(a)在惯性参考系物体所受合力为零,则该物体保持静止或匀速运动的状态;(b)在任何惯性参考系所描述的物理现象都是相同的;(c)两不同惯性参考系间的相对运动,不一定是匀速运动。
A.abc皆正确;B.只有ab正确;
C.只有bc正确;D.只有ac正确。
西工大18春《理论力学》在线作业
西工大18春《理论力学》在线作业(单选题) 1: 1A: AB: BC: CD: D正确答案:(单选题) 2: 如图所示,匀质长方体的高度h为30厘米,宽度b为20厘米,重量G=600N,放在粗糙水平面上,它与水平面的静摩擦系数f是0.4。
要使物体保持平衡,作用在其上的水平力P的最大值为( )牛。
A 100B 200C 150D 250A: AB: BC: CD: D正确答案:(单选题) 3: 1A: AB: BC: CD: D正确答案:(单选题) 4: 1A: AB: BC: CD: D正确答案:(单选题) 5:立方体的各边和作用在该物体上各力的方向如图所示,各力的大小分别是:F1=100N,F2=50N,OA=4cm,OB=5cm,OC=3cm。
图中力F1对轴x力矩为()N*m。
A 3B -3C 2D 0A: AB: BC: CD: D正确答案:(单选题) 6: 1A: AB: BC: CD: D正确答案:(单选题) 7: 1正确答案:(单选题) 8: 1A: AB: BC: CD: D正确答案:A: AB: BC: CD: D正确答案:(单选题) 10: 一刚体作瞬时平动,此瞬时该刚体上各点()。
A: 速度和加速度均相同B: 速度相同而加速度不相同C: 速度和加速度都不相同D: 速度不同而加速度可能相同正确答案:(单选题) 11: 1A: AB: BC: CD: D正确答案:(单选题) 12: 1A: AB: BC: CD: D正确答案:(单选题) 13: 1A: AB: BC: CD: D正确答案:A: AB: BC: CD: D正确答案:(单选题) 15:力沿其作用线由D点滑移到E点(见图),则A、B、C三铰处的约束反力()。
A 都不变B 都改变C 只有C铰反力不变D 只有C铰反力改变正确答案:(单选题) 16:已知F1,F2,F3,F4一平面汇交力系,而且这四个力矢有如图所示关系,则()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
ω1 O1
图2
vr
B
va
O2 ω1 O1 ve
理论力学模拟试题一
2. 选择题(把正确答案的序号填入括号内)
在图1.3中所示的力多边形中,将符合下列矢量关系的分图 号填入: 图()是P+Q+W-F=0的关系a
Q
W F (a) P Q
W F (b) Q
W
P
F
图1.3
(c)
理论力学模拟试题一
(2)在图1.4中,如果物块重G=40N,力P=20N,物块与地 面之间的摩擦因数f = 0.2,则其摩擦力的大小等于 (a) 11.46 N (b) 0 (c) 10 N (d) 20 N P 分析: ∑Fx = 0,
二.选择题(把正确答案的序号填入括号内) 1.在z轴的点O和点A,分别作用着沿x轴正向和与y轴平行的力F 和 Q(图1),其中P=4N,Q=8N,OA=3m,这两个力合成的最后结 果是( C )。 (A)一个力 (B)一个力偶 (C)一个力螺旋 (D)或一个力偶,或一个力螺旋 z A O
图1
z
A Q
B r2 C
O
r1
L0
α
图1.13(a)
理论力学模拟试题一
解:首先取轮B为研究对象,如图1.13(b)所示。 ε2 根据刚体平面运动微分方程,得 m2aC S m2 g sinα F (1) aC 2
m2 g
C
S B
m2 r2 ( ) 2 Fr2 2
(2)
α
(3) A S
F
N
又
aC r2 2
n C a C
z
l
QtC y
A Qn C
ω ε
ml 4 2 2
ml 3
2
图1.10
§ 5-2 惯性力系的简化
综上所述: 1、刚体作平动
向质心简化
● 主矩
● 主矢 RQ= (-mi ai ) =-mR aC 2、刚体做定轴转动 ● 主矢
M Q=0
向固定轴简化
t n RQ=-mRaC=-mR (aC aC )
理论力学模拟试题一
支座O的反力 A NOy r1 NOx O L0
No x
m2 (3L0 m1 gr1 sin ) (m1 3m2 )r1
S
m1g
图1.13(c)
No y
m2 (3L0 m1 gr1 sin ) m1 g sinα (m1 3m2 )r1
B r2 C
2
(b)
r 2 2 ( ) r Rr
O R r C 图1.5 ω
r(R 2r ) 2 (d) Rபைடு நூலகம்r
分析:
vC r ,
2 2 (r ) v t n aC 0, aC aC C Rr Rr
(b)
理论力学模拟试题一
(4)弹簧无变形的原长为2l,刚度系数为k固定在A,B两点,如图 1.6所示。现将弹簧的中心O拉到C,OC⊥AB,且OC=b,则弹性 力所做的功等于。 (a) (b) (c) (d) 分析:
R C vC A
图1.12(b)
ω
又
vC cos30 v A r
故杆AC的角速度
AC
vCA 2 3r l 3l
(顺钟向)
理论力学模拟试题一
加速度分析和计算,如图1.15()所示。由基点法得
t n aC a A aCA aCA
(2)
aA
O
其中
A
an
CA
aA C atCA
最后得轮B的角加速度
aC 2 3 r R 9 l
2
2 0
图1.12(c)
(逆钟向)
理论力学模拟试题一
3.在图 1.13所示得提升机构中,在鼓轮 A 上作用矩为 L0 的常值 力偶,使轮B在与水平成α角的斜面上滚动而不滑动地向上运 动。假设 A 和 B 分别是半径为 r1 和 r2 的匀质圆盘,质量分别为 m1和m2,绳索伸出段与斜面平行,不计绳重和轴承摩擦。求: 轮心C的加速度,斜面对轮B的滑动摩擦力和支座O的反力。 A
y P x
MO=Q· AO Q y R'
图1
P x
2.在图2所示机构中,若取O1A杆上的点A为动点,动系与O2B 杆固连,定系与机座固连,则当O1A杆与O2B杆垂直时,该瞬时 有( C)。 (A)vr = 0, ve ≠ 0 (B)vr= ve =0 (C)vr ≠ 0, ve = 0 (D)vr ≠ 0, ve ≠0 B
k 2 W (1 2 2 ), 2
k( l 2 b2 l)2
k( l b l)
2 2
2
l
l
b O C B
A
2k( l b l )
2 2
2
k (2 l 2 b 2 2l) 2 / 2
图1.6
(d)
1 0,
2 2 l 2 b 2 2l
2 ak 2vr0 4 3r0
理论力学模拟试题一
(4)已知匀质杆AB的质量为m,长度为l,以角速度ω和角加 速度ε绕固定轴z转动,如图1. 10所示,则杆AB上各点的惯性力 向点A简化的结果是 主矢的大小等于———————————— 主矩的大小等于———————————— 分析: anC =lω2/2, atC =lε/2 QnC =mlω2 /2 , QtC =mlε/2 atC x
N Ar (P 2 N Ay ) cos30 2G
理论力学模拟试题一
2、曲柄OA长r,以匀角速度ω绕水平轴O转动,通过连杆AC 带动半径为R的轮B在固定水平面上滚动而不滑动。求当 OA⊥AC如图1.12(a)所示瞬时,轮B的角速度和角加速度。 ω0 A
C R
图1.12(a)
O
30°
B
A S
0 N o y S sinα m1 g
NOy r1 NOx O
联立求解以上方程,得轮心C的加速度
m1g
图1.13(c)
L0
2( L0 m2 gr1 sin ) aC (m1 3m2 )r1
斜面对轮B的滑动摩擦力
m2 ( L0 m2 gr1 sin ) F (m1 3m2 )r1
O1
ω
图1.1
理论力学模拟试题一
(4) 某刚体的质量为M,质心在点C,如图1.2所示,3根轴z ,z1和z2彼此平行。已知该刚体对轴z1的转动惯量Iz1,则该 刚体对轴z2的转动惯量
I z2 I z1 M (a b)
必须是质心轴
2
( ×)
z1 a
z b
z2
C
图1.2 刚体对任一轴的转动惯量,等于它对该轴相平行且通过质心 的轴的转动惯量,加上刚体的质量与两个轴之间距离平方的 乘积。这就是转动惯量的平行轴定理。
理论力学模拟试题一
1. 是非题(正确的在括号内画√,错的画×)
(1)如果作用在刚体上的平面任意力系具有合力,则该合力 是滑动矢量,而力系的主矢是自由矢量,这两个矢量的大小相 等、方向相同。
(2)当刚体受3个不平行力作用时,只要这3个力的作用线汇 交于同一点,则该刚体一定处于平衡状态。 1.(√) 2.(× )
理论力学模拟试题一
解:速度分析和计算,如图1.12(b )所示。由基点法得
vC v A vCA
(1)
将式(1)投影到CA方向,得
ω0 O
vA A
30°
vCA v A tan30
故轮B的角速度
B ωAC vA vC
vC r 2 3r (逆钟向) R R cos30 3R
A
H C
B D
E
M
图1.11(a)
理论力学模拟试题一
NAy 解:取整个系统为研究对象,为了简化 力矩的计算,可将力G和G'同时平移到滑轮 中心E,如图(b)虚线所示。 A P
( 1)
NAx F
NBy B NBx D y x E (b) G
m
B (F) 0
G'
1 AB N Ay AB P BE G 0 2 然后取杆AD为研究对象,受力图如(c)所示。
理论力学模拟试题一
(3)行星轮系如图1.1所示,匀质轮Ⅱ由杆O1O2带动沿固 定轮Ⅰ作纯滚动。两轮的半径分别为r1和r 2 ,轮Ⅱ的质 量为M,杆 O1O2的角速度为ω,则轮Ⅱ的动能 为
T
1 M (r1 r2 ) 2 2 2
(× )
Ⅱ
Ⅰ R1
O2
r2
轮Ⅱ平面运动
1 1 2 2 T Mv O2 I O2 2 2 2
m
D
( F ) 0,
NAy
NAx
AD cos 30 P AD cos 30 N Ay AD sin 30 N Ax 0 2
( 2)
A 30° NDy F ND P D (c)
理论力学模拟试题一
由式(1)和(2)求得
N Ay P 2 3P 4 3G G 2 6 3
分析: AB杆平移
B
l
2
图1.7
§ 4–2
摩擦角
滑动摩擦的性质
最大总反力FRm对法向反力FN的偏角f 。 FRm Fmax 最大总反力 FRm=FN+Fmax
f
FN
Fm f s FN tan f fs FN FN
由此可得重要结论:
摩擦角的正切=摩擦系数
Fm tan f FN
● 对转轴的主矩 3、刚体作平面运动 ● 主矢 RQ mR aC
M zQ J z
