完全平方公式(一)演示文稿
合集下载
完全平方公式第一课时ppt课件
(1) (4m+n)2 解: (4m+n)2=(4m)2 +2•(4m)•n +n2
(a+b)2= a2 + 2 a b +b2 =16m2 +8mn +n2
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
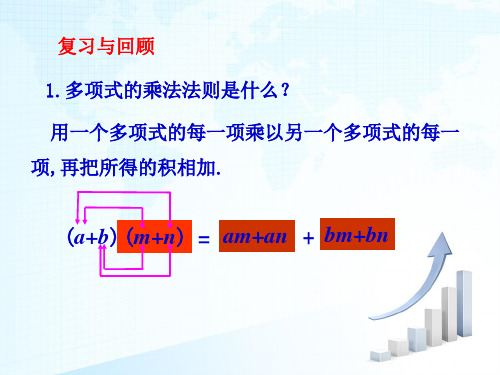
复习与回顾 1.多项式的乘法法则是什么? 用一个多项式的每一项乘以另一个多项式的每一 项,再把所得的积相加.
(a+b)(m+n) = am+an + bm+bn
完全平方公式的几何意义 和的完全平方公式:
b ab
b²
(a+b)² a a² ab
a
b
(a+b)2= a²+ 2ab + b²
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
完全平方公式的几何意义 差的完全平方公式:
思考:(a+b)2与(-a-b)2相等吗? (a-b)2与(b-a)2相等吗?
相等 相等
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
练习
1.运用完全平方公式计算:
(a+b)2= a2 + 2 a b +b2 =16m2 +8mn +n2
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
复习与回顾 1.多项式的乘法法则是什么? 用一个多项式的每一项乘以另一个多项式的每一 项,再把所得的积相加.
(a+b)(m+n) = am+an + bm+bn
完全平方公式的几何意义 和的完全平方公式:
b ab
b²
(a+b)² a a² ab
a
b
(a+b)2= a²+ 2ab + b²
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
完全平方公式的几何意义 差的完全平方公式:
思考:(a+b)2与(-a-b)2相等吗? (a-b)2与(b-a)2相等吗?
相等 相等
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
练习
1.运用完全平方公式计算:
完全平方公式ppt课件

4. 解法:
(1)先把二次方程化为完全 平方公式的形式: ax² + bx + c = 0
完全平方公式
(2)然后将方程按照完全平方公式的标准形式:
(x + p)² + q = 0
01
(5)求出方程的根:
x1 = -p + √(-q)
04
x2 = -p - √(-q)
(3)求出p、q的值:
02
p = -b/2a q = c - b²/4a
一、完全平方公式
演讲人 2023-01-14
目录
01
02
完全平方公式
实例
完全平方公式
1. 定义:
完全平方公式,又称为对称二 次方程,指的是可以表示为一
个完全平方式的二次方程。
2. 标准形式:
ax² + bx + c = 0
3. 用途:
完全平方公式可以用来解决二 次方程,求解方程的根,从而
解决一些数学问题。
04
0 5
(1)将二次方程化为完全平方公式的形式:
x² - 10x + 25 = 0
(3)求出p、q的值:
p = -10/2 q = 25 - 100/4
实例
x1 = 5 + √24 01
03 x1 = 9
(5)求出方程 的根:x2 = 5 - √2 0204 x2 = 1
谢谢
03
(4)由求出的p、q值代入完全平方公式中:
(x + p)² + q = 0
实例
例1:解x² - 10x + 25 = 0
在右侧编辑区输入内容
(2)按照完全平方公式的标准形式:
8.3完全平方公式PPT课件

完全平方公式的数学表达式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方公式的文字叙述:
两数和(或差)的平方,等于 它们的平方和,加(或减)它们的 积的2倍。
.
5
首(a+平b方)2=,a尾2 平+2方ab,+b2
公式特点:
乘(a-积b的)2=2倍a2放-中2a央b。+b2
1、左边是一个二项式的完全平方;
2、右边积为二次三项式;
3、积中两项为两数的平方和;
4、另一项是两数积的2倍,且与乘式 中间的符号相同;
5 、公式中的字母a,b可以表示数,单 项式和多项式。
.
6
讨论
你能根据图8.8 -1和图8.8 -2 中的面积说 明完全平方公式吗?
b
a
a
b
图 8.8-1
b a
b a 图8.8-2
.
11
练习:运用完全平方公式计算: 1) (a+2b)2 2) (a-2b)2 3) (m-4n)2 4) (4n-m)2
.
12
学一学
例例2 运题用解完全析平方公式计算:
(1) 1022;
(2) 992
变形
解: (1) 1022 = (100+2)2 =1002+2×100×2+22
=10000+400+4 =10404
完全平方公式 的几何意义
和的完全平方公式:
b ab b²
(a+b)²
a a² ab
ab
(ab)2 a 2+2ab+b 2
完全平方公式(1)PPT课件

第14章 整式乘除与因式分解
14.2.2 乘法公式
---完全平方公式
2020年9月28日
1
教学目标
使学生理解完全平方公式,掌握完全平方公 式的结构特 征 ,并会用这两个公式进行计算.
重点 :完全平方公式的结构特征及公式 直接运用
难点 :对公式中字母a,b的广泛含义的理
解 与正确应用 .
2020年9月28日
2
复习提问:
1、多项式的乘法法则是什么?
用一个多项式的每一项乘以另一个多 项式的每一项,再把所得的积相加.
(a+b) (m+n) = am+an + bm+bn
2020年9月28日
3
算一算:
(a+b)2 =(a+b) (a+b)
= a2 +ab +ab +b2 = a2 +2ab+b2
(a-b)2 =(a-b) (a-b)
2020年9月28日
5
完全平方公式 的图形理解
完全平方和公式:
b ab b²
(a+b)²
a a² ab
ab
× (ab)2 a 2+2ab+b 2
(x+y) =x +y 判断 2020年9月28日
2 22
6
完全平方公式 的图形理解
完全平方差公式:
b ab b²
a
a² ab
(a-b)²
ab
(ab)2 a 2 ababb2
的符号相同。
首平方,尾平方,积的两倍 中间放,符号与前面一个样
4、公式中的字母a,b可以表示数,单项式和
多项式。 2020年9月28日
14.2.2 乘法公式
---完全平方公式
2020年9月28日
1
教学目标
使学生理解完全平方公式,掌握完全平方公 式的结构特 征 ,并会用这两个公式进行计算.
重点 :完全平方公式的结构特征及公式 直接运用
难点 :对公式中字母a,b的广泛含义的理
解 与正确应用 .
2020年9月28日
2
复习提问:
1、多项式的乘法法则是什么?
用一个多项式的每一项乘以另一个多 项式的每一项,再把所得的积相加.
(a+b) (m+n) = am+an + bm+bn
2020年9月28日
3
算一算:
(a+b)2 =(a+b) (a+b)
= a2 +ab +ab +b2 = a2 +2ab+b2
(a-b)2 =(a-b) (a-b)
2020年9月28日
5
完全平方公式 的图形理解
完全平方和公式:
b ab b²
(a+b)²
a a² ab
ab
× (ab)2 a 2+2ab+b 2
(x+y) =x +y 判断 2020年9月28日
2 22
6
完全平方公式 的图形理解
完全平方差公式:
b ab b²
a
a² ab
(a-b)²
ab
(ab)2 a 2 ababb2
的符号相同。
首平方,尾平方,积的两倍 中间放,符号与前面一个样
4、公式中的字母a,b可以表示数,单项式和
多项式。 2020年9月28日
【信息技术应用能力提升工程 】A3演示文稿设计与制作 初中数学《完全平方公式》主题说明

2.你能自己设计一个图形解释这一公式吗?
3.分析完全平方公式的结构特点,并用语言来描述完全平方公式.
结构特点:左边是二项式(两数和(差))的平方;
右边是两数的平方和加上(减去)这两数乘积两倍.
主要内容 语言描述:两数和(或差)的平方,等于这两数的平方和加+3)2=(m+3)(m+3)=m2+3m+3m+9=m2+2×3m+9=m2+6m+9
(2+3x)2=(2+3x)(2+3x)=4+2×3x+2×3x+9x2=4+2×2×3x+9x2=4+12x+9x2
2.再举两例验证你的发现. 3 你能用自己的语言叙述这一公式吗? 二探究新知:
1. (a-b)2=?你是怎样做的?.
《完全平方公式(1)》主题说明
基本信息 能力维度
县(市、 区)
学校
姓名
□学情分析 教学设计 □学法指导 □学业评价
所属环境 多媒体教学环境 □混合学习环境 □智慧学习环境
微能力点 A3 演示文稿设计与制作
教学环境 多媒体
课题名称 完全平方公式(1)
学科 数学
一:引入 1.观察下列算式及其运算结果,你有什么发现?
(1)(2x−3)2 ; (2) (4x+5y)2 ;
(3) (mn−a)2
例 2 利用完全平方公式计算:
(1) (-1-2x)2 ; (2) (-2x+1)2
三练习计算:
(1 x 2y)2 2
; (2xy 1 x)2 ;(n+1)2-n2 5
四小结:1. 完全平方公式和平方差公式不同:
完全平方公式(共16张PPT)

点评小组 5组
知识综合应用 探究:
(书面展示)
9组
1组
8组 6组
5组
要求: ⑴ 先点评对错;再点评思路方法,应该注意的问 题,力争进行必要的变形拓展。 ⑵ 其他同学认真倾听、积极思考、记好笔记、大 胆质疑。
纠
错 练 习
指出下列各式中的错误, 并加以改正: 2 2 (1) (2a−1) =2a −2a+1; (2) (2a+1)2=4a2 +1; 2 2 (3) (a−1) =a −2a−1.
(a b) a 2ab b
2 2
2
学习目标:
公式进行简单的计算,提高计算能力; 全平方公式的应用技巧; 提高学习数学的兴趣和热爱生活的情感。
1.能准确推导出完全平方公式,并能运用
2.通过自主学习,小组合作,探究总结完
3.激情参与,阳光展示,充分感知数学美,
预习反馈
小组 第一组 第二组 第三组 第四组 第五组 第六组 第七组 第八组 第九组
本节课你的收获是什么?
注意完全平方公式和平方差公式不同:
形式不同.
, 结果不同:
(a b)2=a2 2ab+b2;
(a+b)(a−b)=a2−b2.
整理巩固
要求:整理巩固探究问题
落实基础知识 完成知识结构图
当堂检测
要求:学生自主完成 答案:见教师用书
课堂评价
学科班长: 1.回扣目标 总结收获 2.评出优秀小组和个人
用不同的形式表示实验田 a 的总面积, 并进行比较.
直 2 总面积 = ( a + b ) ; 接 法一 求 间 接 总面积= a2+ ab+ ab+ b2. 法二 求
完全平方公式ppt课件
(1) (2x+3y)2 (2) (2x-3y)2 (3) (-2x+3y)2 (4) (-2x-3y)2
小结:当所给的二项式 中两项符号相同时,一 般选用“和”的完全 平方公式;
当所给的二项式 中两项的符号相反时, 一般选用“差”的完 全平方差公式.
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
本节课你学到了什么?
本节课你的收获是什么?
注意完全平方公式和平方差公式不同:
形式不同. 完全平方公式的结果 是三项, 结果不同: 即 (a b)2=a2 2ab+b2;
运用公式计算: 1.(a-b)(a+b)(a2+b2) 2.(2-1)(2+1)(22+1) (24+1)…… (232+1)+1
本标准适用于已投入商业运行的火力 发电厂 纯凝式 汽轮发 电机组 和供热 汽轮发 电机组 的技术 经济指 标的统 计和评 价。燃 机机组 、余热 锅炉以 及联合 循环机 组可参 照本标 准执行 ,并增 补指标 。
1.(2x+y-z)(2x-y+z) 2.(a+2b-1)2
右边是 两数的平方差.
应用平方差公式的注意事:
☾ 弄清在什么情况下才能使用平方差公式:
做一做 本标准适用于已投入商业运行的火力发电厂纯凝式汽轮发电机组和供热汽轮发电机组的技术经济指标的统计和评价。燃机机组、余热锅炉以及联合循环机组可参照本标准执行,并增补指标。
课件《完全平方公式》课件PPT_人教版1
(1)第一天有a个男孩一起去了老人家,老人一共 给了这些孩子多少块糖?
(2)第二天有b个女孩一起去了老人家,老人一共 给了这些孩子多少块糖?
(3)第三天有(a+b)个孩子一起去了老人家,老人一 共给了这些孩子多少块糖?
(4)这些孩子第三天得到的糖果数与前两天他们得 到的糖果总数哪个多?多多少?为什么?
设置情境,探究新知
有一位老人非常喜欢孩子,每当有孩子到他家做 客时,老人都要拿出糖果招待他们.来一个孩子,老 人就给这个孩子一块糖,来两个孩子,老人就给每个 孩子两块糖,来三个孩子,就给每人三块糖……
(1)第一天有a个男孩一起去了老人家,老人一 共给了这些孩子多少块糖?
a2 块 (2)第二天有b个女孩一起去了老人家,老人一 共给了这些孩子多少块糖?
简记:首平方,尾平方,积的2倍放中间。
设置情境,探究新知
例题讲解与练习 例 运用完全平方公式计算: (1)(2x - 3)2;(2)(4x + 5y)2;(3)(mn - a)2 .
解:(1)(2x - 3)2 =(2x)2 -2 2x 3+32 =4x2 -12x+9;
(2)(4x + 5y)2 = (4x)2 2 4x 5y (5y)2 = 16x2 40xy 25y2;
探究
设置情境,探究新知
一块边长为a m的正方形实验田,如图所示,因
需要将其边长增加b m,构成四块田地,种植不同的
新品种.用不同的形式表示实验田的总面积,并进行
比较.
bm
你发现了什么?
am
am
bm
设置情境,探究新知
bm
方法一:
直接求得:总面积=(a+b)2 m2 .
(2)第二天有b个女孩一起去了老人家,老人一共 给了这些孩子多少块糖?
(3)第三天有(a+b)个孩子一起去了老人家,老人一 共给了这些孩子多少块糖?
(4)这些孩子第三天得到的糖果数与前两天他们得 到的糖果总数哪个多?多多少?为什么?
设置情境,探究新知
有一位老人非常喜欢孩子,每当有孩子到他家做 客时,老人都要拿出糖果招待他们.来一个孩子,老 人就给这个孩子一块糖,来两个孩子,老人就给每个 孩子两块糖,来三个孩子,就给每人三块糖……
(1)第一天有a个男孩一起去了老人家,老人一 共给了这些孩子多少块糖?
a2 块 (2)第二天有b个女孩一起去了老人家,老人一 共给了这些孩子多少块糖?
简记:首平方,尾平方,积的2倍放中间。
设置情境,探究新知
例题讲解与练习 例 运用完全平方公式计算: (1)(2x - 3)2;(2)(4x + 5y)2;(3)(mn - a)2 .
解:(1)(2x - 3)2 =(2x)2 -2 2x 3+32 =4x2 -12x+9;
(2)(4x + 5y)2 = (4x)2 2 4x 5y (5y)2 = 16x2 40xy 25y2;
探究
设置情境,探究新知
一块边长为a m的正方形实验田,如图所示,因
需要将其边长增加b m,构成四块田地,种植不同的
新品种.用不同的形式表示实验田的总面积,并进行
比较.
bm
你发现了什么?
am
am
bm
设置情境,探究新知
bm
方法一:
直接求得:总面积=(a+b)2 m2 .
完全平方公式(1)PPT文档共35页
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
完全平方公式(1)
56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
完全平方公式(1)
56、死去何所道,托体同山阿。 57、春秋多佳日,登高赋新诗。 58、种豆南山下,草盛豆苗稀。晨兴 理荒秽 ,带月 荷锄归 。道狭 草木长 ,夕露 沾我衣 。衣沾 不足惜 ,但使 愿无违 。 59、相见无杂言,但道桑麻长。要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
《完全平方公式》ppt课件人教版初中数学1
=m2+2mn+n2+2mp+2np+p2
(1)(p+1)2 =(p+1)(p+1)= ____________;
(2)(m+2)2 =(m+2)(m+2)= ____________;
(1)(6a+5b)2
(2)(a-b)2
(1)a²+b²=
。
师一共给了这些孩子多少块糖?
(a+b)²=
。
(3)1022
2 2 2 (4)ab=
。
共同特点:(a b) a 2ab b 解:原式=4m2-4m+1
(3)(p-1)2 =(p-1)(p-1)=_____________;
2、“探究”两数差的平方有什么共同特点? (a+b)² - 2ab
= x2 + 2·x·2y+(2y)2
(3)(p-1) =(p-1)(p-1)=_____________; 2 (2)(m+2)2 =(m+2)(m+2)= ____________;
和(或差)的平方 它们的积的两倍
9x2 12
4y2
-4m
a2 +2ab
你能根据109思考的两个图的面积验证公式吗?
完全平方和公式:
完全平方差公式:
b ab b²
b ab b²
a a² ab
a
a² ab
ab
(a b)2 a 2+2ab +b2
ab
(a b)2 a2 ab ab b2
a2 2ab b2
=(p+1)(p+1)=
____________;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3) (mn−a)2
首平方,尾平方,两倍乘积放中央。
1.计算: (1) ( 1 x − 2y)2 ; 2 1 2 (2) (2xy+ x ) ; 5 (3)(n +1)2 − n2 ;
(4) (4x+0.5)2 ;
(5) (2x2-3y2)2
b
公式: (a+b)2= a2+ 2ab + b2.
动脑筋
想一想
完全平方公式
的证明
(a+b)2=a2+2ab+b2 ; (a−b)2= a2 −2ab+b2.
(1) 你能用多项式的乘法法则来说明它成立吗?
(2) 小颖写出了如下的算式:(a−b)2= [a+(−b)]2
完全平方公式
例2 利用完全平方公式计算: (1) (-1-2x)2 ; (2) (-2x+1)2
(a -b )2 = a2-2 a b + b2 (-1-2x)2 =(-1)2+2· (-1)· (-2x)+(-2x)2=1+4x+4x2 方法2: (a +b )2 = a2+2 a b + b2 (-1-2x)2 =[-(1+2x)]2=(1+2x)2=1+4x+4x2 方法3: 还有其他 方法吗?
(1) (-1-2x)2 =(-1)2-2· (-1)· 2x+(2x)2=1+4x+4x2
从不同的角度来看同一问题,常常会 有不同的方法。
完全平方公式
例2 利用完全平方公式计算: (1) (-1-2x)2 ; (2) (-2x+1)2
(2) (-2x+1)2 =(-2x)2 +2· (-2x)· 1+12=4x2-4x+1 (a +b )2 = a2+2 a b + b2 方法2: (-2x+1)2 =(2x-1)2 =4x2-4x+1
1. 平方差公式: (a+b)(a−b)= a2 − b2;
公式的结构特征: 左边是 两个二项式的乘积, 即两数和与这两数差的积. 右边是 两数的平方差.
2. 应用平方差公式的注意事项:
☾ 弄清楚在什么情况下才能使用平方差公式.
完全平方公式
(a+b)2 = a2+2ab+b2 . (a−b)2 = a2−2ab+b2 . 结构特征: 左边是 二项式 (两数和 (差)) 的平方; 右边是 两数的平方和 加上 (减去)
这两数乘积的两倍.
(a+b)2= a2+2ab+b2 几 b 何 解 释: a
(a -b )2 = a2-2 a b + b2
首平方,尾平方,两倍乘积放中央, 加减看前方,同加异减。
1. 注意完全平方公式和平方差公式不同:
形式不同. 结果不同: 完全平方公式的结果是三项, 即 (a b)2=a2 2ab+b2;
平方差公式的结果 是两项, 即 (a+b)(a−b)=a2−b2. 2. 在解题过程中要准确确定a和b,对照公式原形的两边, 做到 不丢项、不弄错符号、2ab时不少乘2。 3. 口诀:首平方,尾平方,两倍乘积放中央, 加减看前方,同加异减。
ab
b2 ab
b
a2
a
(a−b)2 = a2−2ab+b2 b a−b a−b (a−b)2 b(a−b)
语言表述:
两数和(差)的平方 等于这两数的平方和
用自己的语 言叙述上面 的公式
a
加上 (减去) 这两数乘积的两倍. (a−b)2
= a2 −ab −b(a−b) = a2−2ab+b2 .
ab
a
完全平方公式
例1 利用完全平方公式计算: (1) (2x−3)2 ; (2) (4x+5y)2 ;
(1) (2x−3)2 =(2x)2-2· (2x)· 3+32=4x2-12x+9 (a -b )2 = a2-2 a b + b2 (2)(4x+5y)2=(4x)2+2· (4x)· (5y)+(5y)2=16x2+40xy+25y2 (a +b )2 = a2+2 a b + b2 (3)(mn-a)2 =(mn)2-2· mn· a+a2=m2n2-2amn+a2
她是怎么想的? 推证 你能继续做下去吗? (a+b)2 = (a+b)(a+b) =a2+ab+ ab+b2 =a2+2ab+ b2; 2= [a+(−b)]2 ( a − b ) 利用两数和的 = a 2 + 2 a (−b) +(−b) 2 完全平方公式 2. 2 b + a 2a b 推证公式 − =
作业
1. 基础训练:教材习题1.13 .
2. 拓展练习: (a+b)2与(a-b)2有怎样的联系?能否用一个等式来 表示两者之间的关系,并尝试用图形来验证你的 结论?
一块边长为a米的正方形实验田, 因需要将其边长增加 b 米。 形成四块实验田,以种植不同的 新品种(如图1—6). 用不同的形式表示实验田的 总面积, 并进行比较.
b
探索: 你发现了什么?
2 直 接 总面积= (a+b) ; 法一 求 间 接 总面积= a2+ ab+ ab+ b2. 法二 求
a
a 图1 —6
指出下列各式中的错误,并加以改正: (1) (2a−1)2=2a2−2a+1; (2) (2a+1)2=4a2 +1; (3) (a−1)2=a2−2a−1.
解: (1) 第一数被平方时, 未添括号; 第一数与第二数乘积的2倍 少乘了一个2 ; 应改为: (2a−1)2= (2a)2−2•2a•1+1; (2) 少了第一数与第二数乘积的2倍 (丢了一项); 应改为: (2a+1)2= (2a)2+2•2a•1 +1; (3) 第一数平方未添括号, 第一数与第二数乘积的2倍 错了符号; 第二数的平方 这一项错了符号; 应改为: (a−1)2=(a)2−2•(a )•1+12;
