测量误差的基本知识汇总
测量学 测量误差基本知识
B 观测者的误差
C 测量误差
D 外界条件的变化
难度系数 c
若观测量的真值为X,观测值为li(i=1,2,…,n),其算术 平均值为L,则描述观测值的(真)误差的正确表达式是 (A )
A 观测值的(真)误差为 i= li -X; B 观测值的(真)误差为 i = X-L; C 观测值的(真)误差为 i = L-X; D 观测值的(真)误差为 i= li -X;
难度系数 A
L1、L2、L3为一组等精度观测值,其误差分别为-7mm, -2mm, +7mm,则它们的精度为( A )
A L1、L2、L3的精度相同; B L1最高、L3最低; C L3最高、L1最低; D L2最高、L1与L3相同 。
难度系数 B
丈量了D1、D2两段距离,其观测值及中误差分别为: D1=105.53m±0.05m,D2=54.60m±0.05m,这说明 ( A B ).
A D1和D2的中误差相同, B D1的相对精度高于D2的相对精度 C D1和D2的中误差不相同 D D1的相对精度低于D2的相对精度 E D1的相对精度与D2的相对精度相同。
难度系数 B
难度系数 B
精度指标
衡量精度的指标有:( A C D )
A 中误差
B 对中误差
C 相对误差
D 容许误差
E 偶然误差
难度系数 C
若水平角测量的中误差为6,则其极限误差可以取 值为( C E )
A 3
B 6
C 12
D 15
E 18
难度系数 C
观测值L1、L2为同一组等精度观测值,其含义是( C D E ) A L1、L2的真误差相等 B L1、L2的改正数相等 C L1、L2的中误差相等 D L1、L2的观测条件基本相同 E L1、L2服从同一种误差分布
工程测量 测量误差的基本知识汇总

6
二、偶然误差的规律性
在相同的观测条件下,
独立的观测 358个三角形的全部内角,每个三角形 内角之和应等于180度,但由于误差的 影响往往不等于180度,计算各内角和 的真误差,并按误差区间的间隔0.2秒 进行统计。
真误差 =观测值—真值
i Li 1800
7
误差分布表
误差 区间
工程测量
第五章 测量误差的基本知识
1
5.1
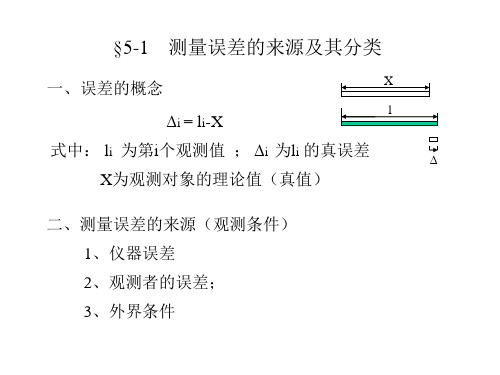
测量误差的概念
一、误差的来源与分类
什么是误差 误差产生的原因 误差的性质和分类 误差的消除
2
1、测量误差的定义
真值:观测量客观上存在的一个能代表 其真正大小的数值,一般用X表示。 观测值:对该量观测所得的值,一般用 Li表示 。 真误差:观测值与真值之差, 一般用i= Li -X表示。
(K/n)/d△
个数K 46 41 33 21 16 13 5 2 0 177
+△ 频率K/n 0.128 0.115 0.092 0.059 0.045 0.036 0.014 0.006 0 0.495
(K/n)/d△
1.20~1.40
1.40~1.60 >1.60
0.630 0.560 0.460 0.320 0.235 0.180 0.085 0.055 0
xn
相互独立
K n xn
2 2 Kn mn
2 2 mZ K12 m12 K 2 m2
19
非线性函数的误差传播定律:
Z f ( x1 , x2 xn ) f f f dZ dx1 dx2 dxn x1 x2 xn f f f Z x1 x2 xn x1 x2 xn f 2 2 f 2 2 f 2 2 m ( ) m1 ( ) m2 ( ) mn x1 x2 xn
测量误差的基本知识.

1)相同测量程序;2)相同测量条
件;3)相同观测人员;4)相同测量设
备;5)相同地点。
4
一、测量误差的几个名词术语
5、等精度测量:在同一条件下进行的一系列重 复测量。
6、误差公理:一切测量都具有误差,误差自始 至终存在于所有科学试验的过程之中。
研究测量误差的目的:寻找产生误差的原因, 认识误差的规律、性质,进而找出减少误差 的途径与方法以求获得尽可能接近真值的测 量结果。
7
1、 按误差的表示形式分
【例】要测稍小于80℃的温度,现在0.5级 的0~300℃和1.0级的0~100℃的两个温 度计,试问采用哪个温度计较好?
解:精度等级A=△x/(xmax-xmin)×100 %
∴ε=△x/x= A×(xmax-xmin)/x
用0.5级时:ε1=300×0.5%/80=1.875%
从上述计算结果不难得出被测电源 电动势和内阻置信区间(K取3)内的测 量值分别为:
Ex Eˆ kˆEˆ 1.5150 0.0009V
Rx Rˆ kˆRˆ 0.37 0.03
44
4、 最小二乘法原理及其应用
2)在曲线拟合和回归分析中的应用 [例] 已知某一热敏电容传感器的温度
和电容值的实测数据如下表所示,试用 最小二乘法原理求其特性表达式。
I
A
用
【例】右图为电源电动 r 势E和电源内阻r的测 U
V
R
量电路,根据电路理 论,测量方程为已知
E
等精度重复测量的重
复测量的数据如下所
示,试求出E和r的估
计值和标准差。
37
4、 最小二乘法原理及其应用
i
Ii/mA
Ui/V
1
3.293
测量误差的基本知识

m乙 =
=
= 4.3
n
6
12
二、相对误差
l 绝对误差 :真误差、中误差 l 相对误差: 在某些测量工作中,绝对误差不能完全
反映出观测的质量。 相对误差K—— 等于误差的绝对值与相应观测值的
比值。常用分子为1的分式表示,即:
相对误差
=
误差的绝对值 观测值
=1 T
13
l 相对中误差:当误差的绝对值为中误差m 的绝对值时, K称为~,即 k=1/m 。
3
1.系统误差
l 系统误差:在相同的观测条件下,对某一未知量进行一系列 观测,若误差的大小和符号保持不变,或按照一定的规律变 化,这种误差称为~ 。
l 系统误差产生的原因 : 仪器工具上的某些缺陷;观测者的 某些习惯的影响;外界环境的影响。
l 系统误差的特点: 具有累积性
4
系统误差消减方法 ❖1、在观测方法和观测程序上采取一定的措施;
中误差、相对误差、极限误差和容许误差
10
一、中误差
在测量实践中观测次数不可能无限多,实际应用中,以 有限次观测个数n计算出标准差的估值定义为中误差m,作 为衡量精度的一种标准:
m = ±sˆ = ± [ ]
n
在测量工作中,普遍采用中误差来评定测量成果的精度。
11
l 有甲、乙两组各自用相同的条件观测了六个三角 形的内角,得三角形的闭合差(即三角形内角和 的真误差)分别为:
例:经纬仪的LL不垂直于VV对测角的影响
5
2.偶然误差 l 偶然误差:在相同的观测条件下,对某一未知量 进行一系列观测,如果观测误差的大小和符号没有 明显的规律性,即从表面上看,误差的大小和符号 均呈现偶然性,这种误差称为 ~。 l 产生偶然误差的原因: 主要是由于仪器或人的感 觉器官能力的限制,如观测者的估读误差、照准误 差等,以及环境中不能控制的因素(如不断变化着的 温度、风力等外界环境)所造成。
测量误差的基本知识

§5.5误差传播定律的应用
一、水准测量的误差分析
每站的高差为:h = a - b ;m读≈ ±3mm
一站的高差中误差:m站 =
≈ ±4mm
线路n站,则总高差:
取3倍中误差为限差,则普通水准路线的容许误 差为 :
二、水平角观测的误差分析
用DJ6经纬仪进行测回法观测水平角,那么用盘 左盘右观测同一方向的中误差为±6 ″,
1、倍数函数:Z=kx 中误差:mz=kmx
2、和差函数 :Z=x1±x2±…±xn 中误差:mz m12 m22 ... mn2
3、线形函数 : Z=k1x1±k2x2±…±knxn 中误差:mz (k1)2 m12 (k2 )2 m22 ... (k n)2 mn2
加权平均值的中误差: M0 = = ±3.2mm
一、一般函数的中误差
设Z=f(x1,x2,…,xn),其中x1,x2,…,xn属于独立自 变量(如直接观测值),他们的中误差分别为 m1,m2,…,mn则函数Z的中误差为 :
mz
(
f x1
)
2
m12
f (
x2
) 2 m22
f ... (
xn
) 2 mn2
二、特殊函数的中误差
小结
• 正确列出函数式; • 检查观测值是否独立; • 求偏微分并代入观测值确定系数; • 套用公式求出中误差。
思考题:一个边长为l的正方形,若测量一 边中误差为ml=±1cm,求周长的中误差? 若四边都测量,且测量精度相同,均为ml, 则周长中误差是多少?
§5.4等精度直接观测值
1.算术平均值原理 假设对某量X 进行了n次等精度的独立观测,得
5.偶然误差的特性
测量学之测量误差基本知识

所谓精度,就是指误差分布的密集或离散的程度,为了衡量 观测值的精度高低,可以用误差分布表、绘制直方图或画出误 差分布曲线的方法进行比较。 衡量精度的标准有以下几种:
中误差 允许误差(极限误差) 相对误差
m 21 22 2n
n
n
例 :对某一距离进行五次丈量,其真误差分别为-6mm 、-5mm、-2mm、+1mm、+6mm,求观测值中误差。 根据上式可知
2. 观测值的和或差函数
函数 Z=x±y 的中误差:
mz2 mx2 my2
或mz
mx2
m
2 y
例2 在三角ABC中,观测了∠A和∠B,其中误差 分别为 mA 6" , mB 8" ,求∠C的中误差?
解: ∵C=180-(A+B) ∴
mc mA2 mB2 62 82 10
2
3
4
5
);
m x2
m 5
3、结论:
Pi mi2 ; (i = 1,2, ……n)
式中:P为权,是任意常数。
水准测量与距离丈量中,各路线的权与该路线的测站数
或距离的公里数成反比。
即
1 pi Ni
或
1 pi Si
同精度观测值的算术平均值的权与观测次数成正比。 即
Pi=Ni
设对某量进行n次观测,其观测值中误差及权分别为: 观测值 l1 , l2 …… ln 中误差 m1, m2 …… mn 权 p1 ,p2 …… pn
则加权平均值为:
x加 p1l1 p2l2 pnln [ pl]
p1 p2 pn
测量误差的基本知识

小结
• 正确列出函数式; • 检查观测值是否独立; • 求偏微分并代入观测值确定系数; • 套用公式求出中误差。 思考题:一个边长为l的正方形,若测量一边中误差为ml=±1cm,求周长
的中误差?若四边都测量,且测量精度相同,均为ml,则周长中误差是多 少?
§5.4等精度直接观测值
1.算术平均值原理 • 假设对某量X 进行了n次等精度的独立观测,得观测值l1,l2,…ln • 算术平均值为 :L=(l1+l2+…ln )/n=[l]/n • 算术平均值原理:当n→∞时,L=X • 证明:∆i=li-X, [∆]=[l]- nX,
mz
(
f x1
)
2
m12
( f x2
) 2 m22
... ( f xn
) 2 mn2
二、特殊函数的中误差
1、倍数函数:Z=kx
中误差:mz=kmx
2、和差函数 :Z=x1±x2±…±xn
中误差:
3、线形函数 : Z=k1x1±k2x2±…±knxn
中误差:
mz m12 m22 ... mn2
此在测量工作中,我们常常取三倍中误差作为偶然误差的容许值(或限差),如果精 度要求较高时,就可以取两倍中误差作为限差,即:
∆容=士 2|m| 或 ∆容=士3|m |
§5.3 误差传播定律
• 误差传播定律:是指描述观测值中误差与其函数中误差之间关系的定律 一、一般函数的中误差
设Z=f(x1,x2,…,xn),其中x1,x2,…,xn属于独立自变量(如直接观测值),他们的 中误差分别为m1,m2,…,mn则函数Z的中误差为 :
• 所以甲组精度高 关于中误差要注意两点 • 中误差(m)与真误差( ∆ )不同,它只是表示某一组
测量误差的基本知识汇总

测量误差的基本知识在测量工作中,对某量(如某一个角度、某一段距离或某两点间的高差等)进行多次观测,所得的各次观测结果总是存在着差异,这种差异实质上表现为每次测量所得的观测值与该量的真值之间的差值,这种差值称为测量真误差,即:测量真误差=真值-观测值一、误差产生的原因:1.观测者由于观测者感觉器官鉴别能力有一定的局限性,在仪器安置、照准、读数等方面都产生误差。
同时观测者的技术水平、工作态度及状态都对测量成果的质量有直接影响。
2.测量仪器每种仪器有一定限度的精密程度,因而观测值的精确度也必然受到一定的限度。
同时仪器本身在设计、制造、安装、校正等方面也存在一定的误差,如钢尺的刻划误差、度盘的偏心等。
3.外界条件观测时所处的外界条件,如温度、湿度、大气折光等因素都会对观测结果产生一定的影响。
外界条件发生变化,观测成果将随之变化。
上述三方面的因素是引起观测误差的主要来源,因此把这三方面因素综合起来称为观测条件。
观测条件的好坏与观测成果的质量有着密切的联二 观测误差分类: 1.系统误差在相同的观测条件下,对某量进行一系列的观测,若观测误差的符号及大小保持不变,或按一定的规律变化,这种误差称为系统误差。
这种误差往往随着观测次数的增加而逐渐积累。
如某钢尺的注记长度为30m ,经鉴定后,它的实际长度为30.016m ,即每量一整尺,就比实际长度量小0.016m ,也就是每量一整尺段就有+0.016m 的系统误差。
这种误差的数值和符号是固定的,误差的大小与距离成正比,若丈量了五个整尺段,则长度误差为5×(+0.016)=+0.080m 。
若用此钢尺丈量结果为167.213m,则实际长度为:167.213+30213.167×0.0016=167.213+0.089=167.302(m)系统误差对测量成果影响较大,且一般具有累积性,应尽可能消除或限制到最小程度,其常用的处理方法有: 1.检校仪器,把系统误差降低到最小程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测量误差的基本知识在测量工作中,对某量( 如某一个角度、某一段距离或某两点间的高差等 ) 进行多次观测,所得的各次观测结果总是存在着差异,这种差异实质上表现为每次测量所得的观测值与该量的真值之间的差值,这种差值称为测量真误差,即:测量真误差 =真值 - 观测值一、误差产生的原因 :1.观测者由于观测者感觉器官鉴别能力有一定的局限性,在仪器安置、照准、读数等方面都产生误差。
同时观测者的技术水平、工作态度及状态都对测量成果的质量有直接影响。
2.测量仪器每种仪器有一定限度的精密程度,因而观测值的精确度也必然受到一定的限度。
同时仪器本身在设计、制造、安装、校正等方面也存在一定的误差,如钢尺的刻划误差、度盘的偏心等。
3.外界条件观测时所处的外界条件,如温度、湿度、大气折光等因素都会对观测结果产生一定的影响。
外界条件发生变化,观测成果将随之变化。
上述三方面的因素是引起观测误差的主要来源,因此把这三方面因素综合起来称为观测条件。
观测条件的好坏与观测成果的质量有着密切的联二观测误差分类:1.系统误差在相同的观测条件下,对某量进行一系列的观测,若观测误差的符号及大小保持不变,或按一定的规律变化,这种误差称为系统误差。
这种误差往往随着观测次数的增加而逐渐积累。
如某钢尺的注记长度为 30m,经鉴定后,它的实际长度为 30.016m,即每量一整尺,就比实际长度量小0.016m,也就是每量一整尺段就有+0.016m 的系统误差。
这种误差的数值和符号是固定的,误差的大小与距离成正比,若丈量了五个整尺段,则长度误差为 5×(+0.016)=+0.080m。
若用此钢尺丈量结果为 167.213m,则实际长度为:167.213+167.213×0.0016=167.213+0.089=167.302(m) 30系统误差对测量成果影响较大,且一般具有累积性,应尽可能消除或限制到最小程度,其常用的处理方法有:1.检校仪器,把系统误差降低到最小程度。
2.加改正数,在观测结果中加入系统误差改正数,如尺长改正等。
3.采用适当的观测方法,使系统误差相互抵消或减弱,如测水平角时采用盘左、盘右现在每个测回起始方向上改变度盘的配置等。
2.偶然误差在相同观测条件下,对某量作一系列的观测,若观测误差的大小及符号变化没有任何规律性,这种误差称为偶然误差,如估读误差,照准误差等。
从大量的测量实践中发现,虽然偶然误差从表面上看没有任何规律性,但是在相同的观测条件下,当观测次数愈多时,误差群的取值范围却服从一定的统计规律。
1)在一定的观测条件下,偶然误差的绝对值不会超过一定的限值。
2)绝对值小的误差比绝对值大的误差出现的机会多。
3)绝对值相等的正、负误差出现的机会基本相等。
4)偶然误差的算术平均值随着观测次数的无限增加而趋于零。
nlim i 10(5-1)n nn式中:= 1+ 2+⋯+n;i 1n——观测次数。
算术平均值研究误差的目的之一,就是把带有误差的观测值给予适当处理,以求得最可靠值。
取算术平均值的方法,就是其中最常见的一种。
一、原理在等精度观测条件下对某量观测了n 次,其观测结果为 L1,L2,⋯L n。
设该量的真值为 X,观测值的真误差为1,2⋯,n,即1=X - L12=X- L2⋯⋯⋯⋯n= X - L n将上列各式求和得:n=nX-n Li 1i 1n n上式两端各除以 n 得:i 1LX i 1n nn nL令i 1i 1xn n代入上式移项后得:X = x +δδ为 n 个观测值真误差的平均值,根据偶然误差的第四个性质,当 n→∞时,δ→0,则有:nlim i 10n n这时算术平均值就是某量的真值。
即:nLi 1xn在实际工作中,观测次数总是有限的,也就是只能采用有限次数的观测值来求得算术平均值,即:xnL i 1nx 是根据观测值所能求得的最可靠的结果,称为最或是值或算术平均值。
二、最或是误差 (改正数 )及特性最或是值与观测值之差称为最或是误差,又名观测值改正数,用V表示,即:V i = x - L i(i=1,2,⋯ n)取其和得:n nV= nx -Li 1i1nL∵x i 1n∴n(5-4) V 0i 1这是最或是误差的一大特征,用作计算上的校核。
评定观测值精度的标准研究误差的又一目的,是评定观测值的精度。
要判断观测误差对观测结果的影响,必须建立衡量观测值精度的标准,其中最常用的有以下几种:一、中误差1.用真误差来确定中误差在等精度观测条件下,对真值为X的某一量进行n 次观测,其观测值为L1,L2⋯L n,相应的真误差为1,2⋯Δn。
取各真误差平方的平均值的平方根,称为该量各观测值的中误差,以m表示,即:i = X -L in2m i 1(5-5)n2.用改正数来确定中误差在实际工作中,未知量的真值往往不知道,真误差也无法求得,所以常用最或是误差即改正数来确定中误差。
即:V i=x- L i (i=1,2,⋯ n)(5-6)nV 2m i 1(5-7)n1例一设用经纬仪测量某角五次,观测值列于表 5-2 中,求观测直的中误差。
表 5-2观测V=x- L VV观测值 L计算次=L- L0数56°32′20″56°32′1+20-1419600″200+63656°31′3-20+2667640″400+63656°32′5+3000-2457600″56°32′30″L0=56°-200+152+3032′00″05Li 1x L0556°32′00″5校核 V0i 15V 2m i 11520n15 1±19.49″二、容许误差由偶然误差的第一特性可以知道,在一定的观测条件下,偶然误差的绝对值不超过一定的限值。
根据误差理论和大量的实践证明,在一系列等精度观测误差中,大于两倍中误差的个数占总数的5% ,大于三倍中误差的个数占总数的0.3%,因此,测量上常取 2 倍或 3 倍中误差为误差的限值,称为容许误差,即:容容2m3m(5-7)三、相对误差衡量测量成果的精度,有时用中误差还不能完全表达观测结果的优劣。
例如用钢尺分别丈量两段距离,其结果为 100m 和 200m,中误差均为 2cm。
显然,后者的精度比前者要高。
也就是说观测值的精度与观测值本身的大小有关。
相对误差是中误差的绝对值与观测值的比值。
通常以分子为 1 的分数形式来表示,即:mKLK1 L / m如上述前者的相对误差 K10.0201=100500 K2= 0.0201说明后者比前者精度高。
20010000(5-8),后者的相对误差相对误差是个无名数,而真误差、中误差、容许误差是带有测量单位的数值。
误差传播定律及其应用在测量工作中,有些未知量不可能直接测量,或者是不便于直接测定,而是利用直接测定的观测值按一定的公式计算出来。
如高差h=a- b,就是直接观测值a、b 的函数。
若已知直接观测值a、b 的中误差 m a、m b后,求出函数h 的中误差 m h,即为观测值函数的中误差。
一、线性函数F = K1x1±K2x2±⋯± K nXn(5-9)式中: F ——为线性函数;K1——为常数;x1——为观测值。
设 x1的中误差为 m1,函数 F 的中误差为 m F,经推导得:m2F = (K1m1)2 + (K2m2)2 + ⋯ (K n m n)2(5-10)即,观测值函数中误差的平方,等于常数与相应观测值中误差乘积的平方和。
二、非线性函数其分微分为可写成其相应的函数中误差式为即例二1:500 比例尺地形图上,量得A、B 两点间的距离S=163.6mm,其中误差 m s=0.2mm。
求 A、B 两点实地距离 D 及其中误差 m D。
解: D=MS =500×163.6(mm) =81.8(m)(M 为比例尺分母 )m D=Mm S=500×0.2(mm) =±0.1(m)∴D=81.1±0.1(m)例三在三角形 ABC 中,∠ A 和∠ B 的观测中误差 m A和 m B分别为± 3″和± 4″,试推算∠ C 的中误差 m C。
解:∠ C=180°- (∠A+∠B)因为 180°是已知数没有误差,则得;m2C= m 2A+ m 2B∴m C=±5″例四某水准路线各测段高差的观测值中误差分别为h1=18.316m±5mm,h2=8.171m±4mm,h3=- 6.625m±3mm,试求总的高差及其中误差。
解: h = h1 + h2 + h3=15.316+8.171- 6.625=16.862(m)m 2h= m 21+ m 22+m 23=52+42+32m h=±7.1(mm)∴h=16.882m±7.1mm例五设对某一未知量 P,在相同观测条件下进行多次观测,观测值分别为 L1, L2⋯L n,其中误差均为 m,求算术平均值 x 的中误差M。
解:nLx i1L1L2L nn式中的1为常数,根据公式 (5-10),算术平均值的中误差为:n21m1)2+(122+⋯+ (1n2M = (n nm )nm )因为 m1=m2=⋯m n=m,得:M m(5-11) n从公式中可知,算术平均值中误差是观测值中误差的1倍,观n测次数愈多,算术平均值的误差愈小,精度愈高。
但精度的提高仅与观测次数的平方根成正比,当观测次数增加到一定次数后,精度就提高得很少,所以增加观测次数只能适可而止。
例六表 5-2 中,观测次数 n=5,观测值中误差 m=±19.5″,求算术平均值的中误差。
解:M m 19.5=±8.7″n5例七三角形的三个内角之和,在理论上等于180°,而实际上由于观测时的误差影响,使三内角之和与理论值会有一个差值,这个差值称为三角形闭合差。
设等精度观测 n 个三角形的三内角分别为a i、b i和 c i,其测角中误差均为 m = m a= m b=m c,各三角形内角和的观测值与真值180°之差为三角形闭合差fβ1、fβ2、⋯⋯fβnfβi = a i + b i + c i- 180°根据 (5-10)式得中误差关系式为:m2fβ = m2a + m2b + m2c = 3m2β∴ m fβ=±m 3由此得测角中误差为:mβ =±mfβ3按中误差定义,三角形闭合差的中误差为:nfβ2m fβ=±i1n将此式代入上式得:nf β2mβ =±i 1(5-12)3n式 (5-12)称为菲列罗公式,是小三角测量评定测角精度的基本公式。
