含参数的一元二次不等式的解法举例
含参数的一元二次不等式例题

含参数的一元二次不等式例题例题 1解不等式:x^2 2x + a > 0,其中a为参数。
解析:对于一元二次方程x^2 2x + a = 0,其判别式\Delta = 4 4a。
当\Delta 0,即4 4a 0,a > 1时,不等式的解集为R。
当\Delta = 0,即4 4a = 0,a = 1时,不等式化为(x 1)^2 > 0,解集为x ≠ 1。
当\Delta > 0,即4 4a > 0,a 1时,方程x^2 2x + a = 0的两根为x_1 = 1 \sqrt{1 a},x_2 = 1 + \sqrt{1 a},不等式的解集为x 1 \sqrt{1 a}或x > 1 + \sqrt{1 a}。
例题 2解不等式:ax^2 + 2x + 1 > 0,其中a为参数。
解析:当a = 0时,不等式化为2x + 1 > 0,解得x > \frac{1}{2}。
当a ≠ 0时,对于一元二次方程ax^2 + 2x + 1 = 0,其判别式\Delta = 4 4a。
若\Delta 0,即4 4a 0,a > 1,不等式的解集为R。
若\Delta = 0,即4 4a = 0,a = 1,不等式化为(x + 1)^2 > 0,解集为x ≠ 1。
若\Delta > 0,即4 4a > 0,a 1且a ≠ 0,方程ax^2 + 2x + 1 = 0的两根为x_1 = \frac{1 + \sqrt{1 a}}{a},x_2 =\frac{1 \sqrt{1 a}}{a}。
当0 a 1时,不等式的解集为x \frac{1 \sqrt{1 a}}{a}或x > \frac{1 + \sqrt{1 a}}{a}。
当a 0时,不等式的解集为\frac{1 + \sqrt{1 a}}{a} x\frac{1 \sqrt{1 a}}{a}。
含参数的一元二次不等式

含参数的一元二次不等式的解法
解含参数的一元二次不等式,通常情况下,均需分类讨论,那么如何讨论呢?对含参一元二次不等式常用的分类方法有三种:
一、按2x 项的系数a 的符号分类,即0,0,0<=>a a a ;
例1 解不等式:()0122>+++x a ax
例2 解不等式()00652≠>+-a a ax ax
分析 因为0≠a
,0>∆,所以我们只要讨论二次项系数的正负。
二、按判别式∆的符号分类,即0,0,0<∆=∆>∆;
例3 解不等式042>++ax x
分析 本题中由于2x 的系数大于0,故只需考虑∆与根的情况。
例4 解不等式()()R m x x m ∈≥+-+014122
三、按方程02=++c bx ax 的根21,x x 的大小来分类,即
212121,,x x x x x x <=<;
例5 解不等式)0( 01)1(2≠<++
-a x a a x 例6 解不等式06522>+-a
ax x ,0≠a
练习、(1)解关于x 的不等式:.0)2(2
>+-+a x a x (2)解关于x 的不等式:.01)1(2
<++-x a ax (3)解关于x 的不等式:.012
<-+ax ax。
含参数的一元二次不等式的解法高中数学

含参数的一元二次不等式的解法高中数学一元二次不等式是高中数学中重要的内容之一,它与一元二次方程不同,需要通过特定的方法来解决。
当一元二次不等式中出现参数时,解法也会有所不同。
本文将介绍含参数的一元二次不等式的解法。
首先,我们来看一个简单的例子,假设有不等式 f(x) =ax^2+bx+c > 0,其中a、b、c为实数且不为零。
我们的目标是确定x的取值范围使得不等式成立。
步骤一:将不等式化简为标准形式首先,我们需要将不等式化简为标准形式,即形如(ax^2+bx+c)>0的形式。
若不等式已经处于此形式,则可以直接进行下一步。
若不等式不满足此形式,则需要移项合并同类项,将不等式转化为标准形式。
步骤二:确定基本情况下的解法对于标准形式的一元二次不等式,我们可以利用图像法或代数法来解决。
对于a>0和a<0的两种情况,基本的解法如下:1. 当a>0时:- 如果a>0,二次函数的开口朝上,函数图像是一个开口朝上的抛物线。
此时的不等式解集为抛物线上方的实数集。
- 若抛物线与x轴有两个交点,我们可以通过求解对应的一元二次方程,求出两个交点x1和x2。
然后我们可以得到解集: x<x1 或x>x2- 若抛物线与x轴只有一个交点,我们可以求解的结果只有一个交点x0,此时解集为:x<x0 或 x>x0。
2. 当a<0时:- 如果a<0,二次函数的开口朝下,函数图像是一个开口朝下的抛物线。
此时的不等式解集为抛物线下方的实数集。
- 若抛物线与x轴有两个交点,我们可以通过求解对应的一元二次方程,求出两个交点x1和x2。
然后我们可以得到解集: x1<x<x2- 若抛物线与x轴没有交点,则解集为空集:ø步骤三:含参数时的解法当一元二次不等式中存在参数时,解法稍有不同。
我们以一个具体的例子来说明。
例题:对于不等式f(x) = (a+b)x^2+(b+c)x+c>0,其中a,b,c 为实数且不为零。
含参数的一元二次不等式的解法

含参数的一元二次不等式的解法含参一元二次不等式常用的分类方法有三种:一、按$x$项的系数$a$的符号分类,即$a>0$,$a=0$,$a<0$。
例1:解不等式$ax+(a+2)x+1>2$分析:本题二次项系数含有参数,$\Delta=(a+2)^2-4a=a+4>0$,故只需对二次项系数进行分类讨论。
解:当$a>0$时,解得方程$ax+(a+2)x+1=0$的两根$x_1=-\frac{a+2+\sqrt{a+4}}{2a}$,$x_2=-\frac{a+2-\sqrt{a+4}}{2a}$,因为$a>0$,所以$x_1x_2$或$x<x_1$,即$x\in\left(-\infty,\frac{a+2-\sqrt{a+4}}{2a}\right)\cup\left(\frac{a+2+\sqrt{a+4}}{2a},+\infty\right)$。
当$a=0$时,不等式为$2x+1>2$,解得$x>\frac{1}{2}$,即解集为$x>\frac{1}{2}$。
当$a<0$时,解得方程$ax+(a+2)x+1=0$的两根$x_1=-\frac{a+2-\sqrt{a+4}}{2a}$,$x_2=-\frac{a+2+\sqrt{a+4}}{2a}$,因为$a<0$,所以$x_1<x_2$。
所以解集为$x_1<x<x_2$,即$x\in\left(\frac{a+2-\sqrt{a+4}}{2a},\frac{a+2+\sqrt{a+4}}{2a}\right)$。
例2:解不等式$ax-5ax+6a>(a\neq0)^2$分析:因为$a\neq0$,$\Delta>0$,所以我们只需讨论二次项系数的正负。
解:当$a>0$时,解得方程$ax-5ax+6a=0$的两根$x_1=2$,$x_2=3$,因为$a>0$,所以$x_13$,即$x\in\left(-\infty,2\right)\cup\left(3,+\infty\right)$。
含参一元二次不等式的解法

变式3: 设不等式mx 2 x m 1 0对于满足 | m | 2的一切
2
m值都成立,则x的取值范围。
ax 5 例3.已知关于x的不等式 2 0的解集为 M x a (1) 当a 4 时,求集合 M ; (2)若3 M , 且 5 M , 求实数a的取值范围。 5 x 4x 5 4 0 解: (1) a 4 时,得 2 0, ( x 2)( x 2) x 4
2
ax 2. 1的解集为{x | x 1或x 2}, 求a. x 1
例 2: 已知关于x的不等式(k 2 4k 5) x 2 4(1 k ) x 3 0 的解集为R, 求实数k的取值范围。
变式1:解集为空集 2 x 2 2mx m 变式2:如果不等式 1对一切x R都成立, 2 4x 6x 3 则实数m的取值范围是
5 3a 5 解: (2) 3 M , 0, a 9 或 a 3 9a 5a 5 5 M , 25 a 0或 0, 25 a 即 (a 1)(a 25) 0, 1 a 25 5 综上,a 的取值范围是a | a 或a 9 a | 1 a 25 3 5 a | 1 a 或 9 a 25 3
例1、解不等式 (1)2 x ax 2 0;
2
(2)ax ( a 2) x 2 0
2
练习:解不等式
x (a a ) x a 0
2 2 3
练习 1. 已知不等式ax bx c 0的解集为
2
{x | x }, 其中 0, 求不等式 cx bx a 0的解集.
5 故 x 2, 或 x 2 4
含参数的一元二次不等式

含参数的一元二次不等式的解法含参一元二次不等式常用的分类方法有三种:一、按2x 项的系数a 的符号分类,即0,0,0<=>a a a ;例1 解不等式:()0122>+++x a ax分析:本题二次项系数含有参数,()044222>+=-+=∆a a a ,故只需对二次项 系数进行分类讨论。
解:∵()044222>+=-+=∆a a a 解得方程 ()0122=+++x a ax 两根,24221a a a x +---=a a a x 24222++--= ∴当0>a 时,解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<++-->a a a x a a a x x 242242|22或 当0=a 时,不等式为012>+x ,解集为⎭⎬⎫⎩⎨⎧>21|x x 当0<a 时, 解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+---<<++--a a a x a a a x 242242|22 例2 解不等式()00652≠>+-a a ax ax分析 因为0≠a ,0>∆,所以我们只要讨论二次项系数的正负。
解 ()()032)65(2>--=+-x x a x x a∴当0>a 时,解集为{}32|><x x x 或;当0<a 时,解集为{}32|<<x x二、按判别式∆的符号分类,即0,0,0<∆=∆>∆;例3 解不等式042>++ax x分析 本题中由于2x 的系数大于0,故只需考虑∆与根的情况。
解:∵162-=∆a∴当()4,4-∈a 即0<∆时,解集为R ;当4±=a 即Δ=0时,解集为⎭⎬⎫⎩⎨⎧≠∈2a x R x x 且;当4>a 或4-<a 即0>∆,此时两根分别为21621-+-=a a x ,21622---=a a x ,显然21x x >, ∴不等式的解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧----+->21621622a a x a a x x 〈或 例4 解不等式()()R m x x m ∈≥+-+014122解 因,012>+m ()()2223414)4(m m -=+--=∆ 所以当3±=m ,即0=∆时,解集为⎭⎬⎫⎩⎨⎧=21|x x ; 当33<<-m ,即0>∆时,解集为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+--+-+>1321322222m m x m m x x 〈或; 当33>-<m m 或,即0<∆时,解集为R 。
含参数的一元二次不等式的解法
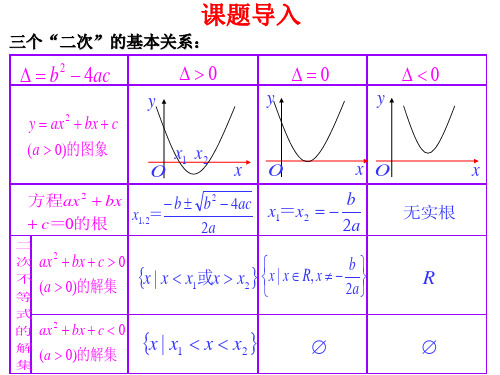
2、上述不等式所对应的一元二次方程的特征是什么? 二次项前面没有参数、可因式分解
3、若将条件a>1去掉,该不等式如何求解?
分类讨论,比较两根a与1的大小关系
引导探究 变式训练:
1、解关于x的不等式 x2-ax - (a+1) >0
2、解关于x的不等式 ax2-(a+1)x+1>0
数学思想:分类讨论思想
当堂练习(10分钟)
基础题1.解关于x的不等式:x2 + 5ax + 6a2 > 0
2.解关于x的不等式:ax2 + (6a+1)x + 6 > 0
探究题: 已知常数 a R, 解关于x的不等式: ax2 2x a 0
当堂诊学(10分钟)
请同学们根据下面提供的答案自我订正:
思考:
{x x 5 或x 6}
2
R
{x 2 x 1}
3
2
1、解一元二次不等式时要考虑哪些要素?
2、若对于一个一元二次不等式中项的系数含有参数,
该如何解决呢?
解关于x的不等式x2-(a+1)x+a>0(a>1)
引导探究 解关于x的不等式x2-(a+1)x+a>0(a>1)
探究: 1、解一元二次不等式应考虑它的哪些要素?
当a <0时,解集为:{x︱x> -3a或x< -2a};
1:
当a =0时,解集为: {x︱x∈R且x≠0};
当a >0时,解集为:{x︱x> -2a或x< -3a}.
1.当a
0时,解集为x
6
含参数的一元二次不等式

-a
1 (-a)
-a
(1)-a<1(2) -a=1 (3)-a>1
例2
解不等式ax +(a-1)x-1>0(a R)
2
二次项含有参数应如何求解?
考点
含参数的一元二次不等式
y x y
x1
O
x2
x1
O
x2
ห้องสมุดไป่ตู้
x
解不等式ax2 +(a-1)x-1>0(a R)
2
,
显然
x1 x 2
a a 2 16 x2 2
∴原不等式的解集为:
a a 2 16 a a 2 16 x x 或 x 〈 2 2
成果验收
课堂练习:
若不等式( 1-a)x2 4 x 6 0的解集是{-3<x<1}, 求实数a的值.
mx2-2x-m+1的图象全部在x轴下方.
当m=0时,1-2x<0, 1 即当x> 时,不等式恒成立,不满足题意; 2 当m≠0时,函数f(x)=mx2-2x-m+1为二次函数, 需满足开口向下且方程mx2-2x-m+1=0无解,即
m 0 , 则m无解. 4 4m(1 m) 0
例1 不等式ax2 +(a-1)x+ a-1<0对所有实数x∈R 都成立,求a的取值范围.
分析:开口向下,且与x轴无交点 。 解:由题目条件知: (1) a < 0,且△ < 0. 因此a < -1/3。 (2)a = 0时,不等式为-x-1 <0 不符合题意。 1 a | a 综上所述:a的取值范围是 3
