运筹学之对偶单纯形法
运筹学-单纯形法灵敏度对偶
若新增约束如下：
max z 50x1 100x2 x1 x2 300 2x1 x2 400 x2 250 10x1 30x2 5000(电力约束) x1, x2 , 0
x1 x2 s1
把最优解x1=50,x2 =250代入电力约束 1050+30 250=80005000 新约束不满足,最优解变化
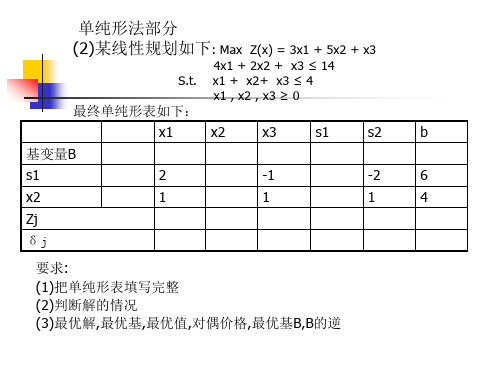
例题：已知某线性规划初始可行基是（S1 S2 S3 a1）， 最终单纯形表如下，求对偶价格不变时的△bi变化范围
x1 x2 s1
50 100 0
X1 50
1
0
0
S3 0
0
0
0
X2 100 0
1
0
s1 0
0
0
1
Zj
50 100 0
δj
0
0
0
（1） △b1的变化范围： ?
（2） △b2的变化范围：?
（3） △b3的变化范围： ? （4） △b4的变化范围：?
1 0 1 2 0.5
B1 p6'
2
1
1
0.5
2
0 0 1 1.5 1.5
Z6' 50 0.5 0 (2) 100 1.5 175
' 6
C6
Z6'
150 175
25
δ6´<0，最优解不变，即仍生产Ⅰ50件，Ⅱ100件。
2、变量xk系数列由pk变为pk´，在最终单纯形表 上xk是基变量
x1 x2 s1
50 100 0
X1 50 1
0
0
S3 0
0
0
0
X2 100 0
1
0
s1 0
0
运筹学 对偶单纯形法
=min{j’ / akj’┃akj’<0}=r’/akr’那么 xr为进基变量,转4； 4.以akr’为转轴元,作矩阵行变换使其变为1,该
列其他元变为0,转2。
2.对偶单纯形法
例3.2：求解线性规划问题：
1.线性规划对偶问题
对称形式： (P) Max z = cT x s.t. Ax ≤ b x ≥0 “Max -- ≤ ”
互为对偶 (D) Min f = bT y s.t. AT y ≥ c y ≥0 “Min-- ≥”
线性规划的对偶模型
原问题（或对偶问题） 约束条件右端项 目标函数变量的系数 目标函数 max 约 束 条 件 m个 ≤ ≥ = n个 变 量 ≥0 ≤0 无约束 对偶问题（或原问题） 目标函数变量的系数 约束条件右端项 目标函数 min m个 ≥0 ≤0 无约束 n个 ≥ ≤ = 约 束 条 件 变 量
否
所有aik
计算
0
否
是
Hale Waihona Puke 0 bi be min aik 0 aik aek
计算
j min aej 0 k < aej aek
以为中心元素进行迭代
以为中心元素进行迭代
单纯形法和对偶单纯形法步骤
2.对偶单纯形法 对偶单纯形法的适用范围 对偶单纯形法适合于解如下形式 的线性规划问题
0 x4 0 1 0 0 0 1 0 0 0 1 0 0
0 x5 0 0 1 0 -1 -1 1 -100 -1 1 1 -50
I
θ i 300 400 250 50 75
运筹学及其应用4.3 对偶单纯形法
min w= 2x1+3x2+4x3+0x4+0x5 x1+2x2+ x3-x4＝ 1 2x1- x2+3x3– x5＝4 x1,x2,x3,x4,x5≥ 0
min w= 2x1+3x2+4x3+0x4+0x5 -x1-2x2- x3+x4＝ -1 -2x1+x2-3x3+x5＝ -4 x1,x2,x3,x4,x5≥ 0
4
234 000
0
x1 x2 x3 x4 -1 -2 -1
x4 x5 b 1 0 -1
max
2 −2
4 ，
−3
=
−1
0 x5 -2* 1 -3 0 1 -4
σ 234 000
0 x4 0 -2.5 0.5 1 -0.5 1
2 x1 1 -0.5 1.5 0 -0.5 2
σ 0 4 1 0 1 -4
步骤：(1)保持σj ≥ 0，j= 1,···,n，确定XB，建立计算表格； (2)判别XB = B-1b ≥ 0是否成立？ ①若成立，XB为最优基变量； ②若不成立，转(3)；
1
步骤：(1)保持σj ≥ 0，j= 1,···,n，确定XB，建立计算表格；
(2)判别XB = B-1b ≥ 0是否成立？ ①若成立，XB为最优基变量； ②若不成立，转(3)；
5
• 作业 • P81 1.12(1)
6
§3 对偶单纯形法
单纯形法：由 XB = B-1b ≥ 0，使σj ≥ 0，j = 1,···,m 对偶单纯形法：由σj ≥ 0(j= 1,···,n)，使XB = B-1b ≥ 0 相同点：都用于求解原问题
韩伯棠管理运筹学(第三版)_第六章_单纯形法的灵敏度分析与对偶
迭代 基
次数 变 量
CB
x1 x2 。 s1 50 100 0
s2
s3
0 0b
x1 50 1 0 1
0 -1 50
S2 0 0 0 -2
1 1 50
2
x2 100 0 1 0
0 1 250
zj
50 100 50 0 50
σj=cj-zj
0 0 -50
0 -50 2750 0
❖
从上表可以发现设备台时数的约束方程中的松弛变量S1
j ck akj 0, ck akj j ,
当a kj
0, ck
j
akj
,这里 j
akj
0;
当a kj
0, ck
j
akj
,这里 j
akj
0;
而当j k时, k ck ck zk ck ck zk ckaKK ,
因为xk是基变量,知 k 0, akk 1,故知 k 0.
x1 x2 s1 50 100 0 1 01 0 0 -2 0 10
s2
s3
00
b
0 -1 50
1 1 50
0 1 250
zj σj=cj-zj
50 100 50 0 0 -50
0 50 0 -50
Z= 27500
先对非基变量s1的目标函数的系数C3进行灵敏度 分析。这里σ3=-50，所以当C3 的增量ΔC3≤-(-50)即 ΔC3≤50时，最优解不变，也就是说S1的目标函数的系 数C′3=C3+△C3≤0+50=50时，最优解不变。
规划问题的对偶价格就不变。而要使所有的基变量仍然
是基变量只要当bj 变化成b′j =bj+△bj时，原来的基不变所 得到的基本解仍然是可行解，也就是所求得的基变量的
应用运筹学基础：线性规划（4）-对偶与对偶单纯形法
应⽤运筹学基础：线性规划（4）-对偶与对偶单纯形法这⼀节课讲解了线性规划的对偶问题及其性质。
引⼊对偶问题考虑⼀个线性规划问题：$$\begin{matrix}\max\limits_x & 4x_1 + 3x_2 \\ \text{s.t.} & 2x_1 + 3x_2 \le 24 \\ & 5x_1 + 2x_2 \le 26 \\ & x \ge0\end{matrix}$$ 我们可以把这个问题看作⼀个⽣产模型：⼀份产品 A 可以获利 4 单位价格，⽣产⼀份需要 2 单位原料 C 和 5 单位原料 D；⼀份产品 B 可以获利 3 单位价格，⽣产⼀份需要 3 单位原料 C 和 2 单位原料 D。
现有 24 单位原料 C，26 单位原料 D，问如何分配⽣产⽅式才能让获利最⼤。
但假如现在我们不⽣产产品，⽽是要把原料都卖掉。
设 1 单位原料 C 的价格为 $y_1$，1 单位原料 D 的价格为 $y_2$，每种原料制定怎样的价格才合理呢？⾸先，原料的价格应该不低于产出的产品价格（不然还不如⾃⼰⽣产...），所以我们有如下限制：$$2y_1 + 5y_2 \ge 4 \\ 3y_1 + 2y_2 \ge3$$ 当然也不能漫天要价（也要保护消费者利益嘛- -），所以我们制定如下⽬标函数：$$\min_y \quad 24y_1 + 26y_2$$ 合起来就是下⾯这个线性规划问题：$$\begin{matrix} \min\limits_y & 24y_1 + 26y_2 \\ \text{s.t.} & 2y_1 + 5y_2 \ge 4 \\ & 3y_1 + 2y_2 \ge 3 \\ & y \ge 0\end{matrix}$$ 这个问题就是原问题的对偶问题。
对偶问题对于⼀个线性规划问题（称为原问题，primal，记为 P） $$\begin{matrix} \max\limits_x & c^Tx \\ \text{s.t.} & Ax \le b \\ & x \ge 0\end{matrix}$$ 我们定义它的对偶问题（dual，记为 D）为 $$\begin{matrix} \min\limits_x & b^Ty \\ \text{s.t.} & A^Ty \ge c \\ & y \ge 0\end{matrix}$$ 这⾥的对偶变量 $y$，可以看作是对原问题的每个限制，都⽤⼀个变量来表⽰。
对偶单纯形法
1. 换出变量的确定原则
常数列中最小的负元素所在的行所对应的基变量为换出变量.
p11-1
§3.4 灵敏度分析
运筹学
灵敏度分析——研究系数变化对最优解的影响.
一、改变价值向量
在最终表内, cr的变化只引起检验数的变化, 需重新计算检验数.
§3.3 对偶单纯形法
运筹学
一、对偶单纯形法与单纯形法的区别
对 运用对偶单纯形法时, 不需要引入人工变量, 但必须先给 定原问题的一个对偶可行基本解.
二、对偶单纯形法的求解方法
▲ 以求解下述线性规划 问题为例
min z 2x1 3x2 4x3 s.t. x1 2x2 x3 3
二、改变资源向量
在最终表内, br的变化只引起右端项的变化, 需重新计算右端项. 利用B-1(b+b).
三、改变A中的一列
通常是非基变量所对应的列, 需重新计算检验数.
四、增加一个新的约束条件
五、增加一个新的变量
p11-2
运筹学
作业：P81第1.12题之（2）； 第1.13题
p11-3
对偶单纯形法的计算步骤_实用运筹学：案例、方法及应用_[共3页]
![对偶单纯形法的计算步骤_实用运筹学：案例、方法及应用_[共3页]](https://img.taocdn.com/s3/m/2b3f6b0576a20029bc642d90.png)
41第2章对偶理论与灵敏度分析即y 是对偶问题（D ）的一个可行解。
条件式（2-21）称为对偶可行性条件，即最优性条件式（2-20）与对偶可行性条件式（2-21）是等价的，因此，如果一个原始可行基B 是原问题（P ）的最优基，则1=B y c B -就是对偶问题（D ）的一个可行解，此时对应的目标函数值1B w=yb =c B -，等于原问题（P ）的目标函数值，可知1=B y c B -也是对偶问题（D ）的最优解。
若原问题（P ）的一个基本解1=0B b x ⎛⎞⎜⎟⎝⎠-对应的检验数向量满足条件式（2-20），即 =(,)=0,0B N N B σσσc c B N -1（-）≤则称x 为（P ）的一个正则解。
于是可知，原问题（P ）的正则解x 与对偶问题（D ）的可行解y 是一一对应的，它们由同一个基B 所决定，我们称这一基为正则基。
因此，我们可以设想另一条求解思路，即在迭代过程中，始终保持对偶问题解的可行性，而原问题的解由不可行逐渐向可行性转化，一旦原问题的解也满足了可行性条件，也就达到了最优解。
也即在保持正则解的正则性不变条件下，在迭代过程中，使原问题解的不可行性逐步消失，一旦迭代到可行解时，即达到了最优解。
这正是对偶单纯形法的思路，这个方法并不需要把原问题化为对偶问题，利用原问题与对偶问题的数据相同（只是所处位置不同）这一特点，直接在反映原问题的单纯形表上进行运算。
2.3.2 对偶单纯形法的计算步骤求解如下标准形式线性规划问题：max =z cx s.t.0Ax =bx ⎧⎨⎩≥对偶单纯形法的计算步骤如下：（1）找一个正则基B 和初始正则解(0)x ；将原问题化为关于基B [不妨设12=(,,,)m B P P P ]的典式，列初始对偶单纯形表，如表2-5所示。
表2-5 对偶单纯形表12 1 2 12121c 1x 1'b 1 0 … 0 1+1'm a 1+2'm a … 1'n a 2c 2x 2'b 01 02+1'm a 2+2'm a … 2'n am c m x'm b 0…1 +1'mm a +2'mm a … 'mn a c j -z j0 0 0+1m σ+2m σ…n σ（2）若1=b'B b -≥0，则停止计算，当前的正则解1=x B b -，即为原问题的最优解；否则转下一步。
(运筹学大作业)单纯性法与对偶单纯性法的比较
对偶单纯形法与单纯形法对比分析1．教学目标：通过对偶单纯形法的学习，加深对对偶问题的理解2．教学内容：1）对偶单纯形法的思想来源 2）对偶单纯形法原理3．教学进程：1）讲述对偶单纯形法解法的来源：所谓对偶单纯形法，就是将单纯形法应用于对偶问题的计算，该方法是由美国数学家C.莱姆基于1954年提出的，它并不是求解对偶问题解的方法，而是利用对偶理论求解原问题的解的方法。
2）为什么要引入对偶单纯形法：单纯形法是解线性规划的主要方法，对偶单纯形法则提高了求解线性规划问题的效率，因为它具有以下优点： （1）初始基解可以是非可行解, 当检验数都为负值时, 就可以进行基的变换, 不需加入人工变量, 从而简化计算； （2）对于变量多于约束条件的线性规划问题,用对偶单纯形法可以减少计算量,在灵敏度分析及求解整数规划的割平面法中,有时适宜用对偶规划单纯形法。
由对偶问题的基本性质可以知道，线性规划的原问题及其对偶问题之间存在一组互补的基解，其中原问题的松弛变量对应对偶问题的变量，对偶问题的剩余变量对应原问题的变量；这些互相对应的变量如果在一个问题的解中是基变量，则在另一问题的解中是非基变量；将这对互补的基解分别代入原问题和对偶问题的目标函数有z=w 。
据此可知，用单纯形法求解线性规划问题时，在得到原问题的一个基可行解的同时，在检验数行得到对偶问题的一个基解，并且将两个解分别代入各自的目标函数时其值相等。
我们知道，单纯形法计算的基本思路是保持原问题为可行解（这时一般其对偶问题为非可行解）的基础上，通过迭代，增大目标函数，当其对偶问题的解也为可行解时，就达到了目标函数的最优值。
那么对偶单纯形法的基本思想可以理解为保持对偶问题为可行解（这时一般原问题为非可行解）的基础上，通过迭代，减小目标函数，当原问题也达到可行解时，即达到了目标函数的最优值。
其实对偶单纯形法本质上就是单纯形法, 只不过在运用时需要将单纯形表旋转一下而已。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5.换基运算： 1 1
1 1
0 0
min Z 4x1 x2 3x3
x1 x2 x3 x4 5 x1 x2 4x3 x5 3 x1 , x2 , x3 , x4 , x5 0
单
x1 x2 x3 x4 x5 常数列
纯 形
x42 -1 -1
-1 -1
0
-5 (1)
表
x5 -1 1
式，可 用两阶 段法求
x1 , x2 , x3 , x4 , x5 0 解，麻
烦！
min Z 4x1 x2 3x3
x1 x2 x3 x4 5 x1 x2 4x3 x5 3 x1 , x2 , x3 , x4 , x5 0
注：对偶单纯形法适用于目标函数系数都 0，不等 式约束都 0 的问题。
单
x1 x2 x3 x4 x5 常数列
纯 形
x2 1
1
1 -1 0
5 (1)
表
x5 -2 0
3
11
-8
检验数 34 01
23
10 0
-05
二.对偶单纯形法的迭代步骤： 例2-8
2.最优性检验：
若当前常数列 0，则得到最
优表。否则转下一步。
min Z 4x1 x2 3x3
x1 x2 x3 x4 5 x1 x2 4x3 x5 3 x1 , x2 , x3 , x4 , x5 0
优 表
检验数
0
x4
x5 常数 min Z 2x1 2x2 x4
0
x1 x2 x3 5
x1 x2 x4 6 6x1 2x2 x5 21
x1, x2 , x3 , x4 , x5 0
一.对偶单纯形法与单纯形法的区别： 不同之处：
单纯形法：在迭代过程中，始终保持常数列 0 ，而 检验数行由有负检验数逐步变为全部 0
00
x4 x5 常数列
1 0 -5
01 00
-3
0 0
有负分量
注：检验数行 0 ，因此可以用对偶单纯形法求解，
否则不能用。
二.对偶单纯形法的迭代步骤： 例2-8
2.最优性检验：
min Z 4x1 x2 3x3
若当前常数列 0，则得
x1 x2 x3 x4 5
到最优表。否则转下一步。 x1 x2 4x3 x5 3
x1 , x2 , x3 , x4 , x5 0
单
x1 x2 x3 x4 x5 常数列
纯 形
x4 -1 -1 -1
10
-5
表
x5 -1 1
4
01
-3
检验数 4 1
3
00
0 0
有负分量
二.对偶单纯形法的迭代步骤： 例2-8
3.确定出基变量：
min Z 4x1 x2 3x3
将常数列中最负分量所在的
检验数
0
二.对偶单纯形法的迭ห้องสมุดไป่ตู้步骤： 求解例2-8
min Z 4x1 x2 3x3
x1 x2 x3 5 标准形 x1 x2 4x3 3 x1, x2 , x3 0
min Z 4x1 x2 3x3 不是典
x1 x2 x3 x4 5 x1 x2 4x3 x5 3
对偶单纯形法：在迭代过程中，始终保持检验数行 0 ， 而常数列由有负分量逐步变为全部 0
最
x1 x2
x3
x4
x5 常数 min Z 2x1 2x2 x4
优
x1 x2 x3 5
表
0
x1 x2 x4 6 6x1 2x2 x5 21
x1, x2 , x3 , x4 , x5 0
4
01
-3
检验数 4 1
3
00
0 0
二.对偶单纯形法的迭代步骤： 例2-8
5.换基运算： 1 1
1 1
0 0
min Z 4x1 x2 3x3
x1 x2 x3 x4 5 x1 x2 4x3 x5 3 x1 , x2 , x3 , x4 , x5 0
单
x1 x2 x3 x4 x5 常数列
二.对偶单纯形法的迭代步骤： 例2-8
1.建立初始单纯形表
j cj CBB1 pj
CB B1b
cj 4 1
3
单 CB
x1 x2 x3
纯0
形 表
0
x4 x5
-1 -1
-1 1
-1 4
检验数 4 1
3
min Z 4x1 x2 3x3
x1 x2 x3 x4 5 x1 x2 4x3 x5 3 x1 , x2 , x3 , x4 , x5 0
纯 形
x2 1
1
1 -1 0
5 (1)
表
x5 --21 10
43
01 1
--38
检验数 4 1
3
00
0 0
二.对偶单纯形法的迭代步骤： 例2-8
5.换基运算： 1 1
1 1
0 0
min Z 4x1 x2 3x3
x1 x2 x3 x4 5 x1 x2 4x3 x5 3 x1 , x2 , x3 , x4 , x5 0
基。
单
x1 x2 x3 x4 x5 常数列
纯 形
x4 -1 -1 -1
10
-5
表
x5 -1 1
4
01
-3
检验数 4 1
3
00
0 0
min{ 4 , 1 , 3 } 1 1 1 1 1
x2为进基变量。若出基变量所在的行中，
所有元素都 0 ，则原问题无可行解。停止计算。
二.对偶单纯形法的迭代步骤： 例2-8
00
0 0
有负分量
二.对偶单纯形法的迭代步骤： 例2-8
4.确定进基变量：
min Z 4x1 x2 3x3
在出基变量所在的行中，找出非基变 量列中的负系数，用相应的检验数分 别除以这些负系数，再取绝对值，所
x1 x2 x3 x4 5 x1 x2 4x3 x5 3
得正比值中最小者相应的非基变量进 x1, x2 , x3 , x4 , x5 0
第二章 线性规划的对偶理论
2.1 对偶线性规划模型 2.2 对偶问题的性质 2.3 对偶单纯形法 2.4 灵敏度分析与参数分析
一.对偶单纯形法与单纯形法的区别：
相同之处：对偶单纯形法与单纯形法都是对单纯形表 进行迭代计算。
当常数列 0，而检验数行都 0 时，单
纯形表是最优表。
最 x1 x2 x3
x1 x2 x3 x4 5
行相应的基变量出基。
x1 x2 4x3 x5 3
min{5, 3} 5 x4为出基变量 x1, x2 , x3 , x4 , x5 0
单
x1 x2 x3 x4 x5 常数列
纯 形
x4 -1 -1 -1
10
-5
表
x5 -1 1
4
01
-3
检验数 4 1
3
单
x1 x2 x3 x4 x5