对偶问题及对偶单纯形法(完整)
合集下载
第三章 线性规划的对偶理论
s.t. AX=b X≥0 由于 AX=b 即 AX=b
AX≤b AX≥b
AX≤b -AX≤-b 所以，原问题可化为 max z=CX s.t. AX≤b -AX≤-b X≥0
A
X≤ -A
b
-b
14
设Y'：AX≤b的对偶变量（行向量） Y''：-AX≤-b的对偶变量（行向量） 按对称形式的对偶关系可得出原问题的对偶问题如下： min w =Y'b-Y''b= （Y'-Y''）b （Yb=bTYT） s.t Y'A-Y''A≥C （ YA=ATYT） Y'≥0，Y''≥0 令Y= Y'-Y''，则对偶问题为 min w =Yb s.t YA≥C Y符号不限 结论：原问题中约束条件为等式，对应的对偶变量 无非负要求；反过来同样成立。
s.t. 2y1+ y2+ 4y3 ≥2
2y1+2y2+ 4y4 ≥3 y1, y2 , y3 , y4 ≥ 0
解：2.首先将原式变形
m axZ 2 x1 3 x 2 4 x 3 2 x 3 x 2 5 x 3 2 3 x1 x 2 7 x 3 3 x1 4 x 2 6 x 3 5 x1 , x 2 , x 3 0
对于非对称形式的规划，可以按照下面的对应关系直接给 出其对偶规划。 （1）对原问题模型为“max，约束条件为≤”或“min，约 束条件为≥” 的形式，对应的对偶规划的变量大于 0 ；反之， 若原问题模型为“max，≥”或“min，≤” 的形式，对应的 对偶规划的变量小于0。 （ 2 ）原问题线性规划的决策变量大于 0 ，则对偶问题的模 型为“max，约束条件为≤”或“min，约束条件为≥” 的形 式；若原问题线性规划的决策变量小于0；则对偶问题的模型 为“max，≥”或“min，≤” 的形式。
运筹学 对偶单纯形法
3.若所有akj’≥0( j = 1,2,…,n )，则原问题 无可行解,停止;否则,若有akj’<0 则选
=min{j’ / akj’┃akj’<0}=r’/akr’那么 xr为进基变量,转4； 4.以akr’为转轴元,作矩阵行变换使其变为1,该
列其他元变为0,转2。
2.对偶单纯形法
例3.2：求解线性规划问题：
1.线性规划对偶问题
对称形式： (P) Max z = cT x s.t. Ax ≤ b x ≥0 “Max -- ≤ ”
互为对偶 (D) Min f = bT y s.t. AT y ≥ c y ≥0 “Min-- ≥”
线性规划的对偶模型
原问题（或对偶问题） 约束条件右端项 目标函数变量的系数 目标函数 max 约 束 条 件 m个 ≤ ≥ = n个 变 量 ≥0 ≤0 无约束 对偶问题（或原问题） 目标函数变量的系数 约束条件右端项 目标函数 min m个 ≥0 ≤0 无约束 n个 ≥ ≤ = 约 束 条 件 变 量
否
所有aik
计算
0
否
是
Hale Waihona Puke 0 bi be min aik 0 aik aek
计算
j min aej 0 k < aej aek
以为中心元素进行迭代
以为中心元素进行迭代
单纯形法和对偶单纯形法步骤
2.对偶单纯形法 对偶单纯形法的适用范围 对偶单纯形法适合于解如下形式 的线性规划问题
0 x4 0 1 0 0 0 1 0 0 0 1 0 0
0 x5 0 0 1 0 -1 -1 1 -100 -1 1 1 -50
I
θ i 300 400 250 50 75
=min{j’ / akj’┃akj’<0}=r’/akr’那么 xr为进基变量,转4； 4.以akr’为转轴元,作矩阵行变换使其变为1,该
列其他元变为0,转2。
2.对偶单纯形法
例3.2：求解线性规划问题：
1.线性规划对偶问题
对称形式： (P) Max z = cT x s.t. Ax ≤ b x ≥0 “Max -- ≤ ”
互为对偶 (D) Min f = bT y s.t. AT y ≥ c y ≥0 “Min-- ≥”
线性规划的对偶模型
原问题（或对偶问题） 约束条件右端项 目标函数变量的系数 目标函数 max 约 束 条 件 m个 ≤ ≥ = n个 变 量 ≥0 ≤0 无约束 对偶问题（或原问题） 目标函数变量的系数 约束条件右端项 目标函数 min m个 ≥0 ≤0 无约束 n个 ≥ ≤ = 约 束 条 件 变 量
否
所有aik
计算
0
否
是
Hale Waihona Puke 0 bi be min aik 0 aik aek
计算
j min aej 0 k < aej aek
以为中心元素进行迭代
以为中心元素进行迭代
单纯形法和对偶单纯形法步骤
2.对偶单纯形法 对偶单纯形法的适用范围 对偶单纯形法适合于解如下形式 的线性规划问题
0 x4 0 1 0 0 0 1 0 0 0 1 0 0
0 x5 0 0 1 0 -1 -1 1 -100 -1 1 1 -50
I
θ i 300 400 250 50 75
对偶单纯形法
y4 y5 cj
－2 －1 0
15 24 5 y1 y2 y3 0 ［－6］ ［－ ］ －1 －2 －1 －5 15 0 －5 15 －5/4 15/2 15/2 24 1 0 0 1 0 0 5 1/6 [-2/3] 1 0 1 0
0 y4 1 0 0 －1/6 －1/3 4
0 y5 0 1 0 0 1 0
C-CBB-1A≥0
对于标准线性规划问题：
min f = CX
max z = bY
s.t. AT Y ≥ C
AX = b s.t. X ≥ 0
最优基B
可行基B 对偶可行基B 单纯形法 保持可行性 对偶单纯形法 保持对偶可行性
可行基B
对偶可行基B
可行基B
对偶可行基B
对于标准线性规划问题：
min f = CX AX = b s.t. X ≥ 0
•
下面通过例题说明对偶单纯形法的步骤：
例3 用对偶单纯形法求解线性规划问题： min w = 15 y1 + 24 y2 + 5 y3
6 y2 + y3 ≥ 2 y1 + 2 y2 + y3 ≥ 1 ：先将问题改写为：
' min w = 15 y1 + 24 y2 + 5 y3 min w = 15 y1 + 24 y2 + 5 y3 + 0 y4 + 0 y5
对偶单纯形法
对偶单纯形法并不是求解对偶问题解的方法，而是利 用对偶理论求解原问题的解的方法。 对于标准线性规划问题：
min f = CX AX = b s.t. X ≥ 0
max z = bY T s.t. A Y ≥ C
(完整版)对偶单纯形法详解
2.3 对偶单纯形法
一、什么是对偶单纯形法？
对偶单纯形法是应用对偶原理求解原始 线性规划的一种方法——在原始问题的单 纯形表格上进行对偶处理。
注意：不是解对偶问题的单纯形法！
二、对偶单纯形法的基本思想 1、对“单纯形法”求解过程认识的提升— —
从更高的层次理解单纯形法 初始可行基（对应一个初始基本可行解）
3 4
x1, x2 , x3, x4, x5 0
以此形式进行列表求解，满足对偶单纯形 法的基本条件，具体如下：
CB
XB
0
x4
0
x5
cj -2 -3 -4 0 0
xj b
x1 x2 x3 x4 x5
-3
-1 -2 -1 1 0
-4
-2 1 -3 0 1
-Z
0
-2 -3 -4 0 0
比
值 -2/-2 --- -4/-3 --- ---
2/5
11/5
-2 -3 -4 0 0 x1 x2 x3 x4 x5
0 1 -1/5 -2/5 1/5 1 0 7/5 -1/5 -2/5
cj-zj
0
0 0 -3/5 -8/5 -1/5
最优解: X*=（11/5，2/5, 0, 0, 0）T，
最优值: minW= -maxZ* = -[11/5×(-2)+2/5×(-3)]= 28/5
将三个等式约束两边分别乘以-1，然后
列表求解如下：
CB
XB
0
y3
0
y4
0
y5
-Z
比
cj yj b
-3 -9 0 y1 y2 y3
00 y4 y5
-2
-1 -1 1 0 0
一、什么是对偶单纯形法？
对偶单纯形法是应用对偶原理求解原始 线性规划的一种方法——在原始问题的单 纯形表格上进行对偶处理。
注意：不是解对偶问题的单纯形法！
二、对偶单纯形法的基本思想 1、对“单纯形法”求解过程认识的提升— —
从更高的层次理解单纯形法 初始可行基（对应一个初始基本可行解）
3 4
x1, x2 , x3, x4, x5 0
以此形式进行列表求解，满足对偶单纯形 法的基本条件，具体如下：
CB
XB
0
x4
0
x5
cj -2 -3 -4 0 0
xj b
x1 x2 x3 x4 x5
-3
-1 -2 -1 1 0
-4
-2 1 -3 0 1
-Z
0
-2 -3 -4 0 0
比
值 -2/-2 --- -4/-3 --- ---
2/5
11/5
-2 -3 -4 0 0 x1 x2 x3 x4 x5
0 1 -1/5 -2/5 1/5 1 0 7/5 -1/5 -2/5
cj-zj
0
0 0 -3/5 -8/5 -1/5
最优解: X*=（11/5，2/5, 0, 0, 0）T，
最优值: minW= -maxZ* = -[11/5×(-2)+2/5×(-3)]= 28/5
将三个等式约束两边分别乘以-1，然后
列表求解如下：
CB
XB
0
y3
0
y4
0
y5
-Z
比
cj yj b
-3 -9 0 y1 y2 y3
00 y4 y5
-2
-1 -1 1 0 0
[经济学]单纯形法与对偶问题
![[经济学]单纯形法与对偶问题](https://img.taocdn.com/s3/m/0043005331b765ce05081479.png)
’小于0，可知
c1≤50时，也就是x1的 目标函数c1’在0≤c1’≤100时最优解不变。
j ' min a 1 j 0 50 。这样可以知道当-50≤Δ a ' 1 j
3 50 j ' 50，有 max a 0 1 j 50 同样有 a13 1 a'1 j
δj δj Max a'kj 0 ΔCk Min a'kj 0（其中 k是某个固定的值， j是1到n的所有数） a' a' kj kj
管 理 运 筹 学
7
§1
单纯形表的灵敏度分析
例： 目标函数：Max z=50X1+100X2 约束条件：X1+X2≤300 2X1+X2≤400 X2≤250 X1，X2≥0 最优单纯形表如下 迭代次数 基变量 X1 S2 X2 ZJ CJ -ZJ
管 理 运 筹 学
2
第六章 单纯形法的灵敏度分析与对偶问题
• §1 • §2 • §3 • §4
单纯形表的灵敏度分析 线性规划的对偶问题 对偶规划的基本性质 对偶单纯形法
管
理
运
筹
学
3
单纯形表
管
理
运
筹
学
4
§1
单纯形表的灵敏度分析
一、目标函数中变量系数Ck灵敏度分析（在什么范围内变化， 最优解不变，与第二章，第三章联系起来） 在线性规划的求解过程中，目标函数系数的变动将会影响检 验数的取值，但是，当目标函数的系数的变动不破坏最优判 别准则时，原最优解不变，否则，原最优解将发生变化，要 设法求出新的最优解。下面我们具体的分析 1.在最终的单纯形表里，X k是非基变量 由于约束方程系数增广矩阵在迭代中只是其本身的行的初等 变换与Ck没有任何关系， 所以当Ck变成Ck+ Ck时，在最终单纯形表中其系数的增广 矩阵不变，又因为Xk是非基变量，所以基变量的目标函数的 系数不变，即CB不变，可知Zk也不变，只是Ck变成了Ck+ Ck。这时 K= Ck-Zk就变成了 Ck+ Ck- Zk= K+ Ck。 要使原来的最优解仍为最优解，只要 K+ Ck≤0即可，也 就是Ck的增量 Ck≤ - K。
c1≤50时，也就是x1的 目标函数c1’在0≤c1’≤100时最优解不变。
j ' min a 1 j 0 50 。这样可以知道当-50≤Δ a ' 1 j
3 50 j ' 50，有 max a 0 1 j 50 同样有 a13 1 a'1 j
δj δj Max a'kj 0 ΔCk Min a'kj 0（其中 k是某个固定的值， j是1到n的所有数） a' a' kj kj
管 理 运 筹 学
7
§1
单纯形表的灵敏度分析
例： 目标函数：Max z=50X1+100X2 约束条件：X1+X2≤300 2X1+X2≤400 X2≤250 X1，X2≥0 最优单纯形表如下 迭代次数 基变量 X1 S2 X2 ZJ CJ -ZJ
管 理 运 筹 学
2
第六章 单纯形法的灵敏度分析与对偶问题
• §1 • §2 • §3 • §4
单纯形表的灵敏度分析 线性规划的对偶问题 对偶规划的基本性质 对偶单纯形法
管
理
运
筹
学
3
单纯形表
管
理
运
筹
学
4
§1
单纯形表的灵敏度分析
一、目标函数中变量系数Ck灵敏度分析（在什么范围内变化， 最优解不变，与第二章，第三章联系起来） 在线性规划的求解过程中，目标函数系数的变动将会影响检 验数的取值，但是，当目标函数的系数的变动不破坏最优判 别准则时，原最优解不变，否则，原最优解将发生变化，要 设法求出新的最优解。下面我们具体的分析 1.在最终的单纯形表里，X k是非基变量 由于约束方程系数增广矩阵在迭代中只是其本身的行的初等 变换与Ck没有任何关系， 所以当Ck变成Ck+ Ck时，在最终单纯形表中其系数的增广 矩阵不变，又因为Xk是非基变量，所以基变量的目标函数的 系数不变，即CB不变，可知Zk也不变，只是Ck变成了Ck+ Ck。这时 K= Ck-Zk就变成了 Ck+ Ck- Zk= K+ Ck。 要使原来的最优解仍为最优解，只要 K+ Ck≤0即可，也 就是Ck的增量 Ck≤ - K。
对偶与对偶单纯形法的应用
y1+2y2
≥50
y1 + y2+y3 ≥100
其中y1，y2，y3均≥0
其对偶问题是？
17
• Max z=50x1 +100x2 • x1 +x2 ≤300 • 2x1+x2 ≤400 • x2 ≤250 • x1，x2≥0
18
（二）若原问题为（弱对偶性定理） maxZ=CX AX ≤b X ≥0 其对偶问题为 Minw=Yb YA ≥C Y ≥0 若X为原问题任一可行解，Y为对偶问题任一 可行解，则必有CX ≤Yb
3}=-3;
确定进基变量：θ=min{δ/akj,akj<0}={-15/-5} 从而确定主元素akr，以此为中心做初等行变换。
39
对偶单纯性表2
ci
-12 -16 -15 0 0
CB B b y1 y2 y3 y4 y5
0 y4 -2 -2 -4 0 1 0
-15 y3 3/5 2/5 0 1 0 -1/5
9
记忆宝典： 1、Max——Min 2、C ——b
3、无约束等于0，个数m变n。 4、max就反正，min就正反。（约束条 件——变量）
10
示例：转化为对偶问题
mz a 3 x x 1 4 x 2 6 x 3
2 x1 3 x 2 6 x3 440 , 6 x1 4 x 2 x3 100 , 5 x1 3 x 2 x3 200 , x1 , x 2 , x3 0
δ -6 -16 0 0 -3
确定出基变量：bk=min{bi , bi<0}=min{15}=-15;
确定进基变量：θ=min{δ/akj,akj<0}={-6/-2, -16/-4}=3
应用运筹学基础：线性规划（4）-对偶与对偶单纯形法
应⽤运筹学基础：线性规划（4）-对偶与对偶单纯形法这⼀节课讲解了线性规划的对偶问题及其性质。
引⼊对偶问题考虑⼀个线性规划问题：$$\begin{matrix}\max\limits_x & 4x_1 + 3x_2 \\ \text{s.t.} & 2x_1 + 3x_2 \le 24 \\ & 5x_1 + 2x_2 \le 26 \\ & x \ge0\end{matrix}$$ 我们可以把这个问题看作⼀个⽣产模型：⼀份产品 A 可以获利 4 单位价格，⽣产⼀份需要 2 单位原料 C 和 5 单位原料 D；⼀份产品 B 可以获利 3 单位价格，⽣产⼀份需要 3 单位原料 C 和 2 单位原料 D。
现有 24 单位原料 C，26 单位原料 D，问如何分配⽣产⽅式才能让获利最⼤。
但假如现在我们不⽣产产品，⽽是要把原料都卖掉。
设 1 单位原料 C 的价格为 $y_1$，1 单位原料 D 的价格为 $y_2$，每种原料制定怎样的价格才合理呢？⾸先，原料的价格应该不低于产出的产品价格（不然还不如⾃⼰⽣产...），所以我们有如下限制：$$2y_1 + 5y_2 \ge 4 \\ 3y_1 + 2y_2 \ge3$$ 当然也不能漫天要价（也要保护消费者利益嘛- -），所以我们制定如下⽬标函数：$$\min_y \quad 24y_1 + 26y_2$$ 合起来就是下⾯这个线性规划问题：$$\begin{matrix} \min\limits_y & 24y_1 + 26y_2 \\ \text{s.t.} & 2y_1 + 5y_2 \ge 4 \\ & 3y_1 + 2y_2 \ge 3 \\ & y \ge 0\end{matrix}$$ 这个问题就是原问题的对偶问题。
对偶问题对于⼀个线性规划问题（称为原问题，primal，记为 P） $$\begin{matrix} \max\limits_x & c^Tx \\ \text{s.t.} & Ax \le b \\ & x \ge 0\end{matrix}$$ 我们定义它的对偶问题（dual，记为 D）为 $$\begin{matrix} \min\limits_x & b^Ty \\ \text{s.t.} & A^Ty \ge c \\ & y \ge 0\end{matrix}$$ 这⾥的对偶变量 $y$，可以看作是对原问题的每个限制，都⽤⼀个变量来表⽰。
第三章对偶单纯形法
··
≥ (c1,c2,…,cn)
y1，y2，…，ym≥0
m个变量，n个约束条件
2﹒约束条件全部为“=”的对偶
原问题：
max z=CX
max z=CX
max z=CX
AX＝b
等价
AX≤b AX≥b
AX≤b 等价 －AX≤－b
X≥0
min ω=(Y1,Y2) A
(Y1,Y2) －A Y1,Y2≥0
b －b
承租
出让代价应不低于 用同等数量的资源 自己生产的利润。
厂家能接受的条件：
出 用同让6等代y数价2量应的不y资低3 源于 2 5 y自1 己生2产y2的利y润3。 1
收购方的意愿：
min w 15 y 24 y 5 y
1
2
3
Ⅰ
Ⅱ
D
设备A
0
设备B
6
调试工序
1
5 15时 2 24时 1 5时
利润（元） 2
x1 0, x2 , x3 0, x4无限制max变S量个数5n y1 约4束y方2 程个6数yn3
2、求下列问题的对偶问题 min Z 2x1 3x2 5x3 x4
4x1 x2 3x3 2x4 5
s.t
3x1 2x2 7x4 2x1 3x2 4x3
4 x4
6
s.t
3﹒约束条件为“≥”的对偶
原问题：
max z=CX
max z=CX
对
AX≥b
等价
－AX≤ － b
偶
X≥0 min ω=Yb
对偶 问题
X≥0
问
题
min ω=Y1 (－ b)
YA ≥C Y≤0
令Y= － Y1
对偶单纯形法
1.对偶问题模型2.对偶例子，总结特点3.对偶的相关性质定理4.对偶单纯形法1.对偶问题模型例：某化工厂利用R1、R2、R3三种原料，生产Q1、Q2两种产品，生产每公斤产品所需的各单位原料、工厂所拥有的个资源最大量及每公斤产品销售利润如下表所示，问每天应生产多少公斤Q1、Q2才能使利润最大。
原料-产品-利润表设每天生产Q1、Q2的产品量为x1，x2，可得到约束方程Max s=0.7 x1 +1.2 x23x+ 10x2≤3004x1 + 5x2≤2009x1 + 4x2≤360x1≥0, x2≥0现在的问题是，如果另一个化工厂想全部购买该厂R1、R2、R3三种原料，那么该厂在什么条件下出售这三种原料，才能使该厂在经济收入上不低于用等量的三种原料生产Q1、Q2产品获得的最大利润。
设三种原料出售单价分别为u1, u2, u3, 可得到约束方程Min W= 300 u1 +200u2 +360 u3+4u2 +9 u3≥0.73 u10 u1 +5 u2 +9u3≥ 1.2u1≥0, u2≥0, u3≥0一半钱这问题成为L，后者为其对偶问题成为D比较两个线性规划模型，其特征有目标函数的要求上两者相反，s求max，w求min右端向量和目标函数的价值系数两者对调约束方程两者符号相反，s是“≤”，w是“≥”由s的约束方程书引入了同等数量的另一组非负变量u=( u1, u2, u3)T,且作为w的决策变量，约束方程数由m个变为n个2.对偶问题及其转化方对偶问题在理论和实践方面有着广泛的应用在某些情况下线性规划的对偶问题比原解问题更容易对偶变量对原问题的解提供了重要的经济意义在处理一般型初始模型时可以不引入人工变量而采用对偶单纯形法直接处理，减少计算量推证出若干重要性质和定理作为线性规划灵敏度分析的重要工具例：求下列线性规划的对偶问题：Max s= x1 +2 x2s.t. x1 -2x2≤2x1≤9-x1 + x2≤5x1≥0, x2≥0解：其对偶问题为：min w=2y1+9y2+5y3s.t. y1+y2-y3≥1-2y2+y3≥2y1≥0, y2≥0, y3≥0需要注意的是，如果原问题的目标函数为求极小，其目标函数的系数需要乘-1变成求极大，如果某些约束为“≥”，则这些约束需乘-1，变成“≤”，才能产生相应的对偶问题。
单纯形法和对偶问题
第六章 单纯形法的灵敏度分析与对偶问题
• • • •
§1 §2 §3 §4
单纯形表的灵敏度分析 线性规划的对偶问题 对偶规划的基本性质 对偶单纯形法
管
理
运
筹
学
1
单纯形表
管
理
运
筹
学
2
§1 单纯形表的灵敏度分析
一、目标函数中变量系数Ck灵敏度分析（在什么范围内变化， 最优解不变，与第二章，第三章联系起来） 在线性规划的求解过程中，目标函数系数的变动将会影响检 验数的取值，但是，当目标函数的系数的变动不破坏最优判 别准则时，原最优解不变，否则，原最优解将发生变化，要 设法求出新的最优解。下面我们具体的分析 1.在最终的单纯形表里，X k是非基变量 由于约束方程系数增广矩阵在迭代中只是其本身的行的初等 变换与Ck没有任何关系， 所以当Ck变成Ck+ Ck时，在最终单纯形表中其系数的增广矩 阵不变，又因为Xk是非基变量，所以基变量的目标函数的系 数不变，即CB不变，可知Zk也不变，只是Ck变成了Ck+ Ck。 这时 K= Ck-Zk就变成了Ck+ Ck- Zk= K+ Ck。要使原来的 最优解仍为最优解，只要 K+ Ck≤0即可，也就是Ck的增量 Ck≤- K。
由于单纯形表的迭代是约束方程的增广矩阵的行变换，Pk变成Pk’仅仅影响最终单纯形表上第k列
数据，包括Xk的系数列、Zk以及 ，这时最终单纯形表上的Xk的系数列就变成了B-1Pj’,而Zk就变成 k
CBB-1Pk’，新的检验数 迭代以求出最优。 例 以第二章例1为基础，设该厂除了生产Ι，Ⅱ种产品外，现在试制成一个新产品Ⅲ，已知生产产品
实际意义可以描述为：设备台时数在250与325之间变化，则设备台时
• • • •
§1 §2 §3 §4
单纯形表的灵敏度分析 线性规划的对偶问题 对偶规划的基本性质 对偶单纯形法
管
理
运
筹
学
1
单纯形表
管
理
运
筹
学
2
§1 单纯形表的灵敏度分析
一、目标函数中变量系数Ck灵敏度分析（在什么范围内变化， 最优解不变，与第二章，第三章联系起来） 在线性规划的求解过程中，目标函数系数的变动将会影响检 验数的取值，但是，当目标函数的系数的变动不破坏最优判 别准则时，原最优解不变，否则，原最优解将发生变化，要 设法求出新的最优解。下面我们具体的分析 1.在最终的单纯形表里，X k是非基变量 由于约束方程系数增广矩阵在迭代中只是其本身的行的初等 变换与Ck没有任何关系， 所以当Ck变成Ck+ Ck时，在最终单纯形表中其系数的增广矩 阵不变，又因为Xk是非基变量，所以基变量的目标函数的系 数不变，即CB不变，可知Zk也不变，只是Ck变成了Ck+ Ck。 这时 K= Ck-Zk就变成了Ck+ Ck- Zk= K+ Ck。要使原来的 最优解仍为最优解，只要 K+ Ck≤0即可，也就是Ck的增量 Ck≤- K。
由于单纯形表的迭代是约束方程的增广矩阵的行变换，Pk变成Pk’仅仅影响最终单纯形表上第k列
数据，包括Xk的系数列、Zk以及 ，这时最终单纯形表上的Xk的系数列就变成了B-1Pj’,而Zk就变成 k
CBB-1Pk’，新的检验数 迭代以求出最优。 例 以第二章例1为基础，设该厂除了生产Ι，Ⅱ种产品外，现在试制成一个新产品Ⅲ，已知生产产品
实际意义可以描述为：设备台时数在250与325之间变化，则设备台时
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第9页
(二)非对称型对偶问题
max z c1x1 c2x2 c3x3 c3x3 s.t. a11x1 a12 x2 a13x3 a13x3 b1
a21x1 a22 x2 a23x3 a23x3 b2 a2a1x21x1 a2a2 x222x2 a2a3x233x3 a2a3x233x3 b2b2 a31x1 a32x2 a33x3 a33x3 b3
n个
约
≥
束
≤
条 件
=
第14页
例2、写出下述线性规划问题的对偶问题
max z 2x1 3x2 5x3 x4
s.t. x1 x2 3x3 x4 5 2x1 2x3 x4 4 x2 x3 x4 6 x1 0,x2, x3 0, x4无约束
解：设对偶变量为 y1, y2, y3，则对偶问题为
对偶问题（D）
第6页
二、原问题与对偶问题的对应关系
P max z 3x1 4x2
s.t. x1 x2 6 y1
x1
2 x2 x2
8 3
y2 y3
x1, x2 0
矩阵形式：
max z (3
4)
x1 x2
s.t. 1 1
min w b1y1 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a31 y3 c1
a12 y1 a22 y2 a32 y3 c2
a13 y1 a23 y2 a33 y3 c3 y1 0，y2无约束，y3 0
第11页
(二)非对称型对偶问题
max z = c1x1 + c2x2 + c3x3 s.t. a11x1 + a12x2 + a13x3 ≤ b1
a21x1 + a22x2 + a23x3 = b2 a31x1 + a32x2 + a33x3 ≥ b3
原问题（原对问偶题问题）
y1 y2 y3
目标函数 max 目标函数的系数 约束条件右端常数
目标函数的系数
3个
≥0
变
≤0
量
无符号限制
23个
约
≥
束
≤
条
=
件
第13页
二、原问题与对偶问题的对应关系
原问题（对偶问题）
目标函数 max
目标函数的系数
约束条件右端常数
约 m个
束≤
条 件
≥
=
n个
变
≥0
量
≤0
无符号限制
对偶问题（原问题）
目标函数 min
约束条件右端常数
目标函数的系数
m个
≥0
变
≤0
量
无符号限制
min w 5y1 4 y2 6 y3
s.t. y1 2 y2 2
y1
y3 3
3y1 2 y2 y3 5
y1 y2 y3 1
y1 0, y2 0, y3无约束
第15页
例3、写出下述线性规划问题的对偶问题
min z 2x1 3x2 5x3 x4
s.t. x1 x2 3x3 x4 5 2x1 2x3 x4 4 x2 x3 x4 6 x1 0,x2, x3 0, x4无约束
y3
4
y1, y2 , y3 0
yj 表示对第 j 种资源的估价
y1
min
w 6
8
3
y2
s.t.
1 1
1 2
0 1
y1 y2 y3
y3
3
4
y1
y2 y3
max z c1x1 c2x2 c3x3 c3x3 s.t. a11x1 a12 x2 a13x3 a13x3 b1
aaa222a111xxx2111x1 aaa222a222xxx22222x2 aaa222a333xxx23333x3 aaa222a333xxx23333x3 bbb222b2 a3a13x11x1 a3a23x22x2 a3a33x33x3 a3a33x33x3 b3b3 x1, x2 , x3, x3 0
对偶变量
y1 y2 y2 y3
第10页
(二)非对称型对偶问题
令 y2 y2 -y2，y3 y3
min w b1y1 b2 y2 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a21 y2 a31 y3 c1
x1≥0, x2≤0, x3无约束
约
3个
束
≤
min w b1y1 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a31 y3 c1
条
≥
件
=
a12 y1 a22 y2 a32 y3 c2 a13 y1 a23 y2 a33 y3 c3 y1 0，y2无约束，y3 0
a12 y1 a22 y2 a22 y2 a32 y3 c2 a13 y1 a23 y2 a23 y2 a33 y3 c3 a13 y1 a23 y2 a23 y2 a33 y3 c3 y1, y2 , y2, y3 0
第2页
一、对偶问题的提出
对同一问题从不同角度考虑，有两种对立的描述。
例例如1：、平应面如中何矩安形排的面生积产与计周划长，的使关系一天的总利润最大？
周某长企一业定生面产积甲最、大乙的两矩种形产是品正，方要形用: 面A、积B一、定C周三长种最不短同的的矩原形料是。正每方生形产1 吨甲产品，需耗用三种原料分别为1，1，0单位；生产1吨乙产品，需耗用三 种原料分别为1，2，1单位。每天原料供应的能力分别为6，8，3单位。又知 道每生产1吨甲产品企业利润为300元，每生产1吨乙产品企业利润为400元。
原料
单位利润
产品
A
B
C
（百元）
甲
1
1
0
3
乙
1
2
1
4
供应量
6
8
3
第3页
假设该企业决策者决定不生产甲、乙产品，而是将厂
里的例现1有、资应源如外何售安。排决生策产者计应划怎，样使制一定天每的种总资源利的润收最费大？
标准才合理？
原料
单位利润
产品
A
B
C
（百元）
甲
1
1
0
3
乙
1
2
1
4
供应量
6
8
3
设 xj 表示第 j 种产品每天的产量
对偶问题： x1, x2 , x3, x3 0
min w b1y1 b2 y2 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a21 y2 a31 y3 c1
a12 y1 a22 y2 a22 y2 a32 y3 c2 a13 y1 a23 y2 a23 y2 a33 y3 c3 a13 y1 a23 y2 a23 y2 a33 y3 c3 y1, y2 , y2, y3 0
max z = 3x1 + 4x2 s.t. x1 + x2 ≤ 6
x1 + 2x2 ≤ 8 x2 ≤ 3
x1 ≥ 0 , x2 ≥ 0
第4页
分析问题：
1、出让例每1、种资应源怎的样收制入定不收能费低标于准自才己合生理产时？的可获利润；
2、定价不能太高，要使对方能够接受。
原料
单位利润
产品
A
BC（百元） Nhomakorabea第8页
(二)非对称型对偶问题
max z = c1x1 + c2x2 + c3x3 s.t. a11x1 + a12x2 + a13x3 ≤ b1
a21x1 + a22x2 + a23x3 = b2 a31x1 + a32x2 + a33x3 ≥ b3 x1≥0, x2≤0, x3无约束 分析：化为对称形式。令 x2 x2，x3 x3 x3 (x3 0, x3 0)
6
1 0
2 1
x1 x2
8 3
x1 x2
0
max z=CX s.t. AX ≤b
X≥0
D min w 6 y1 8y2 3y3
s.t. y1 y2 3
y1
2
y2
min w 6 y1 8y2 3y3
s.t. y1 y2 3
y1
2
y2
y3
4
y1, y2 , y3 0
原问题（对偶问题）
目标函数 max
目标函数的系数
约束条件右端常数
约
3个
束
≤
条
≥
件
=
23个
变
≥0
量
≤0
无符号限制
对偶问题（原问题）
目标函数 min
约束条件右端常数
3个
变
≥0
量
≤0
无符号限制
对偶问对题偶（问原题问题）
目标函数 min
约束条件右端常数
目标函数的系数
(二)非对称型对偶问题
max z c1x1 c2x2 c3x3 c3x3 s.t. a11x1 a12 x2 a13x3 a13x3 b1
a21x1 a22 x2 a23x3 a23x3 b2 a2a1x21x1 a2a2 x222x2 a2a3x233x3 a2a3x233x3 b2b2 a31x1 a32x2 a33x3 a33x3 b3
n个
约
≥
束
≤
条 件
=
第14页
例2、写出下述线性规划问题的对偶问题
max z 2x1 3x2 5x3 x4
s.t. x1 x2 3x3 x4 5 2x1 2x3 x4 4 x2 x3 x4 6 x1 0,x2, x3 0, x4无约束
解：设对偶变量为 y1, y2, y3，则对偶问题为
对偶问题（D）
第6页
二、原问题与对偶问题的对应关系
P max z 3x1 4x2
s.t. x1 x2 6 y1
x1
2 x2 x2
8 3
y2 y3
x1, x2 0
矩阵形式：
max z (3
4)
x1 x2
s.t. 1 1
min w b1y1 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a31 y3 c1
a12 y1 a22 y2 a32 y3 c2
a13 y1 a23 y2 a33 y3 c3 y1 0，y2无约束，y3 0
第11页
(二)非对称型对偶问题
max z = c1x1 + c2x2 + c3x3 s.t. a11x1 + a12x2 + a13x3 ≤ b1
a21x1 + a22x2 + a23x3 = b2 a31x1 + a32x2 + a33x3 ≥ b3
原问题（原对问偶题问题）
y1 y2 y3
目标函数 max 目标函数的系数 约束条件右端常数
目标函数的系数
3个
≥0
变
≤0
量
无符号限制
23个
约
≥
束
≤
条
=
件
第13页
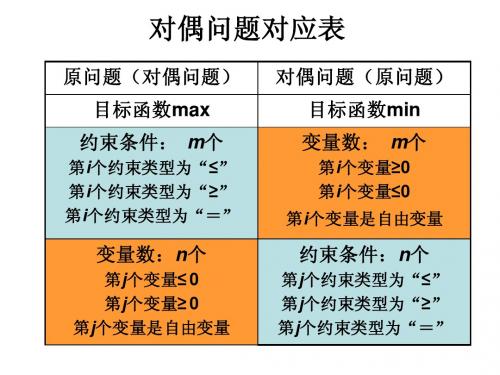
二、原问题与对偶问题的对应关系
原问题（对偶问题）
目标函数 max
目标函数的系数
约束条件右端常数
约 m个
束≤
条 件
≥
=
n个
变
≥0
量
≤0
无符号限制
对偶问题（原问题）
目标函数 min
约束条件右端常数
目标函数的系数
m个
≥0
变
≤0
量
无符号限制
min w 5y1 4 y2 6 y3
s.t. y1 2 y2 2
y1
y3 3
3y1 2 y2 y3 5
y1 y2 y3 1
y1 0, y2 0, y3无约束
第15页
例3、写出下述线性规划问题的对偶问题
min z 2x1 3x2 5x3 x4
s.t. x1 x2 3x3 x4 5 2x1 2x3 x4 4 x2 x3 x4 6 x1 0,x2, x3 0, x4无约束
y3
4
y1, y2 , y3 0
yj 表示对第 j 种资源的估价
y1
min
w 6
8
3
y2
s.t.
1 1
1 2
0 1
y1 y2 y3
y3
3
4
y1
y2 y3
max z c1x1 c2x2 c3x3 c3x3 s.t. a11x1 a12 x2 a13x3 a13x3 b1
aaa222a111xxx2111x1 aaa222a222xxx22222x2 aaa222a333xxx23333x3 aaa222a333xxx23333x3 bbb222b2 a3a13x11x1 a3a23x22x2 a3a33x33x3 a3a33x33x3 b3b3 x1, x2 , x3, x3 0
对偶变量
y1 y2 y2 y3
第10页
(二)非对称型对偶问题
令 y2 y2 -y2，y3 y3
min w b1y1 b2 y2 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a21 y2 a31 y3 c1
x1≥0, x2≤0, x3无约束
约
3个
束
≤
min w b1y1 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a31 y3 c1
条
≥
件
=
a12 y1 a22 y2 a32 y3 c2 a13 y1 a23 y2 a33 y3 c3 y1 0，y2无约束，y3 0
a12 y1 a22 y2 a22 y2 a32 y3 c2 a13 y1 a23 y2 a23 y2 a33 y3 c3 a13 y1 a23 y2 a23 y2 a33 y3 c3 y1, y2 , y2, y3 0
第2页
一、对偶问题的提出
对同一问题从不同角度考虑，有两种对立的描述。
例例如1：、平应面如中何矩安形排的面生积产与计周划长，的使关系一天的总利润最大？
周某长企一业定生面产积甲最、大乙的两矩种形产是品正，方要形用: 面A、积B一、定C周三长种最不短同的的矩原形料是。正每方生形产1 吨甲产品，需耗用三种原料分别为1，1，0单位；生产1吨乙产品，需耗用三 种原料分别为1，2，1单位。每天原料供应的能力分别为6，8，3单位。又知 道每生产1吨甲产品企业利润为300元，每生产1吨乙产品企业利润为400元。
原料
单位利润
产品
A
B
C
（百元）
甲
1
1
0
3
乙
1
2
1
4
供应量
6
8
3
第3页
假设该企业决策者决定不生产甲、乙产品，而是将厂
里的例现1有、资应源如外何售安。排决生策产者计应划怎，样使制一定天每的种总资源利的润收最费大？
标准才合理？
原料
单位利润
产品
A
B
C
（百元）
甲
1
1
0
3
乙
1
2
1
4
供应量
6
8
3
设 xj 表示第 j 种产品每天的产量
对偶问题： x1, x2 , x3, x3 0
min w b1y1 b2 y2 b2 y2 b3 y3 s.t. a11 y1 a21 y2 a21 y2 a31 y3 c1
a12 y1 a22 y2 a22 y2 a32 y3 c2 a13 y1 a23 y2 a23 y2 a33 y3 c3 a13 y1 a23 y2 a23 y2 a33 y3 c3 y1, y2 , y2, y3 0
max z = 3x1 + 4x2 s.t. x1 + x2 ≤ 6
x1 + 2x2 ≤ 8 x2 ≤ 3
x1 ≥ 0 , x2 ≥ 0
第4页
分析问题：
1、出让例每1、种资应源怎的样收制入定不收能费低标于准自才己合生理产时？的可获利润；
2、定价不能太高，要使对方能够接受。
原料
单位利润
产品
A
BC（百元） Nhomakorabea第8页
(二)非对称型对偶问题
max z = c1x1 + c2x2 + c3x3 s.t. a11x1 + a12x2 + a13x3 ≤ b1
a21x1 + a22x2 + a23x3 = b2 a31x1 + a32x2 + a33x3 ≥ b3 x1≥0, x2≤0, x3无约束 分析：化为对称形式。令 x2 x2，x3 x3 x3 (x3 0, x3 0)
6
1 0
2 1
x1 x2
8 3
x1 x2
0
max z=CX s.t. AX ≤b
X≥0
D min w 6 y1 8y2 3y3
s.t. y1 y2 3
y1
2
y2
min w 6 y1 8y2 3y3
s.t. y1 y2 3
y1
2
y2
y3
4
y1, y2 , y3 0
原问题（对偶问题）
目标函数 max
目标函数的系数
约束条件右端常数
约
3个
束
≤
条
≥
件
=
23个
变
≥0
量
≤0
无符号限制
对偶问题（原问题）
目标函数 min
约束条件右端常数
3个
变
≥0
量
≤0
无符号限制
对偶问对题偶（问原题问题）
目标函数 min
约束条件右端常数
目标函数的系数