晶胞计算专题
晶胞计算习题
1.回答下列问题(1)金属铜晶胞为面心立方最密堆积, 边长为acm。
又知铜的密度为ρ g·cm－3, 阿伏加德罗常数为_______。
(2)下图是CaF2晶体的晶胞示意图, 回答下列问题：①Ca2＋的配位数是______, F－的配位数是_______。
②该晶胞中含有的Ca2＋数目是____, F－数目是_____, ③CaF2晶体的密度为ag·cm－3, 则晶胞的体积是_______(只要求列出算式)。
2.某些金属晶体(Cu、Ag、Au)的原子按面心立方的形式紧密堆积, 即在晶体结构中可以划出一块正立方体的结构单元, 金属原子处于正立方体的八个顶点和六个侧面上, 试计算这类金属晶体中原子的空间利用率。
（2）（3）3、单晶硅的晶体结构与金刚石一种晶体结构相似, 都属立方晶系晶胞, 如图：（1）将键联的原子看成是紧靠着的球体, 试计算晶体硅的空间利用率（计算结果保留三位有效数字, 下同）。
（2）已知Si—Si键的键长为234 pm, 试计算单晶硅的密度是多少g/cm3。
4、金晶体的最小重复单元(也称晶胞)是面心立方体, 如图所示, 即在立方体的8个顶点各有一个金原子, 各个面的中心有一个金原子, 每个金原子被相邻的晶胞所共有。
金原子的直径为d, 用NA表示阿伏加德罗常数, M表示金的摩尔质量。
请回答下列问题：(1)金属晶体每个晶胞中含有________个金原子。
(2)欲计算一个晶胞的体积, 除假定金原子是刚性小球外, 还应假定_______________。
(3)一个晶胞的体积是____________。
(4)金晶体的密度是____________。
5.1986年, 在瑞士苏黎世工作的两位科学家发现一种性能良好的金属氧化物超导体, 使超导工作取得突破性进展, 为此两位科学家获得了1987年的诺贝尔物理学奖, 实验测定表明, 其晶胞结构如图所示。
（4）（5）（6）（1）根据所示晶胞结构, 推算晶体中Y、Cu、Ba和O的原子个数比, 确定其化学式。
3.1.2晶胞的有关计算++课件
长a；金的密度钾的密度ρ。
①立方体对角线=4r
体 心 立
棱长 a 4r 3
方
②密度
紧
密
堆
积
2.如图是Fe单质的晶胞模型。已知晶体密度为d g·cm－3，铁原子的半径为__4_3_×__3__d_1·_1N_2A__ _×__1_0_7 _nm(用含有d、NA的代数式表示)。
知识梳理
3. 配位数的计算
二、晶胞中粒子配位数计算
5.硅化镁是一种窄带隙n型半导体材料，在光电子器件、能源 器件、激光、半导体制造等领域具有重要应用前景。硅化镁 的晶胞参数a＝0.639 1 nm，属于面心立方晶胞，结构如图所 示。Si原子的配位数为__8___。
根据晶胞结构，以面心Si原子为基准，同一晶胞内等距离且最近的Mg原子有4个， 紧邻晶胞还有4个Mg原子，共8个，故Si原子的配位数为8。
1 1/2 水平1/4 竖1/3 1/6
体心 1 面心 1/2 棱边 水平1/4 竖1/6 顶点 1/12
知识梳理
2. 晶胞边长、粒子间距、晶体密度的计算
知识梳理 晶体（晶胞）密度计算 （立方晶胞）
(1)思维流程
(2)计算公式
①先确定一个晶胞中微粒个数N（均摊法）
②再确定一个晶胞中微粒的总质量
③最后求晶胞的密度
配位数
一个粒子周围最邻近且等距离的的粒子数称为配位数
离子晶体的配位数： 指一个离子周围最接近且等距离的异种电性离子的数目。
简单立方：配位数为6
面心立方：配位数为12
体心立方：配位数为8
离子晶体的配位数 以NaCl晶体为例
①找一个与其他粒子连接情况最清晰的粒子，如右图中 心的黑球(Cl－)。 ②数一下与该粒子周围距离最近的粒子数，如右图标数 字的面心白球(Na＋)。确定Cl－的配位数为6，同样方法 可确定Na＋的配位数也为6。
选修三专题：晶胞计算
第1页共6页晶胞计算晶胞计算是晶体考查的重要知识点之一，也是考查学生分析问题、解决问题能力的较好素材。
晶体结 构的计算常常涉及如下数据：晶体密度、 N A 、M 、晶体体积、微粒间距离、微粒半径、夹角等，密度 的表达式往往是列等式的依据。
解决这类题，一是要掌握晶体 均摊法”的原理，二是要有扎实的立体 几何知识，三是要熟悉常见晶体的结构特征，并能融会贯通，举一反三。
有关晶胞各物理量的关系：1、晶胞质量二晶胞占有的微粒的质量二晶胞占有的微粒数X NM A 02、空间利用率二对角线长= 2a o ⑵体对角线长=,3a o ⑶体心立方堆积4r = 3a （r 为原子半径）。
⑷面心立方堆积4r = .2a （r 为原子半径）。
对于立方晶胞，可简化成下面的公式进行各物理量的计算：a 3Xp>N A = n XM ， a 表示晶胞的棱长，p 表示密度，N A 表示阿伏加德罗常数的值，n 表示1 mol 晶胞中所含晶体的物质 的量，M 表示摩尔质量，a 3XpX N A 表示1 mol 晶胞的质量。
1、【2012全国1】（6） ZnS 在荧光体、光导体材料、涂料、颜料等行业 中应用广泛。
立方ZnS 晶体结构如下图所示，其晶胞边长为540.0 pm .密 度为 _____________ 列式并计算），a 位置S 2-离子与b 位置Zn 2+离子之间的 距离 ____ pm （列示表示）f270—或估也一或心巧4.1 i "- :sin ——-—22、【2013全国1】（6）在硅酸盐中，SiO 4-四面体（如下图（a ））通过共用顶角氧离子可形成岛状、 链状、层状、骨架网状四大类结构型式。
图（b ）为一种无限长单链结构的多硅酸根，其中 Si 原子的 杂化形式为 _____________ ， Si 与 O 的原子数之比为 _________ ，化学式为 ____________________ 。
晶胞计算专题
3
V晶胞 s 2h 2
3r2 2 2 6 r 8 3
Байду номын сангаас
2r3
空间利用率= V微粒100%
V晶胞
2 4 r3
3 100% 8 2r3
=74%
【堆积方式及性质小结】
堆积方式 晶胞类型 空间利 配位数 用率
实例
简单立方 简单立方 堆积 体心立方 体心立方 密堆积 六方最密 六方 堆积 面心立方 面心立方 最密堆积
晶胞计算 ---密度、空间利用率
1.会计算晶胞中的粒子数 2.掌握晶胞中各线段的关系，结合数学 思想解决密度和空间占有率计算的问题
立方晶胞中各线段之间的关系如下：
V=a3
一、晶胞密度的求算 1、已知金属金是面心立方最密堆积，金原 子半径为r cm，计算：金晶胞棱长；金的密 度。 ①面对角线 = 4r
52％ 68% 74% 74%
6
Po
8
Na、K、Fe
12 Mg、Zn、Ti 12 Cu、Ag、Au
练习：已知铜晶胞是面心立方晶胞，该晶胞的边 长为3.6210-10m，每一个铜原子的质量为 1.05510-25kg ，试回答下列问题：
（1）一个晶胞中“实际”拥有的铜原子数是多少？ （2）该晶胞的体积是多大？ （3）利用以上结果计算金属铜的密度。
4 58.5g
mol1 N A (2acm)3
mol1
29.25 a3 NA
g cm3
5.如图所示，CsCl晶体中最近的Cs+之间距 离为s阿伏加德罗常数为NA摩尔质量为M
求晶体的密度
二、 晶胞中空间利用率的计算
微粒数×1个微粒体积
空间利用率=
晶胞体积
(1)简单立方：
晶胞计算专题PPT课件
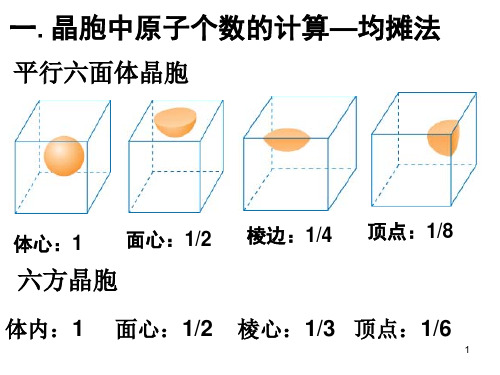
平行六面体晶胞
体心：1 面心：1/2
六方晶胞
棱边：1/4
顶点：1/8
体内：1 面心：1/2 棱心：1/3 顶点：1/6
1
习题1、钙-钛矿晶胞结构如图所示。 观察钙-钛矿晶胞结构，求该晶体中， 钙、钛、氧的微粒个数比为多少？
1:1:3
2
习题2、混合键型晶体——石墨，结构如图所示。
10
mol1
29.25 g cm3
a3 NA
4
2、已知金属金是面心立方紧密堆积，金原 子半径为r cm，计算：金晶胞棱长；金的密 度 面对角线 = 4r
棱长 = 2 2 r
5
3、已知金属 钾是体心立方紧密堆积,钾原 子半径为r cm,请计算：钾晶胞棱长； 钾的密度
棱长=4 3 r/3 体对角线=4r
(1)简单立方： 微粒数为：8×1/8 = 1 空间利用率： 4лr3/3 = 52.36% (2r)3
8
（2）体心立方：微粒数为：8×1/8 + 1 = 2
空间利用率： 2*4лr3/3 (2根号2r)3
9
（4）面心立方：微粒数：8×1/8 + 6×1/2 = 4 空间利用率：
4×4лr3/3 = 74.05% (2×1.414r)3
6
4、若已知下列各晶胞的棱长，你能 求出下列数据吗？
（1）氯化钠晶胞中，钠Байду номын сангаас子和氯离子最小间距
（2）氯离子和氯离子的最小间距
（3）氯化铯晶胞中，铯离子和氯离子的最小间距
（4）硫化锌晶胞中，硫离子和锌离子的最小间距
（5）金刚石晶胞中碳碳键键长 7
三、 晶胞中空间利用率的计算
《晶胞计算专题》课件
发展趋势
晶胞计算将更加智能化、高效化，融合人工智能和 大数据技术，提升计算效率和可预测性。
应用领域
晶胞计算将扩展到更广泛的领域，如药物设计、能 源储存和量子计算。
结论
晶胞计算的价值
晶胞计算为材料科学和化学提供了一种有效的 计算工具，可以加速材料研究和创新。
发展与完善
晶胞计算仍需进一步发展和完善，不断改进算 法和工具，提升计算精度和可靠性。
相关技术
晶胞计算涉及原子模型构建、 能量计算、力场优化等技术， 综合运用多种工具和方法。
晶胞计算的原理
1 晶体结构的描述
晶胞计算通过确定晶格常数和原子位置来描述晶体的结构，揭示材料的有序排列。
2 晶格常数和原子位置的确定
利用计算方法可以确定晶体的晶格常数和原子位置，精确描述晶体的几何结构。
3 原子的运动
晶胞计算的案例
1
材料性质的计算
通过晶胞计算，可以预测材料的力学性质、热学性质和电学性质，进而优化材料 设计。
2
晶格缺陷的模拟
利用晶胞计算，可以模拟材料中的缺陷、固溶体和晶界等结构，研究其对材料性 能的影响。
3
催化反应的机理研究
通过晶胞计算，可以揭示催化反应的机理和活性位点，指导催化剂设计和优化。
晶胞计算的展望
晶胞计算专题
介绍晶胞计算的概念和应用领域，以及相关的技术和工具。深入剖析晶体结 构描述、算法原理和计算案例，并展望未来的发展趋势。
晶胞计算的概述
什么是晶胞计算？
晶胞计算是一种利用计算机 模拟晶体结构和性质的方法， 可以预测材料的性能和行为。
应用领域
晶胞计算广泛应用于材料科 学、化学和能源领域，例如 材料设计、催化剂开发和电 池研究。
晶胞计算专题教育课件
2d
a
（3）一种金原子旳质量可表达为M/NA
空间利用率= X100%
晶胞所含旳原子体积总和
晶胞体积
例如，面心立方晶胞
=74%
空间利用率 =
每个晶胞中含4个原子
×100%
a ：晶胞单位长度 R ：原子半径
1:2
例1：
例2：
如图直线交点处旳圆圈为NaCl晶体中Na+或Cl-所处位置，晶体中，每个Na+周围与它最接近旳且距离相等旳Na+个数为：____
12
金刚石晶体中具有共价键形成旳C原子环，其中最小旳C环上有_____个C原子。
例3：
6
石墨晶体旳层状构造，层内为平面正六边形构造（如图），试回答下列问题：（1）图中平均每个正六边形占有C原子数为____个、占有旳碳碳键数为____个。（2）层内7个六元环完全占有旳C原子数为_____个，碳原子数目与碳碳化学键数目之比为_______.
晶胞计算方法
1、顶点：一种立方体旳顶点由八个相同旳立方体在共用，则平均每个立方体只分到其1/8.
晶胞中金属原子数目旳计算措施(平均值)
1、顶点：一种立方体旳顶点由八个相同旳立方体在共用，则平均每个立方体只分到其1/8.
2、面：
1/2
晶胞中金属原子数目旳计算措施(平均值)
1、顶点：一种立方体旳顶点由八个相同旳立方体在共用，则平均每个立方体只分到其1/8.
12
30
600
巩固练习三：
已知晶体旳基本单元是由12个硼原子构成旳（如右图），每个顶点上有一种硼原子，每个硼原子形成旳化学键完全相同，经过观察图形和推算，可知此基本构造单元是一种正____面体。
20
高考化学晶胞的相关计算专项训练与热点解答题组合练附解析
高考化学晶胞的相关计算专项训练与热点解答题组合练附解析一、晶胞的相关计算1．2Mg Si具有反萤石结构，晶胞结构如图所示，其晶胞参数为0.635nm。
下列叙述错误的是（）A．Si的配位数为8B．紧邻的两个Mg原子的距离为0.635 2nmC．紧邻的两个Si原子间的距离为20.6352⨯nmD．2Mg Si的密度计算式为()337A76g cm0.63510N--⋅⨯2．Fe、HCN与K2CO3在一定条件下发生如下反应：Fe＋6HCN＋2K2CO3=K4Fe(CN)6＋H2↑＋2CO2↑＋2H2O，回答下列问题：(1)此化学方程式中涉及的第二周期元素的电负性由小到大的顺序为________。
(2)配合物K4Fe(CN)6的中心离子的价电子排布图为______，该中心离子的配位数是_______。
(3)1mol HCN分子中含有σ键的数目为_______，HCN分子中碳原子轨道杂化类型是_______，与CN－互为等电子体的阴离子是_______。
(4)K2CO3中阴离子的空间构型为_________，其中碳原子的价层电子对数为____________。
(5)冰的晶体结构模型如图，它的晶胞与金刚石相似，水分子之间以氢键相连接，在一个晶胞中有________个氢键，若氢键键长为d nm，则晶体密度(g·cm－3)计算式为_______ (用N A表示阿伏加德罗常数的值)。
3．据《科技日报》报道，我国科学家研制成功一系列石墨烯限域的3d过渡金属中心(Mn、Fe、Co、Ni、Cu)催化剂，在室温条件下以H2O2为氧化剂直接将CH4氧化成C的含氧化合物。
请回答下列问题：（1）在Mn、Fe、Co、Ni、Cu中，某基态原子核外电子排布遵循“洪特规则特例”（指能量相同的原子轨道在全满、半满、全空状态时，体系的能量最低），该原子的外围电子排布式为_____。
（2）在3d过渡金属中，基态原子未成对电子数最多的元素是_____（填元素符号）。
有关晶胞计算专题课件
晶胞优化算法
总结词
晶胞优化算法是一种用于优化晶体结构的算法，通过迭代方 式不断调整晶胞参数以达到能量最低状态。
详细描述
晶胞优化算法通过迭代方式不断调整晶胞的几何参数和原子 坐标，以最小化晶体的总能量。该算法可以用于预测晶体的 稳定结构、相变温度等，有助于理解晶体材料的结构和性质 。
01
晶胞计算应用
通过晶胞计算，可以预测新材料的稳 定性和性质，为新材料的发现和设计 提供理论指导。此外，晶胞计算还可 以优化材料的结构和性能，提高材料 的稳定性和可靠性。
药物分子设计
总结词
晶胞计算在药物分子设计中具有重要作用，可以预测药物分子的性质和行为。
详细描述
通过晶胞计算，可以模拟药物分子的化学反应过程和行为，预测药物的活性、选择性、药代动力学等性质，为新 药研发提供理论支持。此外，晶胞计算还可以优化药物分子的结构和性质，提高药物的疗效和安全性。
VASP具有高效、灵活和可扩展性强的特点，支持多种计算模式，包括静态能量计算 、分子动力学模拟、过渡态搜索等。
Materials Studio
Materials Studio是一款由BIOVIA开 发的材料科学计算软件，提供了丰富 的建模和模拟工具，用于研究材料的 结构、性质和行为。
Materials Studio还提供了强大的可 视化工具，可以直观地展示材料的结 构和性质，方便用户进行数据分析和 结果解读。
性能。
高分子聚合物的晶胞计算
总结词
高分子聚合物是一类重要的材料，广泛应用于日常生活和工业生产中。了解其晶胞结构有助于优化材 料性能。
详细描述
高分子聚合物的晶胞由多个单体单元组成，通过共价键连接在一起。每个单体单元可以具有不同的化 学结构和性质，从而影响整个聚合物的性能。了解聚合物的晶胞结构有助于预测其物理和化学性质， 如熔点、溶解性等。
高中化学——晶胞的结构与计算专题练习(带答案)
高中化学——晶胞的结构与计算专题练习（带答案解析）一、单选题1．快离子导体是一类具有优良导电能力的固体电解质。
图1(Li3SBF4)和图2是潜在的快离子导体材料的结构示意图。
温度升高时，NaCl晶体出现缺陷，晶体的导电性增强。
该晶体导电时，③迁移的途径有两条：途径1：在平面内挤过2、3号氯离子之间的狭缝(距离为x)迁移到空位。
途径2：挤过由1、2、3号氯离子形成的三角形通道(如图3，小圆的半径为y)迁移到空位。
已知：氯化钠晶胞参数a=564pm，r(Na+)=95pm，r(Cl-)=185pm下列说法不正确的是A．第二周期元素中第一电离能介于B和F之间的元素有4种B．图1所示晶体中，每个Li+与4个呈四面体结构的离子相邻C．氯化钠晶体中，Na+填充在氯离子形成的正八面体空隙中D．温度升高时，NaCl晶体出现缺陷，晶体的导电性增强，该晶体导电时，③迁移的途径可能性更大的是途径12．某铜的氯化物常作工业催化剂，其晶胞结构如图所示，晶胞中C、D两原子核间距为298pm。
N，则下列说法正确的是设阿伏加德罗常数的值为AA．Cu的+2价比+1价稳定，是因为最外层电子达到半充满结构CuClB．此氯化物的化学式为2C．晶胞中Cu位于Cl形成的四面体空隙D ．Cu 与Cl倍 3．Al x CoO y 的立方晶胞如图所示，已知处在体心处的原子为Co ，晶胞参数anm ，下列说法错误的是A ．x=1，y=3B ．该晶胞的密度为23-33A1.3410g cm a N ⨯⋅ C ．该晶胞的俯视图为D ．晶体中一个Al 周围与其最近的O 的个数为64．某立方晶系的锑钾()Sb K -合金可作为钾离子电池的电极材料，下图表示1/8晶胞。
下列说法中错误的是A ．该晶胞的体积为33038a 10cm -⨯B ．K 和Sb 原子数之比为3:1C ．与K 最邻近的Sb 原子数为4D ．该晶胞的俯视图为5．2CaC 的晶胞与NaCl 相似，但由于22C -的结构导致晶胞沿一个方向拉长(如图)，已知2CaC 的摩尔质量为1M g mol -⋅，若阿伏加德罗常数的值为A N ，下列说法错误．．的是A ．2Ca +填充在22C -围成的八面体空隙中B ．每个2Ca +周围等距紧邻的22C -有6个C ．两个最近2Ca +D ．2CaC 晶体密度的计算式为3230A 4g cm 10M N a b --⋅⨯ 6．某镁镍合金储氢后所得晶体的立方晶胞如图1(为便于观察，省略了2个图2的结构)，晶胞边长为apm 。
晶胞的相关计算专项训练知识点-+典型题及解析
晶胞的相关计算专项训练知识点-+典型题及解析一、晶胞的相关计算1．元素X位于第4周期，其基态原子的内层轨道全部排满电子，且最外层电子数为2；元素Y基态原子的3p轨道上有1对成对电子。
X与Y形成的化合物的晶胞结构如图所示，下列关于该晶体的说法正确的是（）A．该晶体属于原子晶体B．X2+的配位数为8，Y2-的配位数为4C．与每个Y2-距离最近且相等的Y2-共有12个D．该晶体的熔点比氧化锌高2．根据下列结构示意图，判断下列说法中正确的是A．在CsCl晶体中，距Cs+最近的Cl-有6个B．在CaF2晶体中，Ca2+周围距离最近的F-有4个C．在SiO2晶体中，每个晶胞中含有4个Si原子和8个O原子D．在铜晶体中，每个铜原子周围距离最近的铜原子有12个3．钯(Pd)、锌及其化合物在合成酮类物质中有极其重要的作用，如图为合成的反应过程：回答下列问题：(1)I原子价电子排布式为___________，其能量最高的能层是___________(填能层符号)。
(2)H、C、O三种元素的电负性由大到小的顺序为___________。
(3) 中碳原子的杂化方式为___________。
(4)ZnCl2溶液中加入足量氨水，发生的反应为ZnCl2＋4NH3·H2O＝[Zn(NH3)4]Cl2＋4H2O。
①上述反应涉及的物质中，固态时属于分子晶体的是___________。
②NH3的空间构型为___________。
③1 mol [Zn(NH3)4]Cl2中含有___________mol σ键。
(5)Zn和Cu可形成金属互化物(ZnCu)，该金属互化物中所有金属原子均按面心立方最密堆积，若所有Cu均位于晶胞的面心，则Zn位于晶胞的___________。
(6)金属钯的堆积方式如图所示：①该晶胞中原子的空间利用率为___________(用含π的式子表示)。
②若该晶胞参数a＝658 pm，则该晶胞密度为___________(列出计算表达式)g·cm－3。
计算专题晶胞的计算
晶胞的计算二、常见的晶胞计算题：晶胞密度ρ =m(晶胞)/V(晶胞)空间利用率=[V(球总体积)/V(晶胞体积)]×100% 【注】1m ＝10dm ＝102cm ＝103mm ＝106um ＝109nm ＝1012pm① 简单立方堆积：假设球的半径为r cm ，则该堆积方式的空间利用率为：② 体心立方堆积：假设球的半径为r cm ，则该堆积方式的空间利用率为：③ 面堆积：，则该堆积方式的空间利用率为：Mg/mol ，N A 为阿伏伽德罗常数的数值，试计算该晶胞的密度：总结】必须掌握的常见晶胞及晶体结构分子晶体：干冰、冰晶胞图形、晶胞组成特点；原子晶体：金刚石（晶体硅）、二氧化硅晶胞组成特点、边长（体积、密度、原子最近距离）的计算方式；金属晶体：四种堆积方式的名称、图形、代表金属、边长（体积、密度、原子最近距离）的计算方式；离子晶体：NaCl 、CsCl 、CaF 2晶胞图形、晶胞组成、边长（体积、密度、原子最近距离）的计算方式。
【练习】中学化学教材中展示了NaCl 晶体结构，它向三维空间延伸得到完美晶体。
NiO(氧化镍)晶体的结构与NaCl 相同，Ni 2+与最临近O 2-的核间距离为a cm ，计算NiO晶体的密度(已知NiO 的摩尔质量为74.7 g/mol)。
(2)天然和绝大部分人工制备的晶体都存在各种缺陷，例如在某氧化镍晶体中就存在如图所示的缺陷：一个Ni 2+空缺，另有两个Ni 2+被两个Ni 3+所取代。
其结果为晶体仍呈电中性，但化合物中Ni 和O 的比值却发生了变化。
某氧化镍样品组成为Ni 0.97O ，试计算该晶体中Ni 3+ 与Ni 2+的离子个数之比。
第二类：晶胞灵活变形及计算【例1：2012年新课标·37】【化学——选修3物质结构与性质】(15分)VIA 族的氧、硫、硒(Se)、碲(Te)等元素在化合物中常表现出多种氧化态，含VIA 族元素的化合物在研究和生产中有许多重要用途。
化学晶胞的相关计算专项训练知识归纳总结附解析
化学晶胞的相关计算专项训练知识归纳总结附解析一、晶胞的相关计算1．2020年，自修复材料、自适应材料、新型传感材料等智能材料技术将大量涌现，为生物医疗、国防军事以及航空航天等领域发展提供支撑。
（1）我国科研工作者基于丁二酮肟氨酯基团的多重反应性，研制了一种强韧、自愈的超级防护材料，其中的分子机制如图所示。
Cu在元素周期表中位于_____区，M层中核外电子能量最高的电子云在空间有_____个伸展方向。
C、N、O第一电离能由大到小的顺序为_____________（2）氧化石墨烯基水凝胶是一类新型复合材料，对氧化石墨烯进行还原可得到还原氧化石墨烯，二者的结构如图所示：还原石墨烯中碳原子的杂化形式是______，上图中氧化石墨烯转化为还原石墨烯时，1号C 与其相邻 C原子间键能的变化是_____________（填“变大”、“变小”或“不变”），二者当中在水溶液中溶解度更大的是____________ （填物质名称），原因为__________________（3）砷化硼是近期受到广泛关注一种III—V半导体材料。
砷化硼为立方晶系晶体，该晶胞中原子的分数坐标为：B：（0，0，0）；（，，0）；（，0，）；（0，，）；……As：（，，）；（，，）；（，，）；（，，）请在图中画出砷化硼晶胞的俯视图．．．．．．．．．．．___________，已知晶体密度为dg/cm3，As半径为a pm，假设As、B原子相切，则B原子的半径为_________pm（写计算表达式）。
2．近期我国学者研制出低成本的电解“水制氢”催化剂——镍掺杂的磷化钴三元纳米片电催化剂（0.10.9Ni Co P ）。
回答下列问题：(1)Co 在元素周期表中的位置为_________，Co 2+价层电子排布式为______________。
(2)Co 、Ni 可形成()()323366Co NH Cl K Co NO ⎡⎤⎡⎤⎣⎦⎣⎦、、4Ni(CO)、()346Ni NH SO ⎡⎤⎣⎦等多种配合物。
晶胞的相关计算专项训练练习题及解析
晶胞的相关计算专项训练练习题及解析一、晶胞的相关计算1．根据下列结构示意图，判断下列说法中正确的是A．在CsCl晶体中，距Cs+最近的Cl-有6个B．在CaF2晶体中，Ca2+周围距离最近的F-有4个C．在SiO2晶体中，每个晶胞中含有4个Si原子和8个O原子D．在铜晶体中，每个铜原子周围距离最近的铜原子有12个2．补铁剂常用于防治缺铁性贫血，其有效成分般为硫酸亚铁、琥珀酸亚铁、富马酸亚铁和乳酸亚铁等。
回答下列问题：（1）能表示能量最低的亚铁离子的电子排布式是__(填标号)。
a.[Ar]3d54s2b.[Ar]3d54s1c.[Ar]3d64s2d.[Ar]3d6（2）琥珀酸即丁二酸(HOOCCH2CH2COOH)，在琥珀酸分子中电负性最大的原子是__，碳原子的杂化方式是__；琥珀酸亚铁中存在配位键，在该配位键中配位原子是__，中心原子是__。
（3）富马酸和马来酸互为顺反异构体，其电离常数如下表：物质名称K a1K a2富马酸()7.94×10-4 2.51×10-5马来酸() 1.23×10-2 4.68×10-7请从氢键的角度解释富马酸两级电离常数差别较小，而马来酸两级电离常数差别较大的原因：__。
（4）β-硫酸亚铁的晶胞结构如图所示，其晶胞参数为a=870pm、b=680pm、c=479pm，α=β=γ=90°，Fe2+占据晶胞顶点、棱心、面心和体心。
在该晶胞中，硫酸根离子在空间上有__种空间取向，晶胞体内硫酸根离子的个数是__，铁原子周围最近的氧原子的个数为__；设阿伏加德罗常数的值为N A，则该晶体的密度是__g·cm-3(列出计算表达式)。
3．新型冠状病毒来势汹汹，但是它依然可防可控。
84消毒液具有强氧化性，可将冠状病毒外的包膜破坏后使RNA被降解，使病毒失活，以达到灭菌的效果。
制取84消毒液的氯气可用加热浓盐酸和MnO2混合物来制取，也可用浓盐酸和KClO3直接混合来制取。
晶胞计算专题优秀课件
晶胞计算专题优秀课件一、引言晶胞计算（also known as晶体结构预测、晶格计算或晶体成像计算）是一种用于预测固体材料的晶体结构的方法。
晶胞计算使用原子坐标和生成能量来优化晶格，并预测出稳定的晶体结构。
本课件将介绍晶胞计算的基本原理和方法。
二、晶胞计算的原理1.单位胞单位胞是最基本的晶体结构单元，它通过周期性排列来描述整个晶体的结构。
在晶胞计算中，通过优化晶胞的参数和原子坐标来获得最稳定的晶体结构。
2.势能函数晶胞计算使用势能函数来描述晶体的稳定性。
势能函数通常由两部分组成：晶格势能和原子间相互作用势能。
通过优化势能函数，可以得到晶体的最低稳定态。
3.优化算法晶胞计算使用优化算法来晶格参数和原子坐标的最优解。
常用的算法包括梯度下降法和遗传算法等。
三、晶胞计算的方法1.第一性原理方法第一性原理方法是一种基于量子力学的方法，通过求解薛定谔方程来预测材料的性质。
常用的第一性原理方法包括密度泛函理论（DFT）和蒙特卡洛方法等。
2.经验势方法经验势方法是一种基于经验公式的方法，通过对已知晶体结构进行统计分析来预测新材料的结构。
经验势方法常用的模型包括伦敦分子力场（Lennard-Jones potential）和Brenner势能等。
3.动力学方法动力学方法是一种基于分子动力学模拟的方法，通过模拟原子在晶体中的运动来预测晶格的稳定态。
常用的动力学方法包括蒙特卡洛模拟和分子动力学模拟等。
四、晶胞计算的应用1.新材料的设计晶胞计算可以用于设计新材料的晶体结构和性能。
通过预测材料的结构和稳定性，可以帮助研发人员选择最佳的材料组合。
2.功能性材料的研究晶胞计算可以用于研究功能性材料的晶体结构和性能。
例如，可以通过计算材料的电子结构来预测其导电性和光学性质。
3.材料的相变研究晶胞计算可以用于研究材料的相变过程。
通过模拟材料在不同温度和压力下的结构变化，可以预测材料的相变点和相变机制。
五、总结晶胞计算是一种重要的预测材料性质和晶体结构的方法。
化学晶胞的相关计算专项训练试题含答案
化学晶胞的相关计算专项训练试题含答案一、晶胞的相关计算1．已知某离子晶体的晶胞示意图如图所示，其摩尔质量为Mg/mol，阿伏加德罗常数的值为N A，晶体的密度为dg/cm3下列说法中正确的是A．晶体晶胞中阴、阳离子的个数都为1B．晶体中阴、阳离子的配位数都是4C．该晶胞可能是NaCl的晶胞D．该晶体中两个距离最近的阳离子的核间距为4M/(N A d)cm2．铁(Fe)、铜(Cu)、银(Ag)是常见的金属元素，它们的单质及其化合物在生活中有广泛应用。
(1)Ag 与 Cu 在同一族，则 Ag 在周期表中________ (填“s”、“p”、“d”或“ds”)区；[Ag(NH3)2]+中Ag+空的 5s 轨道和 5p 轨道以sp 杂化成键，则该配离子的空间构型是________。
(2)基态 Cu+的简化电子排布式为________。
(3)表中是 Fe 和 Cu 的部分电离能数据：请解释 I2(Cu)大于 I2(Fe)的主要原因：________。
元素Fe Cu第一电离能 I1/kJ·mol－1759746第二电离能 I2/kJ·mol－115611958(4)亚铁氰化钾是食盐中常用的抗结剂，其化学式为 K4[Fe(CN)6]。
①CN-的电子式是________；1mol 该配离子中含σ 键数目为________。
②该配合物中存在的作用力类型有________ (填字母)。
A．金属键 B．离子键 C．共价键 D．配位键 E.氢键 F.范德华力(5)氧化亚铁晶体的晶胞结构如图所示。
已知：氧化亚铁晶体的密度为ρg•cm﹣3，N A代表阿伏加德罗常数的值。
在该晶胞中，与 Fe2+紧邻且等距离的 Fe2+数目为________，Fe2+与O2﹣最短核间距为________pm。
3．氮及其化合物有许多用途。
回答下列问题：（1）基态Mn 原子的电子排布式为________，锰的第三电离能比铁的第三电离能大，这是因为________________________________________________________。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例2.氢气是重要而洁净的能源，要利用氢气作能源， 必须安全有效地储存氢气。某种合金材料有较大的储氢
容量，其晶胞如图所示。则这种合金的化学式为（ D）
A．LaNi6 B． LaNi3 C．LaNi4 D． LaNi5
晶胞计算专题
3.正三棱柱
顶点： 1/12 面心： 1/2 （上、下）棱：1/4 中棱： 1/6
介电常数高,在小型变
Ba
压器、话筒和扩音器
中都有应用。其晶体
Ti
的结构示意图如右图
O
所示。则它的化学式
为（D）
A.BaTi8O12 C. BaTi2O4
B. BaTi4O6 D. BaTiO3
晶胞计算专题
2.现有甲、乙、丙、丁四种晶胞，可推知甲晶
体中与的粒子个数比为——1—:—1——；乙晶体 的 化学式为——D—C—2——或—C—2—D—；丙晶体的化学式 为—E—F—或——F—E ；丁晶体的化学式为—X—Y—2。Z
晶胞计算专题
金晶体的晶胞是面心立方晶胞，金原子的直径 为d，用NA表示阿伏加德罗常数，M表示金 的摩尔质量。
(1)欲计算一个晶胞的体积，除假定金原子是钢 性小球外，还应假定 各面对角线上。的三个球两两相切
(2)一个晶胞的体积是多少?
(3)金晶体的密度是多少?
设晶胞边长为a，则有a2+a2=(2d)2，即a= 2 d
1
3 73
62
2
4
面心：1/2
2
顶点：1/8
1
1
体心：1 晶胞计算专题
一、晶胞中粒子个数计算规律
1.立方晶胞
晶胞 顶角 棱上 面上
立方体 1/8 1/4 1/2
中心 1
晶胞计算专题
顶角 棱上 面上 中心
例1.下面晶胞中含有粒子个数
A+
A+= 4 ×1/8=1/2
BB-= 4 ×1/8=1/2
A与B离子的个数比等于 1:1 该物质化学式可 表示为:__A__B___
棱长a =2 2r
②密度
晶胞计算专题
二、晶胞密度的求算
例4.已知：晶体中Na+和 Cl-间最小距离为a cm,计 算NaCl晶体的密度。
458.5gmol1 NA (2acm)3
mol1
29.25 gcm3
a3 NA
晶胞计算专题
拓展 （1）利用均摊法计算该晶胞中含___4___个NaCl
（2）若Na+和Cl-间的最近距离为0.5x10-8cm， 求：晶体的密度
①棱长a = 2r ②密度
晶胞计算专题
二、晶胞密度的求算
2.已知金属 钾是体心立方紧密堆积,钾原子半 径为r cm,请计算：钾晶胞棱长；钾的密度。 ①立方体对角线=4r 棱长a=4r/ 3
②密度
晶胞计算专题
二、晶胞密度的求算 3、已知金属金是面心立方紧密堆积，金原子 半径为r cm，计算：金晶胞棱长；金的密度 。 ①面对角线 = 4r
BA
甲
DC
乙
F
E
丙
Z
X
Y
丁
晶胞计算专题
3、看图写化学式：
晶胞计算专题
A2BC2
4、最近发现一种由钛原子和碳 原子构成的气态团簇分子，如 下图所示，顶角和面心的原子 是钛原子，棱的中心和体心的 原子是碳原子，它的化学式 是 Ti14C13 。
晶胞计算专题
2.正六棱柱晶胞
顶点： 1/6 面心： 1/2 （上、下）棱：1/4 晶胞计算专题 中棱： 1/3
晶胞计算专题
课程标准
1.会计算晶胞中的粒子数 2.掌握晶胞中各线段的关系，结合数学 思想解决密度和空间占有率计算的问题
晶胞计算专题
晶胞中金属原子数目的计算方法(平均值)
顶点算1/8
棱算1/4
面心算1/2
体心算1
晶胞计算专题
已知铜晶胞是面心立方晶胞，该晶胞的边长为 3.6210-10m，每一个铜原子的质量为 1.05510-25kg ，试回答下列问题：
ClNa+
例5.如图所示，CsCl晶体中最近的Cs+之间距 离为s阿伏加德罗常数为NA摩尔质量为M 求晶体的密度
晶胞计算专题
三、 晶胞中空间利用率的计算
空间利用率=
微粒数×1个微粒体积 晶胞体积
(1)简单立方：
微粒数为：8×1/8 = 1
空间利用率：
4лr3/3 = 52.36% (2r)3
×100% =74%
晶胞计算专题
a ：晶bcc 胞单位长度 R ：原子半径
4R 3a a 4 R 3
一个晶胞含原子数 n = 2
空间利用率＝ 2(4R3
a3
/ 3)
100%
2(4R3 / 3)
(4R / 3)3
100%
68%
晶胞计算专题
平行六 面体
无隙并置
晶胞计算专题
请看:
4
8 51
棱边：1/4
8×1/8 + 6×1/2 + 4 = 8
晶胞计算专题金 刚 石 ຫໍສະໝຸດ 胞 示 意 图晶胞计算专题
拓展练习1：
某晶胞结构如 图所示，晶胞中 各微粒个数分别 为：
铜___3_____个 钡___2_____个 钇___1_____个 氧___7_____个
晶胞计算专题
课堂检测：
1.钛酸钡的热稳定性好,
（1）一个晶胞中“实际”拥有的铜原子数是多少？ （2）该晶胞的体积是多大？ （3）利用以上结果计算金属铜的密度。
解：（1）8 1/8+6 1/2=4
（2）V=a3=(3.6210-10m)3=4.74 10-29m3
m 4 1.05510-25kg
(3)ρ= =
=8.9 103 Kg/m3
V
4.74 10-29m3
晶胞计算专题
例3.某晶体的一部分如右图所示，这种晶
体中A、B、C三种粒子数之比是( B )
A.3∶9∶4
B.1∶4∶2
C.2∶9∶4
D.3∶8∶4
A B C
晶胞计算专题
二、晶胞密度计算：
立方晶胞中各线段之间的关系如下：
V=a3
晶胞计算专题
二、晶胞密度的求算 1.已知金属钋是简单立方堆积，钋原子半径 为r cm，计算：钋晶胞棱长；钋的密度。
2d
所以一个晶胞的体积为( 2 d)3=2 2 d3
（3）一个金原子的质量可表示为M/NA
a
ρ= m = 4 M/NA
V
2 2 d3
晶胞计算专题
晶胞所含的原子体积总和
空间利用率=
晶胞体积
X100%
例如，面心立方晶胞
2d
每个晶胞中含4个原子
a
空间利用率 =
4d 4X 3π 2 ( 2 d)3
3
a= 2 d
晶体化学式确定——晶胞内不同微粒的个数最简整数比
晶胞计算专题
确定化学式
A= 1 B= 4 ×1/8=1/2
A2B
晶胞计算专题
确定化学式
A= 4 ×1/4=1 B= 8 ×1/8=1 C= 1
ABC
晶胞计算专题
思考
金刚石晶胞
（1）C原子位于晶胞 的哪些位置，分别有 几个？
（2）实际含有原子 个数应为？