理想气体的内能
物理学24-理想气体的内能

张宏浩
1
பைடு நூலகம்
三、理想气体的内能
分子间相互作用 可以忽略不计 分子间相互作用的势能=0
理想气体的内能=所有分子的热运动动能之总和
i i 1mol理想气体的内能为 E 0 N A ( kT ) RT 2 2
M i 一定质量理想气体的内能为 E RT M mol 2
温度改变,内能改变量为 E M
当温度极低时,转动自由度 r 也被“冻结”, 任何分子都可视为只有平动自由度。
4
刚性分子理想气体内能:
f E kT N 2 f R T N A 2 NA f RT 2
:气体系统的摩尔(mol)数
5
根据
求等体热容
小结:
练习 就质量而言,空气是由76%的N2,23%的O2 和1%的Ar三种气体组成,它们的分子量分别为28、 32、40。空气的摩尔质量为28.910-3kg,试计算1mol 空气在标准状态下的内能。
3
3
3 3 M 28 . 9 10 1 % 0 . 289 10 kg Ar质量 3
M3 0.289 摩尔数 n3 0.007 M mol 3 40 1mol空气在标准状态下的内能
i3 i1 i2 E n1 RT n2 RT n3 RT 2 2 2 1 ( i1 n1 i2 n2 i3 n3 )RT 2
内能: E N( k p) p ij
i j
E (T ,V )
(i>j)
由 T 决定
由 V 决定
3
对理想气体: p ij 0 , E E (T ) ;
对刚性分子(rigid molecule):v 0 ,i t r
理想气体的内能、热容和焓

4
(2)由图可以看出:
PaVa = PcVc ∴Ta = Tc ⇒ ΔU = 0
P (atm )
a 3
2
b
1
c
o 1 2 3 V(10−3m3)
(3)由热力学第一定律得:
Q = ΔU + A = 405.2J
5
二、理想气体的热容
1. 热容、比热容、摩尔热容
设系统温度升高 dT ,所吸收的热量为dQ
在等压过程中,dp=0,故 pdVm = RdT 将其代入 Cp,mdT = CV ,mdT + pdVm 得:
Cp,mdT = CV ,mdT + RdT 等式两边约去dT得:
迈耶公式 C p,m = Cv,m + R
表明:理想气体定压摩尔热容等于定体摩尔热容与普适
气体常量R之和。
C p,m > CV ,m
质量之比。
c
=
C m
=
1 m
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠
M:摩尔质量
摩尔热容Cm:物质的量为v的该物质的热容C与v之比。
Cm
=
C
ν
=1
ν
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠
=
cm
ν
=
Mc
或: c = Cm
M
单位: J·mol-1·K-1
(1)定体摩尔热容CV, m:
CV ,m
=1
ν
⎛ ⎜⎝
dQ dT
⎞ ⎟⎠V
(2)定压摩尔热容Cp, m:
热容:
C = lim ΔQ = dQ ΔT →0 ΔT dT
单位:J/K
(1)定体热容:
CV
ch.1-7 理想气体的内能
dH Cp dT
(1.7.6)
H
C dT H p 0
此即理想气体焓的积分表达式。
3.理想气体的迈尔公式
由式(1.7.4)、(1.7.2)和(1.7.7)可得
C p C V nR
(1.7.7)
上式称为迈尔公式,它给出了理想气体的定压热容 量与定容热容量之差。当年迈尔正是由这个关系最先得 到了热功当量。引入γ表示定压热容量与定容热容量的 比值:
§1.7
理想气体的内能
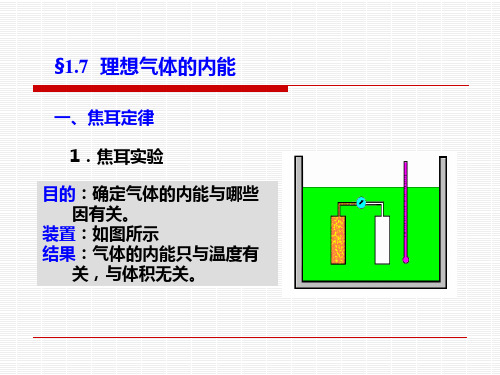
一、焦耳定律 1.焦耳实验 目的:确定气体的内能与哪些 因有关。 装置:如图所示 结果:气体的内能只与温度有 关,与体积无关。
2.焦耳定律
1845年,焦耳用自由膨胀实验研究了气体的内能,得 出气体内能仅仅是温度的函数而与体积无关这一重要结论。 这条结论称为焦耳定律,可表示为
U U U (T )或 0 V T
(1.7.3)
2.理想气体的焓 根据焓的定义(1.6.6)式和理想气体物态方程,可得理 想气体的焓为 H= U + pV = U + nRT (1.7.4)
可以看出, H也仅是T的函数,因此,对于理想气体, 式(1.6.7)的偏导数也可写成
dH Cp dT
(1.7.5)
(1.6.7)的偏导数也可写成 将上式积分,得
后来,人们发现焦耳实验的结果不够可靠。
(1.7.1)
于是,焦耳和汤姆逊在1852年用节流方法重新做了实 验,并发现实际气体的内能不仅是温度的函数而且还是体 积的函数。不过,焦耳定律在实际气体压强趋于零的极限 情形下是正确的,所以可认为它是理想气体所遵守的定律。 即,理想气体的内能只是温度的函数而与体积无关。 可表达为 U=U(T)
6.4X 能量均分定理 理想气体的内能

刚性近似下, s = 0, i = t + r, 分子的平均总能量:
3 2 kT(单原子分子) i tr 5 E Ek kT kT kT(双原子分子) 2 2 2 6 2 kT 3kT(多原子分子)
当温度极低时,转动自由度 r 也被“冻结”, 任何气体分子都可视为只有平动自由度 , 就如 同单原子分子。这时, r = 0, s = 0, i = t, i t 分子的平均总能量 E Ek kT kT 2 2
1.52102 ( J / m3 )
(4) 0.3 mol气体的内能
i 5 E RT 0.3 8.31 273 1.7 10 3 J 2 2
例2:贮存有氮气的容器以速度100米/秒运动。若该容 器突然停止,问容器中温度将升多少?
已知:u
100m / s, i 5, 28 10 kg / mol
常温下热运动能kt为0026ev故转动状态很容易被激发而振动状态很少被激发因此故转动状态很容易被激发而振动状态很少被激发因此在常温下理想气体分子可近似看成是刚性的在常温下理想气体分子可近似看成是刚性的只需考虑其平动和转动自由度而不必考虑其振动自由度
6.4 能量均分定理 理想气体的内能
引言:前面我们研究气体动能时,把分子看作弹性 小球的集合,人们发现用这一模型去研究单原子气体问 题时,理论与实际符合得很好,但是用这一模型去研究 多原子分子时,理论值与实验值相差甚远。 1857年克劳修斯提出:将理想气体模型稍作修改。 即不能将所有分子都看成质点,对结构复杂的多原子 分子,考虑分子的能量时,要考虑分子各种运动的能 量。即不但要考虑分子的平动,还要考虑其转动和分 子内原子之间的振动。 下面我们来考察包括平动、转动、及振动在内的理 想气体能量。
理想气体内能

解
kT 2π d2 p
1 2 π ( 3 1 .1 .3 1 1 0 8 1 2 0 ) 0 2 0 3 2 1 .0 7 1 1 3 5 m 3 0 8 .7 1 1 8 m 0
22 π (3 1 .1 .3 1 0 1 8 1 0 2 ) 0 0 2 3 2 1 .3 7 3 1 3 3 3 0 m 6 .6m 2
CV,m
CP,m
γ
He
12.61 20.953 20.90 1.67
H2
20.47 28.83 1.41
N2
20.78 20.09 1.40 20.56 28.88 1.40
O2
21.16 29.61 1.40
H2O
27.8 36.2 1.31
CH4 24.93 33.24 1.33 27.2 35.2 1.30
3R
25.1Jmol1 K1
§7-7 分子的平均碰撞次数和平均自由程
气体分子 平均速率
v 1.60 RT M mol
氮气分子在27°C时的平均速率为476m/s.
气体分子热运动平均速率高, 矛盾 但气体扩散过程进行得相当慢。
克劳修斯指出:气体分子的速度虽然很大,但前 进中要与其他分子作频繁的碰撞,每碰一次,分 子运动方向就发生改变,所走的路程非常曲折。
一、平均碰撞次数
假 每个分子都是有效直径为d 的弹性小球。
定 只有某一个分子A以平均速率 v运动,
其余分子都静止。
d
v
d
v
A
d
d
v
d
v
A
d
球心在圆柱 体内的分子
运动方向上,以 d 为半径的圆柱体内的分子都将
与分子A 碰撞
理想气体等温可逆内能公式

理想气体等温可逆内能公式
理想气体等温可逆内能公式是指在等温可逆过程中,理想气体内能的计算公式。
根据热力学第一定律,气体的内能变化等于对气体做功和气体所吸收的热量之和,即ΔU=W+Q。
在等温可逆过程中,气体所吸收的热量Q等于热力学温度T与气体所吸收的热量dQ 之积,即Q=TdS。
根据熵的定义S=nClnT+nRlnV+常数,可知等温可逆过程中熵的变化ΔS=nRln(Vf/Vi)。
在等温可逆过程中,气体所做的功W等于PdV,因为过程是可逆的,所以气体的压强始终等于外界压强P0。
根据理想气体状态方程PV=nRT,可得P=nRT/V。
将上式代入W=PdV中,可得W=nRTln(Vf/Vi)。
因此,在等温可逆过程中,理想气体内能变化ΔU=W+Q=nRTln(Vf/Vi)+nRTln(Vf/Vi)=nRTln(Vf/Vi)×2。
根据热力学第二定律,等温可逆过程中ΔS=Q/T=nRln(Vf/Vi),以及ΔS=
ΔU/T,可得ΔU=nRTln(Vf/Vi)。
因此,理想气体等温可逆内能公式为ΔU=nRTln(Vf/Vi)。
- 1 -。
热力学第一定律对理想气体的应用

热力学第一定律对理想气体的应用
热力学第一定律(也称为能量守恒定律)对理想气体的应用提供了重要的物理洞察和计算方法。
以下是热力学第一定律在理想气体中的一些应用:
1.内能变化计算:热力学第一定律表明,理想气体的内能变化等于吸收的热量减去对外界做的功。
根据该定律,我们可以计算理想气体的内能变化,即ΔU = Q - W,其中ΔU 表示内能变化,Q 表示吸收的热量,W 表示对外界做的功。
2.等容过程计算:等容过程是指理想气体在体积不变的条件下发生的过程。
根据热力学第一定律,对于等容过程,ΔU = Q,即内能变化等于吸收的热量。
这使得我们可以根据所吸收的热量计算内能的变化。
3.等压过程计算:等压过程是指理想气体在恒定压力下发生的过程。
根据热力学第一定律,对于等压过程,Q = ΔU + W,即吸收的热量等于内能变化加上对外界所做的功。
这使得我们可以根据所做的功和内能变化计算吸收的热量。
4.等温过程计算:等温过程是指理想气体在恒定温度下发生的过程。
根据热力学第一定律,对于等温过程,Q = W,即吸收的热量等于对外界所做的功。
这意味着在等温过程中,吸收的热量和所做的功相等。
第19讲能量均分定理理想气体的内能

教学要求了解速率分布函数、分子速率的实验测定、麦克斯韦速率分布律。
理解气体分子的方均根速率、刚性分子的自由度。
掌握气体的能量均分定理,理想气体的内能。
7.4 能量均分定理 理想气体的内能前面讨论分子热运动时,把分子视为质点,只考虑分子的平动。
气体的能量是与分子结构有关的,除了单原子分子可看作质点外,一般由两个以上原子组成的分子,不仅有平动,而且还有转动和分子内原子间的振动。
为了确定分子的各种运动形式的能量的统计规律,需要引用力学中有关自由度的概念。
7.4.1自由度完全描述系统在空间位置所需独立坐标的数目,称为系统的自由度。
考察分子运动的能量时,不能再把各种分子都当作质点处理,从而还要考虑其它运动形式(如转动和振动等)的自由度。
气体分子按其结构可分为单原子分子、双原子分子和三原子或多原子分子。
当分子内原子间距离保持不变(不振动)时,这种分子称为刚性分子,否则称为非刚性分子,对于非刚性双原子分子或多原子分子,由于在原子之间相互作用力的支配下,分子内部还有原子的振动,因此还应考虑振动自由度。
但是由于关于分子振动的能量,经典物理不能给出正确的说明,正确的说明需要量子力学;另外在常温下用经典方法认为分子是刚性的也能给出与实验大致相符的结果;所以作为统计概念的初步,下面只讨论刚性分子的自由度。
1 单原子分子如氦(He)、氖(Ne)、氩(Ar)等分子只有一个原子,可看成自由质点,所以有3个平动自图7-3 分子的自由度(a )单原子分子 (b )双原子分子(c )三原子分子zzzααγββθ由度[如图7-3(a )]。
2 刚性双原子分子如氢 (H 2)、氧( O 2)、氮(N 2)、一氧化碳(CO)等分子,两个原子间联线距离保持不变。
就像两个质点之间由一根质量不计的刚性细杆相连着(如同哑铃),确定其质心C 的空间位置,需3个独立坐标(x ,y ,z );确定质点连线的空间方位,需两个独立坐标(如α,β), 而两质点绕连线的的转动没有意义(因为相对该连线的转动惯量J 是非常小的,从而与该连线相应的转动动能212J ω可以忽略不计)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
14、一定质量的理想气体状态变化过程如图所示,第1种变化是从A 到B ,第2种变化是从A到C ,比较两种变化过程( ).(A)A 到C 过程气体吸收热量较多 (B)A 到B 过程气体吸收热量较多 (C)两个过程气体吸收热量一样 (D)两个过程气体内能增加相同15、一定质量的理想气体,当它发生如图所示的状态变化时,哪一个状态变化过程中,气体吸收热量全部用来对外界做功( ).(A)由A 至B 状态变化过程 (B) 由B 至C 状态变化过程 (C) 由C 至D 状态变化过程 (D) 由D 至A 状态变化过程16、一定质量的理想气体可经不同的过程从状态Ⅰ(p 、V 1、T 1)变到状态Ⅱ(p 2、V 2、T 2),已知T 2>T 1,在这些过程中( ). (A)气体一定都从外界吸收热量(B)气体和外界交换的热量都是相等的 (C)外界对气体做的功都是相等的 (D)气体内能的变化量都是相等的 28、如图所示,是一定质量理想气体的p -V1关系图像(p 为气体压强,V 为气体体积),图中A 、B 、C 三点代表该气体的3个不同的状态,若气体先后沿两段直线AC 、BC 发生由A 经C 至B 的状态变化过程,那么在这整个过程中( ).(A)外界对气体做正功,气体内能增加 (B) 外界对气体做正功,气体内能减少 (C) 外界对气体做负功,气体内能增加 (D) 外界对气体做负功,气体内能减少31、如图所示为一定质量的理想气体的状态变化图像.A 、B 、C 三个状态的热力学温度分别为T A 、T B 和T C ,状态变化沿箭头所指的方向进行.那么,( ).(A) T B -T C =T B -T A ,且B →C 过程放出的热量等于A →B 过程吸收的热量. (B) T C -T B =T A -T B ,且B →C 过程吸收的热量等于A →B 过程放出的热量. (C) T C -T B =T A -T B ,且B →C 过程吸收的热量大于A →B 过程放出的热量. (D) T C -T B >T A -T B ,且B →C 过程吸收的热量等于A →B 过程放出的热量.33、一定质量的理想气体,从状态A 变化到状态B ,如图所示,AB 平行于Op 轴,由此可以断定,气体在状态变化过程中( ) (A )气体分子无规则热运动减缓 (B )气体内能增加 (C )气体分子热运动的平均动能不变 (D )气体体积增大36、一定质量的理想气体,在下列变化过程中,其分子无规则运动肯定加剧的是( ).(A)等温压缩(B)等压压缩(C)等温膨胀(D)等压膨胀37、一定质量的理想气体,经过如下状态变化后,其中气体内能可能增加的是()(A)先等温压缩,再等压压缩(B)先等压压缩,再等容升压(C)先等容压缩,再等温压缩(D)先等容降压,再等压膨胀39、一定质量的气体可经过不同的过程从状态(p1、V1、T1)变到状态(p2、V2、T2),已知T2>T1,则在这不同过程中()(A)气体一定都从外界吸收热量(B)气体和外界交换的热量都是相等的(C)外界对气体所做的功都是相等的(D)气体内能的变化量都是相等的40、一定质量的理想气体由状态a 变化到状态b ,经历不同的变化过程的图像如图所示,由图线可知()(A)图线(1)所示的过程中气体的内能不变(B)图线(4)所示的过程中气体不做功(C)图线(2)、(3)所示的过程中外界压缩气体做功(D)图线(2)、(3)、(4)所示的过程中气体向外界放热49、要使一定质量的理想气体由某一状态经过一系列变化,又回到初始状态,下列可能实现这一要求的过程是( ).(A)先等容吸热,再等温吸热,最后等压压缩(B)先等压升温,再等容吸热,最后等温放热(C)先等温膨胀,再等压升温,最后等容吸热(D)先等容放热,再等压降温,最后等温吸热58、一定质量的理想气体,封闭在带活塞的汽缸中,气体从状态a开始,经历ab、bc、cd、da四个状态回到a状态,如图所示,其中气体对外界做功的过程是________过程,从外界吸热的过程是________过程。
61、一定质量的理想气体从状态R出发,分别经历图所示的4种不同过程发生状态变化.其中气体从外界吸热并对外界做正功的过程是( ).(A)R→A(B)R→B(C)R→C(D)R→D63、如图所示,一定质量的理想气体从状态1到状态2,不论经历什么样的变化过程,这一定质量的气体必然(A)向外界放出热量;(B)从外界吸收热量;(C)对外界做功;(D)内能增加。
67、一定质量的理想气体经如图所示的一系列变化过程.过程AB、BC、CA的图像恰组成一个圆周.OA、OB为圆周的切线,C是圆周上离开原点O最远的点心.由图可以判定( )(A)在过程AB中气体体积不断增大(B)在过程BC中气体体积不断减小(C)在过程CA中气体对外做功(D)在过程BCA中气体吸热73、如图所示的绝热容器中间用隔板分成两部分.左侧存有理想气体,右侧是真空.把隔板抽掉,让左侧气体自由膨胀到右侧直至平衡.( ).(A)气体对外做功,内能减少,温度降低(B)气体对外做功,内能不变,温度不变(C)气体不做功,内能不变, 压强不变(D)气体不做功,内能不变,温度不变,但压强减小75、有一个氢气瓶,由于压强不大,可以把其中的氢气视作理想气体,瓶中氢气的p-T图线如图所示的1→2.则它( ).(A)正在灌气(B)正在用气(C)内能减少(D)内能增加76、一定质量的理想气体,其状态变化图线如图所示,1→2→3.那么这3个状态的温度T1、T2、T3以及吸、放热量的关系是( ).(A)T2-T1=T2-T3, 1→2吸收的热量等于2→3放出的热量(B)T2-T1=T2-T3, 1→2吸收的热量小于2→3放出的热量(C)T2-T1=T2-T3, 1→2吸收的热量大于2→3放出的热量(D)T2-T1>T2-T3, 1→2吸收的热量等于2→3放出的热量78、一定质量的理想气体,从某一状态开始经过若干个状态变化过程,最终又回到最初的状态。
则在这些状态变化的过程中()(A)在其中任一过程中,只要气体膨胀对外做功,就一定吸热(B)在其中任一过程中,只要气体吸热,它的温度就一定升高(C)无论变化到哪一个状态,它的状态参量总满足pV/T为一恒量(D)所变化到的状态pV乘积越大,气体在该状态的内能越大79、对于一定质量的理想气体,在下列各种过程中,可能发生的过程是( ) (A ) 气体膨胀对外做功,温度升高 (B ) 气体吸热,温度降低 (C ) 气体放热,压强增大 (D ) 气体放热,温度不变80、对于一定质量的理想气体,下述说法中正确的是(A)状态改变时,热力学能一定改变; (B)等温过程,气体不吸热也不放热; (C)气体放热时,温度不一定降低; (D)气体压缩时,热力学能一定增加.1 (2013徐州摸底)如图所示,一定质量的理想气体从状态A 变化到状态B ,已知在此过程中,气体内能增加100J ,则该过程中气体 (选填“吸收”或“放出”)热量 J .答案:吸收 300解析:一定质量的理想气体从状态A 变化到状态B ,体积增大,对外做功W=p △V=1.0×105×2.0×10-3J=2.0×102J..。
根据热力学第一定律,该过程中气体吸收热量300J 。
2(2013江苏常州模拟)一定质量的理想气体压强p 与热力学温度T 的关系图象如图所示,AB 、BC 分别与p 轴和T 轴平行,气体在状态A 时的压强为p 0、体积为V 0,在状态B 时的压强为2p 0,则气体在状态B 时的体积为 ;气体从状态A 经状态B 变化到状态C 的过程中,对外做的功为W ,内能增加了ΔU ,则此过程气体(选填“吸收”或“放出”)的热量为 .答案: V0/2 (1分) 吸收 (1分) △U+W (4分)(2)解析:对AB 过程,温度不变,由玻意耳定律可知,气体在状态B 时的体积为V= V 0/2;气体从状态A 经状态B 变化到状态C 的过程中,对外做的功为W ,内能增加了ΔU ,由热力学第一定律,此过程气体吸收的热量为△U+W .00p 2p6(9分)(2013长春市四模)一定质量的理想气体从状态A 变化到状态B 再变化到状态C ,其状态变化过程的p -V 图象如图所示。
已知该气体在状态A 时的温度为27℃。
求:①该气体在状态B 、C 时的温度分别为多少摄氏度?②该气体从状态A 到状态C 的过程中是吸热还是放热?传递的热量是多少?(9分)【参考答案】①-73℃;27℃ ②吸热;200J【命题立意】考查学生应用理想气体状态方程解决问题的能力。
【解 析】①气体从状态A 到状态B :得200B T =K 即73B t =-℃ (3分) 气体从状态B 到状态C :得300C T =K 即27C t =℃ (3分) ②气体从状态A 到状态C 过程中是吸热 (1分) 吸收的热量200Q P V =∆=J (2分)8(9分)(2013江西省金溪一中质检)一定质量的理想气体从状态A 变化到状态B ,再变化到状态C ,其状态变化过程的P-T 图象如图所示。
已知该气体在状态A 时的体积为1×10-3m 3。
求: ①该气体在状态C 时的体积;②该气体从状态A 到状态B 再到状态c 的过程中,气体与外界传递的热量解析:①A 、B 两状态体积相等,则有……①(2分)得:,从B 到C 压强相同,则:(2分);;又因:故:(2分)②由于A 到B 再到C 的过程中温度先向外散热,再温度升高从外界吸热,最后A 和C 的温度相同,因此气体内能相同,因为气体向外界传递的热量为零(3分) 10.(10分)(2013甘肃省兰州市模拟)如图所示,一定质量的理想气体,处在A 状态时,温度为t A =27︒C,气体从状态A 等容变化到状态M ,再等压变化到状态B ,A 、M 、B 的状态参量如图所示。
求:①状态B 的温度;②从A 到B 气体对外所做的功。
(取1atm =1.0⨯105P a )解析:①设A 状态和状态B 的温度、体积、压强分别为T 1、、V 1、P 1,T 2、、V 2、P 2,由已知可得T 1、=300K V 1=3m 3 P 1=2.5atm T 2=? V 2=6m 3 P 2=1atm ,从A 到B 由理想气体状态方程,222111T V P T V P =得 …………………① …………………② ②从A 到M 是等容变化,不做功;从M 到B 是等压变化,做的功为,J 100.3J 3100.1m 3atm 1553⨯=⨯⨯=⋅=∆=V P W ,…………………③所以从A 到B 气体对外做的功为J 100.3W 5AB ⨯=………………………………………………………④ ①②步每步3分,③④每步2分。
