六年级奥数蝴蝶模型讲解学习
六年级数学奥数培优教案(下册)图形问题之蝴蝶模型

蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
类型 1:任意四边形中的蝴蝶模型① S 1 ⨯ S 3 = S 2 ⨯ S 4 (上、下两部分面积的积等于左、右两部分面积的积);② S 1 : S 4 = S 2 : S 3 = (S 1 + S 2 ): (S 4 + S 3 )= AO : OC (左:右 = 左和:右和)类型 2:梯形中的蝴蝶模型① S 2 = S 4 ;② S 1 ⨯ S 3 = S 2 ⨯ S 4 ;③OC AO s s s s s s s s :)(:)(::34213241=++==④)(::::::224231ab ab ab b a s s s s 上下平方,左右=⑤梯形 S 的对应份数为 (a + b )2【例1】如图,某公园的外轮廓是四边形 ABCD ,被对角线 AC 、BD 分成四个部分,△ AOB面积为 1 平方千米,△BOC 面积为 2 平方千米,△COD 的面积为 3 平方千米,公园由陆地面积是 6.92 平方千米和人工湖组成,求人工湖的面积是多少平方千米?【例2】如图,边长为 1 的正方形 ABCD 中,BE=2EC ,CF=FD ,求△AEG 的面积.【例3】梯形 ABCD 的对角线 AC 与 BD 交于点 O ,已知梯形上底为 2,且△ABO 的面积等于△BOC 面积的32 ,求△AOD 与△BOC 的面积之比. 专题:图形问题之蝴蝶模型【例4】正方形 ABCD 的面积是 120 平方厘米, BE =31AB , BF = 21BC ,四边形 BGHF 的面积是多少平方厘米?1、如图,四边形被两条对角线分成4个三角形,则△BGC 的面积为 ;AG:GC=2、如图,四边形ABCD 的对角线AC 与BD 交于点O 若△ABD的面积等于△BCD 的面积的31,且AO=2,DO=3,那么CO 的 长度是DO 的 倍。
蝴蝶模型(基础)(知识讲解)(学生版)

蝴蝶模型(基础)知识讲解(学生版)蝴蝶模型是一种用于描述和理解复杂系统中非线性关系的模型。
它基于混沌理论和蝴蝶效应,通过简单的数学方程,展示了微小的初始差异如何随着时间的推移导致巨大的系统变化。
这个模型不仅在数学和物理学中有重要应用,还可以帮助我们理解自然界和日常生活中的许多现象。
一、什么是蝴蝶模型?蝴蝶模型,也称为洛伦兹系统,是由美国气象学家爱德华·洛伦兹在1960年代提出的。
洛伦兹在研究天气预报时发现,即使是微小的初始条件变化,也会导致长期天气预报的巨大差异。
这个发现后来被称为“蝴蝶效应”,即“蝴蝶在巴西扇动翅膀,可能会在美国的德克萨斯州引发龙卷风”。
二、蝴蝶模型的方程dx/dt = σ(y x)dy/dt = x(ρ z) ydz/dt = xy βz其中,x、y、z是系统的状态变量,而σ、ρ、β是参数,通常取σ = 10, ρ = 28, β = 8/3。
这些参数的取值对于系统的行为有着重要影响。
三、蝴蝶模型的特性蝴蝶模型具有几个显著特性,使其成为一个有趣的研究对象:1. 混沌性:蝴蝶模型的解表现出混沌行为,这意味着即使初始条件非常接近,随着时间的推移,解也会迅速分离。
2. 敏感性:蝴蝶模型对初始条件非常敏感,微小的变化会导致长期行为的巨大差异。
3. 吸引子:蝴蝶模型的解趋向于一个复杂的几何形状,称为“洛伦兹吸引子”。
这个吸引子是混沌系统的典型特征。
四、蝴蝶模型的应用蝴蝶模型不仅在理论研究中有着重要地位,它在实际应用中也展现出广泛的价值。
例如:1. 气象学:蝴蝶模型有助于理解天气预报的不确定性,以及为什么长期天气预报难以准确。
2. 经济学:蝴蝶模型可以用来模拟经济系统的复杂动态,如股市波动和宏观经济预测。
3. 生态学:蝴蝶模型可以用来研究生态系统中的种群动态和生物多样性。
通过学习蝴蝶模型,我们可以更好地理解复杂系统的行为,以及如何在不同领域中应用这些知识。
希望这个基础讲解能够帮助你入门,激发你对混沌理论和非线性动力学的兴趣。
2019年数学奥数6年级终极培优详解(第4讲)图形问题之蝴蝶模型

蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。通过构造模型,一 方面可以使不规则四边形的面积关系与四边形内的三角形相联系; 另一方面, 也可以得到 与面积对应的对角线的比例关系。
类型 1:任意四边形中的蝴蝶模型
① S1 S3 S2 S4 (上、下两部分面积的积等于左、右两部分面积的积);
是多少平方厘米?
1 AB, BF
3
1 BC ,四边形 BGHF 的面积
2
1、如图,四边形被两条对角线分成 4 个三角形,则△ BGC 的
面积为
;AG:GC=
2、如图,四边形 ABCD 的对角线 AC 与 BD 交于点 O 若△ ABD
的面积等于△ BCD 的面积的 1 ,且 AO=2, DO=3,那么 CO 的 3
【例 2】如图,边长为 1 的正方形 ABCD 中, BE=2EC, CF=FD ,求△ AEG的面积.
【例 3】梯形 ABCD 的对角线 AC 与 BD 交于点 O,已知梯形上底为 2 ,且△ ABO的面积 等于△ BOC面积的 2 ,求△ AOD与△ BOC的面积之比.
3
【例 4】正方形 ABCD 的面积是 120 平方厘米, BE
长度是 DO 的
倍。
3、梯形的下底是上底的 1.5 倍,△ OBC 的面积是 9cm2 ,
则△ AOD 的面积是
4、正方形 ABCD的面积是 57 平方厘米, E 是 AB的中点, F 是 BC
的中点,则四边形 BGHFABCD是梯形,△ ADE面积是 1.8 ,△ ABF 的面积是 9 ,△ BCF 的面积是 27 .那么阴影△ AEC面积是多少?
② S1 : S4 S2 : S3
S1 S2 : S4 S3 AO : OC (左:右
小学奥数-几何五大模型(蝴蝶模型)知识讲解

小学奥数-几何五大模型(蝴蝶模型)模型三 蝴蝶模型(任意四边形模型)任意四边形中的比例关系(“蝴蝶定理”):S 4S 3S 2S 1O DCBA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径。
通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系。
【例 1】 (小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?ODCBA【分析】 根据蝴蝶定理求得312 1.5AOD S =⨯÷=△平方千米,公园四边形ABCD 的面积是123 1.57.5+++=平方千米,所以人工湖的面积是7.5 6.920.58-=平方千米【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =?任意四边形、梯形与相似模型B【解析】 ⑴根据蝴蝶定理,123BGC S ⨯=⨯V ,那么6BGC S =V ;⑵根据蝴蝶定理,()():12:361:3AG GC =++=. (???)【例 2】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示)。
如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍。
ABCDOH GA BCD O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形。
六年级奥数蝴蝶模型(供参考)

蝴蝶模型一、蝴蝶模型与任意四边形在任意四边形中,两对角线将四边形分成四个三角形,两组相对三角形面积之积相等。
推导:由等积变形模型可知:二、蝴蝶模型与梯形①②推导:① 同上② 过点A 作三角形ABC 的高1h ,过点D 作△BCD 的高2h21h h =∴(两平行线之间高相等)三、蝴蝶模型与平行四边形(一) ①②推导:① 同上② BCD ABC S S ∆∆= ACD BCD S S ∆∆= (同底等高)即:对角平行四边形面积乘积相等(在平行四边形ABCD 内作两条分别平行于两组相对边的线段GH 、EF ) 推导:连接GE 、EH 、HF 、FG ,过点E 作EM 垂直于GH 于点M同理可得:321S S OGF =∴∆ 221S S OFH =∆ 421S S EOH =∆ 由蝴蝶定理可知:EOH OGF OFH OGE S S S S ∆∆∆∆⨯=⨯四、蝴蝶模型与长方形(一) ①②即:对角长方形面积乘积相等五、蝴蝶模型与正方形“子母图”——两共线相邻的正方形在上面两个图形中,每组正方形的对角线均互相平行,即a//b 、c//d重要结论:两共线相邻的正方形对角线互相平行。
例1:如下图所示,在梯形ABCD 中,对角线BD ,AC 相交于点O ,△AOD 的面积是6,△AOB 的面积是4,那么梯形ABCD 的面积是多少?分析:梯形ABCD 是四个三角形面积的总和,现已经知道两个三角形的面积,由蝴蝶定理容易求出三角形BOC 和三角形DOC 的面积,进而可以求出梯形ABCD 的面积。
解:由蝴蝶定理可知:S ∆BOC =S ∆AOD =6∴S ∆DOC =6×6÷4=9∴梯形ABCD 的面积是9+6+4+6=25答:梯形ABCD 的面积是25。
例2:如图,求阴影部分的面积。
(单位cm 2)分析:由长方形中的蝴蝶定理“对角长方形面积乘积相等”,可直接求出阴影部分的面积。
解:S 阴影=28×6÷12=14(cm 2)答:阴影部分的面积为14平方厘米。
六年级奥数蝴蝶模型

蝴蝶模型一、蝴蝶模型与任意四边形在任意四边形中,两对角线将四边形分成四个三角形,两组相对三角形面积之积相等。
推导:由等积变形模型可知:OC AOS S BOC AOB =∆∆ OC AOS S COD AOD =∆∆ COD AODBOC AOB S S S S ∆∆∆∆=∴2431S S S S =即4321S S S S ⨯=⨯∴二、蝴蝶模型与梯形①②推导:① 同上② 过点A 作三角形ABC 的高1h ,过点D 作△BCD 的高2h BC AD //21h h =∴(两平行线之间高相等)121h BC S ABC ⨯⨯=∆221h BC S BDC ⨯⨯=∆BDC ABC S S ∆∆=∴ 3231S S S S +=+∴ 21S S =∴三、蝴蝶模型与平行四边形(一) ①②推导:① 同上② BCD ABC S S ∆∆= ACD BCD S S ∆∆= (同底等高) 4241S S S S +=+∴ 2324S S S S +=+ 21S S =∴ 43S S = OD OB = OC OA = 31S S =∴ 42S S =即:对角平行四边形面积乘积相等(在平行四边形ABCD 内作两条分别平行于两组相对边的线段GH 、EF )推导:连接GE 、EH 、HF 、FG ,过点E 作EM 垂直于GH 于点MEM OG S OGE ⨯⨯=∴∆21EM OG S S ⨯==∴1平行四边形 121S S OGE =∴∆同理可得:321S S OGF =∴∆ 221S S OFH =∆ 421S S EOH =∆ 由蝴蝶定理可知:EOH OGF OFH OGE S S S S ∆∆∆∆⨯=⨯432121212121S S S S ⨯=⨯∴4321S S S S ⨯=⨯∴ 四、蝴蝶模型与长方形(一)①②即:对角长方形面积乘积相等五、蝴蝶模型与正方形“子母图”——两共线相邻的正方形在上面两个图形中,每组正方形的对角线均互相平行,即a//b、c//d 重要结论:两共线相邻的正方形对角线互相平行。
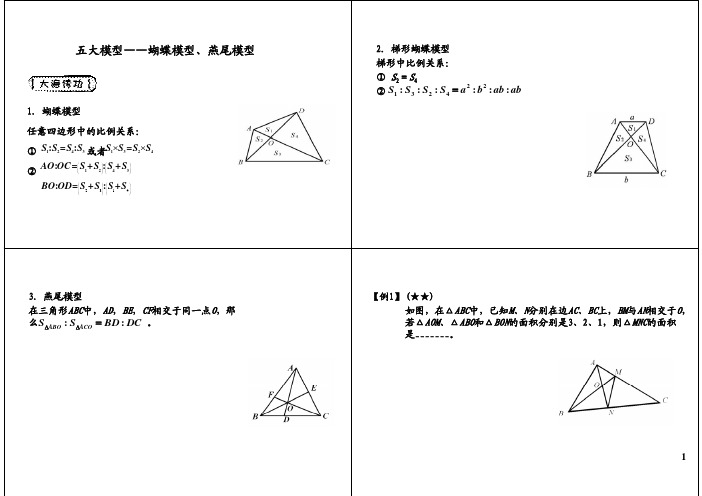
小学六年级奥数 五大模型——蝴蝶模型、燕尾模型
1
【例2】(★★★)
如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分别 为2、5、8平方厘米,那么余下的四边形OFBC的面积为 ___________平方厘米。
【例3】 (★★★)
如图,ABCD长方形中,阴影部分是直角三角形且面积为54,OD 的长是16,OB的长是9。那么四边形OECD的面积是多少?
五大模型——蝴蝶模型、燕尾模型
1.蝴蝶模型
任意四边形中的比例关系:
①
S :S =S :S
12
43
或者S1
S 3
=
S 2
S 4
② AO:OC = S +S : S +S
1
2
4
3
BO:OD= S +S : S +S
ቤተ መጻሕፍቲ ባይዱ
2
3
Aa D S1
S2 O S4
S3
B
C
b
二、本讲经典例题 例1,例4,例6,例7,例8
3.燕尾模型 在三角形ABC中,AD,BE,CF相交于同一点O,那么 SABO : SACO BD : DC 。
4
1
4
3.燕尾模型
在三角形ABC中,AD,BE,CF相交于同一点O,那 么SABO : SACO BD : DC 。
2.梯形蝴蝶模型 梯形中比例关系: ① S2=S4 ② S1 : S3 : S2 : S4 a2 : b2 : ab : ab
六年级奥数蝴蝶模型
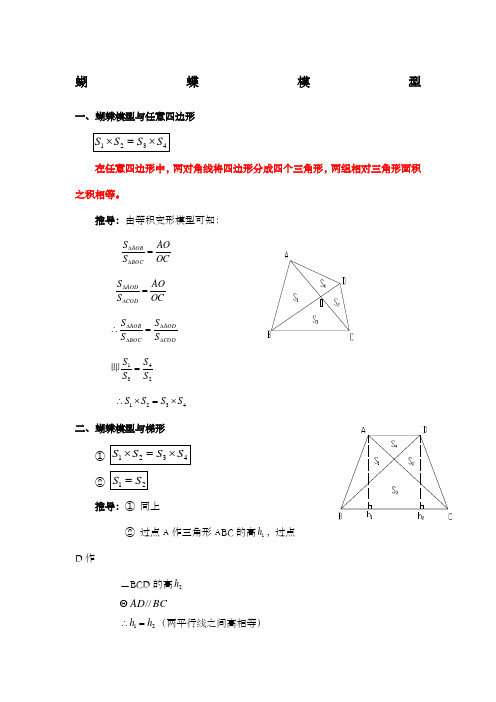
蝴蝶模型一、蝴蝶模型与任意四边形在任意四边形中,两对角线将四边形分成四个三角形,两组相对三角形面积之积相等。
推导:由等积变形模型可知:OC AOS S BOC AOB =∆∆ OC AOS S COD AOD =∆∆ COD AODBOC AOB S S S S ∆∆∆∆=∴2431S S S S =即4321S S S S ⨯=⨯∴二、蝴蝶模型与梯形①②推导:① 同上② 过点A 作三角形ABC 的高1h ,过点D 作△BCD 的高2h BC AD //Θ21h h =∴(两平行线之间高相等)121h BC S ABC ⨯⨯=∆Θ221h BC S BDC ⨯⨯=∆BDC ABC S S ∆∆=∴3231S S S S +=+∴ 21S S =∴三、蝴蝶模型与平行四边形(一) ①②推导:① 同上② BCD ABC S S ∆∆=Θ ACD BCD S S ∆∆= (同底等高) 4241S S S S +=+∴ 2324S S S S +=+ 21S S =∴ 43S S = OD OB =Θ OC OA = 31S S =∴ 42S S =即:对角平行四边形面积乘积相等(在平行四边形ABCD 内作两条分别平行于两组相对边的线段GH 、EF )推导:连接GE 、EH 、HF 、FG ,过点E 作EM 垂直于GH 于点MEM OG S OGE ⨯⨯=∴∆21EM OG S S ⨯==∴1平行四边形121S S OGE =∴∆同理可得:321S S OGF =∴∆ 221S S OFH =∆ 421S S EOH =∆ 由蝴蝶定理可知:EOH OGF OFH OGE S S S S ∆∆∆∆⨯=⨯432121212121S S S S ⨯=⨯∴4321S S S S ⨯=⨯∴ 四、蝴蝶模型与长方形(一) ①②即:对角长方形面积乘积相等五、蝴蝶模型与正方形“子母图”——两共线相邻的正方形在上面两个图形中,每组正方形的对角线均互相平行,即a//b、c//d重要结论:两共线相邻的正方形对角线互相平行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
蝴蝶模型
一、蝴蝶模型与任意四边形
在任意四边形中,两对角线将四边形分成四个三角形,两组相对三角形面积之积相等。
推导:由等积变形模型可知:
OC AO
S S BOC AOB =∆∆ OC AO
S S COD AOD =∆∆ COD AOD
BOC AOB S S S S ∆∆∆∆=∴
2
4
31S S S S =即
4321S S S S ⨯=⨯∴
二、蝴蝶模型与梯形
①
②
推导:① 同上
② 过点A 作三角形ABC 的高1h ,过点D 作
△BCD 的高2h BC AD //Θ
21h h =∴(两平行线之间高相等)
121
h BC S ABC ⨯⨯=∆Θ
22
1
h BC S BDC ⨯⨯=∆
BDC ABC S S ∆∆=∴ 3231S S S S +=+∴ 21S S =∴
三、蝴蝶模型与平行四边形
(一) ①
②
推导:① 同上
② BCD ABC S S ∆∆=Θ ACD BCD S S ∆∆= (同底等高) 4241S S S S +=+∴ 2324S S S S +=+ 21S S =∴ 43S S = OD OB =Θ OC OA = 31S S =∴ 42S S =
即:对角平行四边形面积乘积相等
(在平行四边形ABCD 内作两条分别平行于两组相对边的线段GH 、EF )
推导:连接GE 、EH 、HF 、FG ,过点E 作EM 垂直于GH 于点M
EM OG S OGE ⨯⨯=∴∆21
EM OG S S ⨯==∴1平行四边形 12
1S S OGE =
∴∆
同理可得:321S S OGF =
∴∆ 221S S OFH =∆ 42
1S S EOH =∆ 由蝴蝶定理可知:EOH OGF OFH OGE S S S S ∆∆∆∆⨯=⨯
432121
212121S S S S ⨯=⨯∴
4321S S S S ⨯=⨯∴ 四、蝴蝶模型与长方形
(一)①
②
即:对角长方形面积乘积相等
五、蝴蝶模型与正方形
“子母图”——两共线相邻的正方形
在上面两个图形中,每组正方形的对角线均互相平行,即a//b、c//d 重要结论:两共线相邻的正方形对角线互相平行。
例1:如下图所示,在梯形ABCD 中,对角线BD ,AC 相交于点O ,△AOD 的面积是6,△AOB 的面积是4,那么梯形ABCD 的面积是多少?
分析:梯形ABCD 是四个三角形面积的总和,现已经知道两个三角形的面积,由蝴蝶定理容易求出三角形BOC 和三角形DOC 的面积,进而可以求出梯形ABCD 的面积。
解:由蝴蝶定理可知:
答:梯形ABCD 的面积是25。
例2:如图,求阴影部分的面积。
(单位cm 2)
分析:由长方形中的蝴蝶定理“对角长方形面积乘积相等”,可直接求出阴影部分的面积。
解:
(cm 2)
答:阴影部分的面积为14平方厘米。
例3:下图是两个正方形,大正方形边长是8,小正方形边长是6,求图中阴影部分的面积。
(单位:厘米)
分析:图中阴影部分的面积不能通过面积公式直接得出,因此要将其转化为容易算的部分。
由“子母图中对角线互相平行”这一重要结论可知,连接AC ,所以AC 平行于GE ,由梯形的蝴蝶定理可知,三角形AOG 和三角形COE 面积相等,因此,阴影部分的面积就等于三角形GCE 的面积,即小正方形面积的一半。
解:连接AC
∵AC ∥GE
∴由梯形的蝴蝶定理可知:
∴
(cm 2)
答:阴影部分的面积为18平方厘米。
28 12 6
A
B
D
C
4 6
O
D F
G O
练习题
1.如图,某公园的外轮廓是四边形ABCD,被对角线AC,BD分成四
个部分,△AOB面积为1平方千米,△BOC面积为2平方千米,△COD的面积为3平方千米。
公园由6.92平方千米的陆地和人工湖组成,则人工湖的面积是多少平方千米?
2.如图,长方形ABCD被CE、DF分成四块,已知其中3块的面积分
别为2、5、8平方厘米,求余下的四边形OFBC的
面积。
3.如图,在长方形ABCD中,△ABP的面积为30cm2,△CDQ的面积
为80 cm2,求阴影部分的面积。
4.如图,四边形ABCG和CDEF都是正方形,DC等于12厘米,CB等
于10厘米,求阴影部分的面积。
