专题四立体几何中_如何有效建立空间直角坐标系。
高考数学专题 立体几何中的建系设点问题
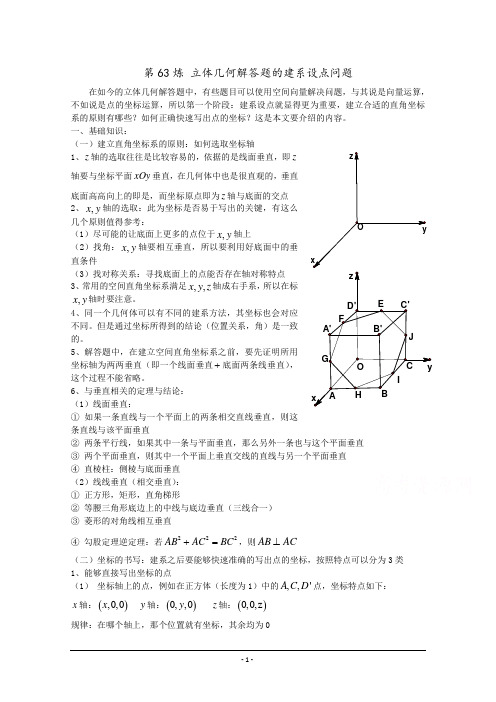
Oyxz FEGH IJ O yx z A'C'B B'C D'A 第63炼 立体几何解答题的建系设点问题在如今的立体几何解答题中,有些题目可以使用空间向量解决问题,与其说是向量运算,不如说是点的坐标运算,所以第一个阶段:建系设点就显得更为重要,建立合适的直角坐标系的原则有哪些?如何正确快速写出点的坐标?这是本文要介绍的内容。
一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、z 轴的选取往往是比较容易的,依据的是线面垂直,即z 轴要与坐标平面xOy 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即为z 轴与底面的交点2、,x y 轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考:(1)尽可能的让底面上更多的点位于,x y 轴上(2)找角:,x y 轴要相互垂直,所以要利用好底面中的垂直条件(3)找对称关系:寻找底面上的点能否存在轴对称特点 3、常用的空间直角坐标系满足,,x y z 轴成右手系,所以在标,x y 轴时要注意。
4、同一个几何体可以有不同的建系方法,其坐标也会对应不同。
但是通过坐标所得到的结论(位置关系,角)是一致的。
5、解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直+底面两条线垂直),这个过程不能省略。
6、与垂直相关的定理与结论: (1)线面垂直:① 如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直② 两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直 ③ 两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直 ④ 直棱柱:侧棱与底面垂直 (2)线线垂直(相交垂直): ① 正方形,矩形,直角梯形② 等腰三角形底边上的中线与底边垂直(三线合一) ③ 菱形的对角线相互垂直④ 勾股定理逆定理:若222AB AC BC +=,则AB AC ⊥(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类 1、能够直接写出坐标的点(1) 坐标轴上的点,例如在正方体(长度为1)中的,,'A C D 点,坐标特点如下:x 轴:(),0,0x y 轴:()0,,0y z 轴:()0,0,z规律:在哪个轴上,那个位置就有坐标,其余均为0(2)底面上的点:坐标均为(),,0x y ,即竖坐标0z =,由于底面在作立体图时往往失真,所以要快速正确写出坐标,强烈建议在旁边作出底面的平面图进行参考:以上图为例: 则可快速写出,H I 点的坐标,位置关系清晰明了111,,0,,1,022H I ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭2、空间中在底面投影为特殊位置的点:如果()'11,,A x y z 在底面的投影为()22,,0A x y ,那么1212,x x y y ==(即点与投影点的横纵坐标相同)由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
建立空间直角坐标系建系的方法及技巧

建立空间直角坐标系建系的方法及技巧建立空间直角坐标系在解决立体几何问题中起着重要作用。
向量法是建系的一种常用方法,它引入了空间向量坐标运算,使解题过程更加简便。
建立适当的坐标系是向量解题的关键步骤之一,一般应使尽量多的点在数轴上或便于计算。
一种建系的方法是利用共顶点的互相垂直的三条棱构建直角坐标系。
例如,在长方体ABCD-A1B1C1D1中,点E、F分别在棱DD1、BB1上,且2DE=ED1,BF=2FB1.要证明点C1在平面AEF内,并求二面角A-EF-A1的正弦值。
另一种建系的方法是利用线面垂直关系构建直角坐标系。
例如,在菱形ABCD中,对角线AC与BD交于点O,AB=5,AC=6,点E、F分别在AD、CD上,AE=CF=,EF交BD于点H。
将△XXX沿EF折到△D'EF的位置,OD'=.要证明D'H⊥平面ABCD,并求二面角B-D'A-C的正弦值。
还有一种建系的方法是利用面面垂直关系构建直角坐标系。
例如,在四棱锥P-ABCD中,侧面PAD是边长为2的等边三角形且垂直于底ABCD,AB=BC=1AD,∠BAD=∠ABC=90°,E是PD的中点。
要证明直线CE//平面PAB,求二面角M-AB-D的余弦值。
有些图形中虽没有明显交于一点的三条直线,但有一定对称关系,例如正三棱柱、正四棱柱等,利用自身对称性可建立空间直角坐标系。
例如,在圆锥D-O-ABC中,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD,ABC是底面的内接正三角形,P为DO上一点,PO=6DO。
要证明PA⊥平面PBC,并求二面角B-PC-E的余弦值。
另外,利用正棱锥的中心与高所在直线也可构建直角坐标系。
建立空间直角坐标系的方法及技巧有多种,根据不同的图形特点选择合适的方法,能够更加高效地解决立体几何问题。
1.中,给定正四棱锥P-ABCD,其所有棱长均为6.底面正方形ABCD的中心在坐标原点,棱AD、BC平行于x轴,棱AB、CD平行于y轴,顶点P在z轴的正半轴上。
如何建立恰当的空间直角坐标系

如何建立恰当的空间直角坐标系引入空间向量坐标运算,使解立体几何问题避免了传统方法进行繁琐的空间分析,只需建立空间直角坐标系进行向量运算,而如何建立恰当的坐标系,成为用向量解题的关键步骤之一.下面通过举例分析建立空间直角坐标系的三个方法.一、利用图形中现成的垂直关系建立坐标系当图形中有明显互相垂直且交于一点的三条直线,可以利用这三条直线直接建系,再写出空间点的坐标.例1、在棱长为1的正方体ABCD —A1B1C1D1中,M、N分别为A I B I和BBi的中点,试建立适当的坐标系,并且写出点A、C、M、N的坐标。
分析:本题中,可以以点D为原点,交于点D的三条直线DA、DC、DD1为坐标轴建立坐标系。
解:建立如下图所示坐标系,把D点视作原点0,分别沿DA、DC、DD1方向为x轴、y轴、z轴的正方向,点A在x轴上,且DA=1,它的横坐标x是1,纵坐标和竖坐标都为零,则A (1 , 0, 0),同样地,点C在y轴上,它的纵坐标y是1,横坐标和竖坐标都点评:对于正方体和长方体,可以直接建立右手直角坐标系,例2、如下图,直棱柱ABC —A1B1C1的底面△ ABC 中,为零,则C ( 0, 1 , 0), M点在面xOy的射影是A,,因此M同A1的横坐标和竖坐标相同,1N( 11, -)•再根据棱长写出各点坐标。
CA=CB=1,/ BCA=90 ° ,又M为AB的中点,I棱AA I =2 , M 、N 分别是A i B i 、A i A 的中点.分析:由题意可知,直线 CA 、CB 、CC i 两两垂直,故可以以点 C 为原点,直线CA 、CB 、CC 1为坐标轴,建立空间直角坐标系。
解:以点C 为原点,直线CA 为x 坐标轴,、CB 为y 坐标轴、CC 1为z 坐标轴,建立 空间直角坐标系。
点A 在X 轴上,且CA =1,它的横坐标x 是1,纵坐标和竖坐标都为零,则 A ( 1,0, 0),同样地,点B 在y 轴上,它的纵坐标 y 是1,横坐标和竖坐标都为零,则B ( 0,1,0), M 点在面xOy 的射影是 A ,因此M 同A 1的横坐标和竖坐标相同,又 M 为AB 的中点,故1 1 1 其纵坐标值为 丄,故M (1,-,1),同理可得N (1,1,-).222点评:对于直棱柱,如果已知条件中出现三条两两垂直的棱, 可以直接建立右手直角坐标系,再根据棱的长度写出各点坐标。
(完整版)立体几何解答题的建系设点问题

立体几何解答题的建系设点问题一、基础知识:(一)建立直角坐标系的原则:如何选取坐标轴1、轴的选取往往是比较容易的,依据的是线面垂直,即轴要与坐标平面z z 垂直,在几何体中也是很直观的,垂直底面高高向上的即是,而坐标原点即xOy 为轴与底面的交点z 2、轴的选取:此为坐标是否易于写出的关键,有这么几个原则值得参考:,x y (1)尽可能的让底面上更多的点位于轴上,x y (2)找角:轴要相互垂直,所以要利用好底面中的垂直条件,x y (3)找对称关系:寻找底面上的点能否存在轴对称特点解答题中,在建立空间直角坐标系之前,要先证明所用坐标轴为两两垂直(即一个线面垂直底面两条线垂直),+这个过程不能省略。
3、与垂直相关的定理与结论:(1)线面垂直:① 如果一条直线与一个平面上的两条相交直线垂直,则这条直线与该平面垂直② 两条平行线,如果其中一条与平面垂直,那么另外一条也与这个平面垂直③ 两个平面垂直,则其中一个平面上垂直交线的直线与另一个平面垂直④ 直棱柱:侧棱与底面垂直(2)线线垂直(相交垂直):① 正方形,矩形,直角梯形② 等腰三角形底边上的中线与底边垂直(三线合一)③ 菱形的对角线相互垂直④ 勾股定理逆定理:若,则222AB AC BC +=AB AC ⊥(二)坐标的书写:建系之后要能够快速准确的写出点的坐标,按照特点可以分为3类1、能够直接写出坐标的点(1) 坐标轴上的点,规律:在哪个轴上,那个位置就有坐标,其余均为0(2)底面上的点:坐标均为,即竖坐标,由于底面在作立体图时往往失真,所以要快速正确写出(),,0x y 0z =坐标,强烈建议在旁边作出底面的平面图进行参考2、空间中在底面投影为特殊位置的点:如果在底面的投影为,那么(即点与投影点的横纵坐标相同)()'11,,A x y z ()22,,0A x y 1212,x x y y == 由这条规律出发,在写空间中的点时,可看下在底面的投影点,坐标是否好写。
立体几何建坐标系

立体几何建坐标系全文共四篇示例,供读者参考第一篇示例:立体几何建坐标系是描述和研究立体图形的重要工具之一。
在三维空间中,我们通常使用三维直角坐标系来描述立体图形的位置和形状。
这种坐标系由三个相互垂直的坐标轴组成,分别是x轴、y轴和z 轴,它们分别对应三维空间中的长度、宽度和高度。
在这个坐标系中,每个点都可以通过三个坐标值来表示,分别表示点在x轴、y轴和z轴上的位置。
用立体几何建坐标系描述一个物体时,首先需要确定一个原点,该原点是坐标轴的交点,通常我们取它为立体图形的重心或者其特定的某一个点。
然后,可以通过在坐标轴上确定一个单位长度来建立坐标系的比例尺。
接下来,可以通过测量物体在x、y、z三个方向上的长度、宽度和高度,来确定物体各个点的坐标值,从而描述整个物体的形状和位置。
利用立体几何建坐标系可以方便地计算立体图形的体积、表面积、中心质心等属性。
通过将三维立体图形分解成一系列的立方体、长方体或圆柱体等基本的几何图形,可以利用数学方法求解各部分的体积,并将它们相加得到整个立体图形的体积。
而对于复杂的立体图形,可以将其分解成多个简单的几何图形,再逐一计算其属性,最后综合得出结果。
这样的方法虽然有时会比较繁琐,但是却是一种较为准确和可靠的计算方式。
立体几何建坐标系不仅可以用于描述静态的立体图形,还可以用于描述立体图形的运动和变形。
通过不断变化物体各个点的坐标值,可以描述其在三维空间中的移动、旋转、缩放等动作。
通过改变一个立方体各个顶点的坐标值,可以实现它在空间中的旋转或者平移。
通过计算不同时间点上各个点的坐标值,可以还原出整个立体图形的运动轨迹,从而研究它的运动规律。
利用立体几何建坐标系还可以进行三维坐标系下的几何投影。
在三维空间中,物体的形状对应着它在每个坐标轴的投影,在三维坐标系下可以进行正投影、侧视投影等操作,将三维空间中的立体图形映射到二维平面上,便于我们观察和研究。
这种投影方法在建筑设计、工程制图等领域中有着广泛的应用。
空间几何体建立空间直角坐标系技巧

空间几何体建立空间直角坐标系技巧建立空间直角坐标系时,可以按照以下步骤进行:
1.确定空间直角坐标系的三个坐标轴方向,一般选择为某轴、y轴和z轴。
2.确定空间直角坐标系的原点,一般选择为三个轴的交点。
3.确定坐标轴的正方向,一般按照右手定则确定,即当右手的大拇指指向某轴正方向,食指指向y轴正方向时,中指所指的方向即为z轴正方向。
4.确定坐标轴的长度和间距,一般选择适当的数值,方便计算。
5.根据需要,可以在空间直角坐标系中建立坐标系网格和标注坐标轴上的刻度值,方便进行坐标计算和表示几何体。
总体说来,建立空间直角坐标系需要考虑方便计算、标注明确、成像清晰等方面,通过实践和熟练掌握,可以更有效地运用空间几何体建模和分析。
高中数学空间直角坐标系的构建策略知识点解析

达标检测
DABIAOJIANCE
1. 如 图 所 示 , 已 知 正 方 体 ABCD - A1B1C1D1 , E , F 分 别 是 正 方 形 A1B1C1D1 和 ADD1A1的中心,则EF和CD所成的角为___4_5_°___.
123
2.在底面为直角梯形的四棱锥S-ABCD中,∠ABC=90°,SA⊥平面ABCD,SA =AB=BC=1,AD=12,则平面SCD与平面SAB所成锐二面角的余弦值为__3_6_.
第三章 空间向量与立体几何
专题突破三 空间直角坐标系的构建策略
利用空间向量的方法解决立体几何问题,关键是依托图形建立空间直角坐标 系,将其他向量用坐标表示,通过向量运算,判定或证明空间元素的位置关 系,以及空间角、空间距离问题的探求.所以如何建立空间直角坐标系显得 非常重要,下面简述空间建系的四种方法,希望同学们面对空间几何问题能 做到有的放矢,化解自如.
跟踪训练1 如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°, 且PA=AD=2,E,F分别是线段PA,CD的中点,求异面直线EF与BD所成 角的余弦值.
二、利用线面垂直关系 例 2 如图,在三棱柱 ABC-A1B1C1 中,AB⊥平面 BB1C1C,E 为棱 C1C 的中点, 已知 AB= 2,BB1=2,BC=1,∠BCC1=π3.试建立合适的空间直角坐标系,求 出图中所有点的坐标.
三、利用面面垂直关系 例3 如图1,在等腰梯形ABCD中,AD∥BC,AB=AD=2,∠ABC=60°, E是BC的中点.将△ABE沿AE折起,使平面BAE⊥平面AEC(如图2),连接BC, BD.求平面ABE与平面BCD所成的锐角的大小.
点评 本题求解关键是利用面面垂直关系,先证在两平面内共点的三线垂直, 再构建空间直角坐标系,然后分别求出两个平面的法向量,求出两法向量夹 角的余弦值,即可得所求的两平面所成的锐角的大小.用法向量的夹角求二面 角时应注意:平面的法向量有两个相反的方向,取的方向不同求出来的角度 就不同,所以最后还应该根据这个二面角的实际形态确定其大小.
巧建系,妙解立体几何题

解题宝典立体几何问题侧重于考查同学们的空间想象能力和逻辑推理能力.在解答立体几何问题时,我们一般只有借助立体几何图形来进行分析,才能快速明确题目中点、线、面的位置关系,找到解题的突破口.建系法是解答立体几何问题的一种重要方法,而运用建系法解答立体几何问题的关键是建立合适的空间直角坐标系,通过空间直角坐标运算求得问题的答案.那么如何选取坐标轴和原点,建立合适的直角坐标系呢?主要有以下两种方法.一、根据几何体的性质和特点建系我们知道,空间直角坐标系中的三个坐标轴相互垂直,并相交于一点.因此,在解答立体几何问题时,可以根据简单几何体的特点和性质,尤其是长方体、直棱柱、直棱锥、圆柱的性质和特点来寻找垂直关系.当图形中出现三条直线两两互相垂直且交于一点时,可以将这三条直线看作坐标轴,将该交点视为坐标原点来建系.例1.(2019年全国卷Ⅱ理科·第17题)如图1,长方体ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.若AE =A 1E ,求二面角B -EC -C 1的正弦值.图1图2分析:本题主要考查了二面角的求法.我们根据长方体的特点和性质可知长方体的所有侧棱都与底面垂直,且底面上由顶点出发的两条棱相互垂直,于是可将底面的其中一个顶点视为原点,以由顶点出发的三条棱为x 、y 、z 轴建立空间直角坐标系.然后根据题目给出的条件,找出相关点的坐标,求出两个平面、BEC 、ECC 1的法向量,再根据公式求出两个平面法向量的夹角余弦值,便可得出夹角的正弦值.解:以点D 为坐标原点,DA 的方向为x 轴的正方向,建立如图2所示的空间直角坐标系D -xyz .设正方形ABCD 的边长为1,||AA 1=2a ,则||A 1E =||AE =a ,所以||EB 1=||EB =a 2+1,因为ABCD -A 1B 1C 1D 1为长方体,所以B 1C 1⊥平面ABB 1A 1,且BE 在平面ABB 1A 1内,因此C 1B 1⊥BE .由题知BE ⊥EC 1,所以BE ⊥平面EB 1C 1.且EB 1在平面EB 1C 1内,则BE ⊥EB 1.在RtΔB 1EB 中,EB 12+EB 2=B 1B 2,即a 2+1+a 2+1=4a 2,所以a =1,所以B (1,1,0),C (0,1,0),E (1,0,1),C 1(0,1,2),所以 CE =(1,-1,1), CB =(1,0,0), CC 1=(0,0,2)设平面BCE 的法向量为n 1=(x 1,y 1,z 1),则ìíî n 1·CE =x 1-y 1+z 1=0, n 1·CB =x 1=0,,解得{x 1=0,z 1=y 1,取 n 1=(0,1,1),设平面CEC 1的法向量为 n 2=(x 2,y 2,z 2),则ìíî n 2·CE =x 2-y 2+z 2=0, n 2·CC 1=2z 2=0,解得{z 2=0,y 2=x 2,取 n 2=(1,1,0),所以cos n 1, n 2=n 1·n 2|| n 1·|| n 2=12.于是sin n 1, n 2=,故二面角B -EC -C 1的正弦值为.例2.如图3,在直三棱柱ABC -A 1B 1C 1中,D ,E 分别是AB 、BB 1的中点,AA 1=AC =CB .求二傅灵欣廖小莲44解题宝典面角D -A 1C -E 的正弦值.图3图4分析:该几何体为直三棱柱,我们可以根据直三棱柱图形的特点和性质来建立空间直角坐标系.直棱柱的侧棱垂直于底面,只要根据题目的条件在直三棱柱的底面找到两条互相垂直且与侧棱有交点的直线,这样三条直线两两便会互相垂直,为建立空间直角坐标系创造了条件.求出相关点的坐标以及二面角所包含的两个平面的法向量,再根据公式便可求出二面角的余弦值,求得夹角的正弦值.解:由AC =CB =得ΔACB 是以∠C 为直角的等腰直角三角形,又因为是直三棱柱ABC -A 1B 1C 1,所以棱CC 1⊥底面ACB .故以点C 为原点、CA 的方向为x 轴,建立如图4所示的空间直角坐标系.设AB =2,则AA 1=AC =CB =AA 1=2,则A (2,0,0),B (0,2,0),D 0),A 1(2,0,2),C (0,0,0),又因为AA 1=BB 1=2,所以E(0,2,于是 CA 1=(2,0,2), CD =0),CE =(0,2,,设平面DA 1C 的法向量为n 1=(x 1,y 1,z 1),则ìíîïï n 1·CA 121+2=0,CD · n 1=2121=0,解得{x 1+z 1=0,x 1+y 1=0,取n 1=(1,-1,-1),设平面A 1CE 的法向量为n 2=(x 2,y 2,z 2),则ìíîïï n 2·AC 1=2x 222=0, CE · n 2=2y 222=0,解得ìíîïïx 2+z 2=0,y 2+12z 2=0,取n 2=(2,1,-2),所以cos n 1, n 2=n 1·n 2|| n 1·||n 2=,则sin n 1, n 2=故二面角D -A 1C -E 的正弦值为.在用建系法解答与长方体、直棱锥有关的立体几何问题时,可以根据长方体、直棱锥本身的性质和特点来建系,若无法根据几何体的性质和特点建系,可以根据题意创造条件来建系.二、利用线面垂直关系建立直角坐标系在建系时,z 轴往往是比较容易选取的,而坐标原点即为z 轴与底面的交点,那么我们只需要确定与z 轴垂直的坐标平面xOy ,且使x 轴、y 轴相互垂直即可.可以根据线面垂直关系来寻找与z 轴垂直的平面.首先要充分利用好底面中的垂直条件,然后根据线面垂直的判断定理得到相应的z 轴以及与z 轴垂直的平面,这样便可建立符合要求的空间直角坐标系.例3(2020年全国Ⅰ卷,第20题)如图5,四棱锥P -ABCD 的底面为正方形,PD ⊥底面ABCD .设平面PAD 与平面PBC 的交线为l .(1)证明:l ⊥平面PDC ;(2)已知PD =AD =1,Q 为l上的点,求PB 与平面QCD 所成角的正弦值的最大值.图5分析:我们可以先根据线面垂直的关系,即PD ⊥底面ABCD 来建立空间直角坐标系.而四棱锥P -ABCD 的底面为正方形,所以正方形的四条邻边相互垂直,于是可以以D 为坐标原点、DA 的方向为x 轴的正方向建立空间直角坐标系.求出相关点的坐标,设45方法集锦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PD 2,CD 2,AE 1
点, PE EC .已知
2 .求:
1.异面直线 PD 与 EC 的距离;
2.二面角 E PC D的大小.
ABC
例 2、(安徽)如图,在四棱锥 O ABCD中,底面 ABCD四边长为 1 的菱形,
4,
OA 底面ABCD , OA 2 , M 为 OA 的中点, N 为 BC 的中点
2
22
44 ,
MN (1 2 , 2 , 1),OP (0, 2 , 2),OD ( 2 , 2 , 2)
(1)
44
2
22
设平面 OCD 的法向量为 n (x, y, z) ,则 n OP 0, n OD 0
2 2
y 2z 0
即
2 x 2
2 y 2z 0 2
zO M
取 z 2 ,解得 n (0, 4, 2)
(3)设点 B 到平面 OCD 的交流为 d ,则 d 为 OB 在向量 n (0, 4, 2) 上的投影的绝对值,
d OB n 2
2
由 OB (1, 0, 2) , 得
n 3 .所以点 B 到平面 OCD 的距离为 3
∵MN n (1 2 , 2 , 1) (0, 4, 2) 0 44
MN‖ 平面OCD
(2) 设 AB 与 MD 所 成 的 角 为 x
∵ AB (1, 0, 0), MD ( 2 , 2 , 1)
,
22
A
B
N
D CP y
∴cos AB MD 1 ,∴
AB MD 2
3 , AB 与 MD 所成角的大小为 3
∵ DG (0,y,z),PC (0,2, 2) ,且 DG· PC 0 ,
则z
2 y ,∴可取 DG (0,1,2) .
∵ EF
再作 EF PC 于 F ,并设 F(0,m,n) ,
3 2
,m
1,n 2
,
且 EF· PC 0 ,则 n
2m
2 2
,∴又取
EF
3 2
,1, 2 22
∵ADP ,∴DP = 2
4
2
MD MA2 AD2 2
,
∴cos MDP DP 1 , MDC MDP
MD 2
3 所以 AB 与 MD 所成角的大小为 3
(3)∵ AB‖平面OCD,∴点 A 和点 B 到平面 OCD 的距离相等,连接 OP,过点 A 作
AQ OP 于点 Q,∵ AP CD,OA CD,∴CD 平面OAP,∴ AQ CD
专题四:高考立体几何专题复习
主要是掌握建立空间直角坐标系的时候,要选择适当的坐标系,我们建
系的原则是:尽量使更多的点落在坐标轴上。同时要注意:紧紧抓住题
目条件中的垂直字眼,然后再考虑如何建系。点的坐标不好写出来时,
记住::一定要把涉及到该点的图形拿出来,使之平面化,再去写点的
坐标!
例 1、如图 2,在四棱锥 P ABCD ,底面 ABCD 为矩形, PD 底面 ABCD , E 是 AB 上一
又 ∵ AQ OP,∴ AQ 平面OCD ,线段 AQ 的长就是点 A 到平面 OCD 的距离
∵OP OD2 DP2 OA2 AD2 DP2 4 1 1 3 2 AP DP 2
2 2,
2
∴ AQ OA AP 2
2 2 2
OP 3 2 3
2
2
,所以点 B 到平面 OCD 的距离为 3
a,12,0
.
(1)∵PE CE ,∴PE· CE 0 ,解得 a
3
2 .∴DE· CE 0 ,即 DE CE ,
又 DE PD ,故 DE 是异面直线 PD 与 EC 的公垂线.
而 DE 1,即异面直线 PD 与 EC 的距离为 1. (2)作 DG PC ,并设 G(0,y,z) ,
方法二(向量法) 作 AP CD 于点 P,如图,分别以 AB,AP,AO 所在直线为 x, y, z 轴建立坐标系
A(0, 0, 0), B(1, 0, 0), P(0, 2 , 0), D( 2 , 2 , 0), O(0, 0, 2), M (0, 0,1), N (1 2 , 2 , 0)
.
由 DG PC , EF PC ,可知 DG 与 EF 的夹角就是所求二面角 的大小,
∴cos DG· EF 2
π
DG EF 2 ,即所求二面角为 4 .
例二:
方法一:(1)证明:取 OB 中点 E,连接 ME,NE ME‖AB,AB‖CD,ME‖CD NE‖OC,平面MNE‖平面OCD MN‖平面OCD (2) CD‖AB, ∴MDC 为异面直线 AB 与 MD 所成的角(或其补角) 作 AP CD于P, 连接 MP ∵OA 平面A B C D ,∴CD MP
O
(Ⅰ)证明:直线 MN‖ 平面OCD ;
(Ⅱ)求异面直线 AB 与 MD 所成角的大小; (Ⅲ)求点 B 到平面 OCD 的距离。
M
A
D
B
NC
答案
例一:解:以 D 为坐标原点, DA,DC,DP 所在直线分别为 x,y,z 轴,建立空(a,0,0),B(a,2,0),C(0,2,0),D(0,0,0),P(0,0,2),E
