磁流变减振器基于Matlab的仿真分析
基于Matlab_Simulink的车用磁流变液制动器设计与仿真

·制造业信息化·Design and Simulationfor a Vehicle Magnetorheological Brake Based on Matlab/SimulinkDING Bai-Qun ,SONG Yu(Traffiic School,Northeast Forestry University,Harbin Heilongjiang 150040,China)Abstract:The structure of a member type vehicle magnetorheological wheel Brake was designed,and its braking torque formula was deducesd as well as the performance simulation model was built based on Matlab/Simulink to analyze the influences on braking torque as structural parameters changing according the rheological characteristics of magnetorheological fluid with the effects of strong magnetic field.The braking torque of vehicle MRF brake designed can satisfy the requirement of a small motor vehicle.Key words:motor vehicle brake ;magnetorheological fluid ;structural design ;simulation0引言磁流变液MRF (Magneto-Rheological Fluids )由高磁导率、低磁滞性的微小软磁性颗粒和非导磁性液体混合而成。
基于磁流变减震器的起落架着陆建模及仿真

基于磁流变减震器的起落架着陆建模及仿真作者:何永勃,苏兴国,刘娜来源:《现代电子技术》2011年第01期摘要:磁流变减震器是一种半主动控制的阻尼装置,可显著改善起落架的减震效果。
针对自行设计的多环形槽结构磁流变减震器,根据流变力学原理,建立了减震器力学模型,并据此建立基于Matlab的起落架系统动态力学模型。
对于不同的机身质量和着陆垂直速度分量,得到励磁电流与振动幅值、频率及稳定时间等参数的关系。
仿真结果表明,选用合适的励磁电流,可方便地控制振动参数,达到较理想的减震效果。
关键词:磁流变减震器;起落架;着陆模型;仿真中图分类号:TN802-34文献标识码:A文章编号:1004-373X(2011)01-0070-04Modeling and Simulation for Landing of Undercarriage Based on Magnetorheological DamperHE Yong-bo, SU Xing-guo, LIU Na(College of Aeronautical Automation, Civil Aviation University of China, Tianjin 300300, China)Abstract: The magnetorheological (MR) damper based on semi-active control is suitable for improving the dynamic performances of aircraft landing gear. For the formerly designed multi-ring groove structure MR damper, a mechanics model is established according to rheological dynamics. Further more, an aircraft landing gear dynamics model used for Matlab simulation is proposed. The relationships between the excitation current and the parameters such as vibration amplitude, frequency and settling time are obtained for different body weight and vertical landing velocity component. The simulation results show that the landing gear vibration parameters is easy to be controlled via a proper control current, and the ideal dynamic performance can be achieved.Keywords: MR damper; undercarriage; landing model; simulation0 引言飞机在着陆过程中,着陆冲击和跑道不平度引起的振动载荷,是造成飞机机体疲劳损伤及动应力、乘客不适及驾驶员地面操纵能力降低的重要因素。
MATLAB环境下汽车减震系统的设计与仿真

on¥3C241 0 and TM8320C671 3 produced
By SAMSUNG and
TI.The system scheme can improve the precision of the system
navigation.and ehence the real·time pedormance of the systam.
文章编号1671-104I(2007)03-0041-02
基于ARM和DSP的INS/GPS组合系统设计
吴俊伟,张雨楠,刘金峰,苑娜 (哈尔滨工程大学自动化学院, 哈尔滨150001)
摘要:为满足组合导航系统要求成本低.体积小、精度高.低功耗的特点。 本文以SAMSUNG公司¥3C241 0型和TI公司TMS320C671 3型芯片为核 心器件设计了一种嵌入式导航计算机系统.此设计可提高系统的精度,更好 地满足系统实时性的要求。 关键词:INS/GPS;ARM¥3C2410;HPI接口:TMS320C67t3 中图分类号:PT277文献标识码:A
是为什么没有任何旅客或驾驶员喜欢这个C=0(相当于减震器粘性 为o’无作用)的值。
;||||㈦!㈡㈦
::::::::
::::::::
—■需常警车饕嚣
●l=c■●芏
i;i i;;※ ;㈡;!:;
图2时域仿真结粜
图3频域1方真结粜
图4时域仿真结果
图5频域仿真结果
3结束语 MATLAB软件是目前比较流行的…种软件,特别在数值训
照型班遮j土盛墨匣
仪器仪表用户
try l
m—pDatabase一>ExecuteSQL(SQLstr); l
catch(CMemoryException+pEx)I/处理内存异常 { pEx一>ReportError0; pEx一>DeleteQ;
磁流变阻尼器的Bingham模型及其Simulink仿真分析-

图 2 Fd 的 S imulink 方框图
图 4 MR 阻尼器在电流变化时力与速度和力与位移的关系曲线
图 3 τy 的 S imulink 方框图
对磁流变阻尼器 Bingham 模型的力学性能进行了测试,其中包括 改变电流、改变频率和改变振幅的情况下对 MR 阻尼器进行的测试, 施加激励为正弦激励.仿真分析工况为:电流分别为 0A、0.5A、1.0A、和 1.5A;频率分别为 0.1Hz、0.25Hz 和 0.5Hz;振幅分别为 2.5mm、5.0mm 和 10.0mm,总工况数为 36.在电流改变情况下,其振幅为 5.0 mm,频率 为 0.5 Hz;频率改变情况下,其振幅为 2.5 mm,电流强度为 1.5 A;振幅 改变情况下,其电流强度为 1.5 A,频率为 0.5 Hz,磁流变阻尼器的力
器的动力学模型,是设计控制策略和实现良好的振动控制效果的重要 因素之一,也是保证模拟的阻尼器输出以及振动控制仿真分析具有较
2
Fd=
12ηLAp
3
πDh
u· +
3LAp h
τysgn(u· )
(1.3)
高可信度的关键因素之一.但是应用流变力学理论分析磁流变阻尼器
式中,L 是活塞有效长度;D 是缸体内径;h 是孔道直径;Ap 是活塞
塑性模型、非线性双粘性模型、非线性滞回模型、粘弹- 塑性模型、修正
由于剪切屈服应力 τy 与磁场强度有关,所以 τy 是控制电流 I 的函
的 Dahl 模型、Bouc- Wen 模型、修正的 Bouc- Wen 模型、现象模型和修 数.本文根据东南大学的徐赵东、郭迎庆[8]研究,剪切屈服应力 τy 和控
(1) 模型建立简单、直观、可操作性强且具有鲜明的层次性; (2) Simulink 模型具有强大的可视化功能; (3) 模型编制具有高度继承性和二次开发能力; (4) 强大的数值积分能力. 3.磁流变阻尼器 Bingham 模型 S imulink 仿真分析 本文所选用的磁流变阻尼器主要性能参数如表 4- 1
基于MATLAB的汽车减震系统分析

基于MATLAB的汽车减震系统分析
邹大勇
【期刊名称】《济源职业技术学院学报》
【年(卷),期】2004(003)004
【摘要】用先进的科学计算软件MATLAB用于汽车防震系统的时域分析和频域分析,充分利用其强大的计算分析和可视化能力,使分析过程具有很强的直观性,且避免传统计算机分析时复杂的软件编程过程.通过该软件平台的应用,大大提高了分析问题、解决问题的能力,同时也减轻了分析工作量.
【总页数】4页(P30-33)
【作者】邹大勇
【作者单位】河南大学计算机与信息工程学院,河南,开封,475001
【正文语种】中文
【中图分类】U463.3
【相关文献】
1.MATLAB环境下汽车减震系统的设计与仿真 [J], 许艳惠
2.基于MATLAB的液压减震器与新型磁流变减震器的对比分析 [J], 谢禹琳;谷腾飞;齐小宝
3.基于MATLAB汽车减震系统的研究 [J], 唐路;章伟康;唐沐天;赵任光
4.基于Matlab的直流电机型位置随动系统分析 [J], 范子荣
5.基于MATLAB的“电力系统分析”仿真平台的设计与实现 [J], 王红艳
因版权原因,仅展示原文概要,查看原文内容请购买。
磁流变减振系统控制算法仿真分析

磁流变减振系统控制算法仿真分析摘要:本文运用模拟技术分析的方法,对磁流变阻尼器减振系统力学模型和动力学特性进行了研究,并以现代控制观点出发建立适宜实际应用的控制策略在外部激励作用下的半主动控制进行了研究。
对多自由度简单屋架结构进行仿真分析。
关键字:磁流变阻尼器、控制、SIMULINK仿真、LQRThis dissertation pays more attentions on the use of theoretical analysis and numerical simulation approach are conducted to characterize the dynamical performance of the MR damper and vibration damping control algorithm for the design and implementation of research. With modern control theory to establish the practical application of appropriate control strategy which can be applied to roof trusses, large space structures under external excitation of the semi-active control.Keyword: Magneto-Rheological damper, Control, SIMULINK、LQR0 引言磁流变液是近年来发展迅速的一种智能材料。
由磁流变阻尼器构成的磁流变减振系统具有阻尼连续可调、功耗低、动态范围宽、响应速度快等特点,是比较理想的半主动减振系统。
磁流变阻尼器减振系统应用于大型结构减振的研究还处于起步阶段,因此对磁流变阻尼器减振系统的控制策略与应用的研究非常有意义。
磁流变液减振器结构设计及仿真结果分析
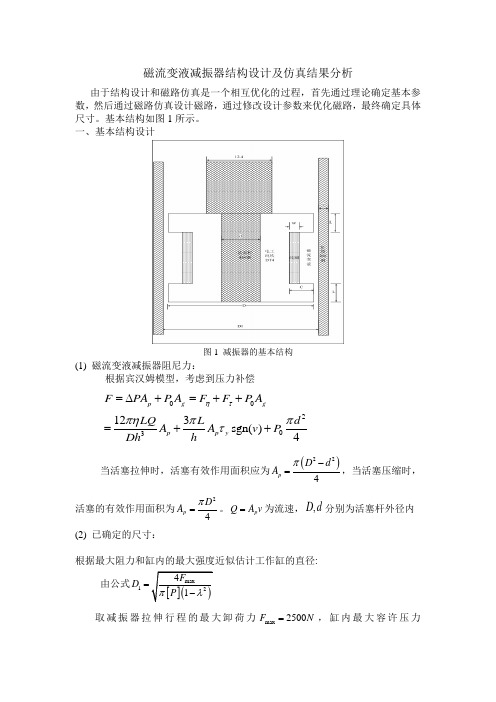
磁流变液减振器结构设计及仿真结果分析由于结构设计和磁路仿真是一个相互优化的过程,首先通过理论确定基本参数,然后通过磁路仿真设计磁路,通过修改设计参数来优化磁路,最终确定具体尺寸。
基本结构如图1所示。
一、基本结构设计图1 减振器的基本结构(1) 磁流变液减振器阻尼力:根据宾汉姆模型,考虑到压力补偿00203123sgn()4p g gp p y F PA P A F F P A LQ L d A A v P Dh h ητπηππτ=∆+=++=++ 当活塞拉伸时,活塞有效作用面积应为()224p D d A π-=,当活塞压缩时,活塞的有效作用面积为24p D A π=。
p Q A v =为流速,,D d 分别为活塞杆外径内(2) 已确定的尺寸:根据最大阻力和缸内的最大强度近似估计工作缸的直径:由公式1D = 取减振器拉伸行程的最大卸荷力max 2500F N =,缸内最大容许压力[]4P MPa =,0.3λ取,得出1=30D ,由此得d=9,若取d=12.4,反算max =2344N F ,仍然满足要求。
工作缸内径130D =,活塞头直径D=28,活塞杆直径d=12.4;工作间隙h=1(3)有效长度: 我国公路路面B, C 及路面占的比重大,建立普通减振器仿真模型,可知减振器的速度一般在O.15m/s 以下,所以根据减振器实验结果,设在O.15m/s,I=OA 时,压缩阻尼力为360N()222203336044L D d d F v p Dh πηπ-=+=零场粘度η=0.8,气体压力02p MPa =,v=0.15m/s由此得出有效长度30L =(4)线圈匝数:当工作电流为2A 时,最大可调阻尼力()22max 3360234436019844y L D d F F N h τπτ-==-=-=44.5y k P a τ=由MRF-J01磁流变液y B τ-曲线最小二乘法拟合得:140y B τ=由于活塞、缸筒等材料的磁导率要比磁流变液高出许多,相对气隙的磁阻来说很小,可以忽略。
基于磁流变动力减振系统的建模与仿真分析

基于磁流变动力减振系统的建模与仿真分析
廖逸杰;张永亮;王恒;姜坤
【期刊名称】《电子科技》
【年(卷),期】2016(029)009
【摘要】将磁流变技术应用于普通CA6140车床跟刀架,设计了一种挤压模式的磁流变动力减振系统.建立了基于磁流变动力减振器的跟刀架系统动力学模型,并通过数值仿真验证了其减振效果.利用Adams软件对磁流变动力减振系统的动力学响应进行仿真分析,仿真结果验证了上述理论分析的正确性,同时也表明磁流变动力减振装置可对车削颤振进行有效的抑制.
【总页数】4页(P75-78)
【作者】廖逸杰;张永亮;王恒;姜坤
【作者单位】上海理工大学机械工程学院,上海200093;上海理工大学机械工程学院,上海200093;上海理工大学机械工程学院,上海200093;上海理工大学机械工程学院,上海200093
【正文语种】中文
【中图分类】TGS02.36
【相关文献】
1.基于磁流变弹性体的汽车减振系统仿真分析 [J], 曹宽宽;邓益民;叶伟强
2.基于磁流变机理的车床减振系统动力学研究 [J], 张玮;张永亮;闫冬;徐振华
3.基于粒子群优化算法的磁流变阻尼器多项式动力学建模方法 [J], 董致臻;冯志敏;
伍广彬;刘小锋
4.基于Matlab的复合电源混合动力汽车建模及动力特性仿真分析 [J], 戚金凤
5.基于半主动控制的磁流变阻尼器建模与仿真分析 [J], 孟建军;张瑞东;陈彦丰因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
磁流变减振器基于Matlab 的仿真分析摘要:基于磁流变减振器在汽车悬架减振系统半主动控制中的广泛应用,根据磁流变液的特点和磁流变减振器阻尼力与结构参数的关系,设计了新型的磁流变减振器,并对影响磁流变减振器性能的参数进行了仿真。
仿真表明,该磁流变减振器设计计算是一种能优化阻尼力的有效算法。
关键词:磁流变减振器;半主动控制;磁流变液1.1减振器的阻尼力计算模型本文选用剪切阀式磁流变阻尼器工作模式进行结构设计,在结构设计前,必须明确该工作模式磁流变液的流变方程,继而推导出磁流变阻尼力的计算模型,这是结构设计过程中的依据所在。
基于剪切阀式磁流变阻尼器的阻尼通道的宽度远大于其阻尼间隙,因而可简化成磁流变液在两相对运动平板之间的运动。
为了简化分析,工作于剪切阀式的磁流变阻尼力可以看成是在阀式工作模式下的阻尼力和剪切工作模式下阻尼力的叠加。
在外加磁场作用下,磁流变液表现Bingham 流体,其磁流变液在平板的流动和速度分布如图1.1所示,其本构关系可用下列方程描述:y u y u y d dd d ηττ+⎪⎪⎭⎫ ⎝⎛=sgn y ττ> (1.1)0=dyduy ττ≤ (1.2)图1.1 磁流变液在平板中的流动和速度分布在阀式工作模式下磁流变液的速度分布如图1.1所示。
假设磁流变液的体积流速Q 在x 方向上一维流动,在y 方向上不流动。
设两平板之间的间隙为h ,长度为L ,宽度为b ,由流体力学可得下列微分方程:⎪⎪⎭⎫⎝⎛∂∂+∂∂+∂∂=∂∂+∂∂y u v x u u t u y x yx xx ρτσ (1.3) 式中u 、v 分别是磁流变液在x 、y 方向上的流动速度;x xy ∂∂σ是磁流变液在x 方向的压力梯度,为了简化将压力梯度是为x 方向线性变化xxy ∂∂σ=lp-∆,l 是阻尼通道的长度;p ∆是阻尼通道两端的压力差;ρ是磁流变液的密度;t 是时间变量;由于流动速度低,可不计惯性效应,0=∂∂yu;令沿x 的剪切应力ττ=xy ,由于磁流变流动的连续性,沿x 方向的速度不变即0=∂∂=∂∂=∂∂tu y u x u 则方程(1.3)简化为: lp ∆=dy d τ (1.4) 对其积分可得:1pD y l+∆=τ (1.5)D 是待定的积分常数。
由公式(1.4)可知,磁流变液受到的剪切应力沿平板间隙是按线性分布的,靠近平板的磁流变液受到的剪切力最大,而中间对称面上的磁流变液受到的剪切应力最小,根据极板两端压差产生的剪切应力与极板附近磁流变液的临界剪切屈服应力比较,当前者小于后者磁流变液静止不动;当前者大于后者将产生如图1.1所示的流体状态,即靠近平板处得磁流变液流动;而中间对称区间的磁流变液不流动。
可将此时的磁流变液的流动分为屈服流动,刚性流动,屈服流动三个区域。
区域 :屈服流动1y 0y ≤≤ 剪切应变率0d ≥dyu,由公式(1.1)可得: dyduηττ+=y (1.6)将公式(1-6)代入公式(1.5)中,并注意u (0)=0,0dydu 1==y u 求解微分方程如下:1y D y Lp dy du +∆=+ητ (1.7) 1y 1y LpD ∆-=τ (1.8)()()122u yy y Lp y -∆=η (1.9) 区域②:刚性流动21y y y ≤≤,剪切应变率0d =dyu,同理可得: ()()2112y Lp y u y u η∆-== (1.10) 区域③:屈服流动h y y ≤≤2,剪切应变率0<dydudyduηττ+=y - (1.11) 将公式(1.11)代入公式(1.5),已知u(h)=0,0du 2==y u dy,求解微分方程得:2y 1-y LpD ∆-=τ (1.12)()()[]22222)(u y h y y Lpy ---∆=η (1.13) 由公式和(1.8)公式(1.13)相减可得刚性流动区得厚度δ为 pL y y ∆=-=τδ2y 12 (1.14)由于存在()()21y u y u ≥=,由公式(1.9)和公式(1.13)可得221)(22p y h L py L -∆=∆ηη (1.15) h y y =+12 (1.16)由公式(1.14)和公式(1.16)可得: p L h y y ∆-=τ21 ;pL h y ∆+=τ2y 2 (1.17) 流经平板间隙的磁流变液的体积流量Q 可有下列得到: ⎥⎦⎤⎢⎣⎡===⎰⎰⎰⎰1212000)()()()(y y y hy h p dy y u dy y u dy y u b dy y bu v A Q (1.18) 代入化简可得()()ηττL p L ph L ph b Qy y 22122∆+∆-∆-= (1.19)经进一步化简可得压差近似公式: y p hcLbh L A τη+=∆312p (1.20) 考虑到阻尼器的实际阻尼通道为环形通道,流动模式下的阻尼力可以表示为: y Pp p hcLA v bh LA pA F τη22420321--=∆-= (1.21) 式中p A 为活塞受压的有效面积。
在移动平板的影响下,磁流变液发生屈服流动,剪切模式下磁流变液的速度分布如图1.2所示。
剪切应变率0≤dydu,则由公式(1.1),剪切应力可表示为: dyduηττ+=y - (1.22) 假如磁流变液的速度是沿y 方向分布如图1.2所示,即hv dy u 0d -=图1.2 剪切模式下磁流变液的速度分布剪切模式下的阻尼力:y bL v hbLL F τητ22b 202--== (1.23)混合工作模式的阻尼力可视为流动模式、剪切模式两种工作模式下的阻尼力的叠加。
即21F F F +=,由于符号的正负只反映活塞运动的方向,因此,整理上式得:y pp bL h cLA v h Lb bh LA F τηη⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+=22224032(1.24)式中参数c 变化范围2-3,本文c=2,因此剪切阀式磁流变阻尼器阻尼力为:y pp bL h LA v h Lb bh LA F τηη⎥⎦⎤⎢⎣⎡++⎥⎦⎤⎢⎣⎡+=24224032(1.25) ()4-2122D D A p π= ; ()242D D b +=π公式可以改为:r e F v C F F F +=+=0τη (1.26)0032224v C v h Lb bhLA F e p =⎥⎦⎤⎢⎣⎡+=ηηη (1.27))(s 240v gn bL h LA F y p ττ⎥⎦⎤⎢⎣⎡+= (1.28)式中粘滞阻尼力系数:h Lb bh LA C pηη22432e +=;库伦阻尼力:)sgn(240v bL h LA F y p ττ⎥⎦⎤⎢⎣⎡+=;0v 为磁流变阻尼器活塞运动速度;sgn 为符号函数;y τ为30-50K a P从上式可以看出磁流变阻尼器的阻尼力由两部分组成,一部分由液体流动时液体粘性产生的粘滞阻尼力,而另一部分由磁流变效应产生的库伦阻尼力组成。
1.2磁流变减振器的仿真分析磁流变减振器的数学模型采用公式1.25,建立磁流变减振器的仿真模型如图1.3所示。
图1.3 仿真模型图1.4Matlab 仿真图由公式(1.25)作为数学模型可进行计算。
F=(3-9-38-210.507.2022.1011.00210.5022.10107.651.107.2024⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯)0V +(11.0022.10210.50107.6511.0043-4-⨯⨯+⨯⨯⨯⨯)31040⨯⨯ =1504.50V +2108上式的计算结果是在阻尼间隙为0.6mm 是计算而得。
在不同的速度下可计算出不同的磁流变阻尼力的值。
图1.4是磁流变减振器的间隙在0.6mm 时,各个速度下阻尼力的大小。
从图中可以看出磁流变减振器的阻尼力随速度的增大而增大。
这符合磁流变减振器对阻尼力的要求。
如上变化可绘制在不同的间隙和不同的速度下,阻尼力的变化关系,表1.1就是磁流变减振器在不同缝隙和不同速度下的阻尼力大小。
表1.1 磁流变减振器的阻尼力随缝隙和速度的变化关系缝隙mm速度s m0.4 0.5 0.70.9 1N 阻尼力0.5 2709.8 2860.25 3161.15 3462.05 3612.5 0.8 1455.12 1491.9 1565.46 1639.02 1675.8 1.0 983.4 1002.25 1039.95 1077.65 1096.5 1.5 810.48 816.1 827.34 838.58 844.2 2.0 597.56 599.95 604.73 609.51 611.9由上表中可以看出,随之缝隙的增加,在一定的速度下,阻尼力是随之缝隙的增加而减小的,在一定的缝隙大小的情况下,随着速的增加,阻尼力是增大的,这与汽车实际的行驶情况是一致的。
1.3总结本章是对磁流变阻尼器的仿真,在仿真的过程中,首先要建立磁流变减振器的数学模型,因为只有建立了磁流变减振器的数学模型,才能为下一步的建立仿真打下基础。
仿真运用的软件为Matlsb 软件,在建立了模块后,输入不同频率和电流来找到最大的阻尼力。
并分析了影响减振器阻尼力大小的速度和电流的因素。
得出了减振器的阻尼力与电流和频率的关系。
参考文献:[1]王金钢,等.磁流变阻尼器阻尼性能仿真研究[J].石油机械,2006,34(10):19-23[2]蒙延佩,等.汽车磁流变阻尼器磁路设计及相关问题[J].功能材料,2006(5):768-770[3]司诰,等.磁流变阻尼器管道流动特性研究[J].功能材料,2006(5):831-833[4]蒋建东.梁锡昌.张博适用于车辆的旋转式磁流变阻尼器研究[期刊论文]-汽车工程2005(1)[5]徐永兴.曹民.磁流变减振器优化的设计计算[J].上海交通大学学报,2004,38(8):1423-1427[6]贺建民等,磁流变减振器的分析与设计,第五届全国磁流变液及其应用学术会议,2008.10[7]徐伟,汽车悬架阻尼匹配研究机减振器设计,农也装备与车辆工程,2009.6[8]Lai C Y,Liao W H.Vibration Control of a Suspension System Via a Magnetorheo logical FluidDamper.Journal of Vibration and Control,2002,8(4):527-547. [9]Yang G,Spencer Jr BF,Carlson JD,et rge scale MR fluid Damper: Modeling and Dyamic Performance Considerations.Engineering Structures,2002,24:309-323。
