初中数学构造平行四边形解题例举学法指导
八年级初二数学华师大版下册同步辅导：构造平行四边形解题
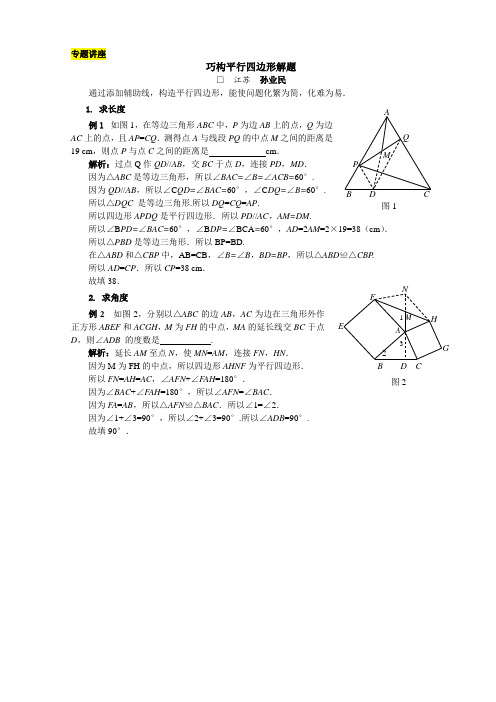
专题讲座巧构平行四边形解题□ 江苏 孙业民通过添加辅助线，构造平行四边形，能使问题化繁为简，化难为易．1. 求长度 例１ 如图1，在等边三角形ABC 中，P 为边AB 上的点，Q 为边AC 上的点，且AP =CQ ．测得点A 与线段PQ 的中点M 之间的距离是19 cm ，则点P 与点C 之间的距离是 cm ． 解析：过点Q 作QD //AB ，交BC 于点D ，连接PD ，MD ． 因为△ABC 是等边三角形，所以∠BAC=∠B=∠ACB=60°.因为QD //AB ，所以∠C QD=∠BAC=60°，∠C DQ=∠B=60°. 所以△DQC 是等边三角形.所以DQ =CQ =AP . 所以四边形APDQ 是平行四边形．所以PD //AC ，AM=DM.所以∠B PD=∠BAC=60°，∠B DP=∠BCA =60°，AD =2AM =2×19=38（cm ）． 所以△PBD 是等边三角形．所以BP=BD.在△ABD 和△CBP 中，AB=CB ，∠B=∠B ，BD=BP ，所以△ABD ≌△CBP . 所以AD =CP ．所以CP =38 cm ．故填38． 2. 求角度例2 如图2，分别以△ABC 的边AB ，AC 为边在三角形外作正方形ABEF 和ACGH ，M 为FH 的中点，MA 的延长线交BC 于点D ，则∠ADB 的度数是 .解析：延长AM 至点N ，使MN =AM ，连接FN ，HN ．因为M 为FH 的中点，所以四边形AHNF 为平行四边形．所以FN =AH =AC ，∠AFN +∠F AH =180°．因为∠BAC +∠F AH =180°，所以∠AFN =∠BAC ．因为F A =AB ，所以△AFN ≌△BAC ．所以∠1=∠2．因为∠1+∠3=90°，所以∠2+∠3=90°.所以∠ADB =90°.故填90°．B C PA M Q 图1 N H G F E 2B DC 1 M A 3 图2。
构造平行四边形解题
构造平行四边形解题作者：王竞进来源：《中学生数理化·八年级数学人教版》2008年第04期平行四边形是基本的几何图形之一，它的应用十分广泛.在解题时，如能根据图形特征，添加辅助线，构造平行四边形，常可化难为易，使问题快速获解.例1如图1，▱ABCD中，E、F为对角线AC上的两点，且AE=CF.M、N分别为边AD、BC上的点，且MD=NB.MN与EF相交于O.求证：EF和MN互相平分.分析1：据图形特征，要证明EF和MN互相平分，易于联想到平行四边形对角线的性质，于是可连接EM、MF、FN、NE，证明四边形MENF为平行四边形即可.证明1：如图2，连接EM、MF、FN、NE.因四边形ABCD为平行四边形，由∠MAE=∠NCF，AM=CN，AE=CF，可得△AEM≌△CFN.∴EM=NF，∠MEA=∠NFC.所以∠MEF=∠NFE.∴EM∥NF，四边形MENF是平行四边形.∴EF和MN互相平分.分析2：结合已知条件，若连接AN、CM，易证四边形ANCM亦为平行四边形（一组对边平行且相等），从而可得AC、MN互相平分.再由AE=CF可知OE=OF，进而结论获证.证明2：如图3，略.例2如图4，已知AC= AB=BD，AE=BE，求证：CD=2CE．分析：由结论，可延长中线CE至点F，使EF=CE，连接AF、BF，则构造了▱AFBC（因对角线互相平分），再证明△DBC≌△FBC，进而推得结论．证明：如图5，延长CE到F，使EF=CE，连接AF、BF.又因AE=BE，∴四边形AFBC是平行四边形.∴AC∥BF，AC=BF．∵AC=BD，∴BD=BF．∵AC= AB，∴∠ACB =∠ABC．又∠DBC=∠ACB+∠BAC=∠ABC+∠ABF=∠FBC，BC= BC，∴△DBC≌△FBC．故CD=CF=2CE．点评：本题也可证CD的一半等于CE.设CD中点为F，连接BF.易知BF=AC=BE.因BF∥AC，故∠FBC=∠ACB=∠ABC.故△CBE≌△CBF.例3如图6，李家庄有一个四边形的池塘ABCD，在它的四个角A、B、C、D处均种有一棵树.李家庄准备开挖池塘养鱼，想使池塘面积扩大一倍，又想保持四棵树不动，并且扩建后仍为四边形.请问：能否实现这一想法？试说明理由.分析：先把这个不规则的四边形通过连对角线，分割成四个三角形，然后再分别构造平行四边形把其面积扩大一倍，使问题得以解决.解：如图7所示，连接AC、BD，分别过点A、C作BD的平行线，分别过点B、D作AC 的平行线，得▱EFGH，即为扩建后符合要求的池塘.点评：利用平行四边形面积是一条对角线所分割出的三角形的面积的2倍，可帮助解决这类构造性问题，如前文中的例4.不能看书一群年轻人在一家旅馆的客房内豪饮狂欢.旅馆的招待员走过来对他们说道：“你们不要这样大喊大叫了！隔壁那位先生说他不能看书了.”“你去告诉他，”一个毛头小伙子说，“他应该感到惭愧，我五岁就能看书了.”。
(文章)构造平行四边形解题
构造平行四边形解题平行四边形是一种特殊的四边形，它的对边平行且相等，对角相等，对角线互相平分．许多几何问题可以通过添加辅助线，构造平行四边形加以解决．一、求线段的长例１如图1，在正△ABC 中，P 为边AB 上一点，Q 为边AC 上一点，且AP =CQ ．今量得A 点与线段PQ 的中点M 之间的距离是19cm ，则P 点到C 点的距离等于 cm ． 分析：作QD //AB ，交BC 于点D ，连接PD ，MD ．由△ABC 为正三角形，易知BP =BD ，AP =DQ ，所以四边形APDQ 为平行四边形．所以AMD 是平行四边形APDQ 的对角线．所以AD =2AM =2×可得PC =AD ．所以PC =38cm ．二、证明线段相等问题例2 如图2，在梯形ABCD 中，AD //BC ，AB =CD ，延长CB 到E ，使EB =AD ，连接AE ．求证：AE =AC ．分析：连接BD ．由AD 与BE 平行且相等，易知四边形AEBD 是平行四边形，所以BD =AE ．因为AC =BD ，所以AE =AC ．三、证明线段和差问题例3 如图3，△ABC 中，D ，F是AB 边上两点，且AD =BF ，作DE //BC ，FG //BC ，分别交AC 于点E ，G ．求证：DE +FG =BC ．分析：作GH //AB 交BC 于点H ．则四边形BHGF 是平行四边形．所以GH =BF =AD ，FG =BH ．因为DE //BC，GH //AB ，所以∠1=∠C ，∠A =∠2．所以△ADE ≌△GHC ．所以DE =HC ．因为BH +四、证明线段倍分问题例4 如图4，已知E 为平行四边形ABCD 中DC 边的延长线上一点，且CE =DC ，连接AE ，分别交BC ，BD 于点F ，G ，连接AC 交BD 于O ，连接OF ．试说明：AB =2OF ． 图3分析：连接BE ．易知四边形ABEC 为平行四边形．由“平行四边形的对角线互相平分”这一性质可得BF =CF ，AO =OC ，所以OF 为△CAB 的中位线，从而得出AB =2OF ．五、证明两直线平行问题例5 如图5，△ABC 中，E ，F 分别是AB ，BC 边的中点，M ，N 是AC 的三等分点，EM ，FN 的延长线交于点D ．求证：AB //CD ．分析：连接BD 交AC 于点O ，连接BM ，BN ．由AE =BE ，AM =MN 可得ED //BN ；由BF =CF ，MN =NC 可得BM //FD ．所以四边形BMDN 是平行四边形．所以OB =OD ，OM =ON ．所以OA =OC ．由此可得出四边形ABCD 是平行四边形．所以AB //CD ．六、证明两直线垂直问题例6如图6，分别以△ABC 的边AB ，AC 为一边在三角形外作正方形ABEF 和ACGH ，M 为FH 的中点．求证：MA ⊥BC ．分析：设MA 的延长线交BC 于点D ，延长AM 至点N ，使MN =AM ，连接FN ，HN ．则四边形AHNF 为平行四边形．所以FN =AH =AC ，∠AFN +∠F AH =180°．因为∠BAC +∠F AH =180°，所以∠AFN =∠BAC ．因为AF =AB ，所以△AFN ≌△BAC ．所以∠1=∠2．因为∠1+∠3=90°，所以∠2+∠3=90°，所以∠ADB =90°．从而得出MA ⊥BC ．。
构造平行四边形解题方略2
D B F
H
C E
G
二、构造平行四边形证
2、如图，AD是 ∆ABC 的边 上的中线， 、如图， 是 的边BC上的中线 上的中线， 求证： 求证：AB+AC﹥2AD ﹥
A
B
○
D
○
C
ቤተ መጻሕፍቲ ባይዱ
F
三、构造平行四边形证
3、如图，分别以 ∆ABC 中的 、AC为边 、如图， 中的AB、 为边 向外作正方形ABEF和正方形 和正方形ACGH，M是 向外作正方形 和正方形 ， 是 BC的中点， 的中点， 的中点 F 求证： 求证：FH=2AM
构造平行四边形解题方略
2011年3月 年 月
一、构造平行四边形证
∆ 1、如图， ABC 中，D在AB上，E在AC的 、如图， 在 上 在 的 延长线上， 连结DE， 延长线上，BD=CE连结 ，交BC于F， 连结 于 ， 外角的平分线交BC的延长线于 ∠BAC外角的平分线交 的延长线于 ， 外角的平分线交 的延长线于G， 且AG//DE。 。 A 求证：BF=CF 求证：
课堂检测
平面上三个等边三角形 ∆ACE、∆ABD、∆BCF 两两共有一个顶点，如图所示， 两两共有一个顶点，如图所示， B 求证： 与 互相平分 求证：CD与EF互相平分
C F
E D A
E A C H G
B
M
D
中考链接
西城二模） （2010西城二模）在△ABC中，点P为BC的中 西城二模 中 为 的中 点． ＜（AB+AC）； （1）如图 ，求证：AP＜（ ）如图1，求证： ＜（ ）； （2）延长 到D，使得 ）延长AB到 ，使得BD=AC，延长 到E， ，延长AC到 ， 使得CE=AB，连结 ． 使得 ，连结DE． 如图2，连结BE， BAC=60° ①如图2，连结BE，若∠BAC=60°，请你探究 线段BE与线段 之间的数量关系． 与线段AP之间的数量关系 线段BE与线段AP之间的数量关系．写出你的结 并加以证明； 论，并加以证明； 请在图3中证明 中证明： ②请在图 中证明：BC≥DE． ．
构造平行四边形证题的技巧
构造平行四边形证题的技巧构造平行四边形证题的技巧一. 构造平行四边形证两线段平行例1. 已知如图，平行四边形ABCD的对角线AC和BD交于O，E、F分别为OB、OD的中点，过O任作一直线分别交AB、CD于G、H。
求证：GF//EH。
证明：连结GE、FH四边形ABCD是平行四边形又四边形EHFG是平行四边形二. 构造平行四边形证两线段相等例2. 如图，中，D在AB上，E在AC的延长线上，BD=CE连结DE，交BC 于F，∠BAC外角的平分线交BC的延长线于G，且AG//DE。
求证：BF=CF分析：过点C作CM//AB交DE于点M，可以证明BD=CM，然后再利用平行四边形的性质得到BF=CF证明：过点C作CM//AB交BE于点M，连接BM、CD，则∠CME=∠ADE四边形BMCD为平行四边形故BF=CF三. 构造平行四边形证线段的不等关系例3. 如图，AD是的边BC上的中线，求证：分析：欲证，即要证，设法将2AD、AB、AC归结到一个三角形中，利用三角形任意两边之和大于第三边来证明。
注意到AD为的中线，故可考虑延长AD到E，使DE=AD，则四边形ABEC为平行四边形。
从而问题得证。
证明：延长AD到E，使DE=AD，连结BE、EC四边形ABEC是平行四边形在中，AE 即2AD<ab+ac< p="">点评：此题是利用三角形三边关系定理、平行四边形的判定，通过延长中线将证明三角形中三条线段间的不等关系，转化为三角形三边之间的关系，从而使问题迎刃而解。
四. 构造平行四边形证线段的倍分关系例4. 如图，分别以中的AB、AC为边向外作正方形ABEF和正方形ACGH，M是BC 的中点，求证：FH=2AM证明：延长AM到D，使MD=AM，连结BD、CD，是BC的中点四边形ABDC为平行四边形又AF=BA，AH=AC=BD故FH=2AM五. 构造平行四边形证两线段互相平分例5. 平面上三个等边三角形两两共有一个顶点，如图所示，求证：CD与EF互相平分分析：要证CD与EF互相平分，须证四边形DFCE是平行四边形证明：连结DE、DF、AF易知AD=AB=BD又AE=AC，AD=AB∠DAE=60°-∠EAB=∠BAC四边形DECF是平行四边形故CD与EF互相平分六. 构造平行四边形证角的`不等关系例6. 如图，在梯形ABCD中，AD//BC，对角线AC>BD求证：∠DBC>∠ACB证明：过点D作DE//AC交BC的延长线于点E，则四边形ACED 是平行四边形又在中，∠DBE>∠E七. 构造平行四边形证线段的和差关系例7. 如图，中，点E、F在边AB上，AE=BF，ED//AC//FG，求证：ED+FG=AC证明：过E作EH//BC交AC于H四边形CHED为平行四边形又AE=BF，同步练习：1. 如图1，在梯形BCED中，DE//BC延长BD、CE交于A，在BD上截取BF=AD。
初中数学初二数学下册《平行四边形》优秀教学案例
一、案例背景
在我国初中数学教育中，平行四边形作为八年级下册数学课程的重要内容，既是培养学生空间观念与几何直观的关键章节，也是提高学生推理能力与解决问题能力的重要载体。本教学案例以初二学生为对象，针对《平行四边形》这一章节，通过创设生活情境，激发学生的学习兴趣，引导学生主动探究平行四边形的性质与判定方法。本案例注重将抽象的数学概念与学生实际生活相结合，采用启发式教学方法，充分调动学生的主体作用，培养他们观察、分析、归纳和解决问题的能力。在教学过程中，关注学生的个体差异，提供不同层次的思考与练习，使每位学生都能在原有基础上得到提高，从而真正实现因材施教、全面发展。
二、教学目标
（一）知识与技能
1.让学生掌握平行四边形的定义，理解其对边平行且相等的性质，并能运用这一性质解决相关问题。
2.使学生掌握平行四边形的判定方法，如对角线互相平分、一组对边平行且相等、两组对边分别相等等，并能运用这些方法判断生活中的平行四边形。
3.培养学生运用平行四边形的性质与判定方法解决实际问题的能力，如计算平行四边形的面积、周长等。
（五）作业小结
1.布置适量的课后作业，包括基础题和提高题，巩固所学知识。
2.设计开放性问题，让学生运用所学知识解决生活中的实际问题，提高他们的创新意识。
3.要求学生在课后进行反思，总结自己在课堂上的收获和不足，为下一节课的学习做好准备。
4.教师及时批改作业，了解学生的学习情况，为下一步的教学提供依据。
4.引导学生将所学知识应用于生活实际，培养他们学以致用、理论联系实际的价值观。
5.培养学生的批判性思维，使他们敢于质疑、勇于探索，形成独立思考的习惯。
三、教学策略
（一）情景创设
人教版数学八年级下册18.1.2平行四边形判定的优秀教学案例
1.布置作业：针对本节课的内容，布置一些具有代表性的练习题，让学生巩固所学知识。
a.画出几个平行四边形，并标出它们的性质。
b.判断以下四边形是否为平行四边形，并说明理由。
c.运用平行四边形的性质解决实际问题。
2.作业评价：对学生的作业进行评价，关注学生的解题思路和方法，及时给予反馈，帮助学生提高。
3.实践探究：组织学生进行动手操作，通过画图、测量等实践活动，让学生在实践中发现平行四边形的性质和判定方法。
4.反思与总结：引导学生对所学知识进行反思和总结，形成自己的知识体系。
（三）情感态度与价值观
1.增强学生对数学学科的兴趣，激发学生的学习热情，培养他们的探究精神。
2.培养学生严谨的学习态度，使学生认识到几何图形在生活中的重要性，提高学生的应用意识。
3.培养学生克服困难的勇气和信心，使学生体验成功解决问题的喜悦，形成积极向上的心态。
4.培养学生的集体荣誉感，使学生学会尊重他人，形成良好的人际关系。
三、教学策略
（一）情景创设
在本章节的教学中，我将创设贴近学生生活的情景，以引发学生的兴趣和思考。例如，可以引用校园建筑中的平行四边形结构，如操场上的跑道、篮球场上的边界线等，让学生感受到数学知识在实际生活中的应用。通过这些情景的引入，让学生认识到平行四边形与我们的生活息息相关，从而激发他们的学习热情。
（二）问题导向
以问题为导向，引导学生主动探究平行四边形的性质和判定方法。在教学过程中，我将设计一系列具有启发性和挑战性的问题，如：
1.如何判断一个四边形是平行四边形？
2.平行四边形具有哪些独特的性质？
3.如何运用这些性质解决实际问题？
（三）小组合作
小组合作是本节课的重要教学策略。我将学生分成若干小组，每组4-6人，让他们在合作交流中共同探讨平行四边形的性质和判定方法。在小组合作中，学生可以互相启发、互相补充，形成集体的智慧。同时，小组合作有助于培养学生的团队精神和沟通能力。
构造平行四边形解题举例
构造平行四边形解题举例浙江江山市长台初中 徐生根 324106平行四边形是初中数学重点，中考中经常出现需要构造平行四边形、利用平行四边形性质证明角相等、线段相等或线段平行等题型.现举例归类分析，供参考.一、 构造平行四边形证明线段平行例1 如图1，AB,CD 交于点O,A C ∥DB,AO=BO,E,F 分别为OC ，OD 的中点，连结AF 、BE,求证：AF ∥BE.分析：从已知条件可证⊿AOC ≌⊿BOD,得到OC=OD,又E 、F 为OC 、OD 的中点，则OE=OF,判断四边形AFBE 为平行四边形，AF ∥BE.证明：连结BF 、AE,因AC ∥DB,故∠C=∠D.在⊿AOC 和⊿BOD 中，由AO=BO,∠AOC=∠BOD,得⊿AOC ≌⊿BOD(ASA),又∵E 、F 为OC 、OD 的中点，则OE=OF,∴四边形AFBE 是平行四边形，∴AF ∥BE.二、构造平行四边形证明两线段相等例2如图2，在R t ⊿ABC 中，∠BAC=90°，延长BA 到D ，使AD=12AB ，点E 、F 分别为BC 、AC 的中点，求证：DF=B E ．分析：要证DF=BE,可以证四边形EBDF 是等腰梯形，但这样比较麻烦，如果连结AE,证明四边形AEFD 是平行四边形，⊿EBA 是等腰三角形，可顺利得DF=BE.证明：连结AE,∵EF 是⊿ABC 的中位线，∴EF ∥AB 且EF=2ABAD ,∴ 四边形AEFD 为平行四边形，DF=AE,又AE 为Rt ⊿ABC 斜边上的中线，则AE=BE,故BE=DF.三、 构造平行四边形证明角相等例3．如图3，已知E 为BC 的中点，A 在DE 上，且AB=CD,求证：∠CDE=∠BAE.分析：由于∠CDE 与∠BAE 在两个不同的三角形中，，且这两个三角形不全等或相似，所以，不能直接比较着两个角的大小，注意到E 为BC 的中点，线段ED 是⊿ABC 的中线，从从而向把中线加倍，构造平行四边形得以解决. 证明：延长DE 到F,使EF=DE,连结FB 、FC 、BD,，易知四边形BFCD 为平行四边形，则BF ∥CD, ∠BFA=∠CDF,BF=CD.∵CD=BA, ∴BF=BA, ⊿BFA 是等腰三角形，∠BFA=∠BAF,即∠BAE=∠CDE.四、构造平行四边形线段的倍分关系例4. 如图4，已知O为平行四边形ABCD对角线的交点，E为DC边延长线上的一点，且CE=CD,连结AE交BC于F点，连OF，求证：AB=2OF.分析：若证AB=2OF,这需证F为BC的中点，连结BE，若四边形ABEC为平行四边形，则F为平行四边形ABCE的对角线交点.证明：连结BE,∵四边形ABCD为平行四边形，∴ AB CD,又∵E为DC延长线上的点，且EC=DC,∴AB EC,∴四边形ABEC为平行四边形，F为BC的中点，∵O为AC的中点，∴OF是⊿CAB的中位线，AB=2OF.五、构造平行四边形证明线段互相平分例5. 如图5，平行四边形ABCD中，E、G、F、H分别是四条边上的点，且AE=CF,BG=DH,试说明：EF与GH互相平分.分析：EF与GH为四边形HEGF的对角线，若能说明四边形HEGF是平行四边形，由平行四边形对角线互相平分这一性质即可得到EF与GH相互平分.证明：连结HE、EG、GF、FH.∵四边形ABCD是平行四边形，∠A=∠C,AD=CB 又∵BG=HD,∴AH=CG,又∵AE=CF,∴△HAE∽△GCF.∴HE=FG同理可得HF=EG,∴四边形EGFH是平行四边形，∴EF与GH互相平分.六、构造平行四边形证明线段的和差关系例6 如图6，四边形ABCD中，AB∥CD，且∠ADC=2∠ABC，试说明:AB=AD+CD.分析：延长DC到E，使DE=AB，连接BE，则四边形ABED为平行四边形，得BE=AD，下面只需说明CE=BE即可.证明：延长DC到E，使DE=AB，连接BE，∵AB∥CD，∴四边形ABED是平行四边形，所以EB=AD，∠ADC=∠ABE.又因为∠ADC=2∠ABC，所以∠ABE==2∠ABC，所以∠ABC=∠EBC.因为∠ECB=∠ABC所以∠EBC=∠ECB，所以EB=EC,因为ED=EC+CD=EB+CD,所以AB=AD+CD.七、构造平行四边形证明两条线段不等例7．如图7，已知AB=AC,D在AB上，E在AC的延长线上，且BD=EC,求证：DE＞BC.分析：由于DE和BC不在同一个三角形中，那么要将DE、BC搬到同一个三角形中解决问题.证明：过D、C分别作BC、BD的平行线DF、CF相交于F点，则四边形BCFD是平行四边形，连结FE,∴BC=DF,BD=CF,∴∠B=∠4,∴CE=BD=CF, ∴∠1=∠2.∵⊿ABC中，AB=AC,∠B=∠3,∴∠3=∠4.∵∠3＞∠5,∴∠4＞∠5,∴∠4+∠1＞∠5+∠2即∠DFE＞∠DEF,∴DE＞DF,即DF＞BC.。
中考数学复习：专题5-2 依据判定 学会构造平行四边形解决问题
专题02 依据判定学会构造平行四边形解决问题【专题综述】平行四边形具有对边相等、对角相等、对角线互相平分等性质，解决某些几何题时，若能根据平行四边形的判定，巧妙地构造出平行四边形，就会化难为易、化繁为简，证明过程简捷．现举例说明.【方法解读】一、说明两线段相等例1 已知：如图1，在四边形ABCD中，AB＝DC，AD＝BC，点E在BC上，点F在AD上，AF＝CE，EF 与对角线BD相交于点O．【举一反三】1 如图所示，在梯形ABCD中，AD∥BC，对角线AC⊥BD，且AC＝5 ㎝，BD＝12 ㎝，则该梯形的两底之和等于____㎝．五、说明线段的倍分关系例5 如图5，已知AB＝A C，B是AD的中点，E是AB的中点，试说明：CD＝2CE．【举一反三】1 如图，在梯形A BCD中，AD∥BC，E是DC的中点，EF∥AB交BC于F，若EF=4，求AB的长.六、解决面积问题例6 如图6，E 是梯形ABCD 腰DC 的中点．试说明：S △ABE ＝21S 梯形ABCD ．【举一反三】1 如图，在四边形ABCD 中，AD ∥BC ，错误!未找到引用源。
，点E 是BC 的中点，连接AE 、BD ．若EA ⊥AB ，BC ＝26，DC ＝12，求△ABD 的面积.【强化训练】1 如图,已知AB =10,点C ,D 在线段AB 上,且AC =DB =2;点P 是线段CD 上的动点,分别以A P ,PB 为边在线段AB 的同侧作等边三角形AEP 和等边三角形PFB ,连接EF ,设EF 的中点为G ;当点P 从点C 运动到点D 时,点G 移动路径的长是_____.2 如图，AC 、BD 是四边形ABCD 的对角线，E 、F 分别是AD 、BC 的中点，M 、N 分别是BD 、AC 的中点． 求证：EF 与MN 互相平分．3 有一块形状如图所示的玻璃，不小心把DEF 部分打碎，现在只测得AB =60cm ，BC =80cm ，∠A =120°，∠B=60°，∠C=150°，你能设计一个方案，根据测得的数据求出AD的长吗？4 已知：如图，在▱ABCD中，∠ADC，∠DAB的平分线DF，AE分别与线段BC相交于点F，E，DF与AE 相交于点G．（1）求证：AE⊥DF；（2）若AD＝10，AB＝6，AE＝4，求DF的长．5 已知，如图，在▱ABCD中，E是CD的中点，F是AE的中点，FC与BE交于点G.求证：GF＝GC.6 如图，在▱ABCD中，∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F，BE与CF相交于点G.(1)求证：BE⊥CF；(2)若AB＝3，BC＝5，CF＝2，求BE的长．7 已知：如图，在梯形ABCD中，AD∥MN∥BC．MN分别交边AB、DC于点M、N．如果AM:MB=2:3，AD=2，BC=7．求MN的长．8 如图，四边形各边中点及对角线中点共六个点中，任取四个点连成四边形中，最多可以有几个平行四边形，证明你的结论.9 如图所示，在形状为平行四边形的一块地ABCD中，有一条小折路EFG．现在想把它改为经过点E的直路，要求小路两侧土地的面积都不变，请在图中画出改动后的小路．10 如图，错误!未找到引用源。
依据判定 学会构造平行四边形解决问题
依据判定学会构造平行四边形解决问题平行四边形具有对边相等、对角相等、对角线互相平分等性质，解决某些几何题时，若能根据平行四边形的判定，巧妙地构造出平行四边形，就会化难为易、化繁为简，证明过程简捷．现举例说明。
一、说明两线段相等例1、已知：如图1，在四边形ABCD中，AB＝DC，AD＝BC，点E在BC上，点F在AD上，AF＝CE，EF与对角线BD相交于点O．试说明：O是BD的中点．分析：观察图形，EF与BD为四边形FBED的对角线，若能说明四边形FBED是平行四边形，根据平行四边形的对角线互相平分这一性质即可得到O是BD的中点。
二、说两线段互相平分例2、如图2，平行四边形ABCD中，E、G、F、H分别是四条边上的点，且AE＝CF，BG＝DH，试说明：EF与GH相互平分．分析：观察图形，EF与HG为四边形HEGF的对角线，若能说明四边形HEGF是平行四边形，根据平行四边形的对角线互相平分这一性质即可得到EF与GH相互平分。
三、说明两线段平行例3、如图3，平行四边形ABCD的对角线AC和BD交于O，E、F分别为OB、OD的中点，过O任作一直线分别交AB、CD于G、H．试说明：GF∥EH．分析：观察图形，GF与EH为四边形GEHF的对边，若能说明四边形EHFG是平行四边形，平行四边形具有对边平行的性质可得GF∥EH．四、说明线段的和差关系例4、如图4，四边形ABCD中，AB∥CD，且∠ADC=2∠ABC，试说明AB=AD+CD分析：延长DC到E，使DE=AB，连接BE，则四边形ABED为平行四边形，得BE=AD，下面只需说明CE=BE即可。
五、说明线段的倍分关系例5、如图5，已知AB＝AC，B是AD的中点，E是AB的中点．试说明：CD＝2CE．分析：延长CE至F，使EF＝CE，连结AF、BF，得四边形AFBC是平行四边形，利用平行四边形的性质证明△DBC ≌△FBC 即可。
六、解决面积问题例6、如图6，E 是梯形ABCD 腰DC 的中点． 试说明：S △ABE ＝21S 梯形ABCD ． 分析：过点E 作MN ∥AB ，交BC 于N ，交AD 的延长线于M ，则四边形ABNM 是平行四边形，△ABE 与四边形ABNM 等底等高，所以S △ABE ＝21S 平行四边形ABNM ，接下来说明S 梯形ABCD ＝S 平行四边形ABNM 即可。
初中数学特殊平行四边形解题模型
1. 我们知道平行四边形的对边平行，因此可以利用相邻角的性质来解题。
2. 如题目给出平行四边形ABCD，我们要证明AD//BC。
3. 根据相邻角的性质，∠ABD和∠BCD是相邻角，因此它们的和为180°。
4. 又因为平行四边形的对边分别平行，所以∠ABD=∠BCD，即两个角相等。
5. 那么根据相等角的性质，∠ABD+∠BCD=180°，即AD//BC成立。
模型二：利用对角线的性质1. 对角线的性质是解决平行四边形问题的另一个重要方法。
2. 给定平行四边形ABCD，我们要证明对角线AC和BD相交于一点O。
3. 因为平行四边形的性质是，对角线互相平分，所以BO=OD，AO=OC。
4. 根据三角形的性质，两边相等且夹角相等，则两个三角形全等。
因此△BOA≌△COD。
5. 根据全等三角形的性质，可以知道∠BOA=∠COD，所以AC与BD 相交于一点O。
1. 辅助线是解决平行四边形问题常用的方法之一。
2. 给定平行四边形ABCD，我们要证明AB//CD。
3. 可以作线段AC的中线，即连接BD的中点M和连接BA的中点N。
4. 根据线段的中线定理，中线等分基底并平行于两个底部，即AM=MC，BN=ND，并且AM//CD，BN//CD。
5. 根据平行线的性质，AB//CD成立。
模型四：利用平移、旋转和对称的方法1. 平移、旋转和对称是解决平行四边形问题中比较灵活的方法。
2. 给定平行四边形ABCD，我们要证明ABCD是一个菱形。
3. 可以将平行四边形ABCD沿着AB向右平移，得到A'B'CD。
4. 然后我们发现A'B'CD是ABCD的旋转图形，它们是共外部定点的两个同圆的切线。
5. 根据旋转体的性质，AB=BC=CD=DA，所以ABCD是一个菱形。
结论：不同的解题模型可以让我们更灵活地应对不同类型的题目，并且提高解题的效率。
通过掌握这些解题模型，我们可以更加轻松地解决平行四边形的相关问题。
八年级数学下册《平行四边形性质的简单应用》优秀教学案例
（四）反思与评价
1.自我反思：引导学生对自己在课堂上的学习过程进行反思，总结自己在学习平行四边形性质方面的优点和不足。
2.同伴评价：组织学生进行同伴评价，让他们在相互评价中学习他人的优点，改进自己的不足。
3.教师评价：教师对学生在课堂上的表现进行客观、全面的评价，既要肯定他们的进步，也要指出需要改进的地方，以促进学生全面发展。
（三）情感态度与价值观
1.激发学生对数学学科的兴趣，培养他们热爱数学的情感。
2.培养学生勇于探索、积极思考的良好学习习惯，增强他们面对困难的信心和毅力。
3.引导学生发现数学与生活的紧密联系，体会数学在现实生活中的重要作用，提高他们的数学素养。
4.培养学生的集体荣誉感，让他们在合作学习中学会互相尊重、互相帮助，形成良好的团队精神。
八年级数学下册《平行四边形性质的简单应用》优秀教学案例
一、案例背景
在我国初中数学教育中，八年级学生已经具备了一定的几何图形认知基础，对于平行四边形的性质也有了初步的理解。《平行四边形性质的简单应用》这一章节旨在帮助学生将理论知识与实际问题相结合，培养他们的逻辑思维能力和解决实际问题的能力。本教学案例以八年级数学下册教材为依据，针对平行四边形在实际问题中的简单应用进行深入剖析，通过设计丰富多样的教学活动，激发学生的学习兴趣，提高他们的几何图形应用能力。在教学过程中，注重引导学生运用所学知识解决生活中的实际问题，以彰显数学学科的魅力和实用性。
二、教学目标
（一）知识与技能
1.理解并掌握平行四边形的基本性质，如对边平行且相等、对角线互相平分等。
2.学会运用平行四边形的性质解决实际问题，如计算平行四边形的面积、周长等。
构造平行四边形巧解题
櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚櫚
（上 接 第 １７ 页 ）
平行四边形．
证明 延 长 ＡＤ 到Ｇ，使 ＤＧ＝ＡＤ，连 接 ＢＧ、ＧＣ，则四边形 ＡＢＧＣ 为平行四边形．
∴ ＡＣ＝ＢＧ， ∵ ＡＣ∥ＢＧ，
在△ＰＭＦ 中，ＰＭ＋ＭＦ＞ＰＦ， 在△ＰＥＮ 中，ＰＮ＋ＥＮ＞ＰＥ， ∴ ＰＭ ＋ＭＦ＋ＰＮ ＋ＥＮ ＞ＰＥ＋ＰＦ， 又 ＰＭ＝ＡＮ，ＰＮ＝ＡＭ，
ＰＭ ∥ＡＣ 交 ＡＢ 于 Ｍ ，
作 ＰＮ ∥ ＡＢ 交 ＡＣ 于
Ｎ ，则 四 边 形 ＡＭＰＮ 为
图５
檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪檪殏
∴ ＡＮ ＋ＥＮ ＋ＡＭ ＋ＭＦ＞ＰＥ＋ＰＦ．
即 ＡＥ＋ＡＦ＞ＰＥ＋ＰＦ．
评析 本题以构造的平行四边形两边
ＰＭ、ＰＮ 为 边 巧 妙 形 成 的 两 个 三 角 形 （即
钟 就 有 一 辆 迎 面 而 过 ，每 隔４０分 钟 就 有 一 辆 从 ３
背面而来，若 某 人 与 公 交 车 均 匀 速 运 动，求 车
站每隔几分钟发出一辆公交车？
简解 某 人 匀 速 向 前 散 步 ４０ 分 钟，迎 面
遇到５辆 （４０ 分 钟 ÷８ 分 钟／辆）公 交 车，立 即
返回，又匀速散步４０ 分 钟，有 ３ 辆 （４０ 分 钟 ÷
∴ ∠Ａ＝ ∠ＢＣＥ． ∵ ∠Ａ＝２∠１，
∴ ∠ＢＣＥ＝２∠１．
∴ ∠１＝ ∠３． ∵ ＡＥ∥ＢＣ，
∴ ∠１＝ ∠２．
∴ ∠２＝ ∠３．
∴ ＤＥ＝ＣＥ．
图１
又 ＡＢ＝ＣＥ，
∴ ＤＥ＝ＡＢ＝４．
∴ ＢＣ＝ＡＥ＝ＡＤ＋ＤＥ＝３＋４＝７． 评析 由构造出的平行四边形，利 用 它 的 性质并结合等腰三角形的判定定理，顺利 完 成
例谈构造平行四边形解题
例谈构造平行四边形解题作者：葛长岭朱记松来源：《中学生数理化·八年级数学人教版》2020年第04期平行四边形（含特殊平行四边形）是几何图形的重要组成部分，也是中考的必考内容之一，几何中的许多问题，若转化为平行四边形（含特殊平行四边形）问题，借助平行四边形（含特殊平行四边形）的边、角、对角线的性质解决，则可以化难为易，事半功倍.这一“转化”过程，通常是通过添加适当的辅助线，来构造平行四边形（含特殊平行四边形）.一构造一般平行四边形例1图1中的①②③分别表示甲、乙、丙三人由A地到B地的路线（箭头表示行进的方向）.其中，H为AB的中点，AE>EB.三人行进路线长度的大小关系为（）.A.甲<乙<丙B.丙<乙<甲C.乙<丙<甲D.甲=乙=丙解析：对于②，延长AG，BK交于点N，得□GEKN，如图2.AG+GE+EK+KB=AG+GN+NK+KB=AN+NB.同理，对于③，AD+DH+HF+FB=AD+DM+MF+FB=AM+MB，如图3.由“角边角”可以判定△ABC≌△ABN≌△ABM.所以有AC=AN=AM，CB=NB=MB.故甲、乙、丙三人行走路线的长度相等，选D.二构造菱形例2如图4，AB=AC=BD，∠A=100°，∠/B=20°.求∠C的大小.解析：以AC，AB为边构造□ABEC.如图5.因AB=AC，故□ABEC是菱形.因∠A=100°，故∠ABE=∠ACE=80°.因∠B=20°.故∠EBD=80°-20°=60°.又AB=BD，AB=BE，则BD=BE，△BED是等边三角形，∠BED=600.所以∠DEC=∠BEC-∠BED=100°-60°=40°.而CE=BE=DF，所以∠ECD=180°-40°/2=70°.所以∠ACD=80°-70°=10°.即为所求.三构造矩形例3如图6所示，CD∥AF，∠CDE=∠BAF，AB⊥BC.∠BCD=124°.∠DEF=80°.求∠AFE 的度數.解析：构造如图7所示的矩形GHMN.∠BCD=124°.可求得∠1=56°.∠G=∠H=90°.∠1+∠GBC=90°.AB⊥BC，∠ABC=90°.因∠2+∠GBC=90°，故∠1=∠2.∠CDE=∠BAF=∠2+∠H=146°.因六边形ABCDEF的内角和为720°，∠DEF=80°，所以∠AFE=134°.点拨：要求∠AFE的度数，关键是求∠CDE，∠BAF的度数.由CD∥AF，AB⊥BC，联想到“一线三直角”模型，通过构造矩形，将六边形问题转化为平行四边形中的矩形问题.事实上，若注意到CD//AF，∠CDE=∠BAF，通过延长AB，DC及AF，DE，构造平行四边形，同样可以使问题解决.。
人教版八年级数学下册18.1.2平行四边形的判定优秀教学案例
3.遵循由浅入深、循序渐进的原则，引导学生逐步掌握平行四边形的判定方法，培养学生的逻辑思维能力和数学素养。
（三）情感态度与价值观
1.培养学生对数学学科的兴趣和爱好，使学生感受到数学的乐趣，提高学生学习数学的积极性。
（三）学生小组讨论
在学生小组讨论环节，我会将学生分成小组，每组需要通过讨论和探究，找出一种判定平行四边形的方法。我会提供一些实例和练习题，引导学生运用所学知识，进行小组合作学习和讨论。在讨论过程中，我会巡回指导，给予学生必要的帮助和提示，促进学生的思考和交流。
（四）总结归纳
在总结归纳环节，我会邀请各小组代表分享他们的讨论成果，让学生展示和阐述他们所找到Байду номын сангаас判定平行四边形的方法。然后，我会对学生的回答进行点评和总结，明确指出平行四边形的判定方法及其适用条件。通过总结归纳，帮助学生梳理和巩固所学知识，提高学生的数学思维能力。
三、教学策略
（一）情景创设
在教学过程中，我会创设贴近学生生活实际的情景，让学生在具体的情境中感受和理解平行四边形的判定。例如，通过展示一些生活中的平行四边形物品，如电梯、推拉门等，引导学生发现平行四边形的特征。同时，我还会设计一些有趣的实践活动，如让学生自己动手制作平行四边形模型，增强学生对平行四边形的直观认识。
五、案例亮点
1.生活情境的创设：本案例通过引入生活中的平行四边形物品，如电梯、推拉门等，让学生在具体的情境中感受和理解平行四边形的特征。这种生活情境的创设使得数学知识与学生的实际生活紧密相连，提高了学生的学习兴趣和积极性。
2.问题导向的教学策略：本案例通过提出一系列问题，引导学生思考和探究。这种问题导向的教学策略使得学生能够在思考和解决问题的过程中，深入理解平行四边形的定义、性质和判定方法，培养了学生的数学思维能力。
构造平行四边形8招
构造平行四边形8招吴健张崇俊平行四边形是特殊的四边形，它具有对边相等、对角相等、对角线互相平分等诸多性质。
在证（解）一些几何问题时，若能根据图形的特征，添加恰当的辅助线构造平行四边形，并利用其性质可使问题化难为易，化繁为简，证明过程极为简便。
下面分类举例说明。
一、构造平行四边形证两线段平行例1 在△ABC，AC>AB，在它的两边AB、AD上分别截取BD=CE，F、G分别是BC 和DE的中点，求证：FG和∠BAC的平分线AT平行。
分析：要证FG∥AT，须证四边形GFKN是平行四边形，而四边形GFKN可通过角平分线AT和中点去构造。
如图。
证明：过B、D分别作AT的垂线，垂足分别为K、N，且分别交AC于M、Q，连接GN、FK，则由AT平分∠BAC，得DN=NQ，又由DG=EG得NG EQ，同理FK MC。
又由TA平分∠BAC，DN⊥AN，BK⊥AK得BD=MQ，又BD=CE，∴QE=MC，∴NG FK。
∴四边形GFKN是平行四边形。
故FG和∠BAC的平分线平行。
二、构造平行四边形证两线段相等例2 如图，△ABC中，AB=AC，E是AB上一点，F是AC延长线上一点，BE=CF，EF交BC于D，求证：DE=DF。
证明：过E作EG∥AC交BC于G，连接CE、GF。
∵AB=AC，∴∠ABC=∠ACB。
∵∠EGB=∠ACB，∴∠ABC=∠EGB，∴EG=BE。
∵BE=CF，∴EG=CF，又EG∥CF，∴四边形EGFC是平行四边形，∴DE=DF。
三、构造平行四边形证两线段互相平分例3 平行四边形ABCD中，E、F分别在AD、BC上，且AE=CF，AF与BE相交于G，CE与DF相交于H，求证EF与GH互相平分。
分析：欲证EF与GH互相平分，只须四边形EGFH为平行四边形，利用已知条件可知四边形AFCE、四边形EBFD都是平行四边形，所以可得AF∥EC，BE∥DF，从而四边形GFHE为平行四边形。
证明：平行四边形ABCD中，AD BC。
八年级数学下册动点问题构成平行四边形解题技巧(一)
八年级数学下册动点问题构成平行四边形解题技巧(一)八年级数学下册动点问题构成平行四边形解题技巧什么是动点问题？动点问题是数学中经常遇到的一类问题，它通常涉及到平行四边形的性质和特点。
解决动点问题需要一定的技巧和方法。
动点问题解题技巧以下是一些解决八年级数学下册动点问题的技巧：•确定动点的位置和性质在解决动点问题时，首先要确定动点的位置和性质。
根据问题所给条件，我们可以确定动点在平行四边形内部、边界上还是延长线上。
这些信息有助于我们确定动点的坐标。
•确定平行四边形的特点平行四边形有一些独特的性质，利用这些性质可以解决动点问题。
例如，平行四边形的对角线相互平分，对角线长相等等。
通过确定平行四边形的特点，我们可以推断出关于动点的一些性质。
•运用向量法或坐标法求解在解决动点问题时，我们可以运用向量法或坐标法来求解。
向量法常用于证明或推导问题，而坐标法常用于具体计算。
具体选择使用哪种方法要根据问题的特点和要求来决定。
•画图辅助解题绘制图形是解决动点问题的重要步骤。
通过画图，我们可以更好地理解问题，并帮助我们找到解题的思路。
画图时，注意要准确绘制出平行四边形的形状和各个元素的位置关系。
•通过推理和运算得出答案在完成前面步骤后，我们可以通过推理和运算来得出最终的答案。
根据题目所要求的内容，进行逻辑推理和数学运算，得出问题的解答。
总结解决八年级数学下册动点问题需要我们熟悉平行四边形的性质和特点，并掌握相应的解题技巧。
通过确定动点的位置和性质、确定平行四边形的特点、运用向量法或坐标法、画图辅助解题以及通过推理和运算得出答案，我们可以有效地解决动点问题。
希望以上技巧能帮助到你解决八年级数学下册动点问题，在数学学习中取得更好的成绩！对于八年级数学下册动点问题构成平行四边形解题，下面给出了更具体的步骤和实例来帮助你更好地理解和应用这些技巧。
1.确定动点的位置和性质首先，从题目中找出关于动点的相关信息，然后根据这些信息来确定动点的位置和性质。
2020—2021学年人教版数学 八年级下册 18.1 平行四边形的解题策略
平行四边形的解题策略【知识储备】一、平行四边形的概念：有两组对边分别平行的四边形叫做平行四边形．二、平行四边形的性质①边：平行四边形的对边相等．②角：平行四边形的对角相等．③对角线：平行四边形的对角线互相平分．三、平行四边形的判定①两组对边分别平行的四边形是平行四边形．②两组对边分别相等的四边形是平行四边形．③一组对边平行且相等的四边形是平行四边形．【经典例题】知识点一、平行四边形的性质例1．如图，▱ABCD中，对角线AC、BD相交于点O，OE⊥BD交AD于点E，连接BE，若ABCD的周长为28，求△ABE的周长.例2．如图,平行四边形ABCD的对角线AC与BD相交于点O，AE⊥BC于E，AB＝，AC＝2，BD＝4.求AE的长.例3．如图，已知△ABC的面积为12，点D在线段AC上，点F在线段BC的延长线上，且BC＝4CF，四边形DCFE是平行四边形，求图中阴影部分的面积.例4．如图，平行四边形ABCD，点F是BC上的一点，连接AF，∠FAD＝60°，AE平分∠FAD，交CD53于点E，且点E是CD的中点，连接EF，已知AD＝5，CF＝3，求EF的长.知识点二、平行四边形的判定例5．如图，在四边形ABCD中，AD∥BC，AD＝5，BC＝18，E是BC的中点．点P以每秒1个单位长度的速度从点A出发，沿AD向点D运动；点Q同时以每秒3个单位长度的速度从点C出发，沿CB向点B运动．点P停止运动时，点Q也随之停止运动，当运动时间t秒时，以点P，Q，E，D为顶点的四边形是平行四边形，求t的值．例6．如图，在等边三角形ABC中，BC＝6cm，射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，点F从点B出发沿射线BC以2cm/s的速度运动．如果点E、F同时出发，设运动时间为t（s）当t多少s时，以A、C、E、F为顶点四边形是平行四边形．例7．如图，在ABCD中，AC与BD交于点M，点F在AD上，AF＝6cm，BF＝12cm，∠FBM＝∠CBM，点E是BC的中点，若点P以1cm/s秒的速度从点A出发，沿AD向点F运动；点Q同时以2cm/秒的速度从点C出发，沿CB向点B运动，点P运动到F点时停止运动，点Q也同时停止运动，当点P运动多少秒时，以P、Q、E、F为顶点的四边形是平行四边形．知识点三、平行四边形的性质与判定例8．如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE．已知∠BAC＝30°，EF⊥AB，垂足为F，连接DF．（1）试说明AC＝EF；（2）求证：四边形ADFE是平行四边形．例9．如图，已知△ABC是等边三角形，点D、F分别在线段BC、AB上，∠EFB＝60°，DC＝EF．（1）求证：四边形EFCD是平行四边形；（2）若BF＝EF，求证：AE＝AD．例10．如图，在中，过B点作BM⊥AC于点E，交CD于点M，过D点作DN⊥AC于点F，交AB于点N．（1）求证：四边形BMDN是平行四边形；（2）已知AF＝12，EM＝5，求AN的长．练习1．如图，四边形ABCD中，对角线AC，BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）A．AB∥DC，AD∥BC B．AB＝DC，AD＝BCC．AO＝CO，BO＝DO D．AB∥DC，AD＝BC练习2．已知四边形ABCD，从下列条件中：（1）AB∥CD；（2）BC∥AD；（3）AB＝CD；（4）BC＝AD；（5）∠A＝∠C；（6）∠B＝∠D．任取其中两个，可以得出“四边形ABCD是平行四边形”这一结论的情况有（）A．4种B．9种C．10种D．13种练习3．在ABCD中，O是AC、BD的交点，过点O与AC垂直的直线交边AD于点E，若ABCD的周长为22cm，则△CDE的周长为（）A．8cm B．10cm C．11cm D．12cm练习4．如图，EF过ABCD对角线的交点O，交AD于点E，交BC于点F，若ABCD的周长为36，OE＝3，则四边形EFCD的周长为（）A．28B．26C．24D．20练习5．如图，▱ABCD的对角线AC，BD交于点O，AC⊥AB，AB＝，且AC：BD＝2：3，那么AC 的长为（）A．2B．C．3D．4练习6如图ABCD的对角线相交于点O，且AB≠AD，过点O作OE⊥BD交BC于点E，若△CDE的周长为10，则ABCD的周长为（）A．14B．16C．20D．18练习7．如图，在ABCD中，对角线AC的垂直平分线分别交AD，BC于点E，F，连接AF，若△ABF 的周长为6，则ABCD的周长为（）A．6B．12C．18D．24练习8．已知一个凸四边形ABCD的四条边的长顺次是a、b、c、d，且a2+ab﹣ac﹣bc＝0，b2+bc﹣bd﹣cd ＝0，那么四边形ABCD一定是（）A．平行四边形B．矩形C．菱形D．梯形练习9．如图，▱ABCD中，点E、F分别在AD、AB上，依次连接EB、EC、FC、FD，图中阴影部分的面积分别为S1、S2、S3、S4，已知S1＝2、S2＝12、S3＝3，则S4的值是（）A．4B．5C．6D．7练习10．如图，在平行四边形ABCD中，AD＝2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，下列结论①∠DCF＝∠BCD；②EF＝CF；③S△BEC＝2S△CEF；④∠DFE＝3∠AEF 中，一定成立的个数有（）A．1个B．2个C．3个D．4个。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初中数学构造平行四边形解题例举学法指导
雷祥红
平行四边形是初中几何中非常重要的内容，它的性质在几何计算和证明中应用十分广泛，在解题中若能根据题目的特征，巧妙添加辅助线，构造平行四边形，能使问题得到快速解答，同时有利于培养同学们良好的思维品质和习惯。
一、证明线段相等
例1. 如图1，在平行四边形ABCD中，E是CD中点，F是AE中点，FC与BE交于点G。
求证：GF＝GC
证明：连结DF，并延长交AB于H，在平行四边形ABCD中，AB∥CD，∵∠DFE＝∠HFA，AF＝FE，∠DEF＝∠FAH，∴△AFH≌△EFD（ASA）∴DE＝AH，∵HB∥DE，∴四边形DHBE为平行四边形，即EG∥DF，又E为CD中点，∴FG＝GC。
例2. 如图2，在△ABC中，AE、BD、CF为中线，FM∥BD，DM∥AB。
求证：MC∥AE
证明：连结AM、FD。
∵FM∥BD，DM∥AB，∴四边形FBDM为平行四边形
∴BF∥DM ∵AF＝BF ∴AF∥DM
∴四边形AFDM为平行四边形
∴AM∥FD
又∵F、D、E分别为AB、AC、BC边中点
∴FD∥EC
∴AM∥EC，
∴四边形AECM为平行四边形
∴MC∥AE。
三、证明线段的和差关系
例3. 如图3，梯形ABCD中，AB∥DC，∠A＋∠B＝90°，M、N分别为AB、DC的中点。
求证：).DC AB (2
1MN -= 证明：过N 分别作NE ∥AD ，NF ∥BC 交AB 于E 、F ，得平行四边形ADNE 和平行四边形NFBC ，∴DN ＝AE ，＝BF ，∠NFE ＝∠B ，∵DN ＝，∠A ＋∠B ＝90°，∴AE ＝BF ，∠NEF ＋∠NFE ＝90°∵AM ＝BM ，∴EM ＝FM ，∴在Rt △NEF 中，
21EF 21MN ==)DC AB (2
1)CN DN AB (21)BF AE AB (-=--=-- 想一想：本题还有别的证法吗？请与同伴交流。
四、求证面积
例4. 如图4，等腰梯形ABCD 中，AB ∥CD ，对角线AC ⊥BD ，DC ＝3cm ，AB ＝8cm 。
求梯形ABCD 的面积。
解：过C 作CF ⊥AB 于F ，作CE ∥BD 交AB 延长线于E ，得平行四边形DBEC ，∴BE ＝DC ，BD ∥CE 。
∵AC ⊥BD ，∴∠ACE ＝Rt ∠，AC ＝CE ，
∴△ACE 为等腰直角三角形。
AE ＝AB ＋BE ＝3＋8＝11cm 。
cm 211AE 21CF ==
， ∴2ABCD cm 4
1212111121CF )AB DC (21S =⨯⨯=⨯+=梯形
五、求线段比
例5. 如图5-1是用12个全等的等腰梯形镶嵌成的图形，这个图形中等腰梯形上底长与下底长之比是______________。
解：过点A 作AE ∥CD 交BC 于E 。
如图5-2，则AE ＝DC ，AD ＝EC ，∵AB ＝CD ，∴AB ＝AE ，易知∠B ＝60°。
∴△ABE 为等边三角形 ∴AB ＝BE ，再由图案可知：AD ＝
AB，则AD＝AB＝BE＝EC，∴AD：BC＝1：2。