离散系统差分方程计算
离散时间系统的数学模型—差分方程
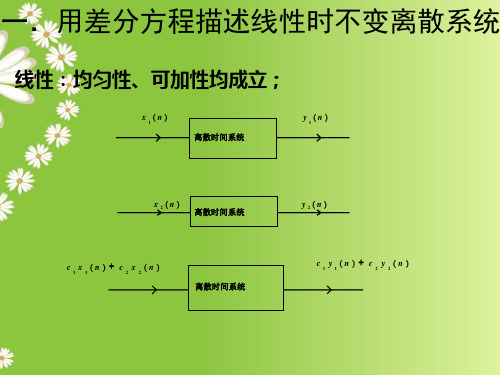
一.用差分方程描述线性时不变离散系统
线性:均匀性、可加性均成立;
x (n) 1
离散时间系统
y (n) 1
x 2 ( n ) 离散时间系统
c x (n ) + c x (n )
x1n+ x2n
x2 n
乘法器:
x1n x1n+ x2n
x2 n
x1 n
x1n x2 n
x2 n
系统框图
乘法器
xn
延时器
axn
a
yn
1
yn 1
E
xn a axn
yn
yn 1
z 1
五.差分方程的特点
(1)输出序列的第n个值不仅决定同一瞬间的输入样值, 而且还与前面输出值有关,每个输出值必须依次保留。
11
22
离散时间系统
y2 (n )
c y (n ) + c y (n )
11
22
时不变性
xn yn,xn N yn N 整个序列右移 N位
x(n)
y(n)
1 1 0 1 2 3 n
1
系统
1 o 1 2 3 4 n
x(n N )
y(n N )
1
1
系统
1 0 1 2 3
yt ynT yn
f t f nT f n
yn yn 1 ayn+ f n
T
yn 1 yn 1+ T f n
1 aT
1 aT
当前输出 前一个输出 输入
差分方程解法及其在离散系统中的应用

差分方程解法及其在离散系统中的应用差分方程是数学中一类重要的离散数学方程,广泛应用于动态系统建模和离散事件系统的分析。
本文将介绍差分方程的解法以及它在离散系统中的应用。
一、差分方程的定义和基本概念差分方程是一种以离散形式描述系统变化的数学方程。
其基本形式为:Δyₙ = f(n, yₙ₋₁)其中,Δyₙ为相邻两个时刻n和n-1之间y的变化量,f(n, yₙ₋₁)为给定时刻n和n-1之间的函数关系。
二、差分方程求解的方法对于简单的差分方程,可以直接通过迭代求解。
例如,对于一阶线性差分方程:Δyₙ = k其中,k为常数。
可以通过重复应用这一关系求解,即:yₙ = y₀ + kₙ其中,y₀为初始条件,kₙ为Δyₙ在不同时刻的取值。
对于更复杂的差分方程,可以采用数值方法求解,如欧拉法、龙格-库塔法等。
这些方法可以通过将差分方程转化为递推方程,并利用数值计算得到近似解。
三、离散系统中差分方程的应用1. 经济学中的应用差分方程可以用来描述经济系统中的离散变化。
例如,经济增长模型中的劳动力增长率、资本积累速度等,都可以通过差分方程来建模和分析。
2. 自然科学中的应用差分方程在物理学、生态学等自然科学领域中也有广泛的应用。
例如,天体运动、人口增长、物种竞争等系统的演化过程都可以用差分方程来描述和预测。
3. 计算机科学中的应用差分方程在计算机科学中的应用也是十分重要的。
例如,计算机网络中数据包的传输、媒体数据的压缩等问题,都可以通过差分方程来建模和解决。
四、差分方程解法的局限性和改进方法虽然差分方程是一种有效的数学工具,但其在一些特殊情况下存在局限性。
例如,对于非线性和高阶差分方程,常常难以求得解析解。
此时,可以利用数值方法进行近似求解,或者采用数值优化算法寻找最佳解。
总结:差分方程是一种重要的离散数学工具,广泛用于动态系统建模和离散事件系统的分析。
通过合适的差分方程求解方法,可以有效地描述和预测各种离散变化的系统。
差分方程及其Z变换法求解

= b0 r[(k + m)T ] + b1r[(k + m − 1)T ] + .......bm−1r[(k + 1)T ] + bm r (kT )
zX 1 ( z ) − zx1 (0) = X 2 ( z )
x2(kT)
z −1
x1(kT) z −1 x2(z) y[(k+1)T] KT
-
x1(0) 1 x1(z)
例2:画出例2所示离散系统的模拟图
y[(k + 1)T ] = -( KT -1) y (kT ) + KTr (kT ) r(kT)+ 1)T ] + ( KT -1) y (kT ) = KTr (kT ) y (k + 1) + ( K -1) y (k ) = Kr (k )
KT-1
三、差分方程的解
差分方程的求解:迭代法、z变换法。 迭代法:将原系统的差分方程化为如下形式:
y[(k + n)T ] = −a1 y[(k + n − 1)T ] − ...... − an −1 y[(k + 1)T ] − an y[kT ] + b0 r[( k + m)T ] + b1r[(k + m − 1)T ] + .......bm −1r[( k + 1)T ] + bm r (kT )
y (kT ) = 0.446 + 1.429(-0.4) k -1.875(-0.6) k
离散系统的差分方程

离散系统的差分方程
哎呀,各位看官,今儿咱来摆摆龙门阵,说说这离散系统的差分方程。
首先咱得搞明白,啥子是离散系统呢?简单说,就像咱们数豆子一样,一颗颗地数,这就是离散;不像流水那样连续不断,那就是连续系统了。
那差分方程又是啥玩意儿呢?说白了,它就是描述离散系统变化规律的数学式子。
就像咱陕西的秦腔一样,有板有眼,差分方程也是一步一步地揭示系统的行为。
咱们先来看看四川话咋个说。
就说这离散系统吧,它就像咱们四川的串串香,一颗颗的串串,就是离散的;而那热辣辣的辣椒油,就是差分方程,它决定了串串的味道变化,让咱们吃得津津有味。
再来说说陕西方言。
离散系统就像咱陕西的黄土高原,一颗颗的土粒儿就是离散的;而差分方程就像那沟沟壑壑,揭示了高原地貌的变化规律,让咱们感受到大自然的鬼斧神工。
最后说说北京话儿。
这离散系统啊,就像咱们老北京的糖葫芦,一颗颗的糖球儿,那就是离散;而差分方程就像那糖衣,它包裹着糖球儿,让糖葫芦甜而不腻,回味无穷。
总而言之,离散系统的差分方程就是用来描述离散系统如何一步步变化的。
它就像咱们各地的方言一样,各有特色,但都揭示了同一个道理。
咱们在日常生活中,也要学会用差分方程的眼光去看待问题,这样才能更好地把握事物的变化规律,做出正确的决策。
差分方程的解法

差分方程的解法1. 引言差分方程是描述离散系统的一种数学工具。
在许多科学领域和工程应用中,差分方程被广泛使用,例如物理学、经济学和计算机科学等。
对于一个给定的差分方程,寻找其解法是非常重要的,因为解法可以帮助我们理解系统的演化和预测其行为。
2. 常用的差分方程解法下面介绍几种常用的差分方程解法:2.1. 递推法递推法是差分方程解法中最常见和最简单的一种方法。
该方法基于差分方程的递推关系,通过迭代计算不同时间步长下的解,并逐步逼近真实解。
递推法适用于一些简单的线性差分方程,例如一阶和二阶差分方程等。
2.2. 特征方程法特征方程法主要用于解线性恒定系数差分方程。
通过将差分方程转化为代数方程,然后求解特征方程的根,可以得到差分方程的通解。
特征方程法适用于一些具有周期性和稳定性的差分方程。
2.3. 变换法变换法是一种将差分方程转化为其他类型方程然后求解的方法。
常见的变换方法有Z变换、拉普拉斯变换和离散傅里叶变换等。
通过变换法,我们可以将差分方程转化为易于求解的形式,从而得到解析解或近似解。
2.4. 迭代法迭代法是一种通过迭代计算逼近差分方程解的方法。
常见的迭代方法有欧拉法、龙格-库塔法和蒙特卡洛方法等。
迭代法适合于解决非线性、复杂或高阶的差分方程,并能够提供数值解。
3. 解法选择的依据在选择差分方程的解法时,我们需要根据差分方程的特性和给定问题的要求来确定一个最合适的解法。
以下是一些选择解法的依据:- 差分方程的类型和形式:不同类型和形式的差分方程可能适用于不同的解法。
- 解的精确性要求:如果需要求得解的精确值,可以选择特征方程法或变换法;如果只需要求得近似解,可以选择递推法或迭代法。
- 计算效率和速度要求:某些解法可能更加高效和快速,适合在大规模计算中使用。
- 可行性和实际性要求:选择对于给定问题实现可行并且实际可行的解法。
4. 结论差分方程的解法多种多样,每种解法都各具特点和适用范围。
在实际应用中,我们需要根据问题的要求和特点选择最合适的解法。
差分方程及其Z变换法求解

例1:右图所示的一阶系统描述它的微分方程为
y(t ) Ke(t ) K (r (t ) y(t ))
y(t ) Ky(t ) Kr (t )
用一阶前向差分方程近似:
(1)
r( t ) e( t ) -
K
1/s
y( t )
y (k 1)T y (kT ) dy y (t ) lim dt T 0 T
由图:x1 (k 1)T x2 (kT )
zX 1 ( z ) zx1 (0) X 2 ( z )
x2(kT)
z
1
x1(kT)
z 1
x1(0) 1
x1 ( z)
x2(z) y[(k+1)T]
例2:画出例2所示离散系统的模拟图
y[(k 1)T ] -( KT -1) y(kT ) + KTr (kT ) r(kT)
y (k 1)T y (kT ) T
(T 很小)
(2)
式中:T为采样周期,(2)代入(1)得:
y (k 1)T (KT 1) y(kT ) KTr(kT )
y(k 1) ( K 1) y(k ) Kr (k )
(3)
二、离散系统差分方程的模拟图
连续系统采用积分器s-1作为模拟连续系统微分方程的主要器件; 与此相对应,在离散系统中,采用单位延迟器z-1。 单位延迟器:把输入信号延迟一个采样周期T秒或延迟1拍。
再利用初始条件,逐次迭代得到各采样时刻的值。
特点:适用于计算机处理求解。 例3:用迭代法解二阶差分方程 y(k+2) +3y(k+1)+2y(k)=1(k)
利用初始条件 y(0)=0, y(1)=1,则有: y(k+2) =-3y(k+1) -2y(k)+1(k) y(2) =-3y(1) -2y(0)+1(0)= -3*1-2*0+1= -2
差分方程求解
差分方程求解什么是差分方程差分方程是离散时间系统模型中常用的数学工具之一。
它描述了在不同时间点上,系统状态之间的关系,其中系统状态是离散的。
差分方程在许多科学领域都有应用,如物理学、工程学和经济学等。
差分方程可以看作是微分方程在离散时间上的等效形式。
微分方程描述了连续时间系统的动态行为,而差分方程描述了离散时间系统的动态行为。
差分方程通常通过递推关系来表示系统状态之间的转移。
差分方程的一般形式差分方程的一般形式可以表示为:x[n+1] = f(x[n], x[n-1], ..., x[n-k])其中,x[n]表示系统在时间点n的状态,f表示系统状态之间的转移函数,k表示系统的阶数。
差分方程的求解方法1. 递推法递推法是一种直接求解差分方程的方法。
通过已知初始条件x[0], x[1], ..., x[k],可以逐步递推得到系统在任意时间点上的状态。
递推法的步骤如下:1.根据初始条件,求得x[k+1];2.迭代计算,依次求得x[k+2], x[k+3], ...。
递推法的优点是简单易用,并且不需要求解复杂的代数方程。
但它的缺点是只能求得系统的局部解,无法得到整个系统的行为。
2. 特征根法特征根法是一种求解差分方程的解析方法。
通过求解差分方程的特征方程,可以得到系统的特征根,进而得到系统的解析解。
特征根法的步骤如下:1.将差分方程转化为对应的特征方程;2.求解特征方程,得到系统的特征根;3.根据特征根的性质,推导得到系统的解析解。
特征根法的优点是能够得到系统的全局解,对于高阶差分方程尤为适用。
但它的缺点是求解过程较为繁琐,需要具备一定的数学知识。
差分方程的应用举例差分方程在许多科学领域都有广泛的应用。
以下是几个常见的应用举例:1. 自然科学中的应用在物理学和工程学等领域中,差分方程常用于描述动态系统的行为。
例如,可以用差分方程描述弹簧振子的运动过程、电路中电流的变化等。
2. 经济学中的应用在经济学中,差分方程常用于描述经济系统的演化过程。
1-3时域离散系统的差分方程描述
an , h(n) = 0,
n≥0 n<0
a <1 稳 系 是 定 统
求差分方程描述的系统的单位抽样响应——MATLAB 求差分方程描述的系统的单位抽样响应
2.2 时域离散系统 时域离散系统 的差分方程描述
线性常系数差分方程 差分方程与系统结构 差分方程的求解 差分方程描述的系统 的线性、 的线性、非时变性 求差分方程描述的系 统的单位抽样响应
x(n)
⊗ ⊕
b0
b0 x(n)
b0 x(n)-a1y(n-1)
y(n)
-a1y(n-1)
⊗
-a1
Z
−1
y(n-1)
求解差分方程——递推法 递推法 求解差分方程
2.2 时域离散系统 时域离散系统 的差分方程描述
线性常系数差分方程 差分方程与系统结构 差分方程的求解 差分方程描述的系统 的线性、 的线性、非时变性 求差分方程描述的系 统的单位抽样响应
求解差分方程y(n)=ay(n-1)+ x(n),y(-1)=1。 求解差分方程 , 。 MATLAB代码: 代码: 代码 a=0.8;ys=1 %设a=0.8 设 xn=[1,zeros(1,30)]; %设x(n)= δ(n),长度 长度N=31 设 长度 B=1;A=[1,-a]; xi=filtic(B,A,ys); yn=filter(B,A,xn,xi); n=0:length(yn)-1; subplot(3,2,1);stem(n,yn,’.’) title(‘(a)’);xlabel(‘n’);ylabel(‘y(n)’)
或者 ai y (n − i ) = ∑ bi x(n − i ), a0 = 1 ∑
i =0 i =0 N M
差分方程状态方程和输出方程
差分方程状态方程和输出方程差分方程是描述离散系统动态行为的数学工具。
它通过将连续时间转化为离散时间,将连续状态转化为离散状态,从而描述系统状态的演化规律。
差分方程的状态方程和输出方程是描述系统状态和输出之间关系的方程。
状态方程描述了系统状态的演化规律。
它包含了系统当前状态与过去状态之间的关系。
状态方程通常采用递推的方法,通过当前状态和输入来计算下一个时刻的状态。
例如,对于一个简单的差分方程状态方程:x(k+1) = A*x(k) + B*u(k)其中,x(k)表示系统在时刻k的状态,u(k)表示系统在时刻k的输入,A和B是状态方程的系数。
这个方程表示系统的下一个状态x(k+1)可以通过当前状态x(k)和输入u(k)以及系数A和B来计算得到。
状态方程可以用来预测系统的未来状态,从而实现对系统的控制。
输出方程描述了系统状态与输出之间的关系。
它将系统的状态映射到系统的输出。
输出方程通常采用线性组合的方式,将系统的状态加权求和得到系统的输出。
例如,对于一个简单的差分方程输出方程:y(k) = C*x(k) + D*u(k)其中,y(k)表示系统在时刻k的输出,C和D是输出方程的系数。
这个方程表示系统的输出y(k)可以通过当前状态x(k)和输入u(k)以及系数C和D来计算得到。
输出方程可以用来观测系统的状态,从而实现对系统的监测和诊断。
差分方程的状态方程和输出方程是描述离散系统的重要工具。
它们可以帮助我们理解系统的动态行为,预测系统的未来状态和输出,实现对系统的控制和监测。
在实际应用中,差分方程的状态方程和输出方程可以通过系统的建模和参数估计得到。
通过对系统的建模和参数估计,我们可以了解系统的结构和参数,从而更好地理解系统的行为并进行系统设计和优化。
差分方程的状态方程和输出方程是描述离散系统动态行为的重要工具。
它们通过描述系统状态和输出之间的关系,帮助我们理解系统的行为,并实现对系统的控制和监测。
差分方程的状态方程和输出方程在自动控制、信号处理、系统建模等领域有着广泛的应用。
差分方程的求解方法与应用
差分方程的求解方法与应用差分方程是一类描述离散系统动态演化的数学模型。
与微分方程相比,差分方程更适用于描述离散时间下的系统变化规律。
在物理、经济、生物等各个领域中,差分方程都有广泛的应用。
本文将介绍差分方程的求解方法以及其在实际问题中的应用。
一、差分方程的求解方法差分方程的求解方法主要有直接求解法和递推求解法两种。
直接求解法是通过将差分方程转化为代数方程组,然后求解方程组得到方程的解。
这种方法适用于一些简单的差分方程,例如线性差分方程。
例如,对于一阶线性差分方程y(n+1) = a*y(n) + b,我们可以通过代入法得到y(n) = (a^n)*y(0) +b*(a^n-1)/(a-1)。
递推求解法是通过递推关系式求解差分方程。
这种方法适用于一些递推性质较强的差分方程,例如递推差分方程。
例如,对于递推差分方程y(n+2) = y(n+1) +y(n),我们可以通过给定初始条件y(0)和y(1),然后利用递推关系式y(n+2) = y(n+1) + y(n)逐步求解出y(2)、y(3)、y(4)等。
二、差分方程的应用差分方程在实际问题中有着广泛的应用。
下面将介绍差分方程在物理、经济和生物领域中的一些应用。
1. 物理领域差分方程在物理领域中的应用非常广泛。
例如,对于自由落体运动,可以通过差分方程描述物体在不同时间点的位置和速度变化。
另外,差分方程还可以用于描述电路中电流和电压的变化规律,从而帮助工程师设计和优化电路。
2. 经济领域经济学中的一些经济模型可以通过差分方程进行建模和求解。
例如,经济增长模型可以用差分方程描述经济发展过程中的变化规律。
此外,差分方程还可以用于描述金融市场中的股票价格变化、货币供给和需求等问题。
3. 生物领域生物学中的一些生态模型和遗传模型可以通过差分方程进行建模。
例如,种群动力学模型可以用差分方程描述不同物种之间的相互作用和数量变化规律。
另外,差分方程还可以用于描述基因传递和突变的过程,从而帮助科学家研究生物遗传学问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.设离散控制系统差分方程为x采样周期T。
试求:(1)
系统的脉冲传递函数。
(2)系统的频率特性表达式。
解:差分方程两边取Z变换,得
脉冲传递函数
频率特性
2.假设离散系统差分方程为。
其中;
,,,。
试求:(1)分析系统的稳定性。
(2),,。
解:(1)对差分方程两边取Z变换,得
特征方程:
解得:;
由于,即系统稳定。
(2)n=0时,
n=1时,
n=2时,
3.某离散控制系统的差分方程为,其中:
,,,,,,。
试求:(1),。
(2)分析稳定性。
解:(1)对差分方程两边Z变换,得
特征方程:
解得:;
由于,所以系统稳定。
(2)n=0时,
n=1时。
4.离散控制系统的差分方程为:,其中
,,时,时。
试求:(1),,。
(2)脉冲传递函数。
解:(1)差分方程两边取Z变换,得
特征方程:
解得:;
由于,所以系统稳定。
(2)n=0时,
n=1时,
n=2时,
5.已知:离散控制系统的差分方程为。
试求:脉冲传
递函数。
系统频率特性
解:对差分方程Z变换,得
频率特性
6.某离散系统的差分方程为=,其中
,。
试求(1)脉冲传递函数,并分析稳定。
(2)
,,。
解:对差分方程两边Z变换,得
()
特征方程:
解得:;
由于,所以系统稳定。
(2)n=0时,
n=1时,
n=2时,y
7.已知离散系统的差分方程为,试求:(1)脉冲传递
函数。
(2)分析系统稳定性
解:(1)对差分方程两边Z变换,得
(2)特征方程:=0
解得:;
由于,所以系统临界稳定。
8.离散系统差分方程为,其中
,;。
试求:,,。
()分析稳定性。
解:(1)n=0时,
n=1时,
n=2时,
(2)对差分方程两边Z变换,得
特征方程:
解得:;
由于,所以系统稳定。
9.某离散系统差分方程为,其中:,
时,;时,。
试求:,,。
(2)分析
稳定性。
解:(1)n=0时,
n=1时,
n=2时,
(2)对差分方程两边Z变换,得
特征方程:
解得:;
由于,所以系统稳定
10.已知离散控制系统的差分方程为,试求:脉冲函数。
解:对差分方程两边Z变换,得。
