柱坐标系和球坐标系下的计算法
三重积分在柱面及球坐标系下的计算
= ∫ dθ ∫
0
2π
R
0
1 2 1 4 2 ( R − ρ ) ρdρ = πR . 2 4
思考： 思考：是否可考虑用切片法来求解？
例2 计算三重积分I = ∫∫∫ ( x + y )dv,
2 2 (V )
z
其中(V )由z = x 2 + y 2 , z = h所围.
解 (V )在xoy面投影域(σ )为圆 : 0 ≤ ρ ≤ h , xy
π
4
θ
y
,0 ≤ ρ ≤ R.
x
∴ I = ∫ dθ
0
2π
∫
π /4
0
dϕ
∫
R
0
ρ 2 ⋅ ρ 2sinϕ dρ
2− 2 5 = πR . 5
练习 试用三种坐标系分别计算三重积分
z
2
σz
I = ∫∫∫ zdv, 其中(V ) : x 2 + y 2 + z 2 ≤ 2 z.
(V )
解法1 解法 直角坐标系(切片法)
1
= 2π ∫ ρ ⋅ 2 1 − ρ 2 dρ
1
4π = . 3
0
解法3 解法 球面坐标系计算
∫∫∫ zdv
(V )
z
2
x2 + y2 + z2 = 2z
球面为 : ρ = 2 cos ϕ , 其中
0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
ϕ
o
π
2
,0 ≤ ρ ≤ 2 cos ϕ .
θ
ρ cos ϕ ⋅ ρ 2 sin ϕdρ
z
• •
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.
柱面坐标系和球面坐标系求三重积分
z x2 y2所围 .
分析 (V )为由半球面与锥面所围,
故可用球面坐标,
y
此 ,0 时 2 ,0 ,0R . x
4
2
I d
/4
d
R22sind
0
0
0
2 2 R5.
5
练习 试用三种坐标系算 分三 别重 计积分
I zdv,其中(V): x2 y2 z2 2z. (V)
解法1 直角坐标(切 系片法 )
x
则 (V )f(c o,s si,n z)d d dz ,
]d d
[ z2(,)f(co ,ssin,z)dz
( ) z1(,)
例1 计算三重积I分 (Vz)dv,
其中(V)由z R2 x2 y2与 z 0所围.
解 (V )向 xo 面 y 投 (x)y 为 影 :0 圆 R , 02 x
I d d
zdz
0
0 1 1 2
x
2012 12d
4 . 3
•1
xy
解法3 球面坐标系计算zdv (V) x2y2z22z
z
2
球面 : 为 2co,s其中
02 ,0,02co .s
2
o
y
I 2d /2d 2coscos2sxind
0
0
0
2/24co5ssind 4 .
0
3
z
h•
此,时 2zh.
I [ h 2dz ]dd ( xy ) 2
•
o•
x
y
( xy )
2d h(3h5)d
0
0
1 h3.
6
思考：本题是否也可考虑用切片法来求解？
4-2-2 球面坐标系下三重积分的计算
柱坐标系和球坐标系
上一页
返回首页
下一页
图 1-5-2
如图 1-5-2 所示，设 z 轴的正向与向量O→M的夹角为 φ，x 轴的正向与O→M0的 夹角为 θ，M 点到原点 O 的距离为 r，则由三个数 r，θ，φ 构成的有序数组 (r，θ，φ)称为空间中点 M 的球坐标.若设投影点 M0 在 xOy 平面上的极坐标为(ρ， θ)，则极坐标 θ 就是上述的第二个球坐标 θ.在球坐标中限定 r≥0,0≤θ<2π， 0≤φ≤π.
则有11＝ ＝ρρcsions
θ， θ，
z＝1，
解之得，ρ＝ 2，θ＝π4.
因此，点 M 的柱坐标为( 2，π4，1).
上一页
返回首页
下一页
由直角坐标系中的直角坐标求柱坐标，可以先设出点 M 的柱坐标为ρ，θ，
z代入变换公式xy＝ ＝ρρcsions
θ， θ，
z＝z.
求 ρ；也可以利用 ρ2＝x2＋y2，求 ρ.利用 tan θ＝yx，
∵(r，θ，φ)＝(3，53π，56π)，
x＝rsin φcos θ＝3sin56πcos53π＝34，
y＝rsin φsin θ＝3sin56πsin53π＝－343，
z＝rcos
φ＝3cos56π＝－3
2
3 .
∴点
M
的直角坐标为(34，－3
4
3，－3
2
3 ).
上一页
返回首页
下一页
类型三 空间点的直角坐标化为球坐标 已知长方体 ABCD－A1B1C1D1 中，底面正方形 ABCD 的边长为 1，
下一页
[质疑·手记] 预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流： 疑问 1： _____________________________________________________ 解惑： _______________________________________________________ 疑问 2： _____________________________________________________ 解惑： _______________________________________________________ 疑问 3： ______________________________________________________ 解惑： _______________________________________________________
圆柱,圆球坐标系
1 ∂ 1 ∂Fφ ∂Fz ∇ ⋅ F (ρ ,φ ,z) = (ρ Fρ ) + + ρ ∂ρ ρ ∂φ ∂z
1
ρ
eρ
eφ ∂ ∂φ ρ Fφ
1
ρ
ez
∇ × F (ρ ,φ ,z )
=
∂ ∂ρ Fρ
∂ ∂z Fz
1.8 圆柱坐标系与球坐标系
CQU
1.8.2 球面坐标系 坐标变量
r ,θ , φ
坐标单位矢量 er , eθ , eφ 位置矢量 线元矢量 面元矢量
= 0, ∂ρ ∂e z = 0, ∂ρ
= −eρ , ∂φ ∂e z = 0, ∂φ
1.8 圆柱坐标系与球坐标系
CQU
圆柱坐标系中的三度表达式
∇ = eρ
∇f =
∂ 1 ∂ ∂ + eφ + ez ∂ρ ρ ∂φ ∂z
∂f 1 ∂f ∂f eρ + eφ + ez ∂ρ ρ ∂φ ∂z
(ρ ≠ 0)
e ρ = cos φ e x + sin φ e y eφ = −sin φ e x + cosφ e y
∂e ρ ∂ρ ∂eφ = 0, ∂e ρ ∂φ ∂eϕ = eφ , =0 ∂z ∂eφ = 0 ∂z ∂e z =0 ∂z ∂e ρ
eρ、eφ、ez对坐标ρ、φ、z求偏导 求偏导
1.8 圆柱坐标系与球坐标系
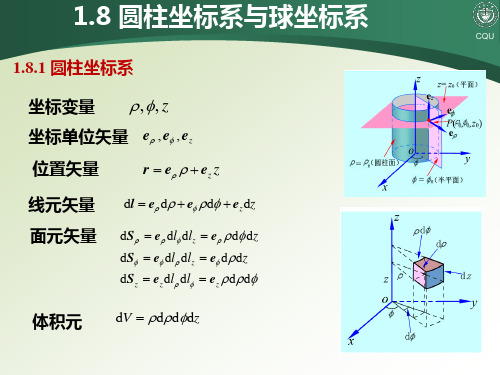
1.8.1 圆柱坐标系 坐标变量
1
CQU
ρ ,φ , z
r = eρ ρ + ez z
dl = eρ dρ + eφ ρ dφ + e z dz
坐标单位矢量 eρ , eφ , e z 位置矢量 线元矢量 面元矢量
三重积分的计算方法
三重积分的计算方法三重积分是在三维空间中对一些实数函数进行积分的计算方法。
它是二重积分的推广，用于求解更复杂的三维问题。
三重积分的计算方法有多种，包括直接计算、柱坐标法、球坐标法和证明法等。
直接计算是最基本的三重积分计算方法。
它将三维空间划分成许多小的立方体或长方体，然后对每个小的体积元素进行积分。
具体步骤如下：1.将被积函数表示为三个独立变量的函数，例如f(x,y,z)。
2.选择一个合适的坐标系，将空间划分成小的体积元素。
通常可以选择笛卡尔坐标系。
3.将整个积分区域划分成小的体积元素，每个体积元素由三个坐标轴上的小区间组合而成。
4.对每个体积元素，计算被积函数在该体积元素上的积分，并将所有体积元素上的积分值加起来。
直接计算方法的优点是直观易懂，适用于简单的积分问题。
但对于复杂的积分区域和被积函数，可能会导致计算量大、步骤繁琐的问题。
柱坐标法是一种使用柱坐标系进行积分计算的方法。
它适用于具有旋转对称性的问题，例如旋转体的体积计算。
柱坐标法的具体步骤如下：1.将被积函数表示为柱坐标系下的函数，即f(ρ,θ,z)。
2.选择合适的积分区域，并确定要积分的极坐标范围。
3. 将柱坐标系下的积分元素表示为dV=ρ dρ dθ dz。
4.将被积函数表示为柱坐标系下的函数，并进行对应的积分计算。
柱坐标法通过利用旋转对称性简化了积分计算，适用于旋转体的体积、质心等相关问题。
球坐标法是一种使用球坐标系进行积分计算的方法。
它适用于具有球对称性的问题，例如球体的体积计算。
球坐标法的具体步骤如下：1.将被积函数表示为球坐标系下的函数，即f(r,θ,φ)。
2.选择合适的积分区域，并确定要积分的球坐标范围。
3. 将球坐标系下的积分元素表示为dV=r^2sinφdr dθ dφ。
4.将被积函数表示为球坐标系下的函数，并进行对应的积分计算。
球坐标法通过利用球对称性简化了积分计算，适用于球体的体积、质心等相关问题。
除了上述方法外，还有一种称作证明法的三重积分计算方法。
在柱坐标系和球坐标系下哈密顿算子的形式
F ( x, y , z ) 1 r sin F F F ex ey ez x y z
F F F 2 sin cos cos sin r sin cos sin cos er cos cos e sin e r
由（1‐12）可以得到：
F 1 F F cos sin x F F F 1 sin cos （1‐13） y F F z z
接下来我们将求在球坐标系下，空间某点 F ( x, y, z ) 分别对 r , , 求偏导数：
F F x F y F z r x r y r z r F F x F y F z （2‐13） x y z F F x F y F z x y z
因为这个矢量为单位矢量，且指向 方向，其向量一定为 e ，即：
e sin ex cos ey 0 ez （2‐10）
因为， 我们得到： e e er ， e cos sin ex cos sin ey sin ez （2‐11） 联立式（2‐6） 、 （2‐10）和（2‐11）我们可以得到：
ex sin cos er cos cos e sin e e y sin sin er cos sin e cos e （2‐12） ez cos er sin e
柱坐标和球坐标系下拉普拉斯算符表达式的简单推导
柱坐标和球坐标系下拉普拉斯算符表达式的简单推导[摘 要]：本文采用多元微积分，利用球坐标与柱坐标、柱坐标与直角坐标变量转换的相同关系，以拉普拉斯算符为例，简化了在柱坐标和球坐标系下拉普拉斯算符表达式的推导。
本文提出了此法在柱坐标和球坐标系下梯度、旋度、散度算符表达式的推导中的适用性，适合广大非数学专业本科生学习与掌握。
[关键词]：拉普拉斯算符；球坐标；柱坐标；多元微积分[中图分类号]：O13 [文献标识码]：A [文章编号]: 1672-1452(2015)**-****-041 引 言在材料科学基础、近代物理、量子力学等课程的内容中，菲克第二定律和薛定谔方程中的拉普拉斯算符在柱坐标系和球坐标系中的表达式十分重要。
在近代物理的课本[1]和材料科学基础的课本[2]上，提到了拉普拉斯算符在柱坐标和球坐标系下的表达式，但没有给出具体的推导过程。
在电动力学课本[3]中,这方面的内容是通过引入“正交曲线坐标系”得出关于拉普拉斯算符的一般结论，再推导出球坐标和柱坐标下的表达式。
但是利用正交曲线坐标系的一般结论进行推导比较抽象，对于非数学专业的同学来说，理解一般性的结论需要较高的数学水平。
现有的文献[4][5]中，有采用多元复合函数微商法则完成推导的，虽然此法在对学生的微积分要求较低，但是所给出的证明计算繁琐，无助于学生直接理解公式的正确性和自主完成推导。
本文给出了用多元微积分导出拉普拉斯算符在柱面坐标系和球面坐标系中表达式的简单方法。
此法仅要求学生掌握基本的多元微积分知识，计算过程简洁美观，便于广大的非数学系专业的学生掌握和理解。
建议在近代物理、量子力学、材料科学基础等课程教材和教学中应用。
2 柱坐标和球坐标下拉普拉斯算符的推导2.1 柱坐标系下的拉普拉斯算符表达式的推导首先，直角坐标系的分量()z y x ,,与柱坐标系的分量()z ,,ϕρ有如下的转换关系：222y x +=ρ（1） x =ϕρcos （2） y =ϕρsin（3） z z =（4）（1）式两端分别对x 和y 求偏导，得ϕρρcos ==∂∂xx（5）ϕρρsin ==∂∂yy（6）（2）两端对x 求偏导，并将（5）式代入，得1sin cos =∂∂-∂∂xx ϕϕρϕρρϕϕsin -=∂∂x（7）同理可知， ρϕϕcos =∂∂y（8）假设所研究的函数为),,(z y x f f =由于z 关于x ，y 是独立的变量，故ρϕϕϕρϕϕρρsin cos ∂∂-∂∂=∂∂∂∂+∂∂∂∂=∂∂f f x f x f x f （9）同理 ρϕϕϕρϕϕρρcos sin ∂∂+∂∂=∂∂∂∂+∂∂∂∂=∂∂f f y f y f y f（10）利用公式（5）（7）（9），对f 求x 的二次偏导2222222222222222222cos sin 2sin sin cos sin 2cos sin cos sin cos sin cos sin sin cos ρϕϕϕρϕρρϕϕρϕϕϕρϕρρϕρϕϕρϕϕϕϕρϕρϕρϕϕρϕϕρϕρϕϕρρ∂∂+∂∂+∂∂+∂∂∂-∂∂=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛∂∂-∂∂-∂∂∂+∂∂-+⎪⎪⎭⎫⎝⎛∂∂+∂∂∂-∂∂=⎪⎭⎫⎝⎛∂∂∂∂∂∂+⎪⎭⎫ ⎝⎛∂∂∂∂∂∂=∂∂f f f f f f f f f f f f x f x x f x xf （11）类似地，计算f 关于y 的二阶偏导数。
(简)3-5利用柱面坐标和球面坐标计算三重积分
0 ≤ r ≤ a,
0 ≤ θ ≤ 2π ,
2π a a
I = ∫∫∫ ( x + y )dxdydz = ∫ dθ ∫ rdr ∫ r 2dz
Ω
0
0
r
a4 a5 π 5 3 = 2π ∫ r (a − r )dr = 2π[a ⋅ − ] = a . 0 10 4 5
a
例 4 求曲面x2 + y2 + z2 ≤ 2a2 与z ≥ x2 + y2 所围 成的立体体积.
解 积分域关于三个坐标面都对称， 积分域关于三个坐标面都对称， 奇函数, 被积函数是 z 的奇函数
z ln( x 2 + y 2 + z 2 + 1) ∫∫∫ x 2 + y 2 + z 2 + 1 dxdydz = 0. Ω
例6
计算 ∫∫∫ ( x + y + z ) dxdydz 其中Ω 是由抛物
2
2
面 z = x + y 和球面 x + y + z = 2 所围成的空 间闭区域.
2 2 2
Ω 2
解
Q ( x + y + z)
2 2 2
2
= x + y + z + 2( xy + yz + zx )
的奇函数, 其中 xy + yz 是关于 y 的奇函数
面对称, 且 Ω 关于 zox 面对称 ∴
所围成的立体如图， 所围成的立体如图，
所围成立体的投影区域如图， 所围成立体的投影区域如图，
D1 : x 2 + y 2 = 16,
0 ≤ θ ≤ 2 π 0 ≤ r ≤ 4 , Ω1 : 2 r ≤ z ≤ 8 2
柱面坐标和球面坐标计算定积分
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
三个有次序的数r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按
逆时针方向转到有向线段 OP 的角，这里 P 为
点 M 在 xoy 面上的投影，这样的三个数 r，， 就叫做点 M 的球面坐标．
规定： 0 r , 0 , 0 2.
y
r
sin
sin
,
z r cos .
如图，
z
球面坐标系中的体积元素为
dv r2 sindrdd ,
f ( x, y, z)dxdydz
dr
d r sin
r
o
d
x
r sind rd
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz，其中 是锥面
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
I2 rdrd r2 fdz
D2
2
利用柱面坐标计算三重积分
z
j r
zdv
dvΒιβλιοθήκη zdvO
dv
a 2 0 2
．
q
x
a y
dv 2 dj dq
2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分
，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz
2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2
3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z
柱坐标系和球坐标系下的计算法
za
x y
2
2
a r , cos 2 z , 4
a : 0 r , 0 , 0 2 , cos 4
I ( x y )dxdydz d d
2 2
2
5 5 1 a 3 2 sin ( 5 0)d a . 10 5 cos 解二 用柱坐标
2 2
将 投到xoy 面得D
x y 1
1
0 2 ,0 r 1, r z 1
(x
2
y z )dv d dr ( r z )rdz
2 2 2 2 0 0 r
2
1
r 4 4 3 2 ( r r )dr 3 3 10 0
_______________________；其值为__________.
二、计算下列三重积分: 2 2 2 2 2 4 z ( x y ) dv 25 ( x y ) 1、 , 其中 是由曲面 及平面z 5 所围成的闭区域.
2、 ( x 2 y 2 )dv ,其中 由不等式
4 5 a a 5 3 2 r (a r )dr 2[a ] a . 0 4 5 10
a
例 4 求曲面 x 2 y 2 z 2 2a 2 与 z 所围 成的立体体积.
x2 y2
解 由锥面和球面围成，
采用球面坐标，
由x
2
y 2 z 2 2a 2 r 2a,
六、求半径为a ,高为h 的均匀圆柱体对于过中心而垂 直于母线的轴的转动惯量 (设密度 1) .
练习题答案
柱坐标和球坐标公式
柱坐标和球坐标公式
在数学和物理学中，柱坐标和球坐标是表示空间中点的两种常用坐标系。
这两种坐标系是笛卡尔坐标系的重要扩展，能够更好地描述三维空间中的点的位置。
柱坐标
柱坐标是三维空间中的一种坐标系，通常用来描述点相对于原点的位置。
在柱坐标系中，一个点的位置由径向(r)、极角(θ)和高度(z)三个坐标值来确定。
柱坐标系和笛卡尔坐标系之间的转换关系如下： - x = r * cos(θ) - y = r * sin(θ) - z = z
其中，r表示点到z轴的距离，θ表示点在xy平面内的极角，z表示点在z轴上的高度。
球坐标
球坐标是另一种常用的三维空间坐标系，用来描述点相对于原点的位置。
球坐标系由径向(r)、极角(θ)和方位角(φ)三个坐标值来确定一个点的位置。
球坐标系和笛卡尔坐标系之间的转换关系如下： - x = r * sin(θ) * cos(φ) - y = r * sin(θ) * sin(φ) - z = r * cos(θ)
其中，r表示点到原点的距离，θ表示点到正z轴的倾角，φ表示点在xy平面上的旋转角度。
柱坐标和球坐标的应用
柱坐标和球坐标在物理学、工程学和计算机图形学等领域有着广泛的应用。
例如，在物理学中，利用柱坐标和球坐标可以更方便地描述和计算力、电场等的分布情况；在工程学中，柱坐标和球坐标可以简化对结构的分析和设计；在计算机图形学中，通过柱坐标和球坐标可以更加自然地进行三维建模和渲染。
总的来说，柱坐标和球坐标是解决三维空间中点位置描述问题的有力工具，它们为研究人员和工程师提供了更多的选择和便利。
通过深入理解柱坐标和球坐标的原理和转换关系，可以更好地应用它们解决实际问题。
5三重积分计算柱面球面坐标系下-DrHuang
第7章 多元函数积分学
7.1 重积分
7.1.3 三重积分的计算(柱面和球面坐标系)
中南大学开放式精品示范课堂高等数学建设组
7.1 重积分
7.1.3 三重积分的计算 (柱面和球面坐标系)
柱
导学及问题讨论
面
柱面坐标介绍
球 面
柱面坐标下计算三重积分 柱面坐标下的三次积分
坐
习例1-4
标 系
计算步骤及适用范围
0
0
1r2
e r2 z2 dz
r2 z2
计算较繁琐甚至无法计算,怎么办？
人们确定航天器某一时刻的具体位置，
是根据某一时刻航天器到地球表面的距离,以
及航天器所处位置的经度 和纬度 ，从而
用有序数组(,， ) 表示航天器的具体位 置那么,如何建立坐标系才能方便得出
，， 的值,从而确定它的位置呢？
)
2d .
f (x, y, z)dxdydz
f ( sin cos, sin sin, cos) 2 sinddd.
y
r
sin
z z
r x2 y2
tan
y x
z z
由定义可知点M的柱面坐标r, , z 的取值范围分别是
r ： 0 r , : 0 2, z : z .
z
三坐标面分别为
r 为常数
为常数
z 为常数
{( x, y, z) | x2 y2 z 1, x2 y2 1}
{(r, , z) | r z 2,0 r 2,0 2 }
{(r, , z) | r z 1,0 r 1,0 2 }
《流体力学》(柱坐标系和求坐标系下)连续方程推导的巧方法
《流体力学》连续方程推导的巧方法施春华,高庆九,李忠贤(南京信息工程大学大气科学学院,江苏南京 210044)摘要:针对柱坐标系和球坐标系下《流体力学》中连续方程形式复杂、理解不便的特点,采用欧拉控制体方法,把“质量通量”整体作为一物理量,从而巧妙地推导了这两类连续方程,该过程物理意义明确、数学算法简单,有助于学生理解。
关键词:连续方程;柱坐标系;球坐标系在大学《流体力学》教学中,连续方程是最基本的内容之一,在很多相关专业课程中得到广泛应用。
相对而言,在直角坐标系中的连续方程形式简单,也易于理解,但在柱坐标系和球坐标系中,连续方程的形式却相对复杂,理解相对困难。
目前,很多参考书[123]对于后两类连续方程要么没有给出具体推导,要么推导过程较为复杂,使数理基础较薄弱的学生难以理解,在此,笔者结合教学中的实际经验,演示柱坐标系和球坐标系下一种物理意义明确、数学理解简单的连续方程的推导过程。
1 连续方程的一般算子形式流体运动的连续方程,是表示流体运动和其质量分布的关系式。
在拉格朗日方法中,某流体块在运动时其体积和形状尽管可发生变化,但它始终由这些流点构成,因此它的质量不变。
由此可见,连续方程实质上是质量守恒定律在“连续介质”(流体)中的应用。
一般的拉格朗日方法考虑,某个别流体微团(质量体)在运动过程中,其随体密度的变化,必然与其体积变化趋势相反,如体积膨胀,它的密度减小,体积收缩,则密度增大。
其算子形式的通用表达式[1](1)一般的欧拉方法考虑,对于某固定位置的空间单位体积元(控制体)来说,该体积元内单位时间的质量变化,与该体积元边界上的质量通量变化相联系,如质量往外流,它的密度减小,反之则增大。
其算子形式的通用表达式[1](2)两种方法的区别:拉格朗日方法多从物理量的定义出发,模型简单容易理解,但数学解析在实际应用中有些困难;欧拉方法则通过适当的数学建模后,能在数学上给出方便的解析,有利于从数学角度更好地理解概念。
球坐标与柱坐标转换
球坐标与柱坐标转换在数学和物理学中，我们经常会遇到需要进行不同坐标系之间的转换的情况。
其中，球坐标系和柱坐标系是两个常用的坐标系，它们有着各自特定的表达形式和应用场景。
在本文中，我们将探讨球坐标系与柱坐标系之间的转换关系和方法。
球坐标系与柱坐标系的定义首先，让我们简单回顾一下球坐标系和柱坐标系的定义。
•球坐标系：在三维空间中，球坐标系由一个原点O、一个距离原点的长度r和两个角度θ和φ来描述一个点P的位置。
其中，r是点P到原点O的距离，θ是点P与正向x轴的夹角（通常0到π），φ是点P投影在xy 平面上与正向x轴的夹角（通常0到2π）。
•柱坐标系：柱坐标系也是三维空间中的一种坐标系，由一个原点O、一个距离原点的长度ρ和两个角度θ和z来描述点P的位置。
其中，ρ是点P 在xy平面上的投影与原点O的距离，θ是点P与正向x轴的夹角（通常0到2π），z是点P在z轴上的高度。
球坐标系到柱坐标系的转换公式现在，我们来探讨如何将一个点的球坐标表示转换为柱坐标表示。
设一个点在球坐标系下的坐标为(r, θ, φ)，我们希望求得该点在柱坐标系下的坐标(ρ, θ, z)。
转换公式如下：•ρ = r sin(φ)•z = r cos(φ)柱坐标系到球坐标系的转换公式同样地，我们也可以探讨将柱坐标系下的坐标(ρ, θ, z)转换为球坐标系下的坐标(r, θ, φ)。
转换公式如下：•r = √(ρ^2 + z^2)•φ = arctan(ρ/z)示例应用以上介绍的球坐标系与柱坐标系的转换公式，在各种工程、科学和数学领域中都有着广泛的应用。
以航空航天领域为例，当我们需要计算飞行器在不同坐标系下的位置时，就会用到这些转换公式来方便地进行坐标变换。
总结起来，球坐标系与柱坐标系之间的转换为我们提供了一种便利的方法，在不同坐标系下描述和计算空间中的物理量。
通过掌握这些转换关系和方法，我们可以更灵活地处理复杂的空间问题，为科学研究和工程实践提供有力支持。
柱坐标与球坐标系
(2)3，56π，53π.
解 ∵(r，φ，θ)＝3，56π，53π，
x＝rsin φcos θ＝3sin
5π 6 cos
53π＝34，
∴y＝rsin φsin θ＝3sin
5π 6 sin
53π＝－3 4 3，
z＝rcos φ＝3cos
56π＝－3
3 2.
∴34，－3
4
3，－3
2
3为所求.
解答
解 由变换公式y＝ρsin θ，
z＝z， 得 x＝4cos π3＝2，y＝4sin π3＝2 3，z＝8. ∴点 P 的直角坐标为感悟
(1)由直角坐标系中的直角坐标求柱坐标，可以先设出点M的柱坐标为 x＝ρcos θ，
(ρ，θ，z)，代入变换公式 y＝ρsin θ，求ρ；也可以利用ρ2＝x2＋y2，求ρ.
答案
梳理
柱坐标系的概念 (1)定义：建立空间直角坐标系Oxyz，设P是空间任意一 点，它在平面Oxy上的射影为Q，用(ρ，θ)(ρ≥0, 0≤θ<2π)表示点Q在平面Oxy上的极坐标.这时点P的位 置可用有序数组 (ρ，θ，z) (z∈R)表示，这样，我们建 立了空间的点与有序数组(ρ，θ，z)之间的一种
z＝z， 利用tan θ＝ y ，求θ，在求θ的时候特别注意角θ所在的象限，从而确定θ
x 的取值.
(2)点的柱坐标和直角坐标的竖坐标相同.
跟踪训练1 (1)已知点M的直角坐标为(0,1,2)，求它的柱坐标； 解 ρ＝ x2＋y2＝ 02＋12＝1. ∵x＝0，y>0，∴θ＝π2. ∴点 M 的柱坐标为(1，π2，2).
2.柱坐标系又称半极坐标系，它是由平面极坐标系及空间直角坐标系中 的一部分建立起来的，空间任一点P的位置可以用有序数组(ρ，θ，z)表 示，(ρ，θ)是点P在Oxy平面上的射影Q的极坐标，z是P在空间直角坐标 系中的竖坐标.
将直角坐标系中的矢量用圆柱和圆球坐标系
将直角坐标系中的矢量用圆柱和圆球坐标系引言在物理和数学领域中，我们经常使用直角坐标系（笛卡尔坐标系）来描述矢量的位置和方向。
然而，在某些情况下，直角坐标系并不是最方便的选择。
为了更好地描述某些问题，我们可以使用其他坐标系，例如圆柱坐标系和球坐标系。
本文将介绍如何将直角坐标系中的矢量用圆柱和圆球坐标系表示。
圆柱坐标系圆柱坐标系是一种二维坐标系，其中一个坐标表示从原点到点的距离，另一个坐标表示与正 x 轴的夹角。
我们可以通过以下公式将直角坐标系中的矢量转换为圆柱坐标系：x = r * cos(theta)y = r * sin(theta)z = z其中，r 是点到原点的距离，theta 是点与正 x 轴的夹角，z 是点在 z 轴上的坐标。
这里的 r 和 theta 均为极坐标，可以通过勾股定理和反三角函数计算出来。
圆球坐标系圆球坐标系是一种三维坐标系，其中一个坐标表示点到原点的距离，另两个坐标表示与正 x 轴和正 z 轴的夹角。
我们可以通过以下公式将直角坐标系中的矢量转换为圆球坐标系：x = r * sin(theta) * cos(phi)y = r * sin(theta) * sin(phi)z = r * cos(theta)其中，r 是点到原点的距离，theta 是点与正 z 轴的夹角，phi 是点在 x-y 平面上与正 x 轴的夹角。
这里的 r、theta 和 phi 均为极坐标，可以通过勾股定理和反三角函数计算出来。
从圆柱坐标系到直角坐标系如果我们已知一个矢量在圆柱坐标系中的表示，我们可以使用以下公式将其转换为直角坐标系：x = r * cos(theta)y = r * sin(theta)z = z其中，r 是点到原点的距离，theta 是点与正 x 轴的夹角，z 是点在 z 轴上的坐标。
通过使用这些公式，我们可以将圆柱坐标系中的矢量转换为直角坐标系。
从圆球坐标系到直角坐标系类似地，如果我们已知一个矢量在圆球坐标系中的表示，我们可以使用以下公式将其转换为直角坐标系：x = r * sin(theta) * cos(phi)y = r * sin(theta) * sin(phi)z = r * cos(theta)其中，r 是点到原点的距离，theta 是点与正 z 轴的夹角，phi 是点在 x-y 平面上与正 x 轴的夹角。
柱坐标转换为球坐标公式
柱坐标转换为球坐标公式柱坐标和球坐标是空间中常用的坐标系之一，它们之间的转换关系可以通过一些简单的公式来表示。
在物理学、数学和工程领域中，经常会遇到需要将柱坐标转换为球坐标的情况。
本文将介绍如何将柱坐标 $(r, \\theta, z)$ 转换为球坐标 $(r', \\theta', \\phi)$ 的公式推导过程。
柱坐标到球坐标的转换首先，我们需要明确柱坐标和球坐标的定义： - 柱坐标 $(r, \\theta, z)$ 中，r 代表点到z轴的距离，$\\theta$ 表示x轴正半轴到点与x轴的夹角，z表示点在z 轴上的高度。
- 球坐标 $(r', \\theta', \\phi)$ 中，r′代表点到原点的距离，$\\theta'$ 表示x轴正半轴到点与x轴的夹角，$\\phi$ 表示点到z轴的夹角。
根据这些定义，可以得到柱坐标到球坐标的转换公式如下：$$ \\begin{align*} r' &= \\sqrt{r^2 + z^2} \\\\ \\theta' &= \\theta \\\\ \\phi &= \\arctan\\left(\\frac{r}{z}\\right) \\end{align*} $$其中，$\\arctan$ 是反正切函数，可以用来求出夹角的大小。
公式推导过程以上公式的推导过程如下：1.首先，根据三角函数的关系，可以得到球坐标到柱坐标的水平距离r和垂直高度z如下：$$ \\begin{align*} r &= r' \\sin\\phi \\\\ z &= r' \\cos\\phi \\end{align*} $$2.将 $r = r' \\sin\\phi$ 代入 $z = r' \\cos\\phi$ 中，可以得到：$$ z = r' \\cos\\left(\\arctan\\frac{r}{z}\\right) $$3.化简上式，可以得到：$$ z = \\frac{r}{\\sqrt{r^2 + z^2}} \\quad \\Rightarrow \\quad r' = \\sqrt{r^2 + z^2} $$4.同样地，根据 $z = r' \\cos\\phi$，可以得到：$$ \\begin{align*} z &= r' \\cos(\\phi) \\\\ z &= r'\\cos\\left(\\arctan\\frac{r}{z}\\right) \\\\ z &= r' \\frac{z}{r'} \\\\ z &= z\\end{align*} $$5.因此，根据 $r = r' \\sin\\phi$，可以得到 $\\phi =\\arctan\\left(\\frac{r}{z}\\right)$。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
z
M ( x, y, z )
0 r ,
0 2,
x
o
r
P(r , )
y
z .
z
r 为常数
圆柱面 半平面 平 面
为常数
z 为常数
z
rd
M ( x, y, z )
z
如图，柱面坐标系中的体积元
o
r
P(r , )
y
dv rdrddz,
4 5 a a 5 3 2 r (a r )dr 2[a ] a . 0 4 5 10
a
例 4 求曲面 x 2 y 2 z 2 2a 2 与 z 所围 成的立体体积.
x2 y2
解 由锥面和球面围成，
采用球面坐标，
由x
2
y 2 z 2 2a 2 r 2a,
dx
2
4 x 2
4 x 2
dy
3( x 2 y 2 )
16 x 2 y 2
0 d0 rdr 3r 2 2 3r d rdr 0 0 16 r
2
2
16 r 2
f ( r cos , r sin , z )dz
③ 若 关于 yoz 面对称
2
(1) 当 f ( x , y, z ) f ( x , y, z ) 时 I 0 ( 2) 当 f ( x , y , z ) f ( x , y , z ) 时
I 2 f ( x , y , z )dv
3
3 ( x , y, z ) | ( x , y, z ) , x 0
f ( r cos , r sin , z )dz ,
2
0
2
d d f ( r sin cos ,
0
6 0
4
r sin sin , r cos )r 2 sin dr
4 0
d 5 d f ( r sin cos ,
0
4 0
a cos 0
r sin dr
4 3
4 0
x y z z r,
2 2 2
D: x y a ,
2 2 2
: r z a,
2 2
0 r a,
0
0 2 ,
2 a a 0 r
I ( x y )dxdydz d rdr r 2dz
注
若 积分区域为球体、球壳或其一部分
被积函数呈 通常采用球坐标。
x y z
2 2
2
而用球坐标后积分区域的球坐标方程比较简单
补充：利用对称性简化三重积分计算
使用对称性时应注意： １、积分区域关于坐标面的对称性；
２、被积函数在积分区域上的关于三个坐标轴的 奇偶性．
一般地，当积分区域 关于 xoy 平面对称，且 被积函数 f ( x , y , z ) 是关于 z 的奇函数，则三重积分 为零，若被积函数 f ( x , y , z ) 是关于 z 的偶函数，则 三重积分为 在 xoy 平面上方的半个闭区域的三重 积分的两倍.
_______________________；其值为__________.
二、计算下列三重积分: 2 2 2 2 2 4 z ( x y ) dv 25 ( x y ) 1、 , 其中 是由曲面 及平面z 5 所围成的闭区域.
2、 ( x 2 y 2 )dv ,其中 由不等式
dz
x
dr
r
f ( x , y, z )dxdydz
y
o
x
d
f (r cos , r sin , z )rdrddz.
然后再把它化为三次积分来计算
积分次序一般是先 z 次 r 后 积分限是根据 r , , z 在积分区域中的变化范围来确定 例1 解
2 2 2 ( x y z )dv , : z
x y
2 2
z
, 4
: 0 r 2a ,
0 , 4
0 2 ,
由三重积分的性质知 V
dxdydz ,
V d d
0 0
2
4
2a
0
r 2 sin dr
3
2
4 0
4 ( 2a ) sin d ( 2 1)a 3 . 3 3
为常数
为常数
z
如图，球面坐标系中的体积元素为d
r sin
dr
r sin d rd d
dv r sindrdd ,
2
r
f ( x , y, z )dxdydz
o
y
d
2 f ( r sin cos , r sin sin , r cos ) r sindrdd .
3
1
注
若空间区域为以坐标轴为轴的圆柱体、 圆锥体或旋转体时，通常情况下总是考 虑使用柱坐标来计算。
例2
ez 2 2 dxdydz, : z x y , z 1, z 2 2 2 x y
解
x r cos y r sin , zz
关键在于定出 的变化范围
练习题
一、填空题: 1 、若 由曲面 z 2 3( x 2 y 2 )和 x 2 y 2 z 2 16 所 围, 则三重积分 f ( x , y , z )dv 表示成直角坐标下
的三次积分是_________________;在柱面坐标下 的三次积分是_________________;在球面坐标下 的三次积分是__________________. 2 2 2 2 z 2 x y 及 z x y 2 、若 由 曲 面 所 围, 将 zdv 表为柱面坐标下的三次积分_________,
在柱坐标系和球坐标系下的计算
一、在柱坐标系下的计算法
设 M ( x , y , z ) 为空间内一点，并设点M 在 xoy 面上的投影 P 的极坐标为 r ,，则这样的三 个数 r , , z 就叫点 M 的柱面坐标．
x r cos , y r sin , z z.
x
然后把它化成对 r , , 的三次积分
具体计算时需要将 用球坐标系下的不等式组表示 积分次序通常是
先r次后
例 3 计算 I ( x 2 y 2 )dxdydz ，其中 是锥面
x 2 y 2 z 2 ， 与平面 z a
解一 用球坐标
(a 0) 所围的立体.
2 (e e ) 2 (e e )dr 2e
2 2 r 1
2
2
二、在球坐标系下的计算法
设 M ( x , y , z ) 为空间内一点，则点M 可用 三个有次序的数 r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按 逆时针方向转到有向线 段 OP 的角，这里 P 为 点 M 在 xoy 面上的投影，这样的三 个数 r，，
za
x y
2
2
a r , cos 2 z , 4
a : 0 r , 0 , 0 2 , cos 4
I ( x y )dxdydz d d
2 2
2
5 5 1 a 3 2 sin ( 5 0)d a . 10 5 cos 解二 用柱坐标
就叫做点 M 的球面坐标．
x r sin cos , y r sin sin , z r cos .
规定
z
x
r
M ( x, y, z )
z
0 r ,
o
A
0 , 0 2.
r 为常数
x
y
P
y
球 面 圆锥面 半平面
(1) f ( x , y , z ) f ( x , y , z ) 时 I 0 ( 2) 当 f ( x , y , z ) f ( x , y , z ) 时
1
I 2 f ( x , y , z )dv
2 ( x , y, z ) | ( x , y, z , y 0)
其值为_______.
3、若空间区域 为二曲面x 2 y 2 az 及 z 2a x 2 y 2 所围, 则其体积可表为三重积分 _______________; 或 二 重 积 分 ______________; 或柱面坐标下的三次积分___________________. 4 、 若 由 不 等 式 x 2 y 2 (z a)2 a 2 , x 2 y 2 z 2 所确定, 将 zdv 表为球面坐标下的三次积分为
六、求半径为a ,高为h 的均匀圆柱体对于过中心而垂 直于母线的轴的转动惯量 (设密度 1) .
练习题答案
一、1 、 dx
2 2 4 x 2 4 x 2 2
dy
16 x 2 y 2 3( x 2 y 2 )
f ( x , y , z )dz f ( x , y , z )dz ,
当f ( x , y, z )关于 ____为奇函数时, f ( x, y, z )dv 0;
z
当f ( x , y , z )关于 ____为偶函数时,
z