高等代数期中模拟题三
高等代数专题研究模拟试题及答案(05春)

高等代数专题研究试题模拟试题(05春)一、单项选择题(每小题3分,本题共15分)1.如果函数f (x )满足条件:对任意x 1与x 2,有)()()(22112211x f q x f q x q x q f +≥+其中( ),则称f (x )是上凸函数.(A) 0,021≥≥q q (B) 021≥⋅q q 且121=+q q(C) ,0,021≥≥q q 且121=⋅q q (D) 0,021≠≠q q 且121=+q q2. 下列环中是非交换环的为( )(A) 整数环Z (B) 剩余类环Z 5(C) n 阶方阵环 (D) 高斯整数环Z [i ]={a +bi ∣a ,b 为整数}3. 剩余类环Z 8的一个真零因子是( ). (A) 3 (B)7 (C) 5 (D) 24. 一副扑克牌有红桃、黑桃、方片和梅花各13张,共52张.从中任取一张,则不同取法有( )种.(A) 52 (B)4 (C) 134 (D) 4135. 将r 个不可区分的小球投入n 个盒子,每一个盒子的容量不超过一个球(n ≥r ),若计算有多少种不同投球方式,应该用( ).(A) 允许重复组合数公式 (B) 不重复组合数公式(C) 允许重复排列数公式 (D) 不重复排列数公式二、填空题(每小题3分,本题共15分)6. 设a 1,a 2,…,a 5是正实数,可构造两组正实数列和 .用柯西不等式,证明25)1...11)(...(521521≥++++++a a a a a a . 7. 若(a ,b )~1,那么(a ,a +b )~ .8. 在有无穷多个元素的域上,设多项式f (x )=a n x n +a n -1x n -1+…+a 0和g (x )=b n x n +b n -1x n-1+…+b 0 ,从代数学的观点,如果 ,则称f (x )=g (x ).9. π是有理数域上的超越元,是因为π不是 多项式的根.10. 计算31019710098100)(P C C += .三、简述题(每小题5分,共10分)11. 试列出三种证明不等式常用的方法.12. 找出整数环Z中的可逆元素,并说明为什么是可逆元素.四、计算题(每小题10,本题共40分)13. 设集合A={ ,a,{a},b},求P(A).14. 设x,y,z为非负实数,且满足x+2y+5z=6求f(x,y,z)=xyz的极大值.15. 求f (x )=2322123+--x x x 的重因式.16. 试求多项式(x 1+x 2+x 3+x 4+x 5)10展开合并同类项后的项数以及2543231x x x x 的系数.四、证明题(每小题10分,本题共20分)17. 设R 是实数集,+R 是正实数集,任给+R 的元素x ,令映射 σ(x )=x lg证明σ是+R 到R 的双射.18. 证明恒等式11--=k n k n nC kC .高等代数专题研究模拟试题(05春) 参考答案一、单项选择题(每小题3分,本题共15分) 1. B .2. C .3. D .4. A .5. B . 二、填空题(每小题3分,本题共15分)6. 521,...,,a a a ,5211,...,1,1a a a . 7. 1. 8. a k =b k (k =0,1,2,…,n ).9. 任何有理系数. 10. 61. 三、简述题(每小题5分,共10分)11.列出三种或三种以上的方法,可得满分5分.参考方法列举:(1)欲证A >B ,可证A -B >0;(2) 当A >0,B >0时,欲证A >B ,可证1>BA ; (3) 欲证A >B ,可证A >C ,C >B ;(4) 欲证A >B ,可将A -B 化为(A -B )2;等.12. 在整数环Z 中,只有1和-1是可逆元素.1是恒等元.因为1和-1都不是零元,但(-1)×(-1)=1,1×1=1,根据可逆的定义知道,它们是可逆元素. (5分)四、计算题(每小题10,本题共40分)13. 由幂集合的定义,P (A)={∅,{∅},{a },{{a }},{b }, (2分){∅,a },{∅,{a }},{∅,b },{a ,{a }},{a ,b },{{a },b } (6分){∅,a ,{a }},{∅,a ,b },{∅,{a },b },{a ,{a },b } (9分){∅,a ,{a },b }} (10分)14. 利用均值不等式x +2y +5z ≥333103523xyz z y x =⋅⋅ (3分)54102761027)52(33=⨯=⨯++≤z y x xyz (9分) 当x =2y =5z 时,得x =2,y =1,z =52时,xyz 的极大值是54. (10分) 15. 只要求出f (x )与f '(x )的公因式即可.(1分)23)(2--='x x x f)1(625)61)((296233)(323---'=+--=x x x f x x x x f (4分) 而 )1)(23(23)(2-+=--='x x x x x f ,有 (f (x ),f '(x ))~(x -1) (8分)所以x -1是f (x )的二重因式. (10分)16. 所求项数为1001!411121314414101510=⨯⨯⨯==-+C C (5分) 2543231x x x x 的系数为12600!2!0!4!1!3!10= (10分)四、证明题(每小题10分,本题共20分)17. 由对数函数的定义域和函数值,知σ(x )=x lg 是+R 到R 的映射.(2分)(1) 任给+R 的两个元素x 1,x 2且x 1≠x 2,由对数函数的严格单调性,有)(lg lg )(2211x x x x σσ=≠= 这表明σ(x )=x lg 是单射. (6分)(2) 任给R 的元素y ,则存在y x 10=属于+R ,则有 σ(x )=y x y ==10lg lg这表明σ(x )=x lg 是满射. (9分)总之,σ是+R 到R 的双射. (10分) 18. )!(!!k n k n k kC kn -⋅⋅= (4分) =))!1(1()!1()!1(----⋅-⋅⋅k n k k n n k (7分) =11))!1()1(()!1()!1(--=-----k n nC k n k n n . (10分)。
2020-2021高中必修三数学上期中模拟试卷附答案(3)

2020-2021高中必修三数学上期中模拟试卷附答案(3)一、选择题1.为研究某种细菌在特定环境下,随时间变化的繁殖情况,得到如下实验数据:由最小二乘法得y 与x 的线性回归方程为ˆˆ0.7yx a =+,则当7x =时,繁殖个数y 的预测值为( ) A .4.9 B .5.25 C .5.95D .6.152.一组数据如下表所示:已知变量y 关于x 的回归方程为+0.5ˆbx ye =,若5x =,则预测y 的值可能为( ) A .5eB .112eC .132eD .7e3.甲、乙两名射击运动员分别进行了5次射击训练,成绩(单位:环)如下: 甲:7,8,8,8,9 乙:6,6,7,7,10;若甲、乙两名运动员的平均成绩分别用12,x x 表示,方差分别为2212,S S 表示,则( )A .221212,x x s s >> B .221212,x x s s >< C .221212,x x s s << D .221212,x x s s <> 4.某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 . 若样本中的青年职工为7人,则样本容量为 A .7B .15C .25D .355.微信中有个“微信运动”,记录一天行走的步数,小王的“微信步数排行榜”里有120个人,今天,他发现步数最少的有0.85万步,最多的有1.79万步.于是,他做了个统计,作出下表,请问这天大家平均走了多少万步?( )A.1.19B.1.23C.1.26D.1.316.远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,如图所示的是一位母亲记录的孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满七进一,根据图示可知,孩子已经出生的天数是()A.336B.510C.1326D.36037.执行如图所示的程序框图,则输出的结果是()A.5B.7C.9D.118.若框图所给的程序运行结果为,那么判断框中应填入的关于k的条件是A.?B.?C.?D.?9.将三枚质地均匀的骰子各掷一次,设事件A=“三个点数之和等于15”,B=“至少出现一个5点”,则概率()|P A B 等于( ) A .5108B .113C .17D .71010.将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m ,第二次出现的点数为n ,向量p u v =(m ,n),q v =(3,6).则向量p u v 与q v共线的概率为( )A .13B .14C .16D .11211.我国古代名著《庄子g 天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是( )A .17?,,+1i s s i i i≤=-= B .1128?,,2i s s i i i≤=-= C .17?,,+12i s s i i i ≤=-= D .1128?,,22i s s i i i≤=-= 12.将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样方法抽取一个容量为50的样本,且随机抽得的号码为003.这600名学生分住在三个营区,从001到200住在第一营区,从201到500住在第二营区,从501到600住在第三营区,三个营区被抽中的人数依次为( ). A .16,26,8B .17,24,9C .16,25,9D .17,25,8二、填空题13.下列说法正确的个数有_________(1)已知变量x 和y 满足关系23y x =-+,则x 与y 正相关;(2)线性回归直线必过点(),x y ;(3)对于分类变量A 与B 的随机变量2k ,2k 越大说明“A 与B 有关系”的可信度越大(4)在刻画回归模型的拟合效果时,残差平方和越小,相关指数2R的值越大,说明拟合的效果越好.x的平均数为90,则该组数据的方差为______.14.已知一组数据:87,,90,89,9315.执行如图所示的框图,输出值______.16.某班按座位将学生分为两组,第一组18人,第二组27人,现采用分层抽样的方法抽取5人,再从这5人中安排两人去打扫卫生,则这两人来自同一组的概率为__________.17.某班全体学生参加英语成绩的频率分布直方图如图,若低于60分的人数是15,则该班的学生人数是__________.18.若按右上图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是__________。
高代期中考试题库及答案

高代期中考试题库及答案一、选择题(每题5分,共20分)1. 设矩阵 \(A\) 为 \(3 \times 3\) 矩阵,且 \(\text{rank}(A) = 2\),则矩阵 \(A\) 的秩是:A. 1B. 2C. 3D. 无法确定答案:B2. 以下哪个选项不是线性代数中的基本概念?A. 向量空间B. 线性映射C. 矩阵D. 微分方程答案:D3. 设 \(\alpha\) 和 \(\beta\) 是两个向量,若 \(\alpha \cdot \beta = 0\),则 \(\alpha\) 和 \(\beta\):A. 正交B. 平行C. 垂直D. 斜交答案:A4. 如果一个矩阵 \(A\) 可以表示为 \(A = PDP^{-1}\),其中 \(P\) 是可逆矩阵,\(D\) 是对角矩阵,则矩阵 \(A\):A. 可对角化B. 正交C. 正定D. 单位答案:A二、填空题(每题3分,共15分)1. 设 \(A\) 是一个 \(n \times n\) 矩阵,若 \(A^2 = A\),则称\(A\) 为幂等矩阵。
若 \(A\) 是幂等矩阵,则 \(A\) 的特征值为______。
答案:0或12. 矩阵 \(A\) 的行列式表示为 \(\text{det}(A)\),若\(\text{det}(A) = 0\),则矩阵 \(A\) 的秩小于______。
答案:n3. 设 \(\lambda\) 是矩阵 \(A\) 的一个特征值,对应的特征向量为\(v\),则 \(A\) 与 \(\lambda\) 乘以单位矩阵 \(I\) 的差 \(A - \lambda I\) 的秩为______。
答案:04. 线性方程组 \(Ax = 0\) 的基础解系由 \(A\) 的零空间的一组基构成,若 \(A\) 是一个 \(3 \times 3\) 矩阵且 \(\text{rank}(A) = 2\),则 \(Ax = 0\) 的基础解系包含______个向量。
高等代数模拟试题

高等代数模拟试题一 选择题(每小题2分,共16分)1 哪个向量组是线性相关的? (A) P[x]中, 1 , 2n, ,,x x x .(B) 2 2P ⨯中, 任意5个矩阵A ,B ,C ,D ,E(C) 在次数≤2的全体多项式以及零多项式所成线性空间3[]P x 中, 1 , 22 1 , 1 x x +-.(D) 3P 中, 123(1,0,0), (1,1,0), (1,1,1)ααα===2在数域P 上 ,下列集合关于通常的加法和数乘是线性空间的有( ) (1) {}(, 0 , ,0 , ),V a b a b P =∈ . (2) {}1212(, , ,)0n V a a a a a =+= (3) {} ()0n nV A Ptr A ⨯=∈=(4) {}()[] (0)0V f x P x f =∈=(A) 1个 (B) 2个 (C) 3个 (D) 4个3下述结论错误的是(A) [,]a b V C = 是实数域上的无限维线性空间. (B) {} n nV A P A A ⨯'=∈=是P 上(1)2n n +维线性空间. (C) {} n nV A P A A ⨯'=∈=-是P 上(1)2n n -维线性空间.(D) ,a b V a b P b a ⎧⎫⎛⎫=∈⎨⎬⎪⎝⎭⎩⎭是P 上4维线性空间. 4.设V =3R ,123123(,,),(,,)x x x y y y αβ==,二元实函数是(,)'A αβαβ=,其中(A)101010100A ⎛⎫ ⎪= ⎪ ⎪⎝⎭, (B) 101010102A ⎛⎫ ⎪= ⎪ ⎪⎝⎭ ,(C)101000100A ⎛⎫ ⎪= ⎪ ⎪⎝⎭, (D) 111110101A -⎛⎫ ⎪= ⎪ ⎪⎝⎭第1页选取上述那个矩阵A 能使V 成为欧氏空间。
5 设A , B ,C 都是n×n 矩阵,且0C ≠,那么(1) CAC ~ A 2C (2) 22~ CB B C (3) ~ CAB ABC (4) ~ CA AC (A) (1) , (2) , (3) , (4) 都正确 (B) (1) , (4) 正确 (C) (1) , (2) , (3) 正确 (D) 都不正确6 下列结论错误的是(A) 如果n 阶复数矩阵A 的最小多项式无重根,那么A 相似于一个对角矩阵 (B) 如果n 阶矩阵A 有n 个线性无关的特征向量,那么A 相似于对角矩阵 (C) 如果n 阶矩阵A 相似于一个对角矩阵,那么A 有n 个不同的特征值 (D) 相似矩阵有相同的特征值 7 能与对角矩阵相似的矩阵是(1) 实对称矩阵 (2) 满足220A A E --= (3) 幂等矩阵 (4) 102003a b c ⎛⎫ ⎪ ⎪ ⎪⎝⎭(A) (1) , (2) , (3) (B) (1) , (2) , (3) ,(4)(C) (1) , (3) , (4) (D) (1), (2) 8 如果四个线性变换1234A A A A ,,,在标准正交基下的矩阵分别是(A)100010001⎛⎫ ⎪- ⎪ ⎪-⎝⎭ (B)011011100⎛⎫⎪- ⎪ ⎪⎝⎭(C)00100⎛⎫⎪⎪⎪-⎝⎭(D) 1000cos sin 0sin cos θθθθ⎛⎫⎪- ⎪ ⎪⎝⎭那么( )不是正交变换。
2020-2021高中必修三数学上期中模拟试题附答案(3)
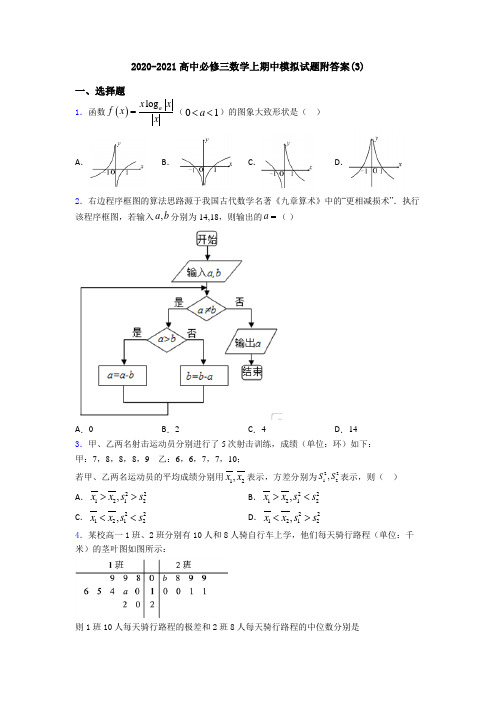
2020-2021高中必修三数学上期中模拟试题附答案(3)一、选择题1.函数()log a x x f x x=(01a <<)的图象大致形状是( )A .B .C .D .2.右边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入,a b 分别为14,18,则输出的a =( )A .0B .2C .4D .143.甲、乙两名射击运动员分别进行了5次射击训练,成绩(单位:环)如下: 甲:7,8,8,8,9 乙:6,6,7,7,10;若甲、乙两名运动员的平均成绩分别用12,x x 表示,方差分别为2212,S S 表示,则( )A .221212,x x s s >> B .221212,x x s s >< C .221212,x x s s << D .221212,x x s s <> 4.某校高一1班、2班分别有10人和8人骑自行车上学,他们每天骑行路程(单位:千米)的茎叶图如图所示:则1班10人每天骑行路程的极差和2班8人每天骑行路程的中位数分别是A .14,9.5B .9,9C .9,10D .14,95.我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目:“一百馒头一百僧,大僧三个更无争.小僧三人分一个,大小和尚各几丁?”.如右图所示的程序框图反映了对此问题的一个求解算法,则输出n 的值为 ( )A .20B .25C .30D .356.已知0,0,2,a b a b >>+=则14y a b=+的最小值是 ( ) A .72B .4C .92D .57.远古时期,人们通过在绳子上打结来记录数量,即“结绳计数”,如图所示的是一位母亲记录的孩子自出生后的天数,在从右向左依次排列的不同绳子上打结,满七进一,根据图示可知,孩子已经出生的天数是( )A .336B .510C .1326D .36038.下列命题:①对立事件一定是互斥事件;②若A ,B 为两个随机事件,则P(A∪B)=P(A)+P(B);③若事件A ,B ,C 彼此互斥,则P(A)+P(B)+P(C)=1;④若事件A ,B 满足P(A)+P(B)=1,则A 与B 是对立事件. 其中正确命题的个数是( )A.1B.2C.3D.49.从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为()A.110B.35C.310D.2510.下列说法正确的是()A.若残差平方和越小,则相关指数2R越小B.将一组数据中每一个数据都加上或减去同一常数,方差不变C.若2K的观测值越大,则判断两个分类变量有关系的把握程度越小D.若所有样本点均落在回归直线上,则相关系数1r11.若同时掷两枚骰子,则向上的点数和是6的概率为()A.16B.112C.536D.51812.某程序框图如图所示,该程序运行后输出的k的值是()A.4B.5C.6D.7二、填空题13.如图所示,在边长为1的正方形OABC中任取一点M.则点M恰好取自阴影部分的概率是.14.某校高一年级有600个学生,高二年级有550个学生,高三年级有650个学生,为调查学生的视力情况,用分层抽样的方法抽取一个样本,若在高二、高三共抽取了48个学生,则应在高一年级抽取学生______个15.如图程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”.执行该程序框图,若输入的a,b分别为98、63,则输出的a=_______.16.甲乙两人一起去游“西安世园会”,他们约定,各自独立地从1到6号景点中任选4个进行游览,每个景点参观1小时,则最后一小时他们同在一个景点的概率是________.17.执行如图所示的流程图,则输出的的值为.18.如左下图是一次数学考试成绩的样本频率分布直方图(样本容量n=200),若成绩不低于60分为及格,则样本中的及格人数是_________。
z34高等代数模拟试卷

05级(06-07学年第一学期)高等代数(二)bB 卷一、选择题(每题3分共30分) 1.以下集合是R n 的子空间的有( )A .(){}1,0,,0,R ,1,n i x x x i n ∈=B .()121,,,0,Z,1,2,,nn i i i x x x x x i n =⎧⎫=∈=⎨⎬⎩⎭∑C .()121,,,1,R ,1,2,,nn i i i xx x x x i n =⎧⎫=∈=⎨⎬⎩⎭∑D .(){}12,,,R ,1,2,,n i x x x x i n ∈=2.方阵A 有n 个不同的特征值是A 可对角化的( )A .必要条件B .充分条件C .充分必要条件D .无关条件 3.n 维线性空间V 的零变换0的像及核的维数分别是( ) A .,0n B .0,n C .,n n D .0,04.线性空间3R 的线性变换,στ定义为()()12312231,,,,x x x x x x x x σ=--,()()12321,,,0,x x x x x τ=,且()31,0,1R α=∈,则()στα+=( )A .()2,0,0B .()2,0,1C .()1,0,0D .()1,0,1 5. [],C a b 的子空间()sin ,sin 2,sin 3L x x x 的维数是( ) A .1 B .2 C .3 D .4 6. 已知线性空间3R 的线性变换()()()12112,,x x x xx σ=+,则()()212,x x σ=( )A .()()()221212,2x x x x +- B .()22221212,4xx x x ++C . ()112,2x x x +D .()121232,43x x x x ++ 7. 设a b A c d ⎛⎫=⎪⎝⎭,()A f λ是A 的特征多项式,则()A f λ的表达式为( ) A .()2T r A A λλ-+ B .()2T r A A λλ++ C .()2Tr A A λλ-- D .()2T r A A λλ+-8. 以下定义的f 是线性空间F n 上的双线性函数的是( )A .()12,3f X X x x =B .()12,n f X X x x x =+++C . ()22212,n f X X x x x =+++ D . (){},,F 0f X X a a =∈-9.设f 为n 元二次型,则( )A .f 正定当且仅当它的正惯性指数等于秩B .f 负定当且仅当它的负惯性指数等于nC .f 正定当且仅当它的正惯性指数等于nD .f 负定当且仅当它的正惯性指数等于0 10.设111111111A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,400B ⎛⎫⎪=⎪ ⎪⎝⎭,那么( ) A.矩阵A 与矩阵B 相似 B. 矩阵A 与矩阵B 合同 C. 矩阵A 与矩阵B 相抵D.矩阵A 与矩阵B 合同但是不相似E. 矩阵A 与矩阵B 相似但是不合同F. 矩阵A 与矩阵B 相似而且合同二、(10分)求整数x 使得()()()1mod 43mod 72mod 15x x x ≡≡-≡.三、(10分)考察自然数列{}n a ,其中011a a ==,当2n ≥时122n n n a a a --=+,请借助线性代数知识,求2007a .四、(10分)设A 为线性空间V 上的线性变换,12,ξξ分别是属于A 的不同特征值12,λλ的特征向量,求证:1.12,ξξ线性无关;2.12ξξ-不是A 的特征向量.五、(10分)设[]3R x 表示实数域上次数不大于3的多项式全体构成的集合,定义()()()11,f g f t g t d t -=⎰,证明(),f g 是[]3R x 内的内积. 六、(10分)考察3K 中的线性变换σ,设123,,εεε为基本单位坐标向量组,且()()()()()()1231,1,0,2,1,1,0,1,1σεσεσε=-==--,向量组()11,1,1η=,()21,1,0η=,()31,0,0η=为3K 的另一组基,求σ在基123,,ηηη下的矩阵.七、(10分)求下列多项式的最大公因式()()(),f x g x ,并求多项式()(),u x v x 使得()()()()()()(),u x f x v x g x f x gx +=,其中()432242fx x x x x =+---,()43222f x x x x x =+---.八、(10分)用直角坐标变换化简下列二次曲面方程,并判断二次曲面的类型:2224410x y xy yz +--+=.。
2020-2021高中必修三数学上期中模拟试卷附答案(4)
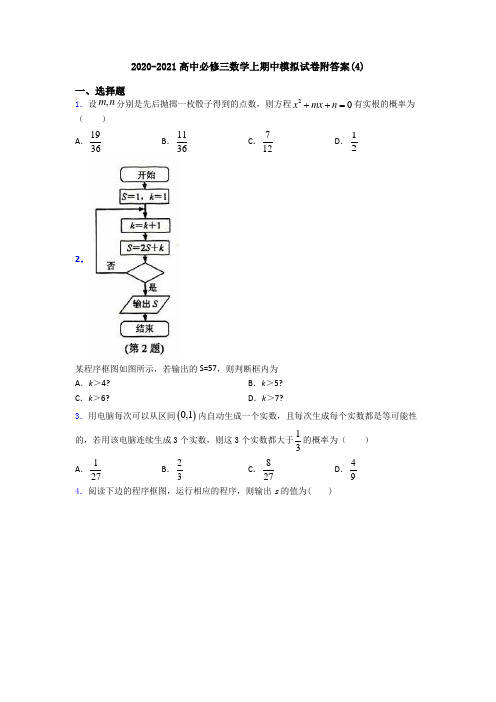
2020-2021高中必修三数学上期中模拟试卷附答案(4)一、选择题1.设,m n 分别是先后抛掷一枚骰子得到的点数,则方程20x mx n ++=有实根的概率为( ) A .1936B .1136C .712D .122.某程序框图如图所示,若输出的S=57,则判断框内为 A .k >4? B .k >5? C .k >6?D .k >7?3.用电脑每次可以从区间()0,1内自动生成一个实数,且每次生成每个实数都是等可能性的,若用该电脑连续生成3个实数,则这3个实数都大于13的概率为( ) A .127B .23C .827 D .494.阅读下边的程序框图,运行相应的程序,则输出s 的值为( )A .1B .0C .1D .35.抛掷一枚质地均匀的骰子,记事件A 为“向上的点数是偶数”,事件B 为“向上的点数不超过3”,则概率()P A B =U ( ) A .12B .13C .23D .566.执行如图所示的程序框图,则输出的n 值是( )A .5B .7C .9D .117.将20名学生任意分成甲、乙两组,每组10人,其中2名学生干部恰好被分在不同组内的概率为( )A .192181020C C C B .1921810202C C C C .1921910202C C C D .192191020C C C 8.为计算11111123499100S =-+-++-…,设计了下面的程序框图,则在空白框中应填入A .1i i =+B .2i i =+C .3i i =+D .4i i =+9.已知0,0,2,a b a b >>+=则14y a b=+的最小值是 ( ) A .72B .4C .92D .510.将一颗骰子掷两次,观察出现的点数,并记第一次出现的点数为m ,第二次出现的点数为n ,向量p u v =(m ,n),q v =(3,6).则向量p u v 与q v共线的概率为( )A .13B .14C .16D .11211.在学校组织的考试中,45名学生的数学成绩的茎叶图如图所示,则该45名学生的数学成绩的中位数为( )A .127B .128C .128.5D .12912.某次测试成绩满分是为150分,设n 名学生的得分分别为()12,,,1n i a a a a N i n ∈≤≤L ,()1150k b k ≤≤为n 名学生中得分至少为k 分的人数.记M 为n 名学生的平均成绩,则( ) A .12150b b b M n ++=LB .12150150b b b M ++=LC .12150b b b M n++>LD .12150150b b b M ++>L二、填空题13.集合{|64,1,2,3,4,5,6}A y y n n ==-=,集合1{|2,1,2,3,4,5,6}n B y y n -===,若任意A∪B 中的元素a ,则a ∈A∩B 的概率是________。
(完整word版)高等代数期中考试题答案

高等代数期中考试题答案一、填空题(每小题3分,共15分)1、___1___,__1/a__2、______3_.3、若4、 (n+1)类5、___n-r__二、1 D 2、 C 3、( D )4、( B )5、 A三、1、解:(1)由于A ),,(),,(321321αααβββ=,其中⎪⎪⎪⎭⎫ ⎝⎛---=101110111A于是 1321321),,(),,(-=A βββααα………………………… (2分) 故由基321,,βββ到基321,,ααα的过渡矩阵为⎪⎪⎪⎭⎫ ⎝⎛--==-1111010111A C ………………………… (3分)(2)⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=241),,(321),,(321),,(321321321ββββββααααC即向量3α在基321,,βββ下的坐标为)2,4,1('.………………………… (5分) 2、故该向量组的一个极大线性无关组为124,,ααα。
3、所以解空间的维数是2, 它的一组基为⎪⎭⎫ ⎝⎛-=0,1,38,911a ,⎪⎭⎫ ⎝⎛-=1,0,37,922a 四、 证明题(本题共4个小题,每小题10分,共计40分) 1、证:因为复数域C 作为实数域R 上的向量空间,维数是2; 而2dim 2=R ,两者维数相同,所以同构。
另证:建立映射),(;:2b a bi a R C →+→σ,验证它为同构映射。
2、证明:向量β可以由r ααα,,,21 线性表示, 则不妨设r r r r a a a a ααααβ++++=--112211 ,其中0≠r a , 若0=r a ,则112211--+++=r r a a a αααβ , 这与β不能由121,,,-r ααα 表示矛盾。
于是11111-----=r rr r r r a a a a a ααβα 。
故向量r α可以由βααα,,,,121-r 线性表示, 即向量组),,,,(121r r αααα- 与),,,,(121βααα-r 能够相互线性表示, 从而),,,,(121r r αααα- 与),,,,(121βααα-r 等价。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、填空题 (将正确答案填在题中横线上。
每小题2分,共10分)
1.若23,x b x ax ++则a ,b 满足条件 .
2.当 t 满足 时, ⎪⎪⎪⎭⎫ ⎝⎛=0111α, ⎪⎪⎪⎭⎫ ⎝⎛-=1312α, ⎪⎪⎪⎭
⎫ ⎝⎛=t 353α 线性相关。
3.设3阶方阵A 满足21,3)A A E O A E -+-=+=则( 。
4.设123212374D -⎛⎫ ⎪=- ⎪ ⎪⎝⎭
163154131-=D , A 2j (j = 1, 2, 3)为元素a 2j 的代数余子式,则 3A 21 + 7A 22 + 4A 23 = .
115. 11, ()211a A a R A a a ⎛⎫ ⎪== ⎪ ⎪⎝⎭
设3阶矩阵若,则= .
二、单项选择题 (每小题仅有一个正确答案, 将正确答案番号填入题干的括号。
每小题2分,共20分) 1. =-0
0000000
000
01
21
n n a a a a ( ) (A) n n n n a a a a 1212)
1()1(--- (B) n n a a a a 121--
(C) n n a a a a 121- (D) 0
123122*********
1223123
123123123
2,,(),()2,23 (C) ,2 (D) ,2322,355A B ααααααααααααααααααααααααααααααα---+++++++++-++-.已知为齐次线性方程组的基础解系,则下列( )仍是该方程组的基础解系.
,
,3,3. 设A 为三阶方阵,A *为A 的伴随矩阵,1,2
A =则 12A A -*+=( ). (A) 6 (B) 16 (C) 2 (D) 12
4. 4阶行列式D 的值为91 ,它的第1行元素为2,3,t+3,-
5. 第1行元素的代数余子式依次为-1,0,6,9,则t =( ).
(A) 1 (B) 2 (C) –20 (D) 20
5. 设 s ααα,,,21 为n 维向量组, 且秩 ,),,,(21r s =ααα 则( ) 。
(A) 该向量组极大无关组唯一
(B) 该向量组极大无关组不唯一
(C) 该向量组中任意r 个向量线性无关
(D) 该向量组中任意 r+1 个向量线性相关
6. 设A 为n 阶矩阵, 且r (A ) = n − 1, α1 , α2 是AX=O 的两个不同的解向量,k 为任意常数, 则 AX=O 的通解为( ).
(A) k α1 (B) k (α1 − α2 ) (C) k (α1 + α2 ) (D) k α2
7. 设A , B 均为n 阶方阵, 下面结论正确的是( ).
(A) 若A + B 可逆, 则 A, B 均可逆 (B) 若A ,B 均可逆, 则 A -B 可逆
(C) 若A ,B 均可逆, 则 AB 可逆 (D) 若A ,B 均可逆, 则 A + B 可逆
222
8. , n , ( ).
(A) ()2 (B)
(C)
(D) A B A B A AB B AB BA A A A B A B +=++=-=-+=+设为阶矩阵运算正确
9.已知方程组
121343
413020200
tx x x x x x x x tx +=⎧⎪++=⎪⎨+=⎪⎪+=⎩ 有非零解,则t=( ).
(A) 4 (B) 14 (C) 2 (D) 12
. () ()
() () A m n AX A A B A C A D A θ⨯=10.设是矩阵,则齐次线性方程组仅有零解的充要条件是()的行向量组线性无关的列向量组线性无关的列向量组线性相关的行向量组线性相关
三、计算题 (每小题10分,共50分)
1. 求432()23331,()f x x x x x f x =-+-+求的有理根。
2.设矩阵A = ⎪⎪⎪⎭⎫ ⎝⎛--110
130
001
,矩阵X 满足等式 XA * + X = 1-A ,求X .
12343. 11321326 ,,,15110312 (1) ,?
(2) ,?p p p p αααα--⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭
设向量组
为何值时该向量组线性无关为何值时该向量组线性相关并在此时求出它的秩和一个极大无关组,并将其余向量用求出的极大无关组线性表出.
4.向量321,,ηηη是4元非齐次线性方程组AX β=的解向量,R (A )=3且
122361200123ηηηη⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭
,, 求AX β=的通解.
5. 设有三维向量组
123211111,1,1,111k k k k k αααβ+⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪==+== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭
(1)k 为何值时,β可由321,,ααα线性表示,且表法唯一;
(2)k 为何值时,β可由321,,ααα线性表示,且表法不唯一;
(3)k 为何值时,β不能由321,,ααα线性表示.
四、证明题 (每小题10分,共20分)
1.,()().
A s n P s s Q n n R PAQ R A ⨯⨯⨯=设为矩阵为可逆矩阵,为可逆矩阵.证明:
23112131231222322313233323
14243
41234 .x a x a x a x a x a x a x a x a x a x a x a x a a a a a ⎧++=⎪++=⎪⎨++=⎪⎪++=⎩2.已知线性方程组
其中,,,互不相同,证明方程组无解。
