[理学]06静定桁架和组合结构--习题
李廉锟《结构力学》(上册)课后习题详解(5-7章)【圣才出品】

第5章静定平面桁架复习思考题1.桁架的计算简图作了哪些假设?它与实际的桁架有哪些差别?答:(1)桁架的计算简图假设①各结点都是无摩擦的理想铰;②各杆轴都是直线,并在同一平面内且通过铰的中心;③荷载只作用在结点上并在桁架的平面内。
(2)桁架的计算简图与实际桁架的差别①结点的刚性。
②各杆轴线不可能绝对平直,在结点处也不可能准确交于一点。
③非结点荷载(例如杆件自重、风荷载等)。
④结构的空间作用,等等。
2.如何根据桁架的几何构造特点来选择计算顺序?答:根据桁架的几何构造特点来选择计算顺序的方法(1)找出零杆根据节点的几何特征和外部受力特点判断出零杆。
(2)选择合适的方法求解桁架①用节点法解简单桁架时,在求出支座反力后,可按与几何组成相反的顺序,从最后的结点开始,依次倒算回去,便能顺利地用结点法求出所有杆件的内力。
②求解联合桁架时,用结点法将会遇到未知力超过两个的结点,可以先用截面法将联合杆件的内力求出,再用结点法求解其它杆件的内力。
③求解复杂桁架时,根据桁架的几何构造特点看,可先算出截面单杆的内力,再选择合适的计算方法求解剩余杆的内力。
3.在结点法和截面法中,怎样尽量避免解联立方程?答:在结点法和截面法中,尽量避免解联立方程的方法:(1)采用结点法时,为避免解联立方程,可改选投影轴方向或者改用力矩平衡方程(向力的汇交点取矩)。
(2)采用截面法时,使用力矩法的关键在于选取合理的力矩中心,因此应尽量选取多力汇交点作为力矩中心;使用投影法的过程中,应尽量选择多个力所在方向作为力分解的坐标轴。
4.零杆既然不受力,为何在实际结构中不把它去掉?答:在实际结构中不把零杆去掉的原因:(1)在实际结构中,工况更复杂,荷载不是一成不变的,荷载改变后,“零杆”可能变为非零杆。
因此,为了保证结构的几何形状在任何载荷作用下都不会改变,零杆不能从桁架中除去。
(2)在理想桁架(做了诸多假设)中“零杆”才是零杆,而实际结构中,零杆的内力也不是零,只是较小而已。
结构力学习题及答案(武汉大学)

结构力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进行几何组成分析。
若是具有多余约束的几何不变体系,则需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1=W 2-1 9-=W 2-3 3-=W 2-4 2-=W 2-5 1-=W 2-6 4-=W2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系 2-9、2-10、2-15具有一个多余约束的几何不变体系 2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
(a)(b)(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
(a)(b)(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。
(a)(b)(c) (d)部分习题答案3-1 (a )m kN M B ⋅=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ⋅=20(上侧受拉),m kN M B ⋅=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ⋅-=40(上侧受拉),m kN M B ⋅-=120(上侧受拉)(b )m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11(下侧受拉)(c )m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10(左侧受拉),m kN M DF ⋅=8(上侧受拉),m kN M DE ⋅=20(右侧受拉) 3-4 m kN M BA ⋅=120(左侧受拉)3-5 m kN M F ⋅=40(左侧受拉),m kN M DC ⋅=160(上侧受拉),m kN M EB ⋅=80(右侧受拉)3-6 m kN M BA ⋅=60(右侧受拉),m kN M BD ⋅=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ⋅=70下(左侧受拉),m kN M DE ⋅=150(上侧受拉),m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0(上侧受拉),m kN M BA ⋅=36.0(右侧受拉) 3-9 m kN M AB ⋅=10(左侧受拉),m kN M BC ⋅=10(上侧受拉) 3-10 (a )错误 (b )错误 (c )错误 (d )正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
静定桁架和组合结构

d A FN1
1
I
0
FN1= - 3FP
d
I d d
FP
例:求图示桁架杆1轴力。
解: 求反力。 取截面I-I右部。 由∑x’=0
a/2
FP I
x’
-
a A FN1 B
FN1
· cos45o+F
cos45o=0
By·
I 1
a/2 FBy= 3FP /4 a/2 a/2 a/2
FN1= FBy =0.75 FP
Ⅰ
FP2
Ⅰ
FP1
Ⅰ
E
ⅡDⅡFra bibliotekFP2
FxD
Ⅰ
FP1
FxE
FxA
A
Ⅲ
B FyB
C
FyD
FyD
Ⅱ
FyE
FyC
FEy
Ⅲ
FyA
Ⅱ
FxA
FyA
FxC
∑MC=0,求出FxD、 FxE FyB
§6-4 结点法与截面法的联合应用
在桁架计算中,对于某一杆件的内 力,如果只用一个的平衡条件或只作一次 截面均无法解决时,可把结点法和截面法 联合起来应用,往往能收到良好的结果。
实例说明。
例:截面隔离体与结点隔离体联合求解杆内力
求a ,b两杆轴力。
Ⅱ
FP
作截面 I - I ∑y=0 FNa cos45o-FNc cos45o+FP=0
取结点K: ∑x=0 FNa = - FNc 2FNa cos45o= - FP FNa = - 0.707FP 作截面Ⅱ-Ⅱ ∑MD=0 →FNb
FNDF= - 1.5kN (压力)
同理可得: FNEB=2.5kN (拉力) FNEG= -1.5kN (压力) 提问:
结构力学-静定桁架和组合结构

N4 β
N2=-N1
N3 N1=N2
N2 N4=N3
6.2桁架的内力分析
找零杆应用
N1=0
P
N2=0
N1=0 N2=P
FP
N1
N2=N1
N3=0
6.2桁架的内力分析
找零杆应用
FP
FP
6.2桁架的内力分析
找零杆训练
P
思考:能否去掉零杆?
对称荷载作用下内力呈对称分布
•其对两由称对D斜轴点称杆上的性轴的竖要力向求K平型:为衡结N零要1=点。N求无2 外N1力=-作N用2 时, 所反以对称荷N1=载N2作=0用下内力呈反对称分布
组合结构的工程应用
6.3组合结构及内力分析
组合结构的内力类型 二力杆只有轴力,方向规定同桁架; 梁式杆可能存在弯矩、剪力和轴力,方向规定同 梁和刚架。
6.3组合结构及内力分析
组合结构的内力分析思路 (1)计算支座反力。 (2)分析找出二力杆和梁式杆。 (3)利用结点法、截面法先计算二力杆轴力, 最后分析梁式杆内力,并作出内力图,方法同梁。
•与对杆称1受轴力垂反直对贯称穿的杆轴力为1 零
•与对称轴重合的杆轴N力=0 为零。 N=0
P
P
PP
P
1
P
P
12
D P
P 1
P
P/2
P P/2
6.2桁架的内力分析
截面法的概念 截取桁架一部分(至少包含
C
D
G
两个结点)为研究对象,利 A E F H B
用平面一般力系的平衡条件计算各杆轴力。
最多求解三个未知量,适用于截开三个链杆情况。 联合桁架优先考虑选用截面法。
第四单元测试题第六章三铰拱、静定桁架和组合结构
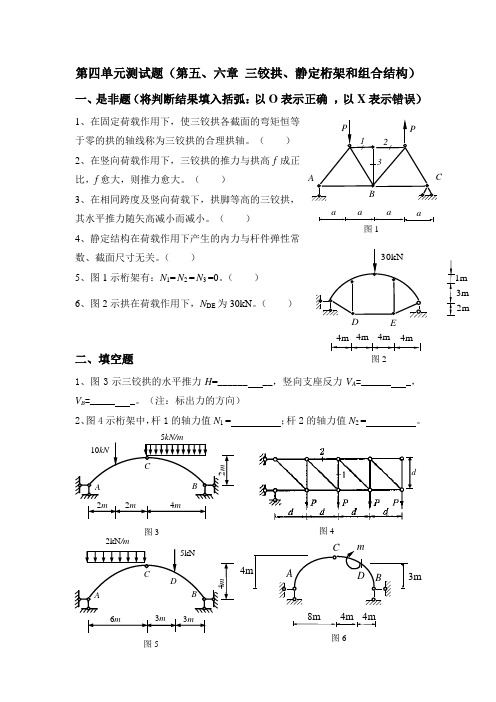
第四单元测试题(第五、六章 三铰拱、静定桁架和组合结构)一、是非题(将判断结果填入括弧:以O 表示正确 ,以X 表示错误)1、在固定荷载作用下,使三铰拱各截面的弯矩恒等于零的拱的轴线称为三铰拱的合理拱轴。
( )2、在竖向荷载作用下,三铰拱的推力与拱高f 成正比,f 愈大,则推力愈大。
( )3、在相同跨度及竖向荷载下,拱脚等高的三铰拱,其水平推力随矢高减小而减小。
( )4、静定结构在荷载作用下产生的内力与杆件弹性常数、截面尺寸无关。
( )5、图1示桁架有:N 1= N 2 = N 3 =0。
( )6、图2示拱在荷载作用下,N DE 为30kN 。
( )二、填空题1、图3示三铰拱的水平推力H =______ __,竖向支座反力V A =______ _,V B =_____ _。
(注:标出力的方向)2、图4示桁架中,杆1的轴力值N 1 = ;杆2的轴力值N 2 = 。
2m2m4m10kNA CB5kN/m2m图33m6m 3mACB4m图5D2kN /m5kN 图4d123PP ABCaaaa图130kND 4m 4m 4m4m1m 图2ABCm 4m3m8m 4m 4mD图63、图5示三铰拱的水平推力H =______ __,竖向支座反力V A =______ _,V B =_____ _。
(注:标出力的方向)4、图6示抛物线三铰拱,矢高为4m ,在D 点作用力偶M = 80kN ·m ,M D 左=_______,M D 右=________。
5、图7示结构CD 杆的内力为_____ _。
6、三铰拱在竖向荷载作用下,其支座反力与三个铰的位置__________关,与拱轴形状_______ 关 。
7、图8示结构固定支座的竖向反力V A = 。
三、选择题1、图8所示桁架中零杆的个数( )。
(提示:不含支座零支杆数)A. 6根B. 7根C. 8根D. 10根 2、图9所示桁架中零杆的个数( )。
3.2静定桁架和组合结构-精选文档

12
D
C
7
10
4
1 C
8
9 A 11
5 6
2
3 B A B
0 0
0
P
13
0
练习:试指出零杆
P P
P
4.2 结点法
14
特殊结点的力学特性
N1=0 N2=0 N1=0 N3 N1 N2=N1 N3=0 N4 N1=N2
N3
N2 N4=N3
P
β
N1
β
N2=-N1
N2=P
?
P
4.3 截面法
15
1 A P 2 3 D P N1 N2 P P D N3 C P C h
E
A F G
Y 0,
Y AC 12 0 , Y AC 12 kN
2m 12kN
1.5m
1.5m
N X Y 12kN 由比例关系得: l l X lY 2 . 5 2 N 12 20 kN 压 力 X 12 16 kN AC AC 1 . 5 1 . 5
二、结点单杆概念
11
结点平面汇交力系中,除某一杆件外,其它所有待求内力的杆件均共线 时,则此杆件称为该结点的结点单杆。
结点单杆的内力可直接根据静力平衡条件求出。
N1 N1
N2
N2
N3
N2 0
N1 0
N1
N2
N 1 N 2 N3 0 N1
零杆
N 1 P
P
N2
N2 0
N N 2 1
上弦杆
6
斜杆
竖杆
桁高
下弦杆
节间 l 跨度
6-3超静定桁架和组合结构

0
1 1 N E 1 2 l A E 1A N 1 2 l E 12 A 22a
P
NP
1 P N E 1 N P l A E 1 A N 1 N P l E 1 A P 23 a 22
a 0.396P -0.604P
(4)解方程
防 灾 科 (5)内力 技 学 院
M图m
第6章 力法
防
11
M
2 1
d
s
EI
FN21 l EA
灾 科 技
2 1.4 104
1.49 2.975 2
2 3
1.49
学 院
1 1.99
106
1.862 5.95
2 2.56
105
1.932 3.09
1 2.02
105
12 0.8
0.000419 m/kN
灾 F N F N 1 X 1 F N P M M 1 X 1 M P
科 技 学 院
第6章 力法
练习 用力法计算下图所示组合结构,求
防 出各桁架杆的轴力,并作梁式杆的弯矩图。
灾 已知梁式杆的抗弯刚度EI=常数,各桁架杆
科 技
的轴向刚度EA=常数,且A=I/16。
学
A
q=10kN /m
C
B
院
结构力学
主讲:王 丽
第6章 力法
§6-4 超静定桁架和组合结构
防 1、超静定桁架结构
灾
杆件只有轴力,故系数和自由项只考虑轴力的影响。
科
ii
Ni2l EA
iP
NiNPl EA
技 例1 求图示超静定桁架的内力。各杆EA为常数。
学
FP
第六章静定桁架和组合结构42页PPT

§6.5 组合结构
• 组合结构由链杆和梁式杆组成。常用于 吊车梁、桥梁的承重结构、房屋中的屋 架。
计算组合结构时应注意: ①注意区分链杆(只受轴力)和梁式杆(受轴力
、剪力和弯矩); ②前面关于桁架结点的一些特性对有梁式杆的结
点不再适用; ③一般先计算反力和链杆的轴力,然后计算梁式
N2 =
13P 3
③1-1以右
MF =NCE6-4P=0,
NCE=3 2P
④2-2以下
F
NCE
CP
X = NCE - X1 = 0,
N1
P NCE=3 2P
X1
=
2 3
P,
N1
=
5 6
P
3、结点法与截面法的联合应用在桁架计算中, 有时联合应用结点法和截面法更为方便。
例题 4
截面法例4
求指定杆的轴力。
MC =0
q=1kN/m
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
f2=0.7m f1=0.5m f =1.2m
66-163-1.2NDE =0
F
C
NDE =15kN
A 15
③截面的剪力和轴力: Q=Ycosα-15sinα N= -Ysinα -15cosα
+ 3.5 -3.5
6kN
3m
D
15
相等。
2、由周边上的K形结点
知各腹杆内力值相等,但正
负号交替变化。所有右上斜
杆同号(设为N),所有右
下斜杆同号(设为-N)。
3、取图示分离体:
d
d
a
F
E
—N
N —N
N
—N D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
N4
5P 4
(压)
结构力学电子教程
6 静定桁架和组合结构
6.23 选用较简便方法计算图示桁架中指定杆的轴力。
D
I II
60kN
1
D I-I截面右部分: II-II截面右部分:
4m
C2
3
I
II
A
B
3m 3m 3m 3m
4m
N1
C N2
N4
3
B
22.5kN
45kN
N5
N3
解:(1)反力如图。 30kN (2)I-I截面右部分
结构力学电子教程
6 静定桁架和组合结构
20kN
20kN C
20kN
(4)以结点C为研究对象
Y 0 :
0 +20
0
3m
D A
XA 0
FE
43m =12m
YA30kN
20
20 C
20
B
YB30kN
1
NCE 20 5
2 20 0 5
NCE 20kN
由对称知 X 0
N (kN)
D
A +60 +60
0 0
3m
A
B
(3)以结点A为研究对象
XA 0
FE
43m =12m
YA30kN
20
20 C
20
N (kN)
D
A +60 +60
+60 +60
1
YB 30kN
Y0:NAD
300 5
NAC30 5=67.08kN
B
2
X0:NAF NAD
0 5
FE
NAF 60kN
30 20kN
D
NDC
NDE
30 5kN
1 1 3P 1
Y 1 0:N 22P 2420 N2
P 4
(拉)
结构力学电子教程
6 静定桁架和组合结构
m
XB
3P 4
1B
P
n
B 3P
P
4
D
C
P
P
2 m
k
4
3k
n
4a
F
N8 N4
E
N3
A
XA 3 P
4
3a
YA 2P
(4)k-k截面上部分
1 1 3 P1
Y 1 0 : N 42 P 2 2 42 0
静定桁架内力计算主要采用结点法与截面法。 结点法的研究对象为结点,平面汇交力系,两个独立的平 衡方程。 截面法是以桁架的某一部分作为研究对象,平面任意力系 ,3个独立的平衡方程。 联合运用结点法和截面法可简化计算。 计算组合结构的内力时,应按与几何组成相反的顺序进行 计算。先轴力杆,再梁式杆。轴力杆只承受轴力,梁式杆除承 受轴力之外,还有弯矩和剪力。
结构力学电子教程
6 静定桁架和组合结构
6 静定桁架和组合结构(4 课时)
本章提要
6.1 桁架的特点和组成分类 6.2 结点法 6.3 截面法 6.4 结点法和截面法的联合应用 6.5 组合结构
*6.6 静定空间桁架 本章小结
思考题
习题
结构力学电子教程
6 静定桁架和组合结构
本章小结
静定桁架的内力计算是假定桁架符合基本假设的前提下进 行的,即桁架各杆为二力杆,桁架内力为轴力。
结构力学电子教程
6 静定桁架和组合结构
课外作业 P88-92
第一次 6.10 、6.15 第二次 6.17、 6.23 第三次 6.28、 6.29(4m改为6m)
结构力学电子教程
6 静定桁架和组合结构
6.10 用结点法求图示桁架各杆的轴力。
20kN
20kN C
20kN
D
解:(1)求支座反力。 (2)判定零杆如图。
+60 +60 B
FE
20kN
30
C
30
10 5kN
10 5kN
NDE
(5)以结点E为研究对象 校核:
由对称知 X 0 Y-10 512200
5
10 5kN
60kN
20kN
10 5kN
60kN
E
结构力学电子教程
6 静定桁架和组合结构6.1 Nhomakorabea 用结点法求图示桁架各杆的轴力。
3m
B 1.333PC 1.333P D
6.28 计算图示组合结构二力杆的轴力,并绘制梁式杆内力图。
q=1kN/m
I-I截面右部分:
q=1kN/m
0 0
3m
I
F
C
G
A +6
+6
+6 B
D
IE
3m 3m 3m 3m
C 6kN
6kN
B
6kN
6kN
6kN
解:反力如图。
Q (kN)
4.5
4.5
M (kNm)
N (kN)
结构力学电子教程
6 静定桁架和组合结构
NAD
A
30
(4)以结点D为研究对象
2
2
2
X 0 :3 05 1 5 N D E 5 1 N D C 5 1 0
Y 0 :3 05 5 2 0 N D E 5 N D C 5 0
30kN NAF
N D E 1 0 5 2 2 . 3 6 k N , N D C 2 0 5 4 4 . 7 2 k N
6.29 计算图示组合结构二力杆的轴力,并绘制梁式杆内力图。
XA 0
5kN E
1 2
A
Dn F
3
m 62m=12m
(2)n-n截面
B
左部分
YA 25kN n-n截面左部分:
10kN N1
YB 10kN
42 M F0:N 1202041020
5kN E
A D N4
25kN
m-m截面左部分:
10kN
N2 F
10kNN5 G
N 1 1 2 55 3 3 .5 1 4 k N ( 压 ) M A 0 : N 25 1 N 25 2 1 0 2 0 C N 2 55 1 1 .1 8 k N ( 压 )
30kN
M C 0 :N 1 4 3 0 3 0 N 1 22.5 k N ( 拉 ) M D 0 : N 2 4 3 0 6 0 N 245kN ( 压 )
(3)II-II截面右部分
X0:22.545N 35 30 N 3 37.5k N ( 拉 )
结构力学电子教程
6 静定桁架和组合结构
0.778P F
0.555P
-P 1.333P
P
0E
0.555P 0.555P 0.555P
-1.555P 0
6m
0.778P
解:
0.778P
A
3m 4m P
结构力学电子教程
6 静定桁架和组合结构
6.17 用截面法求图示桁架指定杆轴力。
n 10kN
10kN 10kN m
G
C
解: (1)反力如图。
3m
B 3P
(2)m-m截面右部分
4
C
M C 0:
P 2 m
a 3P
N6
N1
a 0 24
4a
4
3
n
3 N1
2 P (压 ) 4
(3)n-n截面右部分
A
XA 3 P
P
B 3 P 4
M 0: F
4
3a
YA 2P
D
C
N7
F
N2
E
N3
a
3P
N3
P a 2a 0
2
4
N3
2P (拉) 2
5kN E A
D
25kN
1
2
N6
F N3
(3)m-m截面左部分 M C 0 : N 3 3 2 0 6 1 0 4 1 0 2 0
N 320kN ( 拉 )
结构力学电子教程
6 静定桁架和组合结构
6.19 用截面法求图示桁架指定杆轴力。
m
XB
3P 4
1B
P
N1
n
N5
解: (1)反力如图。
