动态规划 运筹学 例题
《管理运筹学》案例演示(动态规划)

x1
[
]
第一季度生产量加库存量要满足本季度需求量, 又不能超过第一到第四季度的总需求: 最高生产量为6个单位:
2 ≤ x1 + s1 ≤11 0 ≤ x1 ≤ 6
f1 ( s1 )
x1
0 1 2
21
Байду номын сангаас
3
21.5
4
22
5
6
f1 ( s1 )
∗ x1
s1
0
20.5 21.5 20.5
5
第四步:最佳生产决策:第一季度生产5单位产品,期末库存量为 3单位;第二季度不生产,期末库存量为零;第三季度生产6单位 产品,期末库存量为4单位;第四季度不安排生产。
8 100 75 53
A B C
问如何确定三个项目计划的投资额,才能使8千万元的资金投 资后的利润最大。 解: 阶段变量k ( k =1,2, 3 ):每投资一个项目作为一个阶段; 状态变量sk :可以对第k个项目投资的资金数(即投资 第k个项目前的资金数); 决策变量xk:第k 个项目的投资, 0≤xk≤sk;
11 10.5 8 8 8 8 5
6 5 0 0 0 0 0
第三步:第二到第四季度的最佳生产决策; 第二到第四季度的最低生产成本:
f2 (s2 ) = m c2( x2 , s2 ) + f3 (s3 ) in
x2
[
]
约束条件: 由于第一季度期初库存s1= 0,而最高生产量x1= 6 ,市场需求量d1=2,所以,第二季度期初的库存量应为: 第二季度生产量加库存量要满足本季度需求量, 又不能超过第二到第四季度的总需求: 最高生产量为6个单位:
该季度生产量不能超过6个单位:
128503-管理运筹学-习题-06-动态规划

习题6-1. 考虑下面的网络图,箭头上的数字代表相连两个节点之间的距离。
(1)用动态规划找出从节点1到节点10的最短路。
(2)从节点4到节点10的最短路呢?6-2. 从北京到上海的包机的剩余装载能力为2000kg ,某一运输公司现有4种货物需要从北京运输到上海。
每种货物的单位、单位重量和单位运输费用如下表所示。
(1)用动态规划找出包机应该运输的每种货物的单位数。
(2)假设包机同意装载另一批货物,剩余装载能力降为1800kg ,计算结果会怎样变化?6-3. 假定有一个3阶段的过程,每一阶段的产量是需要做出决策的函数。
使用数学符号,问题表述如下:Max ()()()332211d r d r d r ++ s.t.1000321≤++d d d 每个阶段的决策变量和相应的返回值如下所示:6-4. 某制造公司为一家汽车工厂提供发动机的部件,以下是3个月的生产计划的数据。
量是10单位,并且生产批量是10的倍数(例如,10,20或者30单位)。
6-5. 某物流公司雇佣了8名新员工,现决定如何把他们分配到4项作业上。
公司给出了以下每项作业分配不同的作业人员的估计利润表。
(1) 用动态规划决定每项作业应该分配的新员工数目。
(2) 如果公司只雇佣了6名新员工,应该把这些员工分配给哪些作业?6-6. 一个锯木厂采购了一批20ft 长的原木,想要把这些原木切成更短的原木,然后把切后的小原木卖给制造公司。
制造公司已经订购了一批4种尺寸的原木:l 1=3ft ,l 2=7ft ,l 3=11ft ,l 4=16ft 。
锯木厂现在有2000个长度为20ft 的原木的库存,并希望有选择地裁截原木以最大化利润。
假定锯木厂的订单是无限的,唯一的问题就是确定把现有原木裁成的类型以最大化利润。
原木的利润如下表所示:任何裁截类型的长度限制如下:201173321≤++d d d 其中,i d 是长度为i l 的类型的裁截数目,4,3,2,1=i .(1)为这个问题建立动态规划模型,并使用模型解决问题。
运筹学 动态规划-作业及答案
1
第五章 动态规划作业题及答案
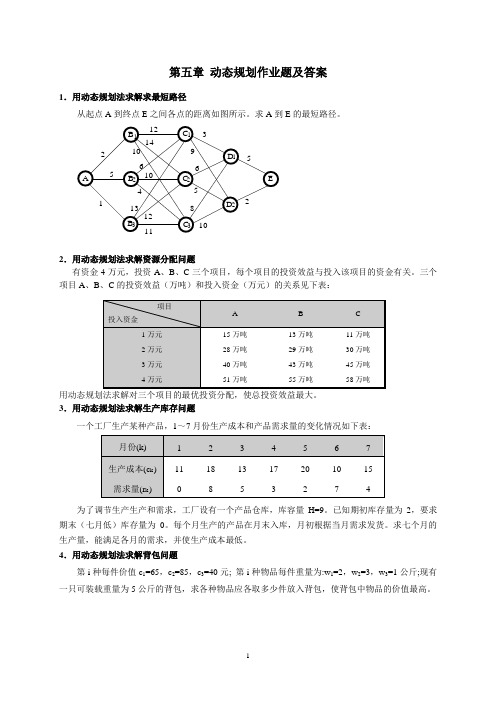
1.用动态规划法求解求最短路径
从起点A 到终点E 之间各点的距离如图所示。
求A 到E 的最短路径。
B A
C B
D B C D E
C 21
23
12
31
2
5
11214
10610
41312113
96
5810
5
2
2.用动态规划法求解资源分配问题
有资金4万元,投资A 、B 、C 三个项目,每个项目的投资效益与投入该项目的资金有关。
三个项目A 、B 、C 的投资效益(万吨)和投入资金(万元)的关系见下表:
用动态规划法求解对三个项目的最优投资分配,使总投资效益最大。
3.用动态规划法求解生产库存问题
一个工厂生产某种产品,1~7月份生产成本和产品需求量的变化情况如下表:
为了调节生产生产和需求,工厂设有一个产品仓库,库容量H=9。
已知期初库存量为2,要求期末(七月低)库存量为0。
每个月生产的产品在月末入库,月初根据当月需求发货。
求七个月的生产量,能满足各月的需求,并使生产成本最低。
4.用动态规划法求解背包问题
第i 种每件价值c 1=65,c 2=85,c 3=40元; 第i 种物品每件重量为:w 1=2,w 2=3,w 3=1公斤;现有一只可装载重量为5公斤的背包,求各种物品应各取多少件放入背包,使背包中物品的价值最高。
运筹学动态规划习题

一、某工厂购进100台机器,准备生产A、B 两种产品。如生产产品A,每台机器每年可 收入45万元,损坏率为65%;若生产产品B, 每台机器每年可收入35万元,损坏率为 35%;估计三年后有新机器出现,旧的机 器将全部淘汰。试问每年应然后安排生产, 使在三年内收入最多?
答案: 第一年将100台机器全部生产产品B,第二年 将余下的机器生产产品B,第三年把所有的 机器生产产品A。三年的总收入为7676.25 万元。
二、某厂有100台机床,能够加工两种零件, 要安排4个月的任务,根据以往经验,用这 些机床加工第一种零件,一个月后损坏率 为1/3;加工第二种零件时,一个月后损坏 率为1/10。又已知机床加工第一种零件时一 个月的受益为10万元,机床加工第二种零 件时一个月的受益为7万元。现安排4个月 的任务,使总收益为最大。
பைடு நூலகம்
• 答案: • 设每个月为一个阶段,共4个阶段。每个阶 段可投入生产的机床数为状态变量SK,加 工第一种零件的机床数为决策变量UK,加 工第二种零件的机床数为SK-UK,阶段指标 函数为DK=7SK+3UK,SK+1=9/10SK-7/30UK。 用逆序的递推方法求解:前两月全部加工 第二种零件,后两月全部加工第一种零件。 其最大收益为2680
• 首先建立动态规划的模型 • 划分成3个阶段,每个阶段决策一个项目 的投资额,每个阶段决策的投资时可以使 用的资金作为状态变量,利润为阶段的指 标函数。 • 利用基本递推方程从第3阶段开始求解 • 给企业的投资额为 95万元 在城市购买房 地产的投资额为 105万元 • 最大利润为 681万元
三、某公司有资金200万元,打算全部参与三 个方面的投资。(1)参与一个企业投资, 当投资额为X1(万元)时,可得利润为 J1=4X1-2(万元);(2)参与一个电视片 制作,当投资额为X2(万元)时,可得利 润为J2=1/16X2-1/5X2-2(万元);(3)在 城市购买房地产,当投资额为X3(万元) 时,可得利润为J3=3X3-10(万元)。又知 投资额的上限为X1≤95万元;X2≤50万元。 用动态规划法决策使总利润最大?
运筹学5(动态规划)

1
2
3
4
下面应用动态规划方法求解例7.1。运用逆序递 推方法求解,即由最后一段到第一段逐步求出各点到 终点的最短路线,最后求出A点到E点的最短路线。 运用逆序递推方法的好处是可以始终盯住目标,不 致脱离最终目标。 例7.1是一个四阶段决策问题,一般可分为四步:
●逆序法求解最短路问题
第一步,从K=4开始
2 S3
3
S4
4
d (C 2 , D1 ) + f 4 ( D1 ) 6+4 =min =5 f 3 ( C2 )=min d (C 2 , D2 ) + f 4 ( D2 ) 2+3 即从 C2 到 E 的最短距离为 5, 其路径为 C2 → D2 →E,相应的决策为
* x 3 ( C 2 ) = D2
1 S1 S2
2 S3
3
S4
4
1
反推,即得到最优决策序列 ,即 x = D2 , x
* 4 * 1
2
3
*
4
*
从城市 A 到城市 E 的最短距离为 17。把各段的最优决策按计算顺序
(A)= B1 , x 2 ( B1 )= C 2 , x 3 ( C 2 ) ( D2 )=E,所以最短路线为 :A→B1→C2 →D2→E.
d ( B1 , C1 ) + f 3 (C1 ) 6+7 f 2 ( B1 ) =min d ( B1 , C2 ) + f 3 (C 2 ) =min 4 + 5 =9 d ( B1 , C3 ) + f 3 (C3 ) 5+5
即 B1 到终点 E 的最短距离为 9, 其路径为 B1→C2→D2→E, 本段的相应 决策为 x
运筹学考试试题

运筹学考试试题
问题一:线性规划
某食品公司有两种包装酱油的产品,产品 A 和产品 B。
产品 A 需
要 2 包的玻璃瓶和 3 包的金属瓶,产品 B 需要 4 包的玻璃瓶和 1 包的金属瓶。
公司每天共有 60 包玻璃瓶和 50 包金属瓶可用于生产。
产品
A 毛利为 10 元/包,产品
B 毛利为 15 元/包。
为了最大限度地提高公司的毛利,请问公司每天应该生产多少包产品 A 和产品 B?
问题二:整数规划
某快递公司需要派送多个包裹,在不同的送货地点停靠。
每个派送地点需要 1 辆专门的送货车。
快递公司最多可以使用 5 辆送货车。
每辆车的容量为 30 个包裹。
每个送货地点的包裹量如下:地点 1 需要 12 个包裹,地点 2 需要 8 个包裹,地点 3 需要 15 个包裹,地点 4 需要 10 个包裹。
每个送货地点停靠一辆车后,可以继续往下一个地点派送。
请问如何安排送货车来最大化送货量?
问题三:动态规划
假设有一个 3×3 的方格矩阵,每个格子里都写有一个正整数。
从左上角出发,每次只能向右或向下移动,直到达到右下角。
路线上所有经过的格子的数字加起来就是这条路径的价值。
求最优路径和的最大值。
问题四:网络流
某市有 4 座工厂,生产不同种类的零件。
每座工厂每天的生产能力不同,且每种零件的需求也不相同。
如何设计一个合理的生产调度方案,使得所有工厂的产量最大化,且满足市场对不同零件的需求?
以上考试试题仅供参考,实际考试内容以试卷内容为准。
祝考试顺利!。
运筹学第七章动态规划
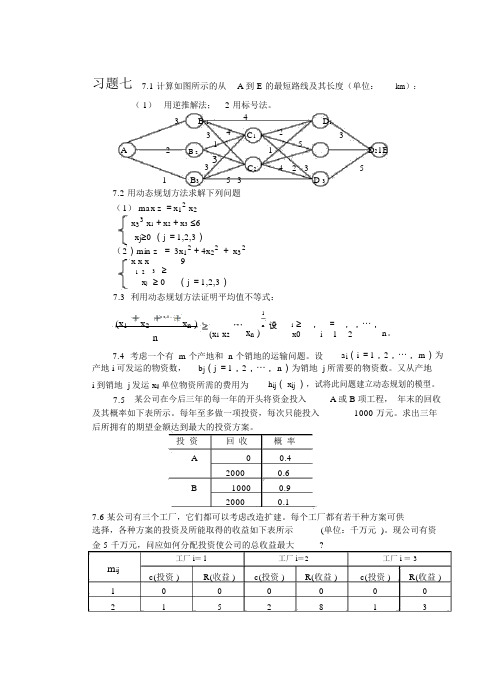
习题七7.1 计算如图所示的从 A 到 E 的最短路线及其长度(单位:km ):( 1) 用逆推解法; 2 用标号法。
3 B 14D 1423C 13A2115D 21EB 2335 C 24 2 351 B 3 3D 37.2 用动态规划方法求解下列问题( 1) max z =x 12 x 2x 33 x 1+x 2+x 3 ≤6 x j ≥0 (j =1,2,3)( 2)min z = 3x 12+4x 22 + x 32x x x91 2 3 ≥x j ≥ 0(j =1,2,3)7.3 利用动态规划方法证明平均值不等式:(x 1x 2x n )1x n ) n设i ≥, = , ,⋯,n 。
n(x 1 x 2x0i127.4 考虑一个有 m 个产地和 n 个销地的运输问题。
设a i (i =1,2,⋯, m )为 产地 i 可发运的物资数,b j (j =1,2,⋯, n )为销地 j 所需要的物资数。
又从产地i 到销地 j 发运 x ij 单位物资所需的费用为h ij ( x ij ),试将此问题建立动态规划的模型。
7.5 某公司在今后三年的每一年的开头将资金投入A 或B 项工程, 年末的回收及其概率如下表所示。
每年至多做一项投资,每次只能投入 1000 万元。
求出三年后所拥有的期望金额达到最大的投资方案。
投 资回 收概 率 A 00.42000 0.6 B1000 0.920000.17.6 某公司有三个工厂,它们都可以考虑改造扩建。
每个工厂都有若干种方案可供选择,各种方案的投资及所能取得的收益如下表所示 (单位:千万元 )。
现公司有资 金 5 千万元,问应如何分配投资使公司的总收益最大?m ij工厂 i = l工厂 i =2 工厂 i = 3c(投资 )R(收益 )c(投资 )R(收益 )c(投资 )R(收益 )1 0 0 0 0 0 0 215281332639——4——412——7.7某厂准备连续 3 个月生产 A 种产品,每月初开始生产。
运筹学第五章动态规划

和 dk 2 (sk ));
(4) 允许决策集: D k ( s k ) ( x k , y k ) 0 ≤ y k ≤ s k ; 0 ≤ x k ≤ 1 0 0 0 ( s k y k )
状态转移方程: s k 1 s k x k y k ,s 1 5 0 0k4,3,2,1
其中s 5 表示第四阶段末的状态; (5) 阶段指标: v k ( s k ,x k ,y k ) q k y k p k x k ,k4,3,2,1;
5.1 动态规划的基本概念和模型
5.1.1 动态规划的基本概念
下面结合实例来介绍动态规划的基本概念:
【例5.1】 如图5.1所示,在处有一水库,现需从点铺设一条 管道到点,弧上的数字表示与其相连的两个地点之间所需修建 的渠道长度,请找出一条由到的修建线路,使得所需修建的渠 道长度最短。
2
A4
3
B
7
(1) 按月份分段: k4,3,2,1;
(2) 状态变量: s k 表示第 k 个月月初的库存量;
(3) 决策变量: dk1(sk表) 示第 k 个月已有库存 s的k 情况下,要定
购的商品量, dk2表(sk示) 第 个月k 已有库存 的商品量(为方便,后面将分别依次用 ,
的 来x sk 情 代k y况 替k 下,要d销k1(售sk )
(6) 动态规划基本方程:
fk(s k) (x k,y m k) a D x k(s k)v k(s k,x k,y k) fk 1 (s k 1 )
f5 (s 5 ) 0 k 4 ,3 ,2 ,1
求解(要求板书) 辅图1
辅图2
辅图3
5.2.3 动态规划的顺序解法
【 例 5.3】 图 5.3 所 示 为 一 水 利 网 络 , A 为 水 库 , 分B 1 ,别B 2 为,B 3 不;C 同1 ,C 的2 ,供C 3 水;D 目1 ,D 的2地,试找出给各供水目的地供水的 最短路线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动态规划运筹学例题
动态规划是运筹学中常用的一种优化技术,它利用规划、三角函数和其他数学技术来解决日常生活中的各种问题,比如最优路线问题、最优资源分配问题、最优出行路线问题等。
本文将通过一个例题,来介绍动态规划的基本思想,以及如何利用动态规划来解决问题。
例题一:已知一条路线,由A点到B点,有N个途经的节点,每个节点之间的距离已知。
求从A到B的最短路线。
按照动态规划的思想,首先将该问题分解为若干个子问题,并根据子问题的解来解决原问题,这种分解和解决问题的方式称为动态规划。
对于上面的问题,可以将其分解为N个子问题,分别是从A到第1个节点、从第1个节点到第2个节点、从第2个节点到第3个节点,以此类推,最后一个子问题是从第N-1个节点到B点的最短路程。
将上面的N个子问题中,从第i个节点到B点的最短路程记为
d[i],由于从第i个节点到B点可能经过i+1、i+2、……、N-1节点,因此要找到d[i],只需要找到经过i+1、i+2、……、N-1节点的最
短路程即可,即求
d[i]=Min{d[i+1]+length[i][i+1],d[i+2]+length[i][i+2],…,d[N
-1]+length[i][N-1]},其中length[i][j]是第i个节点到第j个节点的距离。
以上就是动态规划的解题步骤,它能将原问题分解成若干个子问题,并找到最优解。
对于本例来说,通过上述步骤,就可以得到从A 到B的最短路程。
这种分解和求解问题的方法是动态规划,可以用来解决许多类似的问题,如:1)最优路线问题;2)旅行推销员问题;3)硬币找零问题。
动态规划的一大特点是,他能很好地将问题分解为多个子问题,并能从子问题的解中求解出最优解。
总之,动态规划是一种很有用的优化技术,它可以有效解决各种运筹学问题。
它不仅可以帮助我们解决许多具体问题,而且还能使我们更好地理解问题及其解法。
