2019六年级奥数计数问题及答案

合集下载

小学奥数计数问题练习与答案【三篇】

【导语】成功根本没有秘诀可⾔，如果有的话，就有两个：第⼀个就是坚持到底，永不⾔弃；第⼆个就是当你想放弃的时候，回过头来看看第⼀个秘诀，坚持到底，永不⾔弃，学习也是⼀样需要多做练习。

以下是⽆忧考为⼤家整理的《⼩学奥数计数问题练习与答案【三篇】》供您查阅。

【第⼀篇：整体法经典练习题】经典例题展⽰1：有⼀类各位数字各不相同的五位数M，它的千位数字⽐左右两个数字⼤，⼗位数字也⽐左右两个数字⼤；另有⼀类各位数字各不相同的五位数W，它的千位数字⽐左右两个数字⼩，⼗位数字也⽐左右两个数字⼩。

请问符合要求的数M和W，哪⼀类的个数多？多多少？经典例题展⽰2：游乐园的门票1元1张，每⼈限购1张。

现在有10个⼩朋友排队购票，其中5个⼩朋友只有1元的钞票，另外5个⼩朋友只有2元的钞票，售票员没有准备零钱。

问有多少种排队⽅法,使售票员总能找得开零钱?【第⼆篇：递推⽅法的概述及解题技巧】在不少计数问题中，要很快求出结果是⽐较困难的，有时可先从简单情况⼊⼿，然后从某⼀种特殊情况逐渐推出与以后⽐较复杂情况之间的关系，找出规律逐步解决问题，这样的⽅法叫递推⽅法。

线段AB上共有10个点（包括两个端点），那么这条线段上⼀共有多少条不同的线段？分析与解答：从简单情况研究起： AB上共有2个点，有线段：1条 AB上共有3个点，有线段：1＋2＝3（条） AB上共有4个点，有线段：1＋2＋3＝6（条） AB上共有5个点，有线段：1＋2＋3＋4＝10（条） …… AB上共有10个点，有线段：1＋2＋3＋4＋…＋9＝45（条）⼀般地，AB上共有n个点，有线段： 1＋2＋3＋4＋…＋（n－1）＝n×（n－1）÷2 即：线段数＝点数×（点数－1）÷2【第三篇：计数习题标数法和加法原理的综合应⽤】★★★★）有20个相同的棋⼦，⼀个⼈分若⼲次取，每次可取1个，2个，3个或4个，但要求每次取之后留下的棋⼦数不是3或4的倍数，有（）种不同的⽅法取完这堆棋⼦. 【分析】把20、0和20以内不是3或4的倍数的数写成⼀串，⽤标号法把所有的⽅法数写出来：考点说明：本题主要考察学⽣对于归纳递推思想的理解，具体来说就是列表标数法的使⽤，难度⼀般，只要发现了题⽬中的限制条件，写出符合条件的剩余棋⼦数，然后进⾏递推就可以了。

小学六年级奥数题 10道思维训练题你能答对几道一起进入头脑风暴

小学六年级奥数题 10道思维训练题你能答对几道一起进入头
脑风暴
奥数题并不适合所有学生，因为题本身的难度，远远超出了教材的范围。

孩子不做奥数题很正常，因为很多数学老师要研究一道奥数题很久，甚至找不到答案。

如果孩子在这方面有天赋，我们可以好好培养。

如果孩子不感兴趣，不要勉强。

下面是10道小学六年级的奥数题，难度适中。

你想试试你的手吗？
小学六年级奥数题1.——计数问题
打开，查看更多图片
小学六年级奥数题1.——计数问题
1.答案——
小学六年级奥数题1.——计数问题答案
小学六年级奥数题2.——工程问题
小学六年级奥数题2.——工程问题
2.答案——
答案2
小学六年级奥数题3.——逻辑推理小学六年级奥数题3
3.答案——
答案3
小学六年级奥数题4.——排列组合小学六年级奥数题4
4.答案——
答案4
小学六年级奥数题5.——应用题小学六年级奥数题5
5.答案——
答案5
小学六年级奥数题6.——扶梯问题小学六年级奥数题6
6.答案——
6答案
小学六年级奥数题7.——行程问题小学六年级奥数题7
7.答案——
7.答案
小学六年级奥数题8.——浓度问题
小学六年级奥数题8
8.答案——
8.答案
小学六年级奥数题9.——数论+逻辑推理小学六年级奥数题9
9.答案——
9.答案
小学六年级奥数题10.——分百应用题小学六年级奥数题10
10.答案——
10 答案
祝福孩子们快乐学习，健康成长！。

小学六年级奥数难题100道及答案(完整版)

小学六年级奥数难题100道及答案(完整版)1. 一个数的2/3加上4等于这个数的1/2，求这个数。

解：设这个数为x，根据题意可得方程：(2/3)x + 4 = (1/2)x。

解得x = -24。

2. 一个水池，第一天放水1/3，第二天放水1/4，第三天放水1/5，第四天放水1/6，最后剩下15立方米的水，求水池原来有多少立方米的水。

解：设水池原来有x立方米的水，根据题意可得方程：x * (1 - 1/3 - 1/4 - 1/5 - 1/6) = 15。

解得x = 60。

3. 一个长方形的长比宽多4厘米，周长是32厘米，求长方形的长和宽。

解：设长方形的长为x厘米，宽为y厘米。

根据题意可得方程组：x - y = 4；2x + 2y = 32。

解得x = 10，y = 6。

所以长方形的长为10厘米，宽为6厘米。

4. 一个数的3倍减去5等于这个数的2倍加上7，求这个数。

解：设这个数为x，根据题意可得方程：3x - 5 = 2x + 7。

解得x = 12。

5. 一个三角形的三边长分别为a、b、c，已知a + b > c，a + c > b，b + c > a，求三角形的面积。

解：根据海伦公式，三角形的面积S = sqrt[p * (p - a) * (p - b) * (p - c)]，其中p = (a + b + c) / 2。

将已知的三边长代入公式即可求得三角形的面积。

6. 一个数的5倍减去8等于这个数的3倍加上12，求这个数。

解：设这个数为x，根据题意可得方程：5x - 8 = 3x + 12。

解得x = 10。

7. 一个正方形的边长增加2厘米，面积增加20平方厘米，求原来正方形的边长。

解：设原来正方形的边长为x厘米，根据题意可得方程：(x + 2)^2 - x^2 = 20。

解得x = 4。

所以原来正方形的边长为4厘米。

8. 一个数的4倍加上6等于这个数的3倍加上18，求这个数。

2019-2020年六年级奥数题(含答案)

1．有4箱水果，已知苹果、梨、橘子平均每箱42个，梨、橘子、桃平均每箱36个，苹果和桃平均每箱37个。

一箱苹果多少个？【分析与解】（1）1箱苹果＋1箱梨＋1箱橘子=42×3=136（个）；（2）1箱桃＋1箱梨＋1箱橘子=36×3=108（个）（3）1箱苹果＋1箱桃=37×2=72（个）由（1）（2）两个等式可知：1箱苹果比1箱桃多126－108=18（个），再根据等式（3）就可以算出：1箱桃有（74－18）÷2=28（个），1箱苹果有28＋18=46（个）。

1箱苹果和1箱桃共有多少个：37×2=74（个）1箱苹果比1箱桃多多少个：42×3－36=18（个）1箱苹果有多少个：28＋18=46（个）2．一次数学测验，全班平均分是91.2分，已知女生有21人，平均每人92分；男生平均每人90.5分。

求这个班男生有多少人？【分析与解】女生每人比全班平均分高92－91.2=0.8（分），而男生每人比全班平均分低91.2－90.5=0.7（分）。

全体女生高出全班平均分0.8×21=16.8（分），应补给每个男生0.7分，16.8里包含有24个0.7，即全班有24个男生。

3．小明前几次数学测验的平均成绩是84分，这次要考100分，才能把平均成绩提高到86分。

问这是他第几次测验？【分析与解】100分比86分多14分，这14分必须填补到前几次的平均分84分中去，使其平均分成为86分。

每次填补86－84=2（分），14里面有7个2.所以，前面已经测验了7次，这是第8次测验。

4．小杜从A地到B地，先骑自行车行完全程的一半，每小时行12千米。

剩下的步行，每小时走4千米。

小杜行完全程的平均速度是每小时多少千米？【分析与解】求行完全程的平均速度，应该用全程除以行全程所用的时间。

由于题中没有告诉我们A 地到B地间的路程，我们可以设全程为24千米（也可以设其他数），这样，就可以算出行全程所用的时间是12÷12＋12÷4=4（小时），再用24÷4就能得到行全程的平均速度是每小时6千米。

六年级奥数计数原理与方法练习题

1.正方形ABCD的内部有1999个点，以正方形的4个顶点和内部的1999个点为顶点，将它剪成一些三角形。

问：一共可以剪成多少个三角形？共需剪多少刀？2.甲、乙二人打乒乓球，谁先连胜两局谁赢，若没有人连胜头两局，则谁先胜三局谁赢，打到决出输赢为止。

问：一共有多少种可能的情况？3.经理有4封信先后交给打字员，要求打字员总是先打最近接到的信，比如打完第3封信时第4封信还未到，此时如果第2封信还未打完，那么就应先打第2封信而不能打第1封信。

打字员打完这4封信的先后顺序有多少种可能？4.一个自然数，如果它顺着数和倒着数都是一样的，则称这个数为“回文数”。

例如1331，7，202都是回文数，而220则不是回文数。

问：1到6位的回文数一共有多少个？按从小到大排，第2000个回文数是多少？5.设有长度为1，2，…，9的线段各一条，现在要从这9条线段中选取若干条组成一个正方形，共有多少种不同的取法？这里规定当用2条或多条线段接成一条边时，除端点外，不许重叠。

6.一台晚会上有6个演唱节目和4个舞蹈节目。

求：（1）当4个舞蹈节目要排在一起时，有多少不同的安排节目的顺序？（2）当要求每2个舞蹈节目之间至少安排1个演唱节目时，一共有多少不同的安排节目的顺序？7.在100名学生中，有10人既不会骑自行车又不会游泳，有65人会骑自行车，有73人会游泳，既会骑自行车又会游泳的有多少人？8.在1至100的自然数中，不能被2整除，又不能被3整除，还不能被5整除的数，占这100个自然数的百分之几？9.10个三角形最多将平面分成几个部分？10.四个学生每人做了一张贺年片，放在桌子上，然后每人去拿一张，但不能拿自己做的一张。

问：一共有多少种不同的方法？。

小学奥数计数专题--组合(六年级)竞赛测试.doc

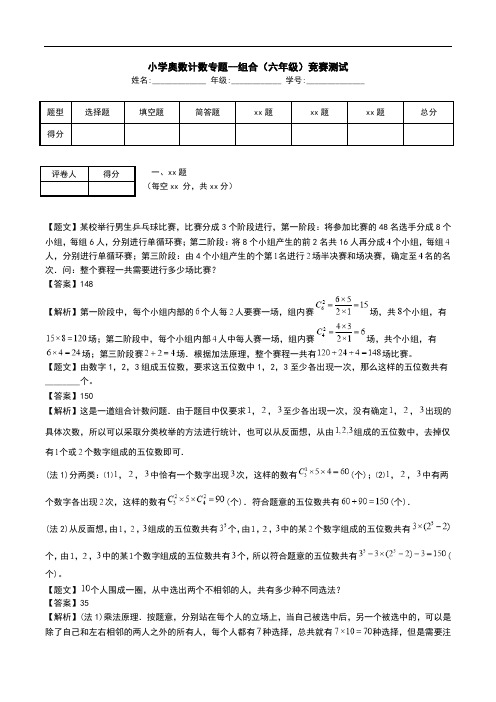
小学奥数计数专题--组合（六年级）竞赛测试姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx 题xx 题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx 分）【题文】某校举行男生乒乓球比赛，比赛分成3个阶段进行，第一阶段：将参加比赛的48名选手分成8个小组，每组6人，分别进行单循环赛；第二阶段：将8个小组产生的前2名共16人再分成个小组，每组人，分别进行单循环赛；第三阶段：由4个小组产生的个第名进行场半决赛和场决赛，确定至名的名次．问：整个赛程一共需要进行多少场比赛？【答案】148【解析】第一阶段中，每个小组内部的个人每人要赛一场，组内赛场，共个小组，有场；第二阶段中，每个小组内部人中每人赛一场，组内赛场，共个小组，有场；第三阶段赛场．根据加法原理，整个赛程一共有场比赛。

【题文】由数字1，2，3组成五位数，要求这五位数中1，2，3至少各出现一次，那么这样的五位数共有________个。

【答案】150【解析】这是一道组合计数问题．由于题目中仅要求，，至少各出现一次，没有确定，，出现的具体次数，所以可以采取分类枚举的方法进行统计，也可以从反面想，从由组成的五位数中，去掉仅有个或个数字组成的五位数即可．(法1)分两类：⑴，，中恰有一个数字出现次，这样的数有(个)；⑵，，中有两个数字各出现次，这样的数有(个)．符合题意的五位数共有(个)．(法2)从反面想，由，，组成的五位数共有个，由，，中的某个数字组成的五位数共有个，由，，中的某个数字组成的五位数共有个，所以符合题意的五位数共有(个)。

【题文】个人围成一圈，从中选出两个不相邻的人，共有多少种不同选法？【答案】35【解析】(法1)乘法原理．按题意，分别站在每个人的立场上，当自己被选中后，另一个被选中的，可以是除了自己和左右相邻的两人之外的所有人，每个人都有种选择，总共就有种选择，但是需要注意的是，选择的过程中，会出现“选了甲、乙，选了乙、甲”这样的情况本来是同一种选择，而却算作了两种，所以最后的结果应该是()(种)．(法2)排除法．可以从所有的两人组合中排除掉相邻的情况，总的组合数为，而被选的两个人相邻的情况有种，所以共有(种)。

2019年六年级数学下学期奥数考试试题含答案

乡镇（街道）学校班级姓名学号 ………密……….…………封…………………线…………………内……..………………不……………………. 准…………………答…. …………题…绝密★启用前2019年六年级数学下学期奥数考试试题含答案题号填空题选择题判断题计算题综合题应用题总分得分考试须知：1、考试时间：100分钟，本卷满分为100分。

2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。

3、请在试卷指定位置作答，在试卷密封线外作答无效，不予评分。

一、填空题（共10小题，每题2分，共计20分）1、陈老师出版了《小学数学解答100问》，获得稿费5000元，按规定，超出800元的部分应缴纳14%的个人所得税。

陈老师应交税（）元。

2、一枝钢笔的单价是a 元，买6枝这样的钢笔需要( )元。

3、在72.5%，79 ，0.7255,0.725 中，最大的数是( )，最小的数是 ( )。

4、妈妈将20000元钱存入银行，定期三年，年利率为2.75%，到期后妈妈可取回本息( )元。

5、分数单位是7 1 的最大真分数是（），它至少再添上（）个这样的分数单位就成了假分数。

6、有一张长48厘米，宽36厘米的长方形纸，如果要裁成若干同样大小的正方形而无剩余，裁成的小正方形的边长最大是( )厘米。

7、一辆汽车从A 城到B 城，去时每小时行30千米，返回时每小时行25千米。

去时和返回时的速度比是（），在相同的时间里，行的路程比是（），往返AB 两城所需要的时间比是（）。

8、1/8的倒数是（）；1的倒数是（）；0.35的倒数是（）。

9、光明饭店今年一月份的营业额是40万元，按规定要缴纳5%的营业税，还要按营业税的7%缴纳城市维护建设税，那么，这个饭店一月份需缴纳营业税（）元和城市维护建设税（）元。

10、在比例尺1：30000000的地图上，量得A 地到B 地的距离是3.5厘米，则A 地到B 地的实际距离是（）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019六年级奥数计数问题及答案
题型：计数问题难度：★★
如果一个大于9的整数，其每个数位上的数字都比它右边数位上的数字小，那么我们称它为"迎春数".那么，小于2008的"迎春数"共有个。

【答案解析】
这是一道组合计数问题.
方法一：枚举法――按位数分类计算.
一、两位数中，"迎春数"个数
(1)十位数字是1，这样的"迎春数"有12，13，…，19，共8个;
(2)十位数字是2，这样的"迎春数"有23，…，29，共7个;
(3)十位数字是3，这样的"迎春数"有34，…，39，共6个;
(4)十位数字是4，这样的"迎春数"有45，…，49，共5个;
(5)十位数字是5，这样的"迎春数"有56，…，59，共4个;
(6)十位数字是6，这样的"迎春数"有67，68，69，共3个;
(7)十位数字是7，这样的"迎春数"有78，79，共2个;
(8)十位数字是8，这样的"迎春数"只有89这1个;
(9)没有十位数字是9的两位的"迎春数";
所以两位数中，"迎春数"共有36个.
二、三位数中，"迎春数"个数
(1)百位数字是1，这样的"迎春数"有123-129，134-139， (189)
共28个;
(2)百位数字是2，这样的"迎春数"有234-239，…，289，共21个;
(3)百位数字是3，这样的"迎春数"有345-349，…，389，共15个;
(4)百位数字是4，这样的"迎春数"有456-459，…，489，共10个;
(5)百位数字是5，这样的"迎春数"有567-569，…，589，共6个;
(6)百位数字是6，这样的"迎春数"有678，679，689，共3个;
(7)百位数字是7，这样的"迎春数"只有789，这1个;
(8)没有百位数字是8，9的三位的"迎春数";
所以三位数中，"迎春数"共有84个.
三、1000-1999的自然数中，"迎春数"个数
(1)前两位数字是12，这样的"迎春数"有1234-1239，…，1289，共21个
(2)前两位数字是13，这样的"迎春数"有1345-1349，…，1389，共15个;
(3)前两位数字是14，这样的"迎春数"有1456-1459，…，1489，共10个;
(4)前两位数字是15，这样的"迎春数"有1567-1569，…，1589，共6个;
(5)前两位数字是16，这样的"迎春数"有1678，1679，1689，共3个;
(6)前两位数字是17，这样的"迎春数"只有1789这1个;
(7)没有前两位数字是18，19的四位的"迎春数";
所以四位数中，"迎春数"共有56个.
四、2000-2008的自然数中，没有"迎春数"
所以小于2008的自然数中，"迎春数"共有36+84+56=176 个.
方法二：利用组合原理?
小于2008的"迎春数"，只可能是两位数、三位数和1000多的数.
计算两位 "迎春数"的个数，它就等于从1-9这9个数字中任意取出2个不同的数字，
每一种取法对应于一个"迎春数"，即有多少种取法就有多少个"迎春数".显然不同的取
法有9×8÷2=36 中，所以两位的"迎春数"共有36个.
同样计算三位数和1000多的数中"迎春数"的个数，它们分别有
9×8×7÷3÷2÷1=84个和8×7×6÷3÷2÷1=56 个.
所以小于2008的自然数中，"迎春数"共有36+84+56=176 个。