三角函数图象的平移和伸缩(后面有高考题练习)
三角函数的平移及伸缩变换(含答案)

三角函数的平移及伸缩变换一、单选题(共8道,每道12分)1.将函数的图象上所有点的纵坐标不变,横坐标缩小到原来的,再把图象上各点向左平移个单位长度,则所得的图象的解析式是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:函数y=Asin(ωx+φ)的图象变换2.已知函数y=f(x)图象上每个点的纵坐标保持不变,横坐标伸长到原来的2倍,然后再将整个图象沿x轴向左平移个单位,沿y轴向下平移1个单位,得到函数,则y =f(x)的表达式时( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:函数y=Asin(ωx+φ)的图象变换3.已知函数,若f(x)的图象向左平移个单位所得的图象与f(x)的图象向右平移个单位所得的图象重合,则的最小值是( )A.2B.3C.4D.5答案:C解题思路:试题难度:三颗星知识点:函数y=Asin(ωx+φ)的图象变换4.已知函数的最小正周期为,将的图象向左平移个单位长度,所得图象关于y轴对称,则的一个值是( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:函数y=Asin(ωx+φ)的图象变换5.偶函数的图象向右平移个单位得到的图象关于原点对称,则的值可以是( )A.1B.2C.3D.4答案:B解题思路:试题难度:三颗星知识点:函数y=Asin(ωx+φ)的图象变换6.已知函数的周期为π,若将其图象沿x轴向右平移a个单位(a >0),所得图象关于原点对称,则实数a的最小值是( )A.πB.C. D.答案:D解题思路:试题难度:三颗星知识点:函数y=Asin(ωx+φ)的图象变换7.函数的图象如图所示,为了得到的图象,则只要将f(x)的图象( )A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度答案:C解题思路:试题难度:三颗星知识点:函数y=Asin(ωx+φ)的图象变换8.将函数的图象向左平移个单位,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:函数y=Asin(ωx+φ)的图象变换。
三角函数图像平移与伸缩练习

三角函数图像平移与伸缩题组练习1.(2020·福建质检)将函数y =sin x 的图像向左平移π2个单位,得到函数y =f (x )的图像,则下列说法正确的是( )A .y =f (x )是奇函数B .y =f (x )的周期为πC .y =f (x )的图像关于直线x =π2对称D .y =f (x )的图像关于点⎝⎛⎭⎫-π2,0对称 答案 D解析 由题意知,f (x )=cos x ,所以它是偶函数,A 错;它的周期为2π,B 错;它的对称轴是直线x =k π,k ∈Z ,C 错;它的对称中心是点⎝⎛⎭⎫k π+π2,0,k ∈Z ,D 对. 2.要得到函数y =cos2x 的图像,只需把函数y =sin2x 的图像( ) A .向左平移π4个单位长度B .向右平移π4个单位长度C .向左平移π2个单位长度D .向右平移π2个单位长度答案 A解析 由于y =sin2x =cos(π2-2x )=cos(2x -π2)=cos[2(x -π4)],因此只需把函数y =sin2x 的图像向左平移π4个单位长度,就可以得到y =cos2x 的图像. 3.若把函数y =f (x )的图像沿x 轴向左平移π4个单位,沿y 轴向下平移1个单位,然后再把图像上每个点的横坐标伸长到原来的2倍(纵坐标保持不变),得到函数y =sin x 的图像,则y =f (x )的解析式为( )A .y =sin(2x -π4)+1B .y =sin(2x -π2)+1C .y =sin(12x +π4)-1D .y =sin(12x +π2)-1答案 B解析 将y =sin x 的图像上每个点的横坐标变为原来的一半(纵坐标保持不变),得到y =sin2x 的图像,再将所得图像向上平移1个单位,得到y =sin2x +1的图像,再把函数y =sin2x +1的图像向右平移π4个单位,得到y =sin2(x -π4)+1的图像,即函数f (x )的图像,所以f (x )=sin2(x -π4)+1=sin(2x -π2)+1,故选B.4.函数y =cos(4x +π3)图像的两条相邻对称轴间的距离为( )A.π8B.π4C.π2 D .π答案 B解析 函数y =cos(4x +π3)图像的两条相邻对称轴间的距离为半个周期,即T 2=2π42=π4.5.将函数y =sin(2x +π4)的图像上各点的纵坐标不变,横坐标伸长到原来的2倍,再向右平移π4个单位,所得到的图像解析式是( )A .f (x )=sin xB .f (x )=cos xC .f (x )=sin4xD .f (x )=cos4x答案 A解析 y =sin(2x +π4)→y =sin(x +π4)→y =sin(x -π4+π4)=sin x .6.(2019·山东理)将函数y =sin(2x +φ)的图像沿x 轴向左平移π8个单位后,得到一个偶函数的图像,则φ的一个可能取值为( )A.3π4B.π4 C .0 D .-π4答案 B解析 把函数y =sin(2x +φ)的图像向左平移π8个单位后,得到的图像的解析式是y =sin(2x +π4+φ),该函数是偶函数的充要条件是π4+φ=k π+π2,k ∈Z ,根据选项检验可知φ的一个可能取值为π4.7.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图像如右图所示,则当t=1100秒时,电流强度是( )A .-5 AB .5 AC .5 3 AD .10 A答案 A解析 由图像知A =10,T 2=4300-1300=1100.∴ω=2πT=100π.∴T =10sin(100πt +φ).(1300,10)为五点中的第二个点,∴100π×1300+φ=π2. ∴φ=π6.∴I =10sin(100πt +π6),当t =1100秒时,I =-5 A ,故选A.8.(2019·福建质检)将函数f (x )=sin(2x +θ)(-π2<θ<π2)的图像向右平移φ(φ>0)个单位长度后得到函数g (x )的图像,若f (x ),g (x )的图像都经过点P (0,32),则φ的值可以是( ) A.5π3 B.5π6 C.π2 D.π6 答案 B解析 因为函数f (x )的图像过点P ,所以θ=π3,所以f (x )=sin(2x +π3).又函数f (x )的图像向右平移φ个单位长度后,得到函数g (x )=sin[2(x -φ)+π3]的图像,所以sin(π3-2φ)=32,所以φ可以为5π6,故选B.9.已知函数y =sin ωx (ω>0)在一个周期内的图像如图所示,要得到函数y =sin(12x +π12)的图像,则需将函数y =sin ωx 的图像向________平移________个单位长度.答案 左,π6解析 由图像知函数y =sin ωx 的周期为T =3π-(-π)=4π, ∴ω=2πT =12,故y =sin 12x .又y =sin(x 2+π12)=sin 12(x +π6),∴将函数y =sin 12x 的图像向左平移π6个单位长度,即可得到函数y =sin(x 2+π12)的图像.10.(2019·重庆文)若将函数f (x )=sin(ωx +φ)⎝⎛⎭⎫ω>0,-π2≤φ<π2图像上每一个点的横坐标缩短为原来的一半,纵坐标不变,再向右平移π6个单位长度得到y =sin x 的图像,则f ⎝⎛⎭⎫π6=________. 答案22解析 将y =sin x 的图像向左平移π6个单位长度可得y =sin ⎝⎛⎭⎫x +π6的图像,保持纵坐标不变,横坐标变为原来的2倍可得y =sin ⎝⎛⎭⎫12x +π6的图像,故f (x )=sin ⎝⎛⎭⎫12x +π6.所以f ⎝⎛⎭⎫π6=sin ⎝⎛⎭⎫12×π6+π6=sin π4=22. 11.若y =A sin(ωx +θ)(A >0,ω>0,|θ|<π2)的图像如图所示,则y =________.答案 2sin(2x +π6)解析 由题图知周期T =1112π-(-π12)=π,∴ω=2ππ=2,且A =2.∴y =2sin(2x +θ).把x =0,y =1代入上式得2sin θ=1, 即sin θ=12.又|θ|<π2,∴θ=π6.即y =2sin(2x +π6).12.(2018·新课标全国Ⅱ文)若函数y =cos(2x +φ)(-π≤φ<π)的图像向右平移π2个单位后,与函数y =sin(2x +π3)的图像重合,则φ=________.答案5π6解析 将y =cos(2x +φ)的图像向右平移π2个单位后得到y =cos[2(x -π2)+φ]的图像,化简得y =-cos(2x+φ),又可变形为y =sin(2x +φ-π2).由题意可知φ-π2=π3+2k π(k ∈Z ),所以φ=5π6+2k π(k ∈Z ),结合-π≤φ<π知φ=5π6.13.若函数y =A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)在闭区间[-π,0]上的图像如图所示,则ω=________.答案 3解析 由函数y =A sin(ωx +φ)的图像可知: T 2=(-π3)-(-23π)=π3,∴T =23π. ∵T =2πω=23π,∴ω=3.14.若函数y =sin2x 的图像向右平移φ(φ>0)个单位,得到的图像恰好关于直线x =π6对称,则φ的最小值是________.答案5π12解析 y =sin2x 的图像向右平移φ(φ>0)个单位,得y =sin2(x -φ)=sin(2x -2φ).因其中一条对称轴方程为x =π6,则2·π6-2φ=k π+π2(k ∈Z ).因为φ>0,所以φ的最小值为5π12.15.设函数y =sin(ωx +φ)(ω>0,φ∈(-π2,π2))的最小正周期为π,且其图像关于直线x =π12对称,则在下面四个结论中:①图像关于点(π4,0)对称;②图像关于点(π3,0)对称;③在[0,π6]上是增函数;④在[-π6,0]上是增函数,所有正确结论的编号为________.答案 ②④解析 ∵y =sin(ωx +φ)的最小正周期为π,∴ω=2ππ=2.又其图像关于直线x =π12对称,得π6+φ=π2+k π(k∈Z ).令k =0,得φ=π3.∴y =sin(2x +π3).当x =π3时,f (π3)=0,∴函数图像关于点(π3,0)对称.所以②正确.解不等式-π2+2k π≤2x +π3≤π2+2k π,得-5π12+k π≤x ≤π12+k π(k ∈Z ),所以④正确.16.(2019·江西景德镇测试)已知函数f (x )=4cos x sin(x +π6)+a 的最大值为2.(1)求实数a 的值及f (x )的最小正周期; (2)在坐标纸上作出f (x )在[0,π]上的图像.答案 (1)a =-1,T =π (2)略解析 (1)f (x )=4cos x (sin x cos π6+cos x sin π6)+a=3sin2x +cos2x +1+a =2sin(2x +π6)+a +1,最大值为3+a =2,∴a =-1.T =2π2=π.(2)列表如下:画图如下:17.(2019·湖北重点中学联考)已知函数f (x )=A sin(ωx +φ)(x ∈R ,A >0,ω>0,|φ|<π2)的部分图像如图所示.(1)试确定函数f (x )的解析式; (2)若f (α2π)=13,求cos(2π3-α)的值.答案 (1)f (x )=2sin(πx +π6) (2)-1718解析 (1)由图像知,f (x )max =A =2,设函数f (x )的最小正周期为T ,则T 4=56-13=12,所以T =2,∴ω=2πT =2π2=π,故函数f (x )=2sin(πx +φ). 又∵f (13)=2sin(π3+φ)=2,∴sin(π3+φ)=1.∵|φ|<π2,即-π2<φ<π2,∴-π6<π3+φ<5π6.故π3+φ=π2,解得φ=π6,∴f (x )=2sin(πx +π6).(2)∵f (α2π)=13,即2sin(π·α2π+π6)=2sin(α2+π6)=13,∴sin(α2+π6)=16.∴cos(π3-α2)=cos[π2-(π6+α2)]=sin(π6+α2)=16.∴cos(2π3-α)=cos[2(π3-α2)]=2cos 2(π3-α2)-1=2×(16)2-1=-1718.。
(完整版)三角函数的平移伸缩变换练习题

三角函数的平移伸缩变换题型一:已知开始和结果,求平移量ϕω【2016高考四川文科】为了得到函数sin()3y x π=+的图象,只需把函数y=sinx 的图象上所有的点( )(A )向左平行移动3π个单位长度 (B) 向右平行移动3π个单位长度 (C ) 向上平行移动3π个单位长度 (D ) 向下平行移动3π个单位长度【】为了得到函数sin(1)y x =+的图象,只需把函数sin y x =的图象上所有的点( ) A .向左平行移动1个单位长度 B .向右平行移动1个单位长度 C .向左平行移动π个单位长度 D .向右平行移动π个单位长度【】要得到函数cos y x =的图象,只需将函数cos y x π⎛⎫=- ⎪3⎝⎭的图象( )(A ).向右平移π6个单位 (B ).向右平移π3个单位 (C ).向左平移π3个单位 (D ).向左平移π6个单位【】要得到函数(21)y cos x =+的图象,只要将函数2y cos x =的图象( ) A .向左平移1个单位 B .向右平移1个单位 C .向左平移12个单位 D .向右平移12个单位【】要得到sin(2)3y x π=-的图象,只需将sin 2y x =的图象 ( )(A )向左平移3π个单位 (B )向右平移3π个单位 (C )向左平移6π个单位 (D )向右平移6π个单位【】.将函数sin 2y x =的图象作平移变换,得到函数sin(2)6y x π=-的图象,则这个平移变换可以是 ( )A. 向左平移6π个单位长度 B. 向左平移12π个单位长度 C. 向右平移6π个单位长度 D. 向右平移12π个单位长度【】为了得到函数4sin(3)()4y x x R π=+∈的图象,只需把函数4sin()()4y x x R π=+∈的图象上所有点( )A 、横坐标伸长到原来的3倍,纵坐标不变B 、横坐标缩短到原来的13倍,纵坐标不变C 、纵坐标伸长到原来的3倍,横坐标不变D 、纵坐标缩短到原来的13倍,横坐标不变.【2015山东】要得到函数4y sin x =-(3π)的图象,只需要将函数4y sin x =的图象( ) (A )向左平移12π个单位 (B )向右平移12π个单位(C )向左平移3π个单位 (D )向右平移3π个单位 【】为了得到函数πsin 23y x ⎛⎫=- ⎪⎝⎭的图像,只需把函数πsin 26y x ⎛⎫=+ ⎪⎝⎭的图像A .向左平移π4个长度单位B .向右平移π4个长度单位C .向左平移π2个长度单位D .向右平移π2个长度单位【】要得到cos(2)4y x π=-的图像,只需将sin 2y x =的图像( )A 向左平移8π个单位B 向右平移8π个单位C 向左平移4π个单位D 向右平移4π个单位【】已知函数()sin 4πf x x ω⎛⎫=+ ⎪⎝⎭()R 0x ω∈>,的最小正周期为π,为了得到函数()cos g x x ω=的图象,只要将()y f x =的图象( )A .向左平移8π个单位长度 B .向右平移8π个单位长度 C .向左平移4π个单位长度D .向右平移4π个单位长度题型二:已知开始,平移量,求结果【】. 将函数sin y x =的图像上所有的点向右平行移动10π个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是 (A )sin(2)10y x π=-(B )sin(2)5y x π=-(C )1sin()210y x π=- (D )1sin()220y x π=-【】函数sin ()y x x =∈R 的图象上所有的点向左平行移动3π个单位长度,再把所得图象上所有点的横坐标缩短到原来的12倍(纵坐标不变),得到的图象所表示的函数是( ) (A )sin(2),3y x x R π=-∈ (B )sin(),26x y x R π=+∈(C )sin(2),3y x x R π=+∈ (D )2sin(2),3y x x R π=+∈【】函数3sin(2)3y x π=+的图象,可由y sinx =的图象经过下述哪种变换而得到 ( )(A )向右平移3π个单位,横坐标缩小到原来的21倍,纵坐标扩大到原来的3倍(B )向左平移3π个单位,横坐标缩小到原来的21倍,纵坐标扩大到原来的3倍(C )向右平移6π个单位,横坐标扩大到原来的2倍,纵坐标缩小到原来的31倍(D )向左平移6π个单位,横坐标缩小到原来的21倍,纵坐标缩小到原来的31倍【】.将函数sin y x =的图象上各点的横坐标扩大为原来的2倍,纵坐标不变,再把所得图象上所有点向左平移3π个单位,所得图象的解析式是 . 【】. 将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是____________▲________________ .【】把函数sin(2)4y x π=+的图像向左平移8π个单位长度,再将横坐标压缩到原来的12,所得函数的解析式为( )。
高考数学三角函数图像平移变换!高考必考内容!3种题型讲解!

⾼考数学三⾓函数图像平移变换!⾼考必考内容!3种题型讲解!题型⼀:函数y=A sin(ωx+φ)的图象及变
换
1.三⾓函数图象变换的思路
先平移后伸缩;先伸缩后平移.值得注意的是,对于三⾓函数图象的平移变换问题,其平移变
换规则是“左加、右减”,并且在变换过程中只变换其⾃变量x,如果x的系数不是1,则需把x的系
数提取后再确定平移的单位长度和⽅向.
题型⼆:由图象求y=A sin(ωx+φ)的解析
式
求函数y=A sin(ωx+φ)+b(A>0,ω>0)中参数的⽅法
(1)求A,b先确定函数的最⼤值M和最⼩值m,则A=(M-m)/2,b=(M+m)/2
(2)求ω先确定函数的周期T,则可得ω=T/2π
(3)求φ
代⼊法.把图象上的⼀个已知点代⼊(此时A,ω,b已知)或代⼊图象与直线y=b的交点求解(此
时要注意交点在上升区间上还是在下降区间上).
题型三:y=A sin(ωx+φ)的图象与性质
函数y=A sin(ωx+φ)的图象与性质是命题的热点,多将图象变换、解析式求法与性质综合⼀起
考查,属中低档题.
常见的命题⾓度有:
(1)图象变换与性质的综合;
(2)解析式的求法与性质的综合;。
三角函数图象求解析式及平移练习题
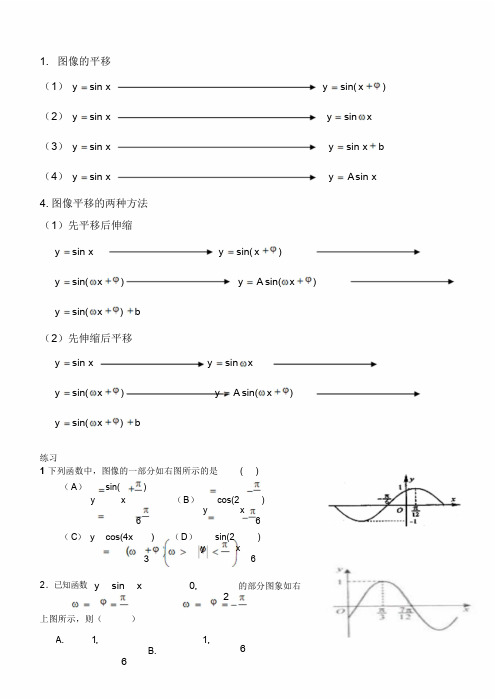
1. 图像的平移(1)y sin x y sin( x ) (2)y sin x y sin x (3)y sin x y sin x b (4)y sin x y A s in x 4. 图像平移的两种方法(1)先平移后伸缩y sin x y sin( x )y sin( x ) y A sin( x )y sin( x ) b(2)先伸缩后平移y sin x y sin xy sin( x ) y A sin( x )y sin( x ) b练习1下列函数中,图像的一部分如右图所示的是( )(A)sin( )y x (B)cos(2 )y x6 6(C)y cos(4x ) (D)sin(2 )y x3 62.已知函数y sin x 0, 的部分图象如右2上图所示,则()A. 1,B.6 1,61C. 2,D.6 2,62.下列函数中,图象的一部分如右图所示的是A. y sin xB. y sin 2x6 6C. y cos 4xD. cos 2y x364、函数y A sin x 的一个周期内的图象如下图,求y 的解析式。
(其中 A 0, 0, )5.已知函数y A sin( x )(A 0,0,| | )的一段图象如图所示,求函数的解析式;6、要得到函数)y 3sin(2 x 的图象,只需将函数y 3 s in 2x 的图象()4(A)向左平移个单位(B)向右平移个单位 4 4 (C)向左平移个单位(D)向右平移个单位8 8 7、将函数y=sin3x 的图象作下列平移可得y=sin(3x+ ) 的图象6(A) 向右平移个单位(B) 向左平移个单位 6 62(C)向右平移个单位(D)向左平移个单位18 188.将函数y sin x 的图象上每点的横坐标缩小为原来的12(纵坐标不变),再把所得图象向左平移个单位,得到的函数解析式为()6xA y sin 2x sin 2 D yB y xC y sin s i nB y xC y sin s i n6 3 2 6 x2 1 29、把函数y cosx 的图象上所有的点的横坐标缩小到原来的一半,纵坐标保持不变,然后把图象向左平移个单位长度,得到新的函数图象,那么这个新函数的解4 析式为x(A)y (B)y (C)y sin 2x(D)y sin 2x cos 2x cos4 2 43.为了得到函数y sin(2x )的图象,可以将函数y cos 2x 的图象()6个单位长度(B) 向右平移(A) 向右平移个单位长度6 3个单位长度(D)向左平移(C)向左平移个单位长度6 34.为得到函数πy x 的图像,只需将函数y sin 2x 的图像()cos 23A .向左平移5π个长度单位B.向右平移125π个长度单位12C.向左平移5π个长度单位D.向右平移65π个长度单位65.将函数y f (x) 的图象上各点的横坐标扩大为原来的 2 倍(纵坐标不变),再将整个图形沿x 轴正向平移,得到的新曲线与函数y 3sin x的图象重合,则f ( x) 3 ()xA. 3sin(2 x )B. 3sin( )3 2 3 C.23sin(2 x ) D.3x 23sin( )2 36.为了得到函数y sin( 2x ) 的图象,可以将函数y cos 2x的图象( )63个单位长度B.向右平移A.向右平移个单位长度6 3个单位长度D.向左平移C.向左平移个单位长度6 37.若将函数y tan x 0 的图像向右平移4 6个单位长度后,与函数y tan x 的图像重合,则的最小值为( )6A.16B.14C.13D.128.设函数 f (x) cos x( >0) ,将y f (x) 的图像向右平移个单位长度后,所得的图像3 与原图像重合,则的最小值等于( )(A )13 (B)3 (C)6 (D)9三角函数图像与性质练习题一.选择题(每小题5分,共100 分)6.将函数y sin x( 0) 的图象按向量 a ,0 平移,平6移后的图象如图所示,则平移后的图象所对应函数的解析式是( )A. y sin( x )B. y sin( x )6 6C. y sin(2 x )D. y sin(2 x )3 3x7.为得到函数y sin( ), x R2 的图像,只需把函数y 2 sin x, x R 的图像上所有的点( )3 6A. 向左平移6 个单位长度,再把所得各点的横坐标缩短到原来的13倍(纵坐标不变)B.向右平移6 个单位长度,再把所得各点的横坐标缩短到原来的13倍(纵坐标不变)个单位长度,再把所得各点的横坐标伸长到原来的 3 倍(纵坐标不变)C.向左平移6个单位长度,再把所得各点的横坐标伸长到原来的 3 倍(纵坐标不变)D.向右平移68.函数 f (x) 2sin x( 0) 在区间,上的最小值是2,则的最小值等于( )3 44A.2 3 B.3 2C.2D.39. 函数 y =sin(2x+)的图象由函数 y=sin2x 的图象经过平移而得到, 这一平移过程可以是 ( ) 3A. 向左平移B.向右平移C.向左平移D.向右平移66 121210. 要得到函数 y= s in(2x- )6的图像,只需将函数 y= c os 2x 的图像 ( )个单位B.向右平移A. 向右平移个单位63个单位D. 向左平移C. 向左平移个单位63 7. 若函数 f (x)sin ( x ) 的图象如图,则和 的取值是 ()yA.1,B.1,3 31C.1 2, 6D.1 2, x 6O29. 函数π y sin 2x 在区间3π ,π的简图是 ( )233y y 1123 xO1O 62361A. B.y y11xO 2631x26 O13xC.D.10.函数y sin(2 x ) cos(2 x ) 的最小正周期和最大值分别为( )6 3A. ,1B. , 2C. 2 ,1D. 2 , 211.已知函数 f (x) sin( x )( 0) 的最小正周期为,则该函数的图象( )35A. 关于点( ,0)3 对称 B.关于直线x对称4C.关于点( ,0)4 对称 D.关于直线x对称311.函数y sin( x )( x R, 0,0 2 ) 的部分图象如图,则( )A. , ,2 43 6B.C. D., ,4 4 45 412.要得到函数y sin x 的图象,只需将函数y cos x 的图象( )A. 向右平移个单位B.向右平移个单位C.向左平移个单位D.向左平移个单位13.设函数 f x sin x 0,0 .若将 f x 的图象沿x 轴向右平移2 16个单位长度,得到的图象经过坐标原点;若将 f x 的图象上所有的点的横坐标缩短到原来的12倍(纵1坐标不变), 得到的图象经过点,16. 则( )A. ,B.6 2 , C.334,8D. 适合条件的, 不存在14.设函数 f (x) sin( x ) 1(0)的导数f (x) 的最大值为3,则f(x)的图象的一条对称轴的6 方程是( )A. xB.9 xC.6xD.3x212.已知函数y A s in( x ) m的最大值为4,最小值为0,最小正周期为,直2 线x是其图象的一条对称轴,则下面各式中符合条件的解析式是()3(A)y 4sin(4 x ) (B)2sin(2 ) 2y x6 3(C)y 2sin(4 x ) 2 (D)2sin(4 ) 2y x3 6π9 函数y=3sin(2 x+3 )的图象,可由y=sin x 的图象经过下述哪种变换而得到6( )(A)向右平移π3 个单位,横坐标缩小到原来的12 倍,纵坐标扩大到原来的3 倍(B)向左平移π3个单位,横坐标缩小到原来的12倍,纵坐标扩大到原来的 3 倍(C)向右平移π6个单位,横坐标扩大到原来的 2 倍,纵坐标缩小到原来的13倍(D)向左平移π6个单位,横坐标缩小到原来的12倍,纵坐标缩小到原来的13倍10 、函数)y s i n(x 在下列哪个区间为增函数. ()43 3(A)][ , (B)[ ,0] (C)[ , ] (D)[ , ]4 4 4 4 2 27、y sin x 的曲线最高点为2, 2 ,离它最近的一个最低点是10, 2 ,则它的解析式xA.f x 2 sin B. 2 sinf x x8 4 8 4xC.f x 2 sin D. 2 sinf x x8 4 8 4如果函数y A s in( x )(A>0,>0,0<<2 ) 的最小值为-2,周期为23,并且经过点(0,- 2 ),求此函数的解析式.7。
2023备考-三角函数专题高频考点《三角函数的平移与伸缩》原卷版

2023备考-三角函数专题高频考点《三角函数的平移与伸缩》(原卷版)三角函数的图象及其变换由函数sin y x =的图象通过变换得到sin()y A x ωϕ=+的图象,有两种主要途径:“先平移后伸缩”与“先伸缩后平移”.在进行图像变换时,提倡先平移后伸缩(先相位后周期),但先伸缩后平移(先周期后相位)在题目中也经常出现,所以必须熟练掌握,无论哪种变化,切记每一个变换总是对变量x 而言的,即图像变换要看“变量x ”发生多大变化,而不是“角”变化多少.真题回顾1.(2022·全国·高考真题(文))将函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭的图像向左平移π2个单位长度后得到曲线C ,若C 关于y 轴对称,则ω的最小值是( ) A .16B .14C .13D .122.(2021·全国(理))把函数()y f x =图像上所有点的横坐标缩短到原来的12倍,纵坐标不变,再把所得曲线向右平移3π个单位长度,得到函数sin 4y x π⎛⎫=- ⎪⎝⎭的图像,则()f x =( )A .7sin 212x x ⎛⎫- ⎪⎝⎭B .sin 212x π⎛⎫+ ⎪⎝⎭C .7sin 212x π⎛⎫- ⎪⎝⎭D .sin 212x π⎛⎫+ ⎪⎝⎭练习挑战1.将函数π()2sin 216f x x ⎛⎫=-- ⎪⎝⎭的图象向左平移π6个单位长度得到函数()g x 的图象,则下列说法错误的是( ) A.函数()g x 的最小正周期是πB.函数()g x 的图象关于点π,112⎛⎫-- ⎪⎝⎭对称C.函数()g x 在ππ,62⎛⎫⎪⎝⎭内单调递减D.函数()g x 在π0,6⎛⎫⎪⎝⎭内的最大值是12.如图是函数sin()()y A x x ωϕ=+∈R 在区间π5π,66⎡⎤-⎢⎥⎣⎦上的图像,为了得到这个函数的图像,需将sin ()y x x =∈R 的图像上所有点( )A.向左平移π3个单位,再把所得图像上各点的横坐标变为原来的12,纵坐标不变 B.向左平移π3个单位,再把所得图像上各点的横坐标变为原来的2倍,纵坐标不变 C.向右平移π6个单位,再把所得图像上各点的横坐标变为原来的12,纵坐标不变 D.向右平移π6个单位,再把所得图像上各点的横坐标变为原来的2倍,纵坐标不变3.要得到函数y =sin 2x 的图象,只需要将函数y =cos ⎝⎛⎭⎫2x -π3的图象( )A .向右平移π6个单位长度 B .向左平移π6个单位长度C .向右平移π12个单位长度 D .向左平移π12个单位长度4.为得到函数)32cos(π+=x y 的图像,只需将函数x y 2sin =的图像( ). A .向左平移125π个单位 B . 向右平移125π个单位 C .向左平移65π个单位 D . 向右平移65π个单位5. 已知)2sin()(π+=x x f ,)2cos()(π-=x x g ,则)(x f 的图像( ). A .与)(x g 图像相同B .与)(x g 图像关于y 轴对称C .是由)(x g 的图像向左平移2π个单位得到 D .是由)(x g 的图像向右平移2π个单位得到6. 已知曲线1cos C y x =:,22πsin 23C y x ⎛⎫=+⎪⎝⎭:,则下面结正确的是( ). A.把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线2CB.把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线2CC.把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线2CD.把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线2C7.已知函数)0)(2sin(21cos cos sin 2sin 21)(2πϕϕπϕϕ<<+-+=x x x f ,其图像过点)21,6(π.(1)求ϕ的值(2)将)(x f 图像上各点的横坐标缩短为原来的21,纵坐标不变,得到函数)(x g y =的图像,求函数)(x g 在]4,0[π上的最大值和最小值。
三角函数的图像和变换以及经典习题和答案
3.4函数sin()y A x ωϕ=+的图象与变换【知识网络】1.函数sin()y A x ωϕ=+的实际意义;2.函数sin()y A x ωϕ=+图象的变换(平移平换与伸缩变换) 【典型例题】 [例1](1)函数3sin()226x y π=+的振幅是 ;周期是 ;频率是 ;相位是 ;初相是 .(1)32; 14π;26x π+;6π (2)函数2sin(2)3y x π=-的对称中心是 ;对称轴方程是;单调增区间是 . (2)(,0),26k k Z ππ+∈;5,212k x k Z ππ=+∈; ()5,1212k k k z ππππ⎡⎤-++∈⎢⎥⎣⎦(3) 将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=- ⎪⎝⎭平移,平移后的图象如图所示,则平移后的图象所对应函数的解析式是( )A .sin()6y x π=+ B .sin()6y x π=- C .sin(2)3y x π=+D .sin(2)3y x π=- (3)C 提示:将函数sin (0)y x ωω=>的图象按向量,06a π⎛⎫=- ⎪⎝⎭平移,平移后的图象所对应的解析式为sin ()6y x πω=+,由图象知,73()1262πππω+=,所以2ω=. (4) 为了得到函数R x x y ∈+=),63sin(2π的图像,只需把函数R x x y ∈=,sin 2的图像上所有的点 ( )(A )向左平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变) (B )向右平移6π个单位长度,再把所得各点的横坐标缩短到原来的31倍(纵坐标不变)(C )向左平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)(D )向右平移6π个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变) (4)C 先将R x x y ∈=,sin 2的图象向左平移6π个单位长度,得到函数2sin(),6y x x R π=+∈的图象,再把所得图象上各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数R x x y ∈+=),63sin(2π的图像(5)将函数x x f y sin )(= 的图象向右平移4π个单位后再作关于x 轴对称的曲线,得到函数x y 2sin 21-=的图象,则)(x f 的表达式是 ( )(A )x cos (B )x cos 2 (C )x sin (D )x sin 2 (5)B 提示: 212sin cos 2y x x =-=的图象关于x 轴对称的曲线是cos 2y x =-,向左平移4π得cos 2()sin 24y x x π=-+=2sin cos x x =[例2]已知函数2()2cos 2,(01)f x x x ωωω=+<<其中,若直线3x π=为其一条对称轴。
三角函数的平移与伸缩变换
三角函数的平移与伸缩变换1、为了得到函数)32sin(π-=x y 的图象,只需把函数)62sin(π+=x y 的图象向____平移_____个单位长度.2、设,0>ω函数2)3sin(++=πωx y 的图象向右平移34π个单位后与原图象重合则ω的最小值是__________.3、将函数x y sin =的图象上所有的点向右平行移动10π个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得函数图象的解析式是_____________.4、将函数x x x f cos sin 3)(-=的图象向左平移m 个单位(m>0),若得到图象对应的函数为偶函数,则m 的最小值是_____________.5、把函数)2||,0)(sin(πϑωϑω<>+=x y 的图象向左平移3π个单位长度,所得曲线的一部分图象如图所示,则( ) A. 6,1πϑω== B. 6,1πϑω-==C. 6,2πϑω== D. 6,2πϑω-==6、已知函数)0,0(2cos )(2>>+=ϖωA x A x f 的最大值为6,其相邻两条对称轴间的距离为4,求.________)20()6()4()2(=+⋅⋅⋅+++f f f f7、右图是函数))(sin(R x x A y ∈+=ϑω在区间)65,6(ππ-上的图象,只要将(1)x y sin =的图象经过怎样的变换? (2)x y 2cos =的图象经过怎样的变换? 8、把x y sin =作何变换可得.1)63sin(8-+=πx y17π12π3xy o1-15π6-π6y x o9、把1)42sin(3+-=πx y 作何变换可得到.sin x y =10、把2)2143sin(21++=x y 作何变换可得到.1)351sin(23++=πx y11、将2)542sin(2++=πx y 做下列变换:(1)向右平移2π个单位长度;(2)横坐标缩短为原来的一半,纵坐标不变; (3)纵坐标伸长为原来的4倍,横坐标不变;(4)沿y 轴正方向平移1个单位,最后得到的函数._________)(==x f y 12、把)(x f y =作如下变换:(1)横坐标伸长为原来的1.5倍,纵坐标不变; (2)向左平移3π个单位长度;(3)纵坐标变为原来的53,横坐标不变;(4)沿y 轴负方向平移2个单位,最后得到函数),423sin(43π+=x y 求).(x f y =13、将)48sin(4ππ+-=x y 作何变换可以得到.sin x y =14、对于)536sin(3x y -=π作何变换可以得到.sin x y =15、把)342cos(3π+=x y 作如下变换:(1)向右平移2π个单位长度;(2)纵坐标不变,横坐标变为原来的31;(3)横坐标不变,纵坐标变为原来的43;(4)向上平移1.5个单位长度,则所得函数解析式为________.16、将x x y cos sin 1+=作何变换可得到.cos sin 2x x y -=17、将x x x y cos sin 3sin 2+=作何变换可得到.sin x y =18、将函数x y sin =的图象向左平移)20(πψψ<≤个单位后,得到函数)6sin(π-=x y 的图象,则._____=ψ19、为了得到函数103lg +=x y 的图象,只需把函数x y lg =的图象作何变换?。
三角函数图象的平移和伸缩(后面有高考题练习)
三角函数图象的平移和伸缩函数sin()y A x k ωϕ=++的图象与函数sin y x =的图象之间可以通过变化A k ωϕ,,,来相互转化.A ω,影响图象的形状,k ϕ,影响图象与x 轴交点的位置.由A 引起的变换称振幅变换,由ω引起的变换称周期变换,它们都是伸缩变换;由ϕ引起的变换称相位变换,由k 引起的变换称上下平移变换,它们都是平移变换.sin y x =2sin 214y x =++ ⎪⎝⎭解:(方法一)①把sin y x =的图象沿x 轴向左平移π4个单位长度,得πsin 4y x ⎛⎫=+ ⎪⎝⎭的图象;②将所得图象的横坐标缩小到原来的12,得πsin 24y x ⎛⎫=+ ⎪⎝⎭的图象;③将所得图象的纵坐标伸长到原来的2倍,得π2sin 24y x ⎛⎫=+ ⎪⎝⎭的图象;④最后把所得图象沿y 轴向上平移1个单位长度得到π2sin 214y x ⎛⎫=++ ⎪⎝⎭的图象.(方法二)①把sin y x =的图象的纵坐标伸长到原来的2倍,得2sin y x =的图象;②将所得图象的横坐标缩小到原来的12,得2sin 2y x =的图象;③将所得图象沿x 轴向左平移π8个单位长度得π2sin 28y x ⎛⎫=+ ⎪⎝⎭的图象;④最后把图象沿y 轴向上平移1个单位长度得到π2sin 214y x ⎛⎫=++ ⎪⎝⎭的图象.说明:无论哪种变换都是针对字母x 而言的.由sin 2y x =的图象向左平移π8个单位长度得到的函数图象的解析式是πsin 28y x ⎛⎫=+ ⎪⎝⎭而不是πsin 28y x ⎛⎫=+ ⎪⎝⎭,把πsin 4y x ⎛⎫=+ ⎪⎝⎭的图象的横坐标缩小到原1π⎛⎫π⎛⎫x+)﹣sin2x+、向左平移个单位个单位个单位个单位按向量A 、B 、C 、D 、3、将函数的图象按向量平移,得到y=f (x )的图象,则f (x )=( )A 、B 、C 、D 、sin (2x )+34、把函数y=(cos3x﹣sin3x)的图象适当变化就可以得到y=﹣sin3x的图象,这个变化可以是()A、沿x轴方向向右平移B、沿x轴方向向左平移C、沿x轴方向向右平移D、沿x轴方向向左平移5、为了得到函数y=的图象,可以将函数y=sin2x的图象()A、向右平移个单位长度B、向右平移个单位长度倍(纵坐标不变),然后个单位,则所得到图象对应的函数解析式为(、、、。
高中数学平移伸缩变换例题
高中数学平移伸缩变换例题
高中数学平移伸缩变换例题指的是涉及平移和伸缩变换的数学问题,通常出现在高中数学课程中。
平移和伸缩是两种基本的几何变换,平移是将图形在平面内沿某一方向移动一定的距离,而伸缩则是改变图形的大小但不改变其形状。
下面提供三道涉及平移和伸缩变换的例题:
1.题目:将函数 y = sin(x) 的图像上所有点向右平移π/6 个单位长度,再把
所得图像上点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是 ___.
2.题目:把函数y = 3sin(2x + π/4) 的图象上各点的横坐标伸长到原来的2
倍(纵坐标不变),再向右平移π/6 个单位长度,所得函数图象的一个对称中心为 ( )
A.(5π/6, 0)
B.(π/6, 0)
C.(π/12, 0)
D. (π/3, 0)
3.题目:函数 f(x) = 3sin(2x - π/3) 的图像为 C,下列结论中正确的是 ___.
①函数 f(x) 的最小正周期为π;
②函数 f(x) 在区间 (-π/12, 5π/12) 内是增函数;
③由函数 f(x) 的图像向右平移π/3 个单位长度可以得到函数 g(x) = 3sin2x 的图像;
④由已知图像可作出的 y = 3sin(x - π/3) 的一个图像是:先作 y = 3sinx 的图像,然后将所得图像上所有点向左平移π/3 个单位长度.
这些例题涉及了平移和伸缩变换的基本概念和性质,通过解决这些问题,学生可以加深对平移和伸缩变换的理解,提高解决相关问题的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数图象的平移和伸缩
函数sin()y A x k ωϕ=++的图象与函数sin y x =的图象之间可以通过变化A k ωϕ,,,来相互转化.A ω,影响图象的形状,k ϕ,影响图象与x 轴交点的位置.由A 引起的变换称振幅变换,由ω引起的变换称周期变换,它们都是伸缩变换;由ϕ引起的变换称相位变换,由k 引起的变换称上下平移变换,它们都是平移变换.
既可以将三角函数的图象先平移后伸缩也可以将其先伸缩后平移. 变换方法如下:先平移后伸缩
sin y x =的图象ϕϕϕ<−−−−−−−→向左(>0)或向右(0)
平移个单位长度
得sin()y x ϕ=+的图象()ωωω
−−−−−−−−−→横坐标伸长(0<<1)或缩短(>1)
1
到原来的纵坐标不变 得sin()y x ωϕ=+的图象()A A A >−−−−−−−−−→纵坐标伸长(1)或缩短(0<<1)
为原来的倍横坐标不变 得sin()y A x ωϕ=+的图象(0)(0)
k k k ><−−−−−−−→向上或向下平移个单位长度
得sin()y A x k ϕ=++的图象. 先伸缩后平移
sin y x =的图象(1)(01)
A A A ><<−−−−−−−−−→纵坐标伸长或缩短为原来的倍(横坐标不变)
得sin y A x =的图象(01)(1)
1
()
ωωω
<<>−−−−−−−−−→横坐标伸长或缩短到原来的纵坐标不变 得sin()y A x ω=的图象
(0)(0)
ϕϕϕω
><−−−−−−−→向左或向右平移
个单位
得sin ()y A x x ωϕ=+的图象(0)(0)
k k k ><−−−−−−−→向上或向下平移个单位长度
得sin()y A x k ωϕ=++的图象. 例1 将sin y x =的图象怎样变换得到函数π2sin 214y x ⎛
⎫=++ ⎪⎝
⎭的图象.
解:(方法一)①把sin y x =的图象沿x 轴向左平移π4个单位长度,得πsin 4y x ⎛
⎫=+ ⎪⎝
⎭的
图象;②将所得图象的横坐标缩小到原来的12,得πsin 24y x ⎛
⎫=+ ⎪⎝⎭的图象;③将所得图象的
纵坐标伸长到原来的2倍,得π2sin 24y x ⎛
⎫=+ ⎪⎝
⎭的图象;④最后把所得图象沿y 轴向上平移
1个单位长度得到π2sin 214y x ⎛
⎫=++ ⎪⎝
⎭的图象.
(方法二)①把sin y x =的图象的纵坐标伸长到原来的2倍,得2sin y x =的图象;②将所得图象的横坐标缩小到原来的
1
2
,得2sin 2y x =的图象;③将所得图象沿x 轴向左平移
π8个单位长度得π2sin 28y x ⎛
⎫=+ ⎪⎝⎭的图象;④最后把图象沿y 轴向上平移1个单位长度得到
π2sin 214y x ⎛
⎫=++ ⎪⎝
⎭的图象.
说明:无论哪种变换都是针对字母x 而言的.由sin 2y x =的图象向左平移π
8
个单位长度得到的函数图象的解析式是πsin 28y x ⎛⎫=+ ⎪⎝⎭而不是πsin 28y x ⎛⎫=+ ⎪⎝⎭,把πsin 4y x ⎛
⎫=+ ⎪⎝
⎭的
图象的横坐标缩小到原来的
12,得到的函数图象的解析式是πsin 24y x ⎛
⎫=+ ⎪⎝
⎭而不是
πsin 24y x ⎛
⎫=+ ⎪⎝
⎭.
对于复杂的变换,可引进参数求解.
例2 将sin 2y x =的图象怎样变换得到函数πcos 24y x ⎛
⎫=- ⎪⎝
⎭的图象.
分析:应先通过诱导公式化为同名三角函数.
解:ππsin 2cos 2cos 222y x x x ⎛⎫⎛
⎫==-=- ⎪ ⎪⎝⎭⎝
⎭,
在πcos 22y x ⎛⎫=- ⎪⎝⎭中以x a -代x ,有ππcos 2()cos 2222y x a x a ⎡⎤⎛
⎫=--=-- ⎪⎢⎥⎣⎦⎝
⎭.
根据题意,有ππ22224x a x --=-,得π
8
a =-.
所以将sin 2y x =的图象向左平移π8个单位长度可得到函数πcos 24y x ⎛
⎫=- ⎪⎝
⎭的图象.
练习
1、要得到函数y=2cos (x+)sin (
﹣x )﹣1的图象,只需将函数
y=sin2x+
cos2x 的图象( )
A 、向左平移个单位
B 、向右平移个单位
C 、向右平移
个单位 D 、向左平移
个单位
2、将函数y=3sin (2x+θ)的图象F 1按向量平移得到图象F 2,
若图象F 2关于直线对称,则θ的一个可能取值是( )
A 、
B 、
C 、
D 、
3、将函数的图象按向量平移,得到y=f(x)的图象,则f(x)=()
A、B、
C、D、sin(2x)+3
4、把函数y=(cos3x﹣sin3x)的图象适当变化就可以得到y=﹣sin3x的图象,这个变化可以是()
A、沿x轴方向向右平移
B、沿x轴方向向左平移
C、沿x轴方向向右平移
D、沿x轴方向向左平移
5、为了得到函数y=的图象,可以将函数y=sin2x的图象()
A、向右平移个单位长度
B、向右平移个单位长度
C、向左平移个单位长度
D、向左平移个单位长度
6、把函数y=sinx的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),然后把图象向左平移个单位,则所得到图象对应的函数解析式为()A、B、
C、D、
1、D
2、A
3、D.
4、D.
5、A.
6、D。
