力对点的矩与力对轴的矩(可修改).ppt
合集下载
(完整版)力与力矩

力矩的量纲是距离乘以力;依照国际单位制,力矩的单位是牛顿-米。
虽然牛顿与米的次序,在数学上,是可以变换的。
BIPM (国际重量测量局) 设定这次序应是牛顿-米,而不是米-牛顿。
事实上,力矩与能量的关系是能量和一个对数矢量2π[lnK]的乘积,即t=2πQ[lnK],[lnk]的方向垂直于作用平面。
因此用焦耳做单位也不是错误的。
做圆周运动时,K=e,因此使 1 牛顿-米的力矩,作用一全转,需要恰巧 2*Pi 焦耳的能量。
定义力对物体的作用效应,除移动效应外,还有转动效应。
当然,量纲相同并不尽是巧合;使 1 牛顿-米的力矩,作用一全转,需要恰巧 2*Pi 焦耳的能量。
静力观念当一个物体在静态平衡时,净作用力是零,对任何一点的净力矩也是零。
关于二维空间,平衡的要求是:x,y方向合力均为0,且合力矩为0.力矩电动机所谓的力矩电动机是一种扁平型多极永磁直流电动机。
其电枢有较多的槽数、换向片数和串联导体数,以降低转矩脉动和转速脉动。
力矩电动机有直流力矩电动机和交流力矩电动机两种。
其中,直流力矩电动机的自感电抗很小,所以响应性很好;其输出力矩与输入电流成正比,与转子的速度和位置无关;它可以在接近堵转状态下直接和负载连接低速运行而不用齿轮减速,所以在负载的轴上能产生很高的力矩对惯性比,并能消除由于使用减速齿轮而产生的系统误差。
交流力矩电动机又可以分为同步和异步两种,目前常用的是鼠笼型异步力矩电动机,它具有低转速和大力矩的特点。
一般地,在纺织工业中经常使用交流力矩电动机,其工作原理和结构和单相异步电动机的相同,但是由于鼠笼型转子的电阻较大,所以其机械特性较软。
动力观念力矩是角动量随时间的导数,就像力是动量随时间的导数。
刚体的角动量是转动惯量乘以角速度。
力对点之矩和轴之矩 ppt课件

矢量方向由右手定则确定; 矢量作用在Op点pt课,件垂直于r 和F所在的平面。 4
力对轴之矩的定义
定义:力使物体绕某一轴转动效应的度量,称 为力对该轴之矩.
力
对 轴
FFz
之
矩
实 例
Fx F
Fy
ppt课件
5
ppt课件
6
ppt课件
7
力对点的矩和力对轴的矩
ppt课件
8
ppt课件
9
力对轴之矩代数量的正负号
ppt课件
10
力对轴之矩的计算
方法一 : 将力向垂直于
该轴的平面投影 ,力的投 影与投影至轴的垂直距 离的乘积.
Mz (F) = Fxyd
= 2(OAB)
ppt课件
11
力对轴之矩的计算
方法二: 将力向三个坐 标轴方向分解,分别求三 个分力对轴之矩,然后 将三个分力对轴之矩 的代数值相加。
ppt课件
15
2
z
Mx 0
F
F z F sin 300
1
My
Fza
Fa 2
F y F cos300
M z F ya
y
3 Fa 2
300
or
x
M
y
zFx
Mx xFz
yF ZzFy 0 aF sin 300
1 2
Fa
M z xF ppt课y 件 yFx
• 1、试求图示中力F对O点的矩。
ppt课件
14
• (a)MO (F ) MO (Fx ) MO (Fy ) MO (Fy ) F sin l • (b)MO (F ) F sin l • (c)MO (F ) MO (Fx ) MO (Fy ) F cosFl2 sin (l1 l3) • (d) MO (F ) MO (Fx ) MO (Fy ) MO (Fy ) F sin l12 l22
力和力矩(课堂PPT)

21
N=mg=2.0×103×9.8 =1.96×104(N)
f=N=0.30×1.96×104
=5.88×103 (N) F=f=5.88×103 (N)
为了省力,可在车床底座下搁置 一些圆木或钢管,使车床在圆木 或钢管上滚动前进。
22
2.静摩擦力
(1)静摩擦实验
23
(2)静摩擦力
当一个物体相对于另一个物体有滑动趋势, 而没有相对滑动时,这个物体将受到另一个物 体的阻碍作用,这时产生的摩擦叫做静摩擦。
选择某一标度,如取10mm长的线段表示10N的力,作出 力的平行四边形,则表示F1的线段长30mm,表示F2的线段长 40mm。
用刻度尺量得表示合力F的对角线长为50mm,所以合力 的大小F=10×50/10=50N。
用角度尺量得合力F与力F1的夹角为53。 整个过程如下页动画所示。
35
36
3.多力合成
按力的性质分,有重力、弹力和摩擦力。 按力的作用效果分,有拉力、压力、支持 力、动力、阻力等。
6
二、重力
1.重力 由于地球吸引而使物体受到的力
叫做重力。
重力的方向是竖直向下的。 重力的大小G=mg。
7
例子:苹果成熟从树上落下。
8
2.重心
地球对物体的重 力作用在物体的各个 部分。从效果上看, 我们通常认为整个物 体受到的重力作用在 一个点上,这个点叫 做物体的重心。
平行四边形得
F1=G·sin F2=G·cos
47
§1.3 物体的受力分析
一、牛顿第三定律 二、物体的受力分析
48
一、牛顿第三定律
1.物体间的作用总是相互的
49
2.作用力与反作用力
我们把物体间相互作用的这一对力叫做作 用力与反作用力。如果把其中一个力叫做作用 力,那么另一个力就叫反作用力。
N=mg=2.0×103×9.8 =1.96×104(N)
f=N=0.30×1.96×104
=5.88×103 (N) F=f=5.88×103 (N)
为了省力,可在车床底座下搁置 一些圆木或钢管,使车床在圆木 或钢管上滚动前进。
22
2.静摩擦力
(1)静摩擦实验
23
(2)静摩擦力
当一个物体相对于另一个物体有滑动趋势, 而没有相对滑动时,这个物体将受到另一个物 体的阻碍作用,这时产生的摩擦叫做静摩擦。
选择某一标度,如取10mm长的线段表示10N的力,作出 力的平行四边形,则表示F1的线段长30mm,表示F2的线段长 40mm。
用刻度尺量得表示合力F的对角线长为50mm,所以合力 的大小F=10×50/10=50N。
用角度尺量得合力F与力F1的夹角为53。 整个过程如下页动画所示。
35
36
3.多力合成
按力的性质分,有重力、弹力和摩擦力。 按力的作用效果分,有拉力、压力、支持 力、动力、阻力等。
6
二、重力
1.重力 由于地球吸引而使物体受到的力
叫做重力。
重力的方向是竖直向下的。 重力的大小G=mg。
7
例子:苹果成熟从树上落下。
8
2.重心
地球对物体的重 力作用在物体的各个 部分。从效果上看, 我们通常认为整个物 体受到的重力作用在 一个点上,这个点叫 做物体的重心。
平行四边形得
F1=G·sin F2=G·cos
47
§1.3 物体的受力分析
一、牛顿第三定律 二、物体的受力分析
48
一、牛顿第三定律
1.物体间的作用总是相互的
49
2.作用力与反作用力
我们把物体间相互作用的这一对力叫做作 用力与反作用力。如果把其中一个力叫做作用 力,那么另一个力就叫反作用力。
力矩、力偶与力的平移

§2-2
力矩、力偶与力的平移
一、力对点之矩(力矩)
力对点之矩(力矩)是指力使物体绕某点转动效应 的量度。
矩心O
力臂d
力矩:力的大小(F)与力臂(d)的乘积再冠以适当的正负号(±)来 表示力F 使物体绕O点转动的效应,称为力F 对O 点的矩,简称力矩。
MO (F ) Fd
MO(F)——代数量(标量),单位:N· m。
§2-2 力矩、力偶与力的平移
2.力偶的性质 ①力偶在任意坐标轴上的投影等于零。力偶不能合成 为一个力,也不能用一个力来平衡,力偶只能由力偶 来平衡。
A
F
B
F F cos F cos 0
x
F
力和力偶是静力学的两个 基本要素。力偶对刚体只 有转动效应,而无移动效 x 应。
M
M
M
§2-2力矩、力偶与力的平移
三、力的平移定理
作用于刚体上的力,可平移至 该刚体内任一点,但须附加一力偶, 其力偶矩等于原力对平移点之矩。
M B M B (F ) Fd
F
A
(加)
F F A F' = -F" = F
B
B
d
F
B
MB
F
A
仅适应于同一刚体。
§2-2力矩、力偶与力的平移 力的平移定理的应用:
力矩、力偶与力的平移
例2-3已知Fn、、r,
求力 Fn 对于轮心O的力矩。 解:利用力矩定理计算
M O ( Fn ) M O ( Fr ) M O ( Fτ ) M O ( Fτ ) Fn r cos
Fτ
O
Fn
r
d
力矩、力偶与力的平移
一、力对点之矩(力矩)
力对点之矩(力矩)是指力使物体绕某点转动效应 的量度。
矩心O
力臂d
力矩:力的大小(F)与力臂(d)的乘积再冠以适当的正负号(±)来 表示力F 使物体绕O点转动的效应,称为力F 对O 点的矩,简称力矩。
MO (F ) Fd
MO(F)——代数量(标量),单位:N· m。
§2-2 力矩、力偶与力的平移
2.力偶的性质 ①力偶在任意坐标轴上的投影等于零。力偶不能合成 为一个力,也不能用一个力来平衡,力偶只能由力偶 来平衡。
A
F
B
F F cos F cos 0
x
F
力和力偶是静力学的两个 基本要素。力偶对刚体只 有转动效应,而无移动效 x 应。
M
M
M
§2-2力矩、力偶与力的平移
三、力的平移定理
作用于刚体上的力,可平移至 该刚体内任一点,但须附加一力偶, 其力偶矩等于原力对平移点之矩。
M B M B (F ) Fd
F
A
(加)
F F A F' = -F" = F
B
B
d
F
B
MB
F
A
仅适应于同一刚体。
§2-2力矩、力偶与力的平移 力的平移定理的应用:
力矩、力偶与力的平移
例2-3已知Fn、、r,
求力 Fn 对于轮心O的力矩。 解:利用力矩定理计算
M O ( Fn ) M O ( Fr ) M O ( Fτ ) M O ( Fτ ) Fn r cos
Fτ
O
Fn
r
d
力矩和力偶

公法线
G
A FN
公切线
节圆
20 FN
FN 20 压力角
车轮与钢轨
光滑点接触:
B
FNB
凸轮与顶杆
A
FNA FNA A
两轮齿啮合
O
G
B FNB
C FNC
FR
滑槽与销钉
滑道、导轨:约束力垂直于滑道、导轨,指向待定。
A O
B
FNB
3. 光滑铰链约束
(1) 光滑圆柱铰链 (中间铰链)约束
两个或两个以上物体上做出相同直径的孔并用一 个圆柱形销钉连接起来,即构成圆柱铰链(又称为中 间铰链)。
向,则投影为正
试分别求出图中各力在X轴和Y轴上投影。
已知 F1 100N F2 150N F3 F4 200N ,各力方向如图所示。
【解】可得出各力在x,y轴上的投影为
,
F1x F1 cos 45 100N 0.707 = 70.7N
,
F1y F1 sin 45 100N0.707 = 70.7N
R
F2
F1 a b cx 合力的投影
y
Rx
Ry R
x
试分别求出图中各力的合力在x轴和y轴上投影。
已知 F1 20N F2 40N F3 50N ,各力方向如图所示。
【解】 可得出各力的合力在x、y轴上的投影为
FRx
Fx F1 cos 90 F2 cos 0 F3
3 32 42
,
直于销钉轴线的平面内,通过铰链的中心,
方向未知,常用过铰链中心的两个正交分力
表示 。
A
FAx
FAy A
FAx
FAy
A
B
B
G
A FN
公切线
节圆
20 FN
FN 20 压力角
车轮与钢轨
光滑点接触:
B
FNB
凸轮与顶杆
A
FNA FNA A
两轮齿啮合
O
G
B FNB
C FNC
FR
滑槽与销钉
滑道、导轨:约束力垂直于滑道、导轨,指向待定。
A O
B
FNB
3. 光滑铰链约束
(1) 光滑圆柱铰链 (中间铰链)约束
两个或两个以上物体上做出相同直径的孔并用一 个圆柱形销钉连接起来,即构成圆柱铰链(又称为中 间铰链)。
向,则投影为正
试分别求出图中各力在X轴和Y轴上投影。
已知 F1 100N F2 150N F3 F4 200N ,各力方向如图所示。
【解】可得出各力在x,y轴上的投影为
,
F1x F1 cos 45 100N 0.707 = 70.7N
,
F1y F1 sin 45 100N0.707 = 70.7N
R
F2
F1 a b cx 合力的投影
y
Rx
Ry R
x
试分别求出图中各力的合力在x轴和y轴上投影。
已知 F1 20N F2 40N F3 50N ,各力方向如图所示。
【解】 可得出各力的合力在x、y轴上的投影为
FRx
Fx F1 cos 90 F2 cos 0 F3
3 32 42
,
直于销钉轴线的平面内,通过铰链的中心,
方向未知,常用过铰链中心的两个正交分力
表示 。
A
FAx
FAy A
FAx
FAy
A
B
B
力对点的矩与力对轴的矩
空间力系中,各力作用线与矩心所确定的力矩平面不再重合
F1
F2
F3
F4
F5
O
{ F1、F2、F3、F4 }
{ F1、F2、F4、F5 }
空间力系中,力对矩心的矩取决于三方面(要素)
①力矩的大小(F.d)
②力矩平面在空间中的方位(法线方位)
③力矩平面内,力使物体绕矩心的转向
——需用矢量表示空间力系中力对点的矩
Fv
= MO( Fv ) + MO( Fh )
§2.5 力对轴之矩
一、力对轴之矩的概念
F
xy
z
d
Fz
Fxy
过力 F 的始端做垂直力的平面 xy
将力 F 分解
Fz∥z 轴
Fxy⊥z 轴
定义: Fxy 对 O 点之矩为力 F 对 z 轴之矩:Mz ( F )
即 Mz ( F ) = MO ( Fxy ) =Fxy .d
同理力F 对 ox 轴的矩为
= -Fy.z + Fz .y
力F 对 oy 轴的矩为
= -Fz.x + Fx .z
2.5 力对轴之矩
二、力对点之矩与力对过该点的轴之矩的关系
Fx
Fy
Fz
Fxy
F
O
y
z
x
A
B
y
x
z
O′
A点坐标:x、y、z
F 投影:Fx、Fy、Fz
Mx (F )= yFz – zFy
一、平面力系中力对点的矩
标量
O
F
d
A
B
1. 矩心不一定要选为物体可以绕之转动的固定点。
2. 力为0或力作用线过矩心时,力矩为0。
F1
F2
F3
F4
F5
O
{ F1、F2、F3、F4 }
{ F1、F2、F4、F5 }
空间力系中,力对矩心的矩取决于三方面(要素)
①力矩的大小(F.d)
②力矩平面在空间中的方位(法线方位)
③力矩平面内,力使物体绕矩心的转向
——需用矢量表示空间力系中力对点的矩
Fv
= MO( Fv ) + MO( Fh )
§2.5 力对轴之矩
一、力对轴之矩的概念
F
xy
z
d
Fz
Fxy
过力 F 的始端做垂直力的平面 xy
将力 F 分解
Fz∥z 轴
Fxy⊥z 轴
定义: Fxy 对 O 点之矩为力 F 对 z 轴之矩:Mz ( F )
即 Mz ( F ) = MO ( Fxy ) =Fxy .d
同理力F 对 ox 轴的矩为
= -Fy.z + Fz .y
力F 对 oy 轴的矩为
= -Fz.x + Fx .z
2.5 力对轴之矩
二、力对点之矩与力对过该点的轴之矩的关系
Fx
Fy
Fz
Fxy
F
O
y
z
x
A
B
y
x
z
O′
A点坐标:x、y、z
F 投影:Fx、Fy、Fz
Mx (F )= yFz – zFy
一、平面力系中力对点的矩
标量
O
F
d
A
B
1. 矩心不一定要选为物体可以绕之转动的固定点。
2. 力为0或力作用线过矩心时,力矩为0。
第三章 空间力系

M y (F) M y (Fx ) M y (Fy ) M y (Fz ) Fx z Fz x Mz (F) Fy x Fx y
MO (F)x yFz zFy M x (F ) MO (F ) y zFx xFz M y (F )
MO (F)z xFy yFx M z (F)
1)力 F 的大小为 F Fx2 Fy2 Fz2 5 2 kN
2)力 F 的方向余弦以及与坐标轴的夹角为
cos F ,i 3 0.424; F ,i θ 64.9 52
cos F , j 4 0.566 ; F , j β 55.55 52
cos F ,k 5 0.707 ; F ,k γ 180 45 135 52
Fx F cos , Fy F cos , Fz F cos (3 1)
5
第三章 空间力系
§3-1 空间汇交力系 2)二次投影法(间接投影法)
当力与轴Ox,Oy正向夹角不易确定 时,可先将 F 投影到坐标平面xy上,得 Fxy,再将Fxy投影到x,y轴上,于是投影 的大小为:
Fx Fxy cos F sing cos Fy Fxy sin F sing sin
x
解:由题知:
Fx 4.5kN ;Fy 6.3kN ;Fz 18kN
y Fy
β γ
\力F 的大小
Fz
F Fx2 Fy2 Fz2 19.6 kN
zF
力F 的方向余弦,及与坐标轴的夹角为
cos Fx 4.5 0.220, 76.7
F 19.6
cos Fy 6.3 0.322, 71.1
侧面 风力
b
(a)图为空间汇交力系;(b)图为空间任意力系 (b)图中去了风力为空间平行力系。
MO (F)x yFz zFy M x (F ) MO (F ) y zFx xFz M y (F )
MO (F)z xFy yFx M z (F)
1)力 F 的大小为 F Fx2 Fy2 Fz2 5 2 kN
2)力 F 的方向余弦以及与坐标轴的夹角为
cos F ,i 3 0.424; F ,i θ 64.9 52
cos F , j 4 0.566 ; F , j β 55.55 52
cos F ,k 5 0.707 ; F ,k γ 180 45 135 52
Fx F cos , Fy F cos , Fz F cos (3 1)
5
第三章 空间力系
§3-1 空间汇交力系 2)二次投影法(间接投影法)
当力与轴Ox,Oy正向夹角不易确定 时,可先将 F 投影到坐标平面xy上,得 Fxy,再将Fxy投影到x,y轴上,于是投影 的大小为:
Fx Fxy cos F sing cos Fy Fxy sin F sing sin
x
解:由题知:
Fx 4.5kN ;Fy 6.3kN ;Fz 18kN
y Fy
β γ
\力F 的大小
Fz
F Fx2 Fy2 Fz2 19.6 kN
zF
力F 的方向余弦,及与坐标轴的夹角为
cos Fx 4.5 0.220, 76.7
F 19.6
cos Fy 6.3 0.322, 71.1
侧面 风力
b
(a)图为空间汇交力系;(b)图为空间任意力系 (b)图中去了风力为空间平行力系。
理论力学ppt

三.力对点的矩
z
B
1.力对点的矩
mo(F)
mo(F) = r×F
mo(F)表示力F绕O点
A
r
O
y
转动的效应.O点称为矩
d
x
心.力矩矢是定位矢量.
力矩的三要素:力矩的大小;力矩平面的
方位;力矩在力矩平面内的转向.
力矩的几何意义: mo(F) =±2OAB面积=±Fd 力矩的单位: N·m 或 kN·m
a an2 at2 R 2 4
方向为
tan
at an
R 2R
2
结论: (1)在每一瞬时,转动刚体内所有各点的速度和加速 度的大小,分别与这些点到转轴的距离成正比。
(2)在每一瞬时,转动刚体内所有各点的全加速度 a 的方
向与半径间的夹角 都相同。
速度分布图
加速度分布图
四 刚体的转动惯量与飞轮的作用
1.转动惯量的概念
n
I mi i2 i 1
转动惯量反映物体转动时惯性的大小。物 体的转动惯量,一方面决定于物体的形状 ,另一方面又决定于转动轴的位置。
四 刚体的转动惯量与飞轮的作用
2.飞轮的作用 (1)使转速变化均匀 (2)改善扭转特性,减缓机械振动 (3)改善机器的启动和操纵性能
三.力对点的矩
2.合力距定理
定理:平面汇交力 系的合力对平面内任一 点之距,等于其所有分 力对于同一点力矩的代 数和
四.力偶及其性质
F
1力偶(F ,F)
B A
力偶作用面和力偶臂d.
F´
力偶无合力.因此力偶不能与一个力等效,也不 能用一个力来平衡.力偶只能与力偶等效或平衡.
四.力偶及其性质 2力偶的三要素
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
优选
13
Fxy
过力 F 的始端做垂直力的平面 xy 将力 F 分解
Fz∥z 轴 Fxy⊥z 轴
定义: Fxy 对 O 点之矩为力 F 对 z 轴之矩:Mz ( F )
即 Mz ( F ) = MO ( Fxy ) =Fxy .d
力对某轴之矩,等于力在垂直于该轴的平 面上的分力对该轴与此平面交点的矩。
优选
9
第二章 平面汇交力系与平面力偶系
F
α
Fv
例:求力 F 对 O 的矩。
解:将力 F 沿水平垂直方向分解
则 MO( F ) =Σ MO( Fi ) = MO( Fv ) + MO( Fh )
0 Fsin a2 b2
Fsin a2 b2
优选
8
第二章 平面汇交力系与平面力偶系
§2.5 力对轴之矩
一、力对轴之矩的概念
z
F
Fz
O
xy d
汇交力系的合力对任一点的力矩矢量,等于力系中各分 力对同一点的力矩矢量的矢量和。
——汇交力系合力之矩定理
对于平面汇交力系,各力对力系平面内任一点的矩矢量共 线,因此可看作代数量。
此时合力之矩等于各分力之矩的代数和。
MO( FR ) =优Σ选MO( Fi )
7
第二章 平面汇交力系与平面力偶系
a O
b Fh
优选
1
第二章 平面汇交力系与平面力偶系
§2.4 力对点的矩
一、平面力系中力对点的矩
标量
★注意
O
B
d
F
A
1. 矩心不一定要选为物体可以绕之转动的固定点。
2. 力为0或力作用线过矩心时,力矩为0。
3. 力沿其作用线滑动时,力矩值不变。
4. 必须指明矩心,力优选矩才有意义。
2
第二章 平面汇交力系与平面力偶系
§2.5 力对轴之矩
一、力对轴之矩的概念
z
F
Fz
O
xy d
Fxy
Mz ( F ) =Fxy.d ★:注意
①力对轴之矩是代数量,正负由右手 螺旋法则确定;
②力作用线与轴平行或相交(即力 与轴共面)时,力对该轴矩为零;
③力沿其作用线移动时,它对轴之 矩不变。
优选
10
第二章 平面汇交力系与平面力偶系
§2.5 力对轴之矩
MO(F)
O
①过矩心作垂直于力矩平面的矢量, 其长度表示力矩的大小
②矢量的方向表示力矩平面的法线方向
F
③矢量的指向按右手螺旋法则确定
空间力系中力对优选点的矩矢量 MO(F)
4
第二章 平面汇交力系与平面力偶系
z MO(F)
B
rOA
F A
O
y
d
|MO( F ) |= F.d =2S∆OAB
定义矢量 rOA
力F优选对 oy 轴的矩为 = -Fz.x + Fx .z 11
第二章 平面汇交力系与平面力偶系
§2.5 力对轴之矩
二、力对点之矩与力对过该点的轴之矩的关系
z Fz
A点坐标:x、y、z F 投影:Fx、Fy、Fz
B
O′
F
Mx (F )= yFz – zFy
A O Fx
zx
Fy
Fxy y
My (F )= zFx - xFz Mz (F )= xFy - yFx.
第二章 平面汇交力系与平面力偶系
§2.4 力对点的矩
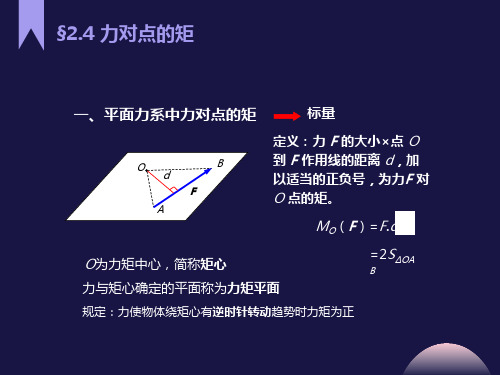
一、平面力系中力对点的矩
标量小×点 O 到 F 作用线的距离 d,加 以适当的正负号,为力F 对 O 点的矩。
MO(F)=F.d
O为力矩中心,简称矩心
=2S∆OAB
力与矩心确定的平面称为力矩平面
规定:力使物体绕矩心有逆时针转动趋势时力矩为正
§2.4 力对点的矩
二、空间力系中力对点的矩
平面力系中,各力作用线与矩心所确定的力矩平面是重合的
{ F1、F2、F3、F4 }
O
F3
F5
F2
F4
F1
{ F1、F2、F4、F5 }
空间力系中,各力作用线与矩心所确定的力矩平面不再重合
优选
3
第二章 平面汇交力系与平面力偶系 空间力系中,力对矩心的矩取决于三方面(要素) ①力矩的大小(F.d) ②力矩平面在空间中的方位(法线方位) ③力矩平面内,力使物体绕矩心的转向 ——需用矢量表示空间力系中力对点的矩
y
力F 对 O 点之矩矢量的解析表达式
x
MO (F )=( yFz – zFy) i + ( zFx – xFz) j +( yFz – zFy) k
力对某点矩矢量在通过该点的优选任一轴上的投影等于力对该轴的1矩2
第二章 平面汇交力系与平面力偶系
[MO( F )]x = Mx ( F ) [MO( F )]y = My ( F ) [MO( F )]z = Mz ( F ) MO (F )=[Mx ( F )] i + [My ( F )] j + [Mz ( F )] k
二、力对点之矩与力对过该点的轴之矩的关系
z Fz
O′
A
O Fx
z y
B F
Fy
Fxy y
x
A点坐标:x、y、z F 投影:Fx、Fy、Fz 力F 对 oz 轴的矩为 Mz ( F ) = MO′ ( Fxy )
= MO′ ( Fx ) + MO′ ( Fy ) = -Fx.y + Fy .x
x
同理力F 对 ox 轴的矩为 = -Fy.z + Fz .y
[MO( F )]z = xFy - yFx
优选
6
第二章 平面汇交力系与平面力偶系
§2.4 力对点的矩
三、汇交力系合力之矩定理
n
对于由n个力组成的汇交力系 FR F1 F2 Fn Fi Fi i 1 MO( FR ) = rOA×FR = rOA×ΣFi =∑(rOA×Fi) =ΣMO( Fi )
MO( F ) = rOA×F
空间力系中,力对点的矩矢量 等于力始点相对于矩心的矢量 与力矢量的矢量积
x
rOA投影(A点坐标):x、y、z rOA = x i +y j +z k
F 投影:Fx、Fy、Fz F =Fx i +Fy j +Fz k
i jk
MO( F ) = rOA×F x y z
优选Fx Fy Fz
5
第二章 平面汇交力系与平面力偶系
i jk MO( F ) = rOA×F x y z
Fx Fy Fz
yFz zFy i zFx xFz j xFy yFx k
——力对点矩矢量的解析表达式
力对点的矩矢量在 x、y、z 轴上的投影
[MO( F )]x = yFz - zFy
[MO( F )]y = zFx - xFz
