相空间中非完整可控力学系统的对称性摄动与绝热不变量
束方平 1211083006 - 欢迎光临苏州科技学院数理学院

2013年数理学院研究生学术报告会时间:11月20日地点:逸夫楼224数理学院2013年11月18日研究生学术报告会论文摘要题目:《凸体p -临界点的性质》报告人:黄星1111081001 指导教师:国起摘要:本文研究了新近引进的p -非对称度及相应的仿射共变p -临界点的一些基本性质。
证明了p -临界点关于p 的连续性)1(+∞<<p ; 研究了当+∞→p 时p -临界点的变化趋势以及收敛凸体列的p -临界点的变化趋势。
题目:《含时滞的非完整力学系统的Noether 对称性和守恒量》 报告人:金世欣1111081002 指导教师:张毅摘要:本文主要研究含时滞的Chetaev 型非完整系统变分问题的Noether 对称性及其守恒量。
首先,依据含时滞的非保守系统的Hamilton 原理以及Lagrange 乘子法,建立含时滞的非完整系统的运动微分方程;其次,根据含时滞的Hamilton 作用量的无限小群变换下的广义准不变性,给出含时滞的非完整系统以及相应完整系统的Noether 广义准对称变换定义和判据;最后,建立含时滞的非完整系统和相应完整系统的Noether 广义准对称变换与守恒量之间的联系。
并举例说明结果的应用。
题目:《混合型渐近非扩张映射合成隐迭代序列的收敛性定理》 报告人:刘涌泉1111081003 指导教师:郭伟平摘要:本文在Banach 空间中讨论了一有限族渐近非扩张自映射与一有限族渐近非扩张非自映射,并获得了其关于合成隐迭代的强收敛和弱收敛定理。
本文的结果推广了一些已有结果。
题目:《(3,p)型二步幂零李代数导子的一个充要条件》报告人:潘林辉1111081004 指导教师:任斌摘要:找出导子的各种等价条件是刻画出李代数的导子代数的有效途径。
本文通过矩阵的巧妙计算, 得到了三维中心的二步幂零李代数导子的一个充要条件。
题目:《几乎凸集的基本性质》报告人:王禹1111081005 指导教师:国起摘要:几乎凸集关于Minkowski 加法,笛卡尔乘积,仿射映射和交集运算下的性质。
广义Birkhoff系统Lie对称性的摄动与绝热不变量

中 图分 类 号 : 3 6 O 1
文 献标 识 码 : A
文章 编 号 : 0 17 1 (0 10 — 3 l0 10 — 19 2 1 )3 0 1一 6
Pe t r a i n t e S m m e re n i b t n a i n sf r r u b to o Li y t isa d Ad a a i I v ra t o c Ge e aie r h f a y t m s n r l d Bi k o z i n S se
d a ai n ai n ft e s se i o ti e . e e d o e p p r a x mp e i gv n t l s a e t ea p ia in o e ib t i v ra to y tm s b an d I t n ft a e , n e a l ie o i u t t h p l t ft c h nh h s l r c o h
r u t. es ls
Ke r s: e e aie i h f a y tm ;L e s mme r ;p ru b t n;a ib t n a in y wo d g n r l d B r of n s se z k i i y t y e r ai t o d a ai i v r t c a
df r n il e u t n n e h n n t s lt n f r t n ,h i y i e e t q ai s u d r te i f i i r soma i s t e L e s mme r f te g n r l e r h f a y tm s f a o i e ma a o t o h e e ai d Bi o n s s y z k i e i
【国家自然科学基金】_无限小变换_基金支持热词逐年推荐_【万方软件创新助手】_20140801
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
2011年 科研热词 推荐指数 特殊无限小变换 2 特殊守恒量 2 守恒量 2 mei守恒量 2 lagrange系统 2 非完整系统 1 翻译方法 1 绝热不变量 1 离散 1 确定方程 1 相对运动动力学 1 独立变量 1 特殊统一对称性 1 特殊noether-lie对称性 1 无限小变换 1 摄动 1 广义hamilton系统 1 广义birkhoff系统 1 对称性 1 变质量 1 动力学系统 1 三体问题 1 noether对称性 1 nielsen方程 1 mei对称性 1 lie对称性 1 kdv 1 hojman守恒量 1 h6non-heiles方程 1 burgers方程 1 appell方程 1
推荐指数 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1
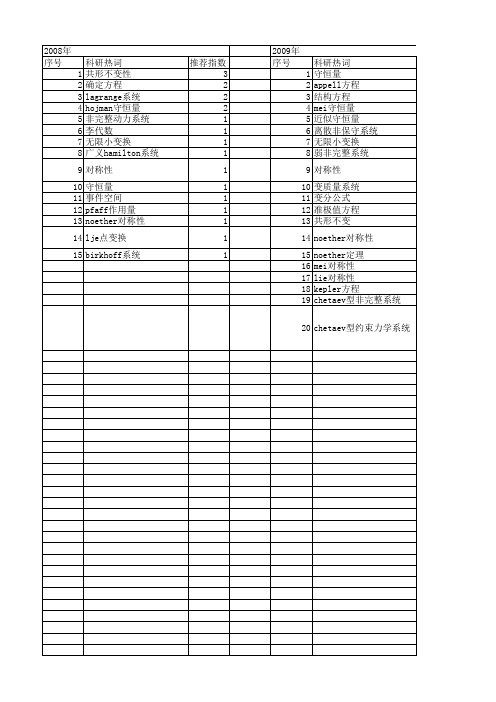
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
科研热词 守恒量 appell方程 结构方程 mei守恒量 近似守恒量 离散非保守系统 无限小变换 弱非完整系统 对称性 变质量系统 变分公式 准极值方程 共形不变 noether对称性 noether定理 mei对称性 lie对称性 kepler方程 chetaev型非完整系统 chetae4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
科研热词 推荐指数 mei对称性 3 noether对称性 2 nielsen方程 2 lie对称性 2 hojman守恒量 2 结构方程 1 约束力学系统 1 积分 1 相对运动动力学系统 1 无限小正则变换 1 无限小变换 1 新的结构方程 1 新的守恒量 1 新守恒量 1 新型守恒量 1 广义tzénoff方程 1 广义birkhoff系统 1 完整系统 1 守恒量 1 nielsen equation, mei symmetry, 1 structural equati mei对称 1 hénon-heiles系统 1 h·non-heiles系统 1 birkhoff系统 1 a型 1 appell方程 1
苏州科技学院学报(自然科学版)2011年总目次

吴健 荣 (9 ) 李元 成 (4 1) 李 燕 (9 1) 徐 孝文 (4 2) 董延 茂 ( 7 2) 魏 杰 ( 2 3)
T/n S J e P O 电极 电催 化 氧 化 氨 氮 的研究 … … … …… … … …… … … …… … 乐 天祥 i O一 bO F — b S 基 于 We ev e 的虚 拟 仿真 系 统研 究 与应 用 … … …… 奚 雪 峰 bS ri s c
Vo . No 4 1 28 .
De c. 2 1 01
2 1 年总 目次 0 1
第 1期
B nc a ah空 间 中一致 , 李 普西 兹 映射 的强 收敛 问 题 …… …… … …… … …… …… …… …… … …… 李 晓南 (1 J 一 )
L b su — t le 型模 糊 C o ut 分 的定 义及 其 基本 性 质 …… …… … …… …… …… 蒋诚 钢 吴 健荣 (6 e ege Si  ̄ s e h qe积 )
基 于 L v n eg Maq ad 算法 的非量 测数 码 相机 影像 纠 正 …… … …… …… … …… …… … …… 杨朝 辉 ( 5 ee b r— ru rt 6) 大 学 生成 绩 变动 分析 及管 理对 策 …… …… … … …… … …… … …… … …… … …… …… 李 晓莉
局部 凸空 间 中带有 约 束 的 向量 极值 问题 的最 优性 条 件 … …… … …… … …… 杨 瑞 朱 建 青 国 马 张 潘 楠 起 ( 2 1) 刚 (6 1) 毅 (9 1) 涛 (8 2) 图 S VS 的 均匀 全色 数 … …… …… …… … …… …… … … …… … …… …… … … …… … 马效 敏 变质 量相 对 运动 动力 学 系统 的对称 性 与守 恒 量 … …… … …… … …… … …… … …… … 岳
相空间中非完整可控力学系统的对称性摄动与绝热不变量

·
z1
( 0) k
( Qs + Λ s )+X
( 0) k
( ε Ws ) , ( 23)
=ε Ws ( ξ s -q sτ )-εWs ( ξ s -q sτ ) =ε Ws ( ξ s -q sτ ) , k =0 时 , 约定 Ws =0 . d Iz z +1 正比于 ε , 即 I z 是该力学系 dt 统的一个 z 阶绝热不变量 . 由上式可得 ,
·
=τ
t
+ξ s
qs
+η s
ps
,
( 9)
约束方程( 1) 和方程( 6) 在无限小变换下保持形式不 变,即 φ β =0 ( β = 1 , …, g ; r =1 , … , b ; s = 1 , …, n ) , ( 10) H * * H · , p s =+Q s + Λ 11) qs = s .( ps qs
· ·
其中 L =L( t , qs , q s ) 为系统的 Lagrange 函数 , Q s = Qs ( t , qs , q s ) 为广义力 , Λ s =Λ s( t , qs , q s , μ r , μ r) 广 义约束反力 . λ t , qs , q s , μ 为约束乘子 . β =λ β( r , μ r) 引入广义动量和 Hamilton 函数
·
* * *
H H · , p s =+Q s + Λ s +ε Ws , ( 17) qs ps
展开 φ β , H ,Qs 和 Λ s , 可得形式不变性确定方程 X ps qs { X
( 0) ( 0)
*
相空间中离散完整系统Mei对称性摄动与绝热不变量

经典 的绝热不 变量是 指在 系统 的某参 数缓 慢 变化时 , 相对 该参 数 的变 化而 改变更 慢 的某一 物理 量【 , 1 绝 0 1 热不 变量又 称缓渐 不变量 或浸 渐不 变量【。实际上 , l 1 】 参数 缓慢 变化等 同于小扰 动作用 。系统在 小扰 动作用 下
g k +6t kq , =q , X = +  ̄
,
.t q , ) kk P (, () 4
ps- + jp, , , , , P, , 十 , k - ^ 9,P ^ ( ^ )
其 中 s为 无 限小参数 , 、
,
和
,
是离 散 生成元 函数 , 表示 全变 分 。
满足方 程
第 2期
张 克军等 : 空间 中 离散 完整 系统 Me 对称性摄 动 与绝 热不 变量 相 i
2 1
o p
: o,
O
s. q
’
, +
’
,
(4 1)
s.
衄
’ (
,
。
( 5 1)
则 相 应 的不 变性 为受扰 动后相 空 间中离散 完整 系统 ( 1 和 (e N i 1 ) 1 ) Me 对称 性 其 中
离散力 学是 近年来 分析力 学 的研究 方 向之一 . 主要思 想是利 用变 分原理 构建 离散算法 。 其 离散 原 有 的连
续系 统 , 尽可 能多地 保 留原 系统 的结 构和 性质 。近年来 , 散力 学系统 动力 学理论 及对称 性与守 恒 量理论 并 离
广义Birkhoff系统Noether对称性的摄动与绝热不变量

( 州科技学院 土木工程学院, 州 25 1) 苏 苏 10 1
摘
要: 研究 广义 Brhf系统对称性 的摄 动与绝热不变量 。首先 , i o k 列写 出广 义 Brhf系统的运动微 i o k
分 方 程 ; 次 , 于 Pa 作 用 量 在 群 的 无 限小 变 换 下 的不 变 性 , 出 了广 义 Brhf系 统 的 N e e 对 其 基 f f 给 i o k ot r h
zHANG Yi ( olg fCvl gn e n , u h u Unv ri f ce c n e h oo y,u h u2 5 1 , hn ) C l eo iiEn ie r g S z o ies yo in ea dT c n lg S z o 1 0 力 学 是 H mio i o k a h n力 学 的推 广 [. 有 完 整 约 束 系 统 和 非 完 整 约 束 系 统 都 能 纳 入 Brh f系 1所 ] i o k
o ti e . n t e e d o e p p r a x mp e i gv n t l s a e t e a p ia in o e r s ls b an d I n ft a e , n e a l s ie o i u t t h p l t ft e u t. h h l r c o h Ke r s a ayi a c a is , e e aie ik o i n s se ; e h rs mmer ; e u b t n a ib t n a i n y wo d : n t l l c me h n c ; g n r l d B r h f a y tm No t e y z t p r r ai ; d a ai i v ra t y t o c
相空间中非完整力学系统的对称性与非Noether守恒量

第2 4卷 第 1 期
20 0 7年 3月
苏 州 科 技 学 院 学 报 ( 然 科 学 版) 自
Jun l fU ies y f cec n eh ooyo uh u(aua Sin e ora nvri ineadT c nlg f zo N trl cec) o to S S
恒量 的研究 取得 了重 要进展 。笔者 进一 步研 究相空 间 中非完 整约束 力学 系统 的对称 性 与非 N ehr ote 守恒
量 。给 出了系统 的 N eh r 称性 、i ote 对 Le对称性 和 Me 对 称性 的判据 , i 研究 了 系统在相 空 间中 的对 称性 之间的 关系 , 得到 了相空 间 中非完 整约束 力学 系统 的两 类非 N eh r ote 守恒 量—— H0 a j n守恒 量 和 Me 守恒 量 。 m i
由力 学 系统 的对 称 性 来 寻 找 系统 的守 恒 量 是数 学 物 理科 学 ,特 别 是 分析 力 学 的一 个 近 代发 展 方 向 。 19 9 2年 , om n由特殊 的 Le 称 性 找到 了 Lgag 统 的一 类非 N e e 守 恒 量【 称 之 为 H j n守恒 Hja i对 arne系 ot r h ” , o ma
量 。 0 0年 , 20 梅凤 翔 提 出了力 学系统 的一 种新 的对称性 [ 即形 式不 变性或 Me 对 称性 。 2 1 , i 由系统 的 Me 对 称性 i
可直 接得到 一类新 的 非 N e e 守恒 量[3可称 为 Me 守恒 量 。 ot r h 3, - - 6 i 近来 , 于力学 系统 的对称 性 与非 N e e 守 关 ot r h
口; £ p , : (, , (: , , ) A (, ) £口 p) 1 … n q,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=τ
t
+ξ s
qs
+η s
ps
,
( 9)
约束方程( 1) 和方程( 6) 在无限小变换下保持形式不 变,即 φ β =0 ( β = 1 , …, g ; r =1 , … , b ; s = 1 , …, n ) , ( 10) H * * H · , p s =+Q s + Λ 11) qs = s .( ps qs
关键词 : 相空间 , 对称性 , 摄动 , 绝热不变量 PACC : 0320 可控力学系统在小扰动作用下的形式不变性摄动和 绝热不变量 , 证明了精确不变量与绝热不变量存在 的条件与形式 , 并举例说明结果的应用 . 1917 年 , Burgers 针对一类特殊的 Hamilton 系统 [ 1] 提出绝热不变量概念 , 绝热不变量又称缓慢不变 量或浸渐不变量 , 它是指当参数在缓慢变化时几 乎不变的量 , 实际上参数的缓慢变化等同于一个小 扰动作用 , 小扰动作用下对称性的改变及其不变量 与力学系统的近可积性之间有密切关系 , 有必要进 [ 3] 行研究 , 本文以此为模型进行研究 . 力学系统的运动依赖于作用力以及所加力的约 束 , 对约束力学系统的研究在物理学中具有重要的 意义 . 可控力学系统作为约束力学系统的扩充 , 长 期以来 , 人们对其研究并不是很多 , 但是随着近代 科学的进步 , 控制 理论在社会 中发挥着 越来越重 要的作用 , 这在很大 程度上 刺激了 可控力 学的发 展 , 使可 控 力 学的 研 究 具 有 重 要 的 理 论 和 现实 [ 4 — 13] 意义 . 文献[ 14 — 28] 研究各种力学系统的对称性摄动 与绝热不变量问题 , 得到了 Noether 形式的绝热不变 量 , 最近 , Zhang 等研究了 Lagrange 系统在小扰动作 用下 Lie 对 称 性 摄 动 , 得 到 Lagrange 系 统 的 一类 [ 29] Hojman 形式的高阶 绝热不变量 . 本文基于力学 系统高阶绝热不变量的定义 , 研究相空间中非完整
·
H · H , p s =+Qs + Λ s , ps qs
g
( 6) ( 7)
+ +
H 0 H· 0 H¨0 τ+ μ rτ + · μ rτ t μ r μ r
·0 H 0 0 · 0 ξ s + Hτ -( Qs +Λ s) ( ξ s -q s τ ) qs
Λ s =
β=1
∑λ
β
φ β qs
·
* * *
H H · , p s =+Q s + Λ s +ε Ws , ( 17) qs ps
展开 φ β , H ,Qs 和 Λ s , 可得形式不变性确定方程 X ps qs { X
( 0) ( 0)
*
*
*
*
在ε Ws 的作用下 , 系统原有的对称性和不变量相应 地发生改变 , 假设这种改变是在系统无扰动的对称 变换基础上发生的小摄动 , 如果 τ ( t , qs , ps ) ,ξ s( t, qs , ps ) 和 η t , qs , ps ) 表示扰动后时间和空间对应 s( 的生成函数 , 则 0 1 2 2 τ=τ +ε τ +ετ + … ξ ξ s =ξ s +ε s +εξ s +… η s =η s +ε η s +εη s +… 且满足 ps ξ s · ·
· 程( 24) ,G ( t , qs , ps , μ 为规范函数 , 则 r , μ r)
k k k k k1
·k
·k
k
·
k
·
k1
k
( 24)
5.算 例
假设系统的 Lagrange 函数为
·2 ·2 L = 1( q +q 2) , 2 1
( 26) ( 27) ( 28)
Iz = ε ( p ξ -H τ +G )= const . ( 25) 是力学系统的一个 z 阶绝热不变量 . 证明 ( 25) 式两边对 t 求导 , 联合( 24) 式,有 ·k d k · k H k H· k I =ε p s ξ τμ s +p sξ s rτ dt z t μ r H¨k H· k H· k rτ p sτ - q sτ · μ ps qs μ r
·
0
0
-H τ +( Qs +Λ s) ( ξ s -q sτ ) +ε Ws ( ξ )+﹒ G =0 , s -q sτ ( 19)
11 期
夏丽莉等 : 相空间中 非完整可控力学系统的对称性摄动与绝热不变量
6185
式中 G 为规范函数 , 若记 G = G +ε G +εG + … X
( 0) k ( 0) k 0 1 2 2
g β =1
·
·
∑
φ β qs = 0 . · δ qs
( 2)
一般情况下方程( 1) 包含控制参数 μ r , 则系统 的运动微分方程可表示为 d dt φ β L L β · - q = Qs + ∑ λ · s β =1 qs qs ( 3)
· ·
g
( s = 1 , …, n ; β =1 , …, g ) ,
z z1 z1 z2 2 1 0 1 z z1
z1
z2
·
z2
· ·
z1 1
z+1
z
·
0
z
=τ
k
t
+ξ s
k
qs
+η s
k
ps
0
·
将( 18) ,( 20) 式代入( 12) ,( 13) ,( 19) 式 ,有 X ( φ β)=0 ,
( 0) k
·
1
3
2
·
2
·
z2
ps qs
{ X { X
( H) }= 0 , ( H) }= X
第 56 卷 第 11 期 2007 年 11 月 1000 -3290 2007 56( 11) 6183 -05
物 理 学 报
ACTA PHYSICA SINICA
Vol . 56 , No . 11 , November , 2007 c2007 Chin . Phys . Soc.
相空间中非完整可控力学系统的对称性摄动 * 与绝热不变量
[ 2]
1. 引
言
2. 系统的运动微分方程
研究一质点系 , 系统的位形由 n 个广义坐标 qs ( s= 1 , … , n) 来确定 . 系统的运动受 g 个 Chetaev 型 非完整可控约束 , φ t , qs , q s , μ β( r , μ r )= 0 ( β =1 , … , g ; r =1 , … , b ; s = 1 , …, n) , ( 1)
0 1 2 2 0 1 2 2
( φ β )= 0 ,
( 0)
( 12)
{ X
( H) }= 0 ,
( 0)
( H) }= X ( Qs + Λ s) .
0 0 0
( 13)
定理 1 如果无限小生成元 τ , ξ s , η s 满足方 程( 12) 和方程( 13) , 且存在规范函数 G =G ( t , qs , ps , μ r , μ r) 满足 p sξ s ·0 ·0 ·
·
,
其中的 H 和 Q s 均表示为 t , qs , ps 的函数 .Λ s 表示 为 t , qs , ps , μ r , μ r 的函数 .
·
0 0 · Hτ =p s ξ s + ps
H -Q - Λ 0 · 0 s s ( ξ s -q s τ ) qs
= ps + =0 . 定理 1 得证 .
夏丽莉 李元成
( 中国石油大学物理科学与技术学院 , 东营 257061) ( 2006 年 8 月 23 日收到 ; 2007 年 3 月 12 日收到修改稿)
研究相空间中非完整可控力学系统的对称 性摄动与 绝热不 变量 .列出 相空间 中未受扰 非完整 可控力 学系统 的形式不变性导致的 Noether 守恒量 . 基 于力学系统高阶绝热不变量的定义 , 研究小扰动作用 下相空间中非完整可 控力学系统的形式不变性摄动与绝热不变量 , 给 出了精确不变 量与绝热 不变量 存在的 条件与 形式 , 并举例 说明结 果的应用 .
( 0) * s * * s *
4. 对称性摄动与绝热不变量
( 8) 首先 , 我们提出相空间中非完整可控力学系统 的高阶不变量的定义 . · 定义 1 若 I z ( t , qs , ps , μ ) 是力学系统 r , μ r , ε 的一个含有小参数 ε 的最高次幂为 z 的物理量 , 其 z +1 时间 t 的一阶导数正比于 ε , 则称 Iz 为力学系统 的 z 阶绝热不变量 . 假设非完整可控力学系统 ( 6) 受到了一个小扰 动ε Ws 的作用 , 则系统的运动微分方程变为 qs =
0 0 0
( 15)
方程( 3) 可表示为正则形式 qs =
·
H · H β , p =+Q s + ∑ λ 5) β · .( ps s qs β= 1 qs
设 系统非 奇异 , 可得 相空间 中与 非完 整系统 ( 1) ,( 3) 相应完整系统的运动方程 qs =
0 0
( 18)
H 0 H· 0 H¨0 H 0 τ- μ ξ rτ - · μ rτ t μ qs s r μ r
0
