正态分布的概率公式
正态分布的简易计算公式和数据分析

正态分布的简易计算公式和数据分析正态分布(也称为高斯分布)在统计学中应用广泛,具有许多重要的性质和特点。
本文介绍了正态分布的简易计算公式以及数据分析方法。
正态分布的计算公式正态分布的概率密度函数(Probability Density Function, PDF)可以表示为以下公式:f(x) = \frac{1}{{\sigma \sqrt{2\pi}}} \cdot e^{-\frac{(x-\mu)^2}{2\sigma^2}}其中,- \( f(x) \) 表示给定随机变量 \( x \) 的概率密度,- \( \mu \) 是均值 (Mean),- \( \sigma \) 是标准差 (Standard Deviation),- \( e \) 是自然对数的底数 (Euler's number).根据公式,我们可以计算给定随机变量 \( x \) 的概率密度,进而进行各种数据分析。
正态分布的数据分析正态分布具有对称性和集中性,因此在数据分析中广泛应用。
下面介绍几个常见的数据分析方法。
1. Z-ScoreZ-Score 是一种衡量数据点在正态分布中相对位置的方法,可以用来判断一个数据点距离均值的偏离程度。
Z-Score 的公式如下:Z = \frac{x - \mu}{\sigma}其中,- \( Z \) 是 Z-Score,- \( x \) 是数据点的值,- \( \mu \) 是正态分布的均值,- \( \sigma \) 是正态分布的标准差.通过计算数据点的 Z-Score,可以判断它在正态分布中的相对位置,例如,Z-Score 大于 2 表示数据点距离均值较远,Z-Score 小于 -2 表示数据点距离均值较近。
2. 累积分布函数累积分布函数 (Cumulative Distribution Function, CDF) 是正态分布中的另一个重要概念,可以用来计算某个值小于等于给定值的概率。
正态分布加减乘除计算公式

正态分布加减乘除计算公式正态分布是一种常见的概率分布,也被称为高斯分布。
它在自然界和社会科学中广泛应用,特别是在统计学和概率论中。
正态分布的概率密度函数可以用以下公式表示:f(x) = 1/(σ√(2π)) * e^(-(x-μ)²/(2σ²))其中,μ是分布的均值,σ是标准差,e是自然对数的底数。
根据该公式,我们可以进行正态分布的加减乘除计算。
让我们来看看正态分布的加法运算。
假设有两个正态分布X和Y,它们的均值分别为μ1和μ2,标准差分别为σ1和σ2。
我们可以将X和Y的概率密度函数相加,得到一个新的正态分布Z,其均值为μ1+μ2,标准差为√(σ1²+σ2²)。
这个过程可以用以下公式表示:Z ~ N(μ1+μ2, √(σ1²+σ2²))接下来,让我们讨论正态分布的减法运算。
假设有两个正态分布X 和Y,它们的均值分别为μ1和μ2,标准差分别为σ1和σ2。
我们可以将X和Y的概率密度函数相减,得到一个新的正态分布Z,其均值为μ1-μ2,标准差为√(σ1²+σ2²)。
这个过程可以用以下公式表示:Z ~ N(μ1-μ2, √(σ1²+σ2²))接下来,让我们来讨论正态分布的乘法运算。
假设有两个正态分布X和Y,它们的均值分别为μ1和μ2,标准差分别为σ1和σ2。
我们可以将X和Y的概率密度函数相乘,得到一个新的正态分布Z,其均值为μ1*μ2,标准差为√((σ1*μ2)²+(σ2*μ1)²)。
这个过程可以用以下公式表示:Z ~ N(μ1*μ2, √((σ1*μ2)²+(σ2*μ1)²))让我们来讨论正态分布的除法运算。
假设有两个正态分布X和Y,它们的均值分别为μ1和μ2,标准差分别为σ1和σ2。
我们可以将X和Y的概率密度函数相除,得到一个新的正态分布Z,其均值为μ1/μ2,标准差为√((σ1/μ2)²+(σ2/μ1)²)。
正态分布 标准差概率公式

正态分布标准差概率公式
正态分布是统计学中常见的一种连续概率分布,也被称为高斯
分布。
它具有许多重要的性质,其中之一就是标准差对概率的影响。
首先,正态分布的概率密度函数可以表示为:
\[ f(x) = \frac{1}{{\sigma \sqrt{2\pi}}} e^{-\frac{(x-
\mu)^2}{2\sigma^2}} \]
其中,\( \mu \) 是分布的均值,\( \sigma \) 是标准差。
标准差对概率的影响可以通过正态分布的标准化来理解。
标准
化后的正态分布具有均值为0,标准差为1。
对于标准正态分布,我
们可以使用 Z 分数来计算概率。
Z 分数可以通过以下公式计算:
\[ Z = \frac{x \mu}{\sigma} \]
其中,\( x \) 是随机变量的取值,\( \mu \) 是均值,
\( \sigma \) 是标准差。
一般来说,我们可以使用 Z 分数来计算标准正态分布中的概率。
例如,要计算随机变量小于某个值的概率,可以将该值代入 Z 分数
公式,然后查找标准正态分布表或使用统计软件来获取相应的概率值。
另外,对于一般的正态分布,我们也可以利用标准化的方法来
计算概率。
首先将给定的数值转化为 Z 分数,然后再通过标准正态
分布表或软件来获取相应的概率。
总之,标准差在正态分布中对概率的影响体现在概率的计算和
解释上,通过标准化可以将一般的正态分布转化为标准正态分布,
从而更方便地计算和解释概率。
希望这个回答能够帮助到你理解正
态分布中标准差对概率的影响。
正态分布分布函数公式fx

正态分布分布函数公式fx正态分布函数是描述连续型随机变量服从正态分布的一种函数形式,通常表示为F(x),其中x为随机变量的取值。
正态分布函数是对正态分布概率密度函数进行积分得到的,在统计学和概率论中有广泛应用。
正态分布函数的公式如下:F(x) = ∫(从-∞到x) f(t) dt其中,F(x)表示随机变量小于等于x的累计概率,f(x)表示概率密度函数,∫表示积分。
正态分布函数的具体计算过程如下:1.根据正态分布的概率密度函数公式:f(x)=(1/(σ√(2π)))*e^(-(x-μ)²/(2σ²))其中,σ表示标准差,μ表示均值,e表示自然对数的底。
2.对概率密度函数进行积分运算:∫(从-∞到x) f(t) dt = ∫(从-∞到x) (1 / (σ√(2π))) *e^(-(t-μ)² / (2σ²)) dt由于正态分布函数没有求解解析解的方法,因此一般采用数值积分方法,如辛普森公式、梯形法则等进行近似计算。
正态分布函数具备以下特点:1.正态分布函数的取值范围是[0,1],表示累计概率的比例值。
2.当x取负无穷时,正态分布函数趋近于0;当x取正无穷时,正态分布函数趋近于13.正态分布函数是一个单调递增函数,即随着随机变量取值的增加,累计概率也会增加。
正态分布函数在实际应用中具有重要作用,它可以用于计算正态分布随机变量在一些特定取值范围内的概率,以及用于计算随机变量在一些阈值以上或以下的概率,进而实现统计推断、假设检验等统计分析方法的应用。
总结起来,正态分布函数是描述连续型随机变量服从正态分布的一种函数形式,采用积分运算对概率密度函数进行计算,用于计算随机变量的累计概率,具有重要的统计学和概率论应用。
标准正态分布概率公式

标准正态分布概率公式标准正态分布是统计学中非常重要的概念,它在各个领域都有着广泛的应用。
在实际问题中,我们经常需要计算标准正态分布的概率,而概率密度函数和累积分布函数是我们计算概率的重要工具。
本文将介绍标准正态分布的概率密度函数和累积分布函数的计算方法,帮助读者更好地理解和运用标准正态分布。
概率密度函数。
标准正态分布的概率密度函数可以用公式表示为:\[f(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\]其中,\(e\)是自然对数的底,\(x\)是随机变量的取值,\(f(x)\)是对应取值的概率密度。
在这个公式中,我们可以看到指数函数的作用,它使得随机变量的取值越偏离均值,概率密度越小。
这也符合我们对正态分布的直观认识,在均值附近的取值概率较大,而远离均值的取值概率较小。
累积分布函数。
标准正态分布的累积分布函数可以用公式表示为:\[Φ(x)=\int_{-∞}^{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt\]其中,\(Φ(x)\)表示随机变量的取值小于等于\(x\)的概率。
通过累积分布函数,我们可以计算出随机变量在某个取值以下的概率,这对于统计推断和假设检验等问题非常有用。
概率计算举例。
现在,我们通过一个例子来说明如何使用标准正态分布的概率密度函数和累积分布函数进行计算。
假设随机变量\(X\)服从标准正态分布,我们需要计算\(P(X≤1.96)\)。
首先,我们可以使用累积分布函数来计算这个概率,即:\[Φ(1.96)=\int_{-∞}^{1.96}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt\]这个积分可以通过数值积分或查表的方式进行计算,最终得到\(Φ(1.96)=0.975\)。
这就意味着随机变量\(X\)小于等于1.96的概率为0.975。
另外,我们也可以使用概率密度函数来计算这个概率,即:\[P(X≤1.96)=\int_{-∞}^{1.96}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt\]同样地,这个积分也可以通过数值积分或查表的方式进行计算,最终得到\(P(X ≤1.96)=0.975\)。
正态分布公式推导

正态分布公式推导正态分布是一种常见的概率分布,其概率密度函数可以通过公式推导而得。
下面将介绍正态分布的起源以及其推导过程。
正态分布在19世纪由高斯(Gauss)引入,也因此被称为高斯分布。
高斯分布具有许多重要的性质,因此在统计学和自然科学中得到了广泛的应用。
正态分布的概率密度函数可以表示为:f(x)=(1/√(2πσ²))*e^((-(x-μ)²)/(2σ²))其中,f(x)是随机变量X的概率密度函数,x是变量的取值,μ是分布的均值,σ²是方差,e是自然对数的底。
下面将推导正态分布的概率密度函数。
首先,考虑标准正态分布,即均值为0,方差为1的正态分布。
其概率密度函数为:f(x)=1/√(2π)*e^(-x²/2)为了将概率密度函数推广到一般的正态分布,我们引入变量Z,用来表示标准正态分布的随机变量。
假设X是一个正态分布的随机变量,其均值为μ,方差为σ²。
我们可以将X表示为:X=μ+σZ其中,Z是标准正态分布的随机变量。
将X的表达式代入概率密度函数,我们得到:f(x)=1/(√(2π)σ)*e^(-((x-μ)/σ)²/2)通过这个表达式,我们可以看出,X是一个以μ为均值,以σ²为方差的正态分布。
为了进一步推导正态分布的公式,我们需要理解正态分布的性质。
具体来说,在正态分布中,68%的观测值位于均值加减1个标准差之间,95%的观测值位于均值加减2个标准差之间,99.7%的观测值位于均值加减3个标准差之间。
这些性质称为“三个标准差法则”或“68-95-99.7法则”。
基于这些性质,我们可以通过对概率密度函数进行适当的变换得到正态分布的常用公式。
首先,我们对标准正态分布的概率密度函数进行变换,得到:∫(-∞, x) (1/√(2π) * e^(-t²/2)) dt = ∫(-∞, (x-μ)/σ) (1/√(2π) * e^(-t²/2)) dt其中,左侧是标准正态分布的累积概率密度函数(CDF),右侧是一般正态分布的CDF。
正态分布条件公式

正态分布条件公式
(实用版)
目录
1.引言
2.正态分布的定义和性质
3.正态分布的条件公式
4.结论
正文
1.引言
正态分布,又称为高斯分布,是一种常见的概率分布。
在自然界和社会科学中的许多现象都遵循正态分布规律,例如人的身高、考试成绩等。
正态分布具有一些重要的性质,如均值、中位数、众数相等,标准差决定了分布的胖瘦等。
2.正态分布的定义和性质
正态分布的概率密度函数为:f(x) = (1 / (σ * sqrt(2π))) * exp(-((x-μ)) / 2σ),其中,μ为均值,σ为标准差。
正态分布的分布图象呈钟型,其均值、中位数、众数相等,即μ=σ=ν。
3.正态分布的条件公式
在实际应用中,我们常常需要根据样本数据来判断总体分布是否为正态分布。
下面介绍一种常用的正态分布检验方法——Kolmogorov-Smirnov 检验。
Kolmogorov-Smirnov 检验是一种基于样本最大差值的检验方法,其步骤如下:
(1) 计算样本的最大差值 Dmax;
(2) 计算 n-1 个区间的中点,记为 xi;
(3) 计算 (xi-μ)/σ的值,记为 z;
(4) 根据 Kolmogorov-Smirnov 分布表,查找对应的临界值 Ks;
(5) 如果计算得到的 z 值小于临界值 Ks,则不能拒绝原假设,即总体分布为正态分布;反之,则拒绝原假设,即总体分布非正态分布。
4.结论
正态分布在实际应用中具有重要意义,理解和掌握正态分布的条件公式,可以帮助我们更好地分析和处理数据。
正态分布概率密度函数
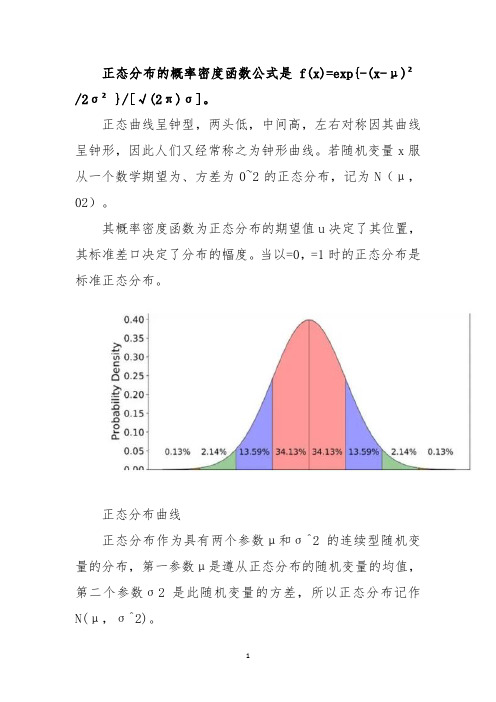
正态分布的概率密度函数公式是f(x)=exp{-(x-μ)²/2σ²}/[√(2π)σ]。
正态曲线呈钟型,两头低,中间高,左右对称因其曲线呈钟形,因此人们又经常称之为钟形曲线。
若随机变量x服从一个数学期望为、方差为0~2的正态分布,记为N(μ,02)。
其概率密度函数为正态分布的期望值u决定了其位置,其标准差口决定了分布的幅度。
当以=0,=1时的正态分布是标准正态分布。
正态分布曲线
正态分布作为具有两个参数μ和σ^2的连续型随机变量的分布,第一参数μ是遵从正态分布的随机变量的均值,第二个参数σ2是此随机变量的方差,所以正态分布记作N(μ,σ^2)。
遵从正态分布的随机变量的概率规律为取μ邻近的值的概率大,而取离μ越远的值的概率越小;σ越小,分布越集中在μ附近,σ越大,分布越分散。
正态分布的密度函数的特点是:关于μ对称,在μ处达到最大值,在正(负)无穷远处取值为0,在μ±σ处有拐点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正态分布的概率公式
正态分布,也称为高斯分布,是统计学中最重要的连续概率分布之一,常用于描述一组连续随机变量的分布情况。
在正态分布中,平均值参数和
标准差参数分别决定了分布的位置和形状。
f(x)=(1/(σ*√(2π)))*e^(-((x-μ)^2)/(2*σ^2))
这个公式可以将变量x对应的概率密度表示为一个正态(高斯)分布
曲线上的一个点的高度。
正态分布的曲线呈钟形,中间最高,两侧逐渐低,左右对称。
在正态分布中,μ决定了曲线的中心位置,σ决定了曲线的宽度,
即标准差越大,曲线分布越宽,相反标准差越小,曲线分布越窄。
1.正态分布曲线在μ处取得最高点,即概率密度最大,随着x离μ
的距离越远,概率密度逐渐减小。
2.曲线的两侧无限延伸,但概率密度会逐渐趋近于0。
约68%的数据
会落在μ±σ内,约95%的数据会落在μ±2σ内,约99.7%的数据会落
在μ±3σ内。
3.正态分布的概率密度总和等于1
4.如果一个随机变量X服从正态分布,那么其线性组合aX+b(其中a
和b为常数)也服从正态分布。
正态分布在实际应用中有着广泛的应用,例如经济学、物理学、心理学、生物学等领域。
通过正态分布的概率公式,可以计算出其中一特定区
间内的概率密度,并用于分析和推断。
如何计算正态分布的概率密度?
要计算正态分布的概率密度,需要给定x的值、μ的值和σ的值,然后根据公式进行计算。
下面以一个例子来说明如何计算正态分布的概率密度:
假设有一个变量X服从正态分布,其均值μ等于50,标准差σ等于10。
我们想要计算X的概率密度在40、50和60的值。
首先,将给定的值代入正态分布的概率密度函数的公式中:
1.当x=40时:
f(40)=(1/(10*√(2π)))*e^(-((40-50)^2)/(2*10^2))
2.当x=50时:
f(50)=(1/(10*√(2π)))*e^(-((50-50)^2)/(2*10^2))
3.当x=60时:
f(60)=(1/(10*√(2π)))*e^(-((60-50)^2)/(2*10^2))
然后,我们可以使用计算器或编程语言中的数学函数来计算指数等操作,得到相应的结果。
最后,根据计算得到的结果,我们可以得到在指定的x值处的概率密度。
从而可以利用这些概率密度进行统计分析、推断和模型拟合等工作。
