2017-2018学年高中数学 考点52 几何证明选讲(含2013年高考试题)新人教A版
2017年全国卷高考数学复习专题——几何证明选讲
2017年全国卷高考数学复习专题——几何证明选讲考点一平行截割定理与相似三角形1.(2014天津,6,5分)如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于点E,过点B 的圆的切线与AD的延长线交于点F.在上述条件下,给出下列四个结论:①BD平分∠CBF;②FB2=FD·FA;③AE·CE=BE·DE;④AF·BD=AB·BF.则所有正确结论的序号是( )A.①②B.③④C.①②③D.①②④答案 D2.(2014广东,15,5分)(几何证明选讲选做题)如图,在平行四边形ABCD中,点E= .在AB上且EB=2AE,AC与DE交于点F,则△CDF的面积△AEF的面积答案9考点二圆的初步3.(2014重庆,14,5分)过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次交圆于B,C.若PA=6,AC=8,BC=9,则AB= .答案 44.(2014陕西,15B,5分)(几何证明选做题)如图,△ABC中,BC=6,以BC为直径的半圆分别交AB,AC于点E,F,若AC=2AE,则EF= .答案 35.(2014湖南,12,5分)如图,已知AB,BC是☉O的两条弦,AO⊥BC,AB=3,BC=22,则☉O的半径等于.答案326.(2014湖北,15,5分)选修4—1:几何证明选讲如图,P为☉O外一点,过P点作☉O的两条切线,切点分别为A,B.过PA的中点Q 作割线交☉O于C,D两点.若QC=1,CD=3,则PB= .答案 47.(2014课标Ⅰ,22,10分)选修4—1:几何证明选讲如图,四边形ABCD是☉O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.(1)证明:∠D=∠E;(2)设AD不是☉O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.解析(1)证明:由题设知A,B,C,D四点共圆,所以∠D=∠CBE.由已知得∠CBE=∠E,故∠D=∠E.(2)设BC的中点为N,连结MN,则由MB=MC知MN⊥BC,故O在直线MN上.又AD不是☉O的直径,M为AD的中点,故OM⊥AD,即MN⊥AD.所以AD∥BC,故∠A=∠CBE.又∠CBE=∠E,故∠A=∠E.由(1)知,∠D=∠E,所以△ADE为等边三角形.8.(2014课标Ⅱ,22,10分)选修4—1:几何证明选讲如图,P是☉O外一点,PA是切线,A为切点,割线PBC与☉O相交于点B,C,PC=2PA,D 为PC的中点,AD的延长线交☉O于点E.证明:(1)BE=EC;(2)AD·DE=2PB2.证明(1)连结AB,AC,由题设知PA=PD,故∠PAD=∠PDA.因为∠PDA=∠DAC+∠DCA,∠PAD=∠BAD+∠PAB,∠DCA=∠PAB,所以∠DAC=∠BAD,从而BE=EC.因此BE=EC.(2)由切割线定理得PA2=PB·PC.因为PA=PD=DC,所以DC=2PB,BD=PB,由相交弦定理得AD·DE=BD·DC,所以AD·DE=2PB2.9.(2014辽宁,22,10分)选修4—1:几何证明选讲如图,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连结DG并延长交圆于点A,作弦AB垂直EP,垂足为F.(1)求证:AB为圆的直径;(2)若AC=BD,求证:AB=ED.证明(1)因为PD=PG,所以∠PDG=∠PGD.由于PD为切线,故∠PDA=∠DBA,又由于∠PGD=∠EGA,故∠DBA=∠EGA,所以∠DBA+∠BAD=∠EGA+∠BAD,从而∠BDA=∠PFA.由于AF⊥EP,所以∠PFA=90°,于是∠BDA=90°.故AB是直径.(2)连结BC,DC.由于AB是直径,故∠BDA=∠ACB=90°.在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而Rt△BDA≌Rt△ACB.于是∠DAB=∠CBA.又因为∠DCB=∠DAB,所以∠DCB=∠CBA,故DC∥AB.由于AB⊥EP,所以DC⊥EP,∠DCE为直角.于是ED为直径.由(1)得ED=AB.10.(2014江苏,21A,10分)选修4—1:几何证明选讲如图,AB是圆O的直径,C、D是圆O上位于AB异侧的两点. 证明:∠OCB=∠D.证明因为B,C是圆O上的两点,所以OB=OC.故∠OCB=∠B.又因为C,D是圆O上位于AB异侧的两点,故∠B,∠D为同弧所对的两个圆周角,所以∠B=∠D.因此∠OCB=∠D.。
2013-2017高考数学全国卷--立体几何汇编(完整资料).doc
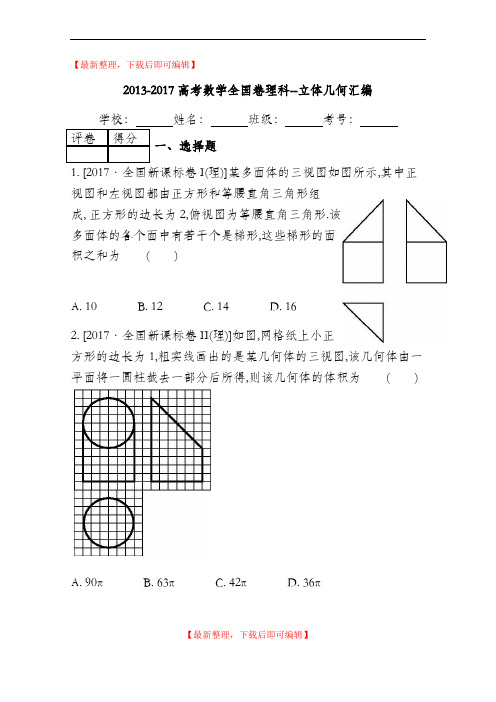
【最新整理，下载后即可编辑】2013-2017高考数学全国卷理科--立体几何汇编学校：姓名：班级：考号：评卷得分一、选择题I(理)]某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成, 正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为()A. 10B. 12C. 14D. 162. [2017·全国新课标卷II(理)]如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为()A. 90πB. 63πC. 42πD. 36π【最新整理，下载后即可编辑】【最新整理，下载后即可编辑】 3. [2017·全国新课标卷II(理)]已知直三棱柱ABC-A 1B 1C 1中,∠ABC=120°,AB=2,BC=CC 1=1,则异面直线AB 1与BC 1所成角的余弦值为 ( )A. √32B. √155C. √105D. √33 4. [2017·全国新课标卷III(理)]已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )A. πB. 3π4C. π2D. .π4 5. [2016·高考全国新课标卷Ⅰ,6]如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是 ( )A. 17πB. 18πC. 20πD. 28π6. [2016·高考全国新课标卷Ⅰ,11]平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α∥平面CB 1D 1,α∩平面ABCD =m ,α∩平面ABB 1A 1=n ,则m ,n 所成角的正弦值为 ( )A. √32B. √22C. √33D. 13【最新整理，下载后即可编辑】7. [2016·高考全国新课标卷Ⅱ,6]如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为 ( )A. 20πB. 24πC. 28πD. 32π8. [2016·高考全国新课标卷Ⅲ,9]如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )A. 18+36√5B. 54+18√5C. 90D. 819. [2016·高考全国新课标卷Ⅲ,10]在封闭的直三棱柱ABC -A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是 ( )A. 4πB. 9π2C. 6πD. 32π310. [2015·高考全国新课标卷Ⅰ,6]《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米【最新整理，下载后即可编辑】 (如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A. 14斛B. 22斛C. 36斛D. 66斛11. [2015·高考全国新课标卷Ⅰ,11]圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为16+20π,则r=( )正视图 俯视图A. 1B. 2C. 4D. 812. [2015·高考全国新课标卷Ⅱ,6]一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为( )A. 18B. 17C. 16D. 15【最新整理，下载后即可编辑】 13. [2015·高考全国新课标卷Ⅱ,9]已知A ,B 是球O 的球面上两点,∠AOB=90°,C 为该球面上的动点.若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为( )A. 36πB. 64πC. 144πD. 256π14. [2014·高考全国新课标卷Ⅰ，12]如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )A. 6√2B. 6C. 4√2D. 4 15. [2014·全国新课标卷Ⅱ,6]如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A. 1727 B. 59 C. 1027 D. 13【最新整理，下载后即可编辑】 16. [2014·全国新课标卷Ⅱ,11]直三棱柱ABC A 1B 1C 1中,∠BCA ＝90°,M ,N 分别是A 1B 1,A 1C 1的中点,BC ＝CA ＝CC 1,则BM 与AN 所成角的余弦值为( ) A. 110 B. 25 C. √3010 D. √22 17. [2013·高考全国新课标卷Ⅰ，6]如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为( )A. 500π3 cm 3B. 866π3 cm 3C. 1372π3 cm 3D.2048π3 cm 318. [2013·高考全国新课标卷Ⅰ，8]某几何体的三视图如图所示，则该几何体的体积为( )A. 16＋8πB. 8＋8πC. 16＋16π D. 8＋16π19. [2013·高考全国新课标卷Ⅱ，4]已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β.直线l 满足l ⊥m ，l ⊥n ，l ⊄α，l ⊄β，则( )A. α∥β且l ∥αB. α⊥β且l ⊥βC. α与β相交，且交线垂直于lD. α与β相交，且交线平行l20. [2013·高考全国新课标卷Ⅱ，7]一个四面体的顶点在空间直角坐标系O－xyz中的坐标分别是(1，0，1)，(1，1，0)，(0，1，1)，(0，0，0)，画该四面体三视图中的正视图时，以zOx平面为投影面，则得到的正视图可以为( )A. B. C. D.评卷得分二、填空题I(理)]如图,圆形纸片的圆心为O,半径为5 cm,该纸片上的等边三角形ABC的中心为O.D,E,F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D,E,F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为.22. [2017·全国新课标卷III(理)]a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60°角时,AB与b成30°角;【最新整理，下载后即可编辑】【最新整理，下载后即可编辑】 ②当直线AB 与a 成60°角时,AB 与b 成60°角;③直线AB 与a 所成角的最小值为45°;④直线AB 与a 所成角的最大值为60°.其中正确的是 .(填写所有正确结论的编号)23. [2016·高考全国新课标卷Ⅱ,14]α,β是两个平面,m ,n 是两条直线,有下列四个命题:①如果m ⊥n ,m ⊥α,n ∥β,那么α⊥β.②如果m ⊥α,n ∥α,那么m ⊥n .③如果α∥β,m ⊂α,那么m ∥β.④如果m ∥n ,α∥β,那么m 与α所成的角和n 与β所成的角相等. 其中正确的命题有 .(填写所有正确命题的编号)三、解答题 I(理)] (本小题满分12分)如图,在四棱锥P-ABCD 中,AB ∥CD ,且∠BAP=∠CDP=90°.(1)证明:平面PAB⊥平面PAD ; (2)若PA=PD=AB=DC ,∠APD=90°,求二面角A-PB-C 的余弦值.25. [2017·全国新课标卷II(理)] (本小题满分12分)如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AB=BC=12AD,∠BAD=∠ABC=90°,E是PD的中点.(1)证明:直线CE∥平面PAB;(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.26. [2017·全国新课标卷III(理)] (本小题满分12分)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D-AE-C的余弦值.【最新整理，下载后即可编辑】【最新整理，下载后即可编辑】27. [2016·高考全国新课标卷Ⅰ,18] (本小题满分12分)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,∠AFD =90°,且二面角D -AF -E 与二面角C -BE -F 都是60°.(1)证明:平面ABEF ⊥平面EFDC ;(2)求二面角E -BC -A 的余弦值.28. [2016·高考全国新课标卷Ⅱ,19] (本小题满分12分)如图,菱形ABCD 的对角线AC 与BD 交于点O ,AB =5,AC =6,点E ,F 分别在AD ,CD 上,AE =CF =54,EF 交BD 于点H .将△DEF 沿EF 折到△D'EF 的位置,OD'=√10.(1)证明:D'H⊥平面ABCD;(2)求二面角B-D'A-C的正弦值.29. [2016·高考全国新课标卷Ⅲ,19] (本小题满分12分) 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明MN∥平面PAB;(2)求直线AN与平面PMN所成角的正弦值.【最新整理，下载后即可编辑】【最新整理，下载后即可编辑】30. [2015·高考全国新课标卷Ⅰ,18](本小题满分12分)如图,四边形ABCD 为菱形,∠ABC=120°,E ,F 是平面ABCD 同一侧的两点,BE ⊥平面ABCD ,DF ⊥平面ABCD ,BE=2DF ,AE ⊥EC.(1)证明:平面AEC ⊥平面AFC ; (2)求直线AE 与直线CF 所成角的余弦值.31. [2015·高考全国新课标卷Ⅱ,19](本小题满分12分)如图,长方体ABCD-A 1B 1C 1D 1中,AB=16,BC=10,AA 1=8,点E ,F 分别在A 1B 1,D 1C 1上,A 1E=D 1F= 4.过点E ,F 的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法和理由);(2)求直线AF 与平面α所成角的正弦值.【最新整理，下载后即可编辑】32. [2014·高考全国新课标卷Ⅰ,19] (本小题满分12分) 如图,三棱柱ABC A 1B 1C 1中,侧面BB 1C 1C 为菱形,AB ⊥B 1C .(1)证明：AC ＝AB 1；(2)若AC ⊥AB 1,∠CBB 1＝60°,AB ＝BC ,求二面角A A 1B 1C 1的余弦值.33. [2014·全国新课标卷Ⅱ，18] (本小题满分12分) 如图,四棱锥P ABCD 中,底面ABCD 为矩形,PA ⊥平面ABCD ,E 为PD 的中点.(1)证明：PB ∥平面AEC ；(2)设二面角D AE C 为60°,AP ＝1,AD ＝√3,求三棱锥E ACD 的体积.【最新整理，下载后即可编辑】34. [2013·高考全国新课标卷Ⅰ，18](本小题满分12分) 如图，三棱柱ABC －A 1B 1C 1中，CA ＝CB ，AB ＝AA 1，∠BAA 1＝60°. (1)证明：AB ⊥A 1C ；(2)若平面ABC ⊥平面AA 1B 1B ，AB ＝CB ，求直线A 1C 与平面BB 1C 1C 所成角的正弦值.35. [2013·高考全国新课标卷Ⅱ，18](本小题满分12分)如图，直三棱柱ABC －A 1B 1C 1中，D ，E 分别是AB ，BB 1的中点，AA 1＝AC ＝CB ＝√22AB .(1)证明：BC 1∥平面A 1CD ；C－E的正弦值.(2)求二面角D－A1【最新整理，下载后即可编辑】。
2017-2018年高考数学真题汇编解析几何及答案详解
2017--2018年高考数学解析几何汇编及答案解析类型一选择填空1、（2018年高考全国卷1文科4）（5分）已知椭圆C：+=1的一个焦点为（2，0），则C的离心率为（）A．B．C．D．【解答】解：椭圆C：+=1的一个焦点为（2，0），可得a2﹣4=4，解得a=2，∵c=2，∴e===．故选：C．2、（2018年高考全国卷1理科8）（5分）设抛物线C：y2=4x的焦点为F，过点（﹣2，0）且斜率为的直线与C交于M，N两点，则•=（）A．5 B．6 C．7 D．8【解答】解：抛物线C：y2=4x的焦点为F（1，0），过点（﹣2，0）且斜率为的直线为：3y=2x+4，联立直线与抛物线C：y2=4x，消去x可得：y2﹣6y+8=0，解得y1=2，y2=4，不妨M（1，2），N（4，4），，．则•=（0，2）•（3，4）=8．故选：D．3、（2018年高考全国卷1理科11）（5分）已知双曲线C：﹣y2=1，O为坐标原点，F为C 的右焦点，过F的直线与C的两条渐近线的交点分别为M，N．若△OMN为直角三角形，则|MN|=（）A．B．3 C．2D．4【解答】解：双曲线C：﹣y2=1的渐近线方程为：y=，渐近线的夹角为：60°，不妨设过F（2，0）的直线为：y=，则：解得M（，），解得：N（），则|MN|==3．故选：B．4、（2018年高考全国卷2文科6）（5分）双曲线=1（a＞0，b＞0）的离心率为，则其渐近线方程为（）A．y=±x B．y=±x C．y=±x D．y=±x【解答】解：∵双曲线的离心率为e==，则=====，即双曲线的渐近线方程为y=±x=±x，故选：A．5、（2018年高考全国卷2文科11）（5分）已知F1，F2是椭圆C的两个焦点，P是C上的一点，若PF1⊥PF2，且∠PF2F1=60°，则C的离心率为（）A．1﹣B．2﹣C．D．﹣1【解答】解：F1，F2是椭圆C的两个焦点，P是C上的一点，若PF1⊥PF2，且∠PF2F1=60°，可得椭圆的焦点坐标F2（c，0），所以P（c，c）．可得：，可得，可得e4﹣8e2+4=0，e∈（0，1），解得e=．故选：D．6、（2018年高考全国卷2理科5）（5分）双曲线=1（a＞0，b＞0）的离心率为，则其渐近线方程为（）A．y=±x B．y=±x C．y=±x D．y=±x【解答】解：∵双曲线的离心率为e==，则=====，即双曲线的渐近线方程为y=±x=±x，故选：A．7、（2018年高考全国卷2理科12）（5分）已知F1，F2是椭圆C：=1（a＞b＞0）的左、右焦点，A是C的左顶点，点P在过A且斜率为的直线上，△PF1F2为等腰三角形，∠F1F2P=120°，则C的离心率为（）A．B．C．D．【解答】解：由题意可知：A（﹣a，0），F1（﹣c，0），F2（c，0），直线AP的方程为：y=（x+a），由∠F1F2P=120°，|PF2|=|F1F2|=2c，则P（2c，c），代入直线AP：c=（2c+a），整理得：a=4c，∴题意的离心率e==．故选：D．8、（2018年高考江苏卷理科12）（5分）在平面直角坐标系xOy中，A为直线l：y=2x上在第一象限内的点，B（5，0），以AB为直径的圆C与直线l交于另一点D．若=0，则点A的横坐标为3．【解答】解：设A（a，2a），a＞0，∵B（5，0），∴C（，a），则圆C的方程为（x﹣5）（x﹣a）+y（y﹣2a）=0．联立，解得D（1，2）．∴=．解得：a=3或a=﹣1．又a＞0，∴a=3．即A的横坐标为3．故答案为：3．9、（2018年高考上海卷2）（4分）双曲线﹣y2=1的渐近线方程为±．【解答】解：∵双曲线的a=2，b=1，焦点在x轴上而双曲线的渐近线方程为y=±∴双曲线的渐近线方程为y=±故答案为：y=±10、（2018年高考上海卷8）（5分）在平面直角坐标系中，已知点A（﹣1，0）、B（2，0），E、F是y轴上的两个动点，且||=2，则的最小值为﹣3．【解答】解：根据题意，设E（0，a），F（0，b）；∴；∴a=b+2，或b=a+2；且；∴；当a=b+2时，；∵b2+2b﹣2的最小值为；∴的最小值为﹣3，同理求出b=a+2时，的最小值为﹣3．故答案为：﹣3．11、（2018年高考上海卷12）（5分）已知实数x1、x2、y1、y2满足：x12+y12=1，x22+y22=1，x1x2+y1y2=，则+的最大值为1．【解答】解：设A（x1，y1），B（x2，y2），=（x1，y1），=（x2，y2），由x12+y12=1，x22+y22=1，x1x2+y1y2=，可得A，B两点在圆x2+y2=1上，且•=1×1×cos∠AOB=，即有∠AOB=60°，即三角形OAB为等边三角形，AB=1，+的几何意义为点A，B两点到直线x+y﹣1=0的距离d1与d2之和，显然d1+d2≤AB=1，即+的最大值为1，故答案为：1．12、（2018年高考上海卷13）（5分）设P是椭圆=1上的动点，则P到该椭圆的两个焦点的距离之和为（）A．2B．2C．2D．4【解答】解：椭圆=1的焦点坐标在x轴，a=，P是椭圆=1上的动点，由椭圆的定义可知：则P到该椭圆的两个焦点的距离之和为2a=2．故选：C．13、（2018年高考浙江卷9）（4分）已知，，是平面向量，是单位向量．若非零向量与的夹角为，向量满足﹣4•+3=0，则|﹣|的最小值是（）A．﹣1 B．+1 C．2 D．2﹣【解答】解：由﹣4•+3=0，得，∴（）⊥（），如图，不妨设，则的终点在以（2，0）为圆心，以1为半径的圆周上，又非零向量与的夹角为，则的终点在不含端点O的两条射线y=（x＞0）上．不妨以y=为例，则|﹣|的最小值是（2，0）到直线的距离减1．即．故选：A．14、（2018年高考浙江卷12）（6分）若x，y满足约束条件，则z=x+3y的最小值是﹣2，最大值是8．【解答】解：作出x，y满足约束条件表示的平面区域，如图：其中B（4，﹣2），A（2，2）．设z=F（x，y）=x+3y，将直线l：z=x+3y进行平移，观察直线在y轴上的截距变化，可得当l经过点B时，目标函数z达到最小值．=F（4，﹣2）=﹣2．∴z最小值可得当l经过点A时，目标函数z达到最最大值：z最大值=F（2，2）=8．故答案为：﹣2；8．15、（2018年高考浙江卷17）（4分）已知点P（0，1），椭圆+y2=m（m＞1）上两点A，B满足=2，则当m=5时，点B横坐标的绝对值最大．【解答】解：设A（x1，y1），B（x2，y2），由P（0，1），=2，可得﹣x1=2x2，1﹣y1=2（y2﹣1），即有x1=﹣2x2，y1+2y2=3，又x12+4y12=4m，即为x22+y12=m，①x22+4y22=4m，②①﹣②得（y1﹣2y2）（y1+2y2）=﹣3m，可得y1﹣2y2=﹣m，解得y1=，y2=，则m=x22+（）2，即有x22=m﹣（）2==，即有m=5时，x22有最大值16，即点B横坐标的绝对值最大．故答案为：5．16、（2018年高考天津卷文科12）（5分）在平面直角坐标系中，经过三点（0，0），（1，1），（2，0）的圆的方程为（x﹣1）2+y2=1（或x2+y2﹣2x=0）．【解答】解：【方法一】根据题意画出图形如图所示，结合图形知经过三点（0，0），（1，1），（2，0）的圆，其圆心为（1，0），半径为1，则该圆的方程为（x﹣1）2+y2=1．【方法二】设该圆的方程为x2+y2+Dx+Ey+F=0，则，解得D=﹣2，E=F=0；∴所求圆的方程为x2+y2﹣2x=0．故答案为：（x﹣1）2+y2=1（或x2+y2﹣2x=0）．17、（2018年高考天津卷文科7）（5分）在平面直角坐标系中，记d为点P（cosθ，sinθ）到直线x﹣my﹣2=0的距离．当θ、m变化时，d的最大值为（）A．1 B．2 C．3 D．4【解答】解：由题意d==，tanα=﹣，∴当sin（θ+α）=﹣1时，d max=1+≤3．∴d的最大值为3．故选：C．18、（2018年高考北京卷理科14）（5分）已知椭圆M：+=1（a＞b＞0），双曲线N：﹣=1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为；双曲线N的离心率为2．【解答】解：椭圆M：+=1（a＞b＞0），双曲线N：﹣=1．若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，可得椭圆的焦点坐标（c，0），正六边形的一个顶点（，），可得：，可得，可得e4﹣8e2+4=0，e∈（0，1），解得e=．同时，双曲线的渐近线的斜率为，即，可得：，即，可得双曲线的离心率为e==2．故答案为：；2．19、（2018年高考天津卷理科7）（5分）已知双曲线=1（a＞0，b＞0）的离心率为2，过右焦点且垂直于x轴的直线与双曲线交于A，B两点．设A，B到双曲线的同一条渐近线的距离分别为d1和d2，且d1+d2=6，则双曲线的方程为（）A．﹣=1 B．﹣=1 C．﹣=1 D．﹣=1【解答】解：由题意可得图象如图，CD是双曲线的一条渐近线y=，即bx﹣ay=0，F（c，0），AC⊥CD，BD⊥CD，FE⊥CD，ACDB是梯形，F是AB的中点，EF==3，EF==b，所以b=3，双曲线=1（a＞0，b＞0）的离心率为2，可得，可得：，解得a=．则双曲线的方程为：﹣=1．故选：C．20、（2018年高考天津卷理科12）（5分）已知圆x2+y2﹣2x=0的圆心为C，直线，（t为参数）与该圆相交于A，B两点，则△ABC的面积为．【解答】解：圆x2+y2﹣2x=0化为标准方程是（x﹣1）2+y2=1，圆心为C（1，0），半径r=1；直线化为普通方程是x+y﹣2=0，则圆心C到该直线的距离为d==，弦长|AB|=2=2=2×=，∴△ABC的面积为S=•|AB|•d=××=．故答案为：．21、（2018年高考北京卷文科10）（5分）已知直线l过点（1，0）且垂直于x轴．若l被抛物线y2=4ax截得的线段长为4，则抛物线的焦点坐标为（1，0）．【解答】解：∵直线l过点（1，0）且垂直于x轴，∴x=1，代入到y2=4ax，可得y2=4a，显然a＞0，∴y=±2，∵l被抛物线y2=4ax截得的线段长为4，∴4=4，解得a=1，∴y2=4x，∴抛物线的焦点坐标为（1，0），故答案为：（1，0）22、（2018年高考北京卷文科12）（5分）若双曲线﹣=1（a＞0）的离心率为，则a=4．【解答】解：双曲线﹣=1（a＞0）的离心率为，可得：，解得a=4．故答案为：4．23、（2018年高考全国卷3文科）8．（5分）直线x+y+2=0分别与x轴，y轴交于A，B两点，点P在圆（x﹣2）2+y2=2上，则△ABP面积的取值范围是（）A．[2，6]B．[4，8]C．[，3] D．[2，3]【解答】解：∵直线x+y+2=0分别与x轴，y轴交于A，B两点，∴令x=0，得y=﹣2，令y=0，得x=﹣2，∴A（﹣2，0），B（0，﹣2），|AB|==2，∵点P在圆（x﹣2）2+y2=2上，∴设P（2+，），∴点P到直线x+y+2=0的距离：d==，∵sin（）∈[﹣1，1]，∴d=∈[]，∴△ABP面积的取值范围是：[，]=[2，6]．故选：A．24、（2018年高考全国卷3文科）10．（5分）已知双曲线C：﹣=1（a＞0，b＞0）的离心率为，则点（4，0）到C的渐近线的距离为（）A．B．2 C．D．2【解答】解：双曲线C：﹣=1（a＞0，b＞0）的离心率为，可得=，即：，解得a=b，双曲线C：﹣=1（a＞b＞0）的渐近线方程玩：y=±x，点（4，0）到C的渐近线的距离为：=2．故选：D．25、（2018年高考全国卷3理科）11．（5分）设F1，F2是双曲线C：﹣=1（a＞0．b＞0）的左，右焦点，O是坐标原点．过F2作C的一条渐近线的垂线，垂足为P，若|PF1|=|OP|，则C的离心率为（）A．B．2 C．D．【解答】解：双曲线C：﹣=1（a＞0．b＞0）的一条渐近线方程为y=x，∴点F2到渐近线的距离d==b，即|PF2|=b，∴|OP|===a，cos∠PF2O=，∵|PF1|=|OP|，∴|PF1|=a，在三角形F1PF2中，由余弦定理可得|PF1|2=|PF2|2+|F1F2|2﹣2|PF2|•|F1F2|COS∠PF2O，∴6a2=b2+4c2﹣2×b×2c×=4c2﹣3b2=4c2﹣3（c2﹣a2），即3a2=c2，即a=c，∴e==，故选：C．26、（2018年高考全国卷3理科）13．（5分）已知向量=（1，2），=（2，﹣2），=（1，λ）．若∥（2+），则λ=．【解答】解：∵向量=（1，2），=（2，﹣2），∴=（4，2），∵=（1，λ），∥（2+），∴，解得λ=．故答案为：．27、（2018年高考全国卷3理科）16．（5分）已知点M（﹣1，1）和抛物线C：y2=4x，过C 的焦点且斜率为k的直线与C交于A，B两点．若∠AMB=90°，则k=2．【解答】解：∵抛物线C：y2=4x的焦点F（1，0），∴过A，B两点的直线方程为y=k（x﹣1），联立可得，k2x2﹣2（2+k2）x+k2=0，设A（x1，y1），B（x2，y2），则x1+x2=，x1x2=1，∴y1+y2=k（x1+x2﹣2）=，y1y2=k2（x1﹣1）（x2﹣1）=k2[x1x2﹣（x1+x2）+1]=﹣4，∵M（﹣1，1），∴=（x1+1，y1﹣1），=（x2+1，y2﹣1），∵∠AMB=90°=0，∴•=0∴（x1+1）（x2+1）+（y1﹣1）（y2﹣1）=0，整理可得，x1x2+（x1+x2）+y1y2﹣（y1+y2）+2=0，∴1+2+﹣4﹣+2=0，即k2﹣4k+4=0，∴k=2．故答案为：228、（2018年高考江苏卷理科）8．（5分）在平面直角坐标系xOy 中，若双曲线﹣=1（a ＞0，b ＞0）的右焦点F （c ，0）到一条渐近线的距离为c ，则其离心率的值是 2 ．【解答】解：双曲线=1（a ＞0，b ＞0）的右焦点F （c ，0）到一条渐近线y=x 的距离为c ，可得：=b=，可得，即c=2a ，所以双曲线的离心率为：e=．故答案为：2．类型二 解答题1.（2017年高考数学北京卷（理））已知抛物线2:2C y px =过点(1,1)P ,过点1(0,)2作直线l 与抛物线C 交于不同的两点,M N ，过点M 作x 轴的垂线分别与直线,OP ON 交于点,A B ，其中O 为原点. （Ⅰ）求抛物线C 的方程，并求其焦点坐标和准线方程； （Ⅱ）求证：A 为线段BM 的中点.解：（Ⅰ）因为抛物线C 过点(1,1)P ，把(1,1)P 代入22y px =，得12p =∴2:C y x =∴焦点坐标1(,0)4，准线为14x =-。
2017-2018学年高中数学考点52几何证明选讲(含2013年高考试题)新人教A版
考点52几何证明选讲一、填空题1.（2013 •天津高考理科• T13）如图,△ ABC 为圆的内接三角形，BD 为圆的弦,且BD// AC.过点 A 作圆的切线与 DB 的延长线交于点 E,AD 与BC 交于点F.若AB=AC,AE=6,BD=5则线段CF 的 长为_______________ .【解析】由相交弦定理 PA • PB 二PD ・PC 得PC = 4，所以弦长CD = 5，故圆心O 到弦 CD 的距离为OC 2 _（；CD ）2二7〜：5二于.【解题指南】 利用圆以及平行线的性质计算【解析】因为AE 与圆相切于点 A,所以A^=EB ・ （EB+BD ）,即62=EB- （EB+5）,所以BE=4,根据 切线的性质有/ BAE=/ ACB,又因为 AB=AC 所以/ ABC 2 ACB,所以/ ABC 2 BAE,所以AE / BC, 因为BD// AC,所以四边形 ACBE 为平行四边形，所以AC=BE=4,BC=AE=6设CF=x,由BD// AC 得 x= 8 ,即 CF=8 . 3 3AC CF BD - BF【答案】,即3 4 —,解得 5 6 -x 8 3.2. （2013 •湖南高考理科AB,CD 相交于点P, PA11）如图，在半径为二 PB = 2, PD =1, 则圆心O 到弦CD 勺距离为【解题指南】 先通过.A= C 及线线平行同位角相等，找出三角形相似 ，再由比例线段求得答案•【解析】 因为 BC//PE 所以.BCD 二/PED.且.A =/C = . PED 二/BAD.PE PD,—二• EPD s APEPE ?二 PA PD = 3 2 二 6.所以 PE 二6.PA PE-4 I【答案】、、6.4. （2013 •北京高考理科・T11）如图， AB 为圆 O 的直径,PA 为圆 O 的切线,PB 与圆 O 相交于 D.若 PA=3,PD ： DB=9： 16,则21【解析】由于PD ： DB=9： 16,设PD=9a,DB=16a,根据切割线定理有 PA=PD ・PB,有a=—,所以59PD=,在 Rt △ PBA 中，有 AB=4.5【解题指南】先用半径表示，再求比值. 【解析】设半径为R AB=3AD=2R.PD=,AB=【解题指南】利用切割线定理求出9 5 5. （2013 •湖北高考理科15）径OC 上的射影为E ,若AB=3ADJ 则 【答案】4. 如图，圆O 上一点C 在直径AB 上的射影为 D,点D 在半 CE 的值为AB.2 1 2 1 22,2 AD=—R,OD=—R,OC=R,CD=、R- R R,3 3 9 3【答案】8. 6.（2013 •陕西高考理科15）如图，弦AB 与 CD 相交于圆O 内一点E 过E 作BC 的平 行线与AD 的延长线相交于点 P 已知PD= 2DA= 2,则PE= _.【解题指南】先通过圆周角相等及线段平行同位角相等得出 ；EPD s 「‘APE,再由比例线段求得答案. 【解析】因为 BC//PE 所以.BCD =• PED.且在圆中• BCD = • BAD = • PED = • BAD. 一一 PE PD —2 — = EPD s APEPE 2 二 PA PD = 3 2 二 6.所以 PE = . 6.PA PE【答案】.6.7. （2013 •广东高考理科15）如图，AB 是圆O 的直径，点C 在圆O 上，延长BC 到 D 使 BC=CD 过C 作圆O 的切线交 AD 于E.若AB=6, ED=2贝U BC _______ .【解题指南】 本题考查几何证明选讲，可先作ABD 的中位线OC 再计算.【解析】设BC 二x ，连接OC ，因为BC =CD, AC _ BD , ABD 是等腰三角形,BC =CD =x, AB =AD =6,ED =2, AE =4，在 ACD 中，CE — AD ，贝UcosC2.2 3CEEO8R-8.lRCE = CD cosCCE2=AC2 - AE2=AD2—DE2，即36—x2—16=x2 -4，解得x =2 3. 【答案】2-、3.8.（ 2013 •广东高考文科・T 15）如图，在矩形ABCD 中，AB —.3, BC =3 , BE _ AC ,垂足为E ，则ED = ______ .【解题指南】本题考查几何证明选讲，可先利用射影定理再结合余弦定理计算/V ）【解析】AB 二心3, BC =3,AC =2.3,. ACB =30 ,AC _ BE , . ：BEC 是直角三角形,3 J 3由射影定理BC 2二AC EC, EC，在 ECD 中，由余弦定理可得 2 人.ED 2 二 EC 2 CD 2 —2EC CD cos60； = 21，即 ED 二 21 .4 2【答案】21 .29.（2013 •天津高考文科・T 13）如图，在圆内接梯形 ABCD 中 , AB / DC 过点A 作圆的 切线与CB 的延长线交于点 E 若AB = AD = 5, BE = 4,则弦BD 的长为 _.【解题指南】 首先利用圆的性质， 得出角的关系，再分别在厶ABE 与△ ABD 中利用正弦定理 求解.【解析】设• BAE ，因为AE 与圆相切于点 A,所以乙BAE ZADB,又因为AB = AD ,所以 ABD =/ADB •,因为 AB / DC 所以 ABD =/CDB = •,所以 ABE =“ADC =2：.即一4 - ,解得cos 〉=?在厶ABD si n t sin （二-3s ） 4BD—，解得BD =戛sin （二-2： ） sin ：215【答案】—在厶ABE 中，由正弦定理得一匪一二-AB ,sin ZBAE sin E 一BD AB ，即sin BAD sin ADB中，由正弦定理得2 10过C作厶ABC的外接圆的切线CD , BD丄CD , BD与外接圆交于点E，则DE的长为【解题指南】直接根据圆的切线及直角三角形的相关性质进行求解【解析】由题意知AB是圆的直径，设圆心为0 ,连接0C ,因为CD是圆的切线，则0C _ CD又因为BD丄CD ,所以0C // BD •因为0A = 0C,. A = 60 ,所以.AC0 =60 0CB =30 ,因为AB = 20,所以BC =10,3 ,因为OC//BD ,所以• CBD =30 •所以BD=15,又因为AB是圆的直径，点E在圆上，AB = 20且ABD = 60 ,所以BE =10,故DE = BD-'BE =15—10=5【答案】5.二、解答题11. （2013 •辽宁高考文科22 ）与（2013 •辽宁高考理科22）相同如图，AB为LI 0的直径，直线CD与L 0相切于E, AD垂直CD于D , BC垂直CD于C , EF垂直AB于F，连接AE, BE .证明：（）FEB =/CEB; （「.）EF2二AD BC.【解题指南】借助等量代换，证明相等关系；利用全等三角形的对应边，角相等【证明】（J由直线CD与L 0相切于E ,得.EAB=/CEB由AB为L 0的直径，得AE _ EB，从而.EAB • • EBF =-231又EF 垂直AB于F，得.FEB EBF ，从而FEB=/CEB2（〔〔）由BC垂直CD于C，得BC — CE又EF 垂直AB 于F= EF _ AB, - FEB =/CEB , BE为公共边，所以Rt・BCE也Rt BFE，所以BC二BF10 （2013 •重庆高考理科・T 14）如图，在厶ABC 中，.C =90°, - A = 60° , AB = 20 ,同理可证，Rt ADE也Rt^AFE，所以AD二AF又在Rt △ AEB 中，EF—AB,所以EF2=AF BF.2综上，EF = AD BC.12. （2013 •新课标I高考文科・T 22）与（2013 •新课标I高考理科22）相同如图，直线AB为圆的切线，切点为B,点C在圆上，/ ABC的角平分线BE交圆于点E, DB 垂直BE 交圆于Do（I）证明：DB=DC（H）设圆的半径为1, BC= ，延长CE交AB于点卩，求厶BCF外接圆的半径。
2017-2018年高考数学立体几何汇编及答案解析
2017—2018年高考数学试题立体几何汇编及答案解析类型一 空间几何体的结构特征与三视图1.【2017浙江，3】某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是A ．12+πB ．32+πC ．123+πD ．323+π【答案】A 【解析】2π1211π3(21)1322V ⨯=⨯⨯+⨯⨯=+，选A. 2.【2017北京，理7】某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为（A ） （B ）（C ） （D ）2 【答案】B 【解析】几何体是四棱锥，如图红色线为三视图还原后的几何体，最长的棱长为正方体的对角线，l == B.3.【2017山东，理13】由一个长方体和两个14圆柱体构成的几何体的三视图如右图，则该几何体的体积为 .【答案】22π+【解析】该几何体的体积为21112211242V π=π⨯⨯⨯+⨯⨯=+． 4．（2018年高考北京卷理科）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（ ）A．1 B．2 C．3 D．4【解答】解：四棱锥的三视图对应的直观图为：PA⊥底面ABCD，AC=，CD=，PC=3，PD=2，可得三角形PCD不是直角三角形．所以侧面中有3个直角三角形，分别为：△PAB，△PBC，△PAD．故选：C．5．（2018年高考数学全国卷1理科）某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）A．2B．2C．3 D．2【解答】解：由题意可知几何体是圆柱，底面周长16，高为：2，直观图以及侧面展开图如图：圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度：=2．故选：B．6．（2018年高考数学全国卷3理科）中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）A． B ． C ． D ．【解答】解：由题意可知，如图摆放的木构件与某一带卯眼的木构件咬合成长方体，小的长方体，是榫头，从图形看出，轮廓是长方形，内含一个长方形，并且一条边重合，另外3边是虚线，所以木构件的俯视图是A ．故选：A ．7．（2018年高考浙江卷）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（ ） A ．2B ．4C ．6D ．8【解答】解：根据三视图：该几何体为底面为直角梯形的四棱柱．如图所示：故该几何体的体积为：V=．故选：C ．8．某多面体的三视图如图所示,则该几何体的体积与其 外接球的体积之比为( )A ．π186B ．π96 C ．π36 D ．π26选A类型二 空间几何体与空间旋转体的面积、体积问题1、如图，半径为4的球O中有一内接圆柱，当圆柱的侧面积最大时，球的表面积与该圆柱的侧面积之差是______.解：如图，2、设球的一条半径与圆柱相应的母线的夹角为α，圆柱侧面积S ＝2π×4sin α×2×4cos α＝32πsin2α，当α＝π4时，S 取最大值32π，此时球的表面积与该圆柱的侧面积之差为32π.3、（2018年高考数学天津卷理科）已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，除面ABCD 外，该正方体其余各面的中心分别为点E ，F ，G ，H ，M （如图），则四棱锥M ﹣EFGH 的体积为 ．【解答】解：正方体的棱长为1，M ﹣EFGH 的底面是正方形的边长为：，四棱锥是正四棱锥，棱锥的高为， 四棱锥M ﹣EFGH 的体积：=．故答案为：．4、(2014·课标Ⅱ)如图，网格纸上正方形小格的边长为1(表示1cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A.1727B.59C.1027D.13解：原来毛坯体积为：π·32·6＝54π(cm 3)，由三视图知该零件由左侧底面半径为2cm ，高为4cm 的圆柱和右侧底面半径为3cm ，高为2cm 的圆柱构成，故该零件的体积为：π·22·4＋π·32·2＝34π(cm 3)，切削掉部分的体积为54π－34π＝20π(cm 3)，故切削掉部分的体积与原来毛坯体积的比值为20π54π＝1027 .故选C.6.【2017课标3，理8】已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为A ．πB ．3π4C ．π2D ．π4【答案】B【解析】由题可知球心在圆柱体中心，圆柱体上下底面圆半径r =则圆柱体体积23ππ4V r h ==，故选B.7.【2017天津，理10】已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为 . 【答案】92π 【解析】设正方体边长为a ，则226183a a =⇒= ，外接球直径为34427923,πππ3382R V R ====⨯=. 8.【2017江苏，6】 如图,在圆柱12,O O 内有一个球O ,该球与圆柱的上、下面及母线均相切.记圆柱12,O O 的体积为1V ,球O 的体积为2V ,则12V V 的值是 ▲ .【答案】32 【解析】设球半径为r ，则2132π2342π3V r r V r ⨯==．故答案为32． 9、（2018年高考数学全国卷3理科）10．（5分）设A ，B ，C ，D 是同一个半径为4的球的球面上四点，△ABC 为等边三角形且面积为9，则三棱锥D ﹣ABC 体积的最大值为（ ） A ．12B ．18C ．24D ．54【解答】解：△ABC 为等边三角形且面积为9，可得，解得AB=6，球心为O ，三角形ABC 的外心为O′，显然D 在O′O 的延长线与球的交点如图：O′C==，OO′==2，则三棱锥D ﹣ABC 高的最大值为：6， 则三棱锥D ﹣ABC 体积的最大值为：=18．故选：B ．10、（2018年高考数学全国卷2理科）16．（5分）已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为，SA 与圆锥底面所成角为45°，若△SAB 的面积为5，则该圆锥的侧面积为40π ．【解答】解：圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为，可得sin ∠AMB==．△SAB 的面积为5，可得sin ∠AMB=5，即×=5，即SA=4．SA 与圆锥底面所成角为45°，可得圆锥的底面半径为：=2．则该圆锥的侧面积：π=40π．故答案为：40π．11、（2018年高考数学全国卷1理科）12．（5分）已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为（ ）A ．B ．C ．D ．【解答】解：正方体的所有棱中，实际上是3组平行的棱，每条棱所在直线与平面α所成的角都相等，如图：所示的正六边形平行的平面，并且正六边形时，α截此正方体所得截面面积的最大，此时正六边形的边长明明就的最大值为：6×=．故选：A．12、（2018年江苏省高考数学试卷）如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为．【解答】解：正方体的棱长为2，中间四边形的边长为：，八面体看做两个正四棱锥，棱锥的高为1，多面体的中心为顶点的多面体的体积为：2×=．故答案为：．类型三点共线、线共点问题1、如图，E，F，G，H分别是空间四边形内AB，BC，CD，DA上的点，且EH与FG交于点O.求证：B，D，O三点共线.证明：∵点E∈平面ABD，点H∈平面ABD，∴EH⊂平面AB D.∵EH∩FG＝O，∴点O∈平面AB D.同理可证点O∈平面BC D.∴点O∈平面ABD∩平面BCD＝B D.即B，D，O三点共线.类型四共面问题1、下列如图所示的正方体和正四面体，P、Q、R、S分别是所在棱的中点，则四个点共面的图形是____________.(填所有满足条件图形的序号)解：易知①③中PS ∥Q R ，∴四点共面.在②中构造如图所示的含点P ，S ，R ，Q 的正六边形，易知四点共面.在④中，由点P ，R ，Q 确定平面α，由图象观察知点S 在平面α外，因此四点不共面.综上知，故填①②③.类型五 异面直线问题1.【2017课标II ，理10】已知直三棱柱111C C AB -A B 中，C 120∠AB =，2AB =，1C CC 1B ==，则异面直线1AB 与1C B 所成角的余弦值为（ ）A ．．5 C ．5D 【答案】C【解析】如图所示，补成四棱柱1111ABCD A B C D - ,则所求角为1111,BC D BC BD C D AB ∠=====因此1cos 5BC D ∠== ，故选C 。
高中数学高考17第一部分 板块二 专题五 解析几何 第3讲 圆锥曲线中的最值、范围、证明问题(大题)
设M(x1，y1)，M′(x2，y2)， 设 MF1 的方程为 x＝my－ 3，
x＝my－ 3，
由x42＋y2＝1
得(m2＋4)y2－2 3my－1＝0，
故yy11＋y2＝y2＝－mm2 221＋＋3m44.，
设F1M与F2N的距离为d，四边形F1F2NM的面积为S，
则 S＝12(|F1M|＋|F2N|)d＝12(|F1M′|＋|F1M|)d＝12|MM′|d＝ S△MF2M′,
2
PART TWO
真题体验 押题预测
真题体验 (2018·全国Ⅰ，文，20)设抛物线C：y2＝2x，点A(2,0)，B(－2,0)，过点A的直线l与 C交于M，N两点. (1)当l与x轴垂直时，求直线BM的方程；
解 当l与x轴垂直时，l的方程为x＝2， 可得点M的坐标为(2,2)或(2，－2). 所以直线 BM 的方程为 y＝12x＋1 或 y＝－12x－1. 即x－2y＋2＝0或x＋2y＋2＝0.
所以 y1＋y2＝2k，y1y2＝－4.
直线 BM，BN 的斜率之和 kBM＋kBN＝x1y＋1 2＋x2y＋2 2＝x2y1＋x1x＋1y22＋x22＋y12＋ y2.
①
将 x1＝yk1＋2，x2＝yk2＋2 及 y1＋y2，y1y2 的表达式代入①式分子，
可得 x2y1＋x1y2＋2(y1＋y2)＝2y1y2＋4kky1＋y2＝－8k＋8＝0.
当且仅当 t2＝92，即 t＝±322时取等号.
故△BPQ
的面积的最大值为
2 2.
热点二 范围问题
圆锥曲线的范围问题的常见解法 (1)几何法：若题目中的条件和结论能明显体现几何特征和意义，则考虑利用图形 性质来解决； (2)代数法：若题目中的条件和结论能体现一种明确的函数关系或不等关系或已知 参数与新参数之间的等量关系等，则可利用这些关系去求参数的范围.
2018年全国各地高考数学试题及解答分类汇编大全(18 选修4：几何证明选讲、坐标系与参数方程、不等式选讲
2018年全国各地高考数学试题及解答分类汇编大全（18选修4：几何证明选讲、坐标系与参数方程、不等式选讲、矩阵与变换）一、几何证明选讲：选修4—1；几何证明选讲1．（2018江苏）[选修4—1：几何证明选讲](本小题满分10分)如图，圆O 的半径为2，AB 为圆O 的直径，P 为AB 延长线上一点，过P 作圆O 的切线，切点为C ．若23PC =，求 BC 的长．1．【答案】2【解析】连结OC ，因为PC 与圆O 相切，所以OC PC ⊥． 又因为23PC =，2OC =，所以224OP PC OC =+=．又因为2OB =，从而B 为Rt OCP △斜边的中点，所以2BC =．二、坐标系与参数方程：选修4-4：坐标系与参数方程1．（2018北京理）在极坐标系中，直线cos sin (0)a a ρθρθ+=>与圆=2cos ρθ相切，则a =__________． 1．【答案】12+【解析】因为222x y ρ=+，cos x ρθ=，sin y ρθ=，由()cos sin 0a a ρθρθ+=>，得()0x y a a +=>， 由2cos ρθ=，得22cos ρρθ=，即22=2x y x +，即()2211x y -+=， 112a -=，12a ∴=±0a >，12a ∴=2．（2018江苏）[选修4—4：坐标系与参数方程](本小题满分10分)在极坐标系中，直线l 的方程为πsin()26ρθ-=，曲线C 的方程为4cos ρθ=，求直线l 被曲线C 截得的弦长．2．【答案】直线l 被曲线C 截得的弦长为3 【解析】因为曲线C 的极坐标方程为4cos ρθ=， 所以曲线C 的圆心为()2,0，直径为4的圆．因为直线l 的极坐标方程为sin 2π6ρθ⎛⎫-= ⎪⎝⎭，则直线l 过()4,0A ，倾斜角为π6，所以A 为直线l 与圆C 的一个交点．设另一个交点为B ，则π6OAB ∠=． 连结OB ，因为OA 为直径，从而π2OBA ∠=，所以4cos6πAB ==．因此，直线l 被曲线C截得的弦长为3．（2018天津理）已知圆2220x y x +-=的圆心为C，直线1,232⎧=-+⎪⎪⎨⎪=-⎪⎩x y t (t 为参数)与该圆相交于A ，B 两点，则ABC △的面积为 .3．【答案】12【解析】由题意可得圆的标准方程为()2211x y -+=， 直线的直角坐标方程为()31y x -=-+，即20x y +-=，则圆心到直线的距离为d ==，由弦长公式可得2AB =则1122ABC S ==△．4．（2018全国新课标Ⅰ文、理）[选修4—4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线1C 的方程为2y k x =+．以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为22cos 30ρρθ+-=． （1）求2C 的直角坐标方程；（2）若1C 与2C 有且仅有三个公共点，求1C 的方程．4.答案：（1）22(1)4x y ++=；（2）423y x =-+ 解答：（1）由22cos 30ρρθ+-=可得：22230x y x ++-=，化为22(1)4x y ++=. （2）1C 与2C 有且仅有三个公共点，说明直线2(0)y kx k =+<与圆2C 相切，圆2C 圆心为(1,0)-，半径为2，则2=，解得43k =-，故1C 的方程为423y x =-+.5．（2018全国新课标Ⅱ文、理）[选修4－4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线C 的参数方程为2cos ,4sin x θy θ=⎧⎨=⎩（θ为参数），直线l 的参数方程为1cos ,2sin x t αy t α=+⎧⎨=+⎩（t 为参数）．（1）求C 和l 的直角坐标方程；（2）若曲线C 截直线l 所得线段的中点坐标为(1,2)，求l 的斜率．5．【答案】（1）221416x y +=，当cos 0α≠，tan 2tan y x αα=⋅+-；当cos 0α=，1x =；（2）2-． 【解析】（1）曲线C 的直角坐标方程为221416x y +=．当cos 0α≠时，l 的直角坐标方程为tan 2tan y x αα=⋅+-， 当cos 0α=时，l 的直角坐标方程为1x =．（2）将l 的参数方程代入C 的直角坐标方程，整理得关于t 的方程()()2213cos 42cos sin 80tt ααα+++-=．①因为曲线C 截直线l 所得线段的中点()1,2在C 内，所以①有两个解，设为1t ，2t ，则120t t +=． 又由①得()12242cos sin 13cos t t ααα++=-+，故2cos sin 0αα+=，于是直线l 的斜率tan 2k α==-．6．（2018全国新课标Ⅲ文、理）[选修4—4：坐标系与参数方程]（10分）在平面直角坐标系xOy 中，O ⊙的参数方程为cos ,sin x y θθ=⎧⎨=⎩（θ为参数），过点(0,且倾斜角为α的直线l 与O ⊙交于A B ，两点． （1）求α的取值范围；（2）求AB 中点P 的轨迹的参数方程．22.答案：见解析 解答：（1）O 的参数方程为cos sin x y θθ=⎧⎨=⎩，∴O 的普通方程为221x y +=，当90α=︒时，直线：:0l x =与O 有两个交点，当90α≠︒时，设直线l的方程为tan y x α=-由直线l 与O 有1<，得2tan 1α>，∴tan 1α>或tan 1α<-，∴4590α︒<<︒或90α︒<<，综上(45,135)α∈︒︒.（2）点P 坐标为(,)x y ，当90α=︒时，点P 坐标为(0,0)，当90α≠︒时，设直线l 的方程为y kx =-1122(,),(,)A x y B x y，∴221x y y kx ⎧+=⎪⎨=-⎪⎩①②有22(1x kx +-=，整理得22(1)10k x +-+=，∴1221x x k +=+，12y y +=，∴2211x ky k ⎧=⎪⎪+⎨⎪=⎪+⎩③④得x k y=-代入④得220x y ++=.当点(0,0)P时满足方程220x y ++=，∴AB 中点的P的轨迹方程是220x y ++=，即221(2x y +=，由图可知，A，(22B --，则02y -<<，故点P的参数方程为cos 2sin 22x y ββ⎧=⎪⎪⎨⎪=-+⎪⎩（β为参数，0βπ<<）.三、不等式选讲选：选修4-5：不等式选讲1．（2018江苏）[选修4—5：不等式选讲](本小题满分10分)若x，y，z为实数，且x+2y+2z=6，求222x y z++的最小值．D．【答案】4【解析】由柯西不等式，得()()()222222212222x y z x y z++++≥++．因为22=6x y z++，所以2224x y z++≥，当且仅当122x y z==时，不等式取等号，此时23x=，43y=，43z=，所以222x y z++的最小值为4．2．（2018全国新课标Ⅰ文、理）[选修4—5：不等式选讲]（10分）已知()11f x x ax=+--．（1）当1a=时，求不等式()1f x>的解集；（2）若()01x∈，时不等式()f x x>成立，求a的取值范围．2.答案：（1）1{|}2x x>；（2）(0,2].解答：（1）当1a=时，21()|1||1|21121xf x x x x xx≥⎧⎪=+--=-<<⎨⎪-≤-⎩，∴()1f x>的解集为1{|}2x x>.（2）当0a=时，()|1|1f x x=+-，当(0,1)x∈时，()f x x>不成立.当0a<时，(0,1)x∈，∴()1(1)(1)f x x ax a x x=+--=+<，不符合题意. 当01a<≤时，(0,1)x∈，()1(1)(1)f x x ax a x x=+--=+>成立.当1a>时，1(1),1()1(1)2,a x xaf xa x xa⎧+-<<⎪⎪=⎨⎪-+≥⎪⎩，∴(1)121a-⋅+≥，即2a≤.综上所述，a的取值范围为(0,2].3．（2018全国新课标Ⅱ文、理）[选修4－5：不等式选讲]（10分） 设函数()5|||2|f x x a x =-+--． （1）当1a =时，求不等式()0f x ≥的解集； （2）若()1f x ≤，求a 的取值范围． 3．【答案】（1）{}|23x x -≤≤；（2）(][),62,-∞-+∞．【解析】（1）当1a =时，()24,12,1226,2x x f x x x x +≤-⎧⎪=-<≤⎨⎪-+>⎩，可得()0f x ≥的解集为{}|23x x -≤≤．（2）()1f x ≤等价于24x a x ++-≥，而22x a x a ++-≥+，且当2x =时等号成立．故()1f x ≤等价于24a +≥， 由24a +≥可得6a ≤-或2a ≥，所以a 的取值范围是(][),62,-∞-+∞．(,6][2,)-∞-+∞4．（2018全国新课标Ⅲ文、理）[选修4—5：不等式选讲]（10分）设函数()|21||1|f x x x =++-． （1）画出()y f x =的图像；（2）当[0,)x ∈+∞，()f x ax b ≤+，求a b +的最小值．4.答案：见解答 解答：（1）13,21()2,123,1x x f x x x x x ⎧-≤-⎪⎪⎪=+-<<⎨⎪≥⎪⎪⎩，如下图：（2）由（1）中可得：3a ≥，2b ≥， 当3a =，2b =时，a b +取最小值， ∴a b +的最小值为5.四、矩阵与变换 选修4-2：矩阵与变换1. （2018上海）行列式4125的值为 。
2013年高考数学预测新课标数学考点预测(19)：几何证明选讲
K
OM .OP = OA ．
（Ⅱ）证明：因为 BK 是圆 O 的切线， BN ⊥ OK ． 同（Ⅰ） ，有
2
2
O
P
M
OB
= ON .OK ，又 OB = OA ，
，即
所以 OP.OM = ON .OK 又 ∠NOP = ∠MOK ，
ON OM ． = OP OK
所以 △ONP ∽△OMK ，故∠OKM = ∠OPN = 90� ． ） 5． （2008 江苏卷理 21 21） 如图， 设△ABC 的外接圆的切线 AE 与 BC 的延长线交于点 E， ∠BAC 的平分线与 BC 交于点 D． A 2 求证： = EB.EC ．
CB=2 2 ，求 EF 的长．
〖解析〗连 PB，BC 切⊙P 于点 B，PB⊥BC， CD=2，CB=2 2 ，由切割线定理得：CB2=CD·CE
B C D ． O A P
F
CE=4，DE=2，BP=1，又∵EF⊥CE EF CE 得： ，EF= 2 = PB CB
∴△CPB∽△CFE，
E
考点三：圆内接四边形的性质定理与判定定理 ) 3.(2008 年南师附中高考数学模拟试卷（最后一卷） 高考数学模拟试卷（最后一卷）) 如图，已知 AD 是ΔABC 的外角∠EAC 的平分线，交 BC 的延长线于点 D，延长 DA 交ΔABC 的外接圆于点 F，连结 FB、FC． （1）求证：FB=FC； （2）求证：FB2=FA·FD； （3）若 AB 是ΔABC 外接圆的直径，∠EAC=120°， BC=6cm，求 AD 的长． 〖解析〗（1）∵AD 平分∠EAC，∴∠EAD=∠DAC． ∵四边形 AFBC 内接于圆，∴∠DAC=∠FBC． ∵∠EAD=∠FAB=∠FCB，∴∠FBC=∠FCB，∴FB=FC． （2）∵∠FAB=∠FCB=∠FBC ，∠AFB=∠BFD，
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
考点52 几何证明选讲一、填空题1.(2013·天津高考理科·T13)如图,△ABC 为圆的内接三角形,BD 为圆的弦,且BD ∥AC.过点A 作圆的切线与DB 的延长线交于点E,AD 与BC 交于点F.若AB=AC,AE=6,BD=5,则线段CF 的长为 .【解题指南】利用圆以及平行线的性质计算.【解析】因为AE 与圆相切于点A,所以AE 2=EB ·(EB+BD),即62=EB ·(EB+5),所以BE=4,根据切线的性质有∠BAE=∠ACB,又因为AB=AC,所以∠ABC=∠ACB,所以∠ABC=∠BAE,所以AE ∥BC,因为BD ∥AC,所以四边形ACBE 为平行四边形,所以AC=BE=4,BC=AE=6.设CF=x,由BD ∥AC 得=AC CF BD BF ,即456=-xx ,解得x=83,即CF=83. 【答案】83.2. （2013·湖南高考理科·Ｔ11）的⊙0中,弦,,2,AB CD P PA PB ==相交于点1PD O =，则圆心到弦CD 的距离为.【解题指南】本题要利用相交弦定理:PA ·PB=PD ·PC 和解弦心三角形22)21(CD r d -=【解析】由相交弦定理PC PD PB PA ∙=∙得4=PC ，所以弦长5=CD ，故圆心O 到弦CD 的距离为234257)21(22=-=-CD OC .【答案】23. 3. （2013·陕西高考文科·Ｔ15）如图, AB 与CD 相交于点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知A C ∠=∠, PD = 2DA = 2, 则PE = .【解题指南】先通过A C ∠=∠及线线平行同位角相等，找出三角形相似,再由比例线段求得答案.【解析】..//BAD PED C A PED BCD PE BC ∠=∠⇒∠=∠∠=∠且所以因为.6.623∽2==⋅=⋅=⇒=⇒∆∆⇒PE PD PA PE PEPDPA PE APE EPD 所以.4. (2013·北京高考理科·T11)如图,AB 为圆O 的直径,PA 为圆O 的切线,PB 与圆O 相交于 D.若PA=3,PD ∶DB=9∶16,则PD= ,AB= .【解题指南】利用切割线定理求出PD,再在Rt △PBA 中利用勾股定理求出AB. 【解析】由于PD ∶DB=9∶16,设PD=9a,DB=16a,根据切割线定理有PA 2=PD ·PB,有a=15,所以PD=95,在Rt △PBA 中,有AB=4. 【答案】 954.5. （2013·湖北高考理科·Ｔ15）如图，圆O 上一点C 在直径AB 上的射影为D ，点D 在半径OC 上的射影为E ，若AB=3AD,则EOCE的值为【解题指南】先用半径表示,再求比值. 【解析】设半径为R ，AB=3AD=2R.AD=23R ,OD=13R ,3R =3cos ,3RC R ==228cos ,339CE CD C R R === 所以EO=R ―CE ―R ― 81,99R R =898.19RCE EO R== 【答案】8.6. （2013·陕西高考理科·Ｔ15）如图, 弦AB 与CD 相交于圆O 内一点E , 过E 作BC的平行线与AD 的延长线相交于点P . 已知PD ＝2DA ＝2, 则PE ＝ .【解题指南】先通过圆周角相等及线段平行同位角相等得出,∽APE EPD ∆∆再由比例线段求得答案. 【解析】..//BAD PED BAD BCD PED BCD PE BC ∠=∠⇒∠=∠∠=∠且在圆中所以因为.6.623∽2==⋅=⋅=⇒=⇒∆∆⇒PE PD PA PE PEPDPA PE APE EPD 所以 【答案】.67.（2013·广东高考理科·Ｔ15）如图，AB 是圆O 的直径，点C 在圆O 上，延长BC 到D 使BC=CD ，过C 作圆O 的切线交AD 于E.若AB=6，ED=2，则BC=______.【解题指南】本题考查几何证明选讲，可先作ABD ∆的中位线OC 再计算.【解析】设BC x =，连接OC ，因为,BC CD AC BD =⊥，ABD ∆是等腰三角形，,6,2,4BC CD x AB AD ED AE ======，在ACD ∆中，CE AD ⊥，则22222CE AC AE AD DE =-=-，即2236164x x --=-，解得x =【答案】8.（2013·广东高考文科·Ｔ15）如图，在矩形ABCD 中，AB =3BC =，BE AC ⊥，垂足为E ，则ED = ．【解题指南】本题考查几何证明选讲，可先利用射影定理再结合余弦定理计算.【解析】3,30,AB BC AC ACB AC BE ===∠=⊥，BEC ∆是直角三角形，由射影定理2,BC AC EC EC =⋅=ECD ∆中，由余弦定理可得222212cos604ED EC CD EC CD =+-⋅=，即2ED =.【答案】2. 9. （2013·天津高考文科·Ｔ13）如图, 在圆内接梯形ABCD 中, AB //DC , 过点A 作圆的切线与CB 的延长线交于点E . 若AB = AD = 5, BE = 4, 则弦BD 的长为 .【解题指南】 首先利用圆的性质，得出角的关系，再分别在△ABE 与△ABD 中利用正弦定理求解.【解析】设∠=BAE α，因为AE 与圆相切于点A ，所以,∠=∠BAE ADB 又因为AB = AD ，所以∠=∠=ABD ADB α，因为AB //DC ,所以∠=∠=ABD CDB α,所以2∠=∠=ABE ADC α.在△ABE 中，由正弦定理得sin sin =∠BE AB BAE E ，即45sin sin(3)=-απα，解得3cos .4=α在△ABD 中，由正弦定理得sin sin =∠∠BD AB BAD ADB ，即5sin(2)sin =-BD παα，解得15.2=BD 【答案】152. 10. （2013·重庆高考理科·Ｔ14）如图，在△ABC 中，090C ∠=，060A ∠=，20AB =，过C 作△ABC 的外接圆的切线CD ，BD ⊥CD ，BD 与外接圆交于点E ，则DE 的长为【解题指南】 直接根据圆的切线及直角三角形的相关性质进行求解【解析】由题意知AB 是圆的直径,设圆心为O ,连接OC ,因为CD 是圆的切线,则CD OC ⊥又因为BD ⊥CD ,所以BD OC //.因为 60,=∠=A OC OA ,所以30,60=∠=∠OCB ACO ,因为20=AB ,所以310=BC ,因为BD OC //,所以30=∠CBD 所以15=BD ,又因为AB 是圆的直径, 点E 在圆上, 20=AB 且 60=∠ABD ,所以10=BE ,故51015=-=-=BE BD DE【答案】5. 二、解答题11. （2013·辽宁高考文科·Ｔ22）与（2013·辽宁高考理科·Ｔ22）相同如图，AB 为O 的直径，直线CD 与O 相切于E , AD 垂直CD 于D ，BC 垂直CD 于C ，EF 垂直AB 于F ，连接,AE BE .证明： ()I FEB CEB ∠=∠;()II 2.EF AD BC =⋅【解题指南】 借助等量代换，证明相等关系；利用全等三角形的对应边，角相等. 【证明】()I 由直线CD 与O 相切于E ,得EAB CEB ∠=∠由AB 为O 的直径，得AE EB ⊥，从而2EAB EBF π∠+∠=又EF 垂直AB 于F ，得2FEB EBF π∠+∠=，从而FEB CEB ∠=∠()II 由BC 垂直CD 于C ，得BC CE ⊥又EF 垂直AB 于F EF AB ⇒⊥，FEB CEB ∠=∠，BE 为公共边， 所以Rt BCE ∆≌Rt BFE ∆，所以BC BF =同理可证，Rt ADE ∆≌Rt AFE ∆，所以AD AF = 又在Rt AEB △中, EF AB ⊥,所以2.EF AF BF =⋅综上，2.EF AD BC =⋅12. （2013·新课标Ⅰ高考文科·Ｔ22）与（2013·新课标Ⅰ高考理科·Ｔ22）相同 如图，直线AB 为圆的切线，切点为B ，点C 在圆上，∠ABC 的角平分线BE 交圆于点E ，DB 垂直BE 交圆于D 。
（Ⅰ）证明：DB=DC ； （Ⅱ）设圆的半径为1，BC=，延长CE 交AB 于点F ，求△BCF 外接圆的半径。
【解析】（Ⅰ）连结DE 交BC 于点G .由弦切角定理得CBE ABE ∠=∠，而∠ABE=∠CBE ，故BCE CBE ∠=∠，CE BE =. 又因为BE DB ⊥，所以DE 为直径，90=∠DCE ， 由勾股定理得DC DB =.（Ⅱ）由（Ⅰ）知，BDE CDE ∠=∠，DC DB =， 故DG 是BC 的中垂线，所以23=BG . 设DE 的中点为O ，连结BO ，则60=∠BOG ， 从而30=∠=∠=∠CBE BCE ABE ，所以BF CF ⊥， 故BCF Rt ∆的外接圆的半径等于23. 13.(2013·江苏高考数学科·T21)如图,AB 和BC 分别与圆O 相切于点D,C,AC 经过圆心O,且BC=2OC.求证:AC=2AD.【解题指南】利用相似三角形证明,主要考查圆的切线性质、相似三角形判定与性质,考查推理论证能力.【证明】连结OD.因为AB 和BC 分别与圆O 相切于点D,C,所以∠ADO=∠ACB=90°. 又因为∠A=∠A,所以Rt △ADO ∽Rt △ACB. 所以BC ACOD AD=,又BC=2OC=2OD, 故AC=2AD.14. （2013·新课标全国Ⅱ高考文科·Ｔ22）与（2013·新课标全国Ⅱ高考理科·Ｔ22）相同如图，CD 为△ABC 外接圆的切线，AB 的延长线交直线CD 于点D ，E 、F 分别为弦AB 与弦AC 上的点，且BC •AE=DC •AF ，B 、E 、F 、C 四点共圆. （1） 证明：CA 是△ABC 外接圆的直径；（2） 若DB=BE=EA,求过B 、E 、F 、C 四点的圆的面积与△ABC 外接圆面积的比值.【解题指南】(1)根据圆的性质及相似知识证得90CBA ∠=︒，可得CA 是ABC ∆外接圆的直径.（2）连接CE ，利用圆的性质，寻求过B 、E 、F 、C 四点的圆的半径长与△ABC 外接圆的半径长的比值，从而确立圆的面积之比.【解析】（1）因为CD 为ABC ∆处接圆的切线，所以DCB A ∠=∠，由题设知BC DCFA EA＝，故CDB ∆∽AEF ∆，所以.DBC EFA ∠=∠因为B ，E ，F ，C 四点共圆，所以CFE DBC ∠=∠，故90EFA CFE ∠=∠=︒ 所以90CBA ∠=︒，因此CA 是ABC ∆外接圆的直径. (2)连结CE ，因为90CBE ∠=︒，所以过B ，E ，F ，C 四点的圆的直径为CE ，由DB ＝BE ，有CE ＝DC ，又222BC DB BA DB =⋅=，所以222246.CA DB BC DB =+=而223DC DB DA DB =⋅=，故过B ，E ，F ，C 四点的圆的面积与ABC ∆外接圆面积的比值为1.2。