等式的性质
等式的性质

a b (c≠ 0) 如果 a = b,那么 c c
3、解一元一次方程的实质就是利用等式的 性质求出未知数的值x=a(常数)
学科网
则 4x +
= 7x
要求: 1、观察等式变形前后两边各 有什么变化 2、应怎么变化可使等式依然相等
(2) 若 3a + 4 = 8
关键:同侧对比 注意符号
则 3a = 8 +
.
你又发现了什么?
你又发现了什么?
• 等式的性质2: 等式两边都乘以 同一个数,或都除以同一个不为 0的数,结果仍相等。
(4) 如果-2x=4, ,那么x =________ 。 -2
(5) 如果2x1 2 3题的括号内,填上使等式成立的依据.
(1)2 x 8
得x 4 ( 2) 3x 2 2 x 得 x 2
1 x2 ( 3) 3 (4) x 5 1 ( 5) y 6
于是 所以 -9x=3 x=-3
1 x 3
练习2:下列各式的变形正确的是( D )
x A.由 0 ,得到 x = 2 2 x B.由 3 ,得到 x = 1 3
x=0 x=9
2 a= C.由-2 a = -3,得到 a = 3
D.由 x-1 = 4,得到 x = 5
3 2
你会吗?
判断对错,对的说明根据等式的哪一条性质;错的 说出为什么。
(1)如果x=y,那么
(× )
(2)如果x=y,那么 x 5 a y 5 a ( √ ) x y (3)如果x=y,那么 5 a 5 a ( × )
5 x 5 y (4)如果x=y,那么
(×)
(5)如果x=y,那么
等式的基本性质教案

等式的基本性质教案引言:等式是数学中非常重要的概念之一,是指两个数或两个代数式用等号连接起来的关系。
等式的基本性质是指在进行等式计算时应该遵循的一些基本规律和原则。
通过学习等式的基本性质,我们可以更好地理解和运用等式,进一步提高我们的数学能力。
本文将介绍等式的基本性质,包括等式的可逆性、等式的传递性、等式的对称性和等式的消去性。
一、等式的可逆性等式的可逆性指的是一个等式两边可以交换位置而不改变等式的真值。
即如果等式A=B成立,那么交换位置后的等式B=A也成立。
这是因为等式的两边具有相等的值,将它们交换位置并不改变它们的值。
例如,如果我们有3+2=5,那么5=3+2也成立。
二、等式的传递性等式的传递性指的是如果等式A=B和等式B=C都成立,那么等式A=C也成立。
这是因为等式的两边具有相等的值,将它们按照传递的顺序连接起来并不改变它们的值。
例如,如果我们有2+3=5和5-1=4,那么2+3=5和5=5-1可以推出2+3=4。
三、等式的对称性等式的对称性指的是一个等式两边可以互换位置而不改变等式的真值。
即如果等式A=B成立,那么等式B=A也成立。
这是因为等式的两边具有相等的值,将它们互换位置并不改变它们的值。
例如,如果我们有a+b=10,那么10=a+b也成立。
四、等式的消去性等式的消去性指的是在等式的两边同时加上(或减去)相同的数(或代数式),所得的新等式仍然成立。
这是因为等式的两边具有相等的值,对它们都加上(或减去)相同的数(或代数式)并不改变它们的值。
例如,如果我们有x+3=8,那么我们可以在两边同时减去3,得到x=5。
结论:通过学习等式的基本性质,我们可以更加灵活地运用等式进行数学计算。
等式的基本性质包括等式的可逆性、等式的传递性、等式的对称性和等式的消去性。
等式的可逆性使我们能够交换等式两边的位置;等式的传递性使我们能够用多个等式推导出新的等式;等式的对称性使我们能够互换等式两边的位置;等式的消去性使我们能够同时加上(或减去)相同的数(或代数式)来简化等式。
等式的性质

◎等式的性质接下来介绍的是化简算式和解方程的知识.一个复杂的算式怎么样化简呢?这就要求我们重新认识等号及加减乘除的概念.我们先来认识一下等式的性质.我们曾经详细地解释过1+1=2中的秘密,这个等式中隐藏着我们看待世界的三个重要的规律:第一,它表示在不同的事物中隐藏着相同的概念;第二,它表示在变化之中总有不变的规律;第三,它表示我们可以通过过程准确地预知结果.接下来,我们就从这些基本规律出发,进一步分析一下等式的性质.我们曾经说过,带有未知数的等式叫作方程,而程的意思就是天平.如果我们把等式看作一架天平的话,很容易就能够根据天平的特征得出等式的三个基本性质:第一,如果我们把等式的左右两边翻转过来,等式依然成立.比如2+3=5,把等式左右反转,得到的是5=2+3.同理,如果a=x,那么x也就等于a.为什么呢?因为等式是天平,把天平左右两侧的东西交换一下位置,天平当然会保持平衡了.我们把等式左右可以相互交换的这种性质,叫作等式的对称性,或者叫作反身性.第二,如果两个数量都跟第三个数相等,那么这两个量也彼此相等.2+3是等于5的,1+4也是等于5的,所以2+3就等于1+4.如果a=c,b=c,那么a=b,这个性质叫作等式的传递性.这个也很容易理解,我们在使用天平的时候,如果称出的两个物体的重量都等于两千克,那么,它们两者的重量肯定是相等的.反身性和传递性都是等式的最基本的性质,那么接下来,我们再看看等式的第三个基本性质.在小学的时候,我们曾经做过这样的题目:有一架天平始终保持着平衡,在天平的左边放着三个桃子,天平右边放着两个桃子和两个橘子,问:一个桃子的重量等于几个橘子的重量?我们知道,在题目中左边的桃子和右边的桃子加橘子的重量是一样的,而天平是一个平衡的杠杆机构.我们在天平的两边同时加上同样重量的东西,或者同时减去同样重量的东西,天平仍然可以保持平衡.现在,在天平的左侧放着三个桃子,右侧放着两个桃子和两个橘子,如果我们把天平两侧同时拿走两个桃子,天平仍然可以保持平衡.这样,在天平的左侧就剩下了一个桃子,而右侧就剩下两个橘子了,这样我们就得到了最终答案:一个桃子的重量等于两个橘子的重量.这个题目在小学阶段我们就非常熟悉了,我们应该从中发现什么规律呢?那就是,在等式的两边经过了相同的运算,结果仍然是相等的.这是等式的最重要的一个性质,任何等式,无论经过了怎样的计算,只要过程相同,那么结果一定是相等的.因为等式两边要经过相同的变化过程,所以这个性质又叫协变性.实际上,这个性质不仅仅存在于天平上,也不仅仅存在于等式中,它是我们这个世界的一个普遍规律.也就是说,从相同的起点出发,经过了相同的方向和相同的路程,最终到达的目的地也一定是相同的;几个相同的事物,经过了相同的变化过程,最终的结果也一定是一样的.比如,几个一模一样的皮球,从一模一样的高度掉落下来,它们掉到了一模一样的地板上,那么我们就可以知道,这几个皮球弹起来的速度、高度及所用的时间一定都是相同的.再比如,几条相同的鱼,经过了相同的烹饪方法,最后色、香、味也会是一模一样的.我们原来所说的,变化的事物里隐藏着不变的东西,这是这个世界的静态原理;现在我们说,相同的事物,经过了相同的运动变化,必然会得到相同的结果,这是这个世界的动态变化原理.这个原理表现在数学上,就是等式的协变性.一切解方程的具体方法,全部都是从这个基本原理中演化出来的.比如:x+3=5.这个算式在小学的时候我们就学过,可是小学的时候是怎么求解的呢?我们当时的思路是,一个东西加一个数以后就变成5了,说明这个数字肯定比5小.那么就用减法,所以x就等于5-3了.结果算对了,可是这个过程是小学的算术思维.那么,当我们学习了等式运算的基本原理以后,要怎么做呢?我们首先要看现在这个算式是什么,希望得到的算式是什么,然后再考虑一下怎么从现在的算式变成我们希望的算式.比如刚才的问题:我们现在的算式是x+3=5,我们希望得到的算式是等号左边只有一个x,右边只有一个得数,那么怎么样从现在的算式得到最终的算式呢?那我们就要看看等号左右两边多什么,怎么样把它去掉.回头再看x+3=5,右边倒是挺简单的,左边除了x外,还多一个+3,那怎么把左边多余的3去掉呢?此时,我们可以使用加减乘除任何的计算方法,也可以随便地使用世界上任何一个数字,但是只有一个要求,那就是:等号左边怎么做了,右边也得同步操作.怎么做可以把左边的加3去掉呢?很简单,再减去一个3就可以了.那左边-3了,右边是不是也得-3呢.对!我们把算式写下来吧:x+3-3=5-3左边的+3-3相互抵消了,就变成了x=5-3,这个时候,等号左边的算式已经干干净净了,右边还多一个减3,那就把它再算出来,5-3=2,最后得到结果:x=2.等式有三个基本性质,第一,等式具有反身性,也就是说等式的左右两边相互对换位置以后,等式仍然成立;第二,等式具有传递性,也就是说,两个式子都和第三个式子相等,那么这两个式子也相等;第三,等式具有协变性,也就是说,等式两边经过了相同的运算以后,等式仍然成立.。
等式的性质

从等式到方程一、等式的基本性质1、等式的两边同加(或同减)同一个数,结果仍然相等;即:若则,b a =.c b c a ±=±2、等式的两边同乘同一个数,结果仍然相等;即:若.,bc ac b a ==则3、等式的两边同除以一个数(不为零),结果仍然相等。
即:若cb c a c b a =≠=则且,0, 4、等式的对称性:即:若a b b a ==则,5、等式的传递性:(等量代换)即:若c a c b b a ===则,,典型例题1、(考查等式的性质及其变形)判断下列说法,并说明理由。
(1)若c b b a +=+,则c a =;(2)若bc ab =,则c a =; (3)若bc b a =,则c a =; (4)若b c b a -=-,则c a =; (5)若1=xy ,则yx 1=; (6)若y xy =,则1=x 。
(7)若31x =,则31=x 。
(8)若z y y x 3,2==,则32x z =。
说明:①在使用等式的性质3时,一定要注意除数不为0的条件,②还要注意题目中的隐含条件,比如1=xy 隐含着0≠y ;而y xy =中则没有。
例2 用适当的数或整式填空,使所得结果仍是等式,并说明是根据哪条性质以及怎样变形的:(1)如果853=+,那么-=83 ;(2)如果632=-x ,那么+=62x ;(3)如果123--=x x ,那么+x 3 1-=;(4)如果521=x ,那么=x ; (5)如果21231-=-x x ,那么-x 31 +-=21 ; (6)如果2)32(4=-x ,那么32-x = ; (7)如果22-=-y x ,那么=x ;(8)如果32y x =,那么=x 3 . 说明:本题是等式性质的应用,可以结合小学加减乘除的逆运算来加深理解。
二、方程:含有未知数的等式叫方程。
1、一元一次方程:只含有一个未知数,且未知数的指数是一次的整式方程。
等式的基本性质

叫做方 未知数的值 )叫做方 )。 。 ) )
(2)求方程的解的过程叫做 解方程 求方程的解的过程叫做( 求方程的解的过程叫做
(3)比x多5的数是 。列方程为 X+5=10 比 多 的数是 的数是10。列方程为( (4)8与x的和是 。方程为 8+X=56 与 的和是 的和是56。方程为( (5)比x少1.06的数是 比 少 的数是21.5。列方程为 的数是 。 ( )。 。 X-1.06=21.5
同学们,你知道小学数学教科书的印刷过程吗? 同学们,你知道小学数学教科书的印刷过程吗?
在一张大纸的 两面分别印上 16页教材。 页教材。 页教材
对折四次后, 对折四次后, 每页的面积是 689.75cm2。
经过装订、 经过装订、裁 边后就成了我 们看到的教科 书。
一、填空。 (1)使方程左右两边相等的 使方程左右两边相等的( 使方程左右两边相等的 程的解。 程的解。
等式两边同时乘或除以一个相同的数( 除外),等式大小不变 除外),等式大小不变。 等式两边同时乘或除以一个相同的数(0除外),等式大小不变。
解方程 3x = 18
x x x
方程两边同时除以同 一个不等于0的数,左 一个不等于 的数, 的数 右两边仍然相等。 右两边仍然相等。
解:3x÷(3)= 18÷(3 ) ÷ ÷ x =(6) (
100g
100+x=250
100+x=100+150 100+150=250, 所以x=150。
100+x=250 x=150
使方程左右两边相等的未知数的值,叫做 方程的解。 像上面,x=150就是方程100+x=250的解。 求方程的解的过程叫做解方程。
等式的性质

b1 5.能 不 能 从 a 3) x b 1得 到 等 式 ( x , a3 b1 为 什 么 ? 反 之 , 能 不 从x 能 得到等式 a3 (a 3) x b 1,为 什 么 ?
6.将 2 x 3 x两 边 同 除 以 , 得2 3, 对 其 中 错 误 x 的 原 因 , 三 名 同 学 归: 纳 甲 : 方 程 本 身 错 误 , 3 x 2x 乙:方程无解 丙 : 方 程 两 边 不 能 同 除 以0 时 请谈谈你的看法
9.解方程:x+7=26.
10.解方程:7x=6x4.
11. 解方程:5x=20.
1 12. 解方程 : x 5 4 3
利用等式性质解一元一 次方程就是把方程 b ax b 0(a 0)变形,最终化为 的形式. x a
方程的解的检验: 一般地,从方程解出未知数的值以后, 可以代入原方程检验,看这个值能够使方 程的两边相等.
次方程 . (1)求 式 子 的 值 (m x)x 4m ) 3m 2 x 6; 2003 ( ( 2)求 关 于 的 方 程 m 3) 2 y x 2的 解. y (
16.已知关于 的方程 b c的解为,求 x ax 1 a b c 1的值
17.已 知3b 2a 1 3a 2b, 利用 等式 的性 质, 试比 较 与b的大 小 a .
第三章 一元一 次方程
3.12 等式的性质
+
等式的性质1 如果a=b,那么ac=bc.
3 3
等式的性质2 如果a=b,那么ac=bc.
a b 如果a b(c 0),那么 . c c
等式还有两条性质:
(1)对称性:如果 b, 那么b a . a ( 2)传递性:如果 b, 且b c, a 则a c .
等式的基本性质

看图列出方程。
xx
x
73
50g
166
用方程表示下面得数量关系。
(1)x加上35等于91。 (2)x得3倍等于57。 (3)x减3得差就是6。 (4)7、8除以x等于1、3。
=
一个苹果和几个橘子重量相等?
等式得基本性质一:
等式得两边同时加上或减去 同一个数,左右两边仍然相等。
X+4=48 x+4-○ 4□ =48 -○ □4
X-4=48 x=b+50
平等衡式得得天两平边两同边时物乘品以都同扩一大个相不同为倍0得数数, , 左天右平两保边持仍平相衡等
等式平得衡两得边天同平时两=除边以物同品一都个缩不小为到0得数,
等式的基本性质
什么就是方程?必须具备哪几个条件 ?
含有 未知数得 等式 叫方程。
必须具备得条件:①就是等式。 ②含有未知数。
平等衡式得得天两平边两同边时加加上上同同样一得个物数品,, 左天右平两保边持仍平相衡等
平等两衡式边得得都天拿两掉平边1两个同花边时瓶减减,天去去平同同还样平一衡得个吗物数?品, , 左天右平两保边持仍平相衡等
原1个来排得球左几和右分几两之个边一皮仍,天球相平重等保量持相平等衡?
大家学习辛苦了,还是要坚持
继续保持安 静
等式得基本性质二:
等式得两边同时乘或除以同一个不 为0得数,左右两边仍然相等。
x÷4=48 x÷4×○4□ =48 ○× □4
x × 4=48 x × 4÷○ □4 =48 ○÷□ 4
2c=24
1、根据等式得基本性质,把下面得等式填写完整。
(1)因为a+b=c, 所以a+b+( 1)5=c+15 (2)因为a+b+35=m+a, 所以( )b+35=m
等式的性质
(4)如果 0.2x=5 那么x=_.
随堂练习:
1.填空并说出是根条性质及怎 样变形(改变式子的形式)
(4)如果 0.2x=5, 那么x=_25_. 答:根据等式性质2,两
边都乘以5。
练习2: 以下等式变形,正确的是( B)
① 由x = y,得到 x+5 = y+5
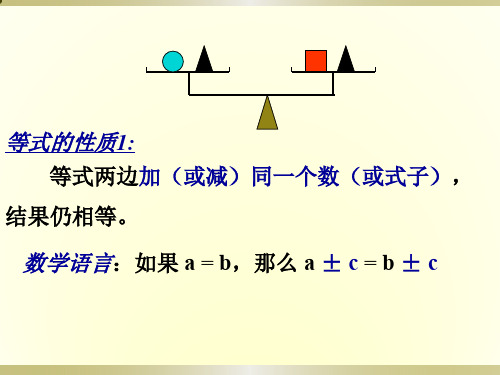
等式的性质1:
等式两边加(或减)同一个数(或式子), 结果仍相等。
数学语言:如果 a = b,那么 a ± c = b ± c
等式的性质2:
等式两边乘同一个数(或式子),或除以同 一个非0的数(或式子)结果仍相等。
数学语言:如果 a = b,那么 a c = b c
如果
a
=
b,那么
a c
bc(c≠ 0)
习惯上,我们写为x=8.
归纳总结
1、等式的两条性质; ① 如果 a = b,那么 a ± c = b ± c ② 如果 a = b,那么 a c = b c 如果 a = b,那么 a b(c≠ 0)
cc
2、解一元一次方程的实质就是利用等式的 性质求出未知数的值
② 若 -x = y,根据_等__式_的__性__质__2_,得到 x =_-__y_ 。
随堂练习: 1.填空并说出是根据等式的哪 条性质及怎样变形(改变式子 的形式) (1)如果3x+7=8,那么
3x=8-______.
随堂练习: 1.填空并说出是根据性质及怎 样变形(改变式子的形式) (1)如果3x+7=8那么 3x=8-_7_;
② 由 2 a +1 = b+1,得到 2 a = b
③ 由 m = n,得到 a m = a n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等式的性质
1.了解等式的两条性质.
2.会用等式的性质解简单的一元一次方程.
阅读教材P 81~82,思考下列问题.
1.等式的性质有哪几条?用字母怎样表示?字母代表什么?
2.解方程的依据是什么?
知识探究
1.如果a =b ,那么a±c =b±c(字母a 、b 、c 可以表示具体的数,也可以表示一个式子).
2.如果a =b ,那么ac =bc.
3.如果a =b(c ≠0),那么a c =b c .
自学反馈
1.已知a =b ,请用“=”或“≠”填空:
(1)3a =3b ;(2)a 4=b 4;(3)-5a =-5b.
2.利用等式的性质解下列方程:
(1)x +7=26;
(2)-5x =20;
(3)-2(x +1)=10.
解:(1)x =19.(2)x =-4.(3)x =-6.
注意用等式的性质对方程进行逐步变形,最终可变形为“x =a ”的形式.
活动1 小组讨论
例 利用等式的性质解下列方程并检验:
(1)x -9=6;
(2)-0.2x =10;
(3)3-13x =2;
(4)-2x +1=0;
(5)4(x +1)=-20.
解:(1)x =15.(2)x =-50.(3)x =3.(4)x =12.(5)x =-6.
运用等式的性质解方程不能漏掉某一边或某一项.
活动2 跟踪训练
利用等式的性质解下列方程并检验:
(1)x +5=8;
(2)-x -1=0;
(3)-2-14x =2;
(4)6x -2=0.
解:(1)x =3.(2)x =-1.(3)=-16.(4)x =13.
活动3 课堂小结
1.等式有哪些性质?
2.在用等式的性质解方程时要注意什么?
会从实际问题中抽象出数学模型,会用一元一次方程解决电话计费等有关方案决策的问题.
阅读教材P104~105探究3的内容,思考题中所提出的问题.知识探究
方案决策问题解题的基本方法是求得每种方案的结果,再结合结果做出判断
自学反馈
某市乘公交车(非空调)每次需投币1.5元或者购买IC卡,每次刷卡扣款1.35元,但办理IC卡时需付工本费15元.问需乘坐公交车多少次时两种收费方式的收费一样?当超过这个次数后哪种收费方式较合算?
解:100次,购买IC卡合算.
活动1小组讨论
例(教材P104探究3)电话计费问题
下表中有两种移动电话计费方式.
考虑下列问题:
(1)设一个月用移动电话主叫为t min(t是正整数).根据上表,列表说明:当t在不同时间范围内取值时,按方式一和方式二如何计费;
(2)观察你的列表,你能从中发现如何根据主叫时间选择省钱的计费方式吗?通过计算验证你的看法.
活动2跟踪训练
某厂招聘运输工,有两种方法来结算工资,一种是每月基本工资300元,每运1吨货给15元;另一种是没有基本工资,每运1吨货给20元.问每月运多少吨货时两种结算方法给的工资一样多?如果某工人每月可运货70吨,那么用哪种结算方法可多拿工资?
解:60吨,用第二种结算方法可多拿工资.
活动3课堂小结
电话计费等有关的方案决策问题.。
