等几何分析
解析几何的基本知识点总结

解析几何的基本知识点总结解析几何是几何学的一个分支,它利用坐标系和代数方法研究几何问题。
通过对解析几何的基本知识点的总结,我们可以更好地理解和应用解析几何的方法。
本文将就解析几何的基本概念、坐标系、直线和曲线等知识点进行详细阐述。
一、基本概念1. 点:解析几何中的基本单位,用坐标表示,通常用大写字母表示,如点A(x₁, y₁)。
2. 线段:由两点确定的有限线段,在解析几何中用两点的坐标表示,如线段AB:AB = √[(x₂-x₁)²+(y₂-y₁)²]。
3. 中点:线段的中点即为线段两端点的均值,设线段AB的中点为M,则M的坐标为[(x₁+x₂)/2, (y₁+y₂)/2]。
4. 斜率:表示直线斜率的概念,在解析几何中常用字母k表示,直线的斜率为k=(y₂-y₁)/(x₂-x₁)。
5. 角度:两条直线之间的旋转角度,用度数或弧度表示。
二、坐标系1. 笛卡尔坐标系:由水平的x轴和垂直的y轴组成,交点为原点O(0,0)。
在这个坐标系下,点的位置可以用有序数对(x, y)表示。
2. 极坐标系:由原点O和极径、极角两个坐标轴组成,极径表示点到原点的距离,极角表示点与x轴正半轴的夹角。
三、直线与曲线1. 直线:由一次方程表示的线段,在解析几何中用方程的形式表示,如直线方程为y=kx+b。
2. 曲线:不是直线的线段,在解析几何中的表示较为复杂,可以通过方程、参数方程或极坐标方程表示,常见的曲线有圆、椭圆、双曲线、抛物线等。
四、常见图形的解析几何表示1. 圆:圆心为(h, k),半径为r,其方程表示为(x-h)²+(y-k)²=r²。
2. 椭圆:椭圆的中心为(h, k),长轴为2a,短轴为2b,其方程表示为(x-h)²/a²+(y-k)²/b²=1。
3. 双曲线:双曲线的中心为(h, k),两支曲线的焦点分别为(f₁, k)和(-f₂, k),其方程表示为(x-h)²/a²-(y-k)²/b²=1。
等几何分析

Let no man ignorant of geometry enter here One may argue the merits of NURBS versus other computational geometry technologies, but their preeminence in engineering design is indisputable. As such, they were the natural starting point for isogeometric analysis and their use in an analysis setting is the focus of this book.Unlike in standard finite element analysis, the B-spline parameter space is local to patches rather than elements.参数空间:设(X1,……,Xn)为来自总体X的样本,(x1,…xn)为相应的样本值,θ是总体分布的未知参数,θ∈Θ,Θ表示θ的取值范围,称Θ为参数空间.基函数:已知一个节点向量,则B样条曲线的基函数递归地定义为分段常数(p=0):对于p=1,2,3,…,它们被定义为:这就是Cox-de递归公式。
对于一个统一的节点向量应用式(2.1)和(2.2)所得的结果显示为图2.3。
对于当p=0和p=1时的B样条曲线函数,与普通的分段常量和线性有限元函数有一样的结果。
二次B样条曲线基函数虽然和有限元中的不一样。
可以从图2.3获得一些很重要的特征除了这些函数是齐次的。
首先最主要的是对一个单位分解,即对任意的,有:其次在整个区间内基函数的值都是非负的(见第6章),这就涉及到发展集中质量的方案。
The third major feature to note is that each pth order function has p −1 continuous derivatives across the element boundaries (i.e., across the knots). This feature has many extremely important implications for the use of splines as a basis for analysis and is one of the most distinctive features of isogeometric analysis. Lastly, the support ofthe B-spline functions of order p is always p + 1 knot spans. It is a common misconception that this increasing support of the functions leads to increased bandwidth in a numerical method. This simply is not the case. As we see in Figure 2.4 for cubics, the total number of functions that any given function shares support with (including itself) is 2p + 1 regardless of whether we are using an FEA basis or B-splines.对不均匀节点向量的利用比对均匀节点向量的利用,让我们获得过更加丰富的性质。
等几何分析

等几何分析研究进展摘要等几何分析是一种刚刚兴起的数值分析方法,对现有的CAE产生了很大的影响。
等几何分析法的出现于发展,缓解和消除了困扰CAE多年的难题,开启了一条结合设计、分析和优化等三方面的途径。
本文阐述了等几何分析产生的背景、意义和相关的定义,还介绍了等几何分析从首先提出到现如今的10年发展历程,包括基础理论体系的发展与完善,新型样条的构建,网格细分方法的研究,计算效率的提高,以及其他方面(如边界条件的施加、接触分析、结构优化等)的进展,展示了等几何分析相对于基于拉格朗日插值的有限元法的优势。
关键字等几何分析有限元NURBS 发展现状1 前言有限元分析是目前应用最广泛的一种数值分析方法,且由于结合了能够高速运算的计算机,有限元法得到了大多数人的支持。
有限元法是将连续的物体离散成有限个单元,单元之间通过节点连接在一起,并将节点处的未知量作为基本未知量,使得无限自由度问题转换成了有限自由度的问题,在利用力学原理近似的求解出未知量。
这一突出优点使得有限元法得到广泛应用,各类有限元软件也层出不穷,如ABAQUS、ANSYS、LS-DYNA、HyperMesh等。
不过这一突出的优点也大大的限制了有限元的进一步发展。
首先,有限元法求得的结果的精确度与网格的细化程度有关,网格越细,则计算结果的精度越高,而计算时间和计算所需的内存也将随之增加,而以目前的水平来看,还无法做到超高精度的细化网格。
Sandia国家实验室曾做过一项统计,在汽车、航空航天和造船行业,大约全部分析时间的80%用于网格划分及划分前的几何模型准备[1]。
其次,网格划分使得应力不连续,且在处理大变形问题中,单元的过度扭曲导致精度严重损失。
第三,网格划分工具对几何形状的识别精度较低,特别是划分复杂高级曲面时无法精确划分,容易划分出大变形网格。
再者,网格划分是建立在几何模型的基础上,若几何模型发生改变,那么须得重新划分网格,花费大量时间。
最后,在处理网格畸变、网格移动如动态裂纹扩展、冲压成型等问题时需要进行网格重构,不仅浪费计算时间,还会损害计算精度[2]。
专题12.23 三角形全等几何模型-“一线三直角”模型(专项练习)(基础篇)
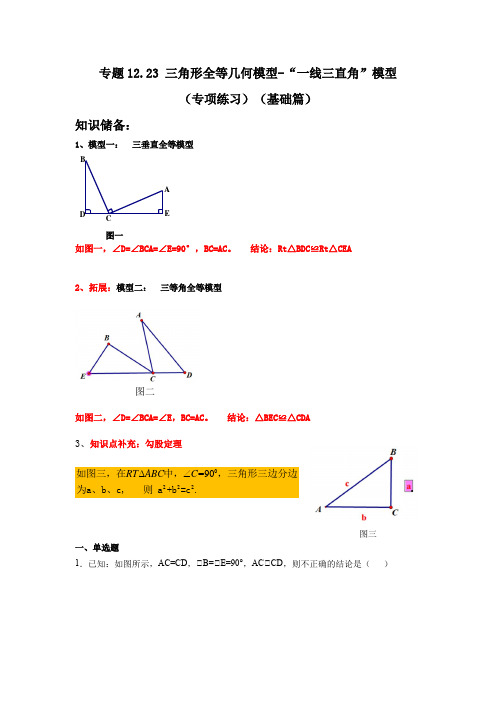
C D E B A 专题12.23 三角形全等几何模型-“一线三直角”模型(专项练习)(基础篇)知识储备:1、模型一: 三垂直全等模型图一如图一,∠D=∠BCA=∠E=90°,BC=AC 。
结论:Rt △BDC ≌Rt △CEA2、拓展:模型二: 三等角全等模型图二如图二,∠D=∠BCA=∠E ,BC=AC 。
结论:△BEC ≌△CDA3、知识点补充:勾股定理0222=90.RT ABC C ∆∠如图三,在中,,三角形三边分边为a 、b 、c,则a +b =c图三一、单选题1.已知:如图所示,AC=CD ,∠B=∠E=90°,AC∠CD,则不正确的结论是( )A .∠1=∠2B .∠A=∠2C .∠ABC∠∠CED D .∠A 与∠D 互为余角2.如图,90ACB ∠=︒,AC BC =,AD CE ⊥,BE CE ⊥,垂足分别为D 、E ,2.5AD cm =, 1.7DE cm =,则BE 的长( ).A .0.8cmB .0.7cmC .0.6cmD .1cm3.如图,在等腰直角三角形ABC 中,90,8C AC ∠=︒=,F 为AB 边的中点,点D ,E 分别在,AC BC 边上运动,且保持AD CE =,连接,,DE DF EF .在此运动变化的过程中,下列结论:∠DEF 是等腰直角三角形;∠四边形CDFE 的面积保持不变;∠AD BE DE +>.其中正确的是( )A .∠∠∠B .∠C .∠D .∠∠二、填空题 4.如图,在等腰Rt∠ABC 中,∠C=90°,AC=7.点O 在BC 上,且CO=1,点M 是AC 上一动点,连接OM ,将线段OM 绕点O 逆时针旋转90°,得到线段OD ,要使点D 恰好落在AB 上,CM 的长度为__________.5.如图,90ACB ∠=︒,CA CB =,AD CE ⊥,BE CE ⊥,垂足分别为D ,E ,3cm =AD ,1.8cm DE =,则BE =______cm .6.如图,()()4,0,0,6A B ,以B 点为直角顶点在第一象限作等腰直角ABC ∆,则C 点的坐标为_________7.如图,点A 在线段DE 上,AB ∠AC ,垂足为A ,且AB =AC ,BD ∠DE ,CE ∠DE ,垂足分别为D 、E ,若ED =12,BD =8,则CE 长为_____.8.如图,AC BC =,AE CD =,AE CE ⊥于点E ,BD CD ⊥于点D ,10AE =,4BD =,则DE 的长是_____.⊥于点F.若9.如图,直线a经过正方形ABCD的顶点A,已知BE a⊥于点E,DF aBE=,83DF=,则线段EF的长为______.10.如图,四边形ABCD中,∠ABC=∠ACD=90°,AC=CD,BC=4cm,则BCD的面积为_____cm2.11.如图,正方形ABCD中,点E、F分别是BC、AB边上的点,且AE∠DF,垂足为点O,∠AOD,则图中阴影部分的面积为_____.三、解答题12.如图:在∠ABC中∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作CF∠AE,垂足为F,过B作BD∠BC交CF的延长线于D.求证:(1)AE=CD.(2)若AC=12cm,求BD的长.13.如图1,在∠ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD∠MN于D,BE∠MN 于E.(1)说明∠ADC∠∠CEB;(2)说明AD+BE=DE;(3)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以说明.14.如图,已知A、B、D在同一条直线上,∠A=∠D=90°,AC=BD,∠1=∠2.求证:∠CBE 是等腰直角三角形.15.在ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD∠MN于点D,BE∠MN 于点E.(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.16.课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示:(1)求证:∠ADC∠∠CEB;(2)已知DE=35cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相同)17.如图,在∠ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足.AE=CF,求证:∠ACB=90°.18.如图,已知在CDE ∆中,12∠=∠,直线AB 经过点E ,DA AB ⊥,CB AB ⊥,垂足分别为A 、B ,AD BE =,求证:AE BC =.19.如图1.∠ABC 中,AG∠BC 于点G ,以A 为直角顶点,分别以AB 、AC 为直角边,向∠ABC 作等腰Rt∠ABE 和等腰Rt∠ACF ,过点E ,F 作射线GA 的垂线,垂足分别为P ,Q .(1)求证:∠EPA∠∠AGB :(2)试探究EP 与FQ 之间的数量关系,并证明你的结论;(3)如图2.若连接EF 交GA 的延长线于H ,由(2)中的结论你能判断EH 与FH 的大小关系吗?并说明理由:(4)在(3)的条件下,若BC =10,AG =12.请直接写出S ∠AEF = .20.如图所示,90,C BE BA ∠=⊥,且,BE BA BD BC =⊥,延长CB 交DE 于点F ,且DF EF =.求证:2AC BF =.21.已知:在直角坐标系中,点()0,3B -,点()1,0C ,点A 在第二象限,,AC BC AC BC =⊥,求点A 的坐标.22.如图,已知:,,,,那么AC 与CE 有什么关系?写出你的猜想并说明理由.参考答案1.A【分析】由题意易得∠ACD=90°,则有∠1+∠2=90°,进而可证三角形全等,然后可排除选项.【详解】解:∠AC∠CD,∠∠ACD=90°,∠∠1+∠2=90°,∠∠B=∠E=90°,∠∠2+∠D=90°,∠∠1=∠D,∠AC=CD,∠∠ABC∠∠CED(AAS),故C正确,∠∠A=∠2,故B正确,∠∠A+∠D=90°,故D正确,∠A选项错误;故选A.【点睛】本题主要考查全等三角形的性质与判定,熟练掌握全等三角形的性质与判定是解题的关键.2.A【分析】证∠CEB和∠ADC全等,得到BE和CD相等,CE和AD相等,即可得到结论;【详解】解:∠BE∠CE,AD∠CE,∠∠E=∠ADC=90°,∠∠EBC+∠BCE=90°,∠∠BCE+∠ACD=90°,∠∠EBC=∠DCA,在∠CEB和∠ADC中,E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∠∠CEB∠∠ADC∠BE=DC ,CE=AD∠AD=2.5cm ,DE=1.7cm ,∠CE=1.7cm ,∠DC=CE -DE=0.8cm ,∠BE=0.8cm ;故选:A .【点睛】本题考查垂直性质的运用,直角三角形的性质的运用,全等三角形的性质和判定,证明三角形全等是解题的关键.3.A【分析】连接CF ,利用SAS 可证ADF CEF ≌,从而得出,=∠=∠DF FE AFD CFE ,从而求出90EFD ∠=︒,即可判断∠;根据全等三角形的性质可得=ADF CEF SS ,从而得出四边形CDFE 的面积为12ABC S ,从而判断∠;延长DF 到G 使FG DF =,连接,EG BG ,证出AD BG =和DE EG =,最后根据三角形的三边关系即可判断∠.【详解】解:如图,连接CF .∠AC BC =,F 为AB 的中点,∠CF AB ⊥,12∠=∠=ACF BCF ACB . ∠90ACB ∠=︒,∠45∠=∠=∠=︒A ACF BCF ,∠CF AF =.又∠AD CE =,∠ADF CEF ≌.∠,=∠=∠DF FE AFD CFE ,∠90AFD CFD ∠+∠=︒,∠90∠+∠=︒CFE CFD ,∠90EFD ∠=︒,∠DEF 是等腰直角三角形.∠正确.∠ADF CEF ≌,∠=ADF CEF S S ,∠四边形CDFE 的面积为12+=+==CDF CEF CDF MDF AFC ABC SS S S S S . ∠11883222=⨯=⨯⨯=ABC S AC BC , ∠四边形CDFE 的面积为16,为定值.∠正确.延长DF 到G 使FG DF =,连接,EG BG .∠AF BF =,∠=∠AFD BFG ,DF FG =,∠ADF BCF ≌△△,∠AD BG =.∠90EFD ∠=︒,∠EF DF ⊥,∠DE EG =.在EBG 中,∠+>BG BE EG ,∠AD BE DE +>.∠正确.∠∠∠均正确,故选A .【点睛】此题考查的是全等三角形的判定及性质、等腰直角三角形的判定和三角形的三边关系,掌握构造全等三角形的方法是解决的关键.4.5【分析】如图,作辅助线;首先证明DOE OMC ∆≅∆,得到OC DE =,CM OE =;其次证明BE DE =,求出OE ,即可解决问题.【详解】解:如图,过点D 作DE OB ⊥于点E ;DEO DOM C ∠=∠=∠,DOE COM COM CMO ∴∠+∠=∠+∠,DOE OMC ∴∠=∠;由题意得:OD OM =;在DOE ∆与OMC ∆中,DOE OMC DEO OCM OD OM ∠=∠⎧⎪∠=∠⎨⎪=⎩,()DOE OMC AAS ∴∆≅∆,1DE OC ∴==,CM OE =;ABC ∆为等腰直角三角形,45B ∴∠=︒,45BDE ∠=︒,1BE DE ∴==,7115OE =--=,5CM OE ∴==,故答案为5.【点睛】本题主要考查了旋转变换的性质、等腰直角三角形的性质、全等三角形的判定等几何知识点及其应用问题;解题的方法是作辅助线,构造全等三角形;解题的关键是灵活运用旋转变换的性质等几何知识点来分析、判断、推理或解答.5.1.2【分析】先根据等角的余角相等得出∠EBC =∠DCA ,再根据AAS 证明∠CEB ∠∠ADC ,然后利用全等三角形的性质并结合已知数据即可求得结果.【详解】解∠BE ∠CE ,AD ∠CE ,∠∠E =∠ADC =90°,∠∠EBC +∠BCE =90°.∠∠BCE +∠ACD =90°,∠∠EBC =∠DCA .在∠CEB 和∠ADC 中,E ADC EBC DCA BC AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠∠CEB ∠∠ADC (AAS),∠BE=DC ,CE=AD =3cm∠DC=CE −DE ,DE =1.8cm ,∠DC =3-1.8=1.2cm ,∠BE =1.2cm故答案为:1.2cm【点睛】本题考查了全等三角形的判定和性质,属于常考题型,难度不大,熟练掌握三角形全等的判定和方法是关键.6.()6,10【分析】过点C 作CD∠y 轴于点D ,由∠ABC 为等腰直角三角形即可得出∠ABC =90°、AB =BC ,通过角的计算即可得出∠ABO =∠BCD ,再结合∠CDB =∠BOA =90°即可利用AAS 证出∠ABO∠∠BCD ,由此即可得出BD 、CD 的长度,进而可得出点C 的坐标.【详解】解:过点C 作CD∠y 轴于点D ,如图所示.∠∠ABC 为等腰直角三角形,∠∠ABC =90°,AB =BC .∠CD∠BD ,BO∠AO ,∠∠CDB =∠BOA =90°.∠∠CBD+∠ABO =90°,∠CBD+∠BCD =90°,∠∠ABO =∠BCD .在∠ABO 和∠BCD 中,==90ABO BCD BOA CDB AB BC ∠=∠⎧⎪∠∠︒⎨⎪=⎩,∠∠ABO∠∠BCD (AAS ),∠BD =AO ,CD =BO ,∠A (4,0),B (0,6),∠BD =4,CD =6,∠点C 的坐标为()6,10,故答案为:()6,10.【点睛】本题结合等腰直角三角形和坐标点综合考查,关键在于辅助线的作法,过C 点作垂直于x 轴的垂线还是垂直于y 轴的垂线是解题关键.7.4【分析】根据已知条件及互余关系可证∠ABD ∠∠CAE ,得出BD =AE =8,AD =CE ,求出AD =4,即可得出答案.【详解】解:∠BD ∠DE ,CE ∠DE ,∠∠D =∠E =90°,∠ABD +∠BAD =90°,∠AB ∠AC ,∠∠BAD +∠EAC =90°,∠∠ABD =∠EAC ,在∠ABD和∠CAE中,D EAB CAABD EAC∠=∠⎧⎪=⎨⎪∠=∠⎩,∠∠ABD∠∠CAE(ASA),∠BD=AE=8,AD=CE,∠AD=ED﹣AE=12﹣8=4,∠CE=4故答案为:4.【点睛】本题考查了全等三角形的判定与性质、等角的余角相等.找到证明三角形全等的条件,证明三角形全等是解题的关键.8.6【分析】根据垂直的定义得到∠AEC=∠D=90°,根据全等三角形的性质即可得到结论.【详解】解:∠AE∠CE于点E,BD∠CD于点D,∠∠AEC=∠D=90°,在Rt∠AEC与Rt∠CDB中AC BC AE CD ⎧⎨⎩==,∠Rt∠AEC∠Rt∠CDB(HL),∠CE=BD=4,CD=AE=10,∠DE=CD−CE=10−4=6,故答案为:6.【点睛】本题考查了全等三角形的判定与性质,解答本题的关键是根据已知条件判定三角形的全等.9.11【分析】根据题意易得∠AEB∠∠DFA,则有BE=AF,DF=AE,进而问题可得解.【详解】解:∠四边形ABCD是正方形,∠AD=AB,∠DAB=90°,∠BE a ⊥,DF a ⊥,∠∠DFA=∠AEB=90°,∠∠FAD+∠ADF=90°,又∠∠FAD+∠BAE=90°,∠∠ADF=∠BAE ,∠∠AEB∠∠DFA ,∠3BE =,8DF =,∠BE=AF=3,DF=AE=8,∠EF=AF+AE=3+8=11;故答案为11.【点睛】本题主要考查全等三角形的判定与性质及正方形的性质,熟练掌握全等三角形的判定与性质及正方形的性质是解题的关键.10.8.【分析】作DH ∠BC ,证明ABC CHD ≌,根据全等三角形的性质得到DH =BC =4,根据三角形的面积公式计算,得到答案.【详解】解:过点D 作DH ∠BC ,交BC 的延长线于点H ,∠∠ABC =90°,∠∠BAC +∠ACB =90°,∠∠ACD =90°,∠∠HCD +∠ACB =90°,∠∠BAC =∠HCD ,在∠ABC 和∠CHD 中,BAC HCD ABC CHD AC CD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠ABC CHD ≌(AAS ),∠DH =BC =4,∠BCD 的面积=1144822BC DH =⨯⨯=(cm 2), 故答案为:8.【点睛】本题考查的是直角三角形的两锐角互余,三角形全等的判定与性质,三角形面积的计算,掌握以上知识是解题的关键.11【分析】先证得∠ADF ≅∠BAE ,再利用等量代换即可求得阴影部分的面积等于∠AOD 的面积.【详解】正方形ABCD 中,∠DAF=∠ABE=90︒,AD=AB ,∠AE∠DF ,∠∠DOA=∠DAF =90︒,∠∠DAO+∠ADF =∠DAO +∠FAO =90︒,∠∠ADF =∠FAO ,在∠ADF 和∠BAE 中, ADF FAO AD ABDAF ABE ∠=∠⎧⎪=⎨⎪∠=∠⎩, ∠∠ADF ≅∠BAE ,∠ADF BAE SS =, ∠ADF AOF BAE AOF S SS S -=-, ∠AOF SS ==阴影.【点睛】本题考查了正方形的性质,全等三角形的判定和性质,证得阴影部分的面积等于∠AOD 的面积是解题的关键.12.(1)见解析;(2)6【分析】(1)根据DB∠BC ,CF∠AE ,得出∠D =∠AEC ,再结合∠DBC =∠ECA =90°,且BC =CA ,证明∠DBC∠∠ECA ,即可得证;(2) 由(1)可得∠DBC∠∠ECA ,可得CE=BD ,根据BC=AC=12cm AE 是BC 的中线,即可得出12CE BC =,即可得出答案. 【详解】证明:(1)证明:∠DB∠BC ,CF∠AE ,∠∠DCB +∠D =∠DCB +∠AEC =90°.∠∠D =∠AEC .又∠∠DBC =∠ECA =90°,且BC =CA , 在∠DBC 和∠ECA 中90D AEC DBC ECA BC AC ∠∠∠∠⎪⎩︒⎧⎪⎨====,∠∠DBC∠∠ECA (AAS ).∠AE =CD ;(2) 由(1)可得∠DBC∠∠ECA∠CE=BD ,∠BC=AC=12cm AE 是BC 的中线, ∠162CE BC cm ==, ∠BD=6cm .【点睛】本题考查了全等三角形的判定和性质,直角三角形斜边上的中线,证明∠DBC∠∠ECA 解题关键.13.(1)见详解;(2)见详解;(3)DE+BE=AD ,理由见详解【分析】(1)由题意易得∠ADC=∠CEB=90°,∠BCE=∠CAD ,进而问题可得证;(2)由(1)可得AD=CE ,BE=CD ,进而根据线段的数量关系可求证;(3)由题意易证∠ADC∠∠CEB,则有AD=CE,BE=CD,进而问题可求解.【详解】解:(1)∠AD∠MN,BE∠MN,∠∠ADC=∠CEB=90°,∠∠ACB=90°,∠∠DCA+∠BCE=90°,∠∠DCA+∠CAD=90°,∠∠BCE=∠CAD,∠AC=CB,∠∠BCE∠∠CAD(AAS);(2)由(1)得:∠BCE∠∠CAD,∠AD=CE,BE=CD,∠DE=DC+CE,∠DE=AD+BE;(3)AD=DE+BE,理由如下:∠AD∠MN,BE∠MN,∠∠ADC=∠CEB=90°,∠∠ACB=90°,∠∠DCA+∠BCE=90°,∠∠DCA+∠CAD=90°,∠∠BCE=∠CAD,∠AC=CB,∠∠BCE∠∠CAD(AAS),∠DC=BE,AD=CE,∠CE=CD+DE,∠AD=DE+BE.【点睛】本题主要考查全等三角形的性质与判定及直角三角形的两个锐角互余,数量掌握全等三角形的性质与判定及直角三角形的两个锐角互余是解题的关键.14.见解析【分析】由题意易证∠ABC∠∠DEB ,则有BC=BE ,∠EBD=∠BCA ,进而问题可证.【详解】证明: 在∠ABC 和∠DEB 中,12A D AC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠∠ABC∠∠DEB (AAS ),∠BC=EB ,∠∠1=∠2,∠2+∠DBE=90°,∠∠1+∠DBE=90°,∠∠CBE=180°﹣(∠1+∠DBE )=90°,∠∠BCE 是等腰直角三角形.【点睛】本题主要考查全等三角形的性质与判定、直角三角形的性质及等腰直角三角形的判定,熟练掌握全等三角形的性质与判定、直角三角形的性质及等腰直角三角形的判定是解题的关键.15.(1)见解析;(2)见解析;(3)DE =BE ﹣AD【分析】(1)由题意易得∠DAC+∠ACD =90°,则∠DAC =∠BCE ,进而可证∠ADC∠∠CEB ,然后根据全等三角形的性质可求解;(2)由题意易得∠CEB=∠ADC=90°,则可求∠CAD=∠BCE ,进而可证∠CAD∠∠BCE ,然后根据全等三角形的性质可求解;(3)根据题意可证∠CAD∠∠BCE ,然后根据全等三角形的性质可求解.【详解】(1)证明:∠AD∠MN ,BE∠MN ,∠∠ADC =∠CEB =90°,∠∠DAC+∠ACD =90°,∠∠ACB =90°,∠∠BCE+∠ACD =90°,∠∠DAC =∠BCE ,在∠ADC 和∠CEB ,ADC CEB DAC ECB AC CB ∠=∠⎧⎪∠=∠⎨⎪=⎩,∠∠ADC∠∠CEB (AAS ),∠CD =BE ,AD =CE ,∠DE =CE+CD =AD+BE ;(2)证明:∠AD∠MN ,BE∠MN ,∠∠ADC =∠CEB =90°,∠∠DAC+∠ACD =90°,∠∠ACB =90°,∠∠BCE+∠ACD =90°,∠∠DAC =∠BCE ,∠AC=BC ,∠∠ADC∠∠CEB ,∠CD =BE ,AD =CE ,∠DE =CE ﹣CD =AD ﹣BE ;(3)解:DE =BE ﹣AD ,理由如下:∠AD∠MN ,BE∠MN ,∠∠ADC =∠CEB =90°,∠∠DAC+∠ACD =90°,∠∠ACB =90°,∠∠BCE+∠ACD =90°,∠∠DAC =∠BCE ,∠AC=BC ,∠∠ADC∠∠CEB ,∠CD =BE ,AD =CE ,∠DE =BE ﹣AD .【点睛】本题主要考查全等三角形的性质与判定及直角三角形的两个锐角互余,熟练掌握全等三角形的性质与判定及直角三角形的两个锐角互余是解题的关键.16.(1)见详解;(2)砌墙砖块的厚度a 为5cm .【分析】(1)根据题意可得AC =BC ,∠ACB =90°,AD∠DE ,BE∠DE ,进而得到∠ADC =∠CEB =90°,再根据等角的余角相等可得∠BCE =∠DAC ,再证明∠ADC∠∠CEB 即可. (2)利用(1)中全等三角形的性质进行解答.【详解】(1)证明:由题意得:AC =BC ,∠ACB =90°,AD∠DE ,BE∠DE ,∠∠ADC =∠CEB =90°,∠∠ACD +∠BCE =90°,∠ACD +∠DAC =90°,∠∠BCE =∠DAC ,在∠ADC 和∠CEB 中ADC CEB DAC BCE AC BC ∠∠∠∠⎧⎪⎨⎪⎩===,∠∠ADC∠∠CEB (AAS );(2)解:由题意得:∠一块墙砖的厚度为a ,∠AD =4a ,BE =3a ,由(1)得:∠ADC∠∠CEB ,∠DC =BE =3a ,AD =CE =4a ,∠DC +CE =BE +AD =7a =35,∠a =5,答:砌墙砖块的厚度a 为5cm .【点睛】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件. 17.见解析【分析】根据题意易得Rt∠ACE∠Rt∠CBF ,则有∠EAC =∠BCF ,然后根据等角的余角相等及领补角可求证.【详解】证明:如图,在Rt∠ACE 和Rt∠CBF 中,AC BC AE CF =⎧⎨=⎩, ∠Rt∠ACE∠Rt∠CBF (HL ),∠∠EAC =∠BCF ,∠∠EAC+∠ACE =90°,∠∠ACE+∠BCF =90°,∠∠ACB =180°﹣90°=90°.【点睛】本题主要考查直角三角形全等的判定与性质,熟练掌握三角形全等的判定条件及性质是解题的关键.18.见解析【分析】根据HL 证明Rt∠DAE∠Rt∠EBC 即可求解.【详解】解:(1)证明:∠ DA∠AB ,CB∠AB ,∠ ∠A =∠B =90°又∠∠1=∠2∠DE =CE在Rt∠DAE 和Rt∠EBC 中,AE CE AD BE=⎧⎨=⎩ ∠Rt∠DAE∠Rt∠EBC (HL )∠AE =BC .【点睛】此题主要考查全等三角形的判定与性质,解题的关键是熟知全等三角形的判定定理.19.(1)证明见解析;(2)结论:EP =FQ ,证明见解析;(3)结论:EH =FH ,理由见解析;(4)60.【分析】(1)根据等腰Rt∠ABE 的性质,求出∠EPA =∠EAB =∠AGB =90°,∠PEA =∠BAG ,根据AAS 推出∠EPA∠∠AGB .(2)根据全等三角形的性质推出EP =AG ,同理可得∠FQA∠∠AGC ,即可得出AG =FQ ,最后等量代换即可得出答案.(3)求出∠EPH =∠FQH =90°,根据AAS 推出∠EPH∠∠FQH ,即可得出EH 与FH 的大小关系.(4)根据全等三角形∠EPH∠∠FQH ,∠EPA∠∠AGB ,∠FQA∠∠AGC ,推出S ∠FQA =S ∠AGC ,S ∠FQH =S ∠EPH ,S ∠EPA =S ∠AGB ,即可求出S ∠AEF =S ∠ABC ,根据三角形面积公式求出即可.【详解】解:(1)如图1,∠∠EAB =90°,EP∠AG ,AG∠BC ,∠∠EPA =∠EAB =∠AGB =90°,∠∠PEA+∠EAP =90°,∠EAP+∠BAG =90°,∠∠PEA =∠BAG ,在∠EPA 和∠AGB 中,EPA BGA PEA BAG AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩∠∠EPA∠∠AGB (AAS ),(2)结论:EP =FQ ,证明:由(1)可得,∠EPA∠∠AGB ,∠EP =AG ,如图1,∠∠FAC =90°,FQ∠AG ,AG∠BC ,∠∠FQA =∠FAC =∠CGA =90°,∠∠FAQ+∠AFQ =90°,∠FAQ+∠GAC =90°,∠∠AFQ =∠GAC ,在∠QFA 和∠GAC 中,FQA CGA FAQ CAG AF AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∠∠QFA∠∠GAC (AAS ),∠AG =FQ ,∠EP =FQ ;(3)结论:EH =FH ,理由:如图,∠EP∠AG ,FQ∠AG ,∠∠EPH =∠FQH =90°,在∠EPH 和∠FQH 中,EHP FHQ EPH FQH EP FQ ∠=∠⎧⎪∠=∠⎨⎪=⎩∠∠EPH∠∠FQH (AAS ),∠EH =FH .(4))∠∠EPH∠∠FQH ,∠EPA∠∠AGB ,∠FQA∠∠AGC ,∠S ∠FQA =S ∠AGC ,S ∠FQH =S ∠EPH ,S ∠EPA =S ∠AGB ,∠S ∠AEF =S ∠EPA +S ∠FQA=S ∠AGB +S ∠AGC=S ∠ABC =12×BC×AG =12×10×12 =60故答案为:60.【点睛】本题属于三角形综合题,主要考查了全等三角形的性质和判定以及等腰直角三角形的性质的综合应用,解题时注意:全等三角形的对应边相等,对应角相等.等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.20.详见解析【解析】【分析】延长BF 至G ,使FG BF =,连结EG ,得BFD GFE ∆∆≌,90DBF G ∠=∠=︒,BF=GF,再证ABC BEG ∆∆≌,得2AC BG BF ==.【详解】证明:延长BF 至G ,使FG BF =,连结EG ,在∠BDF 和∠GEF 中,BF=GF BFD=GFE DF=EF ⎧⎪∠∠⎨⎪⎩,∠BDF GEF ∆∆≌ ,∠90DBF G ∠=∠=︒,BF=GF ,∠BG=2BF ,∠BE∠BA ,∠∠C=∠G=90°,∠A=∠EBG ,在∠ABC 和∠BEG 中,C=G A=EBG AB=BE ∠∠⎧⎪∠∠⎨⎪⎩,∠ABC BEG ∆∆≌,∠AC=BG=2BF.【点睛】本题考查全等三角形的判定和性质,熟练掌握全等三角形的判定与性质定理是解题的关键.21.点A 的坐标为()2,1-【解析】【分析】过点A 作AE x ⊥轴于点E ,先证出ACE CBO ∆∆≌,则CE=BO=3,1AE OC ==,根据点A 在第二象限即可得点A 的坐标.【详解】解:过点A 作AE x ⊥轴于点E ,∠在直角坐标系中,点()0,3B -,点()1,0C ,∠BO=3,OC=1,OC∠OB∠,AC BC AC BC =⊥∠OBC ECA ∠=∠ ,BOC CEA ∠=∠∠ACE CBO ∆∆≌,CE BO ∴==3,1AE OC ==,∠点A 在第二象限,∴点A 的坐标为()2,1-.故答案为点A 的坐标为()2,1-.【点睛】本题考查坐标与图形,全等三角形的判定与性质,解题的关键是通过作辅助线构建全等三角形,要注意第二象限点的坐标符号是(-,+).22.见解析【详解】通过证明两个三角形全等,可以证明两条对应线段相等.。
平移翻折旋转等几何变换的性质分析

平移翻折旋转等几何变换的性质分析平移、翻折、旋转等几何变换是在平面上对图形进行操作的常用方法。
它们具有独特的性质与特点,本文将对这些几何变换的性质进行详细分析。
一、平移的性质分析平移是指将图形按照指定的方向和距离进行移动,而不改变其形状和大小。
平移的性质如下:1. 平移变换是保持图形各点之间距离和相对位置不变的变换。
即使图形进行平移,其各点之间的距离关系和相对位置仍然保持不变。
2. 平移变换的结果是与原图形全等的新图形。
即平移前后的图形在大小和形状上完全相同,只是位置不同。
3. 平移变换可以通过向量的加法来表示。
设图形上一点的坐标为A(x, y),进行平移变换时,将其横向平移a个单位,纵向平移b个单位,则新点的坐标为A'(x+a, y+b)。
二、翻折的性质分析翻折是指沿直线将图形对称地折叠,使得每个点关于折叠线对称,从而得到一个新的图形。
翻折的性质如下:1. 翻折变换是保持图形各点到折叠线的距离不变,但改变图形的相对位置。
即折叠前后的图形各点到折叠线的距离相等。
2. 翻折变换的结果是与原图形全等的新图形。
具体而言,翻折变换前后的图形在大小和形状上完全相同,只是位置不同。
3. 翻折变换可以通过向量的减法来表示。
设图形上一点的坐标为A(x, y),进行翻折变换时,将其关于折叠线的对称点的坐标表示为A'(-x, y')。
三、旋转的性质分析旋转是指围绕指定的旋转中心,按照指定的旋转角度将图形沿逆时针或顺时针方向旋转,从而得到一个新的图形。
旋转的性质如下:1. 旋转变换是保持图形上各点到旋转中心的距离和相对位置不变的变换。
旋转前后的图形各点到旋转中心的距离保持不变,且各点的相对位置不变。
2. 旋转变换的结果是与原图形全等的新图形。
即旋转前后的图形在大小和形状上完全相同,只是位置不同。
3. 旋转变换可以通过矩阵乘法来表示。
设图形上一点的坐标为A(x, y),进行旋转变换时,将其绕旋转中心点逆时针旋转θ角度得到的新点的坐标表示为A'(x', y')。
等几何分析 相场

等几何分析相场等几何分析,又称用几何概念分析,是一种以几何概念替代代数概念,从而获得更直观的结果的分析方法。
它把问题分成一系列的几何问题,以便解决复杂的数学问题。
因此,几何分析引起了许多人的兴趣,并且在科学研究中发挥着重要作用。
几何分析的应用范围很广,其中最重要的一个应用就是用来解决相场的问题,即用空间正交函数描述电场和磁场的强度和分布。
相场是指传统物理问题,即电磁波在介质中传播时,通过它们与电磁场相互作用所产生的场。
必要的假定是,电磁场不受任何介质的影响,并且它可以以空间正交的函数表示。
传统的物理理论要求电磁场的场强可以用空间正交的函数表示,而用几何分析解决这一问题,就可以求出电磁场的场强和分布。
运用几何分析解决相场问题,可以分析电磁场强度和分布,从而求出它们的分布特征,这是传统物理理论无法解决的问题。
因此,等几何分析方法对研究相场有着重要的意义。
首先,几何分析方法可以给出电磁场强度的具体表达式,这在传统物理理论中是不可能实现的。
其次,几何分析方法还可以分析某一特定介质中的电磁场分布特征,从而给出更准确的结论。
等几何分析方法还可以用来解决其它物理问题,比如解释质量积分的质量分布,估算光的传播速度等。
这些都是传统物理理论无法解决的问题,只有通过几何分析方法才能得到准确的结果。
此外,用几何分析方法也可以解决无线电传播中的问题,研究电磁场的冲击波分布等。
最后,用几何分析方法还可以开展更深入的研究,比如宇宙物质和能量的膨胀问题等。
总之,几何分析方法,特别是用几何分析解决相场问题,在科学研究中发挥着重要的作用。
几何分析方法可以提供更准确的结论和更有益的结果,并且它可以用来解决传统物理理论无法解决的问题。
未来,等几何分析方法将更加普及,在科学研究中发挥更为重要的作用。
[复杂型,叶片,数值]叶片类复杂型面电解加工的等几何数值分析方法探讨
叶片类复杂型面电解加工的等几何数值分析方法探讨0 引言航空发动机叶片是发动机的核心部件之一,其叶盆叶背型面是典型的自由曲面,电解加工作为特种加工方法是这类复杂三维型面加工的重要手段,逐渐成为发动机生产领域重要的生产工艺之一。
在电解加工的过程中,由于电场的作用,形成了从工件阳极流向工具阴极的电流,从而构成了电流场。
而对于电解加工的研究,一般认为电解加工的过程已经进入平衡状态,即此时的电场属于稳衡电流场。
Marius Purcar提出应用边界元法仿真电解加工过程中的阳极工件变化,利用解算网格单元节点沿电流密度方向的移动速率获得阳极的形状变化。
随后,基于有限元法开发了与SolidWorks软件集成并能接受STEP,AutoCad,IGES等格式的电解加工过程仿真工具,以此实现了3D环境下的电解加工过程仿真。
J.Kozak提出了稳态条件下电解加工的电场数学模型,指出平衡状态下阴阳极间隙与电势差、电导率、电解指数之间的经验关系。
并基于经验公式研究了加工过程仿真和反求阴极工具形状。
朱荻院士团队也提出了在三维环境下基于有限元法的阴极设计方法,并将方法应用于涡轮机叶片加工的阴极设计中,但应用有限元法降低了优化效率和计算精度。
综上所述,传统数值分析方法都以有限元法、有限差分法和边界元法作为基础方法,这类方法存在一些不足: 1)因为几何建模与数值分析模型采用不同数学描述方法,两者之间需要相互转换,转换常出现模型质量不好的现象。
2)传统有限元法采用多项式基函数的网格单元逼近表示边界,从原理上不能精确表达求解区域边界处的形状,不适于叶片电解加工这类对边界敏感问题的求解。
本文针对以上问题以航空发动机涡轮叶片电解加工的加工间隙电场分布为研究对象,建立了三维加工间隙参数化模型,并基于等几何法数值求解加工间隙的电场分布。
1 叶片电解加工间隙的参数化建模1.1 等几何分析方法的基本思想现有叶片的电解加工数值解法中,叶片工件与阴极工具之间的间隙模型一般采用商用的CAD软件建立,模型中采用的非均匀有理B样条(Non-Uniform Rational BSplines,NURBS)基函数来表示复杂的几何模型;而常用的有限元数值解法采用多项式基函数来逼近复杂边界。
数学几何与解析几何题解题技巧总结
数学几何与解析几何题解题技巧总结数学几何和解析几何是数学中非常重要的分支,它们有着广泛的应用领域,如物理学、工程学、计算机图形学等。
解决数学几何和解析几何问题需要一定的技巧和方法,下面将总结一些常用的解题技巧。
一、数学几何题解题技巧1. 图形的性质分析法在解决数学几何题目时,首先要对给定的图形进行性质分析。
通过观察图形的形状、角度、边长等特征,可以找到一些规律和关系,从而帮助解决问题。
例如,在判断一个四边形是否为矩形时,可以观察其四个角是否都为直角,四条边是否相等等。
2. 利用相似三角形相似三角形是数学几何中常用的重要概念。
当两个三角形的对应角相等,对应边成比例时,可以判断它们为相似三角形。
利用相似三角形的性质,可以求解一些难题。
例如,当两个三角形相似时,可以利用相似比例关系求解未知边长或角度。
3. 利用平行线和垂直线的性质平行线和垂直线是几何中常见的重要概念。
利用平行线和垂直线的性质,可以解决一些几何问题。
例如,当两条直线平行时,它们的对应角相等;当两条直线垂直时,它们的斜率乘积为-1。
4. 利用勾股定理和三角函数勾股定理是解决直角三角形问题的基本工具。
当一个三角形中有一个直角,可以利用勾股定理求解未知边长。
此外,三角函数也是解决三角形问题的重要工具,例如正弦定理、余弦定理等。
二、解析几何题解题技巧1. 坐标系的建立解析几何中,常常需要建立坐标系来描述几何图形。
建立坐标系可以将几何问题转化为代数问题,从而更容易求解。
在建立坐标系时,需要选择合适的原点和坐标轴方向,使得问题的求解更加简便。
2. 利用距离公式和中点公式距离公式和中点公式是解析几何中常用的工具。
距离公式可以求解两点之间的距离,中点公式可以求解线段的中点坐标。
利用这两个公式,可以计算线段的长度、判断三角形是否为等边三角形等。
3. 利用直线和曲线的方程直线和曲线的方程是解析几何中的重要工具。
通过求解直线和曲线的交点,可以解决一些几何问题。
解析几何中的常见图形
解析几何中的常见图形在解析几何中,常见的图形有点、直线、射线、线段、角、三角形、四边形和圆等。
这些图形在几何学中起着重要的作用,并且是我们在求解几何问题时常常会遇到的基本元素。
1. 点点是解析几何中最基本的图形,它是空间中没有大小的位置。
用大写字母表示点,比如A、B、C等。
点没有长度、宽度和厚度,它只有一个确定的位置。
2. 直线直线是由无穷多个点组成的,无限延伸的路径。
直线是解析几何中最基本的图形之一。
我们可以用两个点之间的直线段来表示一条直线,也可以用一条箭头来表示一条无限延伸的直线。
3. 射线射线也是由无穷多个点组成的路径,但它只延伸到一个方向。
射线有一个起点,表示为一个点,然后延伸到一个方向,不会结束。
4. 线段线段是由两个点之间的有限个点组成的路径。
线段有一个起点和一个终点,表示为两个点。
线段有确定的长度,在两个点之间有一个明确的终止点。
5. 角角是由两条射线或线段的交点和其它点组成的图形。
角的大小可以根据两条射线或线段之间的夹角来确定。
6. 三角形三角形是由三条线段组成的图形。
三角形有三个顶点和三条边。
根据三角形的边和角的性质,我们可以判断三角形的类型,如等边三角形、等腰三角形和直角三角形等。
7. 四边形四边形是由四条线段组成的图形。
四边形有四个顶点和四条边。
根据四边形的边和角的性质,我们可以判断四边形的类型,如矩形、正方形、平行四边形和菱形等。
8. 圆圆是由一个中心和一条半径组成的图形。
圆的所有点到中心的距离都相等。
圆在解析几何中有许多重要的性质和定理,在几何问题的求解中经常会用到。
以上就是解析几何中常见的图形。
通过理解和掌握这些图形的性质和特点,我们可以更好地进行几何问题的分析和求解。
三维声腔模态的等几何计算分析
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等几何分析研究进展摘要等几何分析是一种刚刚兴起的数值分析方法,对现有的CAE产生了很大的影响。
等几何分析法的出现于发展,缓解和消除了困扰CAE多年的难题,开启了一条结合设计、分析和优化等三方面的途径。
本文阐述了等几何分析产生的背景、意义和相关的定义,还介绍了等几何分析从首先提出到现如今的10年发展历程,包括基础理论体系的发展与完善,新型样条的构建,网格细分方法的研究,计算效率的提高,以及其他方面(如边界条件的施加、接触分析、结构优化等)的进展,展示了等几何分析相对于基于拉格朗日插值的有限元法的优势。
关键字等几何分析有限元 NURBS 发展现状1 前言有限元分析是目前应用最广泛的一种数值分析方法,且由于结合了能够高速运算的计算机,有限元法得到了大多数人的支持。
有限元法是将连续的物体离散成有限个单元,单元之间通过节点连接在一起,并将节点处的未知量作为基本未知量,使得无限自由度问题转换成了有限自由度的问题,在利用力学原理近似的求解出未知量。
这一突出优点使得有限元法得到广泛应用,各类有限元软件也层出不穷,如ABAQUS、ANSYS、LS-DYNA、HyperMesh等。
不过这一突出的优点也大大的限制了有限元的进一步发展。
首先,有限元法求得的结果的精确度与网格的细化程度有关,网格越细,则计算结果的精度越高,而计算时间和计算所需的内存也将随之增加,而以目前的水平来看,还无法做到超高精度的细化网格。
Sandia国家实验室曾做过一项统计,在汽车、航空航天和造船行业,大约全部分析时间的80%用于网格划分及划分前的几何模型准备[1]。
其次,网格划分使得应力不连续,且在处理大变形问题中,单元的过度扭曲导致精度严重损失。
第三,网格划分工具对几何形状的识别精度较低,特别是划分复杂高级曲面时无法精确划分,容易划分出大变形网格。
再者,网格划分是建立在几何模型的基础上,若几何模型发生改变,那么须得重新划分网格,花费大量时间。
最后,在处理网格畸变、网格移动如动态裂纹扩展、冲压成型等问题时需要进行网格重构,不仅浪费计算时间,还会损害计算精度[2]。
网格是有限元分析的基础,而以上缺陷都是网格划分造成的,是有限元法无法避免的。
基于以上原因,在2005年,Hughes等[3]提出等几何分析的思想。
该方法直接结合了CAD中的几何模型,将其中的几何信息作为有限元分析的输入信息,大大地节省划分网格的时间。
等几何分析与有限元法有许多相同之处,可以说是有限元法的发展,但其具有一套独立的理论体系。
该方法采用描述几何形状的NURBS函数作为基函数,具有几何精确特性,且离散的几何形状不随单元的稀疏而改变,这意味着即使是比较稀疏的网格划分,也能精确描述研究对象的几何形状,具有很高的数值精度[4]。
NURBS本身就具有网格,一个NURBS实体包含若干个NURBS单元,分析时,这些单元成为精确描述几何形状的实体单元。
另外,类似于有限元的网格,NURBS单元也可以细分,基函数的次数也可提高,计算结果更加精确,但几何形状不改变。
于是,Hughes将其命名为等几何分析。
2 等几何分析简介2.1 B 样条基函数由于NURBS 基函数是B 样条基函数的线性组合[5],这里先讨论B 样条基函数的构造。
B 样条基函数由节点矢量构建,如 ,式中u i 为节点,n 和p 分别是B 样条基函数的个数和阶数。
基函数由Cox-de Boor 递推公式定义为[6]:当p =0时,()⎩⎨⎧<<=+其他,0,110,i i i u u u u N 当p >0时,()()()u N u u u u u N u u u u u N p i i p i p i p i i p i i p i 1,11111,,-++++++-+--+--= 由基函数N i,p (u )和控制点P i 可表示出B 样条曲线:()()11,+=≤≤=∑n p n i ip i u u u P u N u C由于B 样条曲线具有局部性质,因而,可将上面的p 次B 样条曲线方程改写为分段表示形式:()()[][]11,,,++-=⊂∈=∑n p i i i p i j j p i u u u u u P u N u C 若给定(m +1)×(n +1)个控制点P i,j (i =1, 2, …, m ,j =1, 2, …, n )的阵列,构成一张控制网格。
又分别给定参数u 和v 的阶数p 和q ,以及两个节点矢量 和V = ,这样,就定义了一张p ×q 次张量积B 样条曲面,方程为:()()()1010,,,,,+=+=≤≤≤≤=∑∑n q m i m p n j ji q j p i v v v u u u P v N u N v u S由于B 样条曲面也具有局部性质,可将其分段表示为:()()()[][][][]1111,,,,,,,,+++-=+-=⊂∈⊂∈=∑∑n q f f m p e p e i e e f q f j j i q j p i u u v v v u u u u u P v N u N v u S 2.2 NURBS 曲线和曲面2.2.1 NURBS 曲线一条p 次NURBS 曲线可以表示为一分段有理多项式矢函数:{}121,,,++=p n u u u U {,1u U ={}121,,,++q n v v v }12,,++p m u u()()()∑∑===n i pi i n i ip i i u N P u N u C 0,0,ωω式中, 被称作权或全因子,分别与控制点相联系。
2.2.2 NURBS 曲面类似于B 样条曲面,NURBS 曲面也可分段表示为:()()()()()∑∑∑∑=====m i nj j i qj p i m i n j j i j i qj p i v N u N P v N u N v u S 00,,,00,,,,,ωω 同样的,一个三变量NURBS 实体也可表示为:()()()()()()()∑∑∑∑∑∑=======m i n j lk kj i rk q j p i m i n j l k k j i k j i rk q j p i w N v N u N P w N v N u N w v u V 000,,,,,000,,,,,,,,,ωω 2.3 计算流程基于NURBS 的等几何分析法的分析思路如下[3]:1)由节点向量积确定NURBS 片;2)通过节点插值将计算域细分为单元;3)每个基函数的支撑域包含少量单元;4)由基函数的控制点定义几何模型;5)采用等参概念,即场变量与几何模型采用相同的基函数表示,而基函数的系数即为自由度或控制变量;6)通过节点插值或基函数阶数可进一步细化单元,有h 型细化、p 型细化和k 型细化;7)采用类似于有限元的方法,可将等参NURBS 片构建的数组组装成全局数组;8)施加Dirichlet 边界条件有几种方法。
最粗糙的方法是加在控制变量上,这种近似法会导致比较大的误差。
然而,对于一些特殊情况,如齐次边界条件,该方法能满足精确度要求。
此外,Dirichlet 边界条件常常通过变分近似法或几何近似法施加。
3 等几何分析的发展3.1 基础理论体系Hughes 等提出了等几何分析的概念后,Bazilevs 等[7]用数学的知识对其进行分析和误差估计,证明了等几何分析的收敛性和稳定性等特征,这个结论为之后等几何分析的发展奠定了扎实的理论基础。
Cottrell 和Hughes [8]研究了等几何分析中网格的细化和近似连续性。
Gomez 等[9]通过等几何分析研究了Cahn-Hilliard),,2,1(n i i =ω),,2,1(n i P i =相域建模问题。
Lipton等[10]研究了等几何离散化的鲁棒性。
Sevilla等[11]提出了增强的NURBS有限元方法。
Shaw和Roy[12]创立了基于NURBS的参数无网格法。
Hughes等[13]人发现对B样条使用高斯积分计算效率并不理想,因而基于Half-Point-rule提出了一种宏单元积分法,该方法比高斯积分成本减少一半.3.2 网格细化等几何分析中主要有3种细化方法[14]:基于节点插入的h型细化方法,基于基函数升阶的p型细化方法以及升阶和节点插入相结合的k型细化方法。
之后,为了提高计算精度,Xu等[15]提出了可优化计算域内部控制点的位置的r型细化方法。
徐岗等[16]在r型细化方法的基础上提出了r-p型细化方法,并应用于二维热传导问题上。
没多久,徐岗、朱亚光等[17]提出了基于局部误差估计的自适应r 细化方法,大大提高计算域参数化的优化效率。
Pilgerstorfer等[18]进一步从理论层面挖掘了计算域参数化以及节点分布对等几何分析求解的影响,发现对一般问题而言,求解误差与计算域的等参数线网格(或等参数面网格)的均匀性及正交性有关,这也为构造适合分析的计算域参数化提供了重要的理论依据。
3.3 新型样条最初的等几何分析采用的基函数是CAD中最广泛应用的B样条和NURBS基函数,后来许多学者陆续采用T样条等新兴样条[19]。
T样条是由Sederberg等[20]在2003年提出的,可以实现局部加密,使单个样条表示复杂模型的能力大大提升。
Bazilevs等[7]率先将T样条用于等几何分析,并用于简单地二维和三维结构问题。
Wang等[21]提出一种将任意非结构化二次网格转化为标准T样条表面的方法。
不过,T样条的局部细分结果依赖于控制网的拓扑结构,其复杂性也是不确定的,另外T样条的混合函数不一定总是线性无关的[22]。
于是,Nguyen-Thanh 等[23]提出了PHT样条(多项式分层T样条),PHT样条是定义在层次T网格上双三次C1连续的样条空间,其继承了NURBS和T样条的所有优点,解决了NURBS和T样条相互转化的困难的问题。
PHT样条具有很好的局部加细性质,这使其在拟合、缝合、简化、自适应曲面重构和等几何分析中得到了广泛的应用[22]。
Bernard Mourrai等[24]研究了一般T网格上的维数计算公式,为将PHT样条向一般情形推广奠定了基础。
3.4 计算效率由于等几何分析法采用了高阶基函数,使得刚度矩阵相比于有限元法要稠密的多,大大地增加了计算时间,为此,许多学者展开了相关的研究。
郭利财等[25]提出了一种基于矩阵分解的并行算法,从刚度矩阵的装配上节省计算时间。
而后他们[26]还提出了直接使用粗网格的精确解作为细网格的初始解,大大提高了迭代速度。
Veiga等[27]提出一种基于重叠加法型施瓦茨预条件算子的重叠计算域分解方法,证明等几OAS算子关于子区域数是可扩展的。
