第一章 几何组成分析
哈工大结构力学题库一章

第一章平面体系的几何组成分析一判断题1. 图示体系是几何不变体系。
()题1图题2图题3图题4图2. 图示体系为几何可变体系。
()3. 图示体系是几何不变体系。
()4. 图示体系是几何不变体系。
()5. 图示体系是几何不变体系。
()题5图题6图题19图题20图6. 图示体系为几何不变有多余约束。
()7. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
()8. 两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必需满足的条件。
()9. 在任意荷载下,仅用静力平衡方程即可确定全不反力和内力的体系是几何不变体系。
()10. 计算自由度W小于等于零是体系几何不变的充要条件。
( )11. 几何可变体系在任何荷载作用下都不能平衡。
( )12. 三个刚片由三个铰相联的体系一定是静定结构。
( )13. 有多余约束的体系一定是超静定结构。
( )14. 有些体系为几何可变体系但却有多余约束存在。
()15. 平面几何不变体系的三个基本组成规则是可以相互沟通的。
()16. 三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
()17. 两刚片用汇交于一点的三根链杆相联,可组成几何不变体系。
()18. 若体系计算自由度W<0,则它一定是几何可变体系。
()19. 在图示体系中,去掉其中任意两根支座链杆后,所余下都是几何不变的。
()20. 图示体系按三刚片法则分析,三铰共线,故为几何瞬变体系。
()21. 有多余约束的体系一定是几何不变体系。
()22. 几何不变体系的计算自由度一定等于零。
()23. 几何瞬变体系的计算自由度一定等于零。
()24. 图中链杆1和2的交点O可视为虚铰。
()题24图二选择题1. 图示体系为:()A.几何不变无多余约束 B.几何不变有多余约束 C.几何常变 D.几何瞬变题1图题2图题3图2. 图示体系为:()A.几何不变无多余约束 B.几何不变有多余约束 C.几何常变 D.几何瞬变3. 图示体系虽有三个多余约束,但为保证其几何不变,哪两根链杆是不能同时去掉的。
几何组成分析分析PPT学习教案

曲 杆)、地基、地球或体系中已经肯定为几何不变的 某个部分都可看作一个平面刚片。
第35页/共57页
O
F
D
B
A
C
E
刚片II
第18页/共57页
两刚片法则:
法则I:两刚片用不全交于一点又不完全平行的三根 链杆相联,所组成的体系是几何不变的。
法则II:两刚片用一个铰和一根不通过该铰的链杆相 联,所组成的体系是几何不变的。
O
F
BD
AC
E
刚片II
O
刚片II
第19页/共57页
二、三刚片法则
平面中三个独立的刚片,共有9个自由 度。要 使这三 个刚片 之间不 发生相 对运动 ,即组 成一个 几何不 变体系 ,那么 这三个 刚片组 成的整 体只能 有3个 自由度 ,从而 整体的 自由度 减少6。
常 变 体 系
两刚片发生相对运动后, 此三根链杆仍互相平行, 故运动将继续发生,此体 系是几何可变体系。
2、常变体系:如果一个几何可变体系可以发生大位 移,则称为常变体系。
第27页/共57页
2、三刚片:
三个刚片用位于同一直线上的三个铰两两相联。
瞬变体系
(a)
铰C可绕两个圆弧的公切线发生一微小移动。微小移 动后,三个铰就不再位于一直线上,运动也就不再继 续,故此体系是一个瞬变体系。
第47页/共57页
练习4
第48页/共57页
练习5
第49页/共57页
练习6
结构力学之平面体系的几何组成分析 ppt课件

B
书写:二元体A-C-B。
PPT课件
22
(二)二元体规则: 增加或去掉二元体不改变原体系的几何 组成性质。
C
A
B
PPT课件
23
例五、 分析图示体系的几何构造:
解:
A
B
D
E
基本铰结三角形ABC符合 三刚片规则,是无多余约
G
C
F
束的几何不变体系;依次
在其上增加二元体A-D-C、 C-E-D、C-F-E、E-G-F后, 体系仍为几何不变体,且 无多余约束。
一、几何构造特性: (一)无多余联系的几何不变体系称为静定 结构。
PPT课件
40
静定结构几何组成的特点是:
任意取消一个约束,体系就变成了 几何可变体系。
PPT课件
41
(二)有多余联系的几何不变体系称为超静 定结构。
特点: 某些约束撤除以后,剩余体系仍
为几何不变体系。
PPT课件
42
二、静力特性: (一)静定结构: 在荷载作用下,可以依据 三个静力平衡条件确定全 部支座反力和内力,且解 答唯一。
用
表示。
几何不变部分
刚片
PPT课件
5
三、自由度:
确定体系位置所需要的独立坐标数目。
点:
y
2
y
o
A( x, y )
平面内点的自由度为
2
PPT课件
x
x
6
刚片:
平面内刚片的自由度为
3
y
( x, y )
y
o
A
3
x
x
PPT课件
7
四、约束(联系): 减少自由度的装置。
于玲玲结构力学第一章_结构的几何构造分析

(2)图 b
刚片 I、II 和 I、III 分别由无穷远处的瞬铰 A、B 相连,由于点 A 和点 B 为同方向的无穷远点,根
据结论(1),两点其实是一点,因此该点与连接刚片 II、III 的铰 C 共线,三点共线,所以该体系为几何
瞬变体系。
(3)图 c
显然为几何常变体系。
(4)图 d
刚片 I、II、III 分别由铰 C 和无穷远处的瞬铰 A、B 相连,由于 A、B 不同方向,所以其连线是一条
(a)
A
(b) A
B
(c)
B
(d)
A
B
C
C
A
B
C
C
(a) E
C
A
D
图 1-5 B
(b) E
C
A
DB
图 1-6
注意:二元体的三个结点都必须是铰接,如图 1-6,b 图中的 CEB 部分是二元体,而 a 图中的 CEB
2
部分不是二元体,区别仅在于 C 结点的连接方式不同。 去掉二元体是体系的拆除过程,应从体系的周边开始进行,而增加二元体是体系的组装过程,应从
结点 F、G、H、I、J 用 10 根链杆分别连于基础和刚片,约束数为 10,因此,
W=1×3+2×5-6-10=-3
2、由计算自由度得出的结论
(1)若 W > 0,则体系缺乏必要约束,是几何常变的。注意:若所分析的体系没有与基础相连,应
将计算出的 W 减去 3,如果仍大于零,才可判断体系为几何常变,否则不是几何常变,详见例 1-3。
刚片,因此铰 O 不是瞬铰;而 b 图中的铰 O 是瞬铰,因为刚片 I、II 和链杆 3 组成一更大的刚片 IV,即
杆 1 和 2 连接的都是刚片 III 和 IV,因此铰 O 是瞬铰。
02结构力学1-几何组成分析

§2-1 基本概念 W = 3m-(3g+2h+b) 四. 计算自由度
例3:计算图示体系的计算自由度 2 1 解法一
9根杆,9个刚片
有几个单铰?
3 3
3根单链杆
2 1
W=3 ×9-(2×12+3)=0
§2-1 基本概念
四. 计算自由度 例3:计算图示体系的计算自由度 铰结链杆体系:完全由两端 铰结的杆件所组成的体系
y 两个刚片一共6个自由 度 加两个单链杆之后:整 个体系有4个自由度 减少2个自由度
x
1单铰=2个单链杆
y
§2-1 基本概念
三. 约束(联系) 约束:减少自由度的装置 实铰 x
两个单链杆
y
y
虚铰 x
x
§2-1 基本概念
三. 约束(联系)
既不平行又不相交于一点 的三个单链杆=一个固定支 座
三个单链杆=一个固定支座?
§2-2 静定结构的组成规则
三边在两边之和大于第三边时,能唯一地组 成一个三角形——基本出发点。
二刚片规则: 二刚片规则: 两个刚片用三根 两个刚片用一 不全平行也不交 个铰和一根不通 于同一点的链杆 过此铰的链杆相 相联,组成无多 联,组成无多余 余联系的几何不 联系的几何不变 变体系。
体系。
§2-2 静定结构的组成规则
x
1单铰=2个约束
§2-1 基本概念
三. 约束(联系) 约束:减少自由度的装置 y
复铰
三个刚片一共9个自由 度 加铰之后:整个体系有 5个自由度 减少4个自由度 x
复铰 等于多少个 单铰?
1连接N个刚片的复铰 =N-1个单铰
§2-1 基本概念
三. 约束(联系) 约束:减少自由度的装置
(完整版)哈工大结构力学题库一章.docx
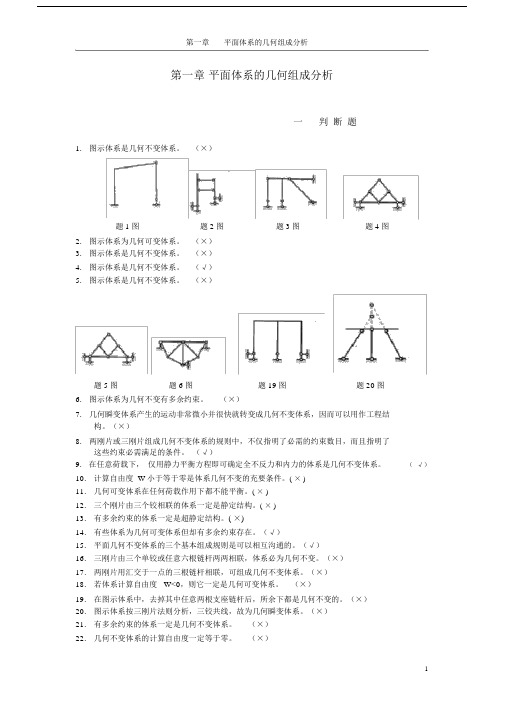
第一章平面体系的几何组成分析一判断题1.图示体系是几何不变体系。
(×)题1图题2图题3图题4图2.图示体系为几何可变体系。
(×)3.图示体系是几何不变体系。
(×)4.图示体系是几何不变体系。
(√)5.图示体系是几何不变体系。
(×)题5图题6图题19图题20图6.图示体系为几何不变有多余约束。
(×)7.几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系,因而可以用作工程结构。
(×)8.两刚片或三刚片组成几何不变体系的规则中,不仅指明了必需的约束数目,而且指明了这些约束必需满足的条件。
(√)9.在任意荷载下,仅用静力平衡方程即可确定全不反力和内力的体系是几何不变体系。
(√)10.计算自由度 W小于等于零是体系几何不变的充要条件。
( × )11.几何可变体系在任何荷载作用下都不能平衡。
( × )12.三个刚片由三个铰相联的体系一定是静定结构。
( × )13.有多余约束的体系一定是超静定结构。
( ×)14.有些体系为几何可变体系但却有多余约束存在。
(√)15.平面几何不变体系的三个基本组成规则是可以相互沟通的。
(√)16.三刚片由三个单铰或任意六根链杆两两相联,体系必为几何不变。
(×)17.两刚片用汇交于一点的三根链杆相联,可组成几何不变体系。
(×)18.若体系计算自由度 W<0,则它一定是几何可变体系。
(×)19.在图示体系中,去掉其中任意两根支座链杆后,所余下都是几何不变的。
(×)20.图示体系按三刚片法则分析,三铰共线,故为几何瞬变体系。
(×)21.有多余约束的体系一定是几何不变体系。
(×)22.几何不变体系的计算自由度一定等于零。
(×)23.几何瞬变体系的计算自由度一定等于零。
(×)24.图中链杆 1 和 2 的交点 O可视为虚铰。
第一章 结构的几何构造分析

(2)体系中约束的布置方式要合理。
17
结构的几何构造分析
二 平面几何不变体系的基本组成规则 1、三刚片规则
三刚片用不在同一直线上的三个单铰两两相联,组成的体系 是几何不变体系,且无多余约束。
2、二刚片规则
两个刚片用三根不完全平行也不交于一同一点的链杆相联, 组成的体系是几何不变体系,且无多余约束。
在对结构进行分析计算前,首先分析体系的几何组成,以确 定其几何不变性,只有几何不变体系才能作为工程结构应用,
因此,几何构造分析的目的为:
1 判别体系是否为几何不变体系,从而决定能否 作为结构应用。
2 掌握几何不变体系的组成规则,便于设计出合理 的结构形式。 3 用以区分体系为静定结构或超静定结构,从而决 2 定采用不同的计算方法。
15
结构的几何构造分析
§1-6 平面几何不变体系的基本组成规则
一 平面几何不变体系应满足的条件 1 计算体系的自由度(或可变度),能否判断体系为几何不 变体系? 平面体系计算自由度(可变度)的计算结果,可能有以下三 种情况: (1)W 0 ,表明体系缺少足够的约束,体系肯定为几何 可变体系。 (2)W 0 ,表明体系具有成为几何不所需的最少约束数 目,此时体系可能为几何不变体系,也可能为几何可变体 系。
5
结构的几何构造分析
约束的种类:
⑴ 链杆: 一根链杆相当一个约束。
y
B
y x A
y
B A
2 1
o
x
o
x
6
结构的几何构造分析
⑵ 单铰:
连接两个刚片的铰称为单铰 。 一个单铰相当于两个 约束。
y
x 1 Ⅰ
A
2 Ⅱ y
o
2006典型例题解析--第1章 几何组成分析

第1章几何组成分析§1 – 1 基本概念1-1-1 名词解释●几何不变体系——结构(静定或超静定)在不考虑材料变形情况下,几何形状和位置不变的体系,称为几何不变体系。
●几何可变体系在不考虑材料变形情况下,形状或位置可变的体系,称为几何可变体系。
●刚片在平面上的几何不变部分。
●自由度确定体系位置所需的独立坐标数目。
●约束(联系)能够减少自由度的装置。
减少自由度的个数为约束个数。
①链杆——相当1个约束②铰——相当2个约束③虚铰——相当2个约束④复铰——相当n-1个单铰的作用●多余联系不能减少自由度的联系,称Array为多余联系。
●必要联系去掉时能够增加自由度(或维持体系不变性必须)的联系。
●瞬变体系几何特征:几何可变体系经过微小位移后成为几何不变体系。
静力特征:受很小的力将产生无穷大内力,因此不能作结构。
1-1-2 分析规则在不考虑材料应变所产生变形的条件下,构成无多余约束几何不变体系(静定结构)的基本规则如下:●三刚片规则三个刚片用不在同一条直线上的三个铰(或虚铰)两两相联。
●二刚片规则2结构力学典型例题解析两个刚片用不交于一点也不全平行的三根链杆相联;或:两个刚片用一个铰和不通过该铰心的链杆相联。
●二元体规则什么是二元体(二杆结点):两根不在同一条直线上的链杆联接一个新结点的装置,称为二元体。
在一个体系上增加或减少二元体不影响其几何不变性。
1-1-3 几何组成分析一般方法(步骤)(1)去二元体(二杆结点)。
(2)分析地基情况:上部体系与地基之间●当有满足二刚片规则的三个联系时,去掉地基,仅分析上部体系;●当少于三个联系时,必为几何常变体系;●当多于三个联系时,将地基当作一个刚片进行分析。
(3)利用规则找大刚片(最简单情况为:三个铰接杆件为刚片)。
(4)使用几何组成规则进行分析。
利用三刚片规则分析时:首先找出三个刚片,(满足三刚片规则的连接条件,即每两个刚片间有一个铰(或虚铰),然后再标出虚铰位置,最后看三个铰是否构成三角形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章几何组成分析
一、是非题(“是”打√,“非”打)
1、图示体系,去掉其中任意一根支座链杆后,剩下部分都是几何不变无多余约束的体系。
()
2、体系几何组成分析中,链杆都能看作刚片,刚片有时能看作链杆,有时不能看作链杆。
()
3、几何不变体系的计算自由度小于或等于0;计算自由度小于或等于0的体系一定是几何不变体系。
()
4、当上部体系只用不交于一点也不全平行的三根链杆与大地相连时,只需分析上部体系的几何组成,就能确定原体系的几何组成。
()
5、图a铰结体系是几何可变体系,图b铰结体系是几何不变体系。
()
(a) (b)
6、几何组成分析中,简单铰结点和简单链杆不能重复利用,复杂铰结点和复杂链杆(这两个概念教学中一般不介绍)可以重复利用。
()
7、体系几何组成分析时,体系中某一几何不变部分,只要不改变它与其余部分的联系,可以替换为另一个几何不变部分,不改变体系的几何组成特
性。
()
8、下图为几何不变体系。
()
9、体系的多余约束对体系的计算自由度、自由度及受力状态都没有影响,故称多余约束。
()
10、瞬变体系就是瞬铰体系。
()
二、选择题
1、图示体系的几何组成是()
A.无多余约束的几何不变体系
B.几何可变体系
C.有多余约束的几何不变体系
D.瞬变体系
2、图示体系的几何组成是()
A、无多余约束的几何不变体系
B、几何可变体系
C、有多余约束的几何不变体系
D、瞬变体系
3、图示体系的几何组成是()
A、无多余约束的几何不变体系
B、几何可变体系
C、有多余约束的几何不变体系
D、瞬变体系
4、图示体系的几何组成是()
A、无多余约束的几何不变体系
B、几何可变体系
C、有多余约束的几何不变体系
D、瞬变体系
5、图示各体系中,几何不变且无多余约束的体系是()
A、图a
B、图b
C、图c
D、图d
(a) (b) (c)
(d)
6、图示体系的几何组成是()
A、无多余约束的几何不变体系
B、几何可变体系
C、有多余约束的几何不变体系
D、瞬变体系
7、图示体系的几何组成是()
A、无多余约束的几何不变体系
B、几何可变体系
C、有多余约束的几何不变体系
D、瞬变体系
8、图示体系的几何组成是()
A、无多余约束的几何不变体系
B、几何可变体系
C、有多余约束的几何不变体系
D、瞬变体系
9、图示体系的几何组成是()
A、无多余约束的几何不变体系
B、几何可变体系
C、有多余约束的几何不变体系
D、瞬变体系
10、图示体系的几何组成是()
A、无多余约束的几何不变体系
B、几何可变体系
C、有多余约束的几何不变体系
D、瞬变体系
三、填空题
1、下图体系的计算自由度W= (),所以该体系为()体系
2、图示桁架受F作用,分别根据结点A和B的平衡求得AB杆轴力为F和0,如何解释这样的矛盾?()
3、图示各体系几何组成分析时,哪些图中的A-B-C可看为二元体去
掉。
()
(a) (b) (c)
(d) (f)
4、图示各体系中,几何不变且无多余约束的体系是()
(a) (b) (c)
(d)
5、图示各体系中,几何瞬变体系是()
(a) (b) (c)
(d)
6、下图体系的几何组成为()
7、下图体系的计算自由度W= ()
一、是非题
1、╳。
水平支座链杆是必要约束。
2、√。
几何组成分析时,只通过两个铰和其他部分相连的几何不变部分可以看作链杆(内力计算时不能这样做)。
3、╳。
计算自由度小于或等于0只是体系几何不变的必要条件。
4、√。
由两刚片法则可知。
5、√。
只需分析上部体系,去二元体,(a)最后剩两个铰结点,(b)最后剩一根链杆。
6、√。
复杂铰结点和复杂链杆可以化为多个简单铰结点和简单链杆考虑。
7、√。
只要是几何不变部分就可以看作刚片。
8、√。
利用第7题的结论,将ABC和CDE换成铰结三角形ABC和CDE。
三角形CDE为刚片Ⅰ,BF为刚片Ⅱ,地基为刚片Ⅲ。
9、╳。
多余约束对体系自由度没有影响,对计算自由度及受力状态有影响。
10、╳。
瞬铰即虚铰。
两根延长线相交的链杆所起的约束作用相当于交点处的一个铰的作用。
而瞬变体系是经微小位移后又成为不变体的一种特殊不变体系。
二、选择题
1.A,BCE为刚片Ⅰ,地基为刚片Ⅱ。
2.B,逐次去二元体。
3.A,AB、BC和地基为三个刚片。
4.D,先去二元体,ABC为刚片Ⅰ,地基为刚片Ⅱ。
5.D
6.A,AB、EF和CD为三个刚片。
7.A,ABC加上二元体A-D-C为刚片Ⅰ,GEF加上二元体E-H-F为刚片Ⅱ。
符合二刚片法则。
8.A,ABC为刚片Ⅰ,DE为刚片Ⅱ,地基为刚片Ⅲ。
9.A,两个L形分别为刚片Ⅰ和Ⅱ,地基为刚片Ⅲ。
10.D,用三刚片法则分析内部,ABDC为刚片Ⅰ,EGHF为刚片Ⅱ,IL为刚片Ⅲ。
三、填空题
1、1,几何可变。
2、该体系为瞬变体系。
3、a、b。
二元体的概念。
4、a、b。
(a)从上至下逐步去二元体;(b)将ABC、CDE和FG看作三个刚片;(c)为几何可变体系,将ABCGFE和DH看作两个刚片;(d)为瞬变体系,将BCF、DE和地基看作三个刚片。
5、a、b。
(a)将ABC、EFD和GH看作三个刚片,地基用AD杆代替;(b)将ABC、DEF和GH看作三个刚片;(c)将AB、CDE和FG看作三个刚片;(d)将AF、BCD和地基看作三个刚片。
FE、ED看作刚片之间的链杆。
6、几何不变且无多余约束体系。
零载法。
7、-3。
B、E处是复杂刚结点。
