《自控原理》典型环节的传递函数
合集下载
自动控制原理课件：2_5系统的传递函数
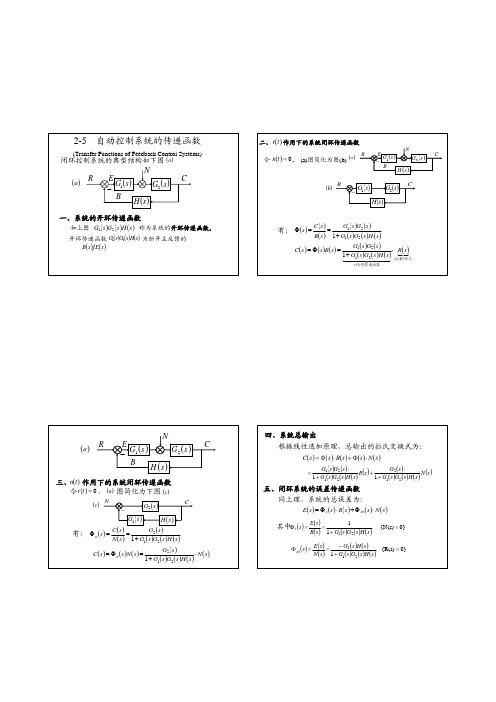
2-5 自动控制系统的传递函数(Transfer Functions of Feedback Control Systems)()s G 1()s H ()s G 2NRBCE−()a 闭环控制系统的典型结构如下图()a 一、系统的开环传递函数如上图称为系统的开环传递函数。
()()()s H s G s G 21开环传递函数为断开主反馈的()()()s H s G s G 21()()s E s B 二、作用下的系统闭环传递函数()t r ()s G 1()s H ()s G 2RC−()b 令, (a)图简化为图(b)()0=t n ()s G 1()s H ()s G 2NRBCE−()a 有：()()()()()()()()s H s G s G s G s G s R s C s 21211+==Φ()()()()()()()()()(){的形式的传递函数对t r r c s R s H s G s G s G s G s R s s C ⋅+=Φ=44434442121211三、作用下的系统闭环传递函数()t n ()a ()c 令，图简化为下图()0=t r ()s G 2()s G 1()s H NC−()c 有：()()()()()()()s H s G s G s G s N s C s n 2121+==Φ()()()()()()()()s N s H s G s G s G s N s s C n ⋅+=Φ=2121()s G 1()s H ()s G 2N RBCE−()a 四、系统总输出根据线性迭加原理，总输出的拉氏变换式为：()()()()()s N s s R s s C ⋅Φ+⋅Φ=()()()()()()()()()()()s N s H s G s G s G s R s H s G s G s G s G 212212111+⋅++⋅=五、闭环系统的误差传递函数同上理，系统的总误差为：()()()()()s N s s R s s E en e ⋅Φ+⋅Φ=()()()()()()0}{N(s) 1121=+==Φs H s G s G s R s E s e 其中：()()()()()()()()0}{R(s) 1212=+−==Φs H s G s G s H s G s N s E s en本章要点•传递函数概念？•怎样建立系统的传递函数？•结构图等效变换、梅森公式作业•2-4•2-5•2-6•在计算机上实现2-6节:MATLAB的应用。
自动控制原理结构图
x5 = a25 x2 + a45 x4
a32
a43
a44
x1
a12 x2
a23
a34
x3
a45 x4
x5
a24
a25
41
自动控制原理结构图
2.信号流图的基本元素 (1) 节点：用来表示变量，用符号“ O ”表示，并在
近旁标出所代表的变量。
2-5 典型环节及其传递函数
1.比例环节
（杠杆，齿轮系，电位器，变压器等）
运动方程式 c(t) = K r(t)
K
传递函数
G(s) = K
1
C(s) = G(s) R(s) = K/s
c(t) = K1(t)
可见，当输入量r(t)=1(t)时，输出量c(t)成比例变化0 。
自动控制原理结构图
c(t) r(t)
－
+
流入量Q 水箱
h
7
自动控制原理结构图
A
4.微分环节 微分方程式为：c(t) T dr(t)
dt
传递函数为： G(s)=Ts
1 r(t)
单位阶跃响应：C(s)Ts 1 T
s
0
t
c(t) = T(t)
c(t)
由于阶跃信号在时刻t = 0有一跃变，
T
其他时刻均不变化，所以微分环节对
阶跃输入的响应只在t = 0时刻产生一
12
nt s
i ndt()
式中，β=cos－1 。响应曲线是按指数衰减振荡的，故称
振荡环节。
j
s1
jd
n
c(t) 1
n
0
t 0 s2
11
自动控制原理结构图
自动控制理论_哈尔滨工业大学_2 第2章线性系统的数学模型_(2.4.1) 典型环节的传递函数PPT
0
t
积分环节在单位阶跃输入下的响应
例：积分器
i2
C
ui R
_
i1
uo
+i1 i2Fra bibliotek1 Rui
(t)
C
d dt
u0
(t )
uo
(t)
1 RC
ui (t)dt
G(s) Uo (s) 1 1 Ui (s) RC s
二、几种典型环节的数学模型
4.微分环节
c(t) d r(t)
斜率1/T
0τ
t
例： • 汽车加速、火箭升空； ——作用力和输出速度
• 加热系统； ——加热量和温度变化
• 励磁回路； ——输入电压和励磁电流
惯性大小用τ来量度。 ——τ越大，接近目标值越慢 ，惯性越大；τ越小，接近 目标值越快，惯性越小。
几乎任何物理系统都包含 大大小小的惯性。
二、几种典型环节的数学模型
滞后环节
二、几种典型环节的数学模型
1.比例环节
y(t) Ku(t)
G(s) Y(s) K U (s)
K——称为比例系数或放大系数，也称为环节的增益，有量纲。
输出量无失真、无滞后、成比例地复现输入。
• 无弹性变形的杠杆；
——作用力和输出力
• 忽略非线性和时间迟后的运算放大器；
——比例放大器的输入电压和输出电压
τ＝RC—时间常数
当 r(t) 1(t) 时， R(s) 1
s
Y(s) s 1 1 s 1 s s 1
t
y(t) e
t=0时，输出幅值为1；
t→∞时，指数衰减至0。
二、几种典型环节的数学模型
2-4 典型环节及其传递函数
1
气阻的数学表达式为 ∆p = R∆q ∆p 式中， 是气体压力降 ； ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量 ； R 是气阻值。 因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) （３）喷嘴一挡板机构 喷嘴一挡板机构由恒节流孔 １，背压室 ２，喷嘴 ３，和挡板 ４ 组成，如图 ２－１８ 所示。 ∆h 它的作用是把输入挡板的微小位移 转换成相应 的气压信号输出。在忽略背压室气容影响时，可把喷嘴 1 2 4 一挡板机构看作一个比例环节，即 3 D ∆p D = k 1 ∆h 式中， 是喷嘴背压的变化； ∆p D ∆h 是挡板开度变化量； 是比例系数。 k1 d （４）放大器 h 在自动控制系统中用得最多的是运算放大 器，它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室 运算放大器一般由集成电路构成，其符号如图 ２－ 3 − 喷嘴 4 − 挡板 １９ 所示。 图 2-17 喷嘴挡板机构结构示意图 图中三角形尖端代表输出端，输出电压为 u 0 (t ) 它有两个输入端，一个是同相输入端 ｂ 用 “十”表示，一个是反相输入端 ａ 用“一”表示。当 放大器工作在放大区而不是饱和区时，输出电压 与同相输入端电压 和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压 之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中， 为开环放大倍数，这个数值很高，可达到 。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点： ①由于开环输入电阻很高，运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高，所以 ｂ 端和 Ｃ 端电位接近相等，即 。 u i2 ≈ ui1 运算放大器本身虽属放大环节，但可用它来组成其他各种基本环节。
气阻的数学表达式为 ∆p = R∆q ∆p 式中， 是气体压力降 ； ( N/m 2 ) ∆q ( N ⋅ s) 是气体重量流量 ； R 是气阻值。 因而它的传递函数为 ∆P( s ) G( s ) = =R ∆Q ( s ) （３）喷嘴一挡板机构 喷嘴一挡板机构由恒节流孔 １，背压室 ２，喷嘴 ３，和挡板 ４ 组成，如图 ２－１８ 所示。 ∆h 它的作用是把输入挡板的微小位移 转换成相应 的气压信号输出。在忽略背压室气容影响时，可把喷嘴 1 2 4 一挡板机构看作一个比例环节，即 3 D ∆p D = k 1 ∆h 式中， 是喷嘴背压的变化； ∆p D ∆h 是挡板开度变化量； 是比例系数。 k1 d （４）放大器 h 在自动控制系统中用得最多的是运算放大 器，它是一个具有高放大倍数直接耦合式放大器。 1 − 恒节流孔 2 − 背压室 运算放大器一般由集成电路构成，其符号如图 ２－ 3 − 喷嘴 4 − 挡板 １９ 所示。 图 2-17 喷嘴挡板机构结构示意图 图中三角形尖端代表输出端，输出电压为 u 0 (t ) 它有两个输入端，一个是同相输入端 ｂ 用 “十”表示，一个是反相输入端 ａ 用“一”表示。当 放大器工作在放大区而不是饱和区时，输出电压 与同相输入端电压 和反相输入 u 0 (t ) u i (t ) u ( t ) 端电压 之间的电压差成正比。即 i1 a u 0 (t ) = k [u i2 (t ) − u i1 ( t )] + 也可写成 b ∆u 0 (t ) = k∆u i (t ) U i1 因而其传递函数为 Ui2 U0 ∆U 0 ( s ) G( s ) = =k 图 2-19 运算放大器符号图 ∆U i ( s ) 式中， 为开环放大倍数，这个数值很高，可达到 。所以集成运算放大器工作在 k 10 6 ~ 10 7 无反馈状态时输入电阻很高。它有以下两个主要特点： ①由于开环输入电阻很高，运算放大器两个输入端的电流接近于零。 ②由于开环放大倍数很高，所以 ｂ 端和 Ｃ 端电位接近相等，即 。 u i2 ≈ ui1 运算放大器本身虽属放大环节，但可用它来组成其他各种基本环节。
自动控制原理课件：2_4典型环节
• 电枢回路电压平衡方程
• 电磁转距方程 • 电动机轴上的转距平衡方程
1)确定输入量、输出量 2)确定动态联系
Ua θc
ua
=
Raia
+ La
dia dt
+ eb
eb = Kbωm
(2)
J
dωm dt
=
Mm
−ML
−
fωm
ua
(1)
Eb Eb
ML
(3) Mm
1
Ia
LaS + Ra
1
ωm
JS + f
电磁力矩 M m = Cmia
Ua eb
La
f1 Mm ML
J1
ωmθm 1/i θc
nω
M2
J2 、f2
原理:直流电动机的工作实质是将输入的
电能转换为机械能，也就是由输入的电枢电压Ua(t) 在电枢回路中产生电枢电流ia (t)，再由电流ia （t）与激磁磁通相互作用产生电磁转距Mm(t)， 从而拖动负载运动。因此，直流电动机的运动方 程可由以下三部分组成。
(4)
Ia Cm
Mm
角速度 ωm = dθm dt
(5)
θm
ωm
S
输出轴转角方程
θm
θc = θm i (6)
1 i
θc
4、传递函数 联结各框图得系统方快图(P39:图表-48)
用结构变换或Mason公式求出传递函数
三、求取系统传递函数的一般方法
步骤： * 1.首先确定出系统的输出信号(被控量等)和输入
信号（如给定值、干扰等）。 * 2.把系统分成若干个典型环节，求出各环节的
传递函数。用信号线把这些方框连接起来，得 到系统的动态结构图。 * 3.对动态结构图进行变换，得到传递函数。
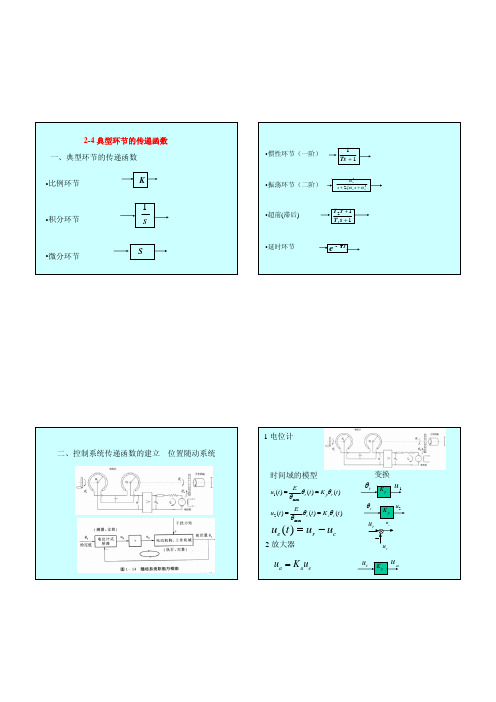
• 电磁转距方程 • 电动机轴上的转距平衡方程
1)确定输入量、输出量 2)确定动态联系
Ua θc
ua
=
Raia
+ La
dia dt
+ eb
eb = Kbωm
(2)
J
dωm dt
=
Mm
−ML
−
fωm
ua
(1)
Eb Eb
ML
(3) Mm
1
Ia
LaS + Ra
1
ωm
JS + f
电磁力矩 M m = Cmia
Ua eb
La
f1 Mm ML
J1
ωmθm 1/i θc
nω
M2
J2 、f2
原理:直流电动机的工作实质是将输入的
电能转换为机械能，也就是由输入的电枢电压Ua(t) 在电枢回路中产生电枢电流ia (t)，再由电流ia （t）与激磁磁通相互作用产生电磁转距Mm(t)， 从而拖动负载运动。因此，直流电动机的运动方 程可由以下三部分组成。
(4)
Ia Cm
Mm
角速度 ωm = dθm dt
(5)
θm
ωm
S
输出轴转角方程
θm
θc = θm i (6)
1 i
θc
4、传递函数 联结各框图得系统方快图(P39:图表-48)
用结构变换或Mason公式求出传递函数
三、求取系统传递函数的一般方法
步骤： * 1.首先确定出系统的输出信号(被控量等)和输入
信号（如给定值、干扰等）。 * 2.把系统分成若干个典型环节，求出各环节的
传递函数。用信号线把这些方框连接起来，得 到系统的动态结构图。 * 3.对动态结构图进行变换，得到传递函数。
自动控制原理--典型环节及其传递函数
hc t hd (t )
l
v
2.3 控制系统的复数域数学模型
4.典型元部件的传递函数
（1）电位计
（1）比例环节
（2）电桥式误差角检测器
（2）微分环节
（3）自整角机
（3）积分环节
（4）测速发电机（交流，直流） （4）惯性环节
（5）电枢控制式直流电动机 （5）振荡环节
（6）两相异步电动机
（6）一阶复合微分环节
特点： 输出量能准确复现输入量，但须延迟一固定的时 间间隔。
在线性控制系统中，系统含有典型环节的情况，反映了系 统的结构和性能。
时滞环节
对于时滞时间很小的时滞环节，常把它展开成泰勒级数，并 略去高次项，得：
W
(
s)
1
s
2
s
2
1
3
s3
2! 3!
1
1s
时滞环节在一定条件下可近似为惯性环节
实例
带钢厚度检测环节
(6)
复习拉普拉斯变换有关内容（13）
用L变换方法解线性常微分方程
0 初条件 n>m
: 特征根（极点） : 相对于 的模态
2.3 控制系统的复数域数学模型
3.传递函数的零点和极点对输出的影响
极点决定模态； 零点影响曲线形状。
4 传递函数的局限性
例 已知某系统在0初条件下的阶跃响应为：
c(t) 1 2 et 1 e4t 33
试求：（1） 系统的传递函数； （2） 系统的增益； （3） 系统的特征根； （4） 画出对应的零极点图； （5） 求系统的单位脉冲响应； （6） 求系统微分方程；
解.（1）
(2) (3) (4) 如图所示 (5)
积分环节实例：
l
v
2.3 控制系统的复数域数学模型
4.典型元部件的传递函数
（1）电位计
（1）比例环节
（2）电桥式误差角检测器
（2）微分环节
（3）自整角机
（3）积分环节
（4）测速发电机（交流，直流） （4）惯性环节
（5）电枢控制式直流电动机 （5）振荡环节
（6）两相异步电动机
（6）一阶复合微分环节
特点： 输出量能准确复现输入量，但须延迟一固定的时 间间隔。
在线性控制系统中，系统含有典型环节的情况，反映了系 统的结构和性能。
时滞环节
对于时滞时间很小的时滞环节，常把它展开成泰勒级数，并 略去高次项，得：
W
(
s)
1
s
2
s
2
1
3
s3
2! 3!
1
1s
时滞环节在一定条件下可近似为惯性环节
实例
带钢厚度检测环节
(6)
复习拉普拉斯变换有关内容（13）
用L变换方法解线性常微分方程
0 初条件 n>m
: 特征根（极点） : 相对于 的模态
2.3 控制系统的复数域数学模型
3.传递函数的零点和极点对输出的影响
极点决定模态； 零点影响曲线形状。
4 传递函数的局限性
例 已知某系统在0初条件下的阶跃响应为：
c(t) 1 2 et 1 e4t 33
试求：（1） 系统的传递函数； （2） 系统的增益； （3） 系统的特征根； （4） 画出对应的零极点图； （5） 求系统的单位脉冲响应； （6） 求系统微分方程；
解.（1）
(2) (3) (4) 如图所示 (5)
积分环节实例：
《自控原理》典型环节的传递函数
3.结构图： 结构图： 结构图 R(S)
1 T2S2+2ξTS +1
C(S)
七、二阶微分环节
d2r(t) dr(t) 2 + r(t) =c(t) 1.微分方程： 微分方程： 微分方程 τ + 2ξτ 2 dt dt
τ：环节的时间常数;ξ：阻尼比。
2.传递函数： 传递函数： 传递函数
G ( s ) = τ S + 2ξτS + 1
G(S)=K
R(S)
K
C(S)
二、积分环节
1.微分方程： c(t)=∫r(t)d(t) 微分方程： 微分方程 ∫ 2.特点： 特点： 特点 输出对输入信号上在时间上的积分。 输出对输入信号上在时间上的积分。 1
3.传递函数： 传递函数： 传递函数
G(S)=
R(S)
S
4.结构图： 结构图： 结构图
1 S
种简单的形式组成，这些典 型的单元，称作典型的环节。
1、比例环节： 、比例环节： 2、积分环节： 、积分环节： 3、纯微分环节： 、纯微分环节：
G(S)=K 1 G(S)= S G(S)=S
1 G(S)= 4、惯性环节： 、惯性环节： TS+1 5、一阶微分环节： G(S)= τS+1 、一阶微分环节： ω2n 6、二阶振荡环节： G(S)= 2 、二阶振荡环节： S +2 ξωnS+ω2n ω 7、二阶微分环节： G ( s ) = τ 2 S 2 + 2ξτS + 1 、二阶微分环节： τ G(S)=e-τs 8、延迟环节： 、延迟环节：
4.结构图： 结构图： 结构图
S
四、惯性环节（一阶环节） 惯性环节（一阶环节）
1 T2S2+2ξTS +1
C(S)
七、二阶微分环节
d2r(t) dr(t) 2 + r(t) =c(t) 1.微分方程： 微分方程： 微分方程 τ + 2ξτ 2 dt dt
τ：环节的时间常数;ξ：阻尼比。
2.传递函数： 传递函数： 传递函数
G ( s ) = τ S + 2ξτS + 1
G(S)=K
R(S)
K
C(S)
二、积分环节
1.微分方程： c(t)=∫r(t)d(t) 微分方程： 微分方程 ∫ 2.特点： 特点： 特点 输出对输入信号上在时间上的积分。 输出对输入信号上在时间上的积分。 1
3.传递函数： 传递函数： 传递函数
G(S)=
R(S)
S
4.结构图： 结构图： 结构图
1 S
种简单的形式组成，这些典 型的单元，称作典型的环节。
1、比例环节： 、比例环节： 2、积分环节： 、积分环节： 3、纯微分环节： 、纯微分环节：
G(S)=K 1 G(S)= S G(S)=S
1 G(S)= 4、惯性环节： 、惯性环节： TS+1 5、一阶微分环节： G(S)= τS+1 、一阶微分环节： ω2n 6、二阶振荡环节： G(S)= 2 、二阶振荡环节： S +2 ξωnS+ω2n ω 7、二阶微分环节： G ( s ) = τ 2 S 2 + 2ξτS + 1 、二阶微分环节： τ G(S)=e-τs 8、延迟环节： 、延迟环节：
4.结构图： 结构图： 结构图
S
四、惯性环节（一阶环节） 惯性环节（一阶环节）
控制工程基础：2.4 传递函数以及典型环节的传递函数
G(s)= 1 Ts 1
•2.4.3.振荡环节（二阶）
G(s)=
1
或
2
T 2s2 2 Ts 1
s2 2s 2
（0< <1)
•2.4.4.积分环节
G(s)= k s
•2.4.5.理想微分环节 •2.4.6.近似微分环节
G(s)=ks
G(s)= kTs Ts+1
• 2.4.7.延迟环节 G(s)= e -τs
N(s) – 分母多项式，又称特征多项式，它决定着系统 响应的基本特点和动态本质。
一般情况下，要求n≥m
G(s) C(s) b0sm b1s m1 bm1s bm M (s) R(s) a0s n a1s n1 an1s an N (s)
m
(s+zi )
K*
i 1 n
于是，由定义得系统传递函数为：
G(s)
C(s) R(s)
b0 s m a0 s n
b1s m1 a1s n1
bm1s bm an1s an
M (s) N(s)
M (s) b0 s m b1s m1 bm1s bm M(s) – 分子多项式
N (s) a0 s n a1s n1 an1s an
2.4 传递函数以及典型环节的传递函数
2.4 传递函数以及典型环节的传递函数
微分方程是在时域中描述系统动态性能的数学 模型，在给定输入量和初始条件下求解微分方 程可以得到系统的输出响应。系统结构和参数 变化时分析较麻烦。
传递函数是在用拉氏变换求解线性常微分方 程的过程中引申出来的概念。
用拉氏变化法求解微分方程时，可以得到控 制系统在复数域的数学模型－传递函数。
传递函数的局限性
典型环节的传递函数
21
一、典型输入信号
1. 阶跃函数：
r(t)
a t 0
a
r(t) 0 t 0
t
单位阶跃函数：
1 t 0 r(t) 1(t) 0 t 0
单位阶跃函数的拉氏变换
R(s) L[1(t)] 1 s
22
2. 速度函数(斜坡函数)：
r(t)
at t 0
r(t)
0
t0
at
t
单位速度函数(斜坡函数)：
传递函数为： G(s)
1
s
积分环节原理图为：
U2(s) 1/ Cf s 1 1 U1(s) R1 R1C f s Tis
4
空载油缸
流量：
Q
f
(t)
A
dx(t) dt
X (s) 1/ A K Q f (s) s s
小惯性电动机
m(s) Km
Ua(s) s
三、理想微分环节 微分方程为：c(t) dr(t)
4. 调节时间ts:整个过渡过程所经历的时间，有时也叫过渡过 程时间。
30
5. 超调量σ%: 响应过程中，输出量
超出稳态值的最大偏差值， 一般用它与稳态值的比值 的百分数表示，即
% h(t p ) h() 100%
h()
6. 振荡次数N:单位阶跃响应曲线在0→ts时间内，穿越稳态 值次数的一半称为振荡次数。
31
7.稳态误差ess:对单位 负反馈系统，当时间t 趋于无穷时，系统单 位阶跃响应的期望值 [即输入量1(t)] 与实际值 (即稳态值)之差，定义为 稳态误差:
ess =1 - h(∞)
当h(∞) =1时，系统的稳态误差为零。
32
注意： σ%
典型环节传递函数
积分环节输入输出关系
积分环节控制实例
5.振荡环节
5.振荡环节
6.延时环节
x ( t ) x t ) o i(
s G (s ) e
特点： 输出滞后于输入，实例
强调几点： 1.传递函数框图中的环节是根据动力学方程来划分的， 一个环节并不一定代表一个物理元件（物理环节或子系统）， 一个物理元件（物理环节或子系统）也不一定就是一个传递函 数环节（也许几个物理元件的特性才组成一个传递函数环节， 也许一个物理元件的特性分散在几个传递函数环节中）。 2.注意区别表示系统结构的物理框图和分析系统的传递 函数框图。 3.同一物理元件在不同系统中的作用不同时，其传递函 数可以不同。 （例如，测速发电机：当输入为角速度时，是比例环节 当输入为角位移时，是微分环节）
传递函数：
G (s ) K
特点： 输入量与输出量成正比 不失真，不延迟 例如：
齿轮传动副
运算放大器
2.惯性环节
dx ( t ) o 动力学方程： T x ( t ) x t ) o i( dt 1 传递函数： G(s) Ts1 特点： 存在储能元件和耗能元件 在阶跃输入下，输出不能立即达到稳态
传递函数框图中的环节是根据动力学方程来划分的一个环节并不一定代表一个物理元件物理环节或子系统一个物理元件物理环节或子系统也不一定就是一个传递函数环节也许几个物理元件的特性才组成一个传递函数环节也许一个物理元件的特性分散在几个传递函数环节中
1.比例环节
( t ) Kx t ) 动力学方程： x o i(
例如：
无源滤波器
k-c系统
3.微分环节
x ( t ) x t ) o i(
G (s) s
特点： 一般不能单独存在；反映输入的变换趋势； 增加系统的阻尼；强化噪声。 例如：
自动控制原理传递函数
自动控制原理传递函数在自动控制系统中，传递函数是一种常用的描述系统动态性能的数学工具。
它反映了系统的输入信号与输出信号之间的关系。
传递函数常用于描述线性、时不变系统，并且在控制系统设计中有着重要的作用。
传递函数可以通过系统的微分方程求得。
对于一个一阶系统，其微分方程一般可以表示为：dy(t)/dt = K*u(t)其中，dy(t)/dt表示系统的输出变量的变化率，K表示系统的增益，u(t)表示系统的输入变量。
通过对上述微分方程进行拉普拉斯变换，可以得到对应的传递函数：Y(s)=K*U(s)/s在上式中，s表示复数变量，Y(s)和U(s)分别表示输出信号和输入信号的拉普拉斯变换。
通过传递函数，我们可以方便地分析系统的动态性能。
传递函数是控制系统设计中的重要工具，它具有以下几个特点：1.表征系统的动态性能：传递函数通过描述输入信号和输出信号之间的关系，反映了系统的动态响应特性。
通过分析传递函数的特性，可以预测系统的稳定性、阻尼性、超调量等重要性能指标。
2.方便进行频域分析：传递函数在频域中有简洁的表达形式，可以方便地进行频域分析。
通过对传递函数进行频率响应分析，可以确定系统的频率特性，为系统的设计和调整提供依据。
3.便于系统设计和优化：传递函数可以直观地表示系统的输入输出关系，便于系统设计和性能调整。
通过对传递函数进行变换和运算，可以方便地进行系统的设计和优化。
可以通过一些常见的传递函数来说明其作用。
以二阶系统为例，其一般传递函数形式为：G(s) = K/(s^2 + 2ξωns + ωn^2)其中，K为系统的增益，ξ为系统的阻尼比，ωn为系统的固有频率。
通过对传递函数的分析，可以得到系统的阶跃响应、频率响应和单位冲激响应等重要特性。
总之，传递函数在自动控制原理中是一种重要的数学工具，通过它可以方便地描述和分析系统的动态特性。
掌握传递函数的分析方法，对于控制系统的设计和优化具有重要的指导意义。
对于自动控制原理的学习和应用，传递函数的掌握是非常重要的一部分。
自动控制原理_2.4典型环节传递函数
B盘以角速度ω 转动时，因 B盘和I 轴
间以滑动键联接，故B盘滑动就会改变
偏心量e；当时e=0，A盘转动而 B盘不
转；e增大， B盘角速度ω 正比的增大， 设K为比例常数，B盘转角为θ (t)。 输入— e 输出—θ (t)
解： (t ) Ke(t )
(t ) K e(t )dt
di(t ) 1 ui (t ) L i(t ) R i(t )dt dt C 1 uo (t ) i(t )dt C
§2.4.6 延时环节（迟延环节）
xo (t ) xi (t )
τ为延迟时间
L[ x0 (t )] L[ xi (t )] G( s ) L[ xi (t )] L[ xi (t )]
当|Ts|<<1时，G(s)=Ts，
才近似为理想的微分环节。
此系统为包含有惯性环节及微分环节的系统。
（1）预见输入（ቤተ መጻሕፍቲ ባይዱ输入提前）
比例环节
R(s) r(t) t
1
1
X o ( s)
xo (t )
o
45
t
比例+微分
R(s) r(t ) t
1 Ts
X o ( s)
xo (t )
K G( s ) Ts 1
K为惯性环节的增益或放大系数；T为时间常数
理想的一阶惯性环节
1 G( s ) Ts 1
例1. 无源滤波电路
ui uo C为电容 R为电阻
1 ui (t ) i (t ) R i (t )dt C 解： 1 uo (t ) i (t )dt C 1 U i (t ) I ( s) R I (s) Cs LT得： 1 U o (t ) I ( s) Cs
自动控制原理课件：2_2传递函数
零状态响应 零输入响应
RC电路对阶跃输入的响应
Uc(0)
•传递函数
例2-1中建立了RC网络的微分方程
RC
duc dt
+ uc
=
ur
如果取零初始状态，有：
RCsU c (s) + Uc (s) = U r (s)
U c (s)
=
1 RCs
+
U 1
r
(s)
传递函数：零初始条件下，系统输出和输入的拉 氏变换之比。
二、传递函数的定义
设线性定常系统的微分方程为：
a0
dn dt n
c(t)
+
a1
d n−1 dt n−1
c(t)
+L+
an−1
d dt
c(t)
+
anc(t)
=
b0
dm dt m
r(t) +
b1
d m−1 dt m−1
r(t) + Lbm−1
d dt
r(t) +
bm r (t )
c(t)为被控量，r(t)为输入量
a0、a1Lan , b0、b1Lbm 为常系数，
由系统结构、参数决定。
设初始值为零，进行拉氏变换：
[a0sn + a1sn−1 +L+ an ]C(s) = [b0sm + b1sm−1 +L+ bm]R(s)
则系统传递函数：
G(s)
=
C(s) R(s)
=
b0 s m a0 s n
+ b1sm−1 + a1sn−1
传递函数经因式分解，可变成如下形
自动控制理论第二章传递函数_图文
解：前向通路4条 独立回路3个
§2.6 一般反馈控制系统
传递函数的各种术语 误差传函 扰动传函 一般控制作用
1. 一般控制系统
前向通道传函 闭环系统的开环传函 系统闭环传递函数 系统在给定作用下的输出
1、由系统输入到系统输出端的信号通路定义为系统 前向主通路(道)[简称主通路或前向通路]
②方框：表示输入、输出信号之间的传递 关系。
③引出点(测量点)：表示信 号引出或测量位置，从同一 点引出的信号完全相同。
④比较点(综合点)：表示两个或两个以上 的信号，在该点相加、减。注意，比较点 处信号的运算符号必须标明正(+)、负(-)， 一般不标者取正号。同时进行运算的信号 必须具有相同的量纲。
梅逊公式
回路总增益 (闭环传函)
第i条前向通 道余子式
第i个前向 通道增益
特征式
例：三级RC滤波网络如
图所示，求传递函数G(s)。
解： 前向通路1条 独立回路5个
两两不接触回路6个
三三不接触回路 特征式 余子式 传递函数
例：试求取图示系统的传递函数
解：前向通路3条
独立回路2个
例：系统结构图如图所示，试求其传递函数
积分器框图
特性：调节系统稳态误差，也称为无差 环节。
电压的传递函数
三、纯微分环节
定义：环节的输出响应正比于输入信号的变化率 。
微分方程 传递函数
测速发电机
四、惯性环节
定义：环节的输出不能立即复现输入，而是经过 一定时间后才能复现输入的变化。
微分方程
传递函数
运算放大器
五、振荡环节
定义：在输入作用下，环节输出响应随时间变化的 过渡过程总是在某一稳定值上下出现衰减振荡，而 最终趋于稳定值。
§2.6 一般反馈控制系统
传递函数的各种术语 误差传函 扰动传函 一般控制作用
1. 一般控制系统
前向通道传函 闭环系统的开环传函 系统闭环传递函数 系统在给定作用下的输出
1、由系统输入到系统输出端的信号通路定义为系统 前向主通路(道)[简称主通路或前向通路]
②方框：表示输入、输出信号之间的传递 关系。
③引出点(测量点)：表示信 号引出或测量位置，从同一 点引出的信号完全相同。
④比较点(综合点)：表示两个或两个以上 的信号，在该点相加、减。注意，比较点 处信号的运算符号必须标明正(+)、负(-)， 一般不标者取正号。同时进行运算的信号 必须具有相同的量纲。
梅逊公式
回路总增益 (闭环传函)
第i条前向通 道余子式
第i个前向 通道增益
特征式
例：三级RC滤波网络如
图所示，求传递函数G(s)。
解： 前向通路1条 独立回路5个
两两不接触回路6个
三三不接触回路 特征式 余子式 传递函数
例：试求取图示系统的传递函数
解：前向通路3条
独立回路2个
例：系统结构图如图所示，试求其传递函数
积分器框图
特性：调节系统稳态误差，也称为无差 环节。
电压的传递函数
三、纯微分环节
定义：环节的输出响应正比于输入信号的变化率 。
微分方程 传递函数
测速发电机
四、惯性环节
定义：环节的输出不能立即复现输入，而是经过 一定时间后才能复现输入的变化。
微分方程
传递函数
运算放大器
五、振荡环节
定义：在输入作用下，环节输出响应随时间变化的 过渡过程总是在某一稳定值上下出现衰减振荡，而 最终趋于稳定值。
自动控制原理典型环节传递函数
即： x（ o t） T 1x（ i t） dt
拉氏变 :X（ os换 ） T 1得 X s（ i s） G(s)
1 Ts
T为积分环节的时间常数
例题：
当 A盘作恒速转动，并靠摩擦力带动
B盘以角速度ω转动时，因 B盘和I 轴
间以滑动键联接，故B盘滑动就会改变 偏心量e；当时e=0，A盘转动而 B盘不 转；e增大， B盘角速度ω正比的增大， 设K为比例常数，B盘转角为θ(t)。 输入— e 输出—θ(t)
x (t ) p1 、p2分别为油缸左、右腔
单位面积上的压力。
o xi—活塞位移 x0—油缸位移
可以认为是一个微分环节 对于这两种机构求其传递函数均为 激磁电压ui恒定，磁通不变。 自动控制原理典型环节传递函数 间以滑动键联接，故B盘滑动就会改变 两者物理模型不同，但数学模型相同，
o
1Ts Xo (s)
1 (设c1) Ts1 k
§2.4.3 微分环节
微分环节具有输出正比于输入的微分
即 xo(t)T x i(t)
G(s)Xo(s)Xi(s)Ts
T为微分环节的时间常数
1、理想的微分环节 G(s) Ts
2、实际的微分环节
G(s) Ts Ts 1
3、微分环节对系统的控制作用
例1、 电压下图为一直流发电机原理
解：
di(t)
1
ui(t)L dt i(t)RCi(t)dt
1
uo(t) Ci(t)d t
LT，得 U Ui0(： (ss))Lc1ssI((sIs))I(s)Rc1sI(s)
G(s)Uo(s)
1
Ui(s) LC 2sRC 1s
n1
LC R C
2L
典型环节的传递函数
LCuo (t ) RCuo (t ) uo (t ) ui (t ) ( LCs 2 RCs 1)U o ( s ) U i ( s )
U o (s) 1 G (s) 2 U i ( s ) LCs RCs 1
2 n 1/( LC ) 2 2 2 s ( R / L) s 1/( LC ) s 2n s n
2
m
c
质量 - 阻尼 - 弹簧系统
其传递函数为 X o (s) k G ( s) 2 X i ( s) m s cs k k/m 2 s (c / m) s k / m
振荡环节传递函数的一般表达式
2 n G ( s) 2 2 s 2n s n
k c 其中,n ， m 2 mk
例7 图2-14所示的无源微分电路
C
i( t )
图 无源微分网络
1 U i (s) I(s) RI(s) 拉氏变换得 Cs u 0 (t) U 0 (s) RI(s) 其中， RCs 1 ui(t) ——输入电压 化简得 U i (s) R U 0 (s) u0(t) ——输出电压 RCs RC=T U ( s ) RCs R——电阻； G (s) 0 K=1 则 C——电容。 U i (s) RCs 1
例
如图所示弹簧-阻尼系统。
Xi(t)
kx i (t ) x 0 (t ) D
dx0 (t ) dt
Xo(t)
kX i (s) X o (s) DsXo (s)
D s 1X o (s) X i (s) k
X (s) 1 G (s) 0 X i (s) D s 1 k
典型环节的传递函数
P18 P28
2.4 典型环节的数学模型P22
思考题：
如何从该框图求得输出 与输入 之间的关系？
2.4 典型环节的数学模型P22
系统是由典型环节组成 常见的几种典型环节 比例、微分、积分、惯性、振荡、滞后 讨论内容
时域特征：微分方程，阶跃响应 复域（s域）特征：传递函数，零极点分布
实例：
测速发电机输出电压与输入角度间的传递函数即
为微分环节。P28 图2-4-9
[实例]
①
R1
理想微分环节
ui
①
C
+
uo
U o ( s) R1Cs Ts U i ( s)
R1
比例微分环节
ui
C R0
+
uo
Uo (s) R1 (1 R0Cs) K(Ts 1) Ui (s) R0
P28
3.阶跃响应及零极点分布
n2 C (s) 2 G(s) 2 R ( s ) s 2n s n
五、 振荡环节（Oscillating Element）
0
c(t)
P28
0 1 1
n
Im jn 1 2
0
单位阶跃响应曲线 [分析]：
p28图222244449999四微分环节derivativeelementp26实例tscsrsusuio????111001????????????tskrcsrrsusuior1iuour0cccc理想微分环节r1iuoucccc比例微分环节带有惯性的微分环节rtuituocrcsrcssusuio????1csrrrzrzszszsxsy112122121???????????111212112?????????????????ktstskcsrrrrcsrrsxsysgcrtrrrk1212??????式中
典型环节的传递函数
15
输出量与输入量对时间积分成正比，即 输出量随时间的增长而不断增长， 增长的斜率为1/T.
R1
Ur
K0
Uc
积分放大器原理
c(t) r(t)
t
4
实例：积分环节的特点是它的输出量为输入 量对时间的积累。如水箱的水位与水流量、 烘箱的温度与热流量、机械运动中的转速 与转矩、位移与速度、速度与加速度、电 容的电量与电流等。
R(s) Ts 1
R1
ur t i1(t)
C1
该环节存在储能元件，典型惯性环节的 微分方程为一阶常微分方程，其特点 是当系统输入有阶跃变化时，系统输 出是由零逐渐跟上，如图所示。(a)为 系统的输入变化，(b)为系统的输出 响应。输出按单调指数规律上升.
7
也就是说，当输入量发生突变时，输出量不能 突变，只能按指数规律逐渐变化，就反映了该环 节具有惯性。
微分环节常用来改善系统的稳态误差。
• 3.理想微分环节
微分方程： 传递函数：
y(t) dx(t)
dt
G(s) Y(s) s
X (s)
实用微分环节：
G(s)
Y (s) X (s)
Ts 1 Ts
动态响应：当x(t)=1(t),R(s)=1/s时， Y (s) G(s)X (s) s • 1
即输出量相对于输入量滞后一个恒定时间。
在延迟时间很小的情况下，延迟环节可 以用一个小惯性环节来代替。
实例：液压油从液压泵到阀控油缸的管道传 输产生的时间上的延迟；热量通过传导因 传输速率低而造成的时间上的延迟；各种 传送带因传送造成的时间上的延迟；晶闸 管整流电路，当控制电压改变时要等到下 一个周期开始后才能响应。
则
y(t) (t)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3.结构图： 结构图： 结构图 R(S)
1 T2S2+2ξTS +1
C(S)
七、二阶微分环节
d2r(t) dr(t) 2 + r(t) =c(t) 1.微分方程： 微分方程： 微分方程 τ + 2ξτ 2 dt dt
τ：环节的时间常数;ξ：阻尼比。
2.传递函数： 传递函数： 传递函数
G ( s ) = τ S + 2ξτS + 1
G(S)=K
R(S)
K
C(S)
二、积分环节
1.微分方程： c(t)=∫r(t)d(t) 微分方程： 微分方程 ∫ 2.特点： 特点： 特点 输出对输入信号上在时间上的积分。 输出对输入信号上在时间上的积分。 1
3.传递函数： 传递函数： 传递函数
G(S)=
R(S)
S
4.结构图： 结构图： 结构图
1 S
C(S)
三、微分环节
1.微分方程： 微分方程： 微分方程 2.特点： 特点： 特点 c(t) = dr(t) dt
输出对输入信号在时间上的微分， 输出对输入信号在时间上的微分， 即输出量与输入量的变化率成正比。 即输出量与输入量的变化率成正比。
3.传递函数： 传递函数： 传递函数
G(S)= S
R(S) C(S)
2 2
3.结构图： 结构图： 结构图
R(S)
τ S + 2ξτS + 1
2 2
C(S)
八、延迟环节
1.微分方程： c(t)=r(t-τ) 微分方程： 微分方程 τ 2.特点： 输出信号与输入信号的波形完全相同， 特点： 输出信号与输入信号的波形完全相同， 特点 但输出量相当于输入量滞后一段时间τ 但输出量相当于输入量滞后一段时间τ。 3.传递函数： 传递函数： 传递函数
4.结构图： 结构图： 结构图
S
四、惯性环节（一阶环节） 惯性环节（一阶环节）
1.微分方程： T dc(t) + c(t) =r(t) 微分方程： 微分方程 dt T:惯性环节的时间常数 2.特点： 特点： 特点 输出延迟地反应输入量的变化规律。 输出延迟地反应输入量的变化规律。
1 3.传递函数： G(S)= 传递函数： 传递函数 TS+1
1 G(S)= 4、惯性环节： 、惯性环节： TS+1 5、一阶微分环节： G(S)= τS+1 、一阶微分环节： ω2n 6、二阶振荡环节： G(S)= 2 、二阶振荡环节： S +2 ξωnS+ω2n ω 7、二阶微分环节： G ( s ) = τ 2 S 2 + 2ξτS + 1 、二阶微分环节： τ G(S)=e-τs 8、延迟环节： 、延迟环节：
τ G(S)=e-τs
4.结构图： 结构图： 结构图
R(S)
τ e-τs
C(S)
τ G(S)=e-τs
=
1
eτ s
1 = 1 2 2 1+τs+ τ s +… 2 τ很小 1 1+τs
1、比例环节： 、比例环节： 2、积分环节： 、积分环节： 3、纯微分环节： 、纯微分环节：
G(S)=K 1 G(S)= S G(S)=S
G(S)=K 1 G(S)= S G(S)=S
1 G(S)= 4、惯性环节： 、惯性环节： TS+1 5、一阶微分环节： G(S)= τS+1 、一阶微分环节： ω2n 6、二阶振荡环节： G(S)= 2 、二阶振荡环节： S +2 ξωnS+ω2n ω 7、二阶微分环节： G ( s ) = τ 2 S 2 + 2ξτS + 1 、二阶微分环节： τ G(S)=e-τs 8、延迟环节： 、延迟环节：
一、比例环节
K为常数； 为常数； 为常数 放大系数； 放大系数； 增益。 增益。
1.微分方程： c(t)=K· r(t） 微分方程： 微分方程 ） 2.特点： 特点： 特点 输出不失真，不延迟，成比例 输变化。
3.传递函数： 传递函数： 传递函数 4.结构图： 结构图： 结构图
§2-4 典型环节的传递函数
环节 环节的传递函数 环节 U1(S) UR(S) 1 I(S) R _ U2(S) 环节的传递函数 1 U2(S) CS
典型环节： 环节的传递函数不外乎是几 典型环节：
种简单的形式组成，这些典 型的单元，称作典型的环节。
1、比例环节： 、比例环节： 2、积分环节： 、积分环节： 3、纯微分环节： 、纯微分环节：
4.结构图： 结构图： 结构图 R(S)
1 TS+1
C(S)
五、一阶微分环节
dr(t) 1.微分方程： c(t)=τ dt + r(t) 微分方程： 微分方程 τ ：一阶微分环节的时间常数 2.特点： 特点： 特点 3.传递函数： 传递函数： 传递函数 输入延迟地反应输出量的变化规律。 输入延迟地反应输出量的变化规律。
G(S)= τS+1
R(S) C(S)
4.结构图： 结构图： 结构图
τS+1
六、二阶振荡环节（二阶环节） 二阶振荡环节（二阶环节）
d2c(t) dc(t) 1.微分方程： T2 微分方程： 微分方程 +2ξT + c(t) =r(t) 2 dt dt T：环节的时间常数;ξ：阻尼比。
1 2.传递函数： G(S)= 2 2 传递函数： 传递函数 T S +2ξTS +1
1 T2S2+2ξTS +1
C(S)
七、二阶微分环节
d2r(t) dr(t) 2 + r(t) =c(t) 1.微分方程： 微分方程： 微分方程 τ + 2ξτ 2 dt dt
τ：环节的时间常数;ξ：阻尼比。
2.传递函数： 传递函数： 传递函数
G ( s ) = τ S + 2ξτS + 1
G(S)=K
R(S)
K
C(S)
二、积分环节
1.微分方程： c(t)=∫r(t)d(t) 微分方程： 微分方程 ∫ 2.特点： 特点： 特点 输出对输入信号上在时间上的积分。 输出对输入信号上在时间上的积分。 1
3.传递函数： 传递函数： 传递函数
G(S)=
R(S)
S
4.结构图： 结构图： 结构图
1 S
C(S)
三、微分环节
1.微分方程： 微分方程： 微分方程 2.特点： 特点： 特点 c(t) = dr(t) dt
输出对输入信号在时间上的微分， 输出对输入信号在时间上的微分， 即输出量与输入量的变化率成正比。 即输出量与输入量的变化率成正比。
3.传递函数： 传递函数： 传递函数
G(S)= S
R(S) C(S)
2 2
3.结构图： 结构图： 结构图
R(S)
τ S + 2ξτS + 1
2 2
C(S)
八、延迟环节
1.微分方程： c(t)=r(t-τ) 微分方程： 微分方程 τ 2.特点： 输出信号与输入信号的波形完全相同， 特点： 输出信号与输入信号的波形完全相同， 特点 但输出量相当于输入量滞后一段时间τ 但输出量相当于输入量滞后一段时间τ。 3.传递函数： 传递函数： 传递函数
4.结构图： 结构图： 结构图
S
四、惯性环节（一阶环节） 惯性环节（一阶环节）
1.微分方程： T dc(t) + c(t) =r(t) 微分方程： 微分方程 dt T:惯性环节的时间常数 2.特点： 特点： 特点 输出延迟地反应输入量的变化规律。 输出延迟地反应输入量的变化规律。
1 3.传递函数： G(S)= 传递函数： 传递函数 TS+1
1 G(S)= 4、惯性环节： 、惯性环节： TS+1 5、一阶微分环节： G(S)= τS+1 、一阶微分环节： ω2n 6、二阶振荡环节： G(S)= 2 、二阶振荡环节： S +2 ξωnS+ω2n ω 7、二阶微分环节： G ( s ) = τ 2 S 2 + 2ξτS + 1 、二阶微分环节： τ G(S)=e-τs 8、延迟环节： 、延迟环节：
τ G(S)=e-τs
4.结构图： 结构图： 结构图
R(S)
τ e-τs
C(S)
τ G(S)=e-τs
=
1
eτ s
1 = 1 2 2 1+τs+ τ s +… 2 τ很小 1 1+τs
1、比例环节： 、比例环节： 2、积分环节： 、积分环节： 3、纯微分环节： 、纯微分环节：
G(S)=K 1 G(S)= S G(S)=S
G(S)=K 1 G(S)= S G(S)=S
1 G(S)= 4、惯性环节： 、惯性环节： TS+1 5、一阶微分环节： G(S)= τS+1 、一阶微分环节： ω2n 6、二阶振荡环节： G(S)= 2 、二阶振荡环节： S +2 ξωnS+ω2n ω 7、二阶微分环节： G ( s ) = τ 2 S 2 + 2ξτS + 1 、二阶微分环节： τ G(S)=e-τs 8、延迟环节： 、延迟环节：
一、比例环节
K为常数； 为常数； 为常数 放大系数； 放大系数； 增益。 增益。
1.微分方程： c(t)=K· r(t） 微分方程： 微分方程 ） 2.特点： 特点： 特点 输出不失真，不延迟，成比例 输变化。
3.传递函数： 传递函数： 传递函数 4.结构图： 结构图： 结构图
§2-4 典型环节的传递函数
环节 环节的传递函数 环节 U1(S) UR(S) 1 I(S) R _ U2(S) 环节的传递函数 1 U2(S) CS
典型环节： 环节的传递函数不外乎是几 典型环节：
种简单的形式组成，这些典 型的单元，称作典型的环节。
1、比例环节： 、比例环节： 2、积分环节： 、积分环节： 3、纯微分环节： 、纯微分环节：
4.结构图： 结构图： 结构图 R(S)
1 TS+1
C(S)
五、一阶微分环节
dr(t) 1.微分方程： c(t)=τ dt + r(t) 微分方程： 微分方程 τ ：一阶微分环节的时间常数 2.特点： 特点： 特点 3.传递函数： 传递函数： 传递函数 输入延迟地反应输出量的变化规律。 输入延迟地反应输出量的变化规律。
G(S)= τS+1
R(S) C(S)
4.结构图： 结构图： 结构图
τS+1
六、二阶振荡环节（二阶环节） 二阶振荡环节（二阶环节）
d2c(t) dc(t) 1.微分方程： T2 微分方程： 微分方程 +2ξT + c(t) =r(t) 2 dt dt T：环节的时间常数;ξ：阻尼比。
1 2.传递函数： G(S)= 2 2 传递函数： 传递函数 T S +2ξTS +1