线段的大小比较和画法
线段的大小比较完整版课件

线段的大小比较完整版课件一、教学内容本节课我们将探讨教材第三章“平面几何初步”中的第二节“线段的大小比较”。
具体内容包括:线段的定义、线段长度的度量方法、以及线段大小比较的方法。
二、教学目标1. 理解并掌握线段的概念及其性质。
2. 学会使用工具测量线段的长度,并能准确进行比较。
3. 能够运用线段大小比较的方法解决实际问题。
三、教学难点与重点教学难点:线段大小比较的方法在实际问题中的应用。
教学重点:线段的定义、测量及大小比较。
四、教具与学具准备教具:尺子、直尺、圆规、多媒体课件。
学具:尺子、直尺、练习本。
五、教学过程1. 实践情景引入通过展示一些日常生活中的实例,如操场的跑道、书本的尺寸等,引导学生理解线段的概念及其在生活中的应用。
2. 知识讲解(1)线段的定义:线段是由两个端点及这两个端点之间的所有点组成的图形。
(2)线段长度的测量:使用尺子、直尺等工具,按照一定的比例进行测量。
(3)线段大小比较:通过比较线段的长度,判断线段的大小。
3. 例题讲解例题1:比较下列线段的长度,指出较长的线段。
解答:通过直接测量或比较,得出结论。
例题2:在下列图形中,找出最长的线段。
解答:观察图形,比较各线段的长度,找出最长的线段。
4. 随堂练习发放练习题,让学生独立完成,巩固所学知识。
六、板书设计1. 线段的定义2. 线段长度的测量3. 线段大小比较4. 例题及解答5. 随堂练习七、作业设计1. 作业题目线段AB:________ 线段CD:________(2)找出下列图形中最长的线段:答案:________2. 答案(1)线段AB:________ 线段CD:________(2)最长的线段:________八、课后反思及拓展延伸1. 反思:本节课学生掌握了线段的概念、测量及大小比较,但在解决实际问题时,还需加强练习。
2. 拓展延伸:引导学生了解线段的性质,如线段的垂直平分线、线段的中点等,为后续学习打下基础。
线段的大小比较完整版课件

线段的大小比较完整版课件一、教学内容本节课我们将探讨教材第五章“平面几何中的基本元素”中第二节“线段的大小比较”。
具体内容包括:线段的定义、线段长度的度量方法、线段大小比较的方法,以及线段等分的概念。
二、教学目标1. 理解线段的定义,掌握线段长度的度量方法。
2. 学会线段大小比较的方法,并能应用于实际问题。
3. 了解线段等分的概念,能够运用等分线段的方法解决相关问题。
三、教学难点与重点教学难点:线段大小比较的方法,线段等分的实际应用。
教学重点:线段的定义,线段长度的度量方法,线段大小比较的方法。
四、教具与学具准备1. 教具:黑板、粉笔、尺子、圆规、直角三角板。
2. 学具:练习本、铅笔、直尺、圆规。
五、教学过程1. 导入:通过展示生活中常见的线段,如跳绳的长度、书桌的长度等,引导学生认识到线段在生活中的广泛应用。
2. 新课导入:(1)讲解线段的定义,强调线段是有限长的直线部分。
(2)介绍线段长度的度量方法,演示如何使用尺子测量线段长度。
(3)引导学生发现,当线段长度相等时,线段大小相同;当线段长度不等时,可以通过比较长度来判断线段的大小。
3. 实践操作:(1)让学生分组讨论,如何比较两条线段的大小。
4. 例题讲解:(1)给出两条线段,让学生比较大小。
(2)通过分析题目,引导学生运用所学知识解决问题。
5. 随堂练习:(1)让学生完成教材第5页的练习题1。
(2)教师挑选部分题目进行讲解,分析解题思路。
6. 知识拓展:(1)介绍线段等分的概念。
(2)演示如何使用尺子和圆规进行线段等分。
(1)回顾本节课所学内容,强调线段大小比较的方法。
(2)提醒学生注意线段等分在实际问题中的应用。
六、板书设计1. 板书线段的大小比较2. 主要内容:(1)线段的定义(2)线段长度的度量方法(3)线段大小比较的方法(4)线段等分的概念及方法七、作业设计1. 作业题目:(1)教材第5页的练习题2。
(2)自编题目:给出两条线段,让学生比较大小,并说明理由。
线段的大小比较和画法

度量法
A
C
B
(3.8㎝)
D (4.1㎝)
叠合法
A
B
(1)如果点B在线段CD上,
C
D
记作AB<CD
A
B
(2)如果点B在线段CD外,
C
D
记作AB>CD
A
B
(3)如果点B与点D重合,
记作AB=CD
C
D
测测眼力吧!
观察下列三组图形,你能看出每组图形 中线段a与b的长短吗
b
a
b
(1)
a
a (2) b
(3)
记做
AB < CD
AB = CD AB > CD
归纳总结:
度量法
数
线段比较的方法
叠合法 形
二、开门见山,引入新知
问题2:老师手里的纸上有一条线段,你 能在你的本上作出一条同样大小的线段来 吗?
a
想一想 画一条线段等于已知线段 问题一、已知线段a,画线段AB,使AB=a. 画 法:(1) 画射线AC ;
3.已知P是线段AB上一点,M,N分别是线段 AB,AP的中点,若AB=16,BP=6,求线段 MN的长度。(请自己画图)
思维测评
3、已知线段AB=12cm,点M是它的一个 三等分点, 则AM=___4_或__8_____cm.
• 直线l上有A、B、C三点,且AB=8cm, BC=5cm,求线段AC的长。
图得到a与b的和、a与b的差呢?
a
a
b
b a
A
B CP A
CB
P
AC=a+b
bCB=a-b源自想一想 问题二:已知线段a、b,画一条线段AB,
a
线段的大小的比较ppt课件
如图,已知线段a,画出线段AB ,使得AB=a.
a
解: 方法二: 1.画一条射线AC;
用直尺和圆
2.在射线AC上截取线段AB=a.
规
A
B
C
以点A为圆心,a
为半径画弧,交射
∴线段AB就是所要画的线段.
线AC于点B.
例题:先观察估计图中线段a,b的大小,然后用比较
线段大小的方法验证你的估计,并用“<”符号连结.
活动室
联结两点的线段的 长度叫做两点之间 的距离.
教学楼
两点之间,线段最短.
练习:下列叙述正确的是( D )
A.联结两点的直线叫做两点之间的距离. B.联结两点的线段叫做两点之间的距离. C.联结两点的直线的长度叫做两点之间的距离. D.联结两点的线段的长度叫做两点之间的距离.
线段是几何图形,两点 之间的距离是一个数量.
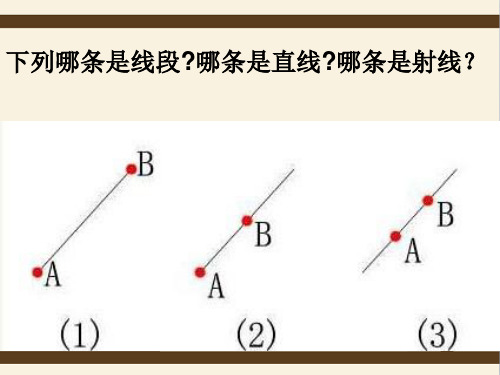
下列哪条是线段?哪条是直线?哪条是射线?
讨论:说一说直线、射线、线段之间的区别与联系.
名称
直线AB 射线AB 线段AB
图形 端点个数 延伸方向 能否度量
AB
AB
A
B
无 一个 两个
向两方无限 延伸
向一方无限 延伸
不向任何一 方延伸
不能 不能
能
线段和射线是直线的一部分.
线段的表示方式
(1)用表示端点的两个大写英文字母表示:
思考:如图为正方体和圆柱体实心木块,小老鼠从表面 爬过,走什么线路,吃到汉堡时爬过的路程最短?
A
自主小结:
1.线段的两种表示方法:
A 两个大写英文字母;
B 记作线段AB
一个小写英文字母.
a
记作线段a
2.线段大小的比较的一般方法:目测法;度量法;叠合法.
线段的大小比较完整版课件

线段的大小比较完整版课件一、教学内容本节课我们将探讨教材第五章“几何初步”中的第二节“线段的大小比较”。
详细内容包括线段的定义、线段长度的测量方法,以及如何直观和准确地比较两条线段的大小。
二、教学目标1. 理解线段的定义,掌握线段长度的测量方法。
2. 学会直观和准确地比较两条线段的大小,并运用到实际问题中。
3. 培养学生的观察能力、逻辑思维能力和实际操作能力。
三、教学难点与重点教学难点:线段大小的准确比较。
教学重点:线段的定义、长度测量方法,以及线段大小比较的方法。
四、教具与学具准备1. 教具:多媒体课件、直尺、三角板、圆规等。
2. 学具:直尺、三角板、练习本等。
五、教学过程1. 实践情景引入:展示一张地图,提出问题:“如何比较地图上两个城市之间的距离?”引导学生思考线段大小比较的实际意义。
2. 知识讲解:a. 线段的定义及性质。
b. 线段长度的测量方法。
c. 线段大小比较的方法。
3. 例题讲解:a. 通过实际操作,比较两条线段的大小。
b. 讲解如何利用工具(如直尺)进行线段长度的测量和比较。
4. 随堂练习:a. 让学生测量并比较教室内不同物品的长度。
b. 在练习本上完成线段大小比较的题目。
六、板书设计1. 线段的定义及性质2. 线段长度的测量方法3. 线段大小比较的方法a. 直观比较b. 工具测量比较七、作业设计1. 作业题目:AB = 5cm,CD = 8cm;EF = 12cm,GH = 15cm。
课本的长度、宽度;笔的长度;课桌的高度。
2. 答案:a. CD > AB,GH > EF。
b. 略。
八、课后反思及拓展延伸1. 反思:本节课学生对线段大小比较的方法掌握程度,以及在实际操作中的表现。
2. 拓展延伸:a. 探讨线段长度与距离的关系。
b. 研究线段大小比较在生活中的应用,如测量地图上的距离、比较物品长度等。
重点和难点解析1. 线段大小比较的方法。
2. 实际操作中测量线段长度的准确性。
比较两条线段的大小和画线段的和差

比较两条线段的大小和画线段的和差
比较两条线段的大小有两种方法:
(1)用移动的方法来比较两条线段的大小.
首先,对齐两条线段的一个端点(起点重合),然后让另一个端点沿相同的方向落下,再根据它们落下的位置来确定线段的大小.
(2)用度量的方法来比较两条线段的大小.
比较两条线段大小的实质是比较它们长度的大小,先用刻度尺量出两条线段的长度,再确定两条线段的大小,这种方法的实质是借助第三个量,来比较两条线段的大小.
画线段的和差也有两种方法:
(1)移动法:把两条线段放到一条直线上,使它们的一个端点重合,若每条线段都在另外一条线段的外部,那么另外两个端点间的线段就是这两条线段的和;若一条线段在另外一条线段内部,那么另外两个端点间的线段就是这两条线段的差.
(2)计算法:先量出已知线段的长度,再计算出它们的和或差,最后画一条线段,使它的长度为前面算得的长度.
画线段的中点、线段的几分之一,一般都采取度量计算的方法.
两点之间,线段最短.两点的距离是两点间线段的长度,它是度量出来的,而不是画出来的,它是一个量,而不是一个形.
例比较下列的高矮,填空并说明理由。
(1)(2)(3)(4)____________________
分析:根据第一种比较方法,将两个人视为两条线段,进行比较。
(3)用度量的方法来比较两条线段的大小。
(1)一高一矮;(2)一样高;(3)一人是120cm,另一人大于120cm;(4)无法比较。
线段的比较与画法

线段的比较与画法简介在几何学中,线段是由两个不同的点确定的一条有限直线。
线段是几何学中常见的基本对象,它在各个学科中都有广泛的应用。
本文将介绍线段的比较与画法,帮助读者更好地了解和运用线段的相关知识。
线段的比较线段的比较是指判断两条线段之间的大小关系。
常见的比较有以下几种情况:1.长度的比较:比较线段的长度,较长的线段在长度上大于较短的线段。
2.线段的位置关系:线段可以分为水平线段、垂直线段和斜线段。
水平线段和垂直线段长度相等时,可以通过比较两条线段的位置关系来判断大小关系。
例如,当两条水平线段的起点相同,端点不同时,端点较远的线段大于端点较近的线段;垂直线段也可以类似地进行比较。
3.斜线段的比较:对于斜线段,可以通过计算斜率来判断大小关系。
斜率是指线段的倾斜程度,可以通过计算线段的起点和终点坐标的差值来得到。
斜率相等时,还需要比较线段的长度。
通过以上几种比较方式,可以判断出不同线段之间的大小关系。
这些比较方法在实际问题中经常被用到,对于解决几何学和工程问题具有重要的意义。
线段的画法在计算机图形学中,我们经常需要绘制线段来表示物体的边界或路径。
下面介绍几种常用的线段画法:1. 数学方法数学方法是最常用的线段画法之一。
通过数学公式表示线段的起点和终点,然后计算线段上的各个点。
通过逐点绘制的方式,将线段画出来。
这种方法简单直观,适用于大多数情况。
2. Bresenham算法Bresenham算法是一种经典的线段绘制算法。
它通过特定的算法计算出线段上的离散点坐标,然后将这些点连接起来,形成线段。
Bresenham算法具有高效性和精确性的特点,被广泛应用于计算机图形学领域。
3. DDA算法DDA算法是另一种常用的线段绘制算法。
它通过计算线段的斜率,然后在直角坐标系上逐个计算出线段上的点。
DDA算法简单易懂,适用于绘制直线和斜线段。
除了以上几种算法之外,还有许多其他的线段绘制算法,如中点画线法、增量算法等。
人教版七年级数学上 直线、射线、线段之线段大小的比较教学ppt(18张)

答:线段AM,MB的长都为3cm。
(2) ∵点M是线段AB的中点
∴AB=2 AM=2 ×4=8 答:线段AB的长为8cm
(经典教学PPT)人教版七年级数学上 4.2 直线、射线、线段之线段大小的比较 教学课 件(18 张PPT)- 导学课 件(示 范)
(经典教学PPT)人教版七年级数学上 4.2 直线、射线、线段之线段大小的比较 教学课 件(18 张PPT)- 导学课 件(示 范)
(经典教学PPT)人教版七年级数学上 4.2 直线、射线、线段之线段大小的比较 教学课 件(18 张PPT)- 导学课 件(示 范)
练习 3、已知线段AB = 4cm,延长AB到C,使BC = 2AB,
若D为AB的中点,则线段DC 的长为__1_0_cm。
4cm
8cm
AD B
C
2cm 2cm + 8cm = 10cm
练习
如图,已知线段a,b。作一条线段,使它等于2a-b。 a
b
(经典教学PPT)人教版七年级数学上 4.2 直线、射线、线段之线段大小的比较 教学课 件(18 张PPT)- 导学课 件(示 范)
(经典教学PPT)人教版七年级数学上 4.2 直线、射线、线段之线段大小的比较 教学课 件(18 张PPT)- 导学课 件(示 范)
பைடு நூலகம்
线段的中点
点M把线段AB分成相等的两条 线段AM与MB,点M叫做线段AB 的中点。
A
MB
几何语言:∵点M是线段AB的中点
1
∴ AM=MB= AB
2
或AB=2 AM=2 MB
1
反之也成立 ∵
AM=MB= AB
2
或AB=2 AM=2 MB
∴点M是线段AB的中点
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A BC
D
l
a b a 所以线段AB=2a-b.
情景活动二
你能用这根绳子正好做一双鞋带吗?
二、概念延伸,思维提升
问题5:如图,已知线段a,求作线段AB=2a.
a
a
a
A
B
CP
AC=2a
点B把线段AC分成相等的两条线段AB与BC,点
B叫做线段AC的中点,可知AB=BC=
1 2
AB.
那么什么叫做三等分点?四等分点呢?
A
BC
(1) AB<AC
(2) AC-AB=BC AC-BC=AB BC+AB=AC
再来测测眼力吧!
在刚才的活动中我们知道了AB<CD,你知道 AB比CD少多少吗?你能用线段表示吗?
C A
BD
AB+BD=CD
CD-AB=BD
你知道如何画线段的和与差吗?
二、概念延伸,思维提升
问题4: 如图,已知线段a和线段b,怎样通过作
AMN
PB
AM MN NP PB 1 AB 4
A
M
B
点M把线段AB分成相等的两条线段AM与MB,我们
把M点叫做线段AB的中点 AM=BM= 1 AB;AB=2AM=2BM 2
AM N B M、N为线段AB的三等分点
AM=MN=NB= 1AB;AB=3AM=3MN=3NB 3
A NMP B
M、N、P为线段AB的四等分点
a
b
1.度量法 2.叠合法(叠合法要注意什么问题?)
度量法
A
C
B
(3.8㎝)
D (4.1㎝)
叠合法
A
B
(1)如果点B在线段CD上,
C
D
记作AB<CD
A
B
(2)如果点B在线段CD外,
C
D
记作AB>CD
A
B
(3)如果点B与点D重合,
记作AB=CD
C
D
测测眼力吧!
观察下列三组图形,你能看出每组图形 中线段a与b的长短吗
可知AC=BC=
1 2
AB
练习:如图,已知点C是线段AB的中点,点D是线 段AC的中点,完成下列填空:
(1)AB= _2_ BC ,BC= _2_ AD (2)BD= _3_ AD
A DC
B
例1如图
(1)如果点P是AB的中点,
则AP=
_
1
2_
AB
A
CPD B
(2)如果点C,1D三等分AB,则 AC=CD= D_ B_ = _3_ AB
图得到a与b的和、a与b的差呢?
a
a
b
b a
A
B CP A
CB
P
AC=a+b
b CB=a-b
想一想 问题二:已知线段a、b,画一条线段AB,
a
使AB=a+b.
b 画法:①先画一条直线l;
②在直线 l上依次截取 AC = a ,CB=b。
AC
所以AB=a+b.
B
l
a
b
想一想
问题三:已知线段a,b(b>a)画一条线段
b
a
b
(1)
a
a (2) b
(3)Байду номын сангаас
比较线段的长短
A
B
C(A) B
D
点A与点C重合,点B落在C、D之间,这时我们说线段AB小 于CD,记作AB<CD。(也可以先测量出线段的长度,再比较.)
想一想,什么情况下线段AB大于线段CD,线段AB等于线段CD?
图形
线段AB与CD的关系 记做
A
B
C
D
AB小于CD AB < CD
AN=MN=MP=PB=
1 4
AB;AB=4AN=4MN=4NP=4PB
情景活动二
B
观察下列步骤,并回答问题
(1)拿出一张白纸 (2)对折这张白纸
C
(3)把白纸展开铺平,发现在边AB上有 个折痕点C,请问AC和BC相等吗?
A
点C把线段AB分成相等的两条线段AC与
BC,点C叫做线段AB的中点(midpoint),
线段PM=___1_2_c_m__.AP=__5_2_c_m__.AN=_6_6_c_m___
A
B
C
D
AB 等于CD
AB = CD
A
B
AB 大于CD
AB > CD
C
D
归纳总结:
度量法
数
线段比较的方法
叠合法 形
二、开门见山,引入新知
问题2:老师手里的纸上有一条线段,你 能在你的本上作出一条同样大小的线段来 吗?
a
想一想 画一条线段等于已知线段 问题一、已知线段a,画线段AB,使AB=a. 画 法:(1) 画射线AC ;
义务第教育四教章科书图形数认学 识七初年步级 上册
4.2 直线、射线、线段 (第2课时)
你能再举出一些比较线段 长短的实例吗?
比较两个人的高矮
比较两根细木条(或绳子)的长短 你能从上面活动得到一些启发吗?
问题:怎样比较两条线段的长短呢?
一、概念延伸,思维提升
问题1:黑板上有两条线段,你能判断一 下它们的长短吗?你有什么方法来验证你 的判断?
(3)CP可以表示成哪两条线段的差?你有几种不 同的表示?
(4)现在告诉你CP=1.5cm,求线段AB的长。
试一试
• 1.已知线段AB=80cm,M为AB的中点,P 在MB上,N为PB的中点,且NB=14cm。
A
MP N B
线段PB=___2_8_c_m__.AM=___4_0_c_m_.BM=__4_0_c_m__
a
(2) 在射线AC上截取AB=a.
所以 AB=a.
A
B
C
注意:不要求写画法,但一定要标清
字母,写出有结论.
二、概念延伸,思维提升
练习1:判断线段AB和CD的大小.
A(C)
B D A(C) D B
图1
图2
A(C) B(D) 图3
(1)如图1,线段AB和CD的大小关系是AB < CD; (2)如图2,线段AB和CD的大小关系是AB > CD; (3)如图3,线段AB和CD的大小关系是AB = CD.
根据图形填空:
1、 AC= _ _ _ _ + _ _ _ _ A B
D
C
2、(如图)增加一个D点,则,AC= _ _ _ _+ _ _ _ _+ _ _ _
3、此时 AC= _ _ _ _+ _ _ _ _ 你还有别的表示方法吗?
二、概念延伸,思维提升
问题3: 如图,线段AB和AC的大小关系是怎样 的?线段AC与线段AB的差是哪条线段?你还能 从图中观察出其他线段间的和、差关系吗?
AC,使AC=b-a。
a
b
画法:①先用直尺画一条直线l;
②在直线l上截取AD = b;
在线段AD上截取DC=a。
所以AC=b-a。
AC
D
l
ba
试一试
已知线段a、b,画线段AB,使AB=2a-b.
解:(1)画一条直线l.
(2)在直线l上顺序截取
a
b
AC=a,CD=a.
(3)在线段AD上截取BD=b.
线段的中点
点M把线段AB分成相等的两条
线段AM与MB,点M叫做线段AB
的中点。
1
A
MB
AM=MB= AB
2
在一张透明的纸上画 一条线段,折叠纸片,使 线段的端点重合,折痕与 线段的交点就是线段的中 点。动手试一试!
类似地,还有线段的三等分点、四等分点等。
A
M NB
AM MN NB 1 AB 3
