2018年高考理科数学导数及应用100题(含答案解析)
2018年高考真题汇编(函数与导数)
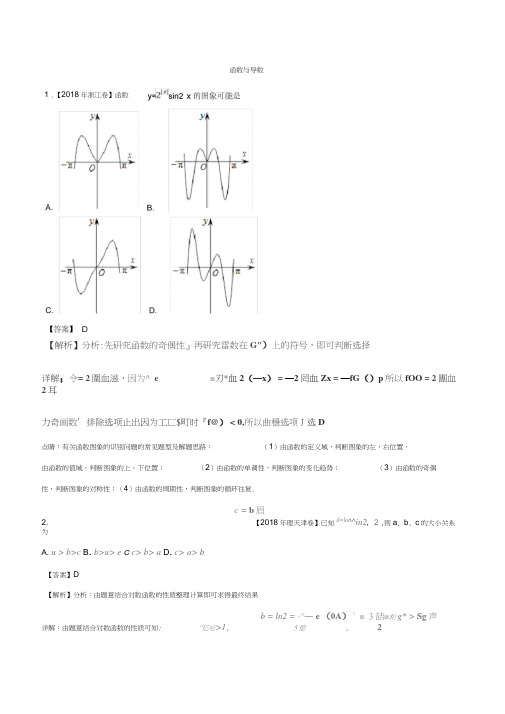
函数与导数1 .【2018年浙江卷】函数【解析】分析:先研究函数的奇偶性』再研究雷数在G")上的符号,即可判断选择详解;令= 2圍血滋,因为^ e =刃*血2(—x) = —2罔血Zx = —fG()p所以fOO = 2團血2耳力奇画数’排除选项止出因为工匸$町时『f@) < 0,所以曲穩选项J选D点睛:有关函数图象的识别问题的常见题型及解题思路:(1)由函数的定义域,判断图象的左、右位置,由函数的值域,判断图象的上、下位置;(2)由函数的单调性,判断图象的变化趋势;(3)由函数的奇偶性,判断图象的对称性;(4)由函数的周期性,判断图象的循环往复.c = b眉2. 【2018年理天津卷】已知il=lo^^in2, 2 ,则a, b, c的大小关系为A. u > b>cB.b>u> e C c> b> a D.c> a> b【答案】D【解析】分析:由题意结合对数函数的性质整理计算即可求得最终结果b = ln2 = -^―e (0A)c= 3詰=和g* > Sg声详解:由题意结合对数函数的性质可知: "忆吆>1, 5慾, 2据此可得:•本题选择D选项.点睛:对于指数幕的大小的比较,我们通常都是运用指数函数的单调性,但很多时候,因幕的底数或指数不相同,不能直接利用函数的单调性进行比较•这就必须掌握一些特殊方法•在进行指数幕的大小比较时,若底数不同,则首先考虑将其转化成同底数,然后再根据指数函数的单调性进行判断•对于不同底而同指数的指数幕的大小的比较,利用图象法求解,既快捷,又准确.龙兰0*3. 【2018年理新课标I卷】已知函数I曲乩北〉心饥巧二“/) + +a .若g (x)存在2个零点,则a的取值范围是A. [ - 1, 0)B. [0 , +R)C. [ - 1 , +R)D. [1 , +R)【答案】C【解析】分析;首先根据存在2个零点,得到方程f CO十""哨两个亀将其转化为金〉二-覽-口有两个解,即直线y =-第-诣曲^二fCO有两个交点”根据題中所给的函数解析式,画出函数f何的團像(将町4掉A再画出直绳=-补并将其上下移动』从图中可臥发现走丄时/龊7=-電-口与曲线y=f^>有两个玄点'从而求得结果.详解:画出函数的图像,7■-了在y轴右侧的去掉,再画出直线卜:讨,之后上下移动,可以发现当直线过点A时,直线与函数图像有两个交点,并且向下可以无限移动,都可以保证直线与函数的图像有两个交点,即方程■有两个解,也就是函数有两个零点,此时满足,即• ,故选C.点睛:该题考查的是有关已知函数零点个数求有关参数的取值范围问题,在求解的过程中,解题的思路是将函数零点个数问题转化为方程解的个数问题,将式子移项变形,转化为两条曲线交点的问题,画出函数的图像以及相应的直线,在直线移动的过程中,利用数形结合思想,求得相应的结果4. 【2018年理新课标I卷】设函数兀心--,若$叩为奇函数,则曲线:在点’ 处的切线方程为A.卜「阙B. H" - '■ - -IC."划D.【答案】D【解析】分析;利用奇函数偶此项系数为零求得"X进而得到的解析式,再对“)求导得出桩戋的斜率©进而求得切线方程.详解;因豹画数雇苛函数J 解得"二4所以』⑴二卯1,门>)二阪y 所臥厂◎二九代町二g所汰曲线y二厲刃在点(啦处的切线方程为y-m))二比建简可得y二知故选D点睛:该题考查的是有关曲线卜在某个点凤煮強;;|处的切线方程的问题,在求解的过程中,首先需要确定函数解析式,此时利用到结论多项式函数中,奇函数不存在偶次项,偶函数不存在奇次项,从而求得相应的参数值,之后利用求导公式求得帀,借助于导数的几何意义,结合直线方程的点斜式求得结果•5. 【2018年全国卷川理】设“=』0目仇2°収,方=衍的帖,贝UA. N + bunbcOB.C. u + bcOca/iD. kb<OCQ +市【答案】B1 i I 11【解析】分析:求出-= io^^ 2t-=lo^.32,得到- +二的范围,进而可得结果。
2018年高考理科数学全国卷二导数压轴题解析

2018年高考理科数学全国卷二导数压轴题解析已知函数2()x f x e ax =-.(1) 若1a =,证明:当0x ≥时,()1f x ≥. (2) 若()f x 在(0,)+∞只有一个零点,求a . 题目分析:本题主要通过函数的性质证明不等式以及判断函数零点的问题考察学生对于函数单调性以及零点存在定理性的应用,综合考察学生化归与分类讨论的数学思想,题目设置相对较易,利于选拔不同能力层次的学生。
第1小问,通过对函数以及其导函数的单调性以及值域判断即可求解。
官方标准答案中通过()()x g x e f x -=的变形化成2()x ax bx c e C -+++的形式,这种形式的函数求导之后仍为2()x ax bx c e -++这种形式的函数,指数函数的系数为代数函数,非常容易求解零点,并且这种变形并不影响函数零点的变化。
这种变形思想值得引起注意,对以后导数命题有着很大的指引作用。
但是,这种变形对大多数高考考生而言很难想到。
因此,以下求解针对函数()f x 本身以及其导函数的单调性和零点问题进行讨论,始终贯穿最基本的导函数正负号与原函数单调性的关系以及零点存在性定理这些高中阶段的知识点,力求完整的解答该类题目。
题目解答:(1)若1a =,2()x f x e x =-,()2x f x e x '=-,()2x f x e ''=-.当[0,ln 2)x ∈时,()0f x ''<,()f x '单调递减;当(ln 2,)x ∈+∞时,()0f x ''>,()f x '单调递增; 所以()(ln 2)22ln 20f x f ''≥=->,从而()f x 在[0,)+∞单调递增;所以()(0)1f x f ≥=,得证. (2)当0a ≤时,()0f x >恒成立,无零点,不合题意.当0a >时,()2x f x e ax '=-,()2x f x e a ''=-.当[0,ln 2)x a ∈时,()0f x ''<,()f x '单调递减;当(ln 2,)x a ∈+∞时,()0f x ''>,()f x '单调递增;所以()(ln 2)2(1ln 2)f x f a a a ''≥=-.当02ea <≤时,()0f x '≥,从而()f x 在[0,)+∞单调递增,()(0)1f x f ≥=,在(0,)+∞无零点,不合题意.当2ea >时,易证2ln 2a a >. (0)10f '=>,(ln 2)0f a '<,由(1)可知,22(2)=(2)10a f a e a '->>.由零点存在性定理可知必然存在一点1(0,ln 2)x a ∈使得1()0f x '=,2(ln 22)x a a ∈,使得2()0f x '=;所以当1(0,)x x ∈时,()0f x '>,()f x 单调递增,12(,)x x x ∈,()0f x '<,()f x 单调递减,2(,)x x ∈+∞,()0f x '>,()f x 单调递增,即当2x x =时()f x 取得极小值2222()x f x e ax =-由2()0f x '=得222x e a x = 从而222222()(2)2x x e f x e ax x =-=-当22x =时,即24e a =时,极小值2()0f x =恰好成立,此时在()f x 在(0,)+∞只有一个零点2x =,满足题意.当224e e a <<时,即212x <<时(易证2xe x在(1,)+∞单调递增),极小值2()0f x >,此时在(0,)+∞无零点,不合题意.x当24e a >时,即22x >时,(0)10f =>,2()0f x <, 32(3)(3)0a f a e a a =-> (易证313x e x >恒成立),由零点存在性定理可知()f x 在区间2(0,)x 和2(,3)x a 各有一根,不合题意.综上所述,24e a =.。
2018高考天津卷理科数学真题与答案解析

2021年普通高等学校招生全国统一考试〔天津卷〕数学〔理工类〕本试卷分为第一卷〔选择题〕和第二卷〔非选择题〕两局部,共150 分,考试用时 120 分钟。
第一卷 1 至 2 页,第二卷 3 至 5 页。
答卷前,考生务必将自己的姓名、准考证号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试完毕后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第I 卷考前须知:1.每题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共 8 小题,每题 5 分,共 40 分。
参考公式:如果事件 A,B互斥,那么P( AB) P( A) P(B) .如果事件 A,B 相互独立,那么P( AB)P( A) P(B) .棱柱的体积公式V Sh ,其中 S 表示棱柱的底面面积,h 表示棱柱的高 .1棱锥的体积公式 VSh,其中S表示棱锥的底面面积,h 表示棱3锥的高 .一.选择题:在每题给出的四个选项中,只有一项为哪一项符合题目要求word 版本整理分享的.(1) 设全集为 R,集合A { x 0x 2} , B{ x x1} ,那么A I (e R B)(A){ x 0x1}(B){ x 0x1}(C){ x 1x2}(D) { x 0x2}x y5,(2) 设变量x,y满足约束条件2x y4,那么目标函数z3x 5y 的最大x y1,y0,值为(A)6(B)19(C) 21(D)45(3)阅读如图的程序框图,运行相应的程序,假设输入 N的值为20,那么输出 T 的值为(A) 1(B) 2(C) 3(D) 4word 版本整理分享(4) 设x R ,那么“| x1 | 1〞是“x31〞的2 2(A)充分而不必要条件(B)必要而不充分条件(C)充要条件(D)既不充分也不必要条件(5) a log 2 e , b ln 2 , c log 11,那么 a,b,c 的大小关系为23(A) a b c(B) b a c(C) c b a(D) c a b(6) 将函数ysin(2x) 的图象向右平移个单位长度,所得图象对应510的函数word 版本整理分享(A) 在区间[3, 5] 上单调递增 (B) 在区间[3, ]上单调4 44递减(C) 在区间[5, 3] 上单调递增 (D) 在区间[3, 2]上单4 22调递减(7) 双曲线x 2y 21( a0, b0) 的离心率为2 ,过右焦点且垂直于a 2b 2x 轴的直线与双曲线交于A ,B 两点.设 A ,B 到双曲线同一条渐近线的距离分别为 d 1和 d 2,且 d 1 d 2 6 ,那么双曲线的方程为(A)x 2y 2 1 (B) x 2y 214 12124(C)x 2 y 2 1(D) x 2y 2 13 993(8) 如图,在平面四边形ABCD 中,ABBC ,AD CD , BAD120,AB AD 1 .uuur uur假设点 E 为边 CD 上的动点,那么AE BE 的最小值为(A)21 (B)3(C)25(D) 316216第二卷考前须知:1. 用黑色墨水的钢笔或签字笔将答案写在答题卡上。
2018全国高考试题分类汇编-导数部分(含解析)

2018年全国高考试题分类汇编-导数部分(含解析)1.(2018·全国卷I高考理科·T5)同(2018·全国卷I高考文科·T6)设函数f=x3+-x2+ax.若f为奇函数,则曲线y=f在点处的切线方程为()A.y=-2xB.y=-xC.y=2xD.y=x2.(2018·全国卷II高考理科·T13)曲线y=2ln(x+1)在点(0,0)处的切线方程为3.(2018·全国卷II高考文科·T13)曲线y=2ln x在点(1,0)处的切线方程为4.(2018·全国Ⅲ高考理科·T14)曲线y=e x在点处的切线的斜率为-2,则a=.5.(2018·天津高考文科·T10)已知函数f(x)=e x ln x,f′(x)为f(x)的导函数,则f′(1)的值为.6.(2018·全国卷I高考理科·T16)已知函数f=2sin x+sin2x,则f的最小值是.7.(12分)(2018·全国卷I高考文科·T21)已知函数f=a e x-ln x-1.(1)设x=2是f的极值点.求a,并求f的单调区间.(2)证明:当a≥时,f≥0.8.(2018·全国Ⅲ高考理科·T21)(12分)已知函数f=ln-2x.(1)若a=0,证明:当-1<x<0时,f<0;当x>0时,f>0.(2)若x=0是f的极大值点,求a.9.(2018·全国Ⅲ高考文科·T21)(12分)已知函数f=-.(1)求曲线y=f在点-处的切线方程.(2)证明:当a≥1时,f+e≥0.10.(本小题13分)(2018·北京高考理科·T18)设函数f(x)=[ax2-(4a+1)x+4a+3]e x.(1)若曲线y=f(x)在点(1,f(1))处的切线方程与x轴平行,求a.(2)若f(x)在x=2处取得极小值,求a的取值范围.11.(本小题13分)(2018·北京高考文科·T19)设函数f(x)=[ax2-(3a+1)x+3a+2]e x.(1)若曲线y=f(x)在点(2,f(2))处的切线斜率为0,求a.(2)若f(x)在x=1处取得极小值,求a的取值范围.12.(12分)(2018·全国卷I高考理科·T21)已知函数f=-x+a ln x.(1)讨论f的单调性.(2)若f存在两个极值点x1,x2,证明:-<a-2.-13.(2018·全国卷II高考理科·T21)(12分)已知函数f(x)=e x-ax2.(1)若a=1,证明:当x≥0时,f(x)≥1.(2)若f(x)在(0,+∞)只有一个零点,求a.14.(2018·全国卷II高考文科·T21)(12分)已知函数f=x3-a.(1)若a=3,求f(x)的单调区间.(2)证明:f(x)只有一个零点.15.(本小题满分14分)(2018·天津高考理科·T20)已知函数f(x)=a x,g(x)=log a x,其中a>1.(Ⅰ)求函数h(x)=f(x)-x ln a的单调区间.(Ⅱ)若曲线y=f(x)在点(x1,f(x1))处的切线与曲线y=g(x)在点(x2,g(x2))处的切线平行,证明x1+g(x2)=-.(Ⅲ)证明当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.16.(本小题满分14分)(2018·天津高考文科·T20)设函数f(x)=(x-t1)(x-t2)(x-t3),其中t1,t2,t3∈R,且t1,t2,t3是公差为d的等差数列.(Ⅰ)若t2=0,d=1,求曲线y=f(x)在点(0,f(0))处的切线方程;(Ⅱ)若d=3,求f(x)的极值;(Ⅲ)若曲线y=f(x)与直线y=-(x-t2)-6有三个互异的公共点,求d的取值范围.17.(本小题满分14分)(2018·江苏高考·T17)某农场有一块农田,如图所示,它的边界由圆O的一段圆弧MPN(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为△CDP,要求A,B均在线段MN上,C,D均在圆弧上.设OC与MN所成的角为θ.(1)用θ分别表示矩形ABCD和△CDP的面积,并确定sinθ的取值范围.(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为4∶3.求当θ为何值时,能使甲、乙两种蔬菜的年总产值最大.18.(本小题满分16分)(2018·江苏高考·T19)记f′(x),g′(x)分别为函数f(x),g(x)的导函数.若存在x0∈R,满足f(x0)=g(x0)且f′(x0)=g′(x0),则称x0为函数f(x)与g(x)的一个“S点”.(1)证明:函数f(x)=x与g(x)=x2+2x-2不存在“S点”.(2)若函数f(x)=ax2-1与g(x)=ln x存在“S点”,求实数a的值.(3)已知函数f(x)=-x2+a,g(x)=,对任意a>0,判断是否存在b>0,使函数f(x)与g(x)在区间(0,+∞)内存在“S点”,并说明理由.19.(2018·浙江高考T22)(本题满分15分)已知函数f(x)=-ln x.(Ⅰ)若f(x)在x=x1,x2(x1≠x2)处导数相等,证明:f(x1)+f(x2)>8-8ln2.(Ⅱ)若a≤3-4ln2,证明:对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.1.【解析】选D.因为f(x)为奇函数,所以f(-x)=-f(x),即a=1,所以f(x)=x3+x,所以f′(0)=1,所以切线方程为y=x.2.【解析】y′=,k==2,所以切线方程为y-0=2(x-0),即y=2x.答案:y=2x3.【解析】y′=,k==2,所以切线方程为y-0=2(x-1)即y=2x-2.答案:y=2x-24.【解析】由y=(ax+1)e x,所以y′=a e x+(ax+1)e x=(ax+1+a)e x,故曲线y=(ax+1)e x在(0,1)处的切线的斜率为k=a+1=-2,解得a=-3.答案:-35.【解析】因为f(x)=e x ln x,所以f′(x)=(e x ln x)′=(e x)′ln x+e x(ln x)′=e x·ln x+e x·,f′(1)=e1·ln1+e1·=e.答案:e6.【解析】方法一:f′(x)=2cos x+2cos2x=4cos2x+2cos x-2=4(cos x+1)-, 所以当cos x<时函数单调减,当cos x>时函数单调增,从而得到函数的减区间为--(k∈Z),函数的增区间为-(k∈Z),所以当x=2kπ-,k∈Z时,函数f(x)取得最小值,此时sin x=-,sin2x=-,所以f(x)min=2×--=-.方法二:因为f(x)=2sin x+sin2x,所以f(x)最小正周期为T=2π,所以f′(x)=2(cos x+cos2x)=2(2cos2x+cos x-1),令f′(x)=0,即2cos2x+cos x-1=0,所以cos x=或cos x=-1.所以当cos x=,为函数的极小值点,即x=或x=π,当cos x=-1,x=π,所以f=-,f=,f(0)=f(2π)=0,f(π)=0,所以f(x)的最小值为-.答案:-7.【解析】(1)f(x)的定义域为(0,+∞),f′(x)=a e x-.由题设知,f′(2)=0,所以a=.从而f(x)=e x-ln x-1,f′(x)=e x-.当0<x<2时,f′(x)<0;当x>2时,f′(x)>0.所以f(x)在(0,2)上单调递减,在(2,+∞)上单调递增.(2)当a≥时,f(x)≥-ln x-1.设g(x)=-ln x-1,则g′(x)=-.当0<x<1时,g′(x)<0;当x>1时,g′(x)>0.所以x=1是g(x)的最小值点.故当x>0时,g(x)≥g(1)=0.因此,当时a≥时,f(x)≥0.8.【解析】(1)当a=0时,f(x)=(2+x)ln(1+x)-2x,f′(x)=ln(1+x)-.设函数g(x)=f′(x)=ln(1+x)-,则g′(x)=.当-1<x<0时,g′(x)<0;当x>0时,g′(x)>0.故当x>-1时,g(x)≥g(0)=0,当且仅当x=0时,g(x)=0,从而f′(x)≥0,当且仅当x=0时,f′(x)=0.所以f(x)在(-1,+∞)上单调递增.又f(0)=0,故当-1<x<0时,f(x)<0;当x>0时,f(x)>0.(2)(i)若a≥0,由(1)知,当x>0时,f(x)≥(2+x)ln(1+x)-2x>0=f(0),这与x=0是f(x)的极大值点矛盾.(ii)若a<0,设函数h(x)==ln(1+x)-.由于当|x|<min时,2+x+ax2>0,故h(x)与f(x)符号相同.又h(0)=f(0)=0,故x=0是f(x)的极大值点,当且仅当x=0是h(x)的极大值点. h′(x)=--=.如果6a+1>0,则当0<x<-,且|x|<min时,h′(x)>0,故x=0不是h(x)的极大值点.如果6a+1<0,则a2x2+4ax+6a+1=0存在根x1<0,故当x∈(x1,0),且|x|<min时,h′(x)<0,所以x=0不是h(x)的极大值点..如果6a+1=0,则h′(x)=---则当x∈(-1,0)时,h′(x)>0;当x∈(0,1)时,h′(x)<0.所以x=0是h(x)的极大值点,从而x=0是f(x)的极大值点.综上,a=-.9.【解析】(1)f(x)的定义域为R,f′(x)=--,显然f(0)=-1,即点(0,-1)在曲线y=f(x)上,所求切线斜率为k=f′(0)=2,所以切线方程为y-(-1)=2(x-0),即2x-y-1=0.(2)方法一(一边为0):令g(x)=-ax2+(2a-1)x+2,当a≥1时,方程g(x)的判别式Δ=(2a+1)2>0,由g(x)=0得,x=-,2,且-<0<2,x,f′(x),f(x)的关系如下①若x∈(-∞,2],f(x)≥f-=-又因为a≥1,所以0<≤1,1<≤e,-≥-e,f(x)+e≥0,②若x∈(2,+∞),ax2+x-1>4a+2-1>0,e x>0,所以f(x)=->0,f(x)+e≥0,综上,当a≥1时,f(x)+e≥0.方法二(充要条件):①当a=1时,f(x)=-.显然e x>0,要证f(x)+e≥0只需证-≥-e, 即证h(x)=x2+x-1+e·e x≥0,h′(x)=2x+1+e·e x,观察发现h′(-1)=0,x,h′(x),h(x)的关系如下所以h(x)有最小值h(-1)=0,所以h(x)≥0即f(x)+e≥0.②当a>1时,由①知,-≥-e,又显然ax2≥x2,所以ax2+x-1≥x2+x-1,f(x)=-≥-≥-e,即f(x)+e≥0.综上,当a≥1时,f(x)+e≥0.方法三(分离参数):当x=0时,f(x)+e=-1+e≥0成立.当x≠0时,f(x)+e≥0等价于-≥-e,等价于ax2+x-1≥-e·e x,即ax2≥-e·e x-x+1等价于a≥--=k(x),等价于k(x)max≤1.k′(x)=--,令k′(x)=0得x=-1,2.x,k′(x),k(x)的关系如下又因为k(-1)=1,k(2)=-<0,所以k(x)max=1,k(x)≤1,x≠0,综上,当a≥1时,f(x)+e≥0.10.【解析】(1)因为f(x)=[ax2-(4a+1)x+4a+3]e x,所以f′(x)=[2ax-(4a+1)]e x+[ax2-(4a+1)x+4a+3]e x=[ax2-(2a+1)x+2]e x. f′(1)=(1-a)e.由题设知f′(1)=0,即(1-a)e=0,解得a=1.此时f(1)=3e≠0,所以a的值为1.(2)由(1)得f′(x)=[ax2-(2a+1)x+2]e x=(ax-1)(x-2)e x.若a>,则当x∈时,f′(x)<0;当x∈(2,+∞)时,f′(x)>0.所以f(x)在x=2处取得极小值.若a≤,则当x∈(0,2)时,x-2<0,ax-1≤x-1<0, 所以f′(x)>0.所以2不是f(x)的极小值点.综上可知,a的取值范围是(,+∞).11.【解析】(1)因为f(x)=[ax2-(3a+1)x+3a+2]e x, 所以f′(x)=[ax2-(a+1)x+1]e x,f′(2)=(2a-1)e2, 由题设知f′(2)=0,即(2a-1)e2=0,解得a=.(2)方法一:由(1)得f′(x)=[ax2-(a+1)x+1]e x=(ax-1)(x-1)e x若a>1,则当x∈时,f′(x)<0.当x∈(1,+∞)时,f′(x)>0.所以f(x)在x=1处取得极小值.若a≤1,则当x∈(0,1)时,ax-1≤x-1<0,所以f′(x)>0.所以1不是f(x)的极小值点.综上可知,a的取值范围是(1,+∞).方法二:f′(x)=(ax-1)(x-1)e x.①当a=0时,令f′(x)=0得x=1.f′(x),f(x)随x的变化情况如下表:所以f(x)在x=1处取得极大值,不合题意.②当a>0时,令f′(x)=0得x1=,x2=1.(ⅰ)当x1=x2,即a=1时,f′(x)=(x-1)2e x≥0,所以f(x)在R上单调递增,所以f(x)无极值,不合题意.(ⅱ)当x1>x2,即0<a<1时,f′(x),f(x)随x的变化情况如下表:所以f(x)在x=1处取得极大值,不合题意.(ⅲ)当x1<x2,即a>1时,f′(x),f(x)随x的变化情况如下表:所以f(x)在x=1处取得极小值,即a>1满足题意.③当a<0时,令f′(x)=0得x1=,x2=1.f′(x),f(x)随x的变化情况如下表:所以f(x)在x=1处取得极大值,不合题意.综上所述,a的取值范围为(1,+∞).12.【解析】(1)f(x)的定义域为(0,+∞),f′(x)=--1+=--.(i)若a≤2,则f′(x)≤0,当且仅当a=2,x=1时f′(x)=0,所以f(x)在(0,+∞)上单调递减.(ii)若a>2,令f′(x)=0得,x=--或x=-.当x∈--∪-时,f′(x)<0;当x∈---时,f′(x)>0.所以f(x)在--,-上单调递减,在---上单调递增.(2)由(1)知,f(x)存在两个极值点,当且仅当a>2.由于f(x)的两个极值点x1,x2满足x2-ax+1=0,所以x1x2=1,不妨设x1<x2,则x2>1.由于--=--1+a--=-2+a--=-2+a--,所以--<a-2等价于-x2+2ln x2<0.设函数g(x)=-x+2ln x,由(1)知,g(x)在(0,+∞)上单调递减,又g(1)=0,从而当x ∈(1,+∞)时,g(x)<0.所以-x2+2ln x2<0,即--<a-2.13.【解析】(1)当a=1时,f(x)≥1等价于(x2+1)e-x-1≤0.设函数g(x)=(x2+1)e-x-1,则g′(x)=-(x2-2x+1)e-x=-(x-1)2e-x.当x≠1时,g′(x)<0,所以g(x)在(0,1)∪(1,+∞)上单调递减.而g(0)=0,故当x≥0时,g(x)≤0,即f(x)≥1.(2)设函数h(x)=1-ax2e-x.f(x)在(0,+∞)上只有一个零点当且仅当h(x)在(0,+∞)上只有一个零点.(i)当a≤0时,h(x)>0,h(x)没有零点;(ii)当a>0时,h′(x)=ax(x-2)e-x.当x∈(0,2)时,h′(x)<0;当x∈(2,+∞)时,h′(x)>0.所以h(x)在(0,2)上单调递减,在(2,+∞)上单调递增.故h(2)=1-是h(x)在[0,+∞)上的最小值.①若h(2)>0,即a<,h(x)在(0,+∞)上没有零点;②若h(2)=0,即a=,h(x)在(0,+∞)上只有一个零点;③若h(2)<0,即a>,由于h(0)=1,所以h(x)在(0,2)上有一个零点,由(1)知,当x>0时,e x>x2,所以h(4a)=1-=1->1-=1->0.故h(x)在(2,4a)有一个零点,因此h(x)在(0,+∞)有两个零点.综上,f(x)在(0,+∞)只有一个零点时,a=.14.【解析】(1)当a=3时,f(x)=x3-3x2-3x-3,f′(x)=x2-6x-3.令f′(x)=0解得x=3-2或3+2.当x∈(-∞,3-2)或(3+2,+∞)时,f′(x)>0;当x∈(3-2,3+2)时,f′(x)<0.故f(x)在(-∞,3-2),(3+2,+∞)上单调递增,在(3-2,3+2)上单调递减.(2)由于x2+x+1>0,所以f(x)=0等价于-3a=0.设g(x)=-3a,则g′(x)=≥0,仅当x=0时g′(x)=0,所以g(x)在(-∞,+∞)上单调递增.故g(x)至多有一个零点.又f(3a-1)=-6a2+2a-=-6--<0,f(3a+1)=>0,故f(x)有一个零点.综上,f(x)只有一个零点.15.【解析】(I)由已知,h(x)=a x-x ln a,有h′(x)=a x ln a-ln a.令h′(x)=0,解得x=0.由a>1,可知当x变化时,h′(x),h(x)的变化情况如表:所以函数h(x)的单调递减区间为(-∞,0),单调递增区间为(0,+∞).(II)由f′(x)=a x ln a,可得曲线y=f(x)在点(x1,f(x1))处的切线斜率为ln a.由g′(x)=,可得曲线y=g(x)在点(x2,g(x2))处的切线斜率为.因为这两条切线平行,故有ln a=,即x2(ln a)2=1.两边取以a为底的对数,得log a x2+x1+2log a(ln a)=0,所以x1+g(x2)=-. (III)曲线y=f(x)在点(x1,)处的切线l1:y-=ln a·(x-x1).曲线y=g(x)在点(x2,log a x2)处的切线l2:y-log a x2=(x-x2).要证明当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线,只需证明当a≥时,存在x1∈(-∞,+∞),x2∈(0,+∞),使得l1和l2重合.即只需证明当a≥时,方程组有解,--由①得x2=,代入②,得-x1ln a+x1++=0③,因此,只需证明当a≥时,关于x1的方程③有实数解.设函数u(x)=a x-xa x ln a+x++,即要证明当a≥时,函数y=u(x)存在零点. u′(x)=1-(ln a)2xa x,可知x∈(-∞,0)时,u′(x)>0;x∈(0,+∞)时,u′(x)单调递减,又u′(0)=1>0,u′[]=1-<0,故存在唯一的x0,且x0>0,使得u′(x0)=0,即1-(ln a)2x0=0.由此可得u(x)在(-∞,x0)上单调递增,在(x0,+∞)上单调递减.u(x)在x=x0处取得极大值u(x0).因为a≥,故ln(ln a)≥-1,所以u(x0)=-x0ln a+x0++=+x0+≥≥0.下面证明存在实数t,使得u(t)<0.由(I)可得a x≥1+x ln a,当x>时,有u(x)≤(1+x ln a)(1-x ln a)+x++=-(ln a)2x2+x+1++,所以存在实数t,使得u(t)<0,因此,当a≥时,存在x1∈(-∞,+∞),使得u(x1)=0.所以,当a≥时,存在直线l,使l是曲线y=f(x)的切线,也是曲线y=g(x)的切线.16.【解析】(Ⅰ)由已知,可得f(x)=x(x-1)(x+1)=x3-x,故f′(x)=3x2-1,因此f(0)=0,f′(0)=-1,又因为曲线y=f(x)在点(0,f(0))处的切线方程为y-f(0)=f′(0)(x-0),故所求切线方程为x+y=0.(Ⅱ)由已知可得f(x)=(x-t2+3)(x-t2)(x-t2-3)=(x-t2)3-9(x-t2)=x3-3t2x2+(3-9)x-+9t2.故f′(x)=3x2-6t2x+3-9.令f′(x)=0,解得x=t2-,或x=t2+.当x变化时,f′(x),f(x)的变化情况如表:所以函数f(x)的极大值为f(t2-)=(-)3-9×(-)=6;函数极小值为f(t2+)=()3-9×=-6.(III)曲线y=f(x)与直线y=-(x-t2)-6有三个互异的公共点等价于关于x的方程(x-t2+d)(x-t2)(x-t2-d)+(x-t2)+6=0有三个互异的实数解,令u=x-t2,可得u3+(1-d2)u+6=0.设函数g(x)=x3+(1-d2)x+6,则曲线y=f(x)与直线y=-(x-t2)-6有三个互异的公共点等价于函数y=g(x)有三个零点.g′(x)=3x2+(1-d2).当d2≤1时,g′(x)≥0,这时g′(x)在R上单调递增,不合题意.当d2>1时,g′(x)=0,解得x1=--,x2=-.易得,g(x)在(-∞,x1)上单调递增,在[x1,x2]上单调递减,在(x2,+∞)上单调递增,g(x)的极大值g(x1)=g-=-+6>0,g(x)的极小值g(x2)=g-=--+6.若g(x2)≥0,由g(x)的单调性可知函数y=g(x)至多有两个零点,不合题意.若g(x2)<0,即(d2-1>27,也就是|d|>,此时|d|>x2,g(|d|)=|d|+6>0,且-2|d|<x1,g(-2|d|)=-6|d|3-2|d|+6<-62+6<0,从而由g(x)的单调性,可知函数y=g(x)在区间(-2|d|,x1),(x1,x2),(x2,|d|)内各有一个零点,符合题意.所以d的取值范围是(-∞,-)∪(,+∞)17.【解析】(1)设PO的延长线交MN于H,则PH⊥MN,所以OH=10.过O作OE⊥BC于E,则OE∥MN,所以∠COE=θ,故OE=40cosθ,EC=40sinθ,则矩形ABCD的面积为2×40cosθ(40sinθ+10)=800(4sinθcosθ+cosθ),△CDP的面积为×2×40cosθ(40-40sinθ)=1600(cosθ-sinθcosθ).过N作GN⊥MN,分别交圆弧和OE的延长线于G和K,则GK=KN=10.令∠GOK=θ0,则sinθ0=,θ0∈.当θ∈[θ0,)时,才能作出满足条件的矩形ABCD,所以sinθ的取值范围是.答:矩形ABCD的面积为800(4sinθcosθ+cosθ)平方米,△CDP的面积为1600(cosθ-sinθcosθ),sinθ的取值范围是.(2)因为甲、乙两种蔬菜的单位面积年产值之比为4∶3,设甲的单位面积的年产值为4k,乙的单位面积的年产值为3k(k>0),则年总产值为4k×800(4sinθcosθ+cosθ)+3k×1600(cosθ-sinθcosθ) =8000k(sinθcosθ+cosθ),θ∈.设f(θ)=sinθcosθ+cosθ,θ∈,则f′(θ)=cos2θ-sin2θ-sinθ=-(2sin2θ+sinθ-1)=-(2sinθ-1)(sinθ+1).令f′(θ)=0,得θ=,当θ∈时,f′(θ)>0,所以f(θ)为增函数;当θ∈时,f′(θ)<0,所以f(θ)为减函数,因此,当θ=时,f(θ)取到最大值.答:当θ=时,能使甲、乙两种蔬菜的年总产值最大.18.【解析】(1)函数f(x)=x,g(x)=x2+2x-2,则f′(x)=1,g′(x)=2x+2.由f(x)=g(x)且f′(x)=g′(x),得-此方程组无解,因此,f(x)与g(x)不存在“S”点.(2)函数f(x)=ax2-1,g(x)=ln x,则f′(x)=2ax,g′(x)=.设x0为f(x)与g(x)的“S”点,由f(x0)=g(x0)且f′(x0)=g′(x0),得-即-(*)得ln x0=-,即x0=-,则a=-=.当a=时,x0=-满足方程组(*),即x0为f(x)与g(x)的“S”点.因此,a的值为.(3)f′(x)=-2x,g′(x)=-,(x≠0),由f′(x0)=g′(x0),得b=-->0,得0<x0<1,由f(x0)=g(x0),得-+a==--,得a=--,令h(x)=x2---a=---,(a>0,0<x<1),设m(x)=-x3+3x2+ax-a,(a>0,0<x<1),则m(0)=-a<0,m(1)=2>0,得m(0)m(1)<0,又m(x)的图象在(0,1)上连续不断,则m(x)在(0,1)上有零点,则h(x)在(0,1)上有零点,则f(x)与g(x)在区间(0,+∞)内存在“S”点.19.【解析】(Ⅰ)函数f(x)的导函数f′(x,由f′(x1)=f′(x2)得-=-,因为x1≠x2,所以+=.由基本不等式得=+≥2.因为x1≠x2,所以x1x2>256.由题意得f(x1)+f(x2)=-ln x1+-ln x2=-ln(x1x2).设g(x)=-ln x,则g′(x)=(-4),所以所以g(x)在(256,+∞)上单调递增,故g(x1x2)>g(256)=8-8ln2,即f(x1)+f(x2)>8-8ln2.(Ⅱ)令m=e-(|a|+k),n=+1,则f(m)-km-a>|a|+k-k-a≥0,f(n)-kn-a<n-≤n<0,所以,存在x0∈(m,n)使f(x0)=kx0+a,所以,对于任意的a∈R及k∈(0,+∞),直线y=kx+a与曲线y=f(x)有公共点.由f(x)=kx+a得k=--.设h(x)=--,则h′(x)=--=--,其中g(x)=-ln x.由(Ⅰ)可知g(x)≥g(16),又a≤3-4ln2,故-g(x)-1+a≤-g(16)-1+a=-3+4ln2+a≤0,所以h′(x)≤0,即函数h(x)在(0,+∞)上单调递减,因此方程f(x)-kx-a=0至多1个实根.综上,当a≤3-4ln2时,对于任意k>0,直线y=kx+a与曲线y=f(x)有唯一公共点.。
【高三数学试题精选】2018年全国高考理科数学导数与积分试题汇编

(Ⅱ)当x 0, 0时,曲线=f (x)与曲线的共点个数即方程根的个数
由,
则h(x)在
h(x)
所以对曲线=f (x)与曲线共点的个数,讨论如下
当时,有0个共点;当= ,有1个共点;当有2个共点;
(Ⅲ)设
令
,且
所以
23.(2018年普通高等学校招生统一考试东数学(理)试题(含答案))设函数( =271828是自然对数的底数, )
(I)求L的方程;
(II)证明除切点(1,0)之外,曲线c在直线L的下方
【答案】解(I)设,则所以所以L的方程为
(II)令,则除切点之外,曲线c在直线的下方等价于满足,且
当时, , ,所以,故单调递减;
当时, , ,所以,故单调递增
所以, ( )
所以除切点之外,曲线c在直线L的下方
又解即变形为,记,则,
(3)若,则= = 0,
∴当≥-2时,≤不可能恒成立,
综上所述,的取值范围为[1, ]
21.(2018年高考湖北卷(理))设是正整数,为正有理数
(I)求函数的最小值;
(II)证明;
(III)设,记为不小于的最小整数,例如, ,令,求的值(参考数Fra bibliotek, , , )
【答案】证明(I)
在上单减,在上单增
(II)由(I)知当时, (就是伯努利不等式了)
当,即时,没有零点,
故关于的方程根的个数为0;
当,即时,只有一个零点,
故关于的方程根的个数为1;
当,即时,
①当时,由(Ⅰ)知
要使,只需使,即;
②当时,由(Ⅰ)知
;
要使,只需使,即;
2018届高考数学(理)热点题型:函数与导数(含答案解析)

函数与导数热点一 利用导数研究函数的性质利用导数研究函数的单调性、极值、最值是高考的热点问题之一,每年必考,一般考查两类题型:(1)讨论函数的单调性、极值、最值,(2)利用单调性、极值、最值求参数的取值范围.【例1】已知函数f (x )=ln x +a (1-x ).(1)讨论f (x )的单调性;(2)当f (x )有最大值,且最大值大于2a -2时,求实数a 的取值范围.解 (1)f (x )的定义域为(0,+∞),f ′(x )=1x -a .若a ≤0,则f′(x )>0,所以f (x )在(0,+∞)上单调递增.若a >0,则当x ∈⎝ ⎛⎭⎪⎫0,1a 时,f ′(x )>0; 当x ∈⎝ ⎛⎭⎪⎫1a ,+∞时,f ′(x )<0, 所以f (x )在⎝ ⎛⎭⎪⎫0,1a 上单调递增,在⎝ ⎛⎭⎪⎫1a ,+∞上单调递减. 综上,知当a ≤0时,f (x )在(0,+∞)上单调递增;当a >0时,f (x )在⎝ ⎛⎭⎪⎫0,1a 上单调递增,在⎝ ⎛⎭⎪⎫1a ,+∞上单调递减. (2)由(1)知,当a ≤0时,f (x )在(0,+∞)上无最大值;当a >0时,f (x )在x =1a 处取得最大值,最大值为f ⎝ ⎛⎭⎪⎫1a =ln 1a +a ⎝ ⎛⎭⎪⎫1-1a =-ln a +a -1.因此f ⎝ ⎛⎭⎪⎫1a >2a -2等价于ln a +a -1<0. 令g (a )=ln a +a -1,则g (a )在(0,+∞)上单调递增,g (1)=0.于是,当0<a <1时,g (a )<0;当a >1时,g (a )>0.因此,实数a 的取值范围是(0,1).【类题通法】(1)研究函数的性质通常转化为对函数单调性的讨论,讨论单调性要先求函数定义域,再讨论导数在定义域内的符号来判断函数的单调性.(2)由函数的性质求参数的取值范围,通常根据函数的性质得到参数的不等式,再解出参数的范围.若不等式是初等的一次、二次、指数或对数不等式,则可以直接解不等式得参数的取值范围;若不等式是一个不能直接解出的超越型不等式时,如求解ln a+a-1<0,则需要构造函数来解.【对点训练】已知a∈R,函数f(x)=(-x2+ax)e x(x∈R,e为自然对数的底数).(1)当a=2时,求函数f(x)的单调递增区间;(2)若函数f(x)在(-1,1)上单调递增,求实数a的取值范围.解(1)当a=2时,f(x)=(-x2+2x)e x,所以f′(x)=(-2x+2)e x+(-x2+2x)e x=(-x2+2)e x.令f′(x)>0,即(-x2+2)e x>0,因为e x>0,所以-x2+2>0,解得-2<x< 2.所以函数f(x)的单调递增区间是(-2,2).(2)因为函数f(x)在(-1,1)上单调递增,所以f′(x)≥0对x∈(-1,1)都成立,因为f′(x)=(-2x+a)e x+(-x2+ax)e x=[-x2+(a-2)x+a]e x,所以[-x2+(a-2)x+a]e x≥0对x∈(-1,1)都成立.因为e x>0,所以-x2+(a-2)x+a≥0对x∈(-1,1)都成立,即a≥x2+2xx+1=(x+1)2-1x+1=(x+1)-1x+1对x∈(-1,1)都成立.令y=(x+1)-1x+1,则y′=1+1(x+1)2>0.所以y=(x+1)-1x+1在(-1,1)上单调递增,所以y <(1+1)-11+1=32.即a ≥32. 因此实数a 的取值范围为a ≥32.热点二 利用导数研究函数零点或曲线交点问题函数的零点、方程的根、曲线的交点,这三个问题本质上同属一个问题,它们之间可相互转化,这类问题的考查通常有两类:(1)讨论函数零点或方程根的个数;(2)由函数零点或方程的根求参数的取值范围.【例2】设函数f(x)=ln x +m x ,m ∈R .(1)当m =e(e 为自然对数的底数)时,求f (x )的极小值;(2)讨论函数g (x )=f ′(x )-x 3零点的个数.解 (1)由题设,当m =e 时,f (x )=ln x +e x ,定义域为(0,+∞),则f ′(x )=x -e x 2,由f ′(x )=0,得x =e.∴当x ∈(0,e),f ′(x )<0,f (x )在(0,e)上单调递减,当x ∈(e ,+∞),f ′(x )>0,f (x )在(e ,+∞)上单调递增,∴当x =e 时,f (x )取得极小值f (e)=ln e +e e =2,∴f (x )的极小值为2.(2)由题设g (x )=f ′(x )-x 3=1x -m x 2-x 3(x >0),令g (x )=0,得m =-13x 3+x (x >0).设φ(x )=-13x 3+x (x >0),则φ′(x )=-x 2+1=-(x -1)(x +1),当x ∈(0,1)时,φ′(x )>0,φ(x )在(0,1)上单调递增;当x ∈(1,+∞)时,φ′(x )<0,φ(x )在(1,+∞)上单调递减.∴x =1是φ(x )的唯一极值点,且是极大值点,因此x =1也是φ(x )的最大值点.∴φ(x )的最大值为φ(1)=23.又φ(0)=0,结合y =φ(x )的图象(如图),可知①当m >23时,函数g (x )无零点;②当m =23时,函数g (x )有且只有一个零点;③当0<m <23时,函数g (x )有两个零点;④当m ≤0时,函数g (x )有且只有一个零点.综上所述,当m >23时,函数g (x )无零点;当m =23或m ≤0时,函数g (x )有且只有一个零点;当0<m <23时,函数g (x )有两个零点.【类题通法】利用导数研究函数的零点常用两种方法:(1)运用导数研究函数的单调性和极值,利用单调性和极值定位函数图象来解决零点问题;(2)将函数零点问题转化为方程根的问题,利用方程的同解变形转化为两个函数图象的交点问题,利用数形结合来解决.【对点训练】函数f (x )=(ax 2+x )e x ,其中e 是自然对数的底数,a ∈R .(1)当a >0时,解不等式f (x )≤0;(2)当a =0时,求整数t 的所有值,使方程f (x )=x +2在[t ,t +1]上有解. 解 (1)因为e x >0,(ax 2+x )e x ≤0.∴ax 2+x ≤0.又因为a >0,所以不等式化为x ⎝ ⎛⎭⎪⎫x +1a ≤0. 所以不等式f (x )≤0的解集为⎣⎢⎡⎦⎥⎤-1a ,0. (2)当a =0时,方程即为x e x =x +2,由于e x >0,所以x =0不是方程的解,所以原方程等价于e x -2x -1=0.令h (x )=e x -2x -1,因为h ′(x )=e x +2x 2>0对于x ∈(-∞,0)∪(0,+∞)恒成立,所以h (x )在(-∞,0)和(0,+∞)内是单调递增函数,又h (1)=e -3<0,h (2)=e 2-2>0,h (-3)=e -3-13<0,h (-2)=e -2>0,所以方程f (x )=x +2有且只有两个实数根且分别在区间[1,2]和[-3,-2]上,所以整数t 的所有值为{-3,1}.热点三 利用导数研究不等式问题导数在不等式中的应用是高考的热点,常以解答题的形式考查,以中高档题为主,突出转化思想、函数思想的考查,常见的命题角度:(1)证明简单的不等式;(2)由不等式恒成立求参数范围问题;(3)不等式恒成立、能成立问题.【例3】设函数f (x )=e 2x -a ln x .(1)讨论f (x )的导函数f ′(x )零点的个数;(2)证明:当a >0时,f (x )≥2a +a ln 2a .(1)解 f (x )的定义域为(0,+∞),f ′(x )=2e 2x -a x (x >0).当a ≤0时,f ′(x )>0,f ′(x )没有零点.当a >0时,设u (x )=e 2x ,v (x )=-a x,因为u (x )=e 2x 在(0,+∞)上单调递增,v (x )=-a x 在(0,+∞)上单调递增,所以f ′(x )在(0,+∞)上单调递增.又f ′(a )>0,当b 满足0<b <a 4且b <14时,f ′(b )<0(讨论a ≥1或a <1来检验),故当a >0时,f ′(x )存在唯一零点.(2)证明 由(1),可设f ′(x )在(0,+∞)上的唯一零点为x 0,当x ∈(0,x 0)时,f ′(x )<0;当x ∈(x 0,+∞)时,f ′(x )>0.故f (x )在(0,x 0)上单调递减,在(x 0,+∞)上单调递增,所以当x =x 0时,f (x )取得最小值,最小值为f (x 0)由于2e2x 0-a x 0=0, 所以f (x 0)=a 2x 0+2ax 0+a ln 2a ≥2a +a ln 2a . 故当a >0时,f (x )≥2a +a ln 2a .【类题通法】1.讨论零点个数的答题模板第一步:求函数的定义域;第二步:分类讨论函数的单调性、极值;第三步:根据零点存在性定理,结合函数图象确定各分类情况的零点个数.2.证明不等式的答题模板第一步:根据不等式合理构造函数;第二步:求函数的最值;第三步:根据最值证明不等式.【对点训练】 已知函数f (x )=ax +ln x (a ∈R ).(1)若a =2,求曲线y =f (x )在x =1处的切线方程;(2)求f (x )的单调区间;(3)设g (x )=x 2-2x +2,若对任意x 1∈(0,+∞),均存在x 2∈[0,1]使得f (x 1)<g (x 2),求a 的取值范围.解 (1)由已知得f ′(x )=2+1x (x >0),所以f ′(1)=2+1=3,所以斜率k =3.又切点为(1,2),所以切线方程为y -2=3(x -1),即3x -y -1=0,故曲线y =f (x )在x =1处的切线方程为3x -y -1=0.(2)f ′(x )=a +1x =ax +1x (x >0),①当a ≥0时,由于x >0,故ax +1>0,f ′(x )>0,所以f (x )的单调增区间为(0,+∞).②当a <0时,由f ′(x )=0,得x =-1a .在区间⎝ ⎛⎭⎪⎫0,-1a 上,f ′(x )>0,在区间⎝ ⎛⎭⎪⎫-1a ,+∞上,f ′(x )<0,所以函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0,-1a ,单调递减区间为⎝ ⎛⎭⎪⎫-1a ,+∞. (3)由已知得所求可转化为f (x )max <g (x )max ,g (x )=(x -1)2+1,x ∈[0,1],所以g (x )max =2,由(2)知,当a ≥0时,f (x )在(0,+∞)上单调递增,值域为R ,故不符合题意.当a <0时,f (x )在⎝ ⎛⎭⎪⎫0,-1a 上单调递增,在⎝ ⎛⎭⎪⎫-1a ,+∞上单调递减,故f (x )的极大值即为最大值,是f ⎝ ⎛⎭⎪⎫-1a =-1+ln ⎝ ⎛⎭⎪⎫-1a =-1-ln(-a ), 所以2>-1-ln(-a ),解得a <-1e 3.。
(完整版)2018年高考全国一卷理科数学答案及解析

2018年普通高等学招生全国统一考试(全国一卷)理科数学参考答案与解析一、选择题:本题有12小题,每小题5分,共60分。
1、设z=,则|z|=A 、0B 、C 、1D 、【答案】C【解析】由题可得i z =+=2i )i -(,所以|z|=1【考点定位】复数2、已知集合A={x|x 2-x-2>0},则A =A 、{x|-1<x<2}B 、{x|-1x 2}C 、{x|x<-1}∪{x|x>2}D 、{x|x -1}∪{x|x 2} 【答案】B【解析】由题可得C R A={x|x 2-x-2≤0},所以{x|-1x 2}【考点定位】集合3、某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:则下面结论中不正确的是:A 、新农村建设后,种植收入减少。
B 、新农村建设后,其他收入增加了一倍以上。
C 、新农村建设后,养殖收入增加了一倍。
D 、新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半。
【答案】A【解析】由题可得新农村建设后,种植收入37%*200%=74%>60%,【考点定位】简单统计4、记S n为等差数列{a n}的前n项和,若3S3=S2+S4,a1=2,则a5=A、-12B、-10C、10D、12【答案】B【解析】3*(a1+a1+d+a1+2d)=(a1+a1+d) (a1+a1+d+a1+2d+a1+3d),整理得:2d+3a1=0; d=-3 ∴a5=2+(5-1)*(-3)=-10【考点定位】等差数列求和5、设函数f(x)=x3+(a-1)x2+ax,若f(x)为奇函数,则曲线y=f(x)在点(0,0)处的切线方程为:A、y=-2xB、y=-xC、y=2xD、y=x【答案】D【解析】f(x)为奇函数,有f(x)+f(-x)=0整理得:f(x)+f(-x)=2*(a-1)x2=0 ∴a=1f(x)=x3+x求导f‘(x)=3x2+1f‘(0)=1 所以选D【考点定位】函数性质:奇偶性;函数的导数6、在ABC中,AD为BC边上的中线,E为AD的中点,则=A、--B、--C、-+D、-【答案】A【解析】AD 为BC 边∴上的中线 AD=AC 21AB 21+ E 为AD 的中点∴AE=AC 41AB 41AD 21+= EB=AB-AE=AC 41AB 43)AC 41AB 41(-AB -=+= 【考点定位】向量的加减法、线段的中点7、某圆柱的高为2,底面周长为16,其三视图如右图,圆柱表面上的点M 在正视图上的对应点为11A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为 A 、B 、C 、3D 、2 【答案】B【解析】将圆柱体的侧面从A 点展开:注意到B 点在41圆周处。
高考数学厦门卷导数的应用历年真题解析

高考数学厦门卷导数的应用历年真题解析一、2018年厦门卷真题解析本文将为您解析2018年厦门卷高考数学导数的应用部分。
在这一部分中,考生需要理解并运用导数的概念和性质来解题。
题目一:设函数f(x)=x^3-3x^2-x+3,已知曲线y=f(x)的切线方程为y=2x+b,求常数b的值。
解析:首先,我们知道曲线y=f(x)的切线方程为y=2x+b,由此可得该切线的斜率为2。
而切线的斜率等于函数在切点处的导数值,所以我们需要求函数f(x)在切点处的导数值。
求导数的过程如下:f'(x) = 3x^2 - 6x - 1由题目中给出的切线方程,可以知道切线与曲线相交的点为(x0,f(x0)),其中斜率为2:2 = f'(x0)代入求得导数的表达式,得到:2 = 3x0^2 - 6x0 - 1化简得:3x0^2 - 6x0 - 3 = 0再进一步化简:x0^2 - 2x0 - 1 = 0通过解这个二次方程可以得到x0的值。
解得:x0 = 1 ± √2因此,在(x0, f(x0))处的切线为:y = 2x + b代入得:f(x0) = 2x0 + b带入x0的值,可以求出b的值。
题目二:已知函数y=f(x)的导数f'(x)=ax^2+2ax-3a,且y=f(x)在点(1, 3)处与直线L相切,求直线L的方程。
解析:题目中给出了函数y=f(x)的导数表达式f'(x)=ax^2+2ax-3a,我们需要根据该导数表达式和已知的切点求直线L的方程。
首先,我们知道函数y=f(x)在点(1, 3)处与直线L相切,那么直线L的斜率就等于函数f(x)在点(1, 3)处的导数值。
因此,直线L的斜率为:k = f'(1) = a + 2a - 3a = a进一步,我们已知直线L与点(1, 3)相切,可以得到直线L的方程为:y - 3 = k(x - 1)将斜率k代入,得到:y - 3 = ax - a化简后可以得到直线L的方程:y - ax = 2a - 3以上就是2018年厦门卷高考数学导数的应用部分的解析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年高考理科数学导数及应用模拟题100题(含答案解析)1.设函数f (x )在R 上存在导函数f′(x ),对任意的实数x 都有f (x )=2x 2﹣f (﹣x ),当x ∈(﹣∞,0)时,f′(x )+1<2x .若f (m+2)≤f (﹣m )+4m+4,则实数m 的取值范围是( )A .[﹣,+∞)B .[﹣,+∞)C .[﹣1,+∞)D .[﹣2,+∞)2.已知函数f (x )=ln (e x+e ﹣x)+x 2,则使得f (2x )>f (x+3)成立的x 的取值范围是( )A .(﹣1,3)B .(﹣∞,﹣3)∪(3,+∞)C .(﹣3,3)D .(﹣∞,﹣1)∪(3,+∞) 3.若2nx x ⎛⎫- ⎪⎝⎭的展开式中第2项与第4项的二项式系数相等,则直线y nx =与曲线2y x =围成的封闭区域的面积为( ). A .223B .12C .323D .364.下列函数中,既是奇函数又存在极值的是( ). A .3y x =B .ln()y x =-C .yD .2y x x=+5.已知函数f (x )满足:f (x )+2f′(x )>0,那么下列不等式成立的是( )A .B .C .D .f (0)>e 2f(4) 6.已知函数f (x )=x 2+2ax ,g (x )=3a 2lnx+b ,设两曲线y=f (x ),y=g (x )有公共点,且在该点处的切线相同,则a ∈(0,+∞)时,实数b 的最大值是( )A .B .C .D .7.由曲线y=x 2与直线y=x+2所围成的平面图形的面积为( )A .B .4C .2D . 8.已知f (x )为定义域为R 的函数,f'(x )是f (x )的导函数,且f (1)=e ,∀x ∈R 都有f'(x )>f (x ),则不等式f (x )<e x的解集为( )A .(﹣∞,1)B .(﹣∞,0)C .(0,+∞)D .(1,+∞)9.若函数f (x )=lnx+x 2﹣ax+a+1为(0,+∞)上的增函数,则实数a 的取值范围是( )A . (﹣∞,22]B .(﹣∞,2]C .[1,+∞)D .[2,+∞)10.直线x=1,x=e 与曲线y=x1,y=x 围成的面积是( ) A .31(2e 23﹣5) B . 31(2e 23﹣1)C .31(2e 23﹣2)D .2e 23﹣5 11.若f (x )=x 3﹣ax 2+1在(1,3)内单调递减,则实数a 的范围是( )A .[,+∞)B .(﹣∞,3]C .(3,)D .(0,3) 12.由曲线y=2,直线y=x ﹣3及x 轴所围成的图形的面积为( )A .12B .14C .16D .18 13.已知函数f (x )=e x﹣ln (x+a )(a ∈R )有唯一的零点x 0,则( )A .﹣1<x 0<﹣B .﹣<x 0<﹣C .﹣<x 0<0D .0<x 0<14.已知函数f (x )=x ﹣1﹣lnx ,对定义域内任意x 都有f (x )≥kx ﹣2,则实数k 的取值范围是( )A .(﹣∞,1﹣]B .(﹣∞,﹣]C .[﹣,+∞)D .[1﹣,+∞)15.已知函数f (x )的导函数图象如图所示,若△ABC 为锐角三角形,则一定成立的是( )A .f (cosA )<f (cosB ) B .f (sinA )<f (cosB )C .f (sinA )>f (sinB )D .f (sinA )>f (cosB )16.已知等差数列{a n }的前n 项和为S n ,且S 10=,则a 5+a 6=( )A .B .12C .6D .17.已知f (x )=cosx ,则f (π)+f′()=( )A .B .C .﹣D .﹣18.若函数f (x )=x 3﹣3x+a 有3个不同的零点,则实数a 的取值范围是( ) A .(﹣2,2) B .[﹣2,2] C .(﹣∞,﹣1) D .(1,+∞)19. 设函数,则( )A .为 f (x )的极大值点B .为f (x )的极小值点C .x=2 为 f (x )的极大值点D .x=2为f (x )的极小值点 20.已知曲线 f (x )=ax 2﹣2在横坐标为1的点 p 处切线的倾斜角为,则a=( )A .B .1C .2D .﹣1 21. .若,则的展开式中常数项为( )A .8B .16C .24D .60 22.函数y=x 2在P (1,1)处的切线与双曲线22a x ﹣22by =1(a >0,b >0)的一条渐近线平行,则双曲线的离心率是( )A .5B .5C .25 D .323.已知定义在R 上的可导函数f (x )的导函数为f′(x ),满足f′(x )<f (x ),且f (x+2)为偶函数,f (4)=1,则不等式f (x )<e x的解集为( ) A .(﹣2,+∞) B .(0,+∞) C .(1,+∞) D .(4,+∞)24.如图所示,正弦曲线y=sinx ,余弦曲线y=cosx 与两直线x=0,x=π所围成的阴影部分的面积为( )A .1B .C .2D .225.函数的最小值为 .26..如图中的曲线为2()2f x x x =-,则阴影部分面积为__________.27.如图中阴影部分的面积等于____________.28.若函数()sin f x x a x =+在R 上递增,则实数a 的取值范围为__________. 29.定积分3112d x x x ⎛⎫-= ⎪⎝⎭⎰__________.30.函数2y x x =-的图像与x 轴所围成的封闭图形的面积等于__________. 31.定义在R 上的函数f (x )满足2f (4﹣x )=f (x )+x 2﹣2,则曲线y=f (x )在点(2,f(2))处的切线方程是 . 32. 已知n=⎰6e 1dx x 1,那么n )x5x (-的展开式中含x 23的项的系数为 . 33.已知函数f (x )满足xf′(x )=(x ﹣1)f (x ),且f (1)=1,若A 为△ABC 的最大内角,则f[tan(A﹣)]的取值范围为.34.点P(x0,y0)是曲线y=3lnx+x+k(k∈R)图象上一个定点,过点P的切线方程为4x﹣y﹣1=0,则实数k的值为.35.D做人处事应从善如流,体现了我们必须坚持正确的价值观,正确处理个人与社会的关系,通过劳动和奉献实现人生价值,②④正确;价值判断和价值选择具有社会历史性,在不同的社会历史条件下,价值判断和选择会不同,因此一个时代的正确的价值判断和价值选择有时并不适用于另一个时代,①普遍适应的说法是错误的,排除①;自觉站在人民的立场上才是最高价值标准,③排除。
故本题答案选D。
【考点定位】人生价值的实现36.函数f(x)=e x(x+sinx+1)在x=0处的切线方程为.37.若曲线y=lnx的一条切线是直线y=x+b,则实数b的值为.38.曲线y=x2与所围成的图形的面积是.39.∫0a(3x2﹣x+1)dx= .40.D【考点】16:蛋白质的合成——氨基酸脱水缩合.菁优网版权所有【分析】1、构成蛋白质的基本单位是氨基酸,每种氨基酸分子至少都含有一个氨基和一个羧基,且都有一个氨基和一个羧基连接在同一个碳原子上,这个碳原子还连接一个氢和一个R基,氨基酸的不同在于R基的不同.2、氨基酸通过脱水缩合形成多肽链,而脱水缩合是指一个氨基酸分子的羧基和另一个氨基酸分子的氨基相连接,同时脱出一分子水的过程;氨基酸形成多肽过程中的相关计算:肽键数=脱去水分子数=氨基酸数一肽链数,游离氨基或羧基数=肽链数+R基中含有的氨基或羧基数,至少含有的游离氨基或羧基数=肽链数.3、分析题图中的3种氨基酸:分析题图中的3种氨基酸的结构简式可知,每种氨基酸只含一个N原子,因此分子式为C22H34O13N6的肽链中含有6个氨基酸;3种氨基酸中每分子甘氨酸和丙氨酸均含2个氧原子,每分子谷氨酸中含有含有4个氧原子.【解答】解:A、由以上分析知,分子式为C22H34O13N6的肽链中含有6个氨基酸,合成1个该多肽链时产生的水分子数=氨基酸数﹣肽链数=6﹣1=5个,A 正确;B 、脱去的水分子数等于形成的肽键数,因此在细胞中合成1个C 22H 34O 13N 6分子要形成5个肽键,B 正确;C 、题图中三种氨基酸分子中只有谷氨酸含有2个羧基,假设谷氨酸的数目为X ,则多肽链中的氧原子数=4X+2(6﹣X )﹣5=13,解得X=3个,C 正确;D 、题图中的3种氨基酸的R 基中均不含氨基,只有谷氨酸的R 基中含有羧基(每分子谷氨酸中含有1个),则1个C 22H 34O 13N 6分子中存在游离的氨基数=肽链数+R 基中含有的氨基数=1+0=1个、存在游离的羧基数=肽链数+R 基中含有的羧基数=1+3=4个,D 错误. 故选:D . 41.函数,数列{a n }的通项公式a n =|f (n )|,若数列从第k 项起每一项随着n 项数的增大而增大,则k 的最小值为 . 42.设函数,若,则x 0的取值范围为 .43.已知函数f (x )=e﹣|x|+cosπx ,给出下列命题:①f (x )的最大值为2;②f (x )在(﹣10,10)内的零点之和为0; ③f (x )的任何一个极大值都大于1. 其中,所有正确命题的序号是 . 44. 曲线,直线x=1,x=e 和x 轴所围成的区域的面积是 .45.已知函数f (x )=(x 2+ax+b )e x ,当b <1时,函数f (x )在(﹣∞,﹣2),(1,+∞)上均为增函数,则2a 2b -+的取值范围是 . 46. 若⎰e1x 2dx=a ,则(x+xa)6展开式中的常数项为 . 47.若函数f (x )=x 2+(a+3)x+lnx 在区间(1,2)上存在唯一的极值点,则实数a 的取值范围为 .48.已知函数f (x )=alnx++1,曲线y=f (x )在点(1,2)处切线平行于x 轴. (Ⅰ)求f (x )的单调区间;(Ⅱ)当x >1时,不等式(x ﹣1)f (x )>(x ﹣k )lnx 恒成立,求实数k 的取值范围. 49.已知函数.(1)求y=f (x )的最大值; (2)当时,函数y=g (x ),(x ∈(0,e])有最小值. 记g (x )的最小值为h (a ),求函 数h (a )的值域. 50.函数()1ln1xf x kx x+=-- . (Ⅰ)讨论()f x 的单调性; (Ⅱ)当()0,1x ∈时,若24e e 1kx kx xx --<- ,求实数k 的取值范围. 51.已知函数21()(1)(1)ln 2f x x a x a x =-+++-,a ∈R .(Ⅰ)当3a =时,求曲线:()C y f x =在点(1,(1))f 处的切线方程.(Ⅱ)当[1,2]x ∈时,若曲线:()C y f x =上的点(,)x y 都在不等式组12,,3,2x x y y x ⎧⎪⎪⎨⎪⎪+⎩≤≤≤≤所表示的平面区域内,试求a 的取值范围. 52.设函数2()ln ()f x x ax x a =+-∈R . (1)若1a =,求函数()f x 的单调区间.(2)若函数()f x 在区间(0,1]上是减函数,求实数a 的取值范围. (3)过坐标原点O 作曲线()y f x =的切线,证明:切点的横坐标为1. 53.设函数21()51623f x x x =++,L 为曲线:()C y f x =在点11,12⎛⎫- ⎪⎝⎭处的切线.(Ⅰ)求L 的方程.(Ⅱ)当15x <-时,证明:除切点11,12⎛⎫- ⎪⎝⎭之外,曲线C 在直线L 的下方.(Ⅲ)设1x ,2x ,3x ∈R ,且满足1233x x x ++=-,求123()()()f x f x f x ++的最大值. 54.已知函数2()(2)ln f x x a x a x =-++(a 为实常数). (Ⅰ)若1x =为()f x 的极值点,求实数a 的取值范围. (Ⅱ)讨论函数()f x 在[1,e]上的单调性.(Ⅲ)若存在[1,e]x ∈,使得()0f x ≤成立,求实数a 的取值范围. 55.设函数1()ln ()f x x a x a x=--∈R . Ⅰ讨论函数()f x 的单调性.Ⅱ若()f x 有两个极值点1x 和2x ,记过点11(,())A x f x ,22(,())B x f x 的直线斜率为k .问:是否存在a ,使得2k a =-?若存在,求出a 的值;若不存在,请说明理由. 56.已知a ∈R ,函数()ln 1af x x x=-+. (Ⅰ)当1a =时,求曲线()y f x =在点(2,(2))f 处的切线方程. (Ⅱ)求()f x 在区间(0,e]上的最小值. 57.函数()e x f x x =⋅. (1)求()f x 的极值.(2)21()2k f x x x ⨯≥+在[1,)-∞+上恒成立,求k 值的集合.58.已知函数2()(2)ln f x x a x a x =-++(a 为实数). (Ⅰ)若2a =-,求函数()y f x =在1x =处的切线方程. (Ⅱ)求函数()f x 的单调区间.(Ⅲ)若存在[1,e]x ∈,使得()0f x ≤成立,求实数a 的取值范围. 59.已知2()xf x e ax =-,()g x 是()f x 的导函数. (Ⅰ)求()g x 的极值;(Ⅱ)若()1f x x ≥+在0x ≥时恒成立,求实数a 的取值范围.60.已知函数21()4f x x =+,1()ln(2e )2g x x =.(Ⅰ)求函数()()y f x g x =-的最小值.(Ⅱ)是否存在一次函数()h x ,使得对于(0,)x ∀∈+∞,总有()()f x h x ≥,且()()h x g x ≥成立?若存在,求出()h x 的表达式;若不存在,说明理由. 61.已知函数()ln(1)ln(1)f x x x =+--.(I )求曲线()y f x =在点(0,())f x 处的切线方程. (II )求证:当(0,1)x ∈时,3()23x f x x ⎛⎫>+ ⎪⎝⎭.(III )设实数k 使得3()3x f x k x ⎛⎫>+ ⎪⎝⎭对(0,1)x ∈恒成立,求k 的最大值.62.已知函数e ()xf x x=.(1)若曲线()y f x =与直线y kx =相切于点P ,求点P 的坐标. (2)令()()(ln )g x f x a x x =--,当0a ≤时,求()g x 的单调区间. (3)当e a ≤,证明:当(0,)x ∈+∞,()0g x ≥. 63.已知函数2()ln f x x a x =+的极值点为2. (1)求实数a 的值. (2)求函数()f x 的极值.(3)求函数()f x 在区间1,e e ⎡⎤⎢⎥⎣⎦上的最值.64.已知函数()()e x f x x a =+,其中e 是自然数的底数,a ∈R . (Ⅰ)求实数()f x 的单调区间.(Ⅱ)当1a <时,试确定函数2()()g x f x a x =--的零点个数,并说明理由. 65.已知曲线:e ax C y =.(Ⅰ)若曲线C 在点(0,1)处的切线为2y x m =+,求实数a 和m 的值.(Ⅱ)对任意实数a ,曲线C 总在直线:l y ax b =+的上方,求实数b 的取值范围. 66.已知函数f(x)=x2+alnx﹣x(a≠0),g(x)=x2.(Ⅰ)求函数f(x)的单调区间;(Ⅱ)若对于任意的a∈(1,+∞),总存在x1,x2∈[1,a],使得f(x1)﹣f(x2)>g (x1)﹣g(x2)+m成立,求实数m的取值范围.67.已知函数f(x)=x2+bx﹣alnx.(1)当a>0时,函数f(x)是否存在极值?判断并证明你的结论;(2)若x=2是函数f(x)的极值点,1和x0是函数f(x)的两个不同零点,且x0∈(n,n+1),求自然数n的值;(3)若对任意b∈[﹣2,﹣1],都存在x∈(1,e),使得f(x)<0成立,求实数a的取值范围.68.已知函数g(x)=(2﹣a)lnx,h(x)=lnx+ax2(a∈R),令f(x)=g(x)+h′(x),其中h′(x)是函数h(x)的导函数.(Ⅰ)当a=0时,求f(x)的极值;(Ⅱ)当﹣8<a<﹣2时,若存在x1,x2∈[1,3],使得|f(x1)﹣f(x2)|>(m+ln3)a﹣2ln3+ln(﹣a)恒成立,求m的取值范围.69.已知函数f(x)=x2﹣1,函数g(x)=2tlnx,其中t≤1.(Ⅰ)如果函数f(x)与g(x)在x=1处的切线均为l,求切线l的方程及t的值;(Ⅱ)如果曲线y=f(x)与y=g(x)有且仅有一个公共点,求t的取值范围.70.已知函数在点(﹣1,f(﹣1))的切线方程为x+y+3=0.(Ⅰ)求函数f(x)的解析式;(Ⅱ)设g(x)=lnx,求证:g(x)≥f(x)在x∈[1,+∞)上恒成立;(Ⅲ)已知0<a<b,求证:.71.已知函数f(x)=x3﹣9x,函数g(x)=3x2+a.(Ⅰ)已知直线l是曲线y=f(x)在点(0,f(0))处的切线,且l与曲线y=g(x)相切,求a的值;(Ⅱ)若方程f(x)=g(x)有三个不同实数解,求实数a的取值范围.72.已知函数f (x )=alnx+21x 2﹣2ax+1(a ∈R). (1)讨论f (x )的单调性;(2)当f (x )有两个极值点x 1,x 2,且2121x x )x (f )x (f ++<m 恒成立时,求m 的取值范围. 73.已知函数f(x)=1x x 2++1,g (x )=x 2e ax (a <0). (Ⅰ)求函数f (x )的单调区间;(Ⅱ)若对任意x 1,x 2∈[0,2],f (x 1)≥g (x 2)恒成立,求a 的取值范围.74.已知函数f (x )=3x ﹣2mx 2﹣3ln (x+1),其中m ∈R(1)若x=1是f (x )的极值点,求m 的值;(2)若0<m <,求f (x )的单调区间;(3)若f (x )在[0,+∞)上的最小值是0,求m 的取值范围.75.已知函数f (x )=m (x ﹣1)e x +x 2(m ∈R ).(1)若m=﹣1,求函数f (x )的单调区间;(2)若对任意的x <0,不等式x 2+(m+2)x >f′(x )恒成立,求m 的取值范围;(3)当m ≤﹣1时,求函数f (x )在[m ,1]上的最小值.76.已知m 为实数,函数f (x )=x 3+x 2﹣3x ﹣mx+2,g (x )=f′(x ),f′(x )是f (x )的导函数.(1)当m=1时,求f (x )的单调区间;(2)若g (x )在区间[﹣1,1]上有零点,求m 的取值范围.77.已知函数f (x )=ln (x ﹣1)﹣k (x ﹣1)+1(k ∈R ).(I )求函数f (x )的单调区间;(II )若f (x )≤0恒成立,试确定实数k 的取值范围;(III )证明:. 78.某连锁分店销售某种商品,每件商品的成本为4元,并且每件商品需向总店交a (1≤a ≤3)元的管理费,预计当每件商品的售价为x (7≤x ≤9)元时,一年的销售量为(10﹣x )2万件.(Ⅰ)求该连锁分店一年的利润L(万元)与每件商品的售价x的函数关系式L(x);(Ⅱ)当每件商品的售价为多少元时,该连锁分店一年的利润L最大,并求出L的最大值.79.已知函数f(x)=为偶函数(1)求实数a的值;(2)记集合E={y|y=f(x),x∈{﹣1,1,2}},λ=lg22+lg2lg5+lg5﹣,判断λ与E 的关系;(3)当x∈[,](m>0,n>0)时,若函数f(x)的值域[2﹣3m,2﹣3n],求实数m,n值.80.已知函数f(x)=x2+lnx.(1)求函数f(x)在[1,e]上的最大值和最小值;(2)求证:当x∈(1,+∞)时,函数f(x)的图象在g(x)=x3+x2的下方.81.已知函数f(x)=﹣4x+m在区间(﹣∞,+∞)上有极大值.(1)求实常数m的值.(2)求函数f(x)在区间(﹣∞,+∞)上的极小值.82.已知函数.(1)当a=0时,求f(x)在点(1,f(1))处的切线方程;(2)是否存在实数a,当0<x≤2时,函数f(x)图象上的点都在所表示的平面区域(含边界)?若存在,求出a的值组成的集合;否则说明理由;(3)若f(x)有两个不同的极值点m,n(m>n),求过两点M(m,f(m)),N(n,f (n))的直线的斜率的取值范围.83.已知f(x)=x3+3ax2+bx+a2(a>1)在x=﹣1时有极值0.(1)求常数 a,b的值;(2)方程f(x)=c在区间[﹣4,0]上有三个不同的实根时,求实数c的范围.84.(14分)已知函数f (x )=lnx ﹣xa ﹣1. (1)若曲线y=f (x )存在斜率为﹣1的切线,求实数a 的取值范围;(2)求f (x )的单调区间;(3)设函数g (x )=xln a x +,求证:当﹣1<a <0时,g (x )在(1,+∞)上存在极小值. 85.(16分)已知f (x )=x 2+mx+1(m ∈R ),g (x )=e x . (1)当x ∈[0,2]时,F (x )=f (x )﹣g (x )为增函数,求实数m 的取值范围;(2)若m ∈(﹣1,0),设函数 G(x)=)x (g )x (f ,H(x)= ﹣41x+45,求证:对任意x 1,x 2∈[1,1﹣m],G (x 1)<H (x 2)恒成立.86.下列关于遗传学基本概念的叙述,正确的是A. 测交后代出现两种性状的现象属于性状分离B. 纯合子自交后代表现出的性状为显性性状C. 相同环境下,基因不同的个体表现型可能相同D. 果蝇的长翅短翅,红眼和复眼都是相对性状87.(14分)如图,已知A ,B 两镇分别位于东西湖岸MN 的A 处和湖中小岛的B 处,点C 在A 的正西方向1km 处,tan ∠BAN=43,∠BCN=4π,现计划铺设一条电缆联通A ,B 两镇,有两种铺设方案:①沿线段AB 在水下铺设;②在湖岸MN 上选一点P ,先沿线段AP 在地下铺设,再沿线段PB 在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km 、4万元∕km .(1)求A ,B 两镇间的距离;(2)应该如何铺设,使总铺设费用最低?88.已知函数f (x )=x 3+ax 2+bx+c ,曲线y=f (x )在点x=﹣1处的切线为l :5x+y ﹣5=0,若时,y=f (x )有极值.(1)求a ,b ,c 的值;(2)求y=f (x )在[﹣3,2]上的最大值和最小值.89. 已知函数. (1)求f (x )的单调区间;(2)当x >0时,,求a 的取值范围.90.已知函数()x f x e =,()()g x ln x a b =++. (Ⅰ)若函数f(x)与g(x)的图像在点 (0,1)处有相同的切线,求a ,b 的值;(Ⅱ)当b=0时,f(x) -g(x)>0恒成立,求整数a 的最大值;(Ⅲ)证明:23ln 2(ln 3ln 2)(ln 4ln 3)+-+-n e [ln(n 1)ln n]e 1+++-<-. 91.(12分)已知函数f (x )=ax (lnx ﹣1)(a≠0).(1)求函数y=f (x )的单调递增区间;(2)当a >0时,设函数g (x )=61x 3﹣f (x ),函数h (x )=g′(x ), ①若h (x )≥0恒成立,求实数a 的取值范围;②证明:ln (1×2×3×…×n )2e <12+22+32+…+n 2(n ∈N*).92.设函数f (x )=mlnx (m ∈R ),g (x )=cosx .(1)若函数h(x)=f(x)+x1在(1,+∞)上单调递增,求m 的取值范围; (2)设函数φ(x )=f (x )+g (x ),若对任意的x ∈(π,23π),都有φ(x )≥0,求m 的取值范围;(3)设m >0,点P (x 0,y 0)是函数f (x )与g (x )的一个交点,且函数f (x )与g (x )在点P 处的切线互相垂直,求证:存在唯一的x 0满足题意,且x 0∈(1,2π). 93.(14分)已知函数f (x )=e x ﹣ax (a 为常数)的图象与y 轴交于点A ,曲线y=f (x )在点A 处的切线斜率为﹣1.(Ⅰ)求a 的值及函数f (x )的极值(Ⅱ)证明:当x >0时,x 2<e x .(Ⅲ)证明:对任意给定的正数c ,总存在x 0,使得当x ∈(x 0,+∞),恒有x 2<ce x .94.(14分)已知函数f(x)= ﹣31x 3+2ax 2﹣3a 2x (a ∈R 且a≠0). (1)当a=﹣1时,求曲线y=f (x )在(﹣2,f (﹣2))处的切线方程;(2)当a >0时,求函数y=f (x )的单调区间和极值;(3)当x ∈[2a ,2a+2]时,不等式|f'(x )|≤3a 恒成立,求a 的取值范围.95.(14分)已知函数f (x )=x 2﹣x ,g (x )=lnx .(Ⅰ)求函数y=xg (x )的单调区间;(Ⅱ)若t ∈[21,1],求y=f[xg (x )+t]在x ∈[1,e]上的最小值(结果用t 表示); (Ⅲ)设h (x )=f (x )﹣21x 2﹣(2a+1)x+(2a+1)g (x ),若a ∈[e ,3],∀x 1,x 2∈[1,2](x 1≠x 2),|2121x x )x (h )x (h --|≤21x x m ⋅恒成立,求实数m 的取值范围. 96.设函数.(1)求f (x )的单调区间及最大值;(2)讨论关于x 的方程|lnx|=f (x )根的个数.97.(12分)已知f (x )=e x ﹣ax 2,曲线y=f (x )在(1,f (1))处的切线方程为y=bx+1.(1)求a ,b 的值;(2)求f (x )在[0,1]上的最大值;(3)证明:当x >0时,e x +(1﹣e )x ﹣xlnx ﹣1≥0.98.已知函数f (x )=(x+1)lnx ,g (x )=a (x ﹣1)(a ∈R ).(Ⅰ)求f (x )的单调区间;(Ⅱ)若f (x )≥g (x )对任意的x ∈[1,+∞)恒成立,求实数a 的取值范围;(Ⅲ)求证:ln2•ln3…lnn>(n ≥2,n ∈N +).99.已知函数,g(x)=b(x+1),其中a≠0,b≠0(1)若a=b,讨论F(x)=f(x)﹣g(x)的单调区间;(2)已知函数f(x)的曲线与函数g(x)的曲线有两个交点,设两个交点的横坐标分别为x1,x2,证明:.100.已知函数f(x)=﹣+(a﹣1)x+lnx.(Ⅰ)若a>﹣1,求函数f(x)的单调区间;(Ⅱ)若a>1,求证:(2a﹣1)f(x)<3e a﹣3.答案1.C【考点】利用导数研究函数的单调性.【分析】利用构造法设g(x)=f(x)﹣x2,推出g(x)为奇函数,判断g(x)的单调性,然后推出不等式得到结果.【解答】解:∵f(x)=2x2﹣f(﹣x),∴f(x)﹣x2+f(﹣x)﹣x2=0,设g(x)=f(x)﹣x2,则g(x)+g(﹣x)=0,∴函数g(x)为奇函数.∵x∈(﹣∞,0)时,f′(x)+1<2x,g′(x)=f′(x)﹣2x<﹣1,故函数g(x)在(﹣∞,0)上是减函数,故函数g(x)在(0,+∞)上也是减函数,若f(m+2)≤f(﹣m)+4m+4,则f(m+2)﹣(m+2)2≤f(﹣m)﹣m2,即g(m+2)<g(﹣m),∴m+2≥﹣m,解得:m≥﹣1,故选:C.2.D【考点】利用导数求闭区间上函数的最值.【分析】先求出+2x,再由f(x)为偶函数,且在(0,+∞)上单调递增,故f(2x)>f(x+3)等价于|2x|>|x+3|,解之即可求出使得f(2x)>f(x+3)成立的x的取值范围.【解答】解:∵函数f(x)=ln(e x+e﹣x)+x2,∴+2x,当x=0时,f′(x)=0,f(x)取最小值,当x>0时,f′(x)>0,f(x)单调递增,当x<0时,f′(x)<0,f(x)单调递减,∵f(x)=ln(e x+e﹣x)+x2是偶函数,且在(0,+∞)上单调递增,∴f (2x )>f (x+3)等价于|2x|>|x+3|,整理,得x 2﹣2x ﹣3>0,解得x >3或x <﹣1,∴使得f (2x )>f (x+3)成立的x 的取值范围是(﹣∞,﹣1)∪(3,+∞). 故选:D .3.C2nx x ⎛⎫- ⎪⎝⎭展开式中第2项与第4项的二项式系数相等, 所以13C C n n =,解得4n =,那么4y x =与2y x =围成的封闭圆形区域的面积为 422323041132(4)d 22440333S x x x x x ⎛⎫=-=-=⨯-⨯= ⎪⎝⎭⎰.故选C . 4.D解:C 、B 不是奇函数,A 在R 上单调递增,无极值,故选D .5.A【考点】利用导数研究函数的单调性.【分析】根据题意可设f (x )=,然后代入计算判断即可.【解答】解:∵f (x )+2f′(x )>0,可设f (x )=,∴f (1)=,f (0)=e 0=1, ∴f (1)>, 故选:A .6.D【考点】利用导数研究曲线上某点切线方程.【分析】分别求出函数f (x )的导数,函数g (x )的导数.由于两曲线y=f (x ),y=g (x )有公共点,设为P (x 0,y 0),则有f (x 0)=g (x 0),且f′(x 0)=g′(x 0),解出x 0=a ,得到b 关于a 的函数,构造函数,运用导数求出单调区间和极值、最值,即可得到b的最大值.【解答】解:函数f(x)的导数为f'(x)=x+2a,函数g(x)的导数为,由于两曲线y=f(x),y=g(x)有公共点,设为P(x0,y0),则,由于x0>0,a>0则x0=a,因此构造函数,由h'(t)=2t(1﹣3lnt),当时,h'(t)>0即h(t)单调递增;当时,h'(t)<0即h(t)单调递减,则即为实数b的最大值.故选D.7.D【考点】定积分.【分析】联立方程组求出积分的上限和下限,结合定积分的几何意义即可得出结果.【解答】解:作出两条曲线对应的封闭区域,如右图:再联立方程,解得x=﹣1或x=2,所以,A(﹣1,1),B(2,4),根据定积分的几何意义,所求阴影部分的面积:S阴影==(﹣x3+x2+2x)=,故选:D.8.A【考点】利用导数研究函数的单调性.【分析】根据题意,令g(x)=,结合题意对其求导分析可得g′(x)>0,即函数g(x)在R上为增函数,又由f(1)=e,可得g(e)==1,而不等式f(x)<e x可以转化为g(x)<g(1),结合函数g(x)的单调性分析可得答案.【解答】解:根据题意,令g(x)=,其导数g′(x)==,又由,∀x∈R都有f'(x)>f(x),则有g′(x)>0,即函数g(x)在R上为增函数,若f(1)=e,则g(e)==1,f(x)<e x⇒<1⇒g(x)<g(1),又由函数g(x)在R上为增函数,则有x<1,即不等式f(x)<e x的解集为(﹣∞,1);故选:A.9.A【考点】利用导数研究函数的单调性.【分析】由函数f(x)=lnx+x2﹣ax+a+1为(0,+∞)上的增函数,可得:f′(x)=+2x﹣a≥0,化为:a≤+2x=g(x),利用导数研究函数的单调性极值与最值即可得出.【解答】解:f′(x)=+2x﹣a,∵函数f(x)=lnx+x2﹣ax+a+1为(0,+∞)上的增函数,∴f′(x)=+2x﹣a≥0,化为:a≤+2x=g(x),g′(x)=2﹣==,可知:x=时,函数g(x)取得极小值即最小值, =2.则实数a的取值范围是a≤2.故选:A.10.A【考点】定积分在求面积中的应用.【分析】利用定积分的几何意义表示出曲边图形的面积,再求值.【解答】解:如图所示,由直线x=1,x=e与曲线y=围成的阴影部分面积是(﹣)dx=dx﹣dx=﹣lnx=﹣﹣1+0=(2﹣5).故选:A.11.A【考点】利用导数研究函数的单调性.【分析】由函数f(x)=x3﹣ax2+1在(0,3)内单调递减转化成f'(x)≤0在(0,3)内恒成立,利用参数分离法即可求出a的范围.【解答】解:∵函数f(x)=x3﹣ax2+1在(0,3)内单调递减,∴f'(x)=3x2﹣2ax≤0在(0,3)内恒成立.即a≥x在(0,3)内恒成立.∵g(x)=x在(0,3]上的最大值为×3=,故a≥∴故选:A.12.D【考点】定积分在求面积中的应用.【分析】由图象得到围成图形的面积利用定积分表示出来,然后计算定积分即可.【解答】解:由曲线y=2,直线y=x﹣3及x轴所围成的图形的面积是+=+()=18,故选D.13.A【考点】利用导数研究函数的单调性;函数零点的判定定理.【分析】利用函数的零点以及方程的根的关系,通过函数的导数,二次导函数判断函数的单调性,利用函数的零点判定定理,推出结果即可.【解答】解:函数f(x)=e x﹣ln(x+a)(a∈R),则x>﹣a,可得f′(x)=e x﹣,f′′(x)=e x+恒大于0,f′(x)是增函数,令f′(x0)=0,则,有唯一解时,a=,代入f(x)可得:f(x0)===,由于f(x0)是增函数,f(﹣1)≈﹣0.63,f()≈0.11所以f(x0)=0时,﹣1.故选:A.14.A【考点】利用导数求闭区间上函数的最值.【分析】问题转化为k≤1+﹣对x∈(0,+∞)恒成立,令g(x)=1+﹣,根据函数的单调性求出g(x)的最小值,从而求出k的范围即可.【解答】解:f(x)=x﹣1﹣lnx,若对定义域内任意x都有f(x)≥kx﹣2,则k≤1+﹣对x∈(0,+∞)恒成立,令g(x)=1+﹣,则g′(x)=,令g′(x)>0,解得:x>e2,令g′(x)<0,解得:0<x<e2,故g(x)在(0,e2)递减,在(e2,+∞)递增,故g(x)的最小值是g(e2)=1﹣,故k≤1﹣,故选:A.15.D【考点】函数的单调性与导数的关系.【分析】根据导数函数图象可判断;f(x)在(0,1)单调递增,(1,+∞)单调递减,由△ABC为锐角三角形,得A+B,0﹣B<A,再根据正弦函数,f(x)单调性判断.【解答】解:根据导数函数图象可判断;f(x)在(0,1)单调递增,(1,+∞)单调递减,∵△ABC为锐角三角形,∴A+B,0﹣B<A,∴0<sin(﹣B)<sinA<1,0<cosB<sinA<1f(sinA)>f(sin(﹣B)),即f(sinA)>f(cosB)故选;D【点评】本题考查了导数的运用,三角函数,的单调性,综合性较大,属于中档题.16.D【考点】等差数列的前n项和;等差数列的通项公式.【分析】利用微积分基本定理、等差数列的通项公式与求和公式及其性质即可得出.【解答】解:∵S10==dx+=+1﹣=1==5(a5+a6),解得a5+a6=,故选:D.【点评】本题考查了微积分基本定理、等差数列的通项公式与求和公式及其性质,考查推理能力与计算能力,属于中档题.17.D【考点】导数的运算.【分析】根据导数的运算法则,求导,然后导入值计算即可【解答】解:f(x)=cosx,则f′(x)=﹣,∴f(π)+f′()=cosπ﹣﹣=﹣﹣=﹣,故选:D【点评】本题考查了导数的运算法则,属于基础题18.A【考点】函数零点的判定定理;利用导数研究函数的单调性;利用导数研究函数的极值.【分析】由函数f(x)=x3﹣3x+a求导,求出函数的单调区间和极值,从而知道函数图象的变化趋势,要使函数f(x)=x3﹣3x+a有3个不同的零点,寻求实数a满足的条件,从而求得实数a的取值范围.【解答】解∵f′(x)=3x2﹣3=3(x+1)(x﹣1),当x<﹣1时,f′(x)>0;当﹣1<x<1时,f′(x)<0;当x>1时,f′(x)>0,∴当x=﹣1时f(x)有极大值.当x=1时,f(x)有极小值,要使f(x)有3个不同的零点.只需,解得﹣2<a<2.故选A.【点评】考查利用导数研究函数的单调性和极值,函数图象的变化趋势,体现了数形结合和运动的思想方法,属中档题.19.D【考点】利用导数研究函数的极值.【分析】求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极小值点即可.【解答】解:f′(x)=﹣+=,(x>0),令f′(x)>0,解得:x>2,令f′(x)<0,解得:0<x<2,故f(x)在(0,2)递减,在(2,+∞)递增,故x=2是函数的极小值点,故选:D.【点评】本题考查了函数的单调性、极值问题,考查导数的应用,是一道基础题.20.A【考点】利用导数研究曲线上某点切线方程.【分析】求得导函数,利用曲线 f(x)=ax2﹣2在横坐标为1的点 p处切线的倾斜角为,可得f′(1)=1,由此可求a的值.【解答】解:求导函数可得f′(x)=2ax,∵曲线 f(x)=ax2﹣2在横坐标为1的点 p处切线的倾斜角为,∴f′(1)=1,∴2a=1,∴a=.故选:A.【点评】本题考查导数的几何意义,考查学生的计算能力,属于基础题.21.C【考点】DB:二项式系数的性质.【专题】38 :对应思想;4O:定义法;5P :二项式定理.【分析】求定积分可得n的值,再利用二项展开式的通项公式,令x的幂指数等于零求得r的值,可得展开式中常数项.【解答】解:=2(sinx+cosx)dx=2(﹣cosx+sinx)=2(﹣cos+cos0+sin﹣sin0)=4,∴的通项公式为T r+1=•2r•y4﹣2r,令4﹣2r=0,可得r=2,∴二项式展开式中常数项是•22=24.故选:C.22.B【考点】双曲线的简单性质.【分析】先根据导数求其切线的斜率,即=2,再根据离心率公式计算即可.【解答】解:由于y=x2,则y′=2x,∴k=y′|x=1=2,∵函数y=x2在P(1,1)处的切线与双曲线﹣=1(a>0,b>0)的一条渐近线平行,∴=2,∴e===,故选:B.【点评】本题考查了导数和几何意义以及双曲线的渐近线方程,求双曲线的离心率,考查了双曲线的标准方程与简单几何性质等知识,属于基础题.23.B【考点】6B:利用导数研究函数的单调性;3N:奇偶性与单调性的综合.【分析】构造函数g(x)=(x∈R),研究g(x)的单调性,结合原函数的性质和函数值,即可求解【解答】解:∵y=f(x+2)为偶函数,∴y=f(x+2)的图象关于x=0对称∴y=f(x)的图象关于x=2对称∴f(4)=f(0)又∵f(4)=1,∴f(0)=1设g(x)=(x∈R),则g′(x)==又∵f′(x)<f(x),∴f′(x)﹣f(x)<0∴g′(x)<0,∴y=g(x)在定义域上单调递减∵f(x)<e x∴g(x)<1又∵g(0)==1∴g(x)<g(0)∴x>0故选B.24.D【考点】69:定积分的简单应用.【分析】由图形可知,阴影部分的面积等于正弦函数与余弦函数图形到的面积,所以利用此区间的定积分可求.【解答】解:由图形以及定积分的意义,得到所求封闭图形面积等价于;故选:D.25.【考点】函数的最值及其几何意义.【分析】令t=(t≥),则函数y=t+,求出导数,判断单调性,即可得到最小值.【解答】解:令t=(t≥),则函数y=t+,导数y′=1﹣,由t2≥2,0<≤,即有y′>0,函数y在[,+∞)递增,可得t=,即x=0时,函数取得最小值,且为.故答案为:.26.8 3210448()d ()d 333S f x x f x x -⎛⎫=-=--= ⎪⎝⎭⎰⎰. 27.1根据题意,所求面积为函数23y x =在区间[0,1]上的定积分值,即该阴影部分面积为1231003d 1x x x ==⎰.28.[1,1]-∵()sin f x x a x =+,()1cos 0f x a x '=+≥在R 上恒成立,cos [1,1]x ∈-.①当0a >时,cos a a x a -≤≤,∴1a --≥,∴01a <≤.②当0a =时,符合要求.③当0a <时,cos a a x a -≤≤,∴1a -≥,∴10a -<≤.综上11a -≤≤.29.8ln3-3112d x x x ⎛⎫- ⎪⎝⎭⎰ 23ln 1x x =- 22(3ln3)(1ln1)=---8ln3=-. 30.16解:函数2y x x =-开口向下,与x 轴围成的封闭图形面积为1232011()d 0236x x x x x ⎛⎫-=-= ⎪⎝⎭⎰. 31.4x+3y ﹣14=0【考点】利用导数研究曲线上某点切线方程.【分析】先根据2f (4﹣x )=f (x )+x 2﹣2,求出函数f (x )的解析式,然后对函数f (x )进行求导,进而可得到y=f(x)在点(2,f(2))处的切线方程的斜率,最后根据点斜式可求导切线方程.【解答】解:∵2f(4﹣x)=f(x)+x2﹣2,∴将x换为4﹣x,可得f(4﹣x)=2f(x)﹣(4﹣x)2+2.将f(4﹣x)代入f(x)=2f(4﹣x)﹣x2+2,得f(x)=4f(x)﹣2(4﹣x)2+4﹣x2+2,∴f(x)=(3x2﹣16x+26),f'(x)=2x﹣,∴y=f(x)在(2,f(2))处的切线斜率为y′=﹣.∴函数y=f(x)在(2,2)处的切线方程为y﹣2=﹣(x﹣2),即为4x+3y﹣14=0.故答案为:4x+3y﹣14=0.32.﹣30【考点】二项式系数的性质.【分析】由定积分求出n=6,从而T r+1=(﹣5)6﹣r,令,解得r=5,由此能求出的展开式中含的项的系数.【解答】解:∵=(lnx)=lne6﹣ln1=6,∴=,T r+1==(﹣5)6﹣r,令,解得r=5,∴的展开式中含的项的系数为: =﹣30.故答案为:﹣30.33.(﹣,0)∪[1,+∞)【考点】利用导数研究函数的单调性;导数的运算.【分析】根据条件构造函数g(x)=xf(x),求函数的导数,结合函数极值和导数之间的关系求函数的极值和单调性即可得到结论.【解答】解:∵xf′(x)=(x﹣1)f(x),∴f(x)+xf′(x)=xf(x)设g(x)=xf(x),则g′(x)=f(x)+xf′(x),即g′(x)=g(x),则g(x)=ce x,∵f(1)=1,∴g(1)=f(1)=1,即g(1)=ce=1,则c=,则g(x)=xf(x)=•e x,则f(x)=,(x≠0),函数的导数f′(x)==,由f′(x)>0得x>1,此时函数单调递增,由f′(x)<0得x<0或0<x<1,此时函数单调递减,即当x=1时,函数f(x)取得极小值,此时f(1)==1,即当x>0时,f(x)≥1,当x<0时,函数f(x)单调递减,且f(x)<0,综上f(x)≥1或f(x)<0,∵A为△ABC的最大内角,∴≤A<π,则0≤A﹣<,则设m=tan(A﹣),则m≥0或m<﹣,∴当m≥0时,f(m)≥1,当m<﹣,f(m)∈(f(﹣),0),即f(m)∈(﹣,0),即f[tan(A﹣)]的取值范围为的值域为(﹣,0)∪[1,+∞),故答案为:(﹣,0)∪[1,+∞)34.2【考点】利用导数研究曲线上某点切线方程.【分析】求出曲线的导函数,把x=x0代入即可得到切线的斜率,然后根据过点P0的切线方程为4x﹣y﹣1=0得出切线的斜率从而求出切点的坐标,最后将切点的坐标代入曲线方程即可求出实数k的值.【解答】解:由函数y=3lnx+x+k知y′=3×+1=+1,把x=x0代入y′得到切线的斜率k=+1,因切线方程为:4x﹣y﹣1=0,∴k=4,∴+1=4,得x0=1,把x0=1代入切线方程得切点坐标为(1,3),再将切点坐标(1,3)代入曲线y=3lnx+x+k,得3=3ln1+1+k,∴k=2.故答案为:2.35.y=2x+3【考点】利用导数研究曲线上某点切线方程.【分析】欲求在x=0处的切线的方程,只须求出其斜率即可,故先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率,从而问题解决.【解答】解:∵f(x)=sinx+e x+2,∴f(x)′=cosx+e x,∴曲线f(x)=sinx+e x+2在点P(0,3)处的切线的斜率为:k=cos0+e0=2,∴曲线f(x)=sinx+e x+2在点P(0,3)处的切线的方程为:y=2x+3,故答案为y=2x+3.36.3x﹣y+1=0【考点】利用导数研究曲线上某点切线方程.【分析】求出函数的导数,可得在x=0处切线的斜率,求得切点坐标,运用斜截式方程可得切线的方程.【解答】解:f′(x)=e x(sinx+cosx+x+2),f′(0)=3,f(0)=1,故切线方程是:y﹣1=3x,即3x﹣y+1=0,故答案为:3x﹣y+1=0.37.﹣1+ln3【考点】利用导数研究曲线上某点切线方程.【分析】求出函数的导数,通过旗下的斜率,列出方程求解即可.【解答】解:曲线y=lnx,可得y′=,曲线y=lnx的一条切线是直线y=x+b,可得=,解得切点的横坐标x=3,则切点坐标(3,ln3),所以ln3=1+b,可得b=﹣1+ln3.故答案为:﹣1+ln3.38.【考点】定积分在求面积中的应用;定积分.【分析】联立两个解析式得到两曲线的交点坐标,然后对函数解析式求定积分即可得到曲线y=x2与所围成的图形的面积.。
