2012北京市高三二模理科数学分类汇编(15)算法初步
2012北京市丰台区2012年高三二模(理科)数学试题及答案
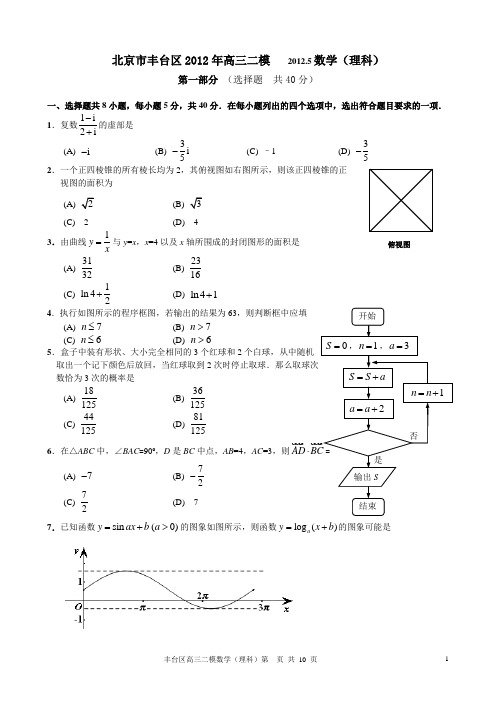
北京市丰台区2012年高三二模 2012.5数学(理科)第一部分 (选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.复数1i 2i-+的虚部是(A) i - (B) 3i 5-(C) –1 (D) 35-2.一个正四棱锥的所有棱长均为2,其俯视图如右图所示,则该正四棱锥的正视图的面积为(A)(B)(C) 2 (D) 43.由曲线1y x=与y =x ,x =4以及x 轴所围成的封闭图形的面积是(A)3132(B)2316(C) 1ln 42+ (D) ln 41+4.执行如图所示的程序框图,若输出的结果为63,则判断框中应填(A) 7n ≤ (B) 7n >(C) 6n ≤ (D) 6n >5.盒子中装有形状、大小完全相同的3个红球和2个白球,从中随机 取出一个记下颜色后放回,当红球取到2数恰为3次的概率是(A) 18125 (B) 36125(C)44125(D)811256.在△ABC 中,∠BAC =90º,D 是BC 中点,AB =4,AC =3,则AD ⋅ (A) 7- (B) 72-(C)72(D) 77.已知函数sin (0)y ax b a =+>的图象如图所示,则函数log ()a y x b =+的图象可能是俯视图(A)(B)(C)(D)8.已知平面上四个点1(0,0)A,22)A,34,2)A ,4(4,0)A .设D 是四边形1234A A A A 及其内部的点构成的点的集合,点0P 是四边形对角线的交点,若集合0{|||||,1,2,3,4}i S P D PP PA i =∈≤=,则集合S 所表示的平面区域的面积为 (A) 2(B) 4 (C) 8(D) 16第二部分 (非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9.在极坐标系中,圆2sin ρθ=的圆心的极坐标是____.10.已知椭圆22221(7x ym mm +=>-上一点M 到两个焦点的距离分别是5和3,则该椭圆的离心率为______. 11.如图所示,AB 是圆的直径,点C 在圆上,过点B ,C 的切线交于点P ,AP 交圆于D ,若AB =2,AC =1,则PC =______,PD =______.12.某地区恩格尔系数(%)y 与年份x 的统计数据如下表:从散点图可以看出y 与x 线性相关,且可得回归方程为ˆˆ4055.25ybx =+,据此模型可预测2012年该地区的恩格尔系数(%)为______.13.从5名学生中任选4名分别参加数学、物理、化学、生物四科竞赛,且每科竞赛只有1人参加,若甲不参加生物竞赛,则不同的选择方案共有 种. 14. 在平面直角坐标系中,若点A ,B 同时满足:①点A ,B 都在函数()y f x =图象上;②点A ,B 关于原点对称,则称点对(A ,B )是函数()y f x =的一个“姐妹点对”(规定点对(A ,B )与点对(B ,A )是同一个“姐妹点对”).那么函数24,0,()2,0,x x f x x x x -≥⎧=⎨-<⎩ 的“姐妹点对”的个数为_______;当PBA函数()x g x a x a =--有“姐妹点对”时,a 的取值范围是______. 三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题共13分)已知函数()cos sin )f x x x x =--.(Ⅰ)求()3f π的值;(Ⅱ)求函数()y f x =在区间[0,]2π上的最小值,并求使()y f x =取得最小值时的x 的值.16.(本小题共13分)某商场举办促销抽奖活动,奖券上印有数字100,80,60,0.凡顾客当天在该商场消费每.超过1000元,即可随机从抽奖箱里摸取奖券一张,商场即赠送与奖券上所标数字等额的现金(单位:元).设奖券上的数字为ξ,ξ的分布列如下表所示,且ξ的数学期望E ξ=22.(Ⅰ)求a ,b (Ⅱ)若某顾客当天在商场消费2500元,求该顾客获得奖金数不少于160元的概率.17.(本小题共14分)在如图所示的几何体中,四边形ABCD 为矩形,平面ABEF ⊥平面ABCD , EF // AB,∠BAF =90º, AD = 2,AB =AF =2EF =1,点P 在棱DF 上.(Ⅰ)若P 是DF 的中点,(ⅰ) 求证:BF // 平面ACP ;(ⅱ) 求异面直线BE 与CP 所成角的余弦值; (Ⅱ)若二面角D -AP -C 3,求PF 的长度.PFEDCAB18.(本小题共13分)已知数列{a n }满足14a =,131n n n a a p +=+⋅+(n *∈N ,p 为常数),1a ,26a +,3a 成等差数列. (Ⅰ)求p 的值及数列{a n }的通项公式; (Ⅱ)设数列{b n }满足2n n nb a n=-,证明:49n b ≤.19.(本小题共14分)在平面直角坐标系xOy 中,抛物线C 的焦点在y 轴上,且抛物线上的点P (x 0,4)到焦点F 的距离为5.斜率为2的直线l 与抛物线C 交于A ,B 两点.(Ⅰ)求抛物线C 的标准方程,及抛物线在P 点处的切线方程;(Ⅱ)若AB 的垂直平分线分别交y 轴和抛物线于M ,N 两点(M ,N 位于直线l 两侧),当四边形AMBN 为菱形时,求直线l 的方程.20.(本小题共13分)设函数()ln ()ln()f x x x a x a x =+--(0)a >. (Ⅰ)当1a =时,求函数()f x 的最小值;(Ⅱ)证明:对∀x 1,x 2∈R +,都有[]11221212ln ln ()ln()ln 2x x x x x x x x +≥++-;(Ⅲ)若211ni i x ==∑,证明:21ln ln 2nni i i x x =≥-∑ *(,)i n ∈N .(考生务必将答案答在答题卡上,在试卷上作答无效)北京市丰台区2012年高三二模数 学(理科)参考答案一、选择题:本大题共8小题,每小题5分,共40分.二、填空题:本大题共6小题,每小题5分,共30分.9.(1,)2π10411,712.31.25 13. 96 14.1,1a >注:第11题第一个空答对得2分,第二个空答对得3分;第14题第一个空答对得3分,第二个空答对得2分.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.解:因为()cos sin )f x x x x =--2sin cos x x x --=1cos 21)sin 222xx +--=12sin 2222x x --=cos(2)62x π+-.(Ⅰ)()cos(2)3362f πππ=⨯+-=22--= ……………………7分 (Ⅱ)因为 [0,]2x π∈,所以2666x ππ7π≤+≤.当 26x π+=π,即512x π=时,函数()y f x =有最小值是12--.当512x π=时,函数()y f x =有最小值是12--. ……………………13分16.解:(Ⅰ)依题意,1000.05806000.722E a b ξ=⨯+++⨯=,所以 806017a b +=.因为 0.050.71a b +++=,所以0.25a b +=.由 806017,0.25,a b a b +=⎧⎨+=⎩ 可得0.1,0.15.a b =⎧⎨=⎩……………………7分(Ⅱ)依题意,该顾客在商场消费2500元,可以可以抽奖2次.奖金数不少于160元的抽法只能是100元和100元; 100元和80元; 100元和60元;80元和80元四种情况. 设“该顾客获得奖金数不少于160元”为事件A ,则()0.050.0520.050.120.050.150.10.10.0375P A =⨯+⨯⨯+⨯⨯+⨯=.答:该顾客获得奖金数不少于160元的概率为0.0375. ……………………13分17.(Ⅰ)(ⅰ)证明:连接BD ,交AC 于点O ,连接OP .因为P 是DF 中点,O 为矩形ABCD 对角线的交点,OBACDEFP所以OP 为三角形BDF 中位线,所以BF // OP ,因为BF ⊄平面ACP ,OP ⊂平面ACP ,所以BF // 平面ACP . ……………………4分 (ⅱ)因为∠BAF =90º, 所以AF ⊥AB ,因为 平面ABEF ⊥平面ABCD , 且平面ABEF ∩平面ABCD = AB ,所以AF ⊥平面ABCD , 因为四边形ABCD 为矩形,所以以A 为坐标原点,AB ,AD ,AF 分别为x ,y ,z 轴,建立如图所示空间直角坐标系O xyz -. 所以 (1,0,0)B ,1(,0,1)2E ,1(0,1,)2P ,(1,C 所以 1(,0,1)2B E =- ,1(1,1,)2C P =-- ,所以cos ,15||||BE C P BE C P BE C P ⋅<>==⋅,即异面直线BE 与CP 所成角的余弦值为15……………………9分(Ⅱ)解:因为AB ⊥平面ADF ,所以平面APF 的法向量为1(1,0,0)n =.设P 点坐标为(0,22,)t t -,在平面APC 中,(0,22,)A P t t =- ,(1,2,0)A C =,所以 平面APC 的法向量为222(2,1,)t n t-=- , 所以121212||cos ,3||||n n n n n n ⋅<>===⋅,解得23t =,或2t =(舍).此时||3PF =. ……………………14分18.解:(Ⅰ)因为14a =,131nn n a a p +=+⋅+,所以1213135a a p p =+⋅+=+;23231126a a p p =+⋅+=+.因为1a ,26a +,3a 成等差数列,所以2(26a +)=1a +3a , 即610124126p p ++=++, 所以 2p =. 依题意,1231n n n a a +=+⋅+, 所以当n ≥2时,121231a a -=⋅+,232231a a -=⋅+,……212231n n n a a ----=⋅+,11231n n n a a ---=⋅+.相加得12212(3333)1n n n a a n ---=+++++- ,所以 113(13)2(1)13n n a a n ---=+--,所以 3nn a n =+.当n =1时,11314a =+=成立,所以 3nn a n =+. ……………………8分(Ⅱ)证明:因为 3nn a n =+,所以 22(3)3n nnnn b n n==+-.因为 2221+11(1)22+1=333n n n nn n n n n b b +++-+-=-,*()n ∈N .若 22+210n n -+<,则12n +>,即 2n ≥时 1n n b b +<.又因为 113b =,249b =,所以49n b ≤. ……………………13分19.解:(Ⅰ)依题意设抛物线C :22(0)x py p =>,因为点P 到焦点F 的距离为5, 所以点P 到准线2p y =-的距离为5.因为P (x 0,4),所以由抛物线准线方程可得12p =,2p =.所以抛物线的标准方程为24x y =. ……………………4分 即 214y x =,所以 1'2y x =,点P (±4,4), 所以 41'|(4)22x y =-=⨯-=-,41'|422x y ==⨯=.所以 点P (-4,4)处抛物线切线方程为42(4)y x -=-+,即240x y ++=; 点P (4,4)处抛物线切线方程为42(4)y x -=-,即240x y --=.P 点处抛物线切线方程为240x y ++=,或240x y --=. ……………………7分(Ⅱ)设直线l 的方程为2y x m =+,11(,)A x y ,22(,)B x y ,联立 242x yy x m⎧=⎨=+⎩,消y 得 2840x x m --=,64160m ∆=+>.所以 128x x +=,124x x m =-, 所以1242x x +=,1282y y m +=+,即A B 的中点为(4,8)Q m +.所以 A B 的垂直平分线方程为1(8)(4)2y m x -+=--.因为 四边形AMBN 为菱形,所以 (0,10)M m +,M ,N 关于(4,8)Q m +对称, 所以 N 点坐标为(8,6)N m +,且N 在抛物线上, 所以 644(6)m =⨯+,即10m =,所以直线l 的方程为 210y x =+. ……………………14分20.解:(Ⅰ)1a =时,()ln (1)ln(1)f x x x x x =+--,(01x <<),则()ln ln(1)ln 1x f x x x x'=--=-.令()0f x '=,得12x =.当102x <<时,()0f x '<,()f x 在1(0,)2是减函数,当112x <<时,()0f x '>,()f x 在1(,1)2是增函数, 所以 ()f x 在12x =时取得最小值,即11()ln22f =. ……………………4分(Ⅱ)因为 ()ln ()ln()f x x x a x a x =+--,所以 ()ln ln()ln x f x x a x a x'=--=-.所以当2a x =时,函数()f x 有最小值.∀x 1,x 2∈R +,不妨设12x x a +=,则121211221111ln ln ln ()ln()2ln()22x x x x x x x x x x a x a x +++=+--≥⋅[]1212()ln()ln 2x x x x =++-. ……………………8分(Ⅲ)(证法一)数学归纳法ⅰ)当1n =时,由(Ⅱ)知命题成立.ⅱ)假设当n k =( k ∈N *)时命题成立,即若1221kx x x +++= ,则112222ln ln ln ln 2k k kx x x x x x +++≥- .当1n k =+时,1x ,2x ,…,121k x +-,12k x +满足 11122121k k x x x x ++-++++= .设11111122212122()ln ln ln ln k k k k F x x x x x x x x x ++++--=++++ ,由(Ⅱ)得11111212212212()()ln[()ln 2]()ln[()ln 2]k k k k F x x x x x x x x x ++++--≥++-++++-=111111212122122122()ln()()ln()(...)ln 2k k k k k x x x x x x x x x x x +++++--++++++-+++ =11111212212212()ln()()ln()ln 2k k k k x x x x x x x x ++++--++++++- .由假设可得 1()ln 2ln 2ln 2k k F x +≥--=-,命题成立.所以当 1n k =+时命题成立.由ⅰ),ⅱ)可知,对一切正整数n ∈N *,命题都成立,所以 若211ni i x ==∑,则21ln ln 2nn ii i xx =≥-∑ *(,)i n ∈N. ……………………13分(证法二)若1221nx x x +++= ,那么由(Ⅱ)可得112222ln ln ln n n x x x x x x +++1212212212()ln[()ln 2]()ln[()ln 2]n n n n x x x x x x x x --≥++-++++- 1212122122122()ln()()ln()(...)ln 2n n n n n x x x x x x x x x x x --=++++++-+++ 1212212212()ln()()ln()ln 2n n n n x x x x x x x x --=++++++-12341234212212()ln()()ln()2ln 2n n n n x x x x x x x x x x x x --≥+++++++++- 121222(...)ln[()ln 2](1)ln 2n n x x x x x x n ≥≥++++++--- ln 2n =-.……………………13分(若用其他方法解题,请酌情给分)。
2012年北京市海淀区高三数学理科二模试卷及答案(WORD版)

北京市海淀区2012高三二模数 学(理科)2012.05一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若sin cos 0θθ<,则角θ是 (A )第一或第二象限角 (B )第二或第三象限角 (C )第三或第四象限角 (D )第二或第四象限角 (2)已知命题p :0x ∃∈R ,021x =.则p ⌝是 (A )0x ∀∈R ,021x ≠ (B )0x ∀∉R ,021x ≠ (C )0x ∃∈R ,021x ≠(D )0x ∃∉R ,021x ≠(3)直线11x ty t =+⎧⎨=-⎩(t 为参数)的倾斜角的大小为(A )4-π (B )4π (C )2π(D )34π(4)若整数,x y 满足1,1,3,2x y x y y ìïïï-?ïïï+?íïïïï£ïïî则2x y +的最大值是 (A )1(B )5(C )2 (D )3(5)已知点12,F F 是椭圆2222x y +=的两个焦点,点P 是该椭圆上的一个动点,那么12PF PF +u u u r u u u u r的最小值是(A )0 (B )1 (C )2 (D)(6)为了得到函数2log y =2log y x =的图象上所有的点的(A )纵坐标缩短到原来的12倍,横坐标不变,再向右平移1个单位长度 (B )纵坐标缩短到原来的12倍,横坐标不变,再向左平移1个单位长度(C )横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位长度(D )横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位长度(7)某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是(A )203(B )43(C )6 (D )4(8)点(,)P x y 是曲线1:(0)C y x x=>上的一个动点,曲线C 在点P 处的切线与x 轴、y 轴分别交于,A B 两点,点O 是坐标原点. 给出三个命题:①PA PB =;②OAB ∆的周长有最小值4+;③曲线C 上存在两点,M N ,使得OMN ∆为等腰直角三角形.其中真命题的个数是(A )1 (B )2 (C )3 (D )0二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上. (9)在面积为1的正方形ABCD 内部随机取一点P ,则PAB ∆的面积大于等于14的概率是_________. (10)已知1021012311(1)x a a x a x a x +=++++L . 若数列123,,,,(111,)k a a a a k k #?Z L 是一个单调递增数列,则k 的最大值是 . (11)在ABC ∆中,若120A ??,5c =,ABC ∆的面积为,则a = .(12)如图,O e 的直径AB 与弦CD 交于点P ,7, 5, 15CP PD AP ===,则DCB Ð=______.(13)某同学为研究函数()1)f x x =#的性质,构造了如图所示的两个边长为1的正方形ABCD 和BEFC ,点P 是边BC 上的一个动点,设CP x =,则()AP PF f x +=. 请你参考这些信息,推知函数()f x 的图象的对称轴是 ;函数()4()9g x f x =-的零点的个数是 .俯视图主视图BEFAB C DP(14)曲线C 是平面内到定点(1,0)A 的距离与到定直线1x =-的距离之和为3的动点P 的轨迹. 则曲线C 与y 轴交点的坐标是 ;又已知点(,1)B a (a 为常数),那么PB PA +的最小值()d a = . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知公差不为0的等差数列{}n a 的前n 项和为n S ,346S a =+,且1413,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列1{}nS 的前n 项和公式. (16)(本小题满分14分)如图所示,PA ^平面ABC ,点C 在以AB 为直径的⊙O 上,30CBA??,2PA AB ==,点E 为线段PB 的中点,点M 在»AB 上,且OM ∥AC . (Ⅰ)求证:平面MOE ∥平面P AC ;(Ⅱ)求证:平面P AC ^平面PCB ;(Ⅲ)设二面角M BP C --的大小为θ,求cos θ的值.(17)(本小题满分13分)某公司准备将100万元资金投入代理销售业务,现有A ,B 两个项目可供选择: (1)投资A 项目一年后获得的利润X且X 1的数学期望E (X 1)=12;(2)投资B 项目一年后获得的利润X 2(万元)与B 项目产品价格的调整有关, B 项目产品价格根据销售情况在4月和8月决定是否需要调整,两次调整相互独立且在4月和8月进行价格调整的概率分别为p (0< p <1)和1-p . 经专家测算评估:B 项目产品价格一年内调整次数X (次)与X 2的关系如下表所示:(Ⅱ)求X 2的分布列;(Ⅲ)若E (X 1)< E (X 2),则选择投资B 项目,求此时 p 的取值范围.(18)(本小题满分13分)ME BOCAP已知椭圆C :22221(0)x y a b a b+=>>的右焦点为(1,0)F ,且点(1,2-在椭圆C 上. (Ⅰ)求椭圆C 的标准方程;(Ⅱ)已知动直线l 过点F ,且与椭圆C 交于A ,B 两点.试问x 轴上是否存在定点Q ,使得716QA QB ⋅=-u u u r u u u r 恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.(19)(本小题满分14分)已知函数21()ln()(0)2f x a x a x x a =--+<. (Ⅰ)求()f x 的单调区间;(Ⅱ)若12(ln 21)a -<<-,求证:函数()f x 只有一个零点0x ,且012a x a +<<+; (Ⅲ)当45a =-时,记函数()f x 的零点为0x ,若对任意120,[0,]x x x ∈且211,x x -=都有21()()f x f x m -≥成立,求实数m 的最大值.(本题可参考数据:99ln 20.7,ln 0.8,ln 0.5945≈≈≈)(20)(本小题满分13分)将一个正整数n 表示为12(*)p a a a p +++?N L 的形式,其中*i a ÎN ,1,2,,i p =L ,且p a a a ≤≤≤Λ21,记所有这样的表示法的种数为)(n f (如4=4,4=1+3,4=2+2,4=1+1+2,4=1+1+1+1,故5)4(=f ).(Ⅰ)写出)5(),3(f f 的值,并说明理由;(Ⅱ)对任意正整数n ,比较)1(+n f 与)]2()([21++n f n f 的大小,并给出证明; (Ⅲ)当正整数6≥n 时,求证:134)(-≥n n f .海淀区高三年级第二学期期末练习数 学(理科)参考答案及评分标准 2012.05一. 选择题:本大题共8小题,每小题5分,共40分.最新整理二.填空题:本大题共6小题,每小题5分,共30分.(9)12(10)6(11(12)45°(13)12x=;2(14)(0,±;1.41,4, 1.41,2,1 1.a aa aa aìï??ïïï+-<?íïï--<<ïïïî或注:(13)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)解:(Ⅰ)设等差数列{}n a的公差为0d¹.因为346S a=+,所以11323362da a d创+=++. ①……………………………………3分因为1413,,a a a成等比数列,所以2111(12)(3)a a d a d+=+. ②……………………………………5分由①,②可得:13,2a d==. ……………………………………6分所以21na n=+.……………………………………7分(Ⅱ)由21na n=+可知:2(321)22nn nS n n++?==+.……………………………………9分所以11111()(2)22nS n n n n==-++. ……………………………………11分所以123111111n nS S S S S-+++++L11111111111()2132435112n n n n=-+-+-++-+--++L21111135()212124(1)(2)n nn n n n+=+--=++++.所以数列1{}nS的前n项和为2354(1)(2)n nn n+++.最新整理……………………………………13分(16)(本小题满分14分)(Ⅰ)证明:因为点E 为线段PB 的中点,点O 为线段AB 的中点,所以 OE ∥PA . ……………………………………1分 因为 PA Ì平面PAC ,OE Ë平面PAC ,所以 OE ∥平面P AC . ……………………………………2分因为 OM ∥AC , 因为 AC Ì平面PAC ,OM Ë平面PAC ,所以 OM ∥平面P AC . ……………………………………3分因为 OE Ì平面MOE ,OM Ì平面MOE ,OE OM O =I ,所以 平面MOE ∥平面P AC . ………………………………………5分(Ⅱ)证明:因为 点C 在以AB 为直径的⊙O 上,所以 90ACB??,即BC AC ⊥.因为 PA ^平面ABC ,BC Ì平面ABC , 所以PA BC ⊥. ……………………………………7分因为 AC Ì平面PAC ,PA Ì平面PAC ,PA AC A =I ,所以 BC ^平面PAC . 因为 BC Ì平面PBC ,所以 平面P AC ^平面PCB . ……………………………………9分(Ⅲ)解:如图,以C 为原点,CA 所在的直线为x 轴,CB 所在的直线为y 轴,建立空间直角坐标系C xyz -. 因为 30CBA??,2PA AB ==,所以2cos30CB =?1AC =.延长MO 交CB 于点D . 因为 OM ∥AC ,所以131, 1,2222MD CB MD CD CB ^=+===.最新整理所以 (1,0,2)P ,(0,0,0)C,B,3(,,0)22M . 所以 (1,0,2)CP =u u u r,CB =u u u r.设平面PCB 的法向量(,,)=x y z m .因为 0,0.CP CBìï?ïíï?ïîu u u r u u u r m m所以(,,)(1,0,2)0,(,,)0,x y z x y z ì?ïïíï?ïî即20,0.x z ì+=ïïíï=ïî令1z =,则2,0x y =-=.所以 (2,0,1)=-m . ……………………………………12分 同理可求平面PMB 的一个法向量n ()=.……………………………………13分 所以 1cos ,5⋅==-⋅m n m n m n . 所以 1cos 5θ=. ………………………………………14分 (17)(本小题满分13分) 解:(Ⅰ)由题意得:0.41,11120.41712.a b a b ++=⎧⎨+⨯+=⎩解得:0.5,0.1a b ==. ……………………………………3分 (Ⅱ)X 2 的可能取值为4.12,11.76,20.40.()[]2 4.12(1)1(1)(1)P X p p p p ==---=-,()[]22211.761(1)(1)(1)(1)P X p p p p p p ==--+--=+-,()220.40(1)P X p p ==-.所以X 2的分布列为:(Ⅲ)由(Ⅱ)可得:()2224.12(1)11.76(1)20.40(1)E Xp p p p p p ⎡⎤=-++-+-⎣⎦211.76p p =-++. ……………………………………11分因为E (X 1)< E (X 2),所以21211.76p p <-++.最新整理所以0.40.6p <<.当选择投资B 项目时,p 的取值范围是()0.4,0.6.……………………………………13分(18)(本小题满分13分) 解:(Ⅰ)由题意知:1c =.根据椭圆的定义得:22a =,即a = ……………………………………3分 所以 2211b =-=.所以 椭圆C 的标准方程为2212x y +=. ……………………………………4分 (Ⅱ)假设在x 轴上存在点(,0)Q m ,使得716QA QB ⋅=-u u u r u u u r 恒成立.当直线l 的斜率为0时,(A B .则7,0)(,0)16m m ?=-. 解得 54m =?. ……………………………………6分 当直线l的斜率不存在时,(1,(1,22A B -.由于557(1,(1,424216+?-?,所以54m ?. 下面证明54m =时,716QA QB ⋅=-u u u r u u u r 恒成立.……………………………………8分显然 直线l 的斜率为0时,716QA QB ⋅=-u u u r u u u r .当直线l 的斜率不为0时,设直线l 的方程为:1x ty =+,()()1122,,,A x y B x y .由221,21x y x ty ìïï+=ïíïï=+ïî可得:22(2)210t y ty ++-=. 显然0∆>.1221222,21.2t y y t y y t ìïï+=-ïï+ïíïï=-ïï+ïî……………………………………10分最新整理因为 111x ty =+,221x ty =+,所以 112212125511(,)(,)()()4444x y x y ty ty y y -?=--+ 2121211(1)()416t y y t y y =+-++2221121(1)24216t t t t t =-+++++ 22222172(2)1616t t t --+=+=-+.综上所述:在x 轴上存在点5(,0)4Q ,使得716QA QB ⋅=-u u u r u u u r恒成立. ……………………………………13分 (19)(本小题满分14分)(Ⅰ)解:()f x 的定义域为(,)a +∞.2(1)'()1a x a xf x x x a x a-++=-+=--. ……………………………………1分令'()0f x =,0x =或+1x a =.当10a -<<时,+10a >,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(0,1)a +,单调递减区间是(,0)a 和(1,)a ++?.……………………………………3分当1a =-时,2'()01x f x x -=≤+. 所以,函数()f x 的单调递减区间是(1,)-+?. ……………………………………4分 当1a <-时,+10a <,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(1,0)a +,单调递减区间是(,1)a a +和(0,)+?.最新整理……………………………………5分(Ⅱ)证明:当12(ln21)0a -<<-<时,由(Ⅰ)知,()f x 的极小值为(0)f ,极大值为(1)f a +.因为(0)ln()0f a a =->,2211(1)(1)(1)(1)022f a a a a +=-+++=->,且()f x 在(1,)a ++?上是减函数,所以()f x 至多有一个零点. ……………………………………7分 又因为211(2)ln 2[2(ln 21)]022f a a a a a a +=--=---<, 所以 函数()f x 只有一个零点0x ,且012a x a +<<+.……………………………………9分(Ⅲ)解:因为412(ln 21)5-<-<-, 所以 对任意120,[0,]x x x ∈且211,x x -=由(Ⅱ)可知:1[0,1)x a ∈+,20(1,]x a x ∈+,且21x ≥. ……………………………………10分因为 函数()f x 在[0,1)a +上是增函数,在(1,)a ++?上是减函数,所以 1()f x (0)f ≥,2()f x (1)f ≤. ……………………………………11分 所以 12()()(0)(1)f x f x f f -?.当45a =-时,1(0)(1)ln()12a f f a a -=--=491ln 542->0. 所以 12()()(0)(1)0f x f x f f -?>. ……………………………………13分所以 21()()f x f x -的最小值为491(0)(1)ln 542f f -=-. 所以 使得21()()f x f x m -≥恒成立的m 的最大值为491ln 542-.……………………………………14分(20)(本小题满分13分)(Ⅰ)解:因为3=3,3=1+2,3=1+1+1,所以3)3(=f .因为5=5,5=2+3,5=1+4,5=1+1+3,5=1+2+2,5=1+1+1+2,5=1+1+1+1+1, 所以7)5(=f . ……………………………………3分 (Ⅱ)结论是)1(+n f )]2()([21++≤n f n f . 证明如下:由结论知,只需证).1()2()()1(+-+≤-+n f n f n f n f最新整理. 因为21≥+n ,把1+n 的一个表示法中11a =的1a 去掉,就可得到一个n 的表示法;反之,在n 的一个表示法前面添加一个“1+”,就得到一个1n +的表示法,即1+n 的表示法中11a =的表示法种数等于n 的表示法种数,所以)()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数,)1()2(+-+n f n f 是2n +的表示法中11a ¹的表示法数.同样,把一个11a ¹的1+n 的表示法中的p a 加上1, 就可得到一个11a ¹的2n +的表示法,这样就构造了从11a ¹的1+n 的表示法到11a ¹的2+n 的表示法的一个对应.所以有).1()2()()1(+-+≤-+n f n f n f n f ……………………………………9分 (Ⅲ)由第(Ⅱ)问可知:当正整数6m ³时,()(1)(1)(2)(6)(5)f m f m f m f m f f --?--吵-L . 又,7)5(,11)6(==f f 所以 ()(1)4f m f m --?. *对于*式,分别取m 为n ,,7,6Λ,将所得等式相加得)5(4)5()(-≥-n f n f .即134)(-≥n n f . ……………………………………13分。
2012届高三二模考试数学试卷(理)及答案

2012届高三模拟考试数学试题数学试题(理科)本试卷共4页,21小题,满分150分.考试用时120分钟.注意事项:1.答卷前,考生要务必填写答题卷上密封线内的有关项目.2.选择题每小题选出答案后,用铅笔把答案代号填在答题卷对应的空格内.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域内;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.请考生保持答题卷的整洁.考试结束后,将答题卷和答题卡交回. 参考公式:锥体的体积公式13V Sh =,其中S 为锥体的底面面积,h 为锥体的高. 一、选择题:本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数(1)i ai ⋅+是纯虚数,则实数a 的值是( )A. 1B. 1-C.0D. 0或1-2.已知集合{||2,A x x x =≤∈R },{2,B x x =≤∈Z },则A B = ( )A. (0,2)B. [0,2]C. {0, 2}D. {0,1,2}3.设25025..12,25,()2.a b c ===,则,,a b c 的大小关系是(C )A.a c b >>B. c a b >>C. a b c >>D.b a c >>4.一空间几何体的三视图如图所示,则该几何体的体积为. A. 1 B. 3 C 6 D. 25.设向量(1,0)a = ,11(,)22b = ,则下列结论正确的是 ( )A.a b =B.2a b ⋅= C. a ∥b D. a b - 与b 垂直6.执行如图1所示的程序框图后,输出的值为5,则P 的取值范围( )A.715816P <≤ B. 1516P > C. 715816P ≤< D.3748P <≤ 7. 下列四个判断:①某校高三一班和高三二班的人数分别是,m n ,某次测试数学平均分分别是,a b ,则这两个班的数学平均分为2a b+; ②10名工人某天生产同一零件,生产的件数是15,17,14,10,15,17,17,16,14,12,设其平均数为a ,中位数为b ,众数为c ,则有b a c >>; ③从总体中抽取的样本12221111(,),(,),,(,),,n nn n i i i i x y x y x y x x y y n n ====∑∑ 若记,则回归直线y =bx a +必过点(,x y )④已知ξ服从正态分布(0N ,2)σ,且(20)0.4P ξ-≤≤=,则(2)0.2P ξ>= 其中正确的个数有: ( )A .0个B . 1 个C .2 个D .3个8. 定义符号函数1,0sgn 0,01,0x x x x >⎧⎪==⎨⎪-<⎩,设111sgn()1sgn()122()()22x x f x f x -+-+=⋅+2()f x ⋅,[0,1]x ∈,其中1()f x =12x +, 2()f x ⋅=2(1)x -, 若1[()][0,)2f f a ∈,则实数a 的取值范围是( )A. 1(0,]4B. 11(,)42C. 11(,]42D. 3[0,]8二、填空题:本大共7小题,考生作答6小题,每小题5分,满分30分.(一)必做题(9~13题)9.. 已知A 是单位圆上的点,且点A 在第二象限,点B 是此圆与x 轴正半轴的交点,记AOB α∠=, 若点A的纵坐标为35.则s i n α=_____________;tan(2)πα-=_______________.10.以抛物线24y x =的焦点为圆心,且被y 轴截得的弦长等于2的圆的方程为__________________.11.从如图所示的长方形区域内任取一个点()y x M ,,则点M 取自阴影部分的概率为____________.12.已知,x y 满足约束条件5000x y x y y ++⎧⎪-⎨⎪⎩≥≤≤,则24z x y =+的最小值是_________.13.设()11f x x x =-++,若不等式121()a a f x a+--≥对任意实数0a ≠恒成立,则x 取值集合是_______________________.(二)选做题(14~15题,考生只能从中选做一题) 14.(几何证明选讲选做题)如图,AB 是圆O 的直径,DE AD =,6,8==BD AB ,则ADAC= ;15.(坐标系与参数方程选做题) 已知直线l 方程是11x ty t =+⎧⎨=-⎩(t 为参数),,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为1ρ=,则圆C 上的点到直线l 的距离最小值是 三、解答题:本大题共6小题,满分80分,解答须写出文字说明、证明过程或演算步骤. 16. (本小题满分12分)已知等比数列{}n a 的前n 项和为n S , 11a =,且1S ,22S ,33S 成等差数列. (1)求数列{}n a 通项公式;(2)设n n b a n =+,求数列{}n b 前n 项和n T .17.(本小题满分14分) 有一个3×4×5的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成60个1×1×1的小正方体,从这些小正方体中随机地任取1个,设小正方体涂上颜色的面数为ξ. (1)求0ξ=的概率; (2)求ξ的分布列和数学期望.18.(本小题满分14分)如图5(1)中矩形ABCD 中,已知2AB =,AD =MN 分别为AD 和BC 的中点,对角线BD 与MN 交于O 点,沿MN 把矩形ABNM 折起,使平面ABNM 与平面MNCD 所成角为60 ,如图5(2).(1) 求证:BO DO ⊥;(2) 求AO 与平面BOD 所成角的正弦值.OABDC MNABDCMNO图6B A19.(本小题满分12分)在ABC ∆中,三个内角A ,B ,C 的对边分别为a ,b ,c ,其中2c =,且cos cos 1A bB a == (1)求证:ABC ∆是直角三角形;(2)如图6,设圆O 过,,A B C 三点,点P 位于劣弧AC ︿上,求PAC ∆面积最大值.20.(本小题满分14分)在直角坐标系xOy 中,动点P 与定点(1,0)F 的距离和它到定直线2x =的距离之比是2,设动点P 的轨迹为1C ,Q 是动圆2222:C x y r +=(12)r <<上一点. (1)求动点P 的轨迹1C 的方程; (2)设曲线1C上的三点1122(,),(,)A x y B C x y 与点F 的距离成等差数列,若线段AC 的垂直平分线与x 轴的交点为T ,求直线BT 的斜率k ;(3)若直线PQ 与1C 和动圆2C 均只有一个公共点,求P 、Q 两点的距离PQ 的最大值.21.(本小题满分14分)已知函数()ln(1)f x x mx =++,当0x =时,函数()f x 取得极大值. (1)求实数m 的值;(2)已知结论:若函数()ln(1)f x x mx =++在区间(,)a b 内导数都存在,且1a >-,则存在0(,)x a b ∈,使得0()()()f b f a f x b a-'=-.试用这个结论证明:若121x x -<<,函数121112()()()()()f x f x g x x x f x x x -=-+-,则对任意12(,)x x x ∈,都有()()f x g x >;(3)已知正数12,,,n λλλL ,满足121n λλλ+++=L ,求证:当2n ≥,n N ∈时,对任意大于1-,且互不相等的实数12,,,nx x x L ,都有1122()n n f x x x λλλ+++>L 1122()()()n n f x f x f x λλλ+++L .2012届高考模拟测试数学试题(理科)参考答案和评分标准一.选择题:CACBD ABB二填空题:9.35(2分)247(3分) 10. 22(1)2x y -+= 11. 13 12. 15- 13. 33(,][,)22-∞-+∞ 14. 4315.1三、解答题: 本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.16.(本题满分14分)解:(1)设数列{}n a 的公比为q ,……………1分若1q =,则111S a ==,21244S a ==,31399S a ==,故13231022S S S +=≠⨯,与已知矛盾,故1q ≠,………………………………………………2分从而得1(1)111n nn a q q S q q--==--,………………………………………………4分由1S ,22S ,33S 成等差数列,得132322S S S +=⨯,即321113411q q q q--+⨯=⨯--, 解得13q =……………………………………………5分 所以11113n n n a a q--⎛⎫=⋅= ⎪⎝⎭.………………………………………………6分(2)由(1)得,11()3n n n b a n n -=+=+,………………………………7分 所以12(1)(2)()n n T a a a n =++++++1(1)(1)(12)12n n b q n nS n q -+=++++=+- ………………………………10分2111()(1)333.12213n n n n n n --+++-=+=-……………………………12分 17.(本题满分12分)(1)60个1×1×1的小正方体中,没有涂上颜色的有6个,61(0)6010P ξ=== … (3分) (2)由(1)可知1(0)10P ξ==;11(1)30P ξ==;2(2)5P ξ==;2(3)15P ξ== … (7分)… (10分)E ξ=0×110+1×1130+2×25+3×215=4730 …(12分)18(本题满分14分)解:(1)由题设,M ,N 是矩形的边AD 和BC 的中点,所以AM ⊥MN, BC ⊥MN, 折叠垂直关系不变,所以∠AMD 是平面ABNM 与平面MNCD 的平面角,依题意,所以∠AMD=60o , ………………………………………………………………………………………………………2分 由AM=DM ,可知△MAD 是正三角形,所以AD=2,在矩形ABCD 中,AB=2,AD=所以,,由题可知,由勾股定理可知三角形BOD 是直角三角形,所以BO ⊥DO ……………………………………………………………………………………… 5分解(2)设E ,F 是BD ,CD 的中点,则EF ⊥CD, OF ⊥CD, 所以,CD ⊥面OEF, OE CD⊥ 又BO=OD ,所以OE ⊥BD, OE⊥面ABCD, OE ⊂面BOD , 平面BOD ⊥平面ABCD过A 作AH ⊥BD ,由面面垂直的性质定理,可得AH ⊥平面BOD ,连结OH ,…………………… 8分 所以OH 是AO 在平面BOD 的投影,所以∠AOH 为所求的角,即AO 与平面BOD 所成角。
2012届北京市房山区高三二模数学理科试题(WORD精校版)

房山区2012年高三第二次模拟试题高三数学(理科)考 生 须知1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共 150分,考试时间为120分钟 。
2. 第Ⅰ卷选择题直接填涂在机读卡上。
3. 第Ⅱ卷非选择题直接写在答题纸上的指定位置,在试卷上作答无效。
4.考试结束后,将机读卡与答题纸一并交回,试卷按学校要求自己保存好。
第I 卷 选择题(共40分)一、选择题:本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项,直接涂在答题纸上。
1. n S 是数列{}n a 的前项和,且2,111++=+n n a a a , 则5S =( ) (A)40 (B)35 (C)30 (D) 252.参数方程2cos (sin x y θθθ=⎧⎨=⎩,,为参数)和极坐标方程6cos ρθ=-所表示的图形分别是( ) (A) 圆和直线 (B) 直线和直线 (C) 椭圆和直线 (D) 椭圆和圆3.正方形ABCD 的边长为1,||AB BC AC ++=( )(A )22 (B )2 (C )1 (D )22 4.在ABC ∆中,6A π=,1,2a b ==,则B = ( )(A)4π (B) 43π (C) 4π或43π (D)6π 或65π5.若x ,y 满足约束条件⎪⎩⎪⎨⎧≤≤≥+-≥+30030x y x y x ,则y x z -=2的最大值为( )(A )9 (B )8 (C )7 (D )66. 如图是某年青年歌手大奖赛中,七位评委为甲乙两名选手打出的分数的茎叶图(其中m 为数字0~9中的一个),去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a 1,a 2,则一定有 ( ) (A )a 1>a 2 (B )a 1<a 2(C )a 1=a 2 (D )a 1,a 2的大小与m 的值有关7.圆2220x y ax +-+=与直线l 相切于点(3,1)A ,则直线l 的方程为( )(A) 250x y --= (B) 210x y --= (C)20x y --= (D) 40x y +-=0795455184464793m甲 乙8.已知定点(1,2)M ,点P 和Q 分别是在直线l :1y x =-和y 轴上动点,则当△MPQ 的周长最小值时,△MPQ 的面积是( )(A)45 (B) 56(C) 1 (D) 235第II 卷 非选择题(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
2012年北京市顺义区高考数学二模试卷(理科)(附答案解析)

2012年北京市顺义区高考数学二模试卷(理科)一.选择题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项)1. 已知集合M={0, 1, 3},N={x|x=3a, a∈M},则集合M∩N=()A.{0}B.{0, 1}C.{0, 3}D.{1, 3}2. 已知i为虚数单位,则复数i(1−i)所对应点的坐标为()A.(−1, 1)B.(1, 1)C.(1, −1)D.(−1, −1)3. “p且q是真命题”是“非p为假命题”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也木必要条件4. 如图给出的是计算12+14+16+⋯+120的值的一个程序框图,判断框内应填入的条件是()A.i<20B.i>20C.i<10D.i>105. 已知直线l:x−y−1=0和圆C:{x=cosθy=1+sinθ(θ为参数,θ∈R),则直线l与圆C的位置关系为()A.直线与圆相交B.直线与圆相切C.直线与圆相离D.直线与圆相交但不过圆心6. 甲乙两人从4门课程中各选修2门,则甲乙两人所选的课程中恰有1门相同的选法有()A.12种B.16种C.24种D.48种7. 一个空间几何体的三视图如图所示,则该几何体的体积为()A.60B.80C.100D.1208. 已知椭圆G:x2a2+y2b2=1(a>b>0)的离心率为√22,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,则满足条件的点M的个数是()A.4B.8C.12D.16二.填空题(本大题共6个小题,每小题5分,共30分,把答案填在答题卡上)若(x+1x)n展开式中第二项与第四项的系数相等,则n=________;展开式中间一项的系数为________.已知数列{a n}的前n项和为S n,对任意n∈N∗都有S n=2a n−1,则a1的值为________,数列{a n}的通项公式a n=________.如图所示:圆O的直径AB=6,C为圆周上一点,∠BAC=30∘,过C作圆O的切线l,过A作直线l的垂线,垂足为D,则CD的长为________.已知O 是坐标原点,点A(−2, 1),若点M(x, y)为平面区域{x −y +1≥0y +1≥0x +y +1≤0,上的一个动点,则OA →⋅OM →的最大值为________.已知A 、B 、P 是双曲线x 2a 2−y 2b 2=1上不同的三点,且A 、B 两点关于原点O 对称,若直线PA ,PB 的斜率乘积k PA ⋅k PB =12,则该双曲线的离心率e =________.已知全集为U ,P ⊈U ,定义集合P 的特征函数为f P (x)={1,x ∈P0,x ∈C U P ,对于A ⊊U ,B ⊊U ,给出下列四个结论:①对∀x ∈U ,有f CU A (x)+f A (x)=1; ②对∀x ∈U ,若A ⊊B ,则f A (x)≤f B (x); ③对∀x ∈U ,有f A∩B (x)=f A (x)⋅f B (x); ④对∀x ∈U ,有f A∪B (x)=f A (x)+f B (x). 其中,正确结论的序号是________.三.解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤).已知向量m →=(2cos x2,1),n →=(cos x2,−1),(x ∈R),设函数f(x)=m →⋅n →. (1)求函数f(x)的值域;(2)已知△ABC 的三个内角分别为A 、B 、C ,若f(A)=13,BC =2√3,AC =3,求边长AB 的值.如图:四棱锥P −ABCD 中,底面ABCD 是平行四边形,∠ACB =90∘,PA ⊥平面ABCD ,PA =BC =1,AB =√2,F 是BC 的中点.(1)求证:DA ⊥平面PAC ;(2)试在线段PD 上确定一点G ,使CG // 平面PAF ;(3)求平面PAF 与平面PCD 所成锐二面角的余弦值.计算机考试分理论考试与实际操作考试两部分进行,每部分考试成绩只记“合格”与“不合格”,两部分考试都“合格”者,则计算机考试“合格”并颁发“合格证书”.甲、乙、丙三人在理论考试中“合格”的概率依次为:45、34、23,在实际操作考试中“合格”的概率依次为:12、23、56,所有考试是否合格相互之间没有影响. (1)假设甲、乙、丙3人同时进行理论与实际操作两项考试,谁获得“合格证书”的可能性大;(2)求这3人进行理论与实际操作两项考试后,恰有2人获得“合格证书”的概率;(3)用X 表示甲、乙、丙3人在理论考试中合格的人数,求X 的分布列和数学期望EX .已知函数f(x)=x −ln x ,g(x)=x +a 2x,(其中a >0).(1)求曲线y =f(x)在(1, f(1))处的切线方程;(2)若x =1是函数ℎ(x)=f(x)+g(x)的极值点,求实数a 的值;(3)若对任意的x 1,x 2∈[1, e],(e 为自然对数的底数,e ≈2.718)都有f(x 1)≤g(x 2),求实数a 的取值范围.已知动圆过点M(2, 0),且被y 轴截得的线段长为4,记动圆圆心的轨迹为曲线C . (1)求曲线C 的方程;(2)过点M 的直线交曲线C 于A ,B 两点,若在x 轴上存在定点P(a, 0),使PM 平分∠APB ,求P 点的坐标.对于定义域为A 的函数f(x),如果任意的x 1,x 2∈A ,当x 1<x 2时,都有f(x 1)<f(x 2),则称函数f(x)是A上的严格增函数;函数f(k)是定义在N ∗上,函数值也在N ∗中的严格增函数,并且满足条件f (f(k))=3k . (I )证明:f(3k)=3f(k);(II )求f(3k−1)(k ∈N ∗)的值;(III )是否存在p 个连续的自然数,使得它们的函数值依次也是连续的自然数;若存在,找出所有的p 值,若不存在,请说明理由.参考答案与试题解析2012年北京市顺义区高考数学二模试卷(理科)一.选择题(本大题共8个小题,每小题5分,共40分,在每小题给出的四个选项中,选出符合题目要求的一项)1.【答案】C【考点】交集及其运算【解析】将集合M中的元素0,1,3分别代入x=3a中计算,确定出集合N中的元素,得到集合N,找出两集合的公共元素,即可求出两集合的交集.【解答】解:∵合M={0, 1, 3},N={x|x=3a, a∈M},∴集合N中的元素为:0,3,9,即N={0, 3, 9},则M∩N={0, 3}.故选C2.【答案】B【考点】复数代数形式的乘除运算复数的代数表示法及其几何意义【解析】先将z化为代数形式,确定好实部虚部,复数与复平面内点的对应关系得出对应的点的坐标.【解答】解:z=i(1−i)=i−i2=1+i,根据复数与复平面内点的对应关系,z对应的点为(1, 1)故选B.3.【答案】A【考点】必要条件、充分条件与充要条件的判断【解析】本题考查判断充要条件的方法,可以根据充要条件的定义判断,本题关键是复合命题真假的判断.【解答】解:由p且q是真命题知,p和q均为真命题,所以非p为假命题,所以“p且q是真命题”是“非p为假命题”的充分条件;由非p为假命题知,p为真命题,但q真假不知,故无法判断p且q真假,所以“p且q是真命题”是“非p为假命题”的不必要条件.故选A 4.【答案】D【考点】循环结构的应用【解析】由程序中的变量、各语句的作用,结合流程图所给的顺序,可知当条件满足时,用1n+s的值代替s得到新的s,并用n+2代替n、用i+1代替i,直到条件满足时,输出最后算出的s值.由此结合题意即可得到本题答案.【解答】解:由题意,该程序按如下步骤运行经过第一次循环得到s=12,n=4,i=2;经过第二次循环得到s=12+14,n=6,i=3;经过第三次循环得到s=12+14+16,n=8,i=4;…看到S中最后一项的分母与i的关系是:分母=2(i−1)∴20=2(i−1)解得i=11时需要输出所以判断框的条件应为i>10.故选D.5.【答案】C【考点】圆的参数方程直线与圆的位置关系【解析】化圆的参数方程为普通方程,求出圆的圆心坐标和半径,然后由点到直线的距离公式求出圆心到直线的距离,和半径比较后即可得到结论.【解答】解:由{x=cosθy=1+sinθ(θ为参数,θ∈R),得x2+(y−1)2=1.所以给出的圆C的圆心是(0, 1),半径为1.又直线l:x−y−1=0,由点到直线的距离公式得到圆心到直线的距离d=√12+(−1)2=√2>1.所以直线l与圆C的位置关系为相离.故选C.6.【答案】C【考点】排列、组合及简单计数问题【解析】间接法:①先求所有两人各选修2门的种数,②再求两人所选两门都相同与都不同的种数,作差可得答案.【解答】解:根据题意,采用间接法:①由题意可得,所有两人各选修2门的种数C42C42=36,②两人所选两门都相同的有为C42=6种,都不同的种数为C42=6,故只恰好有1门相同的选法有36−6−6=24种.故选C7.【答案】B【考点】由三视图求体积【解析】由三视图可知:该几何体是一个横放的直四棱柱,其高为4,底面是一个等腰梯形,上下底边分别为2,8,高为4.据此即可得出体积‘【解答】解:由三视图可知:该几何体是一个横放的直四棱柱,其高为4,底面是一个等腰梯形,上下底边分别为2,8,高为4.∴V=(2+8)×42×4=80.故选B.8.【答案】C【考点】椭圆的定义【解析】以椭圆G的一个顶点和一个焦点构成的线段的垂直平分线与椭圆的交点坐标都是满足条件的点M.【解答】解:设椭圆G:x 2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,左、右顶点分别为A1,A2,下顶点为B1,上顶点为B2,∵椭圆G:x2a2+y2b2=1(a>b>0)的离心率为√22,⊙M过椭圆G的一个顶点和一个焦点,圆心M在此椭圆上,∴A1F1、A1F2、A2F1、A2F2、B1F1、B2F1的垂直平分线与椭圆G的坐标都是满足条件的点M,∴满足条件的点M的个数是12个.故选C.二.填空题(本大题共6个小题,每小题5分,共30分,把答案填在答题卡上)【答案】4,6【考点】二项式定理的应用【解析】由题意可得C n1=C n3,故有1+3=n,求得n的值,从而求得展开式中间一项的系数【解答】解:若(x+1x)n展开式中第二项与第四项的系数相等,则得C n1=C n3,∴1+3=n,则n=4.展开式中间一项的系数为C42=6,故答案为4;6.【答案】1,2n−1【考点】数列递推式【解析】把n=1代入S n=2a n−1就可以求出a1的值;首先表示出s n−1,然后利用a n=s n−s n−1,即可求出通项公式.【解答】解:当n=1时,s1=2a1−1∴a1=1∵S n=2a n−1①∴s n−1=2a n−1−1②①-②得,a n=2a n−2a n−1∴a na n−1=2∴数列{a n}是以1为首项公比为2的等比数列∴数列{a n}的通项公式a n=2n−1故答案为1,2n−1.【答案】3√32【考点】与圆有关的比例线段【解析】连结BC,可得△ABC是以AB为斜边的直角三角形,结合∠BAC=30∘且AB=6算出AC=3√3.由弦切角定理,得Rt△ADC中,∠DCA=∠B=60∘,从而算出CD=AC cos60∘=3√32,得到本题答案.【解答】解:连结BC,∵AB是圆O的直径,∴∠ACB=90∘∵∠BAC=30∘,AB=6,∴BC=12AB=3,AC=√32AB=3√3,∠B=60∘又∵直线CD切圆O于C,∴∠DCA=∠B=60∘因此,Rt △ADC 中,CD =12AC =3√32故答案为:3√32【答案】3【考点】 简单线性规划数量积的坐标表达式 【解析】首先画出可行域,z =OA →⋅OM →代入坐标变为z =x +2y ,即y =−2x +z ,z 表示斜率为−2的直线在y 轴上的截距,故求z 的最大值,即平移直线y =−2x 与可行域有公共点时直线在y 轴上的截距的最大值即可. 【解答】解:如图所示:z =OA →⋅OM →=−2x +y ,即y =2x +z ,首先做出直线l 0:y =2x ,将l 0平行移动,当经过B(−2, −1)点时在y 轴上的截距最大,从而z 最大. 因为B(−2, −1),故z 的最大值为z =2×2−1=3.故答案为:3.【答案】 √62【考点】 双曲线的特性 【解析】设出点点的坐标,求出斜率,将点的坐标代入方程,两式相减,再结合k PA ⋅k PB =12,即可求得结论. 【解答】解:由题意,设A(x 1, y 1),P(x 2, y 2),则B(−x 1, −y 1)∴ k PA ⋅k PB =y 2−y 1x 2−x 1×y 2+y1x 2+x 1=y 22−y 12x 22−x 12∵ x 12a 2−y 12b 2=1,x 22a 2−y 22b 2=1,∴ 两式相减可得y 22−y 12x 22−x 12=b 2a 2∵ k PA ⋅k PB =12,∴ b 2a 2=12∴c 2−a 2a 2=12,∴c 2a 2−1=12∴ c 2a 2=32,∴ e =ca =√62故答案为:√62【答案】 ①、②、③ 【考点】全称命题与特称命题 【解析】利用特殊值法,先设出特殊的集合U ,A ,B ,然后再验证判断四个命题的真假即可得出答案. 【解答】解:利用特殊值法进行求解.设U ={1, 2, 3},A ={1},B ={1, 2}.那么:对于①有f A (1)=1,f A (2)=0,f A (3)=0,f C U A (1)=0,f C U A (2)=1,f C U A (3)=1.可知①正确; 对于②有f A (1)=1=f B (1),f A (2)=0<f B (2)=1,f A (3)=f B (3)=0可知②正确;对于③有f A (1)=1,f A (2)=0,f A (3)=0,f B (1)=1,f B (2)=1,f B (3)=0,f A∩B (1)=1,f A∩B (2)=0,f A∩B (3)=0.可知③正确;对于④有f A (1)=1,f A (2)=0,f A (3)=0,f B (1)=1,f B (2)=1,f B (3)=0,f A∪B (1)=1,f A∪B (2)=1,f A∪B (3)=0可知.④不正确. 故答案为:①、②、③.三.解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤). 【答案】解:(1)∵ 向量m →=(2cos x2,1),n →=(cos x2,−1),(x ∈R)∴ f(x)=m →⋅n →=2cos 2x2−1=cos x , ∵ x ∈R ,∴ f(x)=cos x 的值域为[−1, 1]. (2) f(A)=cos A =13,由余弦定理BC 2=AC 2+AB 2−2AC ⋅AB ⋅cos A ∴ 12=9+c 2−2×3×c ×13,即c 2−2c −3=0 ∴ AB =c =3. 【考点】 余弦定理数量积的坐标表达式【解析】(I 利用向量的数量积公式,结合二倍角公式化简函数,即可求函数f(x)的值域;(2)利用余弦定理,建立方程,即可求c 的值. 【解答】解:(1)∵ 向量m →=(2cos x2,1),n →=(cos x2,−1),(x ∈R) ∴ f(x)=m →⋅n →=2cos 2x2−1=cos x ,∵ x ∈R ,∴ f(x)=cos x 的值域为[−1, 1]. (2) f(A)=cos A =13,由余弦定理BC 2=AC 2+AB 2−2AC ⋅AB ⋅cos A ∴ 12=9+c 2−2×3×c ×13,即c 2−2c −3=0 ∴ AB =c =3.【答案】(1) 证明:∵ 四边形是平行四边形,∴ ∠ACB =∠DAC =90∘, ∵ PA ⊥平面ABCD ,∴ PA ⊥DA ,又AC ⊥DA ,AC ∩PA =A ,∴ DA ⊥平面PAC .(2)解:分别以AC ,AD ,AP 为x 、y 、z 轴建立空间直角坐标系,则A(0,0,0),C(1,0,0),B(1,−1,0),D(0,1,0),F(1,−12,0),P(0,0,1) 设G 为PD 上一点,使CG // 平面PAF ,令PG →=λPD →=(0,λ,−λ),(0≤λ≤√2),GC →=PC →−PG →=(1,−λ,−1+λ) 设平面PAF 法向量为m →=(x,y,z) ∵ AP →=(0,0,1),AF →=(1,−12,0) ∴ {z =0x −y 2=0∴ 可取平面PAF 法向量m →=(1,2,0),要CG // 平面PAF ,∴ m →⋅GC →=0,解得λ=12. ∴ G 为PD 中点时,CG // 平面PAF . (3)解:平面PCD 法向量为n →=(x′,y′,z′) ∵ PC →=(1,0,−1),PD →=(0,1,−1)∴ {x′−z′=0y′−z′=0∴ 可取平面PCD 法向量n →=(1,1,1), ∴ cos <m →,n →>=|m →||n →|˙=√155∴ 所求二面角的余弦值为√155. 【考点】用空间向量求平面间的夹角 直线与平面平行的判定 直线与平面垂直的判定 二面角的平面角及求法【解析】(1)利用平行四边形的性质和平行线的性质可得AD ⊥AC ,再利用线面垂直的性质可得PA ⊥AC ,利用线面垂直的判定定理即可证明;(2)分别以AC ,AD ,AP 为x 、y 、z 轴建立空间直角坐标系,求出平面PAF 法向量m →,要CG // 平面PAF ,可得m →⋅GC →=0,即可求得结论;(3)确定平面PCD 法向量,利用向量的夹角公式,即可求平面PAF 与平面PCD 所成锐二面角的余弦值.【解答】(1) 证明:∵ 四边形是平行四边形,∴ ∠ACB =∠DAC =90∘, ∵ PA ⊥平面ABCD ,∴ PA ⊥DA ,又AC ⊥DA ,AC ∩PA =A ,∴ DA ⊥平面PAC .(2)解:分别以AC ,AD ,AP 为x 、y 、z 轴建立空间直角坐标系,则A(0,0,0),C(1,0,0),B(1,−1,0),D(0,1,0),F(1,−12,0),P(0,0,1)设G 为PD 上一点,使CG // 平面PAF ,令PG →=λPD →=(0,λ,−λ),(0≤λ≤√2),GC →=PC →−PG →=(1,−λ,−1+λ) 设平面PAF 法向量为m →=(x,y,z) ∵ AP →=(0,0,1),AF →=(1,−12,0) ∴ {z =0x −y 2=0∴ 可取平面PAF 法向量m →=(1,2,0),要CG // 平面PAF ,∴ m →⋅GC →=0,解得λ=12. ∴ G 为PD 中点时,CG // 平面PAF . (3)解:平面PCD 法向量为n →=(x′,y′,z′) ∵ PC →=(1,0,−1),PD →=(0,1,−1) ∴ {x′−z′=0y′−z′=0∴ 可取平面PCD 法向量n →=(1,1,1), ∴ cos <m →,n →>=|m →||n →|˙=√155∴ 所求二面角的余弦值为√155. 【答案】解:(1)记“甲获得合格证书”为事件A ,“乙获得合格证书”为事件B ,“丙获得合格证书”为事件C , 则P(A)=45×12=25=3690,P(B)=34×23=12=4590,P(C)=23×56=59=5090 P(C)>P(B)>P(A),所以丙获得合格证书的可能性大.__________ (2)设3人考试后恰有2人获得“合格证书”为事件D , ∴ P(D)=P(A,B,C ¯)+P(A,B ¯,C)+P(A ¯,B,C) =25×12×49+25×12×59+35×12×59=1130.__________ (3)由题意可得X =0,1,2,3., 可得P(X =0)=15×14×13=160,P(X =1)=45×14×13+15×34×13+15×14×23=960,P(X =2)=45×34×13+45×14×23+15×34×23=2660,P(X =3)=45×34×23=2460__________ 故X 的分布列为:∴ EX =0×160+1×960+2×2660+3×2460=13360; __________【考点】离散型随机变量的期望与方差 相互独立事件的概率乘法公式【解析】(1)记“甲、乙、丙获得合格证书”分别为事件A 、B 、C ,由独立事件的概率分别可得P(C),P(B),P(A),比较大小可得结论;(2)设3人考试后恰有2人获得“合格证书”为事件D ,可得P(D)=P(A,B,C ¯)+P(A,B ¯,C)+P(A ¯,B,C),由独立事件和互斥事件的概率公式可得;(3)由题意可得X =0,1,2,3,分别可得可得其对应的概率,进而可得X 的分布列为和数学期望EX . 【解答】解:(1)记“甲获得合格证书”为事件A ,“乙获得合格证书”为事件B ,“丙获得合格证书”为事件C , 则P(A)=45×12=25=3690,P(B)=34×23=12=4590,P(C)=23×56=59=5090 P(C)>P(B)>P(A),所以丙获得合格证书的可能性大.__________ (2)设3人考试后恰有2人获得“合格证书”为事件D , ∴ P(D)=P(A,B,C ¯)+P(A,B ¯,C)+P(A ¯,B,C) =25×12×49+25×12×59+35×12×59=1130.__________ (3)由题意可得X =0,1,2,3.,可得P(X =0)=15×14×13=160,P(X =1)=45×14×13+15×34×13+15×14×23=960, P(X =2)=45×34×13+45×14×23+15×34×23=2660,P(X =3)=45×34×23=2460__________ 故X 的分布列为:∴ EX =0×160+1×960+2×2660+3×2460=13360; __________【答案】解:(1)f(1)=1−ln 1=1,f′(x)=1−1x ,则f′(1)=0,即切线斜率为0, 故曲线y =f(x)在(1, f(1))处的切线方程为y −1=0⋅(x −1),即y =1; (2)ℎ(x)=f(x)+g(x)=x −ln x +x +a 2x=2x +a 2x−ln x ,定义域为(0, +∞),∴ ℎ′(x)=2−a 2x 2−1x =2x 2−x−a 2x 2,令ℎ′(1)=0,解得a 2=1, 又a >0,∴ a =1, 经验证a =1符合条件.(3)对任意的x 1,x 2∈[1, e]都有f(x 1)≤g(x 2)成立,等价于对任意的x ∈[1, e]都有f max (x)≤g min (x)成立, 当x ∈[1, e]时,f ′(x)=1−1x =x−1x≥0,∴ f(x)在[1, e]上单调递增,f max (x)=f(e)=e −1.∵ g ′(x)=1−a 2x 2=(x−a)(x+a)x 2,x ∈[1, e],a >0,∴ ①若0<a≤1,g′(x)≥0,g(x)=x+a2x在[1, e]上单调递增,∴g min(x)=g(1)=1+a2,∴1+a2≥e−1,解得√e−2≤a≤1.②若1<a<e,当1≤x<a时,则g′(x)=(x−a)(x+a)x2<0,当a≤x≤e时,则g′(x)=(x−a)(x+a)x2≥0,∴g(x)在[1, a)上递减,在[a, e]上递增,g min(x)=g(a)=2a≥f max(x)=e−1,解得a≥e−12,又1<a<e,∴a∈(1, e)③当a≥e时,g′(x)=(x−a)(x+a)x2≤0,∴g(x)在[1, e]上递减,g min(x)=g(e)=e+a2e≥f max(x)=e−1,∴a2≥−e恒成立.综上所述a∈[√e−2,+∞).【考点】导数求函数的最值函数在某点取得极值的条件利用导数研究曲线上某点切线方程【解析】(1)求出切点坐标,切线斜率f′(1),由点斜式即可求得切线方程;(2)写出ℎ(x)及其定义域,求出ℎ′(x),由题意得ℎ′(1)=0,解出a值再进行验证即可;(3)对任意的x1,x2∈[1, e]都有f(x1)≤g(x2)成立,等价于对任意的x∈[1, e]都有f max(x)≤g min(x)成立,利用导数易判断f(x)在[1, e]上单调,从而可求得其最大值;求出导数g′(x)=(x−a)(x+a)x2,分0<a≤1,1<a<e,a≥e三种情况进行讨论可得g min(x),然后解不等式f max(x)≤g min(x)可求得a的取值范围;【解答】解:(1)f(1)=1−ln1=1,f′(x)=1−1x,则f′(1)=0,即切线斜率为0,故曲线y=f(x)在(1, f(1))处的切线方程为y−1=0⋅(x−1),即y=1;(2)ℎ(x)=f(x)+g(x)=x−ln x+x+a 2x =2x+a2x−ln x,定义域为(0, +∞),∴ℎ′(x)=2−a2x2−1x=2x2−x−a2x2,令ℎ′(1)=0,解得a2=1,又a>0,∴a=1,经验证a=1符合条件.(3)对任意的x1,x2∈[1, e]都有f(x1)≤g(x2)成立,等价于对任意的x∈[1, e]都有f max(x)≤g min(x)成立,当x∈[1, e]时,f′(x)=1−1x =x−1x≥0,∴f(x)在[1, e]上单调递增,f max(x)=f(e)=e−1.∵g′(x)=1−a2x2=(x−a)(x+a)x2,x∈[1, e],a>0,∴ ①若0<a≤1,g′(x)≥0,g(x)=x+a2x 在[1, e]上单调递增,∴g min(x)=g(1)=1+a2,∴1+a2≥e−1,解得√e−2≤a≤1.②若1<a<e,当1≤x<a时,则g′(x)=(x−a)(x+a)x2<0,当a≤x≤e时,则g′(x)=(x−a)(x+a)x2≥0,∴g(x)在[1, a)上递减,在[a, e]上递增,g min(x)=g(a)=2a≥f max(x)=e−1,解得a≥e−12,又1<a<e,∴a∈(1, e)③当a≥e时,g′(x)=(x−a)(x+a)x2≤0,∴g(x)在[1, e]上递减,g min(x)=g(e)=e+a2e≥f max(x)=e−1,∴a2≥−e恒成立.综上所述a∈[√e−2,+∞).【答案】解:(1)设动圆圆心的坐标为(x, y).依题意,有22+|x|2=(x−2)2+y2,化简得y2=4x.所以动圆圆心的轨迹方程为y2=4x.(2)解法1:设A(x1, y1),B(x2, y2),直线AB的方程为x=my+2.将直线AB的方程与曲线C的方程联立,消去x得:y2−4my−8=0.所以y1+y2=4m,y1y2=−8.若PM平分∠APB,则直线PA,PB的倾斜角互补,所以k PA+k PB=0.∵P(a, 0),则有y1x1−a+y2x2−a=0.将x1=my1+2,x2=my2+2代入上式,整理得2my1y2+(2−a)(y1+y2)(my1+2−a)(my2+2−a)=0,所以2my1y2+(2−a)(y1+y2)=0.将y1+y2=4m,y1y2=−8代入上式,得(a+2)⋅m=0对任意实数m都成立,所以a=−2.故定点P的坐标为(−2, 0).解法2:设A(x1, y1),B(x2, y2),当过点M(2, 0)的直线斜率不存在,则l AB:x=2,A,B两点关于x轴对称,x轴上任意一点P(a, 0)(a≠2)均满足PM平分∠APB,不合题意.当过点M(2, 0)的斜率k存在时(k≠0),设l AB:y=k(x−2),联立{y=k(x−2)y2=4x,消去y得k2x2−4(k2+1)x+4k2=0,△=32k2+16>0,x1+x2=4k2+4k2,x1x2=4,∵PM平分∠APB,则直线PA,PB的倾斜角互补,∴k PA+k PB=0.∵P(a, 0),(a≠2),则有y1x1−a+y2x2−a=0.将y1=k(x1−2)y2=k(x2−2)代入上式,整理得k(x1−2)(x2−a)+k(x2−2)(x1−a)(x1−a)(x2−a)=0,∴k(x1−2)(x2−a)+k(x2−2)(x1−a)=0整理得2x1x2−(x1+x2)(2+a)+4a=0,将x1+x2=4k2+4k2,x1x2=4代入化简得a=−2,故定点P的坐标为(−2, 0).【考点】直线与椭圆结合的最值问题圆锥曲线的轨迹问题【解析】(1)设动圆圆心的坐标为(x, y),利用垂径定理和两点间的距离公式即可得到22+|x|2=(x−2)2+y2,化简即可.(2)解法1:设A(x1, y1),B(x2, y2),直线AB的方程为x=my+2.将直线AB的方程与曲线C的方程联立,消去x得:y2−4my−8=0.得到根与系数的关系y1+y2=4m,y1y2=−8.由PM平分∠APB,则直线PA,PB的倾斜角互补,可得k PA+k PB=0.利用斜率计算公式可得y1x1−a +y2x2−a=0.将x1=my1+2,x2=my2+2代入上式,整理得2my1y2+(2−a)(y1+y2)(my1+2−a)(my2+2−a)=0,即2my1y2+(2−a)(y1+y2)=0.把y1+y2=4m,y1y2=−8代入上式,(a+2)⋅m=0对任意实数m都成立,即可得到a的值;解法2:设A(x1, y1),B(x2, y2),①当过点M(2, 0)的直线斜率不存在,则l AB:x=2,A,B两点关于x轴对称,x轴上任意一点P(a, 0)(a≠2)均满足PM平分∠APB,不合题意.②当过点M(2, 0)的斜率k存在时(k≠0),设l AB:y=k(x−2),与抛物线方程联立,消去y得k2x2−4(k2+1)x+4k2=0,△=32k2+16>0,得到根与系数的关系x1+x2=4k2+4k2,x1x2=4;由已知PM平分∠APB,则直线PA,PB的倾斜角互补,可得k PA+k PB=0.以下类比解法1.【解答】解:(1)设动圆圆心的坐标为(x, y).依题意,有22+|x|2=(x−2)2+y2,化简得y2=4x.所以动圆圆心的轨迹方程为y2=4x.(2)解法1:设A(x1, y1),B(x2, y2),直线AB的方程为x=my+2.将直线AB的方程与曲线C的方程联立,消去x得:y2−4my−8=0.所以y1+y2=4m,y1y2=−8.若PM平分∠APB,则直线PA,PB的倾斜角互补,所以k PA+k PB=0.∵P(a, 0),则有y1x1−a +y2x2−a=0.将x1=my1+2,x2=my2+2代入上式,整理得2my1y2+(2−a)(y1+y2)(my1+2−a)(my2+2−a)=0,所以2my1y2+(2−a)(y1+y2)=0.将y1+y2=4m,y1y2=−8代入上式,得(a+2)⋅m=0对任意实数m都成立,所以a=−2.故定点P的坐标为(−2, 0).解法2:设A(x1, y1),B(x2, y2),当过点M(2, 0)的直线斜率不存在,则l AB:x=2,A,B两点关于x轴对称,x轴上任意一点P(a, 0)(a≠2)均满足PM平分∠APB,不合题意.当过点M(2, 0)的斜率k存在时(k≠0),设l AB:y=k(x−2),联立{y=k(x−2)y2=4x,消去y得k2x2−4(k2+1)x+4k2=0,△=32k2+16>0,x1+x2=4k2+4k2,x1x2=4,∵PM平分∠APB,则直线PA,PB的倾斜角互补,∴k PA+k PB=0.∵P(a, 0),(a≠2),则有y1x1−a+y2x2−a=0.将y1=k(x1−2)y2=k(x2−2)代入上式,整理得k(x1−2)(x2−a)+k(x2−2)(x1−a)(x1−a)(x2−a)=0,∴k(x1−2)(x2−a)+k(x2−2)(x1−a)=0整理得2x1x2−(x1+x2)(2+a)+4a=0,将x1+x2=4k2+4k2,x1x2=4代入化简得a=−2,故定点P的坐标为(−2, 0).【答案】解:(I)证明:∵对k∈N∗,f(f(k))=3k,∴f[f(f(k))]=f(3k)①,由已知f(f(k))=3k,∴f[f(f(k))]=3f(k)②,由①、②得f(3k)=3f(k);(II)若f(1)=1,由已知f(f(k))=3k得f(1)=3,矛盾;设f(1)=a>1,∴f(f(1))=f(a)=3,③由f(k)严格递增,即1<a⇒f(1)<f(a)=3.,∴{f(1)≠1f(1)<3f(1)∈N∗,∴f(1)=2,由③有f(f(1))=f(a)=3,故f(f(1))=f(2)=3,∴f(1)=2,f(2)=3,f(3)=3f(1)=6,f(6)=f(3⋅2)=3f(2)=9,f(9)=3f(3)=18,f(18)=3f(6)=27,f(27)=3f(9)=54,f(54)=3f(18)=81,…依此类推归纳猜出:f(3k−1)=2×3k−1(k∈N∗).下面用数学归纳法证明:(1)当k=1时,显然成立;(2)假设当k=l(l≥1)时成立,即f(3l−1)=2×3l−1,那么当k=l+1时,f(3l)=f(3×3l−1)=3f(3l−1)=3×2×3l−1=2⋅3l.猜想成立,由(1)、(2)所证可知,对k∈N∗f(3k−1)=2×3k−1成立.(III)存在p=3k−1+1,当p个连续自然数从3k−1→2×3k−1时,函数值正好也是p个连续自然数从f(3k−1)=2×3k−1→f(2×3k−1)=3k.【考点】函数恒成立问题【解析】(I)证明:由f(f(k))=3k,得f[f(f(k))]=f(3k)①,再由f(f(k))=3k,得f[f(f(k))]=3f(k)②,联立①②可得结论.(II)由已知易判断f(1)=1不成立,设f(1)=a>1,则f(f(1))=f(a)=3③,由f(k)严格递增,可判断f(1)=2,且f(2)=3,由此可推得f(3)=6,f(9)=3f(3)=18,f(27)=54,…,依此类推归纳猜出:f(3k−1)=2×3k−1(k∈N∗).再用数学归纳法证明即可;(III)由已知及(I)(II)知:当p个连续自然数从3k−1→2×3k−1时,函数值正好也是p个连续自然数从f(3k−1)=2×3k−1→f(2×3k−1)=3k.【解答】解:(I)证明:∵对k∈N∗,f(f(k))=3k,∴f[f(f(k))]=f(3k)①,由已知f(f(k))=3k,∴f[f(f(k))]=3f(k)②,由①、②得f(3k)=3f(k);(II)若f(1)=1,由已知f(f(k))=3k得f(1)=3,矛盾;设f(1)=a>1,∴f(f(1))=f(a)=3,③由f(k)严格递增,即1<a⇒f(1)<f(a)=3.,∴{f(1)≠1 f(1)<3f(1)∈N∗,∴f(1)=2,由③有f(f(1))=f(a)=3,故f(f(1))=f(2)=3,∴f(1)=2,f(2)=3,f(3)=3f(1)=6,f(6)=f(3⋅2)=3f(2)=9,f(9)=3f(3)=18,f(18)= 3f(6)=27,f(27)=3f(9)=54,f(54)=3f(18)=81,…依此类推归纳猜出:f(3k−1)=2×3k−1(k∈N∗).下面用数学归纳法证明:(1)当k=1时,显然成立;(2)假设当k=l(l≥1)时成立,即f(3l−1)=2×3l−1,那么当k=l+1时,f(3l)=f(3×3l−1)=3f(3l−1)=3×2×3l−1=2⋅3l.猜想成立,由(1)、(2)所证可知,对k∈N∗f(3k−1)=2×3k−1成立.(III)存在p=3k−1+1,当p个连续自然数从3k−1→2×3k−1时,函数值正好也是p个连续自然数从f(3k−1)=2×3k−1→f(2×3k−1)=3k.。
2012年北京市怀柔区高三二模数学理试卷及答案

2012年北京市怀柔区高三二模数学理试卷及答案各位考生,2012年高考信息陆续出炉,下面是教育城高考网(/gaokao )小编整理的:2012年北京市怀柔区高三二模数学理试卷及答案,请大家继续关注教育城高考网(/gaokao )。
2012年怀柔区高三年级调研考试 数 学(理科) 2012.4一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中, 有且只有一项是符合题目要求的.1.已知全集U={一l ,0,1,2},集合A={一l ,2},B={0,2},则=⋂B A C U )(A .{0}B .{2}C .{0,l ,2}D .φ2.已知i 为虚数单位,2=iz,则复数=zA .i -1B .i +1C .2iD .-2i 3.“a=2”是“直线ax 十2y=0与直线x+y=l 平行”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.一个四棱锥的三视图如图所示,其中主视图是腰长为1的等腰直角三角形,则这个几何体的体积是 A .21B .1C .23D .2 5.函数2(sin cos )1y x x =+-是A .最小正周期为π2的奇函数B .最小正周期为π2的偶函数C .最小正周期为π的奇函数D .最小正周期为π的偶函数6.过点π4,2A ⎛⎫- ⎪⎝⎭引圆4sin ρθ=的一条切线,则切线长为A .33B .36C .22D .24 7.将图中的正方体标上字母, 使其成为正方体1111ABCD A BC D -, 主视图俯视图同的标字母方式共有A .24种B .48种C .72种D .144种8.若函数()() y f x x R =∈满足()()2f x f x +=,且[]1,1x ∈-时,()21f x x =-,函数()()()lg 01 0x x g x x x ⎧>⎪=⎨-<⎪⎩,则函数()()()h x f x g x =-在区间[]5,5-内的零点的个数为A .5B .7C .8D .10 二、填空题:本大题共6小题,每小题5分,满分30分.9.二项式521⎪⎭⎫ ⎝⎛-x x 的展开式中含4x 的项的系数是 (用数字作答). 10.如图给出的是计算2011151311+⋅⋅⋅+++的值 的一个程序框图,其中判断框内应填入的条件 是 . 11.如图,P A 是圆的切线,A 为切点,PBC 是圆 的割线,且PB PA 3=则=BCPB. 12. 当(1,2)x ∈时,不等式2(1)log a x x -<恒成立,则实数a 的取值范围为 .13.已知不等式组⎪⎩⎪⎨⎧>-≥-≤+122y y x y x 表示的平面区域为,M 若直线13+-=k kx y 与平面区域M 有公共点,则k 的取值范围是 .14.手表的表面在一平面上.整点1,2,…,12这12个数字等间隔地分布在半径为22的圆周上.从整点i到整点(i +1)的向量记作1+i i t t ,则2111243323221t t t t t t t t t t t t ⋅+⋅⋅⋅+⋅+⋅= .三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤. 15.(本小题满分13分)P在ABC ∆中,a b c 、、分别为角A B C 、、的对边,且满足222b c a bc +-=. (Ⅰ)求角A 的值;(Ⅱ)若a =B 的大小为x ,ABC ∆的周长为y ,求()y f x =的最大值.16.(本小题满分14分)如图,在四棱锥S ABCD -中,底面ABCD 是正方形,其他四个侧面都是等边三角形,AC 与BD 的交点为O ,E 为侧棱SC 上一点. (Ⅰ)当E 为侧棱SC 的中点时,求证:SA ∥平面BDE ;(Ⅱ)求证:平面BDE ⊥平面SAC ; (Ⅲ)当二面角E BD C --的大小为45︒ 时,试判断点E 在SC 上的位置,并说明理由.17.(本小题满分13分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产 品作为样本称出它们的重量(单位:克),重量的分组区间为(]495,490,(]500,495,…,(]515,510.由此得到样本的频率分布直方图,如图所示:(Ⅰ)根据频率分布直方图,求重量超过505克的产品数量;(Ⅱ)在上述抽取的40个产品中任职2件,设ξ为重量超过505克的产品数量,求ξ的分布列;(Ⅲ)从流水线上任取5件产品,估计其中恰 有2件产品的重量超过505克的概率.18.(本小题满分13分)已知xxx g e x x ax x f ln )(],,0(,ln )(=∈-=,其中e 是自然常数,R a ∈. (Ⅰ)讨论1=a 时,()f x 的单调性、极值; (Ⅱ)求证:在(Ⅰ)的条件下,1()()2f xg x >+; (Ⅲ)是否存在实数a ,使()f x 的最小值是3,若存在,求出a 的值;若不存在,说明理由.19.(本小题满分14分)已知:椭圆12222=+by a x (0>>b a ),过点)0,(a A -,),0(b B 的直线倾斜角为6π,原点到该直线的距离为23. (Ⅰ)求椭圆的方程;(Ⅱ)斜率大于零的直线过)0,1(-D 与椭圆交于E ,F 两点,若2=,求直线EF 的方程;(Ⅲ)是否存在实数k ,直线2+=kx y 交椭圆于P ,Q 两点,以PQ 为直径的圆过点)0,1(-D ?若存在,求出k 的值;若不存在,请说明理由.20.(本小题满分13分 )定义:对于任意*n ∈N ,满足条件212n n n a a a +++≤且n a M ≤(M 是与n 无关的常数)的无穷数列{}n a 称为T 数列.(Ⅰ)若29n a n n =-+(*n ∈N ),证明:数列{}n a 是T 数列;(Ⅱ)设数列{}n b 的通项为3502nn b n ⎛⎫=- ⎪⎝⎭,且数列{}n b 是T 数列,求常数M 的取值范围;(Ⅲ)设数列1n pc n=-(*n ∈N ,1p >),问数列{}n c 是否是T 数列?请说明理由.参考答案及评分标准一、选择题:本大题共8个小题;每小题5分,共40分.9.10 10.2011≤i 11.2112.]2,1( 13.)0,31[- 14.936- 三、解答题:本大题共6小题,满分80分. 15.(本小题满分13分)在ABC ∆中,a b c 、、分别为角A B C 、、的对边,且满足222b c a bc +-=. (Ⅰ)求角A 的值;(Ⅱ)若a =B 的大小为x ,ABC ∆的周长为y ,求()y f x =的最大值. 解:(Ⅰ)∵222b c a bc +-=,∴2221cos 22b c a A bc +-==又0A π<<, ∴3A π=; -------------------------------------------------------------5分(Ⅱ)∵Aa xb sin sin =, ∴x x x a b sin 2sin 233sin 3sin=⋅=⋅=π同理)32sin(sin sin x C A a c -=⋅=π∴3)6sin(323)32sin(2sin 2++=+-+=ππx x x y∵320,3ππ<<∴=x A ∴)65,6(6πππ∈+x ,∴62x ππ+=即3x π=时,max y =分16.(本小题满分14分)如图,在四棱锥S ABCD-中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.(Ⅰ)当E为侧棱SC的中点时,求证:SA∥平面BDE;(Ⅱ)求证:平面BDE⊥平面SAC;(Ⅲ)当二面角E BD C--的大小为45︒时,试判断点E在SC上的位置,并说明理由.(Ⅰ)证明:连接OE,由条件可得SA∥OE.因为SAË平面BDE,OEÌ平面BDE,所以SA∥平面BDE(Ⅱ)证明:由(Ⅰ)知SO ABCD⊥面,AC BD⊥.建立如图所示的空间直角坐标系.设四棱锥S ABCD-的底面边长为2,则(0, 0, 0)O,(0, 0,S,)0, 0A,()0, 0B,()0, 0C,()0, 0D.所以()0, 0AC=-,()0, 0BD=-.设CE a=(02a<<),由已知可求得45ECO∠=︒.所以(, 0,)22E a,(,)22BE a=.设平面BDE法向量为(,,)x y z=n,则0,BDBE⎧⋅=⎪⎨⋅=⎪⎩nn即0,()0.22yx az=⎧⎪⎨+=⎪⎩令1z=,得(, 0, 1)2aa=-n.易知()0, 0BD=-是平面SAC的法向量.因为(, 0, 1)(0, 0)02aBDa⋅=⋅-=-n,所以BD⊥n,所以平面BDE⊥平面SAC.-------------------------------------9分(Ⅲ)解:设CE a =(02a <<),由(Ⅱ)可知,平面BDE 法向量为(, 0, 1)2aa=-n . 因为SO ABCD ⊥底面,所以(0, 0,OS =是平面SAC 的一个法向量.由已知二面角E BD C --的大小为45︒.所以cos , cos 452OS 〈〉=︒= n ,2=,解得1a =.[ 所以点E 是SC 的中点.-----------------------------------------------------------------14分 17.(本小题满分13分)某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的40件产 品作为样本称出它们的重量(单位:克),重量的分组区间为(]495,490,(]500,495,…,(]515,510.由此得到样本的频率分布直方图,如图所示:(Ⅰ)根据频率分布直方图,求重量超过505克的产品数量;(Ⅱ)在上述抽取的40个产品中任职2件,设ξ为重量超过505克的产品数量,求ξ的分布列;(Ⅲ)从流水线上任取5件产品,估计其中恰 有2件产品的重量超过505克的概率.解:(Ⅰ)重量超过505克的产品数量是12)501.0505.0(40=⨯+⨯⨯件------------2分(Ⅱ)ξ的所有可能取值为0,1,222824063(0)130C P C ξ===,11122824056(1)130C C P C ξ===,21224011(2)130C P C ξ===, ξ的分布列为-------------------------------------------------------9分(Ⅲ)由(Ⅰ)的统计数据知,抽取的40件产品中有12件产品的重量超过505克,其频率为3.0,可见从流水线上任取一件产品,其重量超过505克的概率为3.0,令ξ为任取的5件产品中重量超过505克的产品数,则)3.0,5(~B ξ,故所求的概率为3087.0)7.0()3.0()2(3225===C p ξ-----------------------13分18.(本小题满分13分)已知xxx g e x x ax x f ln )(],,0(,ln )(=∈-=,其中e 是自然常数,R a ∈. (Ⅰ)讨论1=a 时, ()f x 的单调性、极值; (Ⅱ)求证:在(Ⅰ)的条件下,1()()2f xg x >+; (Ⅲ)是否存在实数a ,使()f x 的最小值是3,若存在,求出a 的值;若不存在,说明理由.解:(Ⅰ) x x x f ln )(-=,xx x x f 111)(-=-=' ∴当10<<x 时,/()0f x <,此时()f x 单调递减 当e x <<1时,/()0f x >,此时()f x 单调递增∴()f x 的极小值为1)1(=f -----------------------------------------------------------4分 (Ⅱ) ()f x 的极小值为1,即()f x 在],0(e 上的最小值为1,∴ 0)(>x f ,min ()1f x =……5分 令21ln 21)()(+=+=x x x g x h ,xxx h ln 1)(-=', 当e x <<0时,0)(>'x h ,()h x 在],0(e 上单调递增 ∴min max |)(|12121211)()(x f e e h x h ==+<+== ∴在(1)的条件下,1()()2f xg x >+------------------------------------------------8分 (Ⅲ)假设存在实数a ,使x ax x f ln )(-=(],0(e x ∈)有最小值3,/1()f x a x =-xax 1-=① 当0≤a 时,)(x f 在],0(e 上单调递减,31)()(min =-==ae e f x f ,ea 4=(舍去),所以,此时)(x f 无最小值. ② 当e a <<10时,)(x f 在)1,0(a 上单调递减,在],1(e a上单调递增 3ln 1)1()(min =+==a af x f ,2e a =,满足条件.③ 当e a ≥1时,)(xf 在],0(e 上单调递减,31)()(min =-==ae e f x f ,ea 4=(舍去),所以,此时)(x f 无最小值.综上,存在实数2e a =,使得当],0(e x ∈时()f x 有最小值3.---------------------13分19.(本小题满分14分)已知:椭圆12222=+by a x (0>>b a ),过点)0,(a A -,),0(b B 的直线倾斜角为6π,原点到该直线的距离为23. (Ⅰ)求椭圆的方程;(Ⅱ)斜率大于零的直线过)0,1(-D 与椭圆交于E ,F 两点,若2=,求直线EF 的方程;(Ⅲ)是否存在实数k ,直线2+=kx y 交椭圆于P ,Q 两点,以PQ 为直径的圆过点)0,1(-D ?若存在,求出k 的值;若不存在,请说明理由.解:(Ⅰ)由33=a b ,22232121b a b a +⋅⋅=⋅ ,得3=a ,1=b , 所以椭圆方程是:1322=+y x ---------------------------------------------------------4分 (Ⅱ)设EF :1-=my x (0>m )代入1322=+y x ,得022)3(22=--+my y m , 设),(11y x E ,),(22y x F ,由DF ED 2=,得212y y -=.由322221+=-=+m m y y y ,32222221+-=-=m y y y ----------------------------6分 得31)32(222+=+-m m m ,1=∴m ,1-=m (舍去),(没舍去扣1分) 直线EF 的方程为:1-=y x 即01=+-y x ----------------------------------------9分(Ⅲ)将2+=kx y 代入1322=+y x ,得0912)13(22=+++kx x k (*) 记),(11y x P ,),(22y x Q ,PQ 为直径的圆过)0,1(-D ,则QD PD ⊥,即0)1)(1(),1(),1(21212211=+++=+⋅+y y x x y x y x ,又211+=kx y ,222+=kx y ,得01314125))(12()1(221212=++-=+++++k k x x k x x k . 解得67=k ,此时(*)方程0>∆, ∴存在67=k ,满足题设条件.------------------------------------------------------14分 20.(本小题满分13分 )定义:对于任意*n ∈N ,满足条件212n n n a a a +++≤且n a M ≤(M 是与n 无关的常数)的无穷数列{}n a 称为T 数列.(Ⅰ)若29n a n n =-+(*n ∈N ),证明:数列{}n a 是T 数列;(Ⅱ)设数列{}n b 的通项为3502nn b n ⎛⎫=- ⎪⎝⎭,且数列{}n b 是T 数列,求常数M 的取值范围;(Ⅲ)设数列1n pc n=-(*n ∈N ,1p >),问数列{}n c 是否是T 数列?请说明理由. 解:(Ⅰ) 由29n a n n =-+,得2)1(18)1(2)2(9)2(9222212-=+-+++++-+-=-+++n n n n n n a a a n n n所以数列{}n a 满足212n n n a a a +++≤. 又298124n a n ⎛⎫=--+ ⎪⎝⎭,当n =4或5时,n a 取得最大值20,即n a ≤20.综上,数列{}n a 是T 数列.------------------------------------------------------------4分(Ⅱ)因为11331350(1)50502222n n nn n b b n n ++⎛⎫⎛⎫⎛⎫-=+--+=- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭,所以当1350022n⎛⎫-≥ ⎪⎝⎭即11n ≤时,10n n b b +->,此时数列{}n b 单调递增当12n ≥时,10n n b b +-<,此时数列{}n b 单调递减;故数列{}n b 的最大项是12b ,所以,M 的取值范围是 1236002M ⎛⎫≥- ⎪⎝⎭----------------------------------------9分(Ⅲ)①当12p <≤时, 当1n =时1231,1,1,23p p c p c c =-=-=- 由13252203pc c c +-=-≤得65p ≤,即当615p <≤时符合122++≤+n n nc c c 条件. 若2n ≥,则1≤n p ,此时1n p c n=- 于是 2122(1)(1)2(1)021(1)(2)n n n p p p pc c c n n n n n n ++-+-=-+---=<++++ 又对于*n ∈N 有11n pc n=-<,所以当615p <≤时数列{}n c 是T 数列;②当23p <≤时, 取1n =则:1231,1,1,23p pc p c c =-=-=- 由0322231>-=-+pc c c ,所以23p <≤时数列{}n c 不是T 数列 ③当3p >时, 取1n =则1231,1,1,23p p c p c c =-=-=- 由1325206pc c c +-=>,所以3p >时数列{}n c 不是T 数列. 综上:当615p <≤时数列{}n c 是T 数列;当65p >时数列{}n c 不是T 数列-----------------------------------------------------------------------------13分小编推荐 》》》2012年北京各区高三一模各科试题及答案汇总 2012年北京各区高三二模各科试题及答案汇总 2012年北京各区高三三模各科试题及答案汇总。
北京2012年高考数学最新联考试题分类大汇编(15)算法框图试题解析.pdf
一、学——目标自学、自主学习 (一)学习目标: 1、有感情地朗读诗歌,体会作者的思想感情。
2、揣摩、品味诗歌的语言,体会诗中哲理性的语句。
? 3、联系实际,树立远大理想,并为之奋斗。
(二)作家作品: 1、走近作者:流沙河,原名余勋坦,四川金堂县人,生于1931年。
早在解放前,他在成都二中读书时,就是一个追求光明、酷爱文学的少年。
他加入了进步学生团体“十月读书会”,并在进步报刊上发表文章。
新中国成立时他17岁,正在四川大学农化系读书。
他痛恨自己的地主家庭,决计脱离它而独立生活,毅然辍学前往山区当了小学教员。
1952年转入四川省文联搞专业创作。
1957年1月,流沙河、白航等四位年青诗人在成都创办《星星》诗刊。
“反右”开始,《星星》被指控为“反党刊物”, 1979年底,身穿破棉袄的流沙河又回到《星星》编辑部。
他一边在复刊后的《星星》作编辑工作,一边勤奋地写作。
22年的灾难,不仅没有使他消沉,反而使他的诗更充满激情,更深沉感人,…… 代表作:短篇小说集 《窗》、诗歌集《农村夜曲》、《告别火星》、组诗《草木篇》、《故园六咏》 流沙河诗歌特色:1.构思奇妙,富于浪漫色彩。
2.民族化、群众化结合。
3.形式上:标准的新格律诗,标准的自由体诗。
3、学诗方法:诗是语言的艺术。
诗人的语言就好比画家笔下的线条或色彩,带有一定的灵动性。
理解鉴赏诗歌,就要用普通话正确、流利、有感情地朗读全诗,反复咀嚼这些诗句,细心揣摩诗人的心理历程。
从准确把握诗歌的朗读节奏入手,联系自己的生活体验和阅读积累,感悟诗的意境、情感及表现技巧。
(三)基础自测 1、给加点字注音或根据拼音写汉字。
倔强 ( ) ( ) 鬓发( ) 洗濯 ( ) 黎明( ) 庸人( ) 船舶 ( ) 寂寥( ) 脊梁( ) 连zhuì( ) tuì( )变 哭qì( ) 扒窃( ) diàn( )污 zǔ zhòu( )( )榆阳( ) 荣yù( ) 2、根据课文内容把下列词语填充完整。
2012年北京市朝阳区高考数学二模试卷(理科)(附答案解析)
2012年北京市朝阳区高考数学二模试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1. 已知全集U =R ,集合A ={x|2x >1},B ={x|x 2−3x −4>0},则A ∩C U B =( ) A.{x|0≤x <4} B.{x|0<x ≤4} C.{x|−1≤x ≤0} D.{x|−1≤x ≤4}2. 复数z 满足等式(2−i)⋅z =i ,则复数z 在复平面内对应的点所在的象限是( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限3. 已知双曲线x 2m −y 25=1(m >0)的右焦点与抛物线y 2=12x 的焦点相同,则此双曲线的离心率为( )A.6B.3√22C.32D.344. 在△ABC 中,|AB →|=2,|AC →|=3,AB →⋅AC →<0,且△ABC 的面积为32,则∠BAC 等于( ) A.60∘或120∘ B.120∘ C.150∘ D.30∘或150∘5. 在直角坐标系xOy 中,直线Z 的参数方程为{x =ty =4+t (t 为参数,且t >0);以原点O 为极点,以x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为ρ=4√2sin (θ+π4).则直线l 和曲线C 的公共点有( )A.0个B.l 个C.2个D.无数个6. 下列命题:p :函数f(x)=sin 4x −cos 4x 的最小正周期是π;q :已知向量a →=(λ, 1),b →=(−1, λ2),c →=(−1, 1),则(a →+b →) // c →的充要条件是λ=−1; r :若∫1xa 1dx =1(a >1),则a =e .其中所有的真命题是( ) A.r B.p ,qC.q ,rD.p ,r7. 直线y =x 与函数f(x)={2,x >mx 2+4x +2,x ≤m 的图象恰有三个公共点,则实数m 的取值范围是( )A.[−1, 2)B.[−1, 2]C.[2, +∞)D.(−∞, −1]8. 有一个棱长为1的正方体,按任意方向正投影,其投影面积的最大值是( ) A.1B.3√22C.√2D.√3二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.二项式(ax 2√x)5展开式中的常数项为5,则实数a =________.如图所示的程序框图输出的结果是________.若实数x ,y 满足{x −y +1≤0x ≤0则x 2+y 2的最小值是________.如图,AB 是圆O 的直径,CD ⊥AB 于D ,且AD =2BD ,E 为AD 的中点,连接CE 并延长交圆O 于F .若CD =√2,则AB =________,EF =________.一个工厂生产某种产品每年需要固定投资100万元,此外每生产1件该产品还需要增加投资1万元,年产量为x(x∈N∗)件.当x≤20时,年销售总收入为(33x−x2)万元;当x>20时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为y万元,则y(万元)与x(件)的函数关系式为________,该工厂的年产量为________件时,所得年利润最大.(年利润=年销售总收入-年总投资)在如图所示的数表中,第i行第j列的数记为a i,j,且满足a1,j=2j−1,a i,1=i,a i+1,j+1=a i,j+a i+1,j(i, j∈N∗),MN⊥BC,则此数表中的第5行第3列的数是________;记第3行的数3,5,8,13,22,N为数列{b n},则数列{b n}的通项公式为________.第1行1248…第2行2359…第3行35813……三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.把答案答在答题卡上.已知函数f(x)=√3sin x cos x−cos2x+m(m∈R)的图象过点M(π12, 0).(1)求m的值;(2)在△ABC中,角A,B,C的对边分别是a,b,c,若c cos B+b cos C=2a cos B,求f(A)的取值范围.一个袋子中装有大小形状完全相同的编号分别为1,2,3,4,5的5个红球与编号为1,2,3,4的4个白球,从中任意取出3个球.(1)求取出的3个球颜色相同且编号是三个连续整数的概率;(2)求取出的3个球中恰有2个球编号相同的概率;(3)记X为取出的3个球中编号的最大值,求X的分布列与数学期望.在如图所示的几何体中,四边形ABCD为正方形,EA⊥平面ABCD,EF // AB,AB=4,AE=2,EF=1.(1)若点M在线段AC上,且满足CM=14CA,求证:EM // 平面FBC;(2)求证:AF⊥平面EBC;(3)求二面角A−FB−D的余弦值.已知函数f(x)=a ln x+2a2x+x(a≠0).(1)若曲线y=f(x)在点(1, f(1))处的切线与直线x−2y=0垂直,求实数a的值;(2)讨论函数f(x)的单调性;(3)当a∈(−∞, 0)时,记函数f(x)的最小值为g(a),求证:g(a)≤12e2.在平面直角坐标系x0y中,已知点A(−√2, 0),B(√2,0),E为动点,且直线EA与直线EB的斜率之积为−12.(1)求动点E的轨迹C的方程;(2)设过点F(1, 0)的直线l与曲线C相交于不同的两点M,N.若点P在y轴上,且|PM|=|PN|,求点P的纵坐标的取值范围.已知数列A n:a1,a2,…,a n(n∈N∗, n≥2)满足a1=a n=0,且当2≤k≤n(K∈N∗)时,(a k−a k−1)2=1,令S(A n)=∑a ini=1.(I)写出S(A5)的所有可能的值;(II)求S(A n)的最大值;(III)是否存在数列A n,使得S(A n)=(n−3)24?若存在,求出数列A n;若不存在,说明理由.参考答案与试题解析2012年北京市朝阳区高考数学二模试卷(理科)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.【答案】B【考点】交、并、补集的混合运算【解析】利用全集U=R,B={x|x2−3x−4>0},先求出C U B={x|−1≤x≤4},再由集合A={x|2x>1},求出集合A∩C U B.【解答】解:全集U=R,集合A={x|2x>1}={x|x>0},B={x|x2−3x−4>0}={x|x>4或x<−1},C U B={x|−1≤x≤4},∴A∩C U B={x|0<x≤4}.故选B.2.【答案】B【考点】复数的代数表示法及其几何意义【解析】先根据复数代数形式的乘除运算法则化简复数,然后根据复数的几何意义得到复数z在复平面内对应的点所在的象限.【解答】解:∵(2−i)⋅z=i∴z=i2−i =i(2+i)(2−i)(2+i)=−1+2i5=−15+25i则复数z在复平面内对应的点为(−15, 2 5 )即点所在的象限是第二象限故选B.3.【答案】C【考点】圆锥曲线的共同特征抛物线的求解【解析】确定抛物线的焦点坐标,从而可得双曲线的几何量,由此可求双曲线的离心率.【解答】解:抛物线y2=12x的焦点坐标为(3, 0)∵双曲线x2m−y25=1(m>0)的右焦点与抛物线y2=12x的焦点相同,∴m+5=9∴m=4∴双曲线的离心率为32故选C.4.【答案】C【考点】平面向量数量积的运算【解析】由题意可得∠BAC为钝角,且12×2×3×sin∠BAC=32,解得sin∠BAC=12,从而得到∠BAC的值.【解答】解:∵在△ABC中,|AB→=2,|AC→|=3,AB→⋅AC→<0,且△ABC的面积为32,∴∠BAC为钝角,且12×2×3×sin∠BAC=32,解得sin∠BAC=12,故∠BAC=150∘,故选C.5.【答案】B【考点】直线的参数方程圆的极坐标方程【解析】将参数方程转化为一般直角坐标系的方程,判断直线l和曲线C的公共点个数;【解答】解:∴直角坐标系xOy中,直线Z的参数方程为{x=ty=4+t(t为参数,且t>0);可得y=x+4,②x>0,曲线C方程为ρ=4√2sin(θ+π4),化为标准方程为:(x−2)2+(y−2)2=8,即C为以(2, 2)为圆心,2√2为半径的圆;圆心(2, 2)到直线Z的距离也为2√2,所以直线Z与圆C相切,两者有一个公共点,故选B;6.【答案】D【考点】命题的真假判断与应用 【解析】化简f(x)=sin 4x −cos 4x 后求周期,判断出命题p 为真命题;由(a →+b →) // c →建立λ的方程求解λ;由∫1xa 1dx =1建立关于a 的方程,求出a 的值再判断. 【解答】解:命题P:f(x)=sin 4x −cos 4x=(sin 2x +cos 2x)(sin 2x −cos 2x)=sin 2x −cos 2x =−cos 2x , 所以函数f(x)为π,故命题P 为真命题; 命题q:a →+b →=(λ−1, λ2+1),由(a →+b →) // c →得,−(λ2+1)+(λ−1)=0,解得λ=0或λ=−1, 故命题q 为假命题; 命题r :由∫1xa 1dx =1得,ln a −ln 1=1,解得a =e ,所以命题r 是真命题.故选D . 7.【答案】 A【考点】根的存在性及根的个数判断 【解析】由直线y =x 与函数f(x)={2,x >mx 2+4x +2,x ≤m 的图象恰有三个公共点,作出图象,结合图象,能得到实数m 的取值范围. 【解答】解:解方程组{y =x y =x 2+4x +2,得{x =−2y =−2,或{x =−1y =−1, 由直线y =x 与函数f(x)={2,x >mx 2+4x +2,x ≤m的图象恰有三个公共点,作出图象,结合图象,知−1≤m <2.∴ 实数m 的取值范围是[−1, 2).故选A .8.【答案】 D【考点】平行投影及平行投影作图法 平行投影【解析】首先想象一下,当正方体绕着对角线BD ′所在的直线转动时,体会投影的变化,当正方体为ABCD −A ′B ′C ′D ′投影最大的时候,应该是投影面α和面AB ′C 平行,从而得到结果. 【解答】解:设正方体为ABCD −A ′B ′C ′D ′投影最大的时候,是投影面α和面AB ′C 平行,三个面的投影为三个全等的菱形,其对角线为√2,即投影上三条对角线构成边长为√2的等边三角形. ∴ 投影的面积=2S △AB′C =12×√2×√62×2=√3.故选D .二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.【答案】 1【考点】二项式定理的应用 【解析】先求出二项式展开式的通项公式,再令x 的系数等于0,求得r 的值,即可求得展开式中的常数项.再由常数项为5,求得a 的值.【解答】 解:二项式(ax 2+√x)5的展开式的通项公式为T r+1=C 5r ⋅ a 5−r ⋅x 10−2r ⋅x −r2=C 5r ⋅ a 5−r ⋅x 10−52r ,令10−5r 2=0,解得r =4,故展开式中的常数项为C 51⋅ a 1=5,∴ a =1,故答案为1.【答案】 1023 【考点】等比数列的前n 项和 循环结构的应用【解析】通过分析循环,推出循环规律,利用循环的次数,求出输出结果. 【解答】解:通过循环,可知该循环的作用是求数列的和,循环到1010结束循环, 所以S =1+2+22+23+24+25+26+27+28+29=1023. 故答案为:1023. 【答案】 12【考点】 简单线性规划 【解析】根据已知条件实数x ,y 满足{x −y +1≤0x ≤0则,画出可行域,将x 2+y 2的最小值转化为可行域中的点到原点的最小距离的平方,从而求解; 【解答】解:由已知条件实数x ,y 满足{x −y +1≤0x ≤0画出可行域,如下图:求x 2+y 2的最小值,目标函数z =x 2+y 2,即是图中可行域中的点到原点的最小距离的平方, 可知原点0到直线x −y +1=0的最短距离d =|1|√2=√22, ∴ x 2+y 2的最小值为d 2=12,故答案为12;【答案】 3,2√33【考点】与圆有关的比例线段 【解析】AB 是圆O 的直径,可得∠ACB =90∘.利用射影定理可得CD 2=AD ⋅DB .已知AD =2DB ,CD =√2,可得DB =1,AB =AD +DB =3.已知E 为AD 的中点,可得ED =1.在Rt △CDE 中,利用勾股定理可得CE =√CD 2+DE 2=√3.利用相交弦定理可得:EA ⋅EB =EC ⋅EF ,即可求得EF . 【解答】解:∵ AB 是圆O 的直径,∴ ∠ACB =90∘. ∴ CD 2=AD ⋅DB .∵ AD =2DB ,∴ CD 2=2DB 2, ∵ CD =√2,∴ DB =1, ∴ AB =AD +DB =3.∵ E 为AD 的中点,∴ ED =1.在Rt △CDE 中,CE =√CD 2+DE 2=√3. 由相交弦定理可得:EA ⋅EB =EC ⋅EF , ∴ 1×2=√3EF , ∴ EF =2√33.故答案分别为3,2√33. 【答案】y ={−x 2+32x −100,x ≤20160−x,x >20,16 【考点】函数模型的选择与应用 【解析】根据年利润=年销售总收入-年总投资,确定分段函数解析式,分别确定函数的最值,即可得到结论. 【解答】解:由题意,年利润=年销售总收入-年总投资,则当x ≤20时,年利润y =(33x −x 2)−(100+x)=−x 2+32x −100; 当x >20时,年利润y =260−(100+x)=160−x ;∴ y ={−x 2+32x −100,x ≤20160−x,x >20;当x ≤20时,y =−x 2+32x −100=−(x −16)2+156,∴ x =16时,y 取得最大值156万元; 当x >20时,y =160−x <140万元∵ 156>140,∴ x =16时,利润最大值156万元 故答案为:y ={−x 2+32x −100,x ≤20160−x,x >20;16 【答案】16,b n =2n−1+n +1 【考点】 数列的应用 【解析】(1)由数阵中数的规律,可得:a i,2=(i−1)+i.由此得出a4,2和a5,2的值再结合题中的递推式,即可得到第5行第3列的数;(2)根据题中的递推式,将{b n}的各项依次减去2、3、4、5、6、7、…、n+1,得以1为首项公比为2的等比数列,结合等比数列的通项公式,不难得到数列{b n}的通项公式.【解答】解:(1)根据题意,得a4,2=3+4=7,a5,2=4+5=9,∵a i+1,j+1=a i,j+a i+1,j,∴第5行第3列的数a5,3=a4,2+a5,2=7+9=16;(2)将3,5,8,13,22,39,…,b n,各项依次减去2,3,4,5,6,7,…,n+1,得1,2,4,8,16,32,…,2n−1,∴b n−(n+1)=2n−1,得b n=2n−1+n+1,即为数列{b n}的通项公式故答案为:16,b n=2n−1+n+1三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.把答案答在答题卡上. 【答案】∵sin x cos x=12sin2x,cos2x=12(1+cos2x)∴f(x)=√3sin x cos x−cos2x+m=√32sin2x−12(1+cos2x)+m=√32sin2x−12cos2x−12+m=sin(2x−π6)−12+m∵函数y=fx)图象过点M(π12, 0),∴sin(2⋅π12−π6)−12+m=0,解之得m=12∵c cos B+b cos C=2a cos B,∴结合正弦定理,得sin C cos B+cos C sin B=2sin A cos B∵B+C=π−A,得sin C cos B+cos C sin B=sin(B+C)=sin(π−A)=sin A ∴sin A=2sin A cos B∵△ABC中,sin A>0,∴cos B=12,得B=π3由(1),得f(x)=sin(2x−π6),所以f(A)=sin(2A−π6),其中A∈(0, 2π3)∵−π6<2A−π6<7π6,∴sin(2A−π6)>sin(−π6)=−12,sin(2A−π6)≤sinπ2=1因此f(A)的取值范围是(−12, 1]【考点】两角和与差的三角函数正弦定理【解析】(1)根据二倍角的三角函数公式和辅助角公式,将函数y=f(x)化简,得f(x)=sin(2x−π6)−12+m,再将M点坐标代入,可得m=12;(2)利用正弦定理,将c cos B+b cos C=2a cos B化简整理,得cos B=12,所以B=π3.由此得到函数f(A)=sin(2A−π6),其中A∈(0, 2π3),再结合正弦函数的图象与性质,可得f(A)的取值范围.【解答】∵sin x cos x=12sin2x,cos2x=12(1+cos2x)∴f(x)=√3sin x cos x−cos2x+m=√32sin2x−12(1+cos2x)+m=√32sin2x−12cos2x−12+m=sin(2x−π6)−12+m∵函数y=fx)图象过点M(π12, 0),∴sin(2⋅π12−π6)−12+m=0,解之得m=12∵c cos B+b cos C=2a cos B,∴结合正弦定理,得sin C cos B+cos C sin B=2sin A cos B∵B+C=π−A,得sin C cos B+cos C sin B=sin(B+C)=sin(π−A)=sin A∴sin A=2sin A cos B∵△ABC中,sin A>0,∴cos B=12,得B=π3由(1),得f(x)=sin(2x−π6),所以f(A)=sin(2A−π6),其中A∈(0, 2π3)∵−π6<2A−π6<7π6,∴sin(2A−π6)>sin(−π6)=−12,sin(2A−π6)≤sinπ2=1因此f(A)的取值范围是(−12, 1]【答案】取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率为584.(2)设“取出的3个球中恰有两个球编号相同”为事件B,则P(B)=C41C71C93=13.答:取出的3个球中恰有两个球编号相同的概率为13.(3)X的取值为2,3,4,5.P(X=2)=C21C22+C22C21C93=121,P(X=3)=C21C42+C22C41C93=421,P(X=4)=C21C62+C22C61C93=37,P(X=5)=C11C82C93=13.所以X的分布列为X的数学期望EX=2×121+3×421+4×37+5×13=8521.【考点】离散型随机变量及其分布列离散型随机变量的期望与方差【解析】(1)设“取出的3个球颜色相同且编号是三个连续整数”为事件A,由此能求出取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率.(2)设“取出的3个球中恰有两个球编号相同”为事件B,由此能求出取出的3个球中恰有两个球编号相同的概率.(3)X的取值为2,3,4,5,分别求出P(X=2),P(X=3),P(X=4),P(X=5)的值,由此能求出X的分布列和X的数学期望.【解答】解:(1)设“取出的3个球颜色相同且编号是三个连续整数”为事件A,则P(A)=3+2C93=584.答:取出的3个球的编号恰好是3个连续的整数,且颜色相同的概率为584.(2)设“取出的3个球中恰有两个球编号相同”为事件B,则P(B)=C41C71C93=13.答:取出的3个球中恰有两个球编号相同的概率为13.(3)X的取值为2,3,4,5.P(X=2)=C21C22+C22C21C93=121,P(X=3)=C21C42+C22C41C93=421,P(X=4)=C21C62+C22C61C93=37,P(X=5)=C11C82C93=13.所以X的分布列为X的数学期望EX=2×121+3×421+4×37+5×13=8521.【答案】解:(1)过M作MN⊥BC,垂足为N,连结FN,则MN // AB.又∵CM=14AC,∴MN=14AB.又∵EF // AB且EF=14AB,∴EF // MN.且EF=MN.∴四边形EFNM为平行四边形.∴EM // FN.又FN⊂平面FBC,EM⊄平面FBC,∴EM // 平面FBC.(2)∵EF // AB,∴EF与AB可确定平面EABF,∵EA⊥平面ABCD,∴EA⊥BC.由已知得AB⊥BC且EA∩AB=A,∴BC⊥平面EABF.又AF⊂平面EABF,∴BC⊥AF.在四边形ABFE中,AB=4,AE=2,EF=1,∠BAE=∠AEF=90∘设AF ∩BE =P ,∵ ∠PAE +∠PAB =90∘, ∴ ∠PBA +∠PAB =90∘ 则∠APB =90∘, ∴ EB ⊥AF .又∵ EB ∩BC =B , ∴ AF ⊥平面EBC .(3)以AB 为x 轴,AD 为y 轴,AE 为z 轴建立空间直角坐标系, 则B(4, 0, 0),D(0, 4, 0),F(1, 0, 2). ∴ BD →=(−4,4,0),BF →=(1,−4,2) 设平面BDF 的法向量为m →(a, b, c),则{m →⋅BF →=0˙,解得:m →=(2,2,−1).同理可得,平面AFB 的法向量为n →=(0, 1, 0), ∴ 二面角A −FB −D =<m →,n →>,∴ 二面角A −FB −D 的余弦值为cos (π−<m →,n →>)=cos <m →,n →>=|m →|⋅|n →|˙=23×1=23.【考点】直线与平面平行的判定 直线与平面垂直的判定 用空间向量求平面间的夹角【解析】(1)过M 作MN ⊥BC ,垂足为N ,连结FN ,则MN // AB ,又可得EF // MN ,从而四边形EFNM 为平行四边形,所以EM // FN ,最后根据线面平行的判定定理,即可得到EM // 平面FBC ;(2)先利用线面垂直的性质和勾股定理证出BC ⊥AF ,EB ⊥AF ,从而证出AF ⊥平面EBC ; (3)建立空间直角坐标系,求出两个平面的法向量,求解即可. 【解答】 解:(1)过M 作MN ⊥BC ,垂足为N ,连结FN , 则MN // AB . 又∵ CM =14AC , ∴ MN =14AB .又∵ EF // AB 且EF =14AB , ∴ EF // MN .且EF =MN .∴ 四边形EFNM 为平行四边形. ∴ EM // FN .又FN ⊂平面FBC ,EM ⊄平面FBC ,∴ EM // 平面FBC .(2)∵ EF // AB ,∴ EF 与AB 可确定平面EABF , ∵ EA ⊥平面ABCD , ∴ EA ⊥BC .由已知得AB ⊥BC 且EA ∩AB =A , ∴ BC ⊥平面EABF . 又AF ⊂平面EABF , ∴ BC ⊥AF .在四边形ABFE 中,AB =4,AE =2,EF =1,∠BAE =∠AEF =90∘ 设AF ∩BE =P ,∵ ∠PAE +∠PAB =90∘, ∴ ∠PBA +∠PAB =90∘ 则∠APB =90∘, ∴ EB ⊥AF .又∵ EB ∩BC =B , ∴ AF ⊥平面EBC .(3)以AB 为x 轴,AD 为y 轴,AE 为z 轴建立空间直角坐标系, 则B(4, 0, 0),D(0, 4, 0),F(1, 0, 2). ∴ BD →=(−4,4,0),BF →=(1,−4,2) 设平面BDF 的法向量为m →(a, b, c),则{m →⋅BF →=0˙,解得:m →=(2,2,−1).同理可得,平面AFB 的法向量为n →=(0, 1, 0),∴ 二面角A −FB −D =<m →,n →>,∴ 二面角A −FB −D 的余弦值为cos (π−<m →,n →>)=cos <m →,n →>=|m →|⋅|n →|˙=23×1=23.【答案】解:(1)f(x)的定义域为{x|x >0},f′(x)=ax −2a 2x 2+1(x >0)根据题意,有f′(1)=−2,所以2a 2−a −3=0,解得a =−1或a =32. (2)解:f′(x)=(x−a)(x+2a)x 2(x >0)①当a >0时,因为x >0,由f′(x)>0得(x −a)(x +2a)>0,解得x >a ; 由f′(x)<0得(x −a)(x +2a)<0,解得0<x <a .所以函数f(x)在(a, +∞)上单调递增,在(0, a)上单调递减; ②当a <0时,因为x >0,由f′(x)>0得(x −a)(x +2a)>0,解得x >−2a ; 由f′(x)<0得(x −a)(x +2a)<0,解得0<x <−2a .所以函数f(x)在(−2a, +∞)上单调递增,在(0, −2a)上单调递减;(3)证明:由(2)知,当a ∈(−∞, 0)时,函数f(x)的最小值为g(a),且g(a)=f(−2a)=a ln (−2a)−3a , ∴ g′(a)=ln (−2a)−2,令g′(a)=0,得a =−12e 2.当a 变化时,g′(a),g(a)的变化情况如下表:∴ −12e 2是g(a)在(−∞, 0)上的唯一极值点,且是极大值点,从而也是g(a)的最大值点. 所以g(a)max =g(−12e 2)=12e 2.所以,当a ∈(−∞, 0)时,g(a)≤12e 2成立.【考点】利用导数研究曲线上某点切线方程 利用导数研究函数的单调性【解析】(1)确定f(x)的定义域,利用曲线y =f(x)在点(1, f(1))处的切线与直线x −2y =0垂直,可得f′(1)=−2,从而可求实数a 的值;(2)求导函数,分类讨论,利用导数的正负,即可确定函数f(x)的单调性;(3)由(2)知,当a ∈(−∞, 0)时,函数f(x)的最小值为g(a),且g(a)=f(−2a)=a ln (−2a)−3a ,求导数,求出函数的最大值,即可证得结论.【解答】解:(1)f(x)的定义域为{x|x >0},f′(x)=ax −2a 2x 2+1(x >0)根据题意,有f′(1)=−2,所以2a 2−a −3=0,解得a =−1或a =32. (2)解:f′(x)=(x−a)(x+2a)x 2(x >0)①当a >0时,因为x >0,由f′(x)>0得(x −a)(x +2a)>0,解得x >a ; 由f′(x)<0得(x −a)(x +2a)<0,解得0<x <a .所以函数f(x)在(a, +∞)上单调递增,在(0, a)上单调递减; ②当a <0时,因为x >0,由f′(x)>0得(x −a)(x +2a)>0,解得x >−2a ; 由f′(x)<0得(x −a)(x +2a)<0,解得0<x <−2a .所以函数f(x)在(−2a, +∞)上单调递增,在(0, −2a)上单调递减;(3)证明:由(2)知,当a ∈(−∞, 0)时,函数f(x)的最小值为g(a),且g(a)=f(−2a)=a ln (−2a)−3a , ∴ g′(a)=ln (−2a)−2,令g′(a)=0,得a =−12e 2.当a 变化时,g′(a),g(a)的变化情况如下表:∴ −12e 2是g(a)在(−∞, 0)上的唯一极值点,且是极大值点,从而也是g(a)的最大值点. 所以g(a)max =g(−12e 2)=12e 2.所以,当a ∈(−∞, 0)时,g(a)≤12e 2成立.【答案】 解:(1)设动点E 的坐标为(x, y),∵ 点A(−√2, 0),B(√2,0),E 为动点,且直线EA 与直线EB 的斜率之积为−12, ∴ x+2⋅x−2=−12, 整理,得x 22+y 2=1,x ≠±√2,∴ 动点E 的轨迹C 的方程为x 22+y 2=1,x ≠±√2.(2)当直线l 的斜率不存在时,满足条件的点P 的纵坐标为0, 当直线l 的斜率存在时,设直线l 的方程为y =k(x −1), 将y =k(x −1)代入x 22+y 2=1,并整理,得(2k 2+1)x 2−4k 2x +2k 2−2=0, △=8k 2+8>0,设M(x 1, y 1),N(x 2, y 2),则x 1+x 2=4k 22k 2+1,x 1x 2=2k 2−22k 2+1, 设MN 的中点为Q ,则x Q =2k 22k 2+1,y Q =k(x Q −1)=−k2k 2+1,∴ Q(2k 22k 2+1, −k2k 2+1), 由题意知k ≠0,又直线MN 的垂直平分线的方程为y +k 2k 2+1=−1k(x −2k 22k 2−1),令x =0,得y P =k 2k 2+1=12k+1k,当k >0时,∵ 2k +1k ≥2√2,∴ 0<y P ≤2√2=√24; 当k <0时,因为2k +1k≤−2√2,所以0>y P ≥2√2=−√24. 综上所述,点P 纵坐标的取值范围是[−√24,√24]. 【考点】圆锥曲线的轨迹问题直线与椭圆结合的最值问题 【解析】(1)设动点E 的坐标为(x, y),由点A(−√2, 0),B(√2,0),E 为动点,且直线EA 与直线EB 的斜率之积为−12,知x+2x−2=−12,由此能求出动点E 的轨迹C 的方程.(2)设直线l 的方程为y =k(x −1),将y =k(x −1)代入x 22+y 2=1,得(2k 2+1)x 2−4k 2x +2k 2−2=0,由题设条件能推导出直线MN 的垂直平分线的方程为y +k2k +1=−1k (x −2k 22k −1),由此能求出点P 纵坐标的取值范围.【解答】 解:(1)设动点E 的坐标为(x, y),∵ 点A(−√2, 0),B(√2,0),E 为动点,且直线EA 与直线EB 的斜率之积为−12, ∴ x+√2x−√2=−12,整理,得x 22+y 2=1,x ≠±√2,∴ 动点E 的轨迹C 的方程为x 22+y 2=1,x ≠±√2.(2)当直线l 的斜率不存在时,满足条件的点P 的纵坐标为0, 当直线l 的斜率存在时,设直线l 的方程为y =k(x −1), 将y =k(x −1)代入x 22+y 2=1,并整理,得(2k 2+1)x 2−4k 2x +2k 2−2=0, △=8k 2+8>0,设M(x 1, y 1),N(x 2, y 2),则x 1+x 2=4k 22k 2+1,x 1x 2=2k 2−22k 2+1,设MN 的中点为Q ,则x Q =2k 22k 2+1,y Q =k(x Q −1)=−k2k 2+1, ∴ Q(2k 22k 2+1, −k2k 2+1),由题意知k ≠0,又直线MN 的垂直平分线的方程为y +k 2k 2+1=−1k(x −2k 22k 2−1),令x =0,得y P =k 2k 2+1=12k+1k,当k >0时,∵ 2k +1k≥2√2,∴ 0<y P ≤2√2=√24; 当k <0时,因为2k +1k≤−2√2,所以0>y P ≥2√2=−√24. 综上所述,点P 纵坐标的取值范围是[−√24,√24]. 【答案】解:(I)由题设,满足条件的数列A 5的所有可能情况有: (1)0,1,2,1,0.此时S(A 5)=4;(2)0,1,0,1,0.此时S(A 5)=2; (3)0,1,0,−1,0.此时S(A 5)=0;(4)0,−1,−2,−1,0.此时S(A 5)=−4; (5)0,−1,0,1,0.此时S(A 5)=0;(6)0,−1,0,−1,0.此时S(A 5)=−2; 所以,S(A 5)的所有可能的值为:4,2,0,−2,−4. … (II )由(a k −a k−1)2=1,可设a k −a k−1=c k−1,则c k−1=1或c k−1=−1(2≤k ≤n, k ∈N ∗),因为a n −a n−1=c n−1,所以 a n =a n−1+c n−1=a n−2+c n−2+c n−1=...=a 1+c 1+c 2+...+c n−2+c n−1. 因为a 1=a n =0,所以c 1+c 2+...+c n−1=0,且n 为奇数,c 1,c 2,…,c n−1是由n−12个1和n−12个−1构成的数列.所以S(A n )=c 1+(c 1+c 2)+...+(c 1+c 2+...+c n−1)=(n −1)c 1+(n −2)c 2+...+2c n−2+c n−1. 则当c 1,c 2,…,c n−1的前n−12项取1,后n−12项取−1时S(A n )最大,此时S(A n )=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)=(n−1)24.证明如下:假设c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…c m t 取−1,则c 1,c 2,…,c n−1的后n−12项中恰有t 项第21页 共22页 ◎ 第22页 共22页c n 1,c n 2,…,c n t 取1,其中1≤t ≤n−12,1≤m i ≤n−12,n−12<n i ≤n −1,i =1,2,…,t . 所以S(A n )=(n −1)c 1+(n −2)c 2+⋯+n+12c n−12+n−12c n+12+⋯+2c n−2+c n−1=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)−2[(n −m 1)+(n −m 2)+...+(n −m t )]+2[(n −n 1)+(n −n 2)+...+(n −n t )]=(n−1)24−2∑(t i=1n i −m i )<(n−1)24.所以S(A n )的最大值为(n−1)24. …(III )由(II)可知,如果c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…,c m t 取−1,c 1,c 2,…,c n−1的后n−12项中恰有t 项c n 1,c n 2,…,c n t 取1,则S(A n )=(n−1)24−2∑(t i=1n i −m i ),若S(A n )=(n−3)24,则n −2=2∑(t i=1n i −m i ),因为n 是奇数,所以n −2是奇数,而2∑(t i=1n i−m i )是偶数,因此不存在数列A n ,使得S(A n )=(n−3)24. …【考点】 数列的应用 【解析】(I )由题设,即可满足条件的数列A 5的所有可能情况; (II )确定当c 1,c 2,…,c n−1的前n−12项取1,后n−12项取−1时S(A n )最大,此时S(A n )=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)=(n−1)24.(III )由(II)可知,如果c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…,c m t 取−1,c 1,c 2,…,c n−1的后n−12项中恰有t 项c n 1,c n 2,…,c n t 取1,则S(A n )=(n−1)24−2∑(t i=1n i −m i ),利用条件,分n 是奇数与偶数,即可得到结论.【解答】解:(I)由题设,满足条件的数列A 5的所有可能情况有: (1)0,1,2,1,0.此时S(A 5)=4;(2)0,1,0,1,0.此时S(A 5)=2; (3)0,1,0,−1,0.此时S(A 5)=0;(4)0,−1,−2,−1,0.此时S(A 5)=−4; (5)0,−1,0,1,0.此时S(A 5)=0;(6)0,−1,0,−1,0.此时S(A 5)=−2; 所以,S(A 5)的所有可能的值为:4,2,0,−2,−4. … (II )由(a k −a k−1)2=1,可设a k −a k−1=c k−1,则c k−1=1或c k−1=−1(2≤k ≤n, k ∈N ∗),因为a n −a n−1=c n−1,所以 a n =a n−1+c n−1=a n−2+c n−2+c n−1=...=a 1+c 1+c 2+...+c n−2+c n−1. 因为a 1=a n =0,所以c 1+c 2+...+c n−1=0,且n 为奇数,c 1,c 2,…,c n−1是由n−12个1和n−12个−1构成的数列.所以S(A n )=c 1+(c 1+c 2)+...+(c 1+c 2+...+c n−1)=(n −1)c 1+(n −2)c 2+...+2c n−2+c n−1.则当c 1,c 2,…,c n−1的前n−12项取1,后n−12项取−1时S(A n )最大,此时S(A n )=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)=(n−1)24.证明如下:假设c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…c m t 取−1,则c 1,c 2,…,c n−1的后n−12项中恰有t 项c n 1,c n 2,…,c n t 取1,其中1≤t ≤n−12,1≤m i ≤n−12,n−12<n i ≤n −1,i =1,2,…,t .所以S(A n )=(n −1)c 1+(n −2)c 2+⋯+n+12c n−12+n−12c n+12+⋯+2c n−2+c n−1=(n −1)+(n −2)+⋯+n+12−(n−12+⋯+2+1)−2[(n −m 1)+(n −m 2)+...+(n −m t )]+2[(n −n 1)+(n −n 2)+...+(n −n t )]=(n−1)24−2∑(t i=1n i−m i )<(n−1)24.所以S(A n )的最大值为(n−1)24. …(III )由(II)可知,如果c 1,c 2,…,c n−1的前n−12项中恰有t 项c m 1,c m 2,…,c m t 取−1,c 1,c 2,…,c n−1的后n−12项中恰有t 项c n 1,c n 2,…,c n t 取1,则S(A n )=(n−1)24−2∑(t i=1n i −m i ),若S(A n )=(n−3)24,则n −2=2∑(t i=1n i −m i ),因为n 是奇数,所以n −2是奇数,而2∑(ti=1n i −m i )是偶数,因此不存在数列A n ,使得S(A n )=(n−3)24. …。
北京市海淀区高三数学理科二模试卷及答案(WORD版)
北京市海淀区2012高三二模数 学(理科)2012.05一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)若sin cos 0θθ<,则角θ是 (A )第一或第二象限角 (B )第二或第三象限角 (C )第三或第四象限角 (D )第二或第四象限角 (2)已知命题p :0x ∃∈R ,021x =.则p ⌝是 (A )0x ∀∈R ,021x ≠ (B )0x ∀∉R ,021x ≠ (C )0x ∃∈R ,021x ≠(D )0x ∃∉R ,021x ≠(3)直线11x ty t =+⎧⎨=-⎩(t 为参数)的倾斜角的大小为(A )4-π (B )4π (C )2π(D )34π(4)若整数,x y 满足1,1,3,2x y x y y ìïïï-?ïïï+?íïïïï£ïïî则2x y +的最大值是 (A )1(B )5(C )2 (D )3(5)已知点12,F F 是椭圆2222x y +=的两个焦点,点P 是该椭圆上的一个动点,那么12PF PF +u u u r u u u u r的最小值是(A )0 (B )1 (C )2 (D)(6)为了得到函数2log y =2log y x =的图象上所有的点的(A )纵坐标缩短到原来的12倍,横坐标不变,再向右平移1个单位长度 (B )纵坐标缩短到原来的12倍,横坐标不变,再向左平移1个单位长度(C )横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位长度(D )横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位长度俯视图主视图(7)某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是(A )203(B )43(C )6 (D )4(8)点(,)P x y 是曲线1:(0)C y x x=>上的一个动点,曲线C 在点P 处的切线与x 轴、y 轴分别交于,A B 两点,点O 是坐标原点. 给出三个命题:①PA PB =;②OAB ∆的周长有最小值4+;③曲线C 上存在两点,M N ,使得OMN ∆为等腰直角三角形.其中真命题的个数是(A )1 (B )2 (C )3 (D )0二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上. (9)在面积为1的正方形ABCD 内部随机取一点P ,则PAB ∆的面积大于等于14的概率是_________. (10)已知1021012311(1)x a a x a x a x +=++++L . 若数列123,,,,(111,)k a a a a k k #?Z L 是一个单调递增数列,则k 的最大值是 . (11)在ABC ∆中,若120A ??,5c =,ABC ∆的面积为,则a = .(12)如图,O e 的直径AB 与弦CD 交于点P ,7, 5, 15CP PD AP ===,则DCB Ð=______.(13)某同学为研究函数()1)f x x =#的性质,构造了如图所示的两个边长为1的正方形ABCD 和BEFC ,点P 是边BC 上的一个动点,设CP x =,则()AP PF f x +=. 请你参考这些信息,推知函数()f x 的图象的对称轴是 ;函数()4()9g x f x =-的零点的个数是 .(14)曲线C 是平面内到定点(1,0)A 的距离与到定直线1x =-的距离之和为3的动点P 的轨迹. 则曲线C 与y 轴交点的坐标是 ;又已知点(,1)B a (a 为常数),那么BEFAB C DPPB PA +的最小值()d a = .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知公差不为0的等差数列{}n a 的前n 项和为n S ,346S a =+,且1413,,a a a 成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列1{}nS 的前n 项和公式. (16)(本小题满分14分)如图所示,PA ^平面ABC ,点C 在以AB 为直径的⊙O 上,30CBA??,2PA AB ==,点E 为线段PB 的中点,点M 在»AB 上,且OM ∥AC . (Ⅰ)求证:平面MOE ∥平面P AC ;(Ⅱ)求证:平面P AC ^平面PCB ;(Ⅲ)设二面角M BP C --的大小为θ,求cos θ的值.(17)(本小题满分13分)某公司准备将100万元资金投入代理销售业务,现有A ,B 两个项目可供选择:且X 1的数学期望E (X 1)=12;(2)投资B 项目一年后获得的利润X 2(万元)与B 项目产品价格的调整有关, B 项目产品价格根据销售情况在4月和8月决定是否需要调整,两次调整相互独立且在4月和8月进行价格调整的概率分别为p (0< p <1)和1-p . 经专家测算评估:B 项目产品价格一年内调整次数X (次)与X 2的关系如下表所示:(Ⅱ)求X 2的分布列;(Ⅲ)若E (X 1)< E (X 2),则选择投资B 项目,求此时 p 的取值范围.(18)(本小题满分13分)已知椭圆C :22221(0)x y a b a b+=>>的右焦点为(1,0)F ,且点(1,2-在椭圆C 上. (Ⅰ)求椭圆C 的标准方程;ME BOCAP(Ⅱ)已知动直线l 过点F ,且与椭圆C 交于A ,B 两点.试问x 轴上是否存在定点Q ,使得716QA QB ⋅=-u u u r u u u r 恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.(19)(本小题满分14分)已知函数21()ln()(0)2f x a x a x x a =--+<. (Ⅰ)求()f x 的单调区间;(Ⅱ)若12(ln 21)a -<<-,求证:函数()f x 只有一个零点0x ,且012a x a +<<+; (Ⅲ)当45a =-时,记函数()f x 的零点为0x ,若对任意120,[0,]x x x ∈且211,x x -=都有21()()f x f x m -≥成立,求实数m 的最大值.(本题可参考数据:99ln 20.7,ln 0.8,ln 0.5945≈≈≈)(20)(本小题满分13分)将一个正整数n 表示为12(*)p a a a p +++?N L 的形式,其中*i a ÎN ,1,2,,i p =L ,且p a a a ≤≤≤Λ21,记所有这样的表示法的种数为)(n f (如4=4,4=1+3,4=2+2,4=1+1+2,4=1+1+1+1,故5)4(=f ).(Ⅰ)写出)5(),3(f f 的值,并说明理由;(Ⅱ)对任意正整数n ,比较)1(+n f 与)]2()([21++n f n f 的大小,并给出证明; (Ⅲ)当正整数6≥n 时,求证:134)(-≥n n f .海淀区高三年级第二学期期末练习数 学(理科)参考答案及评分标准 2012.05一. 选择题:本大题共8小题,每小题5分,共40分.二.填空题:本大题共6小题,每小题5分,共30分.(9)12(10)6 (11(12)45° (13)12x =;2 (14)(0,±; 1.41,4, 1.41,2, 1 1.a a a a a a ìï??ïïï+-<?íïï--<<ïïïî或注:(13)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)解:(Ⅰ)设等差数列{}n a 的公差为0d ¹.因为346S a =+, 所以11323362da a d 创+=++. ① ……………………………………3分 因为1413,,a a a 成等比数列,所以2111(12)(3)a a d a d +=+. ② ……………………………………5分由①,②可得:13,2a d ==. ……………………………………6分 所以21n a n =+. ……………………………………7分 (Ⅱ)由21n a n =+可知:2(321)22n n nS n n ++?==+.……………………………………9分所以11111()(2)22n S n n n n ==-++. ……………………………………11分 所以123111111n nS S S S S -+++++L 11111111111()2132435112n n n n =-+-+-++-+--++L 21111135()212124(1)(2)n n n n n n +=+--=++++.所以数列1{}nS 的前n 项和为2354(1)(2)n n n n +++.……………………………………13分(16)(本小题满分14分)(Ⅰ)证明:因为点E 为线段PB 的中点,点O 为线段AB 的中点,所以 OE ∥PA . ……………………………………1分 因为 PA Ì平面PAC ,OE Ë平面PAC ,所以 OE ∥平面P AC . ……………………………………2分因为 OM ∥AC , 因为 AC Ì平面PAC ,OM Ë平面PAC ,所以 OM ∥平面P AC . ……………………………………3分因为 OE Ì平面MOE ,OM Ì平面MOE ,OE OM O =I ,所以 平面MOE ∥平面P AC . ………………………………………5分(Ⅱ)证明:因为 点C 在以AB 为直径的⊙O 上,所以 90ACB??,即BC AC ⊥.因为 PA ^平面ABC ,BC Ì平面ABC , 所以PA BC ⊥. ……………………………………7分因为 AC Ì平面PAC ,PA Ì平面PAC ,PA AC A =I ,所以 BC ^平面PAC . 因为 BC Ì平面PBC ,所以 平面P AC ^平面PCB . ……………………………………9分(Ⅲ)解:如图,以C 为原点,CA 所在的直线为x 轴,CB 所在的直线为y 轴,建立空间直角坐标系C xyz -. 因为 30CBA??,2PA AB ==,所以2cos30CB =?1AC =.延长MO 交CB 于点D . 因为 OM ∥AC ,所以131, 1,222MD CB MD CD CB ^=+===. 所以 (1,0,2)P ,(0,0,0)C,B,3(2M . 所以 (1,0,2)CP =u u u r,CB =u u u r.设平面PCB 的法向量(,,)=x y z m .因为 0,0.CP CBìï?ïíï?ïîu u u r u u u r m m所以(,,)(1,0,2)0,(,,)0,x y z x y z ì?ïïíï?ïî即20,0.x z ì+=ïïíï=ïî 令1z =,则2,0x y =-=.所以 (2,0,1)=-m . ……………………………………12分 同理可求平面PMB 的一个法向量n ()=.……………………………………13分 所以 1cos ,5⋅==-⋅m n m n m n . 所以 1cos 5θ=. ………………………………………14分 (17)(本小题满分13分) 解:(Ⅰ)由题意得:0.41,11120.41712.a b a b ++=⎧⎨+⨯+=⎩解得:0.5,0.1a b ==. ……………………………………3分 (Ⅱ)X 2 的可能取值为4.12,11.76,20.40.()[]2 4.12(1)1(1)(1)P X p p p p ==---=-,()[]22211.761(1)(1)(1)(1)P X p p p p p p ==--+--=+-,()220.40(1)P X p p ==-.所以X 2的分布列为:(Ⅲ)由(Ⅱ)可得:()2224.12(1)11.76(1)20.40(1)E Xp p p p p p ⎡⎤=-++-+-⎣⎦211.76p p =-++. ……………………………………11分因为E (X 1)< E (X 2),所以21211.76p p<-++. 所以0.40.6p <<.当选择投资B 项目时,p 的取值范围是()0.4,0.6.……………………………………13分(18)(本小题满分13分) 解:(Ⅰ)由题意知:1c =. 根据椭圆的定义得:22a =,即a =……………………………………3分 所以 2211b =-=.所以 椭圆C 的标准方程为2212x y +=. ……………………………………4分 (Ⅱ)假设在x 轴上存在点(,0)Q m ,使得716QA QB ⋅=-u u u r u u u r恒成立. 当直线l 的斜率为0时,(A B .则7,0)(,0)16m m ?=-. 解得 54m =?. ……………………………………6分 当直线l的斜率不存在时,(1,(1,22A B -.由于557(1,(1,424216+?-?,所以54m ?. 下面证明54m =时,716QA QB ⋅=-u u u r u u u r 恒成立.……………………………………8分显然 直线l 的斜率为0时,716QA QB ⋅=-u u u r u u u r .当直线l 的斜率不为0时,设直线l 的方程为:1x ty =+,()()1122,,,A x y B x y .由221,21x y x ty ìïï+=ïíïï=+ïî可得:22(2)210t y ty ++-=. 显然0∆>.1221222,21.2t y y t y y t ìïï+=-ïï+ïíïï=-ïï+ïî……………………………………10分 因为 111x ty =+,221x ty =+,所以 112212125511(,)(,)()()4444x y x y ty ty y y -?=--+ 2121211(1)()416t y y t y y =+-++2221121(1)24216t t t t t =-+++++ 22222172(2)1616t t t --+=+=-+.综上所述:在x 轴上存在点5(,0)4Q ,使得716QA QB ⋅=-u u u r u u u r 恒成立.……………………………………13分(19)(本小题满分14分)(Ⅰ)解:()f x 的定义域为(,)a +∞.2(1)'()1a x a xf x x x a x a-++=-+=--. ……………………………………1分令'()0f x =,0x =或+1x a =.当10a -<<时,+10a >,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(0,1)a +,单调递减区间是(,0)a 和(1,)a ++?.……………………………………3分当1a =-时,2'()01x f x x -=≤+. 所以,函数()f x 的单调递减区间是(1,)-+?. ……………………………………4分 当1a <-时,+10a <,函数()f x 与'()f x 随x 的变化情况如下表:所以,函数()f x 的单调递增区间是(1,0)a +,单调递减区间是(,1)a a +和(0,)+?.……………………………………5分(Ⅱ)证明:当12(ln21)0a -<<-<时,由(Ⅰ)知,()f x 的极小值为(0)f ,极大值为(1)f a +.因为(0)ln()0f a a =->,2211(1)(1)(1)(1)022f a a a a +=-+++=->,且()f x 在(1,)a ++?上是减函数,所以()f x 至多有一个零点. ……………………………………7分 又因为211(2)ln 2[2(ln 21)]022f a a a a a a +=--=---<, 所以 函数()f x 只有一个零点0x ,且012a x a +<<+.……………………………………9分(Ⅲ)解:因为412(ln 21)5-<-<-, 所以 对任意120,[0,]x x x ∈且211,x x -=由(Ⅱ)可知:1[0,1)x a ∈+,20(1,]x a x ∈+,且21x ≥. ……………………………………10分因为 函数()f x 在[0,1)a +上是增函数,在(1,)a ++?上是减函数,所以 1()f x (0)f ≥,2()f x (1)f ≤. ……………………………………11分 所以 12()()(0)(1)f x f x f f -?.当45a =-时,1(0)(1)ln()12a f f a a -=--=491ln 542->0. 所以 12()()(0)(1)0f x f x f f -?>. ……………………………………13分所以 21()()f x f x -的最小值为491(0)(1)ln 542f f -=-. 所以 使得21()()f x f x m -≥恒成立的m 的最大值为491ln 542-.……………………………………14分(20)(本小题满分13分)(Ⅰ)解:因为3=3,3=1+2,3=1+1+1,所以3)3(=f .因为5=5,5=2+3,5=1+4,5=1+1+3,5=1+2+2,5=1+1+1+2,5=1+1+1+1+1, 所以7)5(=f . ……………………………………3分 (Ⅱ)结论是)1(+n f )]2()([21++≤n f n f . 证明如下:由结论知,只需证).1()2()()1(+-+≤-+n f n f n f n f因为21≥+n ,把1+n 的一个表示法中11a =的1a 去掉,就可得到一个n 的表示法;反之,在n 的一个表示法前面添加一个“1+”,就得到一个1n +的表示法,即1+n 的表示法中11a =的表示法种数等于n 的表示法种数,所以)()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数,)1()2(+-+n f n f 是2n +的表示法中11a ¹的表示法数.同样,把一个11a ¹的1+n 的表示法中的p a 加上1, 就可得到一个11a ¹的2n +的表示法,这样就构造了从11a ¹的1+n 的表示法到11a ¹的2+n 的表示法的一个对应.所以有).1()2()()1(+-+≤-+n f n f n f n f ……………………………………9分(Ⅲ)由第(Ⅱ)问可知:当正整数6m ³时,()(1)(1)(2)(6)(5)f m f m f m f m f f --?--吵-L. 又,7)5(,11)6(==f f 所以 ()(1)4f m f m --?. *对于*式,分别取m 为n ,,7,6Λ,将所得等式相加得)5(4)5()(-≥-n f n f .即134)(-≥n n f . ……………………………………13分。
2012年北京市各区二模试题分类解析【数学文】(12):算法初步.pdf
结合时代背景,深层领会小说的思想意义。
教学过程 [教学步骤] 一、导语设计 同学们,作为中华民族20世纪的文化伟人,作为伟大的文学家、思想家和革命家的鲁迅,以文艺实现他改变“愚弱的国民”精神的启蒙主义抱负。
在他一生所创作的三十多篇小说中,他最喜欢的是收在小说集《呐喊》中的《孔乙己》。
巴金也说《孔乙己》写得好。
日本有一位作家说孔乙己是最完美的艺术典型,今天,我们就来认识一下孔乙己这个不朽的艺术形象。
(板书文题、作者) 三、诵读,整体感知文意 1.学生默读课文,初步感知文意,疏解下列字词。
(1)注音: (2)释义: 阔绰(chuò ) 羼(chàn) 绽出(zhàn) 拭(shì) 格局:布置的格式。
阔绰:阔气。
污人清白:毁坏人家的名誉。
2.学生自由诵读全文,找出反映下列内容的语句并揣摩其丰富含义。
(1)孔乙己的特殊身份 (2)孔乙己的地位 (3)孔乙己的结局 学生精彩回答,教师提示: (1)概括孔乙己特殊身份的语句:“孔乙已是站着喝酒而穿长衫的唯一的人” 句中“站着喝酒”表明孔乙己生活贫困,经济地位和社会地位都和短衣帮一样;“穿长衫”表明他不愿与“短衣帮”为伍,硬摆读书人的架子;“唯一的”点出了孔乙己的特殊性,他与上层人、下层人都有距离。
3.请学生理清小说情节结构,并概括孔乙己的六个生活片断。
学生回答,教师归结: 六个生活片断是: (1)众人取笑孔乙己脸上又添了新伤疤; (2)众人讥笑孔乙己考不中秀才;(3)孔乙己为偷书作辩解; (4)孔乙己教小伙计识字; (5)孔乙己给小孩子们分茴香豆; (6)侧面交代孔乙己被打断腿。
4.四人学习小组合作探究,分析孔乙己形象。
(1)填写下列句子,探究孔乙己性格中的矛盾表现。
孔乙己是站着喝酒但又_______的人。
孔乙已是穷得将要讨饭但又_______的人。
学生思考、交流,教师明确: 穿长衫 好喝懒做 把“半个秀才也没捞到”当作灵魂伤疤 偶有偷窃 从不拖欠酒钱屡遭冷遇 想和人交流无人关心、可有可无 (2)深入探因 学生合作探究孔乙己矛盾表现的思想原因和社会原因,深刻理解孔乙己形象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x ① f ( x) = e ;
② f ( x ) = −e x ; ④ f ( x) = x − x .
−1
③ f ( x) = x + x −1 ;
则输出函数的序号为( D ) A.① C.③ B.② D.④
S = 0 , n =1,a = 3 S = S +a n = n +1 a =a+2
否
是 输出 S
结束
11) 4.(2012 年昌平二模理 11)如图给出了一个程序框图, 输出相应的 y 值,若要使输入的 x 其作用是输入 x 的值, 值与输出的 y 值相等,则这样的 x 值有 _______个. 答案: 答案:3。
开始
输入 x
x≤2
否 是 是
x≤5
否
y=x2
y=2x-3
y= x -1
输出 y
结束2/2Fra bibliotek年朝阳二模理 10) 2.(2012 年朝阳二模理 10)执行如图所示的程序框图,输出的结果是____ ___. 答案: 答案:13
开始 x=1,y=1,z=2
z=x+y y=z x=y 是 z≤10 否 输出 z 结束 (第 10 题图)
1/2
3.(2012 年丰台二模理 4)执行如图所示的程序框图,若输出的结果为 63,则判断框中应 填( D ) A. n ≤ 7 B. n > 7 C. n ≤ 6 D. n > 6 开始
