第9章--机械振动(阻尼振动和受迫振动)
阻尼振动与受迫振动

【实验目的】1.观测阻尼振动,学习测量振动系统基本参数的方法。
2.研究受迫振动的幅频特性和相频特性,观察共振现象。
3.观察不同阻尼对受迫振动的影响。
【实验原理】当摆轮受到周期性强迫外力矩t M M ωcos 0=的作用,并在有空气阻尼的媒质中运动时(阻尼力矩为 ),其运动方程为t M dt d b k dtd J ωθθθcos 022+--= (1)其中,J 为摆轮的转动惯量,θk -为弹性力矩,0M 为强迫力矩的幅值,ω为强迫力的圆频率。
令J k =20ω,J b=β2,JM m 0=,则(1)式变为 t m dt d dtd ωθωθβθcos 22022=++ (2) 其中,β为阻尼系数,0ω为系统的固有频率,m 为强迫力矩。
当0cos =t m ω时,(2)式即为阻尼振动方程,当0=β,即在无阻尼情况时,(2)式变为简谐振动方程。
方程(2)的通解为()()0201cos cos ϕωθαωθθβ+++=-t t e t (3)由(3)式可见,受迫振动可分为两部分:第一部分,()αωθβ+-t e t 01cos 表示阻尼振动,经过一定时间后衰减消失。
第二部分,说明强迫力矩对摆轮作功,向振动体传递能量,最后达到一个稳定的振动状态,其振幅为()22222024ωβωωθ+-=m(4)它与强迫力矩之间的相位差ϕ为()2022022012T T T T tg -=-=-πβωωβωϕ (5) 由(4)式和(5)式可看出,振幅2θ与相位差ϕ的数值取决于强迫力矩m 、频率ω、固有频率0ω和阻尼系数β四个因素,而与振动起始状态无关。
由()[]04222220=+-∂∂ωβωωω极值条件可得出,当受迫力的圆频率2202βωω-= 时产生共振,θ有极大值。
若共振时的圆频率和振幅分别用r ω 、r θ表示,则dtd b θ-2202βωω-=r (6)2222βωβθ-=m r (7)(6)式和(7)式表示,阻尼系数β越小,共振时圆频率越接近于系统固有频率,振幅也越大。
大学物理学-阻尼振动与受迫振动
v
弹性力
粘滞阻力: f r v
粘滞阻力
x
dx
d 2x
kx
m 2
dt
dt
令k / m 0 , / m 2
2
d2x
dx
2
2
0 x 0
2
dt
dt
大学物理学
k (固有频率)
0
m
(阻尼系数)
2m
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
4.3 阻尼振动与受迫振动
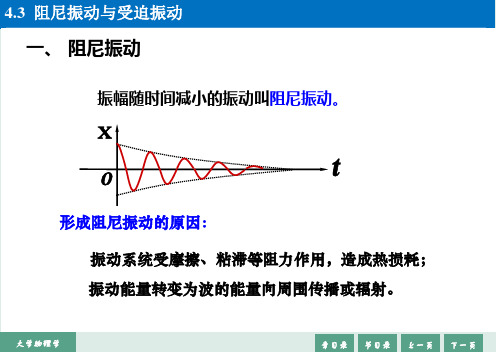
一、 阻尼振动
振幅随时间减小的振动叫阻尼振动。
形成阻尼振动的原因:
振动系统受摩擦、粘滞等阻力作用,造成热损耗;
振动能量转变为波的能量向周围传播或辐射。
大学物理学
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
1. 阻尼振动的微分方程
弹性力:
F kx
(以液体中的水平弹簧振子为例)
阻尼=0
阻尼较小
pr 02 2 2
阻尼较大
共振振幅 :
Ar
大学物理学
f0
2 02 2
O
p
0
共振曲线
章目录
节目录
上一页
下一页
4.3 阻尼振动与受迫振动
2. 速度共振
受迫振动的速度的振幅出现极大值的现象
v pA sin( pt )
大学物理学
章目录
节目录
r
d2x
k
x0
2
2
dt
m J r
5.4阻尼振动和受迫振动

2 p
2 2 0 p
稳态时振动物体速度:
dx A p cos( p t ) dt 2
式中
m A p
f p
2 2 2 2 (0 p ) 4 2 p
在受迫振动中,周期性的驱动力对振动系统提供 能量,另一方面系统又因阻尼而消耗能量,若二者相 等,则系统达到稳定振动状态。
在小阻尼条件下 ( 0 ) ,微分方程的解为:
2
x Ae
t
cos(t )
2 2 其中 0
x Ae
其中 A 和
t
cos(t )
t
为积分常数,由初始条件决定。上式中的
余弦项表征了在弹性力和阻力作用下的周期运动;e 反映了阻尼对振幅的影响。
对于阻尼较小的情形,运动方程之解表为:
x A0e
衰减项
t
cos(t ) A cos( pt )
Hale Waihona Puke 稳态项经过一段时间后,衰减项忽略不计,仅考虑稳态项。
x A cos( pt )
f ( ) 4
2 0 2 2 p 2 2 p
A
tg
共振的应用和防止 应用
共振筛 防止
共鸣箱
1.队或火车过桥时要放慢速度或便步走 2.在振动物体底座加防振垫 3.装修剧场、房屋时使用吸声材料等
2、共
振
对于受迫振动,当外力幅值恒定时,稳定态 振幅随驱动力的频率而变化。当驱动力的角频率 等于某个特定值时,位移振幅达到最大值的现象 称为位移共振。
A
f
2 2 2 2 (0 p ) 4 2 p
dA 0 dp
共振频率
阻尼振动与受迫振动

,可以推出������0 =
2������ ������������ 1−������
2
= ,是阻尼振动振幅衰减到原来 ������−1 需要
,是系统共振锐度或频率选择性的量度。
������������ ������
6. 对数缩减率Λ =
=
2������������ 1−������ 2
,定义为衰减阻尼振动中相邻两
������ ������ 0 ������ 、 ������
=
������ 2 ������������ 2������
2 ������2 0 −������
3. 阻尼振动周期������������ = 4. 时间常数������ = 的时间。 5. 品质因素������ ≡
1 2������ 2������ ������ 1 ������
2 小阻尼(������ 2 − ������0 < 0)时,阻尼振动运动方程的解为 2
������ ������ = ������������ exp −������������ cos
2 ������0 − ������ 2 ������ + ������������ 2
由 上 式 可 知 , 阻 尼 振 动 角 频 率 ������������ = ������2 0 − ������ , 而 周 期 为 ������������ =
[2]
即 ������ 2 ������ ������������ ������ 2 + ������ + ������������ = ������������������ cos ������������ ������������ ������������ 它和弹簧支座固定、摆轮受周期外力矩������������������ cos ������������作用时运动 方程在形式上完全一致,等效外激励力矩的振幅为������������������ ,则对 应的稳态解振幅和相位差分别为 ������������ = ������������ ������2 0
阻尼振动和受迫振动ppt课件

陆果一书讨论阻尼弹簧振子的相图。p168
21
通常称 A p 与 p 的关系曲线为频率响应曲线。
当 Ap maxAp()/ 2时,即相对振幅为 0.707 (即相对强度为1/2) 处曲线宽度,定义为共振 峰的宽度 或共振带宽。可证明在弱阻尼的情
18
讨论:p 0, ApH p /2mp h2 较小
p 0,
H/m H
Ap 2 0
k
p0, Ap 2 H/ m 0 若很小,A p 很大。
3-2 共振
求振幅 Ap 得出
h
对频率的极值,
(02p2)242p2
振幅有极大值:
Ar 2
h
02 2
共振的振幅。
pr 02 22 共振的角频率。
19
pr 02 22 共振的角频率。
k2 A20co 2xsd x1k2 A
2T0 0
4
4
求出势能的时间平均值:
E pT 10 T1 2k2 A co 2(s0t0)d t
k2 A20co 2xsd x1k2 A
2T0 0
4
结论:
* 即弹簧振子的动能和势能的平均值相等,且 等于总机械能的一半
* 任一简谐振动总能量与振幅的平方成正比
co s co s2 co s co s
2
2
合成振动表达式:
x ( t) A co 1 t s ) A (co 2 t s )(
30
附录:三角函数关系式的证明
4 cos cos
22
大学物理机械振动课件

03 阻尼振动
阻尼振动的定义与特点
定义
阻尼振动是指振动系统受到阻力 作用,使得振动能量逐渐减少的
振动过程。
特点
随着时间的推移,振幅逐渐减小, 频率逐渐降低,直至振动停止。
阻尼力
阻尼振动过程中,系统受到的阻力 称为阻尼力,它与振动速度成正比, 方向与振动速度方向相反。
阻尼振动的描述方法
微分方程
阻尼振动的运动方程通常表示为二阶常微分方程,形式为 `m * d²x/dt² + c * dx/dt + k * x = 0`,其中 m、c、k 分别为质量、
振动压路机
利用共振原理来提高压实效果。
振动输送机
利用共振来输送物料,提高输送效率。
受迫振动与共振的能量转换
能量转换过程
外界周期性力对系统做正 功,系统动能增加;阻尼 使系统能量耗散,系统势 能减小。
转换关系
在振动过程中,外界对系 统的总能量输入等于系统 动能和势能的变化之和。
影响因素
阻尼系数、驱动力频率、 物体固有频率等。
能量耗散途径
阻尼振动的能量耗散途径 主要包括与周围介质之间 的摩擦、空气阻力、内部 摩擦等。
能量耗散的意义
阻尼振动的能量耗散有助 于减小系统振幅,避免因 过大振幅导致的结构破坏 或噪声污染等问题。
04 受迫振动与共振
受迫振动的定义与特点
定义:在外来周期性力的持 续作用下,物体发生的振动
称为受迫振动。
确定各简谐振动的振幅、相位差和频 率,在复平面内绘制振动相量,通过 旋转和位移操作找到合成振动的相量 表示。
振动合成的能量法
描述
能量法是通过分析各简谐振动的能量分布和转化,来研究振 动合成过程中的能量传递和平衡。
阻尼振动__受迫振动
实验表明:
物体在外力驱动下振动时,振动稳定后的频率等于外力 驱动的频率,跟物体的固有频率没有关系.
受迫振动物体
T T驱 f f驱
受迫振动实例:
①跳板在人走过时发生的振动 ②机器底座在机器运转时发生的振动 ③听到声音时耳膜的振动 ④电磁打点计时器的振针所做的振动
1.下列振动中属于受迫振动的是(
D.后一时刻的机械能一定小于前一时刻的机械能
【解题指导】在阻尼振动中,振动系统的动能和势能之 和减小.但在一段较短的时间内,动能和势能不一定都减小,关 键要分析动能与势能之间是如何转化的.
思考: 用什么方法才能得到持续的振动呢?
1,驱动力:作用到振动系统周期性的外力 2,受迫振动:物体在外界驱动力作用下的振动 3、受迫振动的特点:受迫振动的频率总等于驱动力 的频率,与系统的固有频率无关
o
t
阻尼振动图象
注意:阻尼振动的振幅是逐渐减小的,但是它的频率是不发生
变化的,频率与振幅是无关的。
2.系统不受外力作用,也不受任何阻力,只在自身 回复力作用下的振动,称为自由振动 又叫做无阻尼振动。
或无阻尼振动图象
自由振动的频率,叫做系统的固有频率
[要点提炼 ] 1.对阻尼振动的理解 (1)同一简谐运动能量的大小表现为 振幅 的大小.
2.阻尼振动和无阻尼振动的比较 振动类型 阻尼振动 比较项目 产生条件 振幅 受到阻力作用 如果没有能量补充,物 体的振幅会 越来越小
无阻尼振动 不受阻力作用或受到 阻力作用,但外界补 充能量 振幅 不变
振动图像 用锤敲锣,由于锣的振 动,发出响亮的锣声, 弹簧振子的振动,单 但锣声越来越弱,振幅 摆的振动 越来越小,属阻尼振动
实例
1.下列说法中正确的是 [ ACD
阻尼振动与受迫振动教案
三、共振的危害与应用
1、共振的危害与防止
例1、(图片说明)18世纪中叶,法国昂热市附近一座长102m的桥,因一队骑兵在桥上经过。他们在指挥官的口令下迈着整齐的步伐过桥,引起桥梁共振,桥梁突然断裂,造成226名官兵和行人丧生。此后,各国都规定大队人马过桥,要便步通过。
例3、(图片说明)微波炉:微波炉加热食品时,炉内有很强的交变电磁场,它使得食物分子中的带电微粒做受迫振动.由于分子间的相互作用,振动的能量最终成为食物分子热运动的动能,提高了食物的温度。
四、思考
对于一个振动系统,如果其位移做的是一个无阻尼简谐振动,则其速度的运动也是简谐振动。
在受迫振动中,位移也在做一个类似于简谐振动的周期性振动
3、知道共振的应用和防止的实例。
教学重点
1、什么是阻尼振动以及阻尼振动的特点。
2、什么是受迫振动,什么是共振及共振产生的条件。
教学难点
1、简谐振动、阻尼振动及受迫振动的区别。
2、共振发生的条件。
教学方法
1、多媒体课件与黑板板书相结合。
2、图片举例,了解共振的应用和防止;
3、实际演示,了解阻尼振动的特点及共振现象。
振动方程
振动特点
特征量
无阻尼简谐振动
等幅振动
机械能守恒
初始条件
系统自身性质
阻尼振动
减幅振动
能量不断衰减
初始条件
阻尼因子
系统自身性质
受迫振动
等幅振动,
需要外界不断补充能量
与策动力的幅值、
频率及阻尼因子有关
1、在张紧的水平绳上挂7个单摆,先让D摆振动起来,其余各摆也随之振动,已知A、D、G三摆的摆长相同,则下列判断正确的是
阻尼振动和受迫振动
横轴:表示驱动力的频率
纵轴:表示受迫振动的振幅
图象的意义:
f驱= f固时,振幅有最大值
f驱与 f固差别越大时,振幅越
小
四、共振的应用和防止
1、共振的应用
①测量发动机转速的转速计
②共振筛
发动机的转速计原理图
共振筛的原理图
生活中的共振现象
美国有一农场农妇,习惯于用吹笛的方式招
关,阻尼越大,振幅减小得越快。
b、物体做阻尼振动时频率不变。
3、自由振动:系统不受外力作用,也不受任
何阻力,只在自身回复力作用下的振动,称
为自由振动。
自由振动的频率,叫做系统的固有频率。来自思考:二、受迫振动
用什么方法才能得到持续的振动呢?
阻尼振动会受到阻力作用,其振幅减小,如
果想让其周期性地振动下去,就需要施加周
第一章 机械振动
4 阻尼振动 受迫振动
如下图所示,在鼓皮上放几颗米粒,猛敲一下鼓,
观察米粒在鼓皮上的运动。
一、阻尼振动
阻尼振动
振动幅
度减小
受到阻力作用
能量的损失
1、定义:系统在振动过程中受到阻力的作用,
振动逐渐消逝,振动能量逐步转变为其他能
量,这种振动叫做阻尼振动。
2、注意:a、振幅减小的快慢跟所受的阻尼有
呼丈夫回家吃饭,可当她有一次吹笛时,居
然发现树上的毛毛虫纷纷坠地而死,惊讶之
余,她到自己的果园吹了几个小时,一下子
将果树上的毛毛虫收拾的一干二净,究其原
因,还是笛子发出的声音引起毛毛虫内脏发
生剧烈共振而死亡。
2、共振的防止
①军队过桥随步走,以免产生周期性驱动力。
2、共振的防止
机械振动中的阻尼振动与受迫振动
机械振动中的阻尼振动与受迫振动在机械系统中,振动是一种普遍存在的现象,它包含着阻尼振动和受迫振动两种类型。
阻尼振动是指系统在一定的阻尼作用下运动的周期性减弱振动,而受迫振动是指系统受到外部力的作用而发生周期性振动。
本文将探讨机械振动中的阻尼振动和受迫振动的特点及其应用。
一、阻尼振动阻尼振动是指振动系统在受到阻力的作用下产生的振动。
阻尼力可以分为粘性阻尼、干摩擦阻尼和液体摩擦阻尼等不同形式。
阻尼振动的特点是振幅逐渐减小,振动频率也逐渐减小。
阻尼振动的主要原因是能量的损失。
当机械系统受到阻尼力的作用时,振动系统的机械能会逐渐转化为热能而损失。
这导致振动幅度逐渐减小,最终停止振动。
例如,摆钟在受到空气阻力的影响下,其摆动幅度会逐渐减小,最终停止。
阻尼振动的应用广泛。
在机械工程中,阻尼振动常常被用于减震和能量吸收的装置设计。
例如,在车辆的悬挂系统中使用减震器,可以有效地缓解车辆行驶中的颠簸感。
同时,阻尼振动还常用于物体的减振和抗震设计,例如建筑物中的隔震装置。
二、受迫振动受迫振动是指振动系统在外部力的作用下产生的振动。
外力可以是周期性的,也可以是非周期性的。
受迫振动的特点是振幅和频率与外力的频率相关。
外力对振动系统的影响可以分为共振和强迫两种情况。
共振是指外力的频率接近或等于振动系统的固有频率时,振动幅度会显著增大。
强迫是指外力的频率与振动系统的固有频率有一定的差别,但仍然能引起系统振动。
受迫振动在实际生活中有许多应用。
例如,在音乐中,乐器的共振现象使得乐器能够产生特定的音调。
另外,受迫振动还在工程领域中有着广泛的应用,如振动筛、振动输送机等。
它们利用外力作用产生振动,以完成特定的分选和输送任务。
三、阻尼振动与受迫振动的关系阻尼振动与受迫振动是机械振动中两种常见的振动类型,它们在某些情况下可以相互转化。
当受迫振动系统存在阻尼时,会产生阻尼振动。
此时,外力的频率与振动系统的固有频率相同或接近时,阻尼振动的幅度会受到外力的影响,产生共振效应。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2) 如果 )
amax > g,
mg − N = ma
小物体能脱离振动物体, 小物体能脱离振动物体,开始分离的位 置由 N = 0 求得
g = amax = −ω x
2
m
x=−
g
ω
2
= −19.6 (cm)
x
初开始分离。 即在平衡位置上方 19.6 cm 初开始分离。
λ = −β ± β −ω
Ae−βt
fv = −γ v
β
2 0
--- 表征阻尼大小的常量
阻尼度
β 当 β < ω (Λ = < 1) 时, ω0 2 λ1, λ2 = −β ± i ω0 − β 2 方程的解为 eλ1t eλ2t 的线性组合 和
2
阻尼振荡(欠阻尼) 阻尼振荡(欠阻尼) a) )
Λ = β / ω0
式中 2β =
γ
x(t) = A0e
若
−β t
cos(ωt +ϕ) + B cos(ωd t + ϕd )
暂态解 定态解
式中 ω =
2 0 2
fd 0 α= m
m k ω0 = m
& x|0 = x|0 = 0 ; ω = ω − β
x
ω −β
2 0
2
过程复杂
t
定态解 t → ∞时 x → Acos(ωt +ϕ)
或 Λ > 1 解为
2 −( β − β 2 −ω0 )t
b)过阻尼(阻尼较大) )过阻尼(阻尼较大)
当
2 β 2 > ω0
x(t) = c1e
c)临界阻尼 )
当
+ c2e
2 −( β + β 2 −ω0 )t
无周期,非振动。 无周期,非振动。
x
o
三种阻尼的比较
b
β =ω
2
2 0
Λ =1
c
t
x(t) = e
9.7 阻尼振动
d2 x 一、无阻尼振动 −kx = m 2 dt 例:水平弹簧谐振子
二、阻尼振动
d2 x 2 + ω0 x = 0 2 dt x = Acos(ω0t +ϕ) ω0 = k
2
m
dx dx 粘性阻力 fv = −γ v −kx − γ =m 2 dt dt 2 ω0 = k / m 固有角频率 d x γ dx k + + x =0 令 2 dt mdt m β = γ / 2m 阻尼系数 2 dx dx 2 + 2β + ω0 x = 0 二阶常系数齐次微分方程 dt 2 dt
A
共振频率
dB 由 =0 dωd
2 0 2 令
小阻尼 阻尼 → 0
ωd = ω − 2β
= ωr
大阻尼
(β << ω0时ωd = ωr = ω0 )
o
ω0
ωP
共振现象的危害
1940 年7月1日美国 Tocama 悬索桥因共振而坍塌 月 日美国
塔科玛大桥.mpg
的拉力作用下可伸长30cm 。现将一 例 一轻弹簧在 60N 的拉力作用下可伸长 物体悬挂在弹簧的下端并在它上面放一小物体, 物体悬挂在弹簧的下端并在它上面放一小物体,它们的总质量 然后释放。 为 4 kg 。待其静止后再向下拉 10cm , 然后释放。问 (1)此小物体是停在振动物体上面还是离开它? )此小物体是停在振动物体上面还是离开它? 需满足何条件? (2)如果使小物体离开,则振幅 A 需满足何条件?二者在 )如果使小物体离开, 何位置开始分离? 何位置开始分离? 解: 设小物体随振动物体的加速度为 a , 按牛顿第二定律有
在
−β t
(c1 + c2t)
a
τ=
1
和过阻尼情形相比,临界阻尼情形下, 和过阻尼情形相比,临界阻尼情形下,物体回到平衡 位置所需时间最短
β
时间, 时间,
1 ≈ 37% 振幅衰减到原来的 e
9.8 受迫振动 共振 周期性驱动力 fd = fd 0 cosωd t 2 dx dx −kx − γ + fd 0 cosωd t = m 2 dt dt d2 x dx 2 + 2β + ω0 x = α cosωd t 2 dt dt
mg − N = ma ∴ N = m( g − a )
m
当 N = 0, 即a = g 时 小物体开始脱离振动物体。 小物体开始脱离振动物体。 由题意可知 A = 10cm, ω = k M = 50 rad ⋅ s −1
2 −2 系统最大加速度 amax = ω A = 5 m ⋅ s
x
故小物体不会离开。 此值小于 g , 故小物体不会离开。
{
将试探 解
x~e
λt 代入上式
特征方程
λ + 2βλ + ω = 0
2 2Байду номын сангаас0
d2 x dx 2 + 2β + ω0 x = 0 dt 2 dt
特征方程 特征根 阻尼系数
2
试探 解
x~e
λt
ω0 = k / m
β = γ / 2m
Ae−βt cosωt
2 λ2 + 2βλ + ω0 = 0 x
2 0
x(t) = A0e
−β t
cos(ωt + ϕ) + B cos(ωd t + ϕd )
α
2 0 2 2 d 2 2 d
得定态解振幅: 得定态解振幅 B =
(ω −ω ) + 4β ω −2βωd 相位: 相位 ϕd = arctan 2 共振频率 2 ω0 −ωd
B和ϕd 与初始条件无关
位移共振
t
T
e = cosθ + i sinθ −iθ e = cosθ − i sinθ (eiθ + e−iθ ) 2 = cosθ (eiθ − e−iθ ) 2i = sinθ
iθ
x(t) = A0e
−β t
cos(ωt +ϕ)
式中 ω =
2 ω0 − β 2
特征根
λ = −β ± β 2 −ω02
