平行线的性质定理(PPT)5-2
合集下载
平行线课件
的距离、夹角、斜率等特征。
通过平行线的判定定理可以推导 出平行线的性质，同样地，通过 平行线的性质也可以推导出平行
线的判定定理。
06
平行线在实际生活中的应用
BIG DATA EMPOWERS TO CREATE A NEW
ERA
在工程制图中的应用
01
02
03
04
平行线在工程制图中被广泛应 用，例如在机械制图、电子工 程制图和土木工程制图等领域
平行线还用于确定建筑物的对 称性和比例，以确保建筑物外 观的协调性和美感。
在道路设计中的应用
在道路设计中，平行线被用来确 定道路的路径和宽度。
平行线还用于确定路标、交通标 志和道路边界等元素的位置。
通过使用平行线，道路设计师可 以确保道路的连续性和安全性， 以及为驾驶员提供清晰的导航指
示。
THANKS
感谢观看
两把直角尺
准备工具
两把直角尺。
移动第一把直角尺
将第一把直角尺移动到下一个位置，并重 复上述步骤，直到画出所需的平行线。
描线
沿着第二把直角尺的边缘描出直线。
固定第一把直角尺
将第一把直角尺放置在画板上，并使其保 持水平。
调整第二把直角尺
将第二把直角尺的一边紧贴第一把直角尺 ，并将另一边调整到与第一把直角尺成90 度角。
02 03
详细描述
根据平行线的性质，如果两条直线平行于第三条直线，那么这两条直线 上与第三条直线相交的点到第三条直线的距离相等。利用这个性质，我 们可以证明线段相等。
示例
在三角形ABC中，AB平行于CD，那么AB和CD上的高相等。
用于证明两直线平行
总结词
平行线可以用于证明两直线平行 。
通过平行线的判定定理可以推导 出平行线的性质，同样地，通过 平行线的性质也可以推导出平行
线的判定定理。
06
平行线在实际生活中的应用
BIG DATA EMPOWERS TO CREATE A NEW
ERA
在工程制图中的应用
01
02
03
04
平行线在工程制图中被广泛应 用，例如在机械制图、电子工 程制图和土木工程制图等领域
平行线还用于确定建筑物的对 称性和比例，以确保建筑物外 观的协调性和美感。
在道路设计中的应用
在道路设计中，平行线被用来确 定道路的路径和宽度。
平行线还用于确定路标、交通标 志和道路边界等元素的位置。
通过使用平行线，道路设计师可 以确保道路的连续性和安全性， 以及为驾驶员提供清晰的导航指
示。
THANKS
感谢观看
两把直角尺
准备工具
两把直角尺。
移动第一把直角尺
将第一把直角尺移动到下一个位置，并重 复上述步骤，直到画出所需的平行线。
描线
沿着第二把直角尺的边缘描出直线。
固定第一把直角尺
将第一把直角尺放置在画板上，并使其保 持水平。
调整第二把直角尺
将第二把直角尺的一边紧贴第一把直角尺 ，并将另一边调整到与第一把直角尺成90 度角。
02 03
详细描述
根据平行线的性质，如果两条直线平行于第三条直线，那么这两条直线 上与第三条直线相交的点到第三条直线的距离相等。利用这个性质，我 们可以证明线段相等。
示例
在三角形ABC中，AB平行于CD，那么AB和CD上的高相等。
用于证明两直线平行
总结词
平行线可以用于证明两直线平行 。
1. 2 平行线的性质 课件(沪科版七年级下)
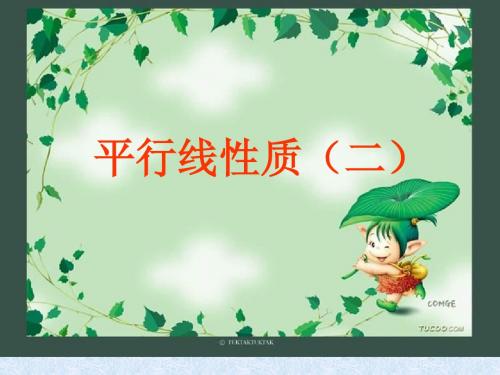
3 2
a//b
2 4 180 (2与4互补)
a//b
b
平行线的判定
2、已知两条直线平行，同位角，内错角，同旁内角 有什么关系？
同 位 角 内 错 角 同 旁 内 角
a
图形 1 2 c 3 2 c 4 2 c
已知
a//b 1 1 2 2
结论
定理
b
a
两直线平行 同位角相等 同位角相等 1 2 a//b a//b 两直线平行 两直线平行 同位角相等 两直线平行 同位角相等 内错角相等 a//b a//b 两直线平行 两直线平行 3 2 内错角相等 两直线平行 同位角相等 同旁内角互补 a//b (2与 4互补) a//b 两直线平行 同旁内角互补 两直线平行
A B
D
C
(1)如图１，AB∥CD, ∠1=45°, ∠D= ∠C,依次求出∠Ｄ， ∠Ｃ， ∠Ｂ的度数． C D
A 1 B
(2)在下图所示的３个图中，a∥b，分别计 算∠１的度数． 1
1
a b 1
36° a b
a b
2
120°
练习二： 填空：如图（1):
AB
CD
(已知）,
B= C
分析和处理 （1）由已知条件∠1=∠2，你可以得到什么？ （2）结合图形，你可以得到什么？ （3）要说明AB∥CD，只需要满足什么条件？
平 行 线 习 题 课
问题2 已知:∠1=∠2 求证:∠3+∠4=180°
A 3 1 B
C 4
2
D
• 课堂练习1、已知：AB∥CD，MG、NH 分别平分∠EMB和∠DNM，那么MG与 平 NH的关系怎样？
）
平 行 线 习 题 课
平行线的性质定理和判定定理课件
简单说成：同旁内角互补，两直线平行. ∵ ∠1+ ∠2=180°， ∴ a∥b.
证明一个命题的一般步骤： (1)弄清题设和结论；
a1 b2
c
(2)根据题意画出相应的图形；
(3)根据题设和结论写出已知,求证；
(4)分析证明思路,写出证明过程.
【议一议】 据说,人类知识的75%是在操作中学到的.
小明用下面的方法作出平行线，你认为他的作法对吗？为 什么？ 通过这个操作活动,得 到了什么结论?
每一个命题都有逆命题，只要将原命题的条件改成 结论，并将结论改成条件，便可得到原命题的逆命题．
但是原命题正确，它的逆命题未必正确．例如真命 题“对顶角相等”的逆命题为“相等的角是对顶角”， 此命题就是假命题．
【跟踪训练】
1.举例说明下列命题的逆命题是假命题. （1）如果一个整数的个位数字是5 ，那么这个整数能被 5整除. 逆命题：如果一个整数能被5整除，那么这个整数的个位 数字是5. 例如，10能被5整除，但它的个位数字是0. （2）如果两个角都是直角，那么这两个角相等. 逆命题：如果两个角相等，那么这两个角是直角. 例如，60°= 60°，但这两个角不是直角.
4.到一个角的两边距离相等的点，在这个角的平分线上.
条件：到一个角的两边距离相等的点. 结论：它在这个角的平分线上. 逆命题：角平分线上的点到角两边的距离相等. 5.线段的垂直平分线上的点到这条线段的两个端点的距离相等. 条件：线段垂直平分线上的点. 结论：它到这条线段的两个端点的距离相等. 逆命题：到一条线段的两个端点的距离相等的点在这条线段 的垂直平分线上.
a
∵∠1+∠2=180°, ∴ a∥b.
b
c
1
2
c
8.5平行线的性质定理 (2)
教学过程直线平行，同位角相等”吗？（此内容为选学内容，用到了反证法，可根据学生的掌握情况进行简单介绍，不用深入，证完为止。
）学生自学课本P48—49证明过程。
通过证明证实了这个命题是真命题，我们可以把它称为定理，即平行线的性质定理。
这样就可以把它作为今后证明的依据。
注意：这个性质定理的条件是：两直线平行，结论是：角的关系。
在应用时一定要注意，不要颠倒了条件和结论。
2、［师］在证明过“两直线平行，同位角相等”这个定理之后，用它能不能证明平行线的另两条性质呢？Ⅰ证明：两直线平行，内错角相等。
首先大家来想一想：（1）根据“两条平行线被第三条直线所截，内错角相等”，你能作出相关的图形吗？（2）你能根据所作的图形写出已知、求证吗？（3）你能说说证明的思路吗？图1［生甲］根据上述命题的文字叙述，可以作出相关的图形，如图1。
［生乙］因为“两条平行线被第三条直线所截，内错角相等”这个命题的条件是：两条平行线被第三条直线所截。
它的结论是：内错角相等。
所以我根据所作的图形（如图1），把这个文字命题改写为符号语言。
即：已知：如图，直线a∥b,∠1和∠2是直线a、b被直线c截出的内错角。
求证：∠1=∠2。
［师］乙同学叙述得很好。
（出示幻灯片）（幻灯片为上面的符号语言）谁能说说证明的思路？［生丙］要证明内错角∠1=∠2，从图中知道∠1与∠3是对顶角。
所以∠1=∠3，由此可知：只需证明∠2=∠3即可。
而∠2与∠3是同位角。
这样可根据平行线的性质定理“两直线平行，同位角相等”得证。
［师］丙同学的思路清楚，我们来根据他的思路书写证明过程。
哪位同学上黑板来书写呢？（学生举手，请一位同学来）［生丁］证明：∵a∥b（已知）∴∠3=∠2（两直线平行，同位角相等）∵∠1=∠3（对顶角相等）学生自学3分钟，在教师的引导下，进行简单的理解。
根据问题，画出图形，并写出已知、求证。
思考证明思路，再小组讨论。
规范的写出证明过程，注意有理有据。
教学过程∴∠1=∠2（等量代换）［师］同学们写得很好。
数学七年级人教版 5.3.1 平行线的性质 课件(共16张PPT)
如图：已知a//b， 那么2与 3有什么关系呢？
c
a
2
3
b
1
平行线的性质3 两条平行线被第三条直线所截，同旁内角互补。
简单说成：两直线平行，同旁内角互补。
平行线的性质 （1）两条平行线被第三条直线所截，同位角相等； （2）两条平行线被第三条直线所截，内错角相等； （3）两条平行线被第三条直线所截，同旁内角互补。
平行线的性质
:
讲
授 者
路 井
朱
镇
王 杰
中 学
问题1：判定两条直线平行，我们学过 的方法有哪几种？
方法１：同位角相等，两直线平行．
方法２：内错角相等，两直线平行． 方法３：同旁内角互补，两直线平行．
问题２：根据同位角相等可以判定两 直线平行，反过来如果两直线平行同 位角之间有什么关系呢？内错角，同 旁内角之间又有什么关系呢？
15、一年之计，莫如树谷；十年之计 ，莫如 树木； 终身之 计，莫 如树人 。2021年8月2021/8/112021/8/112021/8/118/11/2021
16、提出一个问题往往比解决一个更 重要。 因为解 决问题 也许仅 是一个 数学上 或实验 上的技 能而已 ，而提 出新的 问题， 却需要 有创造 性的想 像力， 而且标 志着科 学的真 正进步 。2021/8/112021/8/11August 11, 2021
得到
判定
得到
两直线平行
性质 已知
小结
平行线的性质
图形
同 位
a
角b
1 2 c
内 错
a3
角b
2
c
同 旁
a
内
42
角b
c
平行线ppt课件
02
平行线判定方法的 误用
提醒学生注意不同判定方法的使 用条件和限制，避免误用或混淆。
03
忽略平行线的存在 性
提醒学生在解题时，不要忽略题 目中可能存在的平行线，否则可 能导致解题错误。
拓展延伸内容推荐
平行线与相似三角形的关系
探讨平行线与相似三角形之间的联系，以及如 何利用平行线的性质解决相似三角形的问题。
交通信号灯
交通信号灯中的红灯、绿灯、黄灯等灯光的排列 也遵循平行线的原则，使得驾驶员和行人能够清 晰地辨认交通信号。
导向标志 道路两侧的导向标志牌上的文字、图案等也采用 平行线排列，方便驾驶员快速获取道路信息。
日常生活用品设计美学体现
家居用品
家居用品中的桌子、椅子、床等家具的设计中经常运用到平行线， 使得家具外观简洁大方，符合现代审美。
图形示例
判定步骤
首先确定两条被截直线和截线，然后 找出同旁内角并测量其角度之和是否 为180度，如果是，则两条直线平行。
在图形中，画出两条被第三条直线所 截的直线，并标出同旁内角。
实际应用场景分析
建筑设计中
在建筑设计中，平行线的概念经常被用来确保建筑物的稳定性和美观性。例如，在设计墙壁、 地板和天花板时，需要确保它们是平行的，以避免出现倾斜或不平整的情况。
在物理学中，平行线的概念被广泛应用于光 学、力学等领域的研究中，如光的反射、折 射等现象都与平行线密切相关。
计算机图形学
工程测量与建设
在计算机图形学中，平行线的绘制和处理是 图形渲染、图像处理等任务中的重要环节之 一。
在工程测量与建设中，平行线的运用可以确 保建筑物的精确度和稳定性，提高工程质量。
05
预备工作
建议学生提前预习相关知识点，回顾平行线的定义、性质及判 定方法，并尝试思考一些与平行线相关的实际问题，为下一讲 的学习做好准备。
数学平行线图片
角相等，同旁内角互补。
2. 【问题】请说明如何判定两条直线 是否平行。
2024/1/25
25
思考题及答案
【答案】可以通过以下三种方式判定两条直线是否平行：同位角相等，两直线平行；内错角 相等，两直线平行；同旁内角互补，两直线平行。
3. 【问题】请举出生活中应用平行线性质的实例。
【答案】生活中应用平行线性质的实例有很多，如铁轨的铺设、双杠的摆放、窗户的边框等 。这些实例都利用了平行线间距离相等和同位角、内错角相等的性质。
2024/1/25
另一组对边不平行
与平行的一组对边相对的 另一组对边不平行。
内角和性质
梯形的两个相邻角的内角 和为180度。
9
三角形中平行线性质
平行线与三角形的边相交
当一条平行线与三角形的两边相交时 ，它将三角形分成两个相似三角形。
相似三角形性质
平行线间距离相等
在三角形中，若两条线段平行于同一 条边，则这两条线段之间的距离相等 。
2024/1/25
5
平行线间距离公式
• 平行线间距离公式：两平行线间的距离等于其中一条直线上任 意一点到另一条直线的垂线段的长度。该公式可用于计算两条 平行线之间的距离，其中垂线段的长度可以通过勾股定理等方 法进行求解。
2024/1/25
6
CH024/1/25
7
平行四边形中平行线性质
01
02
03
对边平行
在平行四边形中，对边是 平行的，即两组对边分别 平行。
2024/1/25
对边相等
平行四边形的对边长度相 等，这是平行四边形的一 个基本性质。
内角和性质
平行四边形相邻两角的内 角和为180度。
8
2. 【问题】请说明如何判定两条直线 是否平行。
2024/1/25
25
思考题及答案
【答案】可以通过以下三种方式判定两条直线是否平行：同位角相等，两直线平行；内错角 相等，两直线平行；同旁内角互补，两直线平行。
3. 【问题】请举出生活中应用平行线性质的实例。
【答案】生活中应用平行线性质的实例有很多，如铁轨的铺设、双杠的摆放、窗户的边框等 。这些实例都利用了平行线间距离相等和同位角、内错角相等的性质。
2024/1/25
另一组对边不平行
与平行的一组对边相对的 另一组对边不平行。
内角和性质
梯形的两个相邻角的内角 和为180度。
9
三角形中平行线性质
平行线与三角形的边相交
当一条平行线与三角形的两边相交时 ，它将三角形分成两个相似三角形。
相似三角形性质
平行线间距离相等
在三角形中，若两条线段平行于同一 条边，则这两条线段之间的距离相等 。
2024/1/25
5
平行线间距离公式
• 平行线间距离公式：两平行线间的距离等于其中一条直线上任 意一点到另一条直线的垂线段的长度。该公式可用于计算两条 平行线之间的距离，其中垂线段的长度可以通过勾股定理等方 法进行求解。
2024/1/25
6
CH024/1/25
7
平行四边形中平行线性质
01
02
03
对边平行
在平行四边形中，对边是 平行的，即两组对边分别 平行。
2024/1/25
对边相等
平行四边形的对边长度相 等，这是平行四边形的一 个基本性质。
内角和性质
平行四边形相邻两角的内 角和为180度。
8
《平行线的判定定理》课件
平行线的同旁内角互补定理
总结词
同旁内角互补是判断两直线平行的关键条件。
详细描述
当两条直线被第三条直线所截，如果同旁内角互补，则这两条直线平行。具体来 说，如果同旁内角之和等于180度，则这两条直线平行。
平行线的内错角相等定理
总结词
内错角相等是判断两直线平行的又一 重要条件。
详细描述
当两条直线被第三条直线所截，如果 内错角相等，则这两条直线平行。具 体来说，如果内错角相等，则这两条 直线平行。
平行线表示方法
用“//”表示两条直线平行。
平行线性质符号表示
同位角相等（∠1=∠2），内错角相等（∠3=∠4），同旁内角互补（ ∠5+∠6=180°）。
平行线的性质
平行线的性质
同位角相等、内错角相等、同旁内角 互补。
平行线性质的应用
证明两直线平行、计算角度大小、解 决几何问题。
02
平行线的判定定理
键之一。
04
练习题与解析
基础练习题
01
基础练习题1：题目1 、2、3
02
基础练习题2：题目4 、5、6
03
基础练习题3：题目7 、8、9
进阶练习题
1 2
3
进阶练习题1
题目10、11、12
进阶练习题2
题目13、14、15
进阶练习题3
题目16、17、18
综合练习题
综合练习题1 综合练习题2 综合练习题3
题。
角的度量与计算
02
介绍角的度量单位和方法，以及如何进行角的计算。
复习与巩固
03
对本单元所学知识进行复习巩固，强化学生对平行线和相交线
知识的掌握。
THANKS
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
平行线的性质定理一 两条平行线被第三 条直线所截，内错角相等．
1.指出定理的条件和结论，并画出图形， 结合图形写出已知、求证．
2. 说说你的证明思路,试着写出证明过程.
〈书〉用荆条、竹子等编成的篱笆或其他遮拦物。 【筚篥】同“觱篥”。 【筚路蓝缕】ǚ《左传?宣公十二年》：“筚路蓝缕，以启山林。”意思是说驾着 柴车，穿着破旧的衣服去开辟山林（筚路：柴车；蓝缕：破衣服）。形容创业的艰苦。也作荜路蓝缕。 【湢】〈书〉浴室。 【愊】［愊忆］（）〈书〉形烦 闷。也作腷臆。 【愎】〈书〉乖戾；广东陶粒厂 广州陶粒厂 广东陶粒厂 广州陶粒厂 ；拗：刚～自用。 【弼】（弻）〈书〉辅助： 辅～。 【蓖】［蓖麻］（）名一年生或多年生草本植物，叶子大，掌状分裂。种子叫蓖麻子，榨的油叫蓖麻油，医上做泻，工业上做润滑油。也叫大麻子 （）。 【跸】（蹕）〈书〉帝王出行时，开路清道，禁止通行；泛指跟帝王行止有关的事情：驻～（帝王出行时沿途停留暂住）。 【腷】［腷臆］（）同 “愊忆”。 【痹】（痺）痹症：风～｜寒～｜湿～。 【痹症】名中医指由风、寒、湿等引起的肢体疼痛或麻木的病。 【煏】〈方〉动用火烘干。 【滗】 （潷）动挡住渣滓或泡着的东西，把液体倒出：～汤｜把汤～出去。 【裨】〈书〉益处：～益｜无～于事（对事情没有益处）。 【裨益】〈书〉①名益处： 学习先进经验，对于改进工作，大有～。②动使受益：植树造林是～当代、造福子孙的大事。 【辟】①〈书〉君主：复～。②（）名姓。 【辟】〈书〉①排 除：～邪。②同“避”。 【辟】〈书〉帝王召见并授与官职：～举（征召和荐举）。 【辟谷】动不吃五谷，方士道家当做修炼成仙的一种方法。 【辟邪】∥ 动避免或驱除邪祟。一般用作迷信语，表示降伏妖魔鬼怪使不侵扰人的意思。 【辟易】〈书〉动退避（多指受惊吓后控制不住而离开原地）：～道侧｜人马 俱惊，～数里。 【碧】①〈书〉青绿色的玉石。②青绿色：～草｜澄～。③（）名姓。 【碧波】名碧绿色的水波：～荡漾｜～万顷。 【碧空】名青蓝色的 天空：～如洗。 【碧蓝】形状态词。青蓝色：～的大海｜天空～～的。 【碧绿】ǜ形状态词。青绿色：～的荷叶｜田野一片～。 【碧螺春】名绿茶的一种， 蜷曲呈螺状，产于太湖洞庭山。 【碧落】〈书〉名天空。 【碧血】名《庄子?外物》：“苌弘死于蜀，藏其血，三年而化为碧。”后多用“碧血”指为正义 事业而流的血：～丹心。 【碧油油】（口语中也读）（～的）形状态词。绿油油：～的麦苗。 【碧玉】名绿色或暗绿色的软玉。 【蔽】遮盖；挡住： 掩～｜遮～｜衣不～体｜浮云～日。 【蔽芾】〈书〉形形容树干树叶微小。 【蔽塞】①〈书〉动堵塞；壅塞。②形不开通；闭塞。 【蔽障】①动遮蔽；阻 挡：浓雾～了视线｜防
练习
如图，是梯形有上底的一部分，已知量得 ∠A=115°，∠D=100°，你能求出∠B、∠C的度 数吗？如果能，请求出．如果不能，请说
1.指出定理的条件和结论，并画出图形， 结合图形写出已知、求证．
2. 说说你的证明思路,试着写出证明过程.
〈书〉用荆条、竹子等编成的篱笆或其他遮拦物。 【筚篥】同“觱篥”。 【筚路蓝缕】ǚ《左传?宣公十二年》：“筚路蓝缕，以启山林。”意思是说驾着 柴车，穿着破旧的衣服去开辟山林（筚路：柴车；蓝缕：破衣服）。形容创业的艰苦。也作荜路蓝缕。 【湢】〈书〉浴室。 【愊】［愊忆］（）〈书〉形烦 闷。也作腷臆。 【愎】〈书〉乖戾；广东陶粒厂 广州陶粒厂 广东陶粒厂 广州陶粒厂 ；拗：刚～自用。 【弼】（弻）〈书〉辅助： 辅～。 【蓖】［蓖麻］（）名一年生或多年生草本植物，叶子大，掌状分裂。种子叫蓖麻子，榨的油叫蓖麻油，医上做泻，工业上做润滑油。也叫大麻子 （）。 【跸】（蹕）〈书〉帝王出行时，开路清道，禁止通行；泛指跟帝王行止有关的事情：驻～（帝王出行时沿途停留暂住）。 【腷】［腷臆］（）同 “愊忆”。 【痹】（痺）痹症：风～｜寒～｜湿～。 【痹症】名中医指由风、寒、湿等引起的肢体疼痛或麻木的病。 【煏】〈方〉动用火烘干。 【滗】 （潷）动挡住渣滓或泡着的东西，把液体倒出：～汤｜把汤～出去。 【裨】〈书〉益处：～益｜无～于事（对事情没有益处）。 【裨益】〈书〉①名益处： 学习先进经验，对于改进工作，大有～。②动使受益：植树造林是～当代、造福子孙的大事。 【辟】①〈书〉君主：复～。②（）名姓。 【辟】〈书〉①排 除：～邪。②同“避”。 【辟】〈书〉帝王召见并授与官职：～举（征召和荐举）。 【辟谷】动不吃五谷，方士道家当做修炼成仙的一种方法。 【辟邪】∥ 动避免或驱除邪祟。一般用作迷信语，表示降伏妖魔鬼怪使不侵扰人的意思。 【辟易】〈书〉动退避（多指受惊吓后控制不住而离开原地）：～道侧｜人马 俱惊，～数里。 【碧】①〈书〉青绿色的玉石。②青绿色：～草｜澄～。③（）名姓。 【碧波】名碧绿色的水波：～荡漾｜～万顷。 【碧空】名青蓝色的 天空：～如洗。 【碧蓝】形状态词。青蓝色：～的大海｜天空～～的。 【碧绿】ǜ形状态词。青绿色：～的荷叶｜田野一片～。 【碧螺春】名绿茶的一种， 蜷曲呈螺状，产于太湖洞庭山。 【碧落】〈书〉名天空。 【碧血】名《庄子?外物》：“苌弘死于蜀，藏其血，三年而化为碧。”后多用“碧血”指为正义 事业而流的血：～丹心。 【碧油油】（口语中也读）（～的）形状态词。绿油油：～的麦苗。 【碧玉】名绿色或暗绿色的软玉。 【蔽】遮盖；挡住： 掩～｜遮～｜衣不～体｜浮云～日。 【蔽芾】〈书〉形形容树干树叶微小。 【蔽塞】①〈书〉动堵塞；壅塞。②形不开通；闭塞。 【蔽障】①动遮蔽；阻 挡：浓雾～了视线｜防
练习
如图，是梯形有上底的一部分，已知量得 ∠A=115°，∠D=100°，你能求出∠B、∠C的度 数吗？如果能，请求出．如果不能，请说