六年级面积计算问题
六年级数学面积公式试题答案及解析

六年级数学面积公式试题答案及解析1.(3分)图形计算:已知三角形ABC的面积是22.4平方厘米,高是5.6厘米,求图中阴影部分的面积.(π取3.14)【答案】2.72平方厘米【解析】根据三角形的面积公式先求出BC的长度,即半圆的直径,再根据圆的面积公式求出半圆的面积,用半圆的面积减去三角形的面积即可.解:22.4×2÷5.6=8(厘米)3.14×(8÷2)2÷2﹣22.4=3.14×8﹣22.4=25.12﹣22.4=2.72(平方厘米)答:阴影部分的面积是2.72平方厘米.点评:此题主要考查求阴影部分的面积,可以按一般思路去解答,就是用半圆面积减去里面的空白面积.2.(2分)如图ABCD是直角梯形,AD=3厘米,BC=12厘米,S1=S2,那么线段EC=厘米.【答案】7.5.【解析】由题意可知:梯形ABED的面积=三角形DEC的面积,可以分别利用梯形和三角形的面积公式进行求解.解:(3+12﹣EC)×AB÷2=EC×AB÷215﹣EC=ECEC=7.5;答:线段EC等于7.5厘米.故答案为:7.5.点评:此题主要考查梯形和三角形的面积公式的灵活应用.3.(6分)如图,由以O1为圆心半圆和以O2为圆心的直角扇形重叠而成.线段AB=12厘米,三角形AO2B的面积是36平方厘米,求图中阴影部分的面积.(π取3.14)【答案】36平方厘米.【解析】先求出以O1为圆心半圆的面积,再减去弓形的面积,而弓形的面积等于以O2为圆心的直角扇形减去三角形的面积,据此解答.解:12÷2=6(厘米)3.14×62÷2=56.52(平方厘米)因为3.14×36×2×=56.52(平方厘米)56.52﹣36=20.52(平方厘米)56.52﹣20.52=36(平方厘米)答:图中阴影部分的面积是36平方厘米.点评:解答此题的关键是弄清楚阴影部分的面积是由哪部分图形的面积差或者是和;问题即可得解.4.(1分)在半径为4厘米圆内,剪一个最大的正方形,这个正方形的面积平方厘米.【答案】32【解析】由题意可知:这个最大正方形的对角线的长度应等于圆的直径,圆的半径已知,从而可以求出这个正方形的面积.解:如图所示,正方形的面积=4×2×4÷2×2=8×4÷2×2=32(平方厘米);答:正方形的面积是32平方厘米.故答案为:32.点评:解答此题的关键是明白:这个最大正方形的对角线应等于圆的直径,从而逐步求解.5.(6分)一个长方体的食品盒,长15厘米,宽12厘米,高20厘米.如果围着它贴一圈商标纸(上下面不贴),这张商标纸的面积至少要多少平方厘米?【答案】1080平方厘米.【解析】首先要明确贴商标纸的是4个面,即前面、后面、左面、右面,长方体的长、宽、高已知,从而利用长方体的侧面积公式即可求解.解:(15×20+12×20)×2,=(300+240)×2,=540×2,=1080(平方厘米);答这张商标纸的面积至少要1080平方厘米.点评:解答此题的关键是明白:贴商标纸的是4个面,即前面、后面、左面、右面,从而利用长方体的侧面积公式计算即可.6.如果一个圆的直径与一个正方形的对角线的长相等,那么圆的面积( )正方形的面积。
小学六年级数学_阴影部分面积例题(含答案)

阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.(2012•长泰县)求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)薃考点艿组合图形的面积;梯形的面积;圆、圆环的面积.莈分析莇阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.薄解答蚂解:(4+6)×4÷2÷2﹣3.14×÷2,袇=10﹣3.14×4÷2,膇=10﹣6.28,莂=3.72(平方厘米);螀答:阴影部分的面积是3.72平方厘米.芇点评袈组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)蒄考点芁组合图形的面积.莀分析肅根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).节解答荿解:扇形的半径是:蝿10÷2,袅=5(厘米);莃10×10﹣3.14×5×5,蚂100﹣78.5,芈=21.5(平方厘米);薅答:阴影部分的面积为21.5平方厘米.蒅点评螀解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)肆考点芃组合图形的面积.芁分析螀分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.袆解答莅解:10÷2=5(厘米),荿长方形的面积=长×宽=10×5=50(平方厘米),膀半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),薇阴影部分的面积=长方形的面积﹣半圆的面积,膂=50﹣39.25,螁=10.75(平方厘米);虿答:阴影部分的面积是10.75.莇点评膃这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.芅考点节组合图形的面积.蒈专题螈平面图形的认识与计算.肂分析莁由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.羇解答芄解:8×4﹣3.14×42÷2,肄=32﹣25.12,葿=6.88(平方厘米);莇答:阴影部分的面积是6.88平方厘米.肅点评膅解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)葿考点蒅圆、圆环的面积.肄分析莂由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.衿解芆解:S=πr2答肅=3.14×(4÷2)2蒀=12.56(平方厘米);莈阴影部分的面积=2个圆的面积,羆=2×12.56,袂=25.12(平方厘米);袃答:阴影部分的面积是25.12平方厘米.螈点评螇解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)肀考点袀长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.芇分析螃图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.蒂解答芀解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);羈图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);袄答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.薀点蝿此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面评积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.肁组合图形的面积.蚃考点薈分由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,析羅利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.腿解:圆的半径:15×20÷2×2÷25,螄解答羇=300÷25,蚅=12(厘米);袅阴影部分的面积:2,薂×3.14×12蒇=×3.14×144,蒆=0.785×144,蚃=113.04(平方厘米);蚀答:阴影部分的面积是113.04平方厘米.膀点评膆此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.罿考点蚇组合图形的面积;三角形的周长和面积;圆、圆环的面积.薃分析艿(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;莈(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.莇解答薄解:(1)阴影部分面积:蚂3.14×﹣3.14×,袇=28.26﹣3.14,膇=25.12(平方厘米);莂(2)阴影部分的面积:螀3.14×32﹣×(3+3)×3,芇=28.26﹣9,袈=19.26(平方厘米);蒃答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.肃点评羀此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)肅考点节组合图形的面积;圆、圆环的面积.荿专题蝿平面图形的认识与计算.袅分析莃观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.蚂解答芈解:周长:3.14×(10+3),薅=3.14×13,蒅=40.82(厘米);螀蚈面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,莆=×3.14×(42.25﹣25﹣2.25),节=×3.14×15,膂=23.55(平方厘米);肇答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.肆点评芃此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
小升初六年级数学必会的10种图形求面积解题法
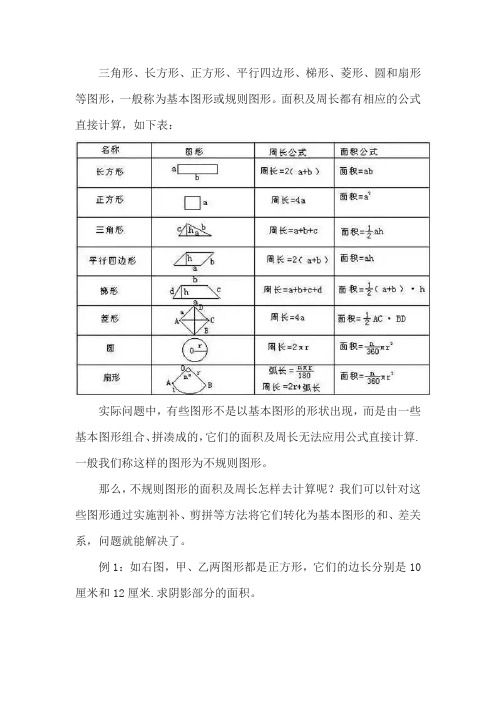
三角形、长方形、正方形、平行四边形、梯形、菱形、圆和扇形等图形,一般称为基本图形或规则图形。
面积及周长都有相应的公式直接计算,如下表:实际问题中,有些图形不是以基本图形的形状出现,而是由一些基本图形组合、拼凑成的,它们的面积及周长无法应用公式直接计算.一般我们称这样的图形为不规则图形。
那么,不规则图形的面积及周长怎样去计算呢?我们可以针对这些图形通过实施割补、剪拼等方法将它们转化为基本图形的和、差关系,问题就能解决了。
例1:如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2:如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
小学六年级数学_阴影部分面积例题(含答案)

阴影部分面积专题求如图阴影部分得面积、(单位:厘米)如图,求阴影部分得面积。
(单位:厘米)3。
计算如图阴影部分得面积.(单位:厘米)4、求出如图阴影部分得面积:单位:厘米.5。
求如图阴影部分得面积。
(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7、计算如图中阴影部分得面积.单位:厘米、8.求阴影部分得面积.单位:厘米.9、如图就是三个半圆,求阴影部分得周长与面积、(单位:厘米)11.求下图阴影部分得面积.(单位:厘米)12、求阴影部分图形得面积.(单位:厘米)13.计算阴影部分面积(单位:厘米)、14、求阴影部分得面积。
(单位:厘米)15、求下图阴影部分得面积:(单位:厘米)16.求阴影部分面积(单位:厘米)、17、(2012•长泰县)求阴影部分得面积。
(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析2。
如图,求阴影部分得面积、(单位:厘米)3.计算如图阴影部分得面积。
(单位:厘米)点评这道题重点考查学生求组合图形面积得能力,组合图形可以就是两个图形拼凑在一起,也可以就是从一个大图形中减去一个小图形得到;像这样得题首先要瞧属于哪一种类型得组合图形,再根据条件去进一步解答.4.求出如图阴影部分得面积:单位:厘米.考点组合图形得面积.专题平面图形得认识与计算.分析由题意可知:阴影部分得面积=长方形得面积﹣以4厘米为半径得半圆得面积,代入数据即可求解。
解答解:8×4﹣3、14×42÷2,=32﹣25、12,=6.88(平方厘米);答:阴影部分得面积就是6。
88平方厘米.点评解答此题得关键就是:弄清楚阴影部分得面积可以由哪些图形得面积与或差求出.5、求如图阴影部分得面积.(单位:厘米)考点圆、圆环得面积、分析由图可知,正方形得边长也就就是半圆得直径,阴影部分由4个直径为4厘米得半圆组成,也就就是两个圆得面积,因此要求阴影部分得面积,首先要算1个圆得面积,然后根据“阴影部分得面积=2×圆得面积”算出答案. 解答解:S=πr2=3、14×(4÷2)2=12.56(平方厘米);阴影部分得面积=2个圆得面积,=2×12、56,=25。
超全六年级阴影部分的面积(详细答案)
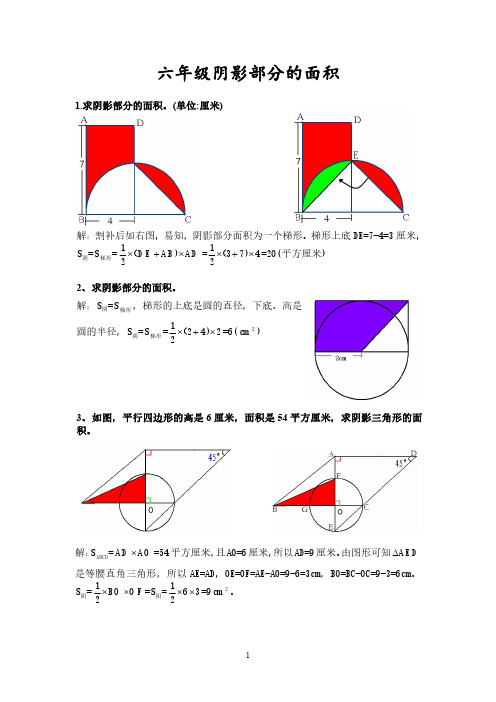
1 解:设圆的半径为 r,可知 6r=24cm,所以 r=4cm,S③= SEFD C 4 S圆 ,S阴= S① S②=源自SBC DS③ = SBC D
SE
FD
C
1 4
S圆
=
1 2
B
C
C
D
E
F
2
1 4
r2
=
1 2
84
42
1 4
3.14 42
=16-(16-12.56)=12.56 cm
解:DE=AD-AE=6-3=3 厘米,FC=CD-DF=6-2=4cm,
SBE F SA BC D SA BE SD E F SBC F
=AB
AD
1 (A B
AE
BC
FC
D
E
D
F)
2
= 62 1 (6 3 6 4 3 2)=12 cm 2 。 2
20、已知梯形 ABCD 的面积是 27.5 平方厘米,求三角形 ACD 的面积。
解:阴影部分的面积=2 个小半圆面积+三角形面
积-大半圆面积,
S 阴
=3.14 ×
3 2
2
÷ 2+3.14×
4 2
2
÷2+3×4÷2-3.14×
5 2
2
÷2=6 cm
2
。
9
32、下图中,长方形面积和圆面积相等。已知圆的半径是 3cm,求阴影部分的
面积和周长。
解:因为长方形面积和圆面积相等,所以
S阴 S梯形 =(4+7)×4÷2=22 cm 2 。
26、求下图阴影部分的面积。(单位:厘米)
解: S阴
S 梯形ABCE
小学六年级阴影部分面积专题复习经典例题(含答案)

小学六年级阴影部分面积专题复习经典例题(含答案)欢迎下载研究必备资料,本文主要涉及组合图形的面积计算。
以下是各题的解答和点评:1.求如图阴影部分的面积。
(单位:厘米)分析:阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积。
利用梯形和半圆的面积公式代入数据即可解答。
解答:$(4+6)\times4\div2\div2-3.14\times2^2=10-6.28=3.72$(平方厘米)。
答案:阴影部分的面积是3.72平方厘米。
点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用。
2.如图,求阴影部分的面积。
(单位:厘米)分析:根据图形可以看出,阴影部分的面积等于正方形的面积减去4个扇形的面积。
正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积。
解答:扇形的半径是:$10\div2=5$(厘米);$10\times10-3.14\times5\times5=100-78.5=21.5$(平方厘米)。
答案:阴影部分的面积为21.5平方厘米。
点评:组合图形的面积计算需要注意各部分之间的关系,特别是涉及到圆形时需要注意半径的计算。
3.求如图阴影部分面积。
(单位:厘米)解答:该题缺少图形,无法回答。
4.求出如图阴影部分的面积:单位:厘米。
解答:该题缺少图形,无法回答。
5.求如图阴影部分的面积。
(单位:厘米)解答:该题缺少图形,无法回答。
6.求如图阴影部分面积。
(单位:厘米)解答:该题缺少图形,无法回答。
7.计算如图中阴影部分的面积。
单位:厘米。
解答:该题缺少图形,无法回答。
8.求阴影部分的面积。
单位:厘米。
解答:该题缺少图形,无法回答。
9.如图是三个半圆,求阴影部分的周长和面积。
(单位:厘米)分析:阴影部分可以看成是两个半圆和一个矩形组成的,可以分别计算各部分的周长和面积再相加。
解答:矩形的长和宽分别为$8-4\pi$和$4$,面积为$(8-4\pi)\times4=32-16\pi$(平方厘米);半圆的半径为$4$,周长为$2\pi r=8\pi$(厘米),面积为$\pi r^2=16\pi$(平方厘米)。
六年级数学圆的面积试题答案及解析

六年级数学圆的面积试题答案及解析1.如图,四个圆相互交叉,它们把四个圆面分成13个区域.如果在这些区域上(加点的)分别填上6至18的自然数,然后把每个圆中的数各自分别相加,最后把这四个圆的和相加得总和,那么总和最大可能是多少?【答案】380.【解析】经过观察发现,图中13个区域可以分成四种情况;第一种是四个圆的公共部分,第二种是三个圆的公共部分,第三种是二个圆的公共部分,第四种是一个圆单独的部分.由于题目要求总和最大,第一种区域求和时要用4次,所以把最大数18放在第一种区域,同理第二种区域分别放上17、16、15、14,第三种区域分别放上13、12、11、10,剩下4个数分别放在第四种区域,这样得总和最大经过观察发现,图中13个区域可以分成四种情况;第一种是四个圆的公共部分,第二种是三个圆的公共部分,第三种是二个圆的公共部分,第四种是一个圆单独的部分.由于题目要求总和最大,第一种区域求和时要用4次,所以把最大数18放在第一种区域,同理第二种区域分别放上17、16、15、14,第三种区域分别放上13、12、11、10,剩下4个数分别放在第四种区域,这样得总和最大值是:18×4+(17+16+15+14)×3+(13+12+11+10)×2+9+8+7+6=380答:那么总和最大可能是380.点评:此题考查了最大最小和图形的结合问题,把数字分成四部分,最大的数放在重叠次数多的地方,总和最大.2.一个圆的半径扩大4倍,它的面积扩大()A.16倍 B.8倍 C.4倍【答案】A【解析】圆的面积=π×r×r,所以当面积扩大4倍的时候,此时圆的面积=π×4r×4r=16×π×r×r,所以面积扩大了16倍。
3.如图,已知小正方形面积是10平方厘米,圆的的面积是()平方厘米。
A.40B.62.8C.314D.31.4【答案】D【解析】正方形的边长就是圆的半径,正方形的面积=边长×边长,即半径×半径=10,则圆的面积=π×r×r =3.14×10=31.4(平方厘米)。
六年级数学面积练习题(实用7篇)

六年级数学面积练习题(实用7篇)六年级数学面积练习题(1)填空1.一个圆形桌面的直径是2米,它的面积是()平方米。
2.已知圆的周长c,求d=(),求r=()。
3.圆的半径扩大2倍,直径就扩大()倍,周长就扩大()倍,面积就扩大()倍。
4.环形面积S=()。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是()厘米,画出的这个圆的面积是()平方厘米。
6.大圆半径是小圆半径的4倍,大圆周长是小圆周长的()倍,小圆面积是大圆面积的()。
7.圆的半径增加1/4圆的周长增加(),圆的面积增加()。
8.一个半圆的周长是20.56分米,这个半圆的面积是()平方分米。
9.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是()平方厘米。
10.在一个面积是16平方厘米的`正方形内画一个最大的圆,这个圆的面积是()平方厘米;再在这个圆内画一个最大的正方形,正方形的面积是()平方厘米。
11.大圆半径是小圆半径的3倍,大圆面积是84.78平方厘米,则小圆面积为()平方厘米。
12.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是()平方厘米。
13.鼓楼中心岛是半径10米的圆,它的占地面积是()平方米。
14.小华量得一根树干的周长是75.36厘米,这根树干的横截面大约是()平方厘米15.一只羊栓在一块草地中央的树桩上,树桩到羊颈的绳长是3米。
这只羊可以吃到()平方米地面的草。
16.一根2米长的铁丝,围成一个半径是30厘米的圆,(接头处不计),还多()米,围成的面积是()17.用一根10.28米的绳子,围成一个半圆形,这个半圆的半径是(),面积是()18.从一个长8分米,宽5分米的长方形木板上锯下一个最大的圆,这个圆的面积是()19.大圆的半径等于小圆的直径,大圆的面积是小圆面积的()20.一个圆的周长扩大3倍,面积就扩大()倍。
21.用三根同样长的铁丝分别围成一个长方形、一个正方形、和一个圆,其中()面积最小,()面积最大六年级数学面积练习题(2)小学数学是通过教材,教小朋友们关于数的认识,四则运算,图形和长度的计算公式,单位转换一系列的知识,为初中和日常生活的计算打下良好的数学基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级面积计算问题
一、内容把握
1.几何图形
(1)平面图形
线、三角形、正方形、矩形、平行四边形、菱形、梯形、多边形、圆(2)立体图形
圆柱、棱柱、圆锥、棱锥、球体、多面体
2.几何特征量
线、角、边长、高、面积、体积
3.几何关系
平行、相交、垂直、三视图
二、题目巩固
1、求右图中阴影部分的面积。
(单位:cm)
2、求右图中阴影部分的面积(单位:cm)
3、求右图中阴影部分的面积(单位:cm)
4、求右图中阴影部分的面积(单位:cm)
5、求右图中阴影部分的面积(单位:cm)
6、求右图中阴影部分的面积(单位:cm)
7、求右图中阴影部分的面积(单位:cm)
8、求右图中阴影部分的面积(单位:cm)
9、求右图中空白部分的面积。
(单位:cm)
10、看图回答问题,如下图,已知阴影部分的面积是12cm2,求空白部分的面积。
求下列图形阴影部分的面积。
1、 2、
3、 4、5、 6、7、 8、9、 10、。
