K字图形中的相似三角形
k字形三角形相似例题

k字形三角形相似例题【原创实用版】目录1.题目背景及要求2.K 字形三角形的定义和性质3.相似三角形的判定方法4.K 字形三角形相似的例题解析5.总结与拓展正文1.题目背景及要求在解决数学问题时,我们经常会遇到一些形状特殊的图形,如 K 字形三角形。
这类题目在初中、高中数学题中比较常见,要求学生掌握一定的解题技巧和方法。
本篇文章主要针对 K 字形三角形的相似问题进行探讨,帮助大家更好地理解和掌握这一类型的题目。
2.K 字形三角形的定义和性质K 字形三角形是指三角形中有两条边相等,且这两条边所在的直线互相垂直。
它具有以下性质:(1)K 字形三角形的两个底角相等;(2)K 字形三角形的两个斜边互相垂直;(3)K 字形三角形的面积可以通过底边和高来计算。
3.相似三角形的判定方法要解决 K 字形三角形相似问题,首先要了解相似三角形的判定方法。
相似三角形的判定方法有以下几种:(1)AA 相似定理:两个角相等,则两个三角形相似;(2)SAS 相似定理:两边和夹角分别相等,则两个三角形相似;(3)SSS 相似定理:三边分别相等,则两个三角形相似。
4.K 字形三角形相似的例题解析例题:如图,在三角形 ABC 中,AB=AC,BD=DC,且∠BDA=90°。
求证:三角形 ABD 与三角形 CBD 相似。
解析:根据题目条件,我们可以得到两个相等的角(∠ADB=∠CDB)和一个相等的边(BD)。
因此,根据 AA 相似定理,我们可以得出三角形 ABD 与三角形 CBD 相似。
5.总结与拓展在解决 K 字形三角形相似问题时,我们要灵活运用相似三角形的判定方法,注意观察题目中给出的条件,寻找相等的角和边。
同时,多做一些类似的例题,提高自己的解题能力和技巧。
K字型复习

“K”字型复习(三等角型相似三角形)引例:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示:等角的顶点在底边上的位置不同得到的相似三角形的结论也不同,当顶点移动到底边的延长线时,形成变式图形,图形虽然变化但是求证的方法不变。
此规律需通过认真做题,细细体会。
课前演练:1.如图,等边△ABC中,边长为6,D是BC上动点,∠EDF=60°(1)求证:△BDE∽△CFD(2)当BD=1,FC=3时,求BE2.如图,等腰△ABC中,AB=AC,D是BC中点,∠EDF=∠B,求证:△BDE∽△DFE3.(2012•朝阳)如图,四边形ABCD是正方形,点E是BC边上一动点(不与B、C重合).连接AE,过点E作EF⊥AE,交DC于点F.(1)求证:△ABE∽△ECF;(2)连接AF,试探究当点E在BC什么位置时,∠BAE=∠EAF,请证明你的结论.精选例题:例1.(2015•贺州)如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B,C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α=,有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或;④0<BE≤,其中正确的结论是(填入正确结论的序号)例2. 如图,在△ABC中,AB=AC=5cm,BC=8,点P为BC边上一动点(不与点B、C重合),过点P作射线PM交AC于点M,使∠APM=∠B;(1)求证:△ABP∽△PCM;(2)设BP=x,CM=y.求y与x的函数解析式,并写出函数的定义域.(3)当△APM为等腰三角形时,求PB的长.当堂巩固:练习1:.(2012秋•洛江区期末)如图,在△ABC中AB=AC=6cm,BC=8cm.点E是线段BC边上的一动点(不含B、C两端点),连结AE,作∠AED=∠B,交线段AB于点D.(1)求证:△BDE∽△CEA;(2)设BE=x,AD=y,请写y与x之间的函数关系式,并求y的最小值.(3)E点在运动的过程中,△ADE能否构成等腰三角形?若能,求出BE的长;若不能,请说明理由.2.(1)在ABC ∆中,5==AC AB ,8=BC ,点P 、Q 分别在射线CB 、AC 上(点P 不与点C 、点B 重合),且保持ABC APQ ∠=∠.①若点P 在线段CB 上(如图10),且6=BP ,求线段CQ 的长;②若x BP =,y CQ =,求y 与x 之间的函数关系式,并写出函数的定义域;(2)正方形ABCD 的边长为5(如图12),点P 、Q 分别在直线..CB 、DC 上(点P 不与点C 、点B 重合),且保持︒=∠90APQ .当1=CQ 时,写出线段BP 的长(不需要计算过程,请直接写出结果).课后巩固练习:1. 如图,在△ABC 中,8==AC AB ,10=BC ,D 是BC 边上的一个动点,点E 在AC 边上,且C ADE ∠=∠. (1) 求证:△ABD ∽△DCE ;(2) 如果x BD =,y AE =,求y 与x 的函数解析式,并写出自变量x 的定义域; (3) 当点D 是BC 的中点时,试说明△ADE 是什么三角形,并说明理由.2. 已知:如图,在△ABC 中,5==AC AB ,6=BC ,点D 在边AB 上,AB DE ⊥,点E 在边BC 上.又点F 在边AC 上,且B DEF ∠=∠. (1) 求证:△FCE ∽△EBD ;(2) 当点D 在线段AB 上运动时,是否有可能使EBD FCE S S ∆∆=4. 如果有可能,那么求出BD 的长.如果不可能请说明理由.3. 如图,在△ABC 中,AB =AC =5,BC =6,P 是BC 上一点,且BP =2,将一个大小与∠B 相等的角的顶点放在P 点,然后将这个角绕P 点转动,使角的两边始终分别与AB 、AC 相交,交点为D 、E 。
相似三角形复习2—K字型
G
B
F
CD
K字型的延伸形式: A
B A
B
∟
G FC
∟
E
D E
G
F
CD
1、如图,等边△ABC的边长为3,点D是BC上一点,
且BD=1,在AC上取点E,使∠ADE=60度,AE长为
()
A. 3 B.2
2
3
C.
7 3
D.
3 4
2、四边形ABCD中,AD∥BC,AB=DC=AD=6, ∠ABC=∠C=70°,点E,F分别在线段AD,DC上, 且∠BEF=110°,若E为AD中点时,DF长为 ________.
在线段AD上是否存在一点E,使得F为CD的中点, 若存在求出AE的长,若不存在,说明理由。
3.如图,直线 l1∥l2∥l3,一等腰直角三角形 ABC 的三个顶 点 A,B,C 分别在 l1,l2,l3 上,∠ACB =90°,AC 交 l2 于点 D.已 知 l1 与 l2 的距离为 1,l2 与 l3 的距离为 3.则AB 的值为( )
1.先明确不变量及不变关系,对于变量,在 静止时刻进行代数化表示。
2.要使△APR∽△PRQ.,已有的相等条件是 什么?根据对应原则,还可以是哪两个角 对应相等?
3.若改为“当t为何值时,△APR与△PRQ相似”,应该如何解答?
4.如图,正△ABC边长为6cm,P,Q同时从 A,B两点出发,分别沿AB,BC匀速运动, 其中点P的速度为1cm/s,点Q的速度为 2cm/s,当Q点到达C点时,两点都停止运 动,设运动时间为t(s),作QR//BA交 AC于点R,连接PR,当t为何值时, △APR∽△PRQ.
1.先明确不变量及不变关系,对于变量,在 静止时刻进行代数化表示。
解读相似三角形中k型图

VS
证明
由于∠BAC=∠DAE且AB/AD=AC/AE=2/3, 根据相似三角形的判定定理,我们可以得 出△ABC∽△ADE。
03
K型图中线段比例关系
比例性质介绍
比例的基本性质
在相似三角形中,对应边之间的 比例是相等的,即如果两个三角 形相似,那么它们的对应边之间 的比值是一个常数。
比例的性质
在相似三角形中,对应高、对应 中线、对应角平分线的比例都等 于相似比。
反思
在学习相似三角形时,可能会出现一些理解上的困难或误区。例如,有些同学可能会认为只要两个三角形的 对应角相等,它们就是相似的,而忽略了对应边成比例的条件。因此,在学习过程中需要不断反思和总结自 己的理解和方法是否正确,并及时纠正错误的认识和做法。同时,还需要多做练习题加深对知识点的理解和
记忆。
THANKS
案例一
建筑设计中的K型图应用。在建筑设计中,经常需要利用相似三角形的性质进行比例计算 和建模。例如,在设计一座建筑时,可以利用K型图求出建筑的高度、宽度等比例关系, 进而进行建筑设计。
案例二
地理测量中的K型图应用。在地理测量中,经常需要利用相似三角形的性质进行距离、高 度等测量。例如,在测量一座山的高度时,可以利用K型图进行建模和计算,从而得出山 的高度。
02
利用K型图的性质
在K型图中,若已知其中一条边的长度,则可以求出另外两条边的长度。
同时,若已知两个角的大小,则可以求出第三个角的大小。
03
证明过程
首先,根据题目中的已知条件,确定K型图中的两个相似三角形。然后,
利用相似三角形的性质,建立比例关系。最后,通过代数运算,证明目
标结论。
案例分析
案例一
已知三角形ABC和三角形ADE相 似,且AB=AC,AD=AE。求证:
k字形三角形相似例题

k字形三角形相似例题
k字形三角形相似例题一道关于图形相似的题目,要求判断两个三角形是否相似。
在这里,我们可以通过计算各个角度和比较边长比例来判断。
首先,我们需要知道K字形三角形的特征:
1. 两个直角三角形(其中一个角为90度,另外两个角分别为45度和4 5度);
2. 两个直角三角形的斜边长度相等;
3. 两个直角三角形的直角边长度比例为1:√2。
现在,假设我们有两个K字形三角形,分别为△ABC和△DEF,我们需要判断它们是否相似。
步骤1:计算各个角度
- 计算△ABC的各个角度:∠A、∠B、∠C
- 计算△DEF的各个角度:∠D、∠E、∠F
步骤2:计算边长比例
- 计算△ABC的边长比例:AB/BC、BC/AC
- 计算△DEF的边长比例:DE/DF、DF/DE
步骤3:比较角度和边长比例
- 比较∠A和∠D是否相等,如果相等,继续比较∠B和∠E是否相等,以及∠C和∠F是否相等;
- 比较边长比例:如果AB/BC = DE/DF 且BC/AC = DF/DE,则可以判断两个三角形相似。
注意事项:
- 如果题目给出的三角形不是K字形,请先判断是否符合K字形三角形的特征;
- 在计算角度和边长比例时,请确保精度,以便更准确地判断相似性;
- 在比较角度和边长比例时,请仔细观察每个条件是否满足,从而得出最终结论。
中考数学专题之“一线三角”(K型图)证相似
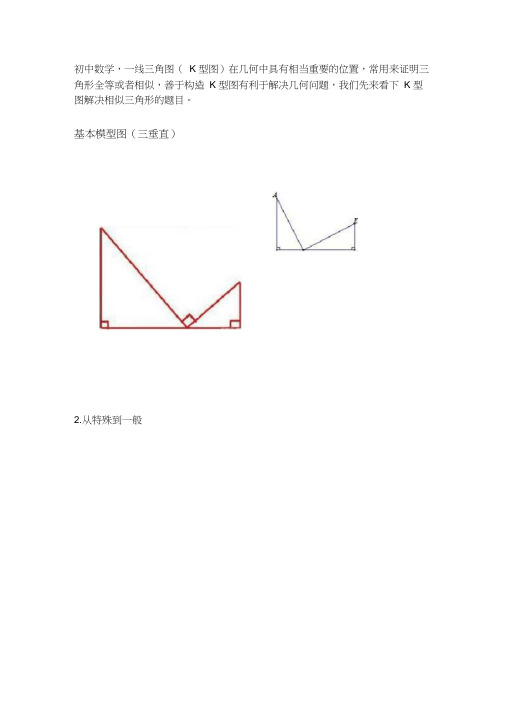
初中数学,一线三角图( K 型图)在几何中具有相当重要的位置,常用来证明三 角形全等或者相似,善于构造 K 型图有利于解决几何问题,我们先来看下 K 型 图解决相似三角形的题目。
基本模型图(三垂直)2.从特殊到一般3.相似中K 型图常见形态(A字型、8 字型)例题1:已知△ABC 中AB=AC、BC=8,D是BC 边上任意一点,AB 边上有一点E,AC 边上有一点F,使∠ EDF= ∠ C. 已知BD=6 、BE=4,求CF的长。
分析:这是一道典型的K 型图,已知∠ EDF= ∠C=∠B,从而可以得到△BDE∽△CFD例题2:如图,已知点A(0,4)、B(4,1),BC⊥x轴于点C,点P 为线段OC 上一点,且PA⊥ PB.求点P 的坐标。
分析:这是三垂直模型图(∠ AOP= ∠AOB= ∠BCP=9°0 ),我们很快可以得到△AOC 与△BCP 相似例题 3:已知矩形 ABCD 中, CD=2 ,AD=3 ,点 P 是 AD 上的一个动点,且和 点 A ,D 不重合,过点 P 作 PE ⊥CP ,交边 AB 于点 E ,设 PD=x ,AE=y ,求 y y 的最大值。
解析:由图可知:∠ A=∠EPC= ∠D=90°,是三垂直模型,可以得到 △EAP ∽△ PDC ,通过比例式得到 x 与 y 的函数关系式,进而求出 y的最大值Zi-1•等∣∣fΔJkBC l AB=AC= 8 , ZDAC=I20°F P为BC的中点,小9>⅜含30:角的透明三角板,便抄角的顶点落在点P,三角板级P点旋無•(L)如图L当三角板的两边分別交AB ∙ AC于点EP时.束证?ABPE^∆CFPJC2)揉仕箝三角板境点PfiH刚囹b惜形叭三超板的两边分别交BA的延长线、边Ae于点E、F.G)搽究Iz ABPE与ZXFP还相似吧?(只需写比结论)©持究2:连结EF, ∆BPE ⅛∆PFE g否相似?请说明環由d® IS EF=ιt, ∆EPF的面枳为S,试用氏的代数式未示S∙rSbS□①求证:ZkOCPSAPDA;②若AOCP与ZXPDA的面枳比为U 4,求边AB州Q(2)若圄1中的点P恰好罡CD边的中点丿求/OAB的度数;<3>如凰2,在⑴条件下,揀去折痕込线段申连结叭动点Jl在纟網AP上〈点M与点P. A 不重合》,动点“在线段AB的延冷虹,且盼PIv送结加交PB于点巧作KElBP于点匚试问当点讥H在移动过程中,线段EF的*度是否发主超匕?若鸡匕说明理由丿若不氐求出线段EF的≡.Zl-4阅渎理解:如團Ii 在四边形ABCD 的边AB 上任取一点E {点E 不与A 、B 重合),分别连接ED 、EC, 可以把四边形APCD 分成三个三角形,如果Rd 有两个三角形相似啟们我把E 叫做四边形ABCP 的边AB 上的“相攸点” > 如杲这三个三角形訓目饥 我们蒯巴E 叫傲四边形ABCD 的边AB 上 的“强«似点"・〈】〉扣图b ZA=ZB=ZPEC=45d ,试判浙点E 罡否定囚边形ΛK D 的边AE 上的相似駄 并说 明理由,(2) 如因2,在矩形ABS P A∙ B. C 、D 四点均在正万形网榕(网格中毎个小正万形的边长为 1>的林点〈卬厨个小正方形的顶点)上,试衽图2中画出矩形ABCD 的边AB 上泪相似点; (3) 如图3,砌返形ABCD 沿CM 折崑 使点D 落在AB 边上的点E 处,若点E 恰好定四边形 Δ≡的边AB 上的T 、窗出忙包・试抹究AB 与DC 的刘蚩关系3己知正方形ABcD 的边长为码 T 以点A 为顶点前笳。
专题14 全等与相似模型-一线三等角(K字)模型(学生版)
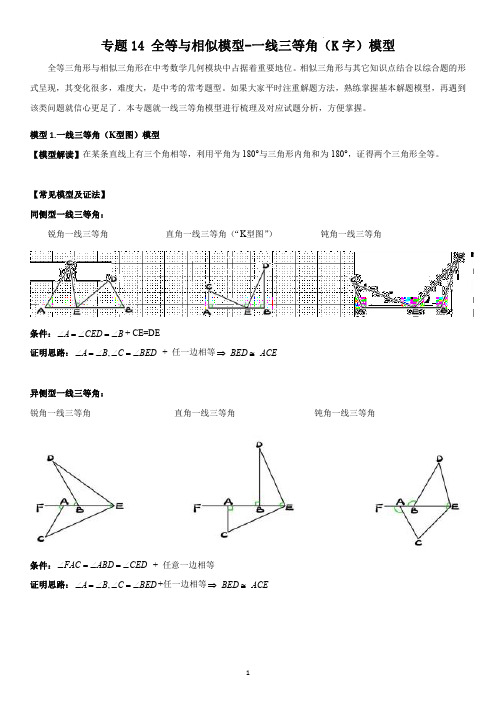
专题14全等与相似模型-一线三等角(K字)模型全等三角形与相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现,其变化很多,难度大,是中考的常考题型。
如果大家平时注重解题方法,熟练掌握基本解题模型,再遇到该类问题就信心更足了.本专题就一线三等角模型进行梳理及对应试题分析,方便掌握。
模型1.一线三等角(K型图)模型【模型解读】在某条直线上有三个角相等,利用平角为180°与三角形内角和为180°,证得两个三角形全等。
【常见模型及证法】同侧型一线三等角:锐角一线三等角直角一线三等角(“K型图”)钝角一线三等角条件:A CED B∠=∠=∠+CE=DE证明思路:,⇒≅∠=∠∠=∠+任一边相等BED ACEA B C BED异侧型一线三等角:锐角一线三等角直角一线三等角钝角一线三等角条件:FAC ABD CED∠=∠=∠+任意一边相等证明思路:,⇒≅∠=∠∠=∠+任一边相等BED ACEA B C BED例1.(2021·山东日照·中考真题)如图,在矩形ABCD 中,8cm AB =,12cm AD =,点P 从点B 出发,以2cm/s 的速度沿BC 边向点C 运动,到达点C 停止,同时,点Q 从点C 出发,以cm/s v 的速度沿CD 边向点D 运动,到达点D 停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v 为_____时,ABP △与PCQ △全等.例2.(2022·黑龙江·九年级期末)(1)如图(1),已知:在△ABC 中,∠BAC =90°,AB =AC ,直线m 经过点A ,BD ⊥直线m ,CE ⊥直线m ,垂足分别为点D 、E .证明∶DE =BD +CE .(2)如图(2),将(1)中的条件改为:在△ABC 中,AB =AC ,D 、A 、E 三点都在直线m 上,并且有∠BDA =∠AEC =∠BAC =α,其中α为任意锐角或钝角.请问结论DE =BD +CE 是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D 、E 是D 、A 、E 三点所在直线m 上的两动点(D 、A 、E 三点互不重合),点F 为∠BAC 平分线上的一点,且△ACF 均为等边三角形,连接BD 、CE ,若∠BDA =∠AEC =∠BAC ,试判断△DEF 的形状.例3.(2022·广东·汕头市潮阳区一模)(1)模型建立,如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.求证:△BEC≌△CDA;,OB=4,将线段AB绕点B逆(2)模型应用:①已知直线AB与y轴交于A点,与x轴交于B点,sin∠ABO=35时针旋转90度,得到线段BC,过点A,C作直线,求直线AC的解析式;②如图3,矩形ABCO,O为坐标原点,B的坐标为(8,6),A,C分别在坐标轴上,P是线段BC上动点,已知点D在第一象限,且是直线y=2x 5上的一点,若△APD是以D为直角顶点的等腰直角三角形,请求出所有符合条件的点D的坐标.例4.(2023·湖南岳阳·统考一模)如图,在ABC中,AB=AC=2,∠B=40°,点D在线段BC上运动(点D不与点B、C重合),连接AD,作∠ADE=40°,DE交线段AC于点E.(1)当∠BDA=115°时,∠EDC=______°,∠AED=______°;(2)线段DC的长度为何值时,△ABD≌△DCE,请说明理由;(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,求∠BDA的度数;若不可以,请说明理由.例5.(2022·浙江杭州·一模)老师在上课时,在黑板上写了一道题:“如图,ABCD 是正方形,点E 在BC 上,DF ⊥AE 于F ,请问图中是否存在一组全等三角形?”小杰同学经过思考发现:△ADF ≌△EAB .理由如下:因为ABCD 是正方形(已知)所以∠B =90°且AD =AB 和AD ∥BC又因为DF ⊥AE (已知)即∠DFA =90°(垂直的意义)所以∠DFA =∠B (等量代换)又AD ∥BC 所以∠1=∠2(两直线平行,内错角相等)在△ADF 和△EAB 中12DFA B AD AB ∠=∠⎧⎪∠=∠⎨⎪=⎩所以△ADF ≌△EAB (AAS )小胖却说这题是错误的,这两个三角形根本不全等.你知道小杰的错误原因是什么吗?我们再添加一条线段,就能找到与△ADF 全等的三角形,请能说出此线段的做法吗?并说明理由.例6.(2022·山东·九年级课时练习)(1)课本习题回放:“如图①,90ACB ∠=︒,AC BC =,AD CE ⊥,BE CE ⊥,垂足分别为D ,E , 2.5cm AD =, 1.7cm DE =.求BE 的长”,请直接写出此题答案:BE 的长为________.(2)探索证明:如图②,点B ,C 在MAN ∠的边AM 、AN 上,AB AC =,点E ,F 在MAN ∠内部的射线AD 上,且BED CFD BAC ∠=∠=∠.求证:ABE CAF ∆∆≌.(3)拓展应用:如图③,在ABC ∆中,AB AC =,AB BC >.点D 在边BC 上,2CD BD =,点E 、F 在线段AD 上,BED CFD BAC ∠=∠=∠.若ABC ∆的面积为15,则ACF ∆与BDE ∆的面积之和为________.(直接填写结果,不需要写解答过程)例7.(2023·贵州遵义·八年级统考期末)过正方形ABCD (四边都相等,四个角都是直角)的顶点A 作一条直线MN .(1)当MN 不与正方形任何一边相交时,过点B 作BE MN ⊥于点E ,过点D 作DF MN ⊥于点F 如图(1),请写出EF ,BE ,DF 之间的数量关系,并证明你的结论.(2)若改变直线MN 的位置,使MN 与CD 边相交如图(2),其它条件不变,EF ,BE ,DF 的关系会发生变化,请直接写出EF ,BE ,DF 的数量关系,不必证明;(3)若继续改变直线MN 的位置,使MN 与BC 边相交如图(3),其它条件不变,EF ,BE ,DF 的关系又会发生变化,请直接写出EF ,BE ,DF 的数量关系,不必证明.模型2.一线三等角模型(相似模型)【模型解读与图示】“一线三等角”型的图形,因为一条直线上有三个相等的角,一般就会有两个三角形的“一对角相等”,再利用平角为180°,三角形的内角和为180°,就可以得到两个三角形的另外一对角也相等,从而得到两个三角形相似.1)一线三等角模型(同侧型)(锐角型)(直角型)(钝角型)条件:如图,∠1=∠2=∠3,结论:△ACE∽△BED.2)一线三等角模型(异侧型)条件:如图,∠1=∠2=∠3,结论:△ADE∽△BEC.3)一线三等角模型(变异型)图1图2图3①特殊中点型:条件:如图1,若C为AB的中点,结论:△ACE∽△BED∽△ECD.②一线三直角变异型1:条件:如图2,∠ABD=∠AFE=∠BDE=90°.结论:△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2:条件:如图3,∠ABD=∠ACE=∠BDE=90°.结论:△ABM∽△NDE∽△NCM.例1.(2023·山东东营·统考中考真题)如图,ABC 为等边三角形,点D ,E 分别在边BC ,AB 上,60ADE ∠=︒,若4BD DC =, 2.4DE =,则AD 的长为()A .1.8B .2.4C .3D .3.2A .3B .5C .2D .1例3.(2022·河南新乡·九年级期中)某学习小组在探究三角形相似时,发现了下面这种典型的基本图形.(1)如图1,在ABC中,∠BAC=90°,ABAC=k,直线l经过点A,BD⊥直线I,CE上直线l,垂足分别为D、E.求证:BDAE=k.(2)组员小刘想,如果三个角都不是直角,那么结论是否仍然成立呢?如图2,将(1)中的条件做以下修改:在ABC中,ABAC=k,D、A、E三点都在直线l上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问(1)中的结论还成立吗?若成立,请你给出证明;若不成立,请说明理由.(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,在ABC中,沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG,ABAE=ACAG=12,AH是BC边上的高,延长HA交EG于点I.①求证:I是EG的中点.②直接写出线段BC与AI之间的数量关系:.边的数量关系.问题探究:(1)先将问题特殊化,如图(2),当90α=︒时,直接写出GCF ∠的大小;(2)再探究一般情形,如图(1),求GCF ∠与α的数量关系.问题拓展:(3)将图(1)特殊化,如图(3),当120α=︒时,若12DG CG =,求BECE 的值.B和射线例5.(2022·山西晋中·一模)阅读材料:我们知道:一条直线经过等腰直角三角形的直角顶点,过另外两个顶点分别向该直线作垂线,即可得三垂直模型”如图①,在ABC 中,90ACB ∠=︒,AC BC =,分别过A 、B 向经过点C 直线作垂线,垂足分别为D 、E ,我们很容易发现结论:ADC CEB △≌△.(1)探究问题:如果AC BC ≠,其他条件不变,如图②,可得到结论;ADC CEB △∽△.请你说明理由.(2)学以致用:如图③,在平面直角坐标系中,直线12y x =与直线CD 交于点()2,1M ,且两直线夹角为α,且3tan 2α=,请你求出直线CD 的解析式.(3)拓展应用:如图④,在矩形ABCD 中,3AB =,5BC =,点E 为BC 边上—个动点,连接AE ,将线段AE 绕点E 顺时针旋转90︒,点A 落在点P 处,当点P 在矩形ABCD 外部时,连接PC ,PD .若DPC △为直角三角形时,请你探究并直接写出BE 的长.校考三模)某数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探【观察与猜想】(1)如图1,在正方形ABCD 中,E ,F 分别是AB ,AD 上的两点,连接则DE CF的值为___________;(2)如图2,在矩形ABCD 中,7AD =,4CD =,E 是AD 上的一点,连接CE ,BD ,若课后专项训练1.(2022·湖南·长沙市二模)如图,等腰直角三角形ABC 的直角顶点C 与坐标原点重合,分别过点A 、B 作x 轴的垂线,垂足为D 、E ,点A 的坐标为(-2,5),则线段DE 的长为()A .4B .6C .6.5D .72.(2022·贵州·凯里一模)如图,在平面直角坐标系中()0,4A 、()6,0C ,BC x ⊥轴,存在第一象限的一点(),25P a a -使得PAB △是以AB 为斜边的等腰直角三角形,则点P 的坐标().A .()3,1或()3,3B .()5,5C .()3,1或()5,5D .()3,3A .()9,3B .()9,23=5.(2021·浙江台州·中考真题)如图,点E,F,G分别在正方形ABCD的边AB,BC,AD上,AF⊥EG.若AB =5,AE=DG=1,则BF=_____.为边的运动过程中,△CEF面积的最小值是.9.(2022·河北保定·模拟预测)如图,桌面上竖直放置着一个等腰直角三角板ABC ,若测得斜边AB 的两端点到桌面的距离分别为AD ,BE .(1)求证:ADC CEB △≌△;(2)若10DE =,7AD =,求BE 的长.10.(2023·浙江·九年级期末)如图,已知ABC 和CDE 均是直角三角形,Rt ACB CED ∠=∠=∠,AC CE =,AB CD ⊥于点F .(1)求证:ABC ≌CDE ;(2)若点B 是EC 的中点,10cm DE =,求AE 的长.11.(2022·江苏·九年级专题练习)【感知模型】“一线三等角”模型是平面几何图形中的重要模型之一,请根据以下问题,把你的感知填写出来:①如图1,ABC 是等腰直角三角形,90C ∠=︒,AE =BD ,则AED ≌_______;②如图2,ABC 为正三角形,,60BD CF EDF =∠=︒,则BDE ≌________;③如图3,正方形ABCD 的顶点B 在直线l 上,分别过点A 、C 作AE l ⊥于E ,CF l ⊥于F .若1AE =,2CF =,则EF 的长为________.【模型应用】(2)如图4,将正方形OABC 放在平面直角坐标系中,点O 为原点,点A 的坐标为(,则点C 的坐标为________.【模型变式】(3)如图5所示,在ABC 中,90ACB ∠=︒,AC BC =,BE CE ⊥于E ,AD ⊥CE 于D ,4cm DE =,6cm AD =,求BE 的长.12.(2022·江苏镇江·二模)模型构建:如图1,AM MN ⊥于点M ,BN MN ⊥于点N ,AB 的垂直平分线交MN 于点P ,连接AP 、BP .若90APB ∠=︒,求证:AM BN MN +=.数学应用:如图2,在ABC 中,D 是BC 上一点,AC AD BD ==,90CAD ∠=︒,8AB =,求ABC 的面积.实际运用:建设“交通强国”是满足人民日益增长的美好生活需要的必然要求.建设“美丽公路”是落实美丽中国建设、回应人民日益增长的美好生活对优美生态环境的需要.如图3是某地一省道与国道相交处的示意图,点Q 处是一座古亭,鹅卵石路QA 、QB 以及AB 两旁栽有常青树,其它区域种植不同的花卉;设计要求QA QB =,QA QB ⊥,AB 是以Q 为圆心、QA 为半径的圆弧(不计路宽,下同).请在图4中画出符合条件的设计图,要求尺规作图,保留作图痕迹,标注必要的字母,写出详细的作法,不要求说明理由;13.(2022·黑龙江·桦南县九年级期中)如图1,在ABC 中,90ACB ∠=︒,AC BC =,直线MN 经过点C ,且AD MN⊥于D ,BE MN ⊥于E .(1)由图1,证明:DE AD BE =+;(2)当直线MN 绕点C 旋转到图2的位置时,请猜想出DE ,AD ,BE 的等量关系并说明理由;(3)当直线MN 绕点C 旋转到图3的位置时,试问DE ,AD ,BE 又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由).14.(2022·黑龙江佳木斯·三模)在ABC 中,90ABC ∠=︒,AB BC =,D 为直线AB 上一点,连接CD ,过点B 作BE CD ⊥交CD 于点E ,交AC 于点F ,在直线AB 上截取AM BD =,连接FM .(1)当点D ,M 都在线段AB 上时,如图①,求证:BF MF CD +=;(2)当点D 在线段AB 点M 在线段BA 的延长线上时,如图②;当点D 在线段BA 的延长线上,点M 在线段AB 的延长线上时,如图③,直接写出线段BF ,MF ,CD 之间的数量关系,不需要证明.15.(2022·安徽·合肥二模)(1)如图1,等腰直角ABC 中,90ACB ∠=︒,CB CA =,线段ED 经过点C ,过A 作AD ED⊥于点D ,过B 作BE ED ⊥于.E 求证:BEC △≌CDA .(2)如图2,已知在平面直角坐标系xOy 中,O 为坐标原点,点A 的坐标为()0,4,点C 的坐标为()3,0-,点B 是平面直角坐标系中的一点,若ABC 是以AC 为直角边的等腰直角三角形,求点B 的坐标;(3)如图3,已知在平面直角坐标系xOy 中,O 为坐标原点,在等腰直角OAB 中,90OAB ∠=︒,4OA AB ==,点M 在线段OB 上从O 向B 运动(运动到点B 停止),以点M 为直角顶点向右上方做等腰直角AMN ,求点N 移动的距离.的两个等腰直角三角形,∠N(3)【拓展探究】在整个运动过程中,请直接写出N点运动的路径长,及CN的最小值.(1)若正方形ABCD的边长为2,E是AD的中点.①如图1,当90∠=︒时,求证:AEF DCEFEC△△;∽18.(2023·广东深圳·九年级校考阶段练习)如图,在ABC 中6cm AB AC ==,8cm BC =,点E 是线段BC 边上的一动点(不含B 、C 两端点),连接AE ,作AED B ∠=∠,交线段AB 于点D .(1)求证:BDE CEA△∽△(2)设BE x =,AD y =,请求y 与x 之间的函数关系式.(3)E 点在运动的过程中,ADE V 能否构成等腰三角形?若能,求出BE 的长;若不能,请说明理由.BC=.点E是线段AD上的动点(点E不20.(2022·湖南郴州·中考真题)如图1,在矩形ABCD中,4AB=,6⊥,交AB于点F.与点A,D重合),连接CE,过点E作EF CE∽;(1)求证:AEF DCE⊥,垂足为G,连接AG.点M是线段BC的中点,连接GM.(2)如图2,连接CF,过点B作BG CF①求AG GM+的最小值;②当AG GM+取最小值时,求线段DE的长.。
k字形三角形相似例题

k字形三角形相似例题相似三角形是指具有相同形状但大小不一定相同的三角形。
在几何学中,相似三角形是一个重要的研究对象。
本文将介绍K字形三角形相似的性质、判定方法及其应用。
一、相似三角形的概念及判定条件相似三角形是指两个三角形的对应角度相等,对应边长成比例。
判定两个三角形相似的条件有:1.两个三角形有两个对应角相等;2.两个三角形的对应边长成比例。
二、K字形三角形相似的性质K字形三角形是指由两个相似三角形组成,其中一个三角形的顶点在另一个三角形的内部。
K字形三角形具有以下性质:1.K字形三角形的两个相似三角形必为全等三角形;2.K字形三角形的相似比为1:1;3.K字形三角形的中心角平分线、角平分线、高、中线、边心距等线段相等。
三、K字形三角形相似的判定方法1.判断两个三角形是否具有相同的形状,即判断它们的对应角是否相等;2.判断两个三角形的边长是否成比例,即判断它们的对应边长是否成比例;3.利用相似比,判断两个三角形是否满足K字形三角形的性质。
四、相似三角形的应用相似三角形在实际生活中有许多应用,如建筑、制图、测量等领域。
通过相似三角形的性质,可以解决一些实际问题,如求解比例、计算距离等。
五、例题解析下面通过一个具体的例子来说明K字形三角形相似的判定过程。
题目:已知三角形ABC和三角形DEF相似,求证:三角形AGF与三角形BHD相似。
证明:1.由于三角形ABC和三角形DEF相似,故有∠ABC = ∠DEF,AB/DE = BC/EF;2.∠AGF = ∠ABC,∠BHD = ∠DEF,故有∠AGF = ∠BHD;3.由于AB/DE = BC/EF,故有AF/BD = AG/BE = FC/BD;4.故三角形AGF与三角形BHD相似。
综上所述,K字形三角形相似的性质、判定方法及应用已为大家讲解清楚。
在解决实际问题时,要学会运用相似三角形的知识,灵活处理问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K 字图形中的相识三角形
一、探究基本图形的性质:
如图∠C=∠D=∠1=90O 时,△APC 与△BPD 有什么关系?
如图∠C=∠D=∠1=60O 时,△APC 与△BPD 有什么关系?
如图∠C=∠D=∠1=n O 时,△APC 与△BPD 有什么关系?
探究:当点C ,点P ,点D 在同一直线上,且满足条件___________________时,△APC 与△BPD 相似。
1 B A C
D P D
1 B
A C P
二、基本图形的应用:
例1:
在矩形ABCD 中,AB=10,AD=8,F 是CD 上一动点,沿EF 折叠后,点C 恰好落在AB 上G 处,E 在BC 上
(1)F 与D 重合时,求折痕EF 的长
(2)BG=6时,能求折痕EF 的长吗?
(3)试求BG 的取值范围
突破题(课后完成):
(4)F 与D 重合时,是否存在过点G 的直线L 、直线DE 与x 轴所围成的三角形和直线L 、直线DE 与y 轴所围成的三角形相似,如果存在,请直接写出解析式,
E E C B
在等边△QCD 中,P 为CD 上一点,B 为QD
上一点,且∠3=60o ,CP=1,BD= . 求△QCD 的边长?
变式1:如图,△QCD 为等边三角形,点A 、P 、B 分别在QC 、CD 、QD 上,且△APB 也为等边三角形
(1)除已知等边三角形的边相等外,请猜想还有哪些边相等,并证明结论
(2)你所证明相等的线段,可以通过怎样的变换相互得到?
变式2:如图所示,在平面直角坐标系中,四边形OABC 是等腰梯形,BC ∥OA ,OA=7,AB=4,∠COA=60o ,点P 为x 轴上的一个动点,点P 不与点O 、点A 重合,连结CP ,过点P 作PD 交AB 于D ,当点P 运动到什么位置时,使得 ∠CPD=∠OAB,且 ,求这时点P 的坐标。
3
2Q C D
P
85AB BD C
已知:等腰梯形ABCD中,AB∥CD,AB<CD, AB=10,BC=3 (1)如图,点M为AB上一点,且满足∠1=∠A,求AM的长;
(2)如图,点M在AB上移动(M不与A、B重合),且满足
∠1=∠A,MN交BC的延长线于点N,设AM=x,CN=y,求y关于x的函数关系式?
N
A M
1、已知:QC=QD=2,∠C=∠D=∠3=45o ,P 在CD 上运动不与C 、D 重合,设CP=x ,QB=y,求y 关于x 的函数关系式
变式:若QC=QD=2,∠C=45o =∠3,点P 在CD 的中点处,∠3绕中点旋转,∠3的两边分别与射线CQ 、DQ 相交于点E 、F ,设CE=x,DF=y
(1)求y 与x 的关系式
(2)∠EPF 在旋转的过程中,△PEF 是否能为等腰三角形?若能,求出等腰三角形时x 的值,若不能,请说明理由。
Q C D P C D P C D P C D P
2、在等腰三角形中,CQ=DQ=8,∠CQD=120o P为CD中点,小惠拿着含30度角的透明三角板,使30o角的顶点落在点P,将三角板绕点P顺时针旋转(1)当三角板的两边分别与QC、QD交于点E、F时,求证△CPE∽△DPF
Q
C
(2)当三角板的两边分别交CQ的延长线,边DQ于点E、F
①探究:△CPE与△DPF还相似吗?
②探究:连接EF,△CPE与△EPF是否相似,试说明理由
③设EF=m,△EPF的面积为S,试用含m的代数式表示S
P。
