模拟曲线
eq参数模拟riaa曲线
eq参数模拟riaa曲线
模拟RIA（Recording Industry Association of America）曲线需要考虑到EQ参数的调整。
RIA曲线是一种标准化的均衡曲线，用于在录制和播放唱片时进行音频信号的均衡处理。
在模拟RIA曲线时，需要考虑到以下几个参数：
1. 频率响应，根据RIA标准，需要在20Hz到20kHz的频率范围内进行均衡处理。
这意味着需要调整EQ参数以使得整个频率范围内的响应符合标准。
2. 增益和衰减，根据RIA标准，需要在不同频率范围内进行不同的增益和衰减。
这意味着需要调整EQ参数以使得不同频率范围内的增益和衰减符合标准。
3. 滤波器类型，RIA曲线通常使用特定类型的滤波器进行均衡处理，比如高通滤波器和低通滤波器。
在模拟RIA曲线时，需要选择合适的滤波器类型，并调整其参数以符合标准。
4. 总谐波失真，在模拟RIA曲线时，需要考虑到EQ参数对总谐波失真的影响。
合适的EQ参数可以帮助减少总谐波失真，从而使
得模拟的RIA曲线更加准确。
总之，模拟RIA曲线需要综合考虑频率响应、增益和衰减、滤波器类型以及总谐波失真等多个方面的EQ参数调整，以确保模拟的曲线符合标准并达到预期的均衡效果。
模拟iphone贝塞尔曲线
模拟iphone贝塞尔曲线
模拟iPhone的贝塞尔曲线，可以使用贝塞尔曲线的数学公式和参数来绘制。
下面是一个简单的示例代码，使用Python语言绘制一个类似于iPhone的贝塞尔曲线：
python复制代码
import numpy as np
import matplotlib.pyplot as plt
# 定义贝塞尔曲线的参数
t = np.linspace(0, 1, 1000)
p0 = (0, 0) # 起点
p1 = (0.5, 0.5) # 控制点
p2 = (1, 0) # 终点
# 计算贝塞尔曲线的坐标
x = (1 - p1[0]) * p0[0] + (1 - p2[0]) * p1[0] * (1 - t) + p2[0] * t
y = (1 - p1[0]) * p0[1] + (1 - p2[0]) * p1[1] * (1 - t) + p2[0] * t
# 绘制贝塞尔曲线
plt.plot(x, y)
plt.scatter([p0[0], p1[0], p2[0]], [p0[1], p1[1], p2[1]], color='red') # 标记控制点
plt.xlim(-1, 2)
plt.ylim(-1, 2)
plt.show()
在这个示例中，我们使用NumPy库生成一组参数t，表示贝塞尔曲线上的点。
然后，我们使用贝塞尔曲线的公式计算每个点的坐标x和y。
最后，我们使用Matplotlib库绘制贝塞尔曲线，并将控制点标记为红色。
你可以根据需要调整控制点的位置和曲线的形状，以模拟不同的iPhone界面元素。
吸波模拟曲线
吸波模拟曲线引言吸波模拟曲线是指在电磁波吸收材料表面进行反射和吸收反射的电磁波形成的曲线。
吸波材料的设计和性能评估是电磁波应用中的关键问题之一。
吸波模拟曲线的研究对于吸波材料的设计和优化具有重要的意义。
什么是吸波模拟曲线吸波模拟曲线是描述吸波材料吸收和反射电磁波的性能的一种函数曲线。
吸波模拟曲线通常由两个部分组成：反射损耗曲线和吸收损耗曲线。
反射损耗曲线反射损耗曲线描述了电磁波在吸波材料表面反射的程度。
反射损耗值越低，说明吸波材料表面对电磁波的反射较少，即更多的电磁波被吸收。
反射损耗曲线通常在一定频率范围内呈现出不同的特征。
吸收损耗曲线吸收损耗曲线描述了电磁波在吸波材料中被吸收的程度。
吸收损耗值越高，说明吸波材料对电磁波的吸收能力越强。
吸收损耗曲线通常在一定频率范围内呈现出不同的特征。
吸波模拟曲线的应用吸波模拟曲线在许多领域具有广泛的应用。
以下是一些典型的应用领域：电磁波吸收材料设计通过分析吸波模拟曲线，可以评估吸波材料的吸收性能。
设计吸波材料时，可以通过调整材料的性质和结构来优化吸波性能，以实现特定频率范围内的高吸收效果。
电磁波隐身技术吸波模拟曲线的研究对于电磁波隐身技术的发展具有重要意义。
通过选择合适的吸波材料和设计合理的结构，可以实现对特定频率范围内电磁波的吸收和控制，从而达到隐身的效果。
电磁波干扰抑制在一些特殊的环境下，电磁波的干扰可能会对系统产生不利影响。
通过使用吸波材料，可以有效地吸收并抑制电磁波干扰，提高系统的稳定性和可靠性。
电磁波检测技术吸波模拟曲线的研究也可以应用于电磁波检测技术。
通过对吸波模拟曲线进行分析，可以确定电磁波的频率和强度，从而实现对电磁波的检测和定位。
吸波模拟曲线的影响因素吸波模拟曲线的形状和特征受到多种因素的影响。
以下是一些常见的影响因素：材料性质吸波材料的性质对吸波模拟曲线影响很大。
例如，吸波材料的介电性能、磁性能、导电性能等都会直接影响吸波性能。
结构设计吸波材料的结构设计也是影响吸波模拟曲线的重要因素。
曲线模拟方法有哪几种图片
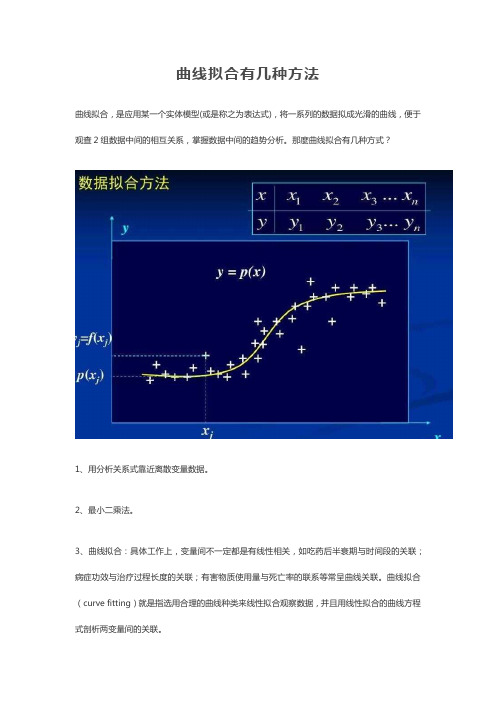
曲线拟合有几种方法
曲线拟合，是应用某一个实体模型(或是称之为表达式)，将一系列的数据拟成光滑的曲线，便于观查2组数据中间的相互关系，掌握数据中间的趋势分析。
那麼曲线拟合有几种方式？
1、用分析关系式靠近离散变量数据。
2、最小二乘法。
3、曲线拟合：具体工作上，变量间不一定都是有线性相关，如吃药后半衰期与时间段的关联；病症功效与治疗过程长度的关联；有害物质使用量与死亡率的联系等常呈曲线关联。
曲线拟合（curve fitting）就是指选用合理的曲线种类来线性拟合观察数据，并且用线性拟合的曲线方程式剖析两变量间的关联。
4、曲线平行线化指曲线拟合的主要方式之一。
针对一些最优控制的材料可以根据简洁的变量转换使之平行线化，那样就可以按最小二乘法基本原理求出转换后变量的直线方程，在具体工作中中常会运用此直线方程制作材料的规范工作中曲线，与此同时依据须要可将此直线方程复原为曲线方程式，完成对材料的曲线拟合。
c++ 贝尔曲线计算模拟两点坐标间的曲线移动轨迹
c++ 贝尔曲线计算模拟两点坐标间的曲线移动轨迹文章标题：深度解析C++中贝尔曲线计算模拟两点坐标间的曲线移动轨迹在现代计算机科学中，C++语言被广泛应用于各种领域，包括图形学和计算机图形学。
其中，贝尔曲线（Bézier curve）是一种常用的数学工具，用于在计算机图形学中模拟两点坐标间的曲线移动轨迹。
本文将从C++语言的角度深入探讨贝尔曲线的计算模拟，旨在帮助读者全面理解和应用贝尔曲线在计算机图形学中的实际应用。
一、贝尔曲线简介在计算机图形学中，贝尔曲线是由一系列控制点和一组特定的数组算法所生成的曲线。
这些控制点决定了贝尔曲线的形状，而贝尔曲线的算法则确定了曲线的平滑度和变化规律。
贝尔曲线广泛用于计算机图形学中的曲线绘制、动画效果和路径规划等方面。
在实际的C++编程中，我们可以通过实现贝尔曲线算法来模拟两点之间的曲线移动轨迹，为计算机图形学和动画效果的实现提供强大的支持。
二、C++中的贝尔曲线计算模拟在C++编程中实现贝尔曲线算法需要考虑诸多因素，包括控制点的设置、贝尔曲线方程的推导和递归求解等。
我们需要确定两个端点和若干个控制点，它们将决定贝尔曲线的形状和路径。
我们可以使用贝尔曲线的递推公式来计算曲线上的点，从而实现曲线的绘制和移动效果。
在C++中，我们可以通过自定义函数或类来实现贝尔曲线算法，并结合图形库或动画库来展现计算结果。
三、C++中贝尔曲线的应用实例为了更具体地说明C++中贝尔曲线的应用，我们可以以一个实际的案例来展示其在计算机图形学中的效果。
假设我们要实现一个动态的曲线路径规划系统，其中涉及到飞机、汽车或无人机的路径模拟。
我们可以利用C++编程语言中的贝尔曲线算法来计算和模拟这些交通工具之间的曲线移动轨迹，从而实现更加真实和生动的动画效果。
四、个人观点和总结通过本文的讨论，我们可以看到C++语言在贝尔曲线计算模拟中的重要作用和实际应用。
贝尔曲线不仅可以用于计算机图形学中的动画效果，还可以应用于路径规划、数据可视化和工程设计等领域。
蒸馏曲线模拟
蒸馏曲线模拟
蒸馏曲线模拟是一种计算机模拟技术，用于模拟和预测不同温度和压力下的蒸馏过程。
这种模拟技术可以帮助工程师优化蒸馏过程，提高产品的质量和产量，并降低能耗和成本。
蒸馏曲线模拟通常使用计算流体动力学（CFD）软件进行。
这些软件可以通过数值方法求解描述蒸馏过程的偏微分方程，例如对流方程、传热方程和传质方程等。
通过输入不同的温度、压力、流量等参数，模拟可以预测蒸馏过程中各种组分的浓度、温度和压力等随时间的变化。
蒸馏曲线模拟可以帮助工程师了解蒸馏塔内的流动和传热传质特性，预测产品的质量和产量，优化进料和操作条件。
例如，通过模拟可以找到最佳的进料位置、最佳的操作压力和温度，以及最佳的再沸器和冷凝器设计等。
此外，模拟还可以用于评估新设计的蒸馏塔的性能，预测其在实际操作中的表现。
总之，蒸馏曲线模拟是一种有效的工具，可以帮助工程师更好地理解和优化蒸馏过程，提高产品的质量和产量，降低能耗和成本。
贝塞尔曲线 模拟轮廓
贝塞尔曲线模拟轮廓贝塞尔曲线是一种数学曲线，它通过控制点来模拟复杂的轮廓。
这种曲线可以用来绘制平滑的曲线，因此在计算机图形学和设计领域被广泛应用。
本文将介绍贝塞尔曲线的基本原理、应用以及如何使用控制点来模拟轮廓。
我们来了解一下贝塞尔曲线的基本原理。
贝塞尔曲线是由一系列控制点组成的曲线，通过调整控制点的位置和数量，可以得到不同形状的曲线。
贝塞尔曲线的关键是通过插值和插值函数来计算曲线上的点。
贝塞尔曲线的插值函数可以通过以下公式表示：B(t) = ∑(i=0 to n) Pi * Bi,n(t)其中，Pi表示控制点，Bi,n(t)表示贝塞尔基函数，t表示参数，n 表示控制点的数量。
贝塞尔基函数可以用递归方式计算，具体公式如下：Bi,n(t) = C(n, i) * (1 - t)^(n-i) * t^i在计算机图形学中，贝塞尔曲线通常是二次或三次曲线。
二次贝塞尔曲线有3个控制点，分别是起始点、控制点和结束点，通过调整控制点的位置可以得到不同形状的曲线。
三次贝塞尔曲线有4个控制点，分别是起始点、两个控制点和结束点，同样可以通过调整控制点的位置来改变曲线的形状。
贝塞尔曲线在计算机图形学和设计领域有广泛的应用。
它可以用来绘制平滑的曲线，比如绘制字体、绘制图形等。
由于贝塞尔曲线可以通过调整控制点来改变曲线的形状，因此在设计中可以用来模拟复杂的轮廓。
比如，可以使用贝塞尔曲线来绘制自然界中的曲线，比如花朵的轮廓、云朵的形状等。
在使用贝塞尔曲线模拟轮廓时，需要注意一些技巧。
首先，要合理选择控制点的位置，以得到满足需求的曲线形状。
其次，可以使用多个贝塞尔曲线来拼接成复杂的轮廓，这样可以更好地模拟真实的形状。
此外，还可以通过调整控制点的权重来改变曲线的形状，比如使曲线更加平滑或更加锐利。
贝塞尔曲线是一种用来模拟轮廓的重要数学工具。
它通过控制点来调整曲线的形状，可以绘制平滑的曲线，并在计算机图形学和设计领域得到广泛应用。
Matlab模拟直流电动机特性曲线
Matlab模拟直流电动机特性曲线简介本文档旨在介绍如何使用Matlab模拟直流电动机的特性曲线。
直流电动机是一种常见的电动机类型，通过控制电流和电压可以实现不同的运行特性。
通过模拟特性曲线，我们可以更好地了解电动机的性能和工作情况。
准备工作在开始之前，需要确保已安装Matlab软件，并具备基本的Matlab编程知识。
另外，需要了解直流电动机的基本原理和特性。
模拟特性曲线的步骤以下是使用Matlab模拟直流电动机特性曲线的步骤：1. 导入必要的库和数据：首先，在Matlab中导入需要使用的库和电动机的基本参数数据。
2. 定义电动机模型：根据电动机的特性方程，定义电动机的模型，包括转矩方程、速度方程和电流方程。
3. 设置输入条件：根据需要模拟的特性曲线类型，设置输入条件，如电压、负载等。
4. 模拟电动机运行：使用定义的电动机模型和设置的输入条件，通过Matlab进行电动机运行的模拟。
5. 绘制特性曲线：根据模拟结果，使用Matlab的绘图功能，绘制电动机的特性曲线。
注意事项在进行电动机特性曲线的模拟时，需要注意以下事项：- 确保输入的参数和条件与实际电动机相符，以获得准确的模拟结果。
- 选择合适的模拟时间和步长，以保证模拟结果的准确性和稳定性。
- 模拟过程中可能出现的错误和异常情况需要进行处理和排除，以确保模拟的有效性。
结论通过使用Matlab进行直流电动机特性曲线的模拟，我们可以更好地了解电动机的性能和工作情况。
这有助于电动机的设计、优化和控制。
同时，我们还需要注意模拟过程中的参数设置和异常情况处理，以确保模拟结果的准确性和可靠性。
以上是关于如何使用Matlab模拟直流电动机特性曲线的简要介绍，希望对您有所帮助。
如有疑问，请随时与我联系。
Matlab对直流电动机特性曲线的仿真模拟
Matlab对直流电动机特性曲线的仿真模
拟
介绍
本文档旨在介绍如何使用Matlab对直流电动机的特性曲线进行仿真模拟。
通过仿真模拟，我们可以更好地了解直流电动机的性能和特性，并进行相关分析。
步骤
1. 导入必要的库和数据
在开始之前，我们需要导入Matlab所需的相关库和数据。
确保你已经安装了Matlab并且具备相关的电动机特性数据。
2. 定义电动机参数
根据你所拥有的电动机特性数据，定义电动机的相关参数，包括额定电压、额定电流、额定转速等。
3. 编写模拟代码
使用Matlab编写模拟代码，根据电动机的参数和特性数据，
模拟电动机的运行过程。
可以使用电动机的等效电路模型来进行仿真。
4. 运行模拟
运行编写好的模拟代码，观察仿真结果。
可以绘制电动机的转
速-负载曲线、转矩-负载曲线等，以便进一步分析电动机的性能。
5. 分析结果
根据模拟结果进行分析，了解电动机在不同负载下的性能表现。
可以计算电动机的效率、功率因素等指标，进一步评估电动机的性能。
注意事项
- 在进行仿真模拟时，需要确保电动机的参数和特性数据准确
无误。
- 在编写模拟代码时，遵循Matlab的语法规范，确保代码的正
确性和可读性。
- 在分析结果时，根据实际需求选择合适的指标和方法，以得
到准确的结论。
以上是关于使用Matlab对直流电动机特性曲线进行仿真模拟的简要介绍和步骤。
希望对你有所帮助！。
comsol 扬声器曲线仿真
Step48
Step49
计算
• Step50 点击【计结果如下图
添加绘图组-FR
• Step51 右键【结果】-【一维绘图组】 • Step52 右键【一维绘图组】-【点图】-选择球体顶点
Step51
Step52-1
Step52-2
设置图表-FR
• Step53 点击
Step37
Step38
Step39
固定约束
• Step40 在【壳】点右键选择【面约束】-【固定约束】 • Step41 选择DP边缘为固定约束
Step40
Step41
面载荷
• Step42 在【壳】点右键选择【面和休载荷】-【面载荷】 • Step43 选择VC作为面载荷对象，【力】设定Z为Fe/AA
Step27
Step28
积分
• Step29 在【定义】点右键选择【组件耦合】-【积分】
• Step30 选择【VC】作为积分目标
Step30
Step29
平均
• Step31 在【定义】点右键选择【组件耦合】-【平均】
• Step32 选择【VC】作为平均目标
Step31
Step32
压力声学
• Step33 右键力声学，频域】添加【内部硬声场边界】及【球面 波辐射】
Step16
Step18
建立群组
DP
• Step19 在【几何1】右键选择【选择】-【显式选择】 • Step20利用隐藏功能，隐藏不需要的部分以方便选择 • Step21 选择边界并选取需要的边界建立群组 DP,VC
Step19-2
Step21 VC
Step19-1
构建并集
origin 模拟二极管拟合曲线
origin 模拟二极管拟合曲线本文旨在介绍如何使用Origin软件进行二极管的模拟，并通过拟合曲线来优化二极管的性能。
在本文中，我们将介绍二极管的原理、Origin软件的基本操作、拟合曲线的概念以及如何使用Origin进行二极管的拟合曲线。
一、二极管原理二极管是一种具有单向导电性的电子元件，它可以将电流从一个方向传导到另一个方向，具有重要的作用在电子线路中。
二极管的导电特性可以通过电路模拟软件进行模拟，以优化其性能。
二、Origin软件操作Origin是一款强大的数据分析软件，可用于数据拟合、绘图等。
以下是使用Origin进行二极管模拟的基本步骤：1. 打开Origin软件并新建一个工作簿。
2. 导入二极管相关的数据，如电压、电流等。
3. 选择合适的拟合类型（线性拟合、非线性拟合等），并设置相关参数。
4. 进行拟合运算，生成拟合曲线。
5. 分析拟合结果，优化二极管的性能。
三、拟合曲线的概念拟合曲线是利用数据与模型之间的对应关系，通过数学方法将数据拟合成一条光滑曲线的过程。
在二极管模拟中，拟合曲线可以帮助我们更好地理解二极管的性能，从而优化其参数。
以下是使用Origin模拟二极管拟合曲线的具体步骤：1. 打开Origin软件并新建一个工作簿，导入二极管相关的数据。
2. 选择合适的拟合类型（如线性拟合），并设置相关参数（如最小二乘法、置信区间等）。
3. 在软件界面的右侧，选择“Graph”菜单，并选择“Line Plot”或“Scatter Plot”，以绘制电压与电流的拟合曲线。
4. 根据拟合结果，优化二极管的性能参数（如反向偏压、正向偏压等）。
5. 进行多次模拟，对比不同参数下的性能表现，最终选择最优参数组合。
五、总结通过以上步骤，我们可以使用Origin软件进行二极管的模拟，并通过拟合曲线来优化二极管的性能。
在实际应用中，我们需要根据具体情况选择合适的拟合类型和参数设置，以获得最佳的模拟结果。
ADINA滞回曲线模拟
收敛控制: 模型计算不收敛一般和网格,时间步长关系比较大,不收敛的时候, 在没有接触等其它非线性效应时,一般首先是考虑步长的因素,再次 考虑网格变形能力。
FOCUSED ON EXCELLENCE
ADINA
FOCUSED ON EXCELLENCE
滞回曲线示例
FOCUSED ON EXCELLENCE
ADINA
载荷使用正玄式加载
FOCUSED ON EXCELLENCE
ADINA
步长必须小于载荷周期，为周期的百分之一较好
FOCUSED ON EXCELLENCE
ADINA
滞回曲线模拟注意的几个事项:
1 材料必须是具有塑性的材料,或者有徐变,蠕变的材料,弹性材料 没有耗能作用.钢结构材料就得选用带有塑性的材料模型； 2 载荷施加是加载卸载式的类型,也就是这个载荷随着时间变化 是正选式的来回交替的.得定义时间函数控制加载载荷； 3 时间步长得是一个载荷周期的百分之一或者更小,不能大于载 荷周期； 4 结果保存,每一步的结果最好都保存,保存结果太少,会跳过中间 的线段,最后出来曲线就不是所要的曲线了。
ADINA
滞回曲线模拟
ADINA技术部
命令流文件：test-zhihui.in 后处理命令流文件：zhihui.plo
FOCUSED ON EXCELLENCE
ADINA
几何模CUSED ON EXCELLENCE
ADINA
外侧使用弹性材料，为钢材参数，里面是土，使用Mohr-Coulomb,有塑性存在
matlab根据excel生成模拟曲线的方法
matlab根据excel生成模拟曲线的方法1. 引言1.1 概述本文旨在介绍如何使用MATLAB根据Excel数据生成模拟曲线的方法。
近年来，数据处理和分析在科学研究、工程设计和商业决策等领域中扮演着越来越重要的角色。
而Excel作为一款常用的电子表格软件，广泛应用于数据整理和存储。
然而，Excel在进行复杂数据处理和曲线拟合方面功能有限，无法满足特定需求。
相对而言，MATLAB作为一种强大的数值计算和科学编程语言，在数据处理、绘图和拟合等方面具备出色的能力。
本文将详细介绍如何利用MATLAB导入Excel中的数据，并使用多种曲线拟合方法、插值方法以及多项式拟合方法生成模拟曲线。
1.2 文章结构本文总共分为五个部分：引言、MATLAB生成模拟曲线方法、模拟曲线生成原理、实践示例与应用案例以及结论与总结。
首先，在引言部分我们将概述文章的目的并介绍本文主要内容。
接着，在第二部分中我们将深入讨论MATLAB和Excel的基本概念，并提供了导入Excel数据到MATLAB的方法。
第三部分将解释模拟曲线的生成原理，包括曲线拟合方法、插值方法和多项式拟合方法。
在第四部分中，我们将通过一个实际案例来展示如何准备和导入示例数据，并详细介绍利用MATLAB生成模拟曲线的步骤。
同时，我们还将通过案例分析和结果展示来验证该方法的有效性。
最后，在结论与总结部分中，我们将总结文章中的主要观点，并讨论本文研究的价值及不足之处。
此外，我们还会提出一些建议以供进一步研究使用。
1.3 目的本文旨在帮助读者了解如何利用MATLAB根据Excel数据生成模拟曲线。
通过本文所介绍的方法，读者可以更加灵活地进行数据处理与分析，并能够针对特定需求生成准确而美观的模拟曲线。
希望本文能为科学研究、工程设计和商业决策等领域提供有价值的参考，推动相关领域技术发展和应用创新。
2. MATLAB生成模拟曲线方法2.1 MATLAB和Excel的基本概念在开始介绍MATLAB生成模拟曲线方法之前，我们先了解一些基本概念。
大漠插件模拟曲线鼠标原理-概述说明以及解释
大漠插件模拟曲线鼠标原理-概述说明以及解释1.引言1.1 概述概述部分的内容应该对整篇文章进行简要介绍，包括介绍大漠插件和曲线鼠标的基本概念以及本文主要讨论的内容。
可以参考以下内容进行编写：引言部分将对大漠插件模拟曲线鼠标原理进行详细探讨。
在当今科技发展的背景下，计算机已经深入到我们生活的各个领域。
作为人与计算机之间的重要交互方式之一，鼠标在我们日常工作和娱乐中扮演着重要角色。
然而，传统鼠标的运动方式只能呈现直线轨迹，无法满足在特定应用场景中需要曲线运动的需求。
曲线鼠标的概念应运而生，它通过特殊的设计和算法，使鼠标能够实现自由曲线运动，进一步提升用户的操作体验和效率。
然而，由于曲线鼠标的硬件设计和价格等限制，其普及程度相对较低。
针对这一问题，本文将引入大漠插件的概念，并详细讨论其在模拟曲线鼠标原理中的应用。
大漠插件是一种功能强大的鼠标操作辅助工具，通过在计算机上安装插件程序，可以模拟人类鼠标操作，实现鼠标的各种运动轨迹，包括曲线运动。
本文的主要目的是通过深入研究大漠插件模拟曲线鼠标原理，探讨其在实际应用中的优势和潜在的应用前景。
通过对插件的定义和作用的介绍，以及对曲线鼠标原理的详细剖析，读者将能够全面了解大漠插件模拟曲线鼠标的工作原理和应用场景。
接下来的章节将会逐步展开，在介绍插件的定义和作用后，我们将详细探讨曲线鼠标的原理，包括其算法和实现方式。
进一步，我们将在结论部分总结插件模拟曲线鼠标的优势，并展望其在未来的应用前景。
通过本文的阅读，读者将对大漠插件模拟曲线鼠标的原理和应用有更深入的了解，希望能够为相关领域的研究和开发提供有益的参考和启示。
1.2 文章结构文章结构部分的内容可以包括以下内容：文章结构要合理安排，能够清晰地表达出论文的逻辑框架和脉络。
通常可以按照以下方式展开：首先，简要介绍整篇文章的组织结构，包括各章节的主要内容和目标。
其次，详细说明每个章节的内容和主题。
比如，在本文中，第一章为引言，主要介绍了整篇文章的背景、目的和结构安排。
fdmnes编码模拟xanes曲线
一、背景介绍众所周知，X射线吸收近边结构（XANES）是一种重要的结构表征技术，通过X射线与原子核内电子之间的相互作用来研究材料的电子结构和化学成分。
而在进行XANES数据模拟时，FDMNES编码成为了研究人员常用的工具之一。
二、FDMNES编码概述1. FDMNES编码简介FDMNES编码是一种常用的用于模拟X射线吸收近边结构（XANES）的计算工具，它基于全势数值计算和密度泛函理论。
通过FDMNES编码，可以模拟材料的XANES光谱，并且能够提供材料中各种原子的对光谱的贡献。
2. FDMNES编码的特点FDMNES编码具有高度的灵活性和可扩展性，可以适用于多种物质体系的XANES数据模拟。
它还能够考虑到材料中的局部结构效应和畸变等因素，能够更准确地描述实际材料的XANES光谱。
三、FDMNES编码模拟XANES曲线的步骤1. 建立模拟体系在进行FDMNES编码模拟时，首先需要准备好模拟的体系结构，包括原子坐标、晶胞参数等信息。
这些信息可以通过实验测量或者理论计算得到。
2. 定义计算参数接下来需要设定FDMNES编码的计算参数，包括计算的能量范围、光子入射方向、晶格参数等。
这些参数会直接影响到模拟得到的XANES 曲线。
3. 进行FDMNES计算一旦建立了模拟体系并定义了计算参数，就可以进行FDMNES编码的计算了。
在计算过程中，FDMNES会考虑到原子的多体效应、晶体场效应等因素，从而得到模拟的XANES光谱曲线。
4. 分析和比对结果对于得到的模拟XANES曲线，需要进行详细的分析和比对。
可以通过与实验测量得到的XANES曲线进行比对，从而验证模拟的准确性，并且得到更深层次的结构信息。
四、FDMNES编码模拟XANES曲线的应用1. 新材料的研究FDMNES编码可以被应用于新材料的研究中，通过模拟XANES曲线可以了解材料的电子结构和化学成分，从而指导实验的设计和研发工作。
2. 催化剂的设计对于催化剂的研究中，FDMNES编码可以帮助科研人员了解材料的电子结构特征，从而设计出更高效的催化剂。
stata 模拟二次曲线
stata 模拟二次曲线
要在Stata中模拟二次曲线，你可以使用内置的“twoway function”命令来实现。
首先，你需要生成一个自变量的序列，然
后计算对应的因变量值，最后使用“twoway function”命令来绘制
二次曲线。
首先，假设你想要模拟二次曲线y = a + bx + cx^2，其中a、
b和c是参数。
你可以按照以下步骤在Stata中实现：
1. 生成自变量的序列，使用“gen”命令生成自变量x的序列，例如，gen x = 1/100。
2. 计算因变量值，使用“gen”命令计算对应的因变量值y，
例如，gen y = 2 + 3x + 0.5(x^2)。
3. 绘制二次曲线，使用“twoway function”命令来绘制二次
曲线，例如，twoway function y = 2 + 3x + 0.5(x^2)。
以上步骤将生成自变量x的序列，计算对应的因变量值y，并
绘制出二次曲线。
你也可以通过调整参数a、b和c来观察二次曲线
的变化。
这样就可以在Stata中模拟二次曲线了。
除了上述方法，你还可以使用“regress”命令拟合二次曲线模型，然后利用拟合的结果来绘制二次曲线。
这样可以更直观地了解
二次曲线的拟合效果。
总的来说，在Stata中模拟二次曲线有多种方法，你可以根据
具体的需求选择合适的方法来实现。
希望这些信息能对你有所帮助。
分子动力学模拟曲线波动
分子动力学模拟曲线波动分子动力学模拟是一种在计算机上模拟原子或分子运动的方法，通过追踪分子之间的相互作用力，可以得到粒子的运动轨迹和相对位置的变化。
在分子动力学模拟中，分子之间的相互作用力通常由势函数或力场来描述。
这些势函数可以是简单的Lennard-Jones势能，也可以是更复杂的分子力场模型，包括键长、键角和二面角等参数。
通过定义粒子之间的相互作用势能，分子动力学模拟可以对系统进行数值求解，从而得到各个粒子的位置、速度和加速度的时间演化。
然而，在分子动力学模拟中，由于计算精度的限制以及计算算法的近似性质，模拟得到的分子运动轨迹存在一定的误差和波动。
这种波动主要包括两个方面。
首先，由于分子之间的相互作用力是通过计算来模拟的，很难完全准确地描述真实物理系统的相互作用。
因此，在模拟过程中，分子的运动轨迹可能会产生一定的偏差，导致模拟结果与实际系统之间存在波动。
其次，在分子动力学模拟中，由于系统的初态和边界条件的选择，以及模拟参数的设置等各种因素的影响，都会对分子的运动轨迹产生一定的影响。
例如，在模拟过程中增加温度或压力的波动，或者改变模拟过程中的步长和时间尺度等，都会对分子的运动轨迹产生一定的影响。
为了减小这种模拟结果的波动，可以采取一些方法来提高计算精度和模拟准确性。
例如，可以增加模拟系统的大小，减小边界效应的影响；可以采用更加精确的计算算法和模型，提高模拟的准确性；还可以通过平均多次模拟结果来减小波动，提高数据的可信度。
总之，分子动力学模拟曲线的波动是由于计算精度的限制和计算算法的近似性质所导致的。
通过采用精确的计算算法和模型，以及增加模拟系统的大小等方法，可以减小模拟结果的波动，提高分子动力学模拟的准确性和可靠性。
模拟计算sn曲线
模拟计算sn曲线
在进行模拟计算sn曲线时，我们使用一种常见的方法来预测或模拟特定系统
或实验的信噪比曲线。
信噪比（Signal-to-Noise Ratio，SNR）是在信号中的有效信
号与噪音强度之间的比例关系，它可以用来评估信号的质量和清晰度。
首先，在进行模拟计算sn曲线之前，我们需要确定要模拟的系统或实验的特
定特征，例如信号的频率、幅度、相位以及噪音的特性。
根据这些特征，我们可以选择合适的模型和算法来进行模拟计算。
其次，为了模拟sn曲线，我们需要定义一个适当的信噪比度量。
常见的度量
方式包括信号功率与噪音功率的比值（即功率信噪比，PSNR）和信号能量与噪音
能量的比值（即能量信噪比，ESNR）。
根据具体的需求，我们选择适当的度量方
式来计算sn曲线。
然后，我们可以使用数学模型或计算模型来进行模拟计算。
数学模型可以用于
解析求解，而计算模型则利用计算机进行数值计算。
在模拟计算时，我们需要确定模型的输入信号和噪音，并对其进行定义和参数化。
根据模型的特点，我们可以利用数值方法或仿真实验来求解sn曲线。
最后，通过进行模拟计算，我们可以得到系统或实验的sn曲线。
这个曲线描
述了信号在不同信噪比下的变化情况，可以用于评估系统的性能和可靠性。
根据这个曲线，我们可以优化系统设计，改善信号传输质量，并提高信噪比。
总之，模拟计算sn曲线是一种有效的方法，可以帮助我们了解信号在不同噪
音强度下的变化情况。
通过模拟计算，我们可以优化系统设计，提高信号传输质量，从而更好地满足实际应用的需求。
一阶多项式 模拟卡曲线拟合
一阶多项式模拟卡曲线拟合
一阶多项式是指只含有一次幂的多项式，通常可以表示为y = ax + b的形式，其中a和b是常数，x是自变量，y是因变量。
一阶多项式也可以被称为线性函数，因为其图像是一条直线。
模拟卡曲线拟合是指使用一阶多项式来拟合实际数据中的曲线趋势。
这种拟合方法常用于统计分析和数据建模中，通过将实际数据点与一条直线进行拟合，可以得到一条最佳拟合直线，从而更好地理解数据的整体趋势。
在进行一阶多项式拟合时，通常会使用最小二乘法来确定最佳拟合直线的系数a和b。
最小二乘法是一种常见的参数估计方法，通过最小化实际数据点与拟合直线之间的残差平方和来确定最佳拟合直线的参数。
需要注意的是，一阶多项式拟合适用于线性关系比较明显的数据，对于非线性关系较强的数据，一阶多项式可能无法很好地拟合曲线趋势。
在这种情况下，可能需要考虑使用更高阶的多项式或者其他非线性拟合方法。
总的来说，一阶多项式可以用来模拟卡曲线拟合，但在实际应用中需要根据数据的特点和拟合效果来选择合适的拟合方法。
企业模拟需求曲线总结(必备4篇)
企业模拟需求曲线总结(必备4篇)企业模拟需求曲线总结第1篇可以在市场部进行广告投入，广告投入是针对具体产品的，广告投入具有时间累积性，但随着时间推移，前面投入的广告对后面季度的影响会越来越弱，例如某公司一季度针对 A 产品投入了 1万元的广告，二季度又投入了 1万元，则在二季度时，A 产品实际累积的广告效应应该大于1万但小于2万元。
企业模拟需求曲线总结第2篇消费者购买产品根据五个因素：n产品功能，产品设计时确定的产品功能特点，功能越符合消费者诉求，销量越高n产品品牌，每期针对产品投入的广告累积效应，效应越大，销量越高n产品价格，每期报价时确定的销售价格，与竞争对手相比，价格越低，销量越高n产品口碑，该产品累计在该类消费者上的销售量及交货量，越高，销量越高n产品销售，该产品对应的销售人员的能力合计，能力越高，销量越高当然不同消费者对以上五个因素权重并不相同，权重越大的因素对最后销量影响也越大。
季度结束后可以去市场部查看产品评价。
当然消费者购买量及订单分配，不会超过您设置的上限数。
每一步决策前，请阅读对应的规则说明。
企业模拟需求曲线总结第3篇可以当季出售的设备：设备上没有在在制品，没有在搬迁中。
线上工人转闲置状态，可以调整到其他有空位的线上。
可以当季出售/退租的厂房：厂房内没有任何设备。
设备在生产中，可以预出售，季度末产品下线后，设备自动出售，工人转闲置状态。
厂房内所有设备都预出售，厂房可以预退租或出售。
季度末，设备出售后，厂房自动退租或出售。
厂房设备的搬迁出售等操作需要到生产车间厂房列表界面去操作。
企业模拟需求曲线总结第4篇在产品设计之前，你需要仔细阅读“系统帮助”->“消费群体”了解整个行业的消费群体特性，然后选择设计最适合的产品来满足此类消费群体。