最新柱、锥、台、球的表面积和体积(有答案)
高中数学必修2立体几何常考题型：柱体、锥体、台体的表面积和体积全面版
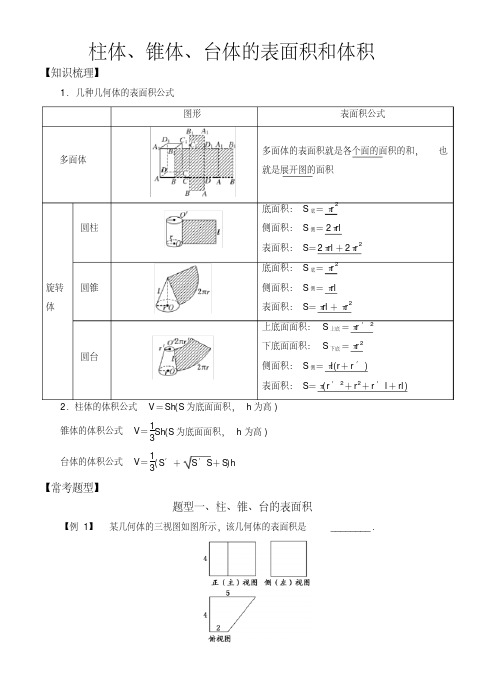
柱体、锥体、台体的表面积和体积【知识梳理】1．几种几何体的表面积公式图形表面积公式多面体多面体的表面积就是各个面的面积的和，也就是展开图的面积旋转体圆柱底面积：S底＝πr2侧面积：S侧＝2πrl表面积：S＝2πrl＋2πr2圆锥底面积：S底＝πr2侧面积：S侧＝πrl表面积：S＝πrl＋πr2圆台上底面面积：S上底＝πr′2下底面面积：S下底＝πr2侧面积：S侧＝πl(r＋r′)表面积：S＝π(r′2＋r2＋r′l＋rl)2．柱体的体积公式V＝Sh(S为底面面积，h为高)锥体的体积公式V＝13Sh(S为底面面积，h为高)台体的体积公式V＝13(S′＋S′S＋S)h【常考题型】题型一、柱、锥、台的表面积【例1】某几何体的三视图如图所示，该几何体的表面积是________．[解析]由三视图，画出几何体的直观图易求得基本量，如图所示，其表面积S＝2＋5×42×2＋4×(2＋4＋5＋5)＝28＋64＝92.[答案]92【类题通法】1．求几何体的表面积问题，通常将所给几何体分成基本几何体，再通过这些基本几何体的表面积进行求和或作差，从而获得几何体的表面积，另外有时也会用到将几何体展开求其展开图的面积进而得表面积．2．结合三视图考查几何体的表面积是高考的热点，解决此类问题的关键是正确地观察三视图，把它还原为直观图，特别要注意从三视图中得到几何体的相关量，再结合表面积公式求解．【对点训练】1．圆台的上、下底面半径分别是10 cm和20 cm，它的侧面展开图的扇环的圆心角是180°，求圆台的表面积．解：如图所示，设圆台的上底面周长为c cm，由于扇环的圆心角是180°，则c＝π·S A＝2π×10，解得SA＝20(cm)．同理可得SB＝40(cm)，所以AB＝SB－SA＝20(cm)．所以S表＝S侧＋S上＋S下＝π×(10＋20)×20＋π×102＋π×202＝1 100π(cm2).题型二、柱、锥、台的体积【例2】已知一个三棱台的上、下底面分别是边长为20 cm和30 cm的正三角形，侧面是全等的等腰梯形，且侧面面积等于上、下底面面积之和，求棱台的高和体积．[解]如图所示，在三棱台ABC-A′B′C′中，O′、O分别为上、下底面的中心，D、D′分别是BC、B′C′的中心，则DD′是等腰梯形BCC′B′的高，所以，S侧＝3×12×(20＋30)×DD′＝75DD′.又A′B′＝20 cm，AB＝30 cm，则上、下底面面积之和为S上＋S下＝34×(202＋302)＝3253(cm2)．由S侧＝S上＋S下，得75DD′＝3253，所以，DD′＝1333(cm)．又∵O′D′＝36×20＝1033(cm)，OD＝36×30＝53(cm)，∴棱台的高h＝O′O＝D′D2－OD－O′D′2＝13332－53－10332＝43(cm)，由棱台的体积公式，可得棱台的体积为V＝h3(S上＋S下＋S上S下)＝433×(3253＋34×20×30)＝1 900(cm3)．【类题通法】求几何体的体积时，要注意利用好几何体的轴截面(尤其为圆柱、圆锥时)，准确求出几何体的高和底面积；同时，对不规则的几何体可利用分割几何体或补全几何体的方法转化为柱、锥、台体的体积计算问题．【对点训练】2．已知圆台的高为3，在轴截面中，母线AA1与底面圆直径AB的夹角为60°，轴截面中的一条对角线垂直于腰，求圆台的体积．解：如图所示，作轴截面A1ABB1，设圆台的上、下底面半径和母线长分别为r、R，l，高为h.作A1D⊥AB于点D，则A1D＝3.又∵∠A1AB＝60°，∴AD＝A1Dtan 60°，即R－r＝3×33，∴R－r＝ 3.又∵∠BA1A＝90°，∴∠BA1D＝60°.∴BD＝A1D·tan 60°，即R＋r＝3×3，∴R＋r＝33，∴R＝23，r＝3，而h＝3，∴V圆台＝13πh(R2＋Rr＋r2)＝13π×3×[(23)2＋23×3＋(3)2]＝21 π．所以圆台的体积为21 π．题型三、简单组合体的表面积和体积【例3】已知△ABC的三边长分别是AC＝3，BC＝4，AB＝5，以AB所在直线为轴，将此三角形旋转一周，求所得旋转体的表面积和体积．[解]如图，在△ABC中，过C作CD⊥AB，垂足为 D.由AC＝3，BC＝4，AB＝5，知AC2＋BC2＝AB2，则AC⊥BC.∵BC·AC＝AB·CD，∴CD＝125，记为r＝125，那么△ABC以AB所在直线为轴旋转所得旋转体是两个同底的圆锥，且底半径r＝12 5，母线长分别是AC＝3，BC＝4，所以S表面积＝πr·(AC＋BC)＝π×125×(3＋4)＝845π，V＝13πr2(AD＋BD)＝13πr2·AB＝13π×1252×5＝485π．所以，所求旋转体的表面积是845π，体积是485π．【类题通法】求组合体的表面积与体积的关键是弄清组合体中各简单几何体的结构特征及组合形式，对于与旋转体有关的组合体问题，要根据条件分清各个简单几何体的底面半径及母线长，再分别代入公式求解．【对点训练】3．某几何体的三视图如图所示，它的体积为()A．12πB．45πC．57πD．81π解析：选C由三视图可知，该几何体是由底面直径为6，高为5的圆柱与底面直径为6，母线长为5的圆锥组成的组合体，因此，体积为V＝π×32×5＋13×π×32×52－32＝57π．【练习反馈】1．若圆锥的高等于底面直径，则它的底面积与侧面积之比为() A．1∶2B．1∶ 3C．1∶ 5 D.3∶2解析：选C设圆锥底面半径为r，则高h＝2r，∴其母线长l＝5r.∴S侧＝πrl＝5πr2，S底＝πr2.2．若长方体的长、宽、高分别为 3 cm、4 cm、5 cm，则长方体的体积为() A．27 cm3B．60 cm3C．64 cm3D．125 cm3解析：选B长方体即为四棱柱，其体积为底面积×高，即为3×4×5＝60 cm3. 3．若圆锥的侧面展开图为一个半径为2的半圆，则圆锥的体积是________．解析：易知圆锥的母线长为2，设圆锥的半径为r，则2πr＝12×2π·２，∴r＝1，则高h＝l2－r2＝ 3.∴V圆锥＝13πr2·h＝13π×3＝33π．答案：3 3π4．圆台的上、下底面半径和高的比为1∶4∶4，母线长为10，则圆台的侧面积为________．解析：已知圆台的上、下底面半径和高的比为1∶4∶4，母线长为10，设圆台上底面的半径为r，则下底面半径和高分别为4r和4r，由100＝(4r)2＋(4r－r)2，得r＝2，故圆台的侧面积等于π(r＋4r)l＝π(2＋8)×10＝100π．答案：100π5．一个正三棱柱的三视图如图所示(单位：cm)，求这个正三棱柱的表面积与体积．解：由三视图知直观图如图所示，则高AA′＝2 cm，底面高B′D′＝2 3 cm，所以底面边长A′B′＝23×23＝4 cm.一个底面的面积为12×23×4＝4 3 cm2.所以S表面积＝2×43＋4×2×3＝(24＋83) cm2，V＝43×2＝8 3 cm3.所以表面积为(24＋83) cm2，体积为8 3 cm3.你曾落过的泪，最终都会变成阳光，照亮脚下的路。
_柱体椎体台体的表面积与体积
(变式) 球的内接长方体的长、宽、高分别为3、
2、 3,求此球体的表面积和体积。
分析：长方体内接于球，则由 球和长方体都是中心对称图形 可知，它们中心重合，则长方
体体对角线与球的直径相等。
解：Q 长方体内接于球
球的直径等于长方体的体对角线长
(2 R)2 32 22 ( 3)2 16 R 2
V Sh
S为底面面积， S分别为上、下底面
S为底面面积，
h为锥体高
面积，h 为台体高
h为柱体高
例3 有一堆规格相同的铁制（铁的密是 7.8g/cm3 ）六 角螺帽共重5.8kg，已知底面是正六边形，边长为 12mm，内孔直径为10mm，高为10mm，问这堆螺 帽大约有多少个（π取3.14）？
解：六角螺帽的体积是六棱柱的体积与圆柱体 积之差，即:
棱柱（圆柱）的高是指两底面之间的距离，即从一 个底面上任意一点向另一个底面作垂线，这点与垂 足（垂线与底面的交点）之间的距离。不一样
锥体体积公式
圆锥的体积公式：
V 1 Sh （其中S为底面面积，h为高） 3
圆锥体积等于同底等高的圆柱的体积的 1． 3
棱锥的体积怎么求？
A’
C’
把三棱锥
B’
以△ABC为
3
什么是锥体的高？
由此可知，棱柱与圆柱的体积公式类似，都是底面 面积乘高；棱锥与圆锥的体积公式类似，都是等于
底面面积乘高的 1． 3
h
台体体积公式
台体的体积
由于圆台(棱台)是由圆锥(棱锥) 截成的，因此可以利用两个锥体 的体积差．得到圆台(棱台)的体积 公式．
V VP ABCD VP ABCD
C C C C C CC C C C C C 锥2、3
棱柱棱台棱锥圆柱圆锥圆台的表面积和体积
棱柱棱台棱锥圆柱圆锥圆台的表面积和体积今天咱们聊聊几种几何图形的表面积和体积，别看它们名字一大堆，实际上说起来还挺有趣的！什么棱柱、棱台、棱锥、圆柱、圆锥、圆台，一听这些名儿就有点头大是不是？但别怕，咱慢慢捋，保证让你不仅明白，而且还觉得挺轻松的。
一、棱柱棱柱嘛，说白了就是两块一样的多边形，通过平行的连接边把它们“拉”到一起，像是一个长方体，但是它的两头可能不一定是矩形，而是其他形状的多边形。
要想算表面积，咱首先得弄清楚，棱柱的表面积就等于两块底面（上面和下面）加上四周的侧面。
底面呢，就像是两片“面包”，每片的面积要算清楚。
然后四周的侧面，就是一圈包着底面的墙壁，一圈一圈的，面积就是每个侧面小长方形的面积加起来。
说得简单点，就是找出每个侧面的长和宽，再加上底面，就搞定了！至于体积，那就更简单了。
棱柱的体积就是底面面积乘以高。
就好像你拿个鞋盒子，底面有多少面积，高度是多少，乘一乘，你就能知道鞋盒能装多少东西了。
是不是挺简单？二、棱台棱台，嘿听起来像个“顶端有点小”的棱柱，对吧？你可以把它想象成一个“上面小下面大”的冰淇淋桶。
它有两个不一样的底面，一个是上面小的，一个是下面大的。
算表面积和体积的思路其实和棱柱差不多，唯一不同的就是你得计算两个不同底面的面积。
像冰淇淋桶那样，底面面积的算法可得分开算，因为上面和下面的底面不一样！不过别紧张，搞清楚底面的面积，侧面的区域也不难算，照着棱柱的办法，慢慢来，搞定它。
体积的话，咱还是按公式来。
棱台的体积就是上下两底面积的平均值，再乘以高。
这就像把一个上小下大的杯子装满水，求的是你能装下多少水的量。
听起来像是数学公式的“变化球”，不过还是挺直白的。
三、棱锥棱锥，这名字是不是也听着有点陌生？其实它就像是一个金字塔的样子。
它的底面可以是多边形，而顶点就是一个“尖尖儿”的点。
表面积呢，首先要计算底面面积，这个好办，底面就是一个多边形，面积根据具体的形状来算。
然后，别忘了加上每个侧面的面积。
空间几何体的表面积和体积(一)
空间几何体的表面积与体积柱体、锥体、台体的表面积与体积[新知初探]1．柱体、锥体、台体的表面积公式2．柱体、锥体、台体的体积公式柱体的体积公式V＝Sh(S为底面面积，h为高)；锥体的体积公式V＝13Sh(S为底面面积，h为高)；台体的体积公式V＝13(S′＋S′S＋S)h.[点睛](1)圆柱、圆锥、圆台的侧面积公式之间的关系：[小试身手]1．判断下列命题是否正确．(正确的打“√”，错误的打“×”) (1)锥体的体积等于底面面积与高之积( ) (2)台体的体积可转化为两个锥体的体积之差( ) 答案：(1)× (2)√2．侧面都是等腰直角三角形的正三棱锥，底面边长为a 时，该三棱锥的表面积是( ) A.3＋34a 2B.34a 2C.3＋32a 2D.6＋34a 2解析：选A ∵侧面都是等腰直角三角形，故侧棱长等于22a ，∴S 表＝34a 2＋3×12×⎝⎛⎭⎫22a 2＝3＋34a 2.3．若圆锥的底面半径为3，母线长为5，则圆锥的体积是________． 解析：由已知圆锥的高h ＝4， 所以V 圆锥＝13π×32×4＝12π.答案：12π柱、锥、台的表面积[典例] 现有一个底面是菱形的直四棱柱，它的体对角线长为9和15，高是5，求该直四棱柱的侧面积．[解] 如图，设底面对角线AC ＝a ，BD ＝b ，交点为O ，对角线A 1C ＝15，B 1D ＝9， ∴a 2＋52＝152，b 2＋52＝92， ∴a 2＝200，b 2＝56.∵该直四棱柱的底面是菱形， ∴AB 2＝⎝⎛⎭⎫AC 22＋⎝⎛⎭⎫BD 22＝a 2＋b 24＝200＋564＝64，∴AB ＝8. ∴直四棱柱的侧面积S ＝4×8×5＝160.(1)求几何体的表面积问题，通常将所给几何体分成基本几何体，再通过这些基本几何体的表面积进行求和或作差，从而获得几何体的表面积，另外有时也会用到将几何体展开求其展开图的面积进而得表面积．(2)结合三视图考查几何体的表面积是高考的热点，解决此类问题的关键是正确地观察三视图，把它还原为直观图，特别要注意从三视图中得到几何体的相关量，再结合表面积公式求解．[活学活用]1．(陕西高考)一个几何体的三视图如图所示，则该几何体的表面积为()A．3πB．4πC．2π＋4 D．3π＋4解析：选D由几何体的三视图可知，该几何体为半圆柱，直观图如图所示．表面积为2×2＋2×12×π×12＋π×1×2＝4＋3π.2．圆台的上、下底面半径和高的比为1∶4∶4，若母线长为10，则圆台的表面积为() A．81π B．100πC．168π D．169π解析：选C先画轴截面，再利用上、下底面半径和高的比求解．圆台的轴截面如图所示，设上底面半径为r，下底面半径为R，则它的母线长为l＝h2＋(R－r)2＝(4r)2＋(3r)2＝5r＝10，所以r＝2，R＝8.故S侧＝π(R＋r)l＝π(8＋2)×10＝100π，S表＝S侧＋πr2＋πR2＝100π＋4π＋64π＝168π.柱体、锥体、台体的体积[典例])A．2π＋2 3 B．4π＋2 3C ．2π＋233D ．4π＋233[解析] 该空间几何体由一圆柱和一正四棱锥组成，圆柱的底面半径为1，高为2，体积为2π，四棱锥的底面边长为2，高为3，所以体积为13×(2)2×3＝233，所以该几何体的体积为2π＋233.[答案] C空间几何体体积问题的常见类型及解题策略(1)求简单几何体的体积．若所给的几何体为柱体、锥体或台体，则可直接利用公式求解．(2)求以三视图为背景的几何体的体积．应先根据三视图得到几何体的直观图，然后根据条件求解．[活学活用]1．已知某圆台的上、下底面面积分别是π，4π，侧面积是6π，则这个圆台的体积是________．解析：设圆台的上、下底面半径分别为r 和R ，母线长为l ，高为h ，则S 上＝πr 2＝π，S 下＝πR 2＝4π，∴r ＝1，R ＝2，S 侧＝π(r ＋R )l ＝6π，∴l ＝2，∴h ＝3，∴V ＝13π(12＋22＋1×2)×3＝733π.答案：733π 2.若某几何体的三视图如图所示，则此几何体的体积等于________． 解析：根据三视图，可知题中的几何体是由一个三棱柱削去一个三棱锥得到的，体积V ＝12×3×4×5－13×12×4×3×3＝24.答案：24几何体体积的求法1.如图所示，正方体ABCD -A 1B 1C 1D 1的棱长为1，E 为线段B 1C 上的一点，则三棱锥A -DED 1的体积为________．解析：V 三棱锥A -DED 1＝V 三棱锥E -DD 1A ＝13×12×1×1×1＝16.答案：162.如图所示，三棱锥的顶点为P ，PA ，PB ，PC 为三条侧棱，且PA ，PB ，PC 两两互相垂直，又PA ＝2，PB ＝3，PC ＝4，求三棱锥P -ABC 的体积V .解：三棱锥的体积V ＝13Sh ，其中S 为底面积，h 为高，而三棱锥的任意一个面都可以作为底面，所以此题可把B 看作顶点，△PAC 作为底面求解．故V ＝13S △PAC ·PB ＝13×12×2×4×3＝4.题点二：分割法3.如图，在多面体ABCDEF 中，已知面ABCD 是边长为4的正方形，EF ∥AB ，EF ＝2，EF 上任意一点到平面ABCD 的距离均为3，求该多面体的体积．解：如图，连接EB ，EC .四棱锥E -ABCD 的体积 V 四棱锥E -ABCD ＝13×42×3＝16. ∵AB ＝2EF ，EF ∥AB ， ∴S △EAB ＝2S △BEF .∴V 三棱锥F -EBC ＝V 三棱锥C -EFB ＝12V 三棱锥C -ABE ＝12V 三棱锥E -ABC ＝12×12V 四棱锥E -ABCD ＝4. ∴多面体的体积V ＝V 四棱锥E -ABCD ＋V 三棱锥F -EBC ＝16＋4＝20. 题点三：补形法4．如图，一个底面半径为2的圆柱被一平面所截，截得的几何体的最短和最长母线长分别为2和3，求该几何体的体积．解：用一个完全相同的几何体把题中几何体补成一个圆柱，如图，则圆柱的体积为π×22×5＝20π，故所求几何体的体积为10π.5．已知四面体ABCD 中，AB ＝CD ＝13，BC ＝AD ＝25，BD ＝AC ＝5，求四面体ABCD 的体积．解：以四面体的各棱为对角线还原为长方体，如图． 设长方体的长、宽、高分别为x ，y ，z ， 则{x 2＋y 2＝13，y 2＋z 2＝20，x 2＋z 2＝25，∴{ x ＝3，y ＝2，z ＝4.∵V D -ABE ＝13DE ·S △ABE ＝16V 长方体， 同理，V C -ABF ＝V D -ACG ＝V D -BCH ＝16V 长方体， ∴V 四面体ABCD ＝V 长方体－4×16V 长方体＝13V 长方体．而V 长方体＝2×3×4＝24，∴V 四面体ABCD ＝8.(1)三棱锥又称为四面体，它的每一个面都可当作底面来处理，这一方法叫作体积转移法(或称等积法)．(2)当所给几何体形状不规则时，无法直接利用体积公式求解，这时可通过分割或补形，将原几何体分割或补形成较易计算体积的几何体，从而求出原几何体的体积．层级一 学业水平达标1．已知某长方体同一顶点上的三条棱长分别为1,2,3，则该长方体的表面积为( ) A ．22 B ．20 C ．10D ．11解析：选A 所求长方体的表面积S ＝2×(1×2)＋2×(1×3)＋2×(2×3)＝22. 2．若某圆锥的高等于其底面直径，则它的底面积与侧面积之比为( ) A ．1∶2 B ．1∶ 3 C ．1∶ 5D.3∶2解析：选C 设圆锥底面半径为r ，则高h ＝2r ，∴其母线长l ＝5r .∴S 侧＝πrl ＝5πr 2，S 底＝πr 2，S 底∶S 侧＝1∶ 5.3.如图是一个几何体的三视图，其中正视图是腰长为2的等腰三角形，俯视图是半径为1的半圆，则该几何体的体积是( )A.433πB.36πC.12π D.33π 解析：选B 由三视图，可知给定的几何体是一个圆锥的一半，故所求的体积为12×13×π×12×3＝36π. 4．已知某圆台的一个底面周长是另一个底面周长的3倍，母线长为3，圆台的侧面积为84π，则该圆台较小底面的半径为( )A ．7B ．6C ．5D ．3解析：选A 设圆台较小底面的半径为r ，则另一底面的半径为3r .由S 侧＝3π(r ＋3r )＝84π，解得r ＝7.5.如图，ABC -A ′B ′C ′是体积为1的棱柱，则四棱锥C -AA ′B ′B 的体积是( )A.13B.12C.23D.34解析：选C ∵V C -A ′B ′C ′＝13V ABC -A ′B ′C ′＝13，∴V C -AA ′B ′B ＝1－13＝23. 6．棱长都是3的三棱锥的表面积S 为________．解析：因为三棱锥的四个面是全等的正三角形，所以S ＝4×34×32＝9 3. 答案：9 37．若圆锥的侧面展开图为一个半径为2的半圆，则圆锥的体积是________． 解析：易知圆锥的母线长l ＝2，设圆锥的底面半径为r ，则2πr ＝12×2π×2，∴r ＝1，∴圆锥的高h ＝l 2－r 2＝3，则圆锥的体积V ＝13πr 2h ＝33π.答案：33π 8．如图是一个几何体的三视图，若它的体积是3 3，则a ＝________.解析：由三视图，可知几何体为一个放倒的直三棱柱，则该几何体的体积V ＝3×⎝⎛⎭⎫12×2×a ＝3 3，所以a ＝ 3.答案： 39．如图，在四边形ABCD 中，∠DAB ＝90°，∠ADC ＝135°，AB ＝5，CD ＝22，AD ＝2，若四边形ABCD 绕AD 旋转一周成为几何体．(1)画出该几何体的三视图； (2)求出该几何体的表面积． 解：(1)如图所示．(2)过C 作CE 垂直AD 延长线于E 点， 作CF 垂直AB 于F 点． 由已知得：DE ＝2，CE ＝2， ∴CF ＝4，BF ＝5－2＝3. ∴BC ＝CF 2＋BF 2＝5. ∴下底圆面积S 1＝25π，台体侧面积S 2＝π×(2＋5)×5＝35π， 锥体侧面积S 3＝π×2×22＝42π， 故表面积S ＝S 1＋S 2＋S 3＝(60＋42)π.10.如图，已知正三棱锥S -ABC 的侧面积是底面积的2倍，正三棱锥的高SO ＝3，求此正三棱锥的表面积．解：如图，设正三棱锥的底面边长为a ，斜高为h ′，过点O 作OE ⊥AB ，与AB 交于点E ，连接SE ，则SE ⊥AB ，SE ＝h ′.∵S 侧＝2S 底， ∴12·3a ·h ′＝34a 2×2. ∴a ＝3h ′.∵SO ⊥OE ，∴SO 2＋OE 2＝SE 2. ∴32＋⎝⎛⎭⎫36×3h ′2＝h ′2.∴h ′＝23，∴a ＝3h ′＝6. ∴S 底＝34a 2＝34×62＝93，S 侧＝2S 底＝18 3. ∴S 表＝S 侧＋S 底＝183＋93＝27 3.层级二 应试能力达标1．正方体的表面积为96，则正方体的体积为( )A ．486B ．64C ．16D ．96解析：选B 设正方体的棱长为a ，则6a 2＝96，∴a ＝4，故V ＝a 3＝43＝64. 2.已知高为3的棱柱ABC -A 1B 1C 1的底面是边长为1的正三角形，如图，则三棱锥B -AB 1C 的体积为( )A.14B.12C.36D.34解析：选D VB -AB 1C ＝VB 1-ABC ＝13S △ABC ×h ＝13×34×3＝34.3．圆柱的一个底面积是S ，侧面展开图是一个正方形，那么这个圆柱的侧面积是( ) A ．4πS B ．2πS C ．πSD.233πS解析：选A 底面半径是Sπ，所以正方形的边长是2πSπ＝2πS ，故圆柱的侧面积是(2πS )2＝4πS .4.一个几何体的三视图如图所示，则该几何体的体积为( ) A.533B.433C.536D. 3 解析：选A 由三视图可知，该几何体是正三棱柱的一部分，如图所示，其中底面三角形的边长为2，故所求的体积为34×22×2－13×34×22×1＝533. 5．已知一个长方体的三个面的面积分别是2，3，6，则这个长方体的体积为________．解析：设长方体从一点出发的三条棱长分别为a ，b ，c ，则{ ab ＝2，ac ＝3，bc ＝6，三式相乘得(abc )2＝6，故长方体的体积V ＝abc ＝ 6.答案： 66．用一张正方形的纸把一个棱长为1的正方体礼品盒完全包住，不将纸撕开，则所需纸的最小面积是________．解析：如图①为棱长为1的正方体礼品盒，先把正方体的表面按图所示方式展成平面图形，再把平面图形尽可能拼成面积较小的正方形，如图②所示，由图知正方形的边长为22，其面积为8.答案：87．如图所示，已知某几何体的三视图如下(单位：cm)．(1)画出这个几何体(不要求写画法)；(2)求这个几何体的表面积及体积．解：(1)这个几何体如图所示．(2)这个几何体可看成是正方体AC1及直三棱柱B1C1Q-A1D1P的组合体．由PA1＝PD1＝2，A1D1＝AD＝2，可得PA1⊥PD1.故所求几何体的表面积S＝5×22＋2×2×2＋2×12×(2)2＝(22＋42)cm2，所求几何体的体积V＝23＋12×(2)2×2＝10(cm3)．8．一个圆锥的底面半径为2 cm，高为6 cm，在其内部有一个高为x cm的内接圆柱．(1)求圆锥的侧面积．(2)当x为何值时，圆柱的侧面积最大？并求出侧面积的最大值．解：(1)圆锥的母线长为62＋22＝210(cm)，∴圆锥的侧面积S1＝π×2×210＝410 π(cm2)．(2)画出圆锥的轴截面如图所示：设圆柱的底面半径为r cm，由题意，知r2＝6－x 6，∴r＝6－x3，∴圆柱的侧面积S2＝2πrx＝2π3(－x2＋6x)＝－2π3[(x－3)2－9]，∴当x＝3时，圆柱的侧面积取得最大值，且最大值为6π cm2.。
圆锥圆柱圆台球的表面积和体积公式
圆锥圆柱圆台球的表面积和体积公式圆锥、圆柱和圆台球是几何学中常见的三个立体图形，它们都具有特定的表面积和体积公式。
在本篇文章中，我将为您介绍这三个图形的定义、特点以及如何计算它们的表面积和体积。
一、圆锥圆锥是由一个圆和与圆上每一点相连的一条线段组成的立体图形。
圆锥有一个顶点和一个底面，底面是一个圆，而顶点则位于底面的正上方。
圆锥的表面积公式为：S = πr² + πrl其中，S表示圆锥的表面积，r表示底面圆的半径，l表示圆锥的斜高。
圆锥的体积公式为：V = (1/3)πr²h其中，V表示圆锥的体积，r表示底面圆的半径，h表示圆锥的高。
二、圆柱圆柱是由两个平行圆面和连接两个圆面的侧面组成的立体图形。
圆柱的底面是一个圆，而圆柱的高则是连接两个底面中心的线段。
圆柱的表面积公式为：S = 2πr² + 2πrh其中，S表示圆柱的表面积，r表示底面圆的半径，h表示圆柱的高。
圆柱的体积公式为：V = πr²h其中，V表示圆柱的体积，r表示底面圆的半径，h表示圆柱的高。
三、圆台球圆台球是由两个平行圆面和连接两个圆面的侧面组成的立体图形，其中一个圆面的半径较大，另一个圆面的半径较小。
圆台球的底面是一个圆，而圆台球的高则是连接两个底面中心的线段。
圆台球的表面积公式为：S = π(R+r)l + πR² + πr²其中，S表示圆台球的表面积，R表示底面较大圆的半径，r表示底面较小圆的半径，l表示圆台球的斜高。
圆台球的体积公式为：V = (1/3)πh(R²+r²+Rr)其中，V表示圆台球的体积，R表示底面较大圆的半径，r表示底面较小圆的半径，h表示圆台球的高。
通过以上公式，我们可以方便地计算出圆锥、圆柱和圆台球的表面积和体积。
这些公式的应用范围广泛，例如在建筑设计、工程测量以及日常生活中都有重要的应用。
在实际问题中，我们可以根据给定的数据，将公式中的参数代入，计算出具体的数值。
柱、锥、台、球的表面积与体积精例
表面积与体积
X
一. 棱柱的侧面积、表面积与体积 1. 直棱柱的侧面积、表面积与体积
S侧=C•h
S表= S侧+2S底 S表= S侧+2S底
V棱柱= S•h
2. 斜棱柱的侧面积、表面积与体积
S侧=C’•L
二. 棱锥的侧面积、表面积与体积
S侧= S△1+S △2 +S △3 +… S表= S侧+S底
2
它的体积是
2cm
俯视图
4_________. 2 cm
4 3
3
例2
已知长方体ABCD-A1B1C1D1的长、宽、高分别 为3，2，1，求沿其表面从点A到点C1的最短距离。 D1 C1 B1 A1 1 C E D
2 2 3
A
B 1
例2
已知长方体ABCD-A1B1D1的长、宽、高分别为3， 2，1，求沿其表面从点A到点C1的最短距离。 D1 C1 B1 F A
A
5 4 B 4
3 C B 4 C
12 5
5
5
A
A
3
C
3
思考：
1.用棱长为1的正方体的体积作为单位体积，下图 长方体的体积的数值为24.假如将体积单位改用棱 长为2的正方体的体积，这个长方体的体积变为多 少？
2.一个正方体和一个圆柱等高,并且侧面积相等。 比较它们的体积哪个大？为什么？ P 3.求证:经过长方体相对两个面 的中心的任意平面,把长方体分 成体积相等的两个柱体。 Q
1
D
2
1 C 2
1
A
3Ba来自 例2已知长方体ABCDD1 A1B1C1D1的长、宽、高分 别为3，2，1，求沿其表面 A1 从点A到点C1的最短距离。 D
柱、锥、台表面积与体积
柱、锥、台的表面积与体积
要点1 柱体的表面积
棱柱的侧面是平行四边形；圆柱的侧面展开图是矩形． 设柱体的底面周长为c ，高为h ，则S 侧＝c·h ，S 表＝S 侧＋2S 底． 要点2 锥体的表面积
棱锥的侧面展开图是由若干个三角形拼成的，因此侧面积为各三角形面积之和；圆锥的侧面展开图为扇形．表面积公式为：S 表＝S 侧＋S 底． 要点3 台体的表面积
棱台的侧面展开图为若干个梯形拼接而成，因此侧面积为各梯形的面积之和，而圆台的侧面展开图为扇环，其侧面积可由大扇形的面积减去小扇形的面积而得到，它们的表面积公式为：S 表＝S 侧＋S 上底＋S 下底． 要点4 柱体、锥体与台体的体积公式
V 柱体＝Sh ，(S 为底面积，h 为柱体的高)． V 锥体＝1
3Sh ，(S 为底面积，h 为锥体的高)． V 台体＝1
3(S ＋SS ′＋S ′)h ， V 柱――――→S ′＝S V 台――――→S ′＝0
V 锥
例1 (1)已知棱长为5的各侧面均为正三角形的四棱锥
S －ABCD ，求它的侧面积、表面积．
(2)一个正方体和一个圆柱等高，并且侧面面积相等，求这个正方体和圆柱的体积之比．
例2(1)已知一圆台上底面半径为2，下底面的半径为3，截得此圆台的圆锥的高为6，求此圆台的体积．
例3某几何体的三视图如图所示，该几何体的体积等于________，表面积等于________．
空间几何体体积计算的常见技巧
1．等积变换法
例如图所示，三棱锥的顶点为P，PA、PB、PC为三条侧棱，且PA、PB、PC两两互相垂直，又PA＝2，PB＝3，PC＝4，求三棱锥P －ABC的体积V.。
圆柱、圆锥、圆台、球的表面积和体积
8． 3.2 圆柱、圆锥、圆台、球的表面积和体积 学习指导核心素养1.知道圆柱、圆锥、圆台、球的表面积和体积公式．2.能用表面积和体积公式解决简单的实际问题．直观想象、数学运算：利用公式计算圆柱、圆锥、圆台、球的表面积与体积．[学生用书P75]1．圆柱、圆锥、圆台的表面积圆柱底面积：S 底＝πr 2侧面积：S 侧＝2πrl 表面积：S ＝2πr (r ＋l ) 圆锥底面积：S 底＝πr 2侧面积：S 侧＝πrl 表面积：S ＝πr (r ＋l ) 圆台上底面面积：S 上底＝πr ′2 下底面面积：S 下底＝πr 2侧面积：S 侧＝πl (r ＋r ′)表面积： S ＝π(r ′2＋r 2＋r ′l ＋rl )2.圆柱、圆锥、圆台的体积 V 圆柱＝πr 2h (r 是底面半径，h 是高)， V 圆锥＝13πr 2h (r 是底面半径，h 是高)，V 圆台＝13 πh (r ′2＋r ′r ＋r 2)(r ′，r 分别是上、下底面半径，h 是高).3．球的表面积和体积 表面积：S ＝4πR 2． 体积：V ＝43πR 3．1．圆柱、圆锥、圆台的侧面积公式之间有什么关系？ 提示：S 圆柱侧＝2πrl ――→r ′＝rS 圆台侧＝π(r ′＋r )l ――→r ′＝0S 圆锥侧＝πrl . 2．球面能展开成平面图形吗？ 提示：不能展开成平面图形．1．判断正误(正确的打“√”，错误的打“×”) (1)圆柱的侧面面积等于底面面积与高的积．( )(2)圆柱、圆锥、圆台的展开图分别是一个矩形、扇形、扇环．( ) (3)决定球的大小的因素是球的半径．( )(4)球面被经过球心的平面截得的圆的半径等于球的半径．( ) 答案：(1)× (2)× (3)√ (4)√2．若圆锥的底面半径为3 ，高为1，则圆锥的体积为( ) A ．π3B ．π2C ．πD ．2π答案：C3．若一个球的直径为 2，则此球的表面积为( ) A ．2π B ．16π C ．8π D ．4π解析：选D ．因为球的直径为 2，所以球的半径为 1，所以球的表面积 S ＝4πR 2＝4π.4．圆柱的侧面展开图是长 12 cm ，宽 8 cm 的矩形，则这个圆柱的体积为( ) A ．288π cm 3B ．192πcm 3C ．288π cm 3或192π cm 3D ．192π cm 3解析：选 C ．当圆柱的高为 8 cm 时， V ＝π×⎝⎛⎭⎫122π 2×8＝288π (cm 3)，当圆柱的高为 12 cm 时，V ＝π×⎝⎛⎭⎫82π 2×12＝192π(cm 3). [学生用书P75]探究点1 圆柱、圆锥、圆台的表面积 [问题探究]求圆柱、圆锥、圆台的表面积时，关键是什么？探究感悟：求圆柱、圆锥的表面积时，关键是求其母线长与底面的半径；求圆台的表面积时，关键是求其母线长与上、下底面的半径．(1)若圆锥的高为3，底面半径为4，则此圆锥的表面积为( ) A ．40π B ．36π C ．26πD ．20π(2)圆台的上、下底面半径和高的比为1∶4∶4，若母线长为10，则圆台的表面积为( ) A ．81π B ．100π C ．168πD ．169π【解析】 (1)圆锥的母线l ＝32＋42 ＝5，所以圆锥的表面积为π×42＋π×4×5＝36π.故选B.(2)圆台的轴截面如图所示，设上底面半径为r ，下底面半径为R ，则它的母线长为l ＝h 2＋（R －r ）2 ＝（4r ）2＋（3r ）2 ＝5r ＝10，所以r ＝2，R ＝8.故S 侧＝π(R ＋r )l ＝π×(8＋2)×10＝100π，S 表＝S 侧＋πr 2＋πR 2＝100π＋4π＋64π＝168π.故选C.【答案】 (1)B (2)C圆柱、圆锥、圆台的表面积的求解步骤解决圆柱、圆锥、圆台的表面积问题，要利用好旋转体的轴截面及侧面展开图，借助于平面几何知识，求得所需几何要素，代入公式求解即可，基本步骤如下：(1)得到空间几何体的展开图； (2)依次求出各个平面图形的面积； (3)将各平面图形的面积相加．1．若一个圆柱的轴截面是面积为9的正方形，则这个圆柱的侧面积为( ) A ．9π B ．12π C ．272πD ．454π解析：选A.由于圆柱的轴截面是面积为9的正方形，则h ＝2r ＝3，所以圆柱的侧面积为2πr ·h ＝9π.2.如图，已知直角梯形ABCD ，BC ∥AD ，∠ABC ＝90°，AB ＝5，BC ＝16，AD ＝4，求以BC 所在直线为轴旋转一周所得几何体的表面积．解：以BC 所在直线为轴旋转一周所得几何体是圆柱和圆锥的组合体，如图．其中圆锥的高为16－4＝12，圆柱的母线长为AD ＝4，圆锥的母线长CD ＝13，故该几何体的表面积为2π×5×4＋π×52＋π×5×13＝130π.探究点2 圆柱、圆椎、圆台的体积(2021·贵州安顺高二期末)若一个圆锥的侧面展开图是半径为3，圆心角为120°的扇形，求该圆锥的体积．【解】 设圆锥底面半径为r ，则由题意得2πr ＝120180·π·3，解得r ＝1.所以底面面积为S ＝πr 2＝π. 又圆锥的高h ＝32－12 ＝22 ，故圆锥的体积V ＝13 Sh ＝13 ×π×22 ＝223π.求圆柱、圆锥、圆台的体积问题，一是要牢记公式，然后观察空间图形的构成，是单一的旋转体，还是组合体；二是注意旋转体的构成，以及圆柱、圆锥、圆台轴截面的性质，从而找出公式中需要的各个量，代入公式计算．1．圆台上、下底面面积分别是π，4π，侧面积是6π，则这个圆台的体积是( ) A ．233 πB ．2 3C ．736πD ．733π解析：选D.S 1＝π，S 2＝4π，所以r ＝1，R ＝2，S 侧＝6π＝π(r ＋R )l ，所以l ＝2，所以h＝3 .所以V ＝13 π(1＋4＋2)×3 ＝733π.故选D.2．若一圆柱与圆锥的高相等，且轴截面面积也相等，那么圆柱与圆锥的体积的比值为( )A ．1B ．12C ．32D ．34解析：选D.设圆柱底面圆半径为R ，圆锥底面圆半径为r ，高都为h ，由已知得2Rh ＝rh ，所以r ＝2R ，所以V 柱∶V 锥＝πR 2h ∶13πr 2h ＝3∶4，故选D.探究点3 球的表面积与体积 [问题探究]用一个平面去截球体，截面是什么形状？该截面的几何量与球的半径之间有什么关系？ 探究感悟：用一个平面去截球体，截面是圆面．在不过球心的截面图中，截面圆与球的轴截面的关系如图所示．其关系为R 2＝d 2＋r 2.用与球心距离为1的平面去截球，所得截面圆的面积为π，则球的表面积为( ) A ．8π3B ．32π3C ．8πD ．82π3【解析】 设球的半径为R ，则截面圆的半径为R 2－1 ，所以截面圆的面积为S ＝π(R 2－1 )2＝(R 2－1)π＝π，所以R 2＝2，所以球的表面积S ＝4πR 2＝8π.故选C. 【答案】 C(1)球的表面积和体积的求解关键因为球的表面积和体积都与球的半径有关，所以在解答这类问题时，设法求出球的半径是解题的关键．(2)球的截面问题的解题技巧①有关球的截面问题，常画出过球心的截面圆，将问题转化为平面中圆的问题． ②解题时要注意借助球半径R 、截面圆半径r 、球心到截面的距离d 构成的直角三角形，即R 2＝d 2＋r 2.1．(2021·江苏徐州高一期中)一个球的表面积是16π，那么这个球的体积为( ) A ．163 πB ．323 πC ．643πD ．2563π解析：选B.设这个球的半径为R ，则4πR 2＝16π，解得R ＝2，所以这个球的体积V ＝43 πR 3＝323π.故选B. 2．两个球的半径相差 1，表面积之差为 28π，则它们的体积之和为________． 解析：设大、小两球半径分别为 R ，r ，则⎩⎪⎨⎪⎧R －r ＝1，4πR 2－4πr 2＝28π，所以⎩⎪⎨⎪⎧R ＝4，r ＝3.所以体积之和为 43 πR 3＋43 πr 3＝364π3 .答案：364π3探究点4 与球有关的切、接问题(1)一个长方体的各个顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为 1，2，3，则此球的表面积为________．(2)如图，在圆柱O 1O 2内有一个球O ，该球与圆柱的上、下底面及母线均相切，记圆柱O 1O 2的体积为V 1，球O 的体积为V 2，则V 1V 2的值是________．【解析】 (1)长方体外接球直径长等于长方体体对角线长，即 2R ＝12＋22＋32 ＝14 ，所以球的表面积 S ＝4πR 2＝14π.(2)设球O 的半径为r ，则圆柱的底面半径为r ，高为2r ，所以V 1V 2 ＝πr 2·2r 43πr 3 ＝32.【答案】 (1)14π (2)32(1)常见几何体与球的切、接问题的解题策略①处理有关几何体外接球或内切球的相关问题时，要注意球心的位置与几何体的关系．一般情况下，由于球的对称性，球心总在特殊位置，比如中心、对角线的中点等．②解决此类问题的实质就是根据几何体的相关数据求球的直径或半径，关键是根据“切点”和“接点”作出轴截面图，把空间问题转化为平面问题来计算．(2)几个常用结论①球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径． ②球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径． ③球与圆柱的底面和侧面均相切，则球的直径等于圆柱的高，也等于圆柱底面圆的直径．将棱长为 2 的正方体木块削成一个体积最大的球，则该球的体积为( )A ．4π3B ．2π3C ．3π2D ．π6解析：选A.由题意知，此球是正方体的内切球，根据其几何特征知，此球的直径与正方体的棱长是相等的，故可得球的直径为 2，故半径为 1，其体积是43 ×π×13＝4π3.[学生用书P77]1．已知圆柱的底面半径r ＝1，母线长l 与底面的直径相等，则该圆柱的表面积为( ) A ．6π B ．8π C ．9πD ．10π解析：选A.因为圆柱的表面积为2πr 2＋2πrl ，r ＝1，l ＝2，所以圆柱的表面积为6π.故选A.2．若球的大圆面积扩大为原来的2倍，球的体积扩大为原来的( ) A ．8倍 B ．4倍 C ．22 倍D ．2倍解析：选C.球的大圆面积扩大为原来的2倍，则球的半径扩大为原来的2 倍，所以球的体积扩大为原来的22 倍．3．设三棱柱的侧棱垂直于底面，所有棱的长都为 a ，顶点都在一个球面上，则该球的表面积为( )A ．πa 2B ．73 πa 2C ．113πa 2D ．5πa 2解析：选B.由题意知，该三棱柱为正三棱柱，且侧棱与底面边长相等，均为 a ．如图，P 为三棱柱上底面的中心，O 为球心，易知 AP ＝23 ×32 a ＝33 a ，OP ＝12a ，所以球的半径 R ＝ OA 满足R 2＝⎝⎛⎭⎫33a 2 ＋⎝⎛⎭⎫12a 2＝712 a 2，故 S 球＝4πR 2＝73 πa 2.4．已知圆台上、下底面半径分别为1，2，高为3，则圆台的体积为__________． 解析：由公式知V 圆台＝13 π(1＋2＋4)×3＝7π.答案：7π5．如图所示，在边长为4的正三角形ABC 中，E ，F 分别是AB ，AC 的中点，AD ⊥BC ，EH ⊥BC ，FG ⊥BC ，D ，H ，G 为垂足，若将正三角形ABC 绕AD 旋转180°，求阴影部分形成的几何体的体积．解：由题意知，旋转后几何体是一个圆锥，从下面挖去一个圆柱，且圆锥的底面半径为2，高为23 ，圆柱的底面半径为1，高为3 .所求旋转体的体积为大圆锥的体积减去里面小圆柱的体积，即V 旋转体＝13 ×π×22×23 －π×12×3 ＝533 π，故所求旋转体的体积为533π. [学生用书P217(单独成册)][A 基础达标]1．在△ABC 中，AB ＝4，BC ＝3，AC ＝5，现以AB 所在直线为轴旋转一周，则所得几何体的表面积为( )A ．24πB ．21πC ．33πD ．39π解析：选A.因为在△ABC 中，AB ＝4，BC ＝3，AC ＝5，所以△ABC 是以∠B 为直角的直角三角形，故以AB 所在直线为轴旋转一周得到的几何体为圆锥，所以圆锥的底面半径为3，母线长为5，所以底面周长为6π，侧面积为12 ×6π×5＝15π，所以几何体的表面积为15π＋π×32＝24π.故选A.2．两个球的体积之比为8∶27，那么这两个球的表面积之比为( ) A ．2∶3 B ．4∶9 C ．2 ∶3D ．8 ∶27解析：选B.设两个球的半径分别为r ，R ，则⎝⎛⎭⎫43πr 3 ∶⎝⎛⎭⎫43πR 3 ＝r 3∶R 3＝8∶27， 所以r ∶R ＝2∶3，所以S 1∶S 2＝r 2∶R 2＝4∶9.3．(多选)如图，一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R 相等，则下列结论正确的是( )A ．圆柱的侧面积为2πR 2B ．圆锥的侧面积为2πR 2C ．圆柱的侧面积与球面面积相等D ．圆柱、圆锥、球的体积之比为3∶1∶2解析：选CD.依题意得球的半径为R ，则圆柱的侧面积为2πR ×2R ＝4πR 2，所以A 错误；圆锥的侧面积为πR ×5 ·R ＝5 πR 2，所以B 错误；球面面积为4πR 2，因为圆柱的侧面积为4πR 2，所以C 正确；因为V 圆柱＝πR 2·2R ＝2πR 3，V 圆锥＝13 πR 2·2R ＝23 πR 3，V 球＝43 πR 3，所以V 圆柱∶V 圆锥∶V 球＝2πR 3∶23 πR 3∶43πR 3＝3∶1∶2，所以D 正确．故选CD.4．将半径为R 的半圆卷成一个圆锥，则它的体积是( ) A ．524 πR 3 B ．58 πR 3 C ．324πR 3 D ．38πR 3 解析：选C.设圆锥的底面半径为r ，则2πr ＝πR ，所以r ＝R2 .所以圆锥的高h ＝R 2－r 2 ＝32R . 所以圆锥的体积V ＝13 πr 2×h ＝13 π(R 2 )2×32 R ＝324πR 3.故选C.5．若两球的体积之和是 12π，经过两球球心的截面圆周长之和为 6π，则两球的半径之差为( )A ．1B ．2C ．3D ．4解析：选 A ．设两球的半径分别为 R ，r (R >r )，则由题意得⎩⎪⎨⎪⎧4π3R 3＋4π3r 3＝12π，2πR ＋2πr ＝6π，解得⎩⎪⎨⎪⎧R ＝2，r ＝1.故 R －r ＝1. 6．一个高为2的圆柱，底面周长为2π，该圆柱的表面积为________.解析：由底面周长为2π可得底面半径为1.S 底＝πr 2＝π，S 侧＝2πr ·h ＝4π，所以S 表＝2S底＋S 侧＝6π.答案：6π7．表面积为3π的圆锥，它的侧面展开图是一个半圆，则该圆锥的底面直径为________． 解析：设圆锥的母线为l ，圆锥底面半径为r ，由题意可知，πrl ＋πr 2＝3π，且πl ＝2πr .解得r ＝1，即圆锥的底面直径为2.答案：28.圆柱形容器内盛有高度为8 cm 的水，若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后，水恰好淹没最上面的铁球(如图所示)，则铁球的半径是________cm.解析：设铁球的半径为x cm ，由题意得πx 2×8＝πx 2×6x －43 πx 3×3，解得x ＝4.答案：49．某组合体的直观图如图所示，它的中间为圆柱形，左右两端均为半球形，若图中r ＝1，l ＝3，试求该组合体的表面积和体积．解：该组合体的表面积S ＝4πr 2＋2πrl ＝4π×12＋2π×1×3＝10π， 该组合体的体积V ＝43 πr 3＋πr 2l ＝43 π×13＋π×12×3＝13π3.10．已知一个圆锥的底面半径为R ，高为H ，在其内部有一个高为x 的内接圆柱． (1)求圆柱的侧面积；(2)x 为何值时，圆柱的侧面积最大？解：(1)作圆锥的轴截面，如图所示．因为rR ＝H －x H，所以r ＝R －RH x ，所以S 圆柱侧＝2πrx ＝2πRx －2πR Hx 2(0<x <H ). (2)因为－2πRH<0，所以当x ＝2πR 4πR H＝H2 时，S 圆柱侧最大．故当x ＝H2时，即圆柱的高为圆锥高的一半时，圆柱的侧面积最大．[B 能力提升]11．一个球与一个正三棱柱的三个侧面和两个底面都相切，已知这个球的体积为323 π，那么这个正三棱柱的体积是( )A ．963B ．163C ．243D ．483解析：选D.由题意可知正三棱柱的高等于球的直径，从棱柱中间平行棱柱底面截得球的大圆内切于正三角形，正三角形与棱柱底面三角形全等，设三角形边长为a ，球半径为r ，由V 球＝43 πr 3＝323 π，得r ＝2.由S 柱底＝12 a ×r ×3＝34 a 2，得a ＝23 r ＝43 ，所以V 柱＝S柱底·2r ＝483 .12．如图，一个盛满溶液的玻璃杯，其形状为一个倒置的圆锥，现放一个球状物体完全浸没于杯中，球面与圆锥侧面相切，且与玻璃杯口所在平面相切，则溢出溶液的体积为( )A ．8327 πB ．4327 πC ．16327πD ．32327π解析：选D.由题意，设球的半径为r ，作出玻璃杯的轴截面，可得一个半径为r 的圆内切于一个边长为4的等边三角形，此等边三角形的高h ＝23 .根据中心(重心)的性质可得，球的半径r ＝13 h ＝233 ，所以球的体积V ＝43 πr 3＝43 π×⎝⎛⎭⎫233 3 ＝32327 π.即溢出溶液的体积为32327π，故选D.13.(多选)如图所示，△ABC 的三边长分别是AC ＝3，BC ＝4，AB ＝5，过点C 作CD ⊥AB ，垂足为D ，下列说法正确的是( )A ．以BC 所在直线为轴，将此三角形旋转一周，所得旋转体的侧面积为15πB ．以BC 所在直线为轴，将此三角形旋转一周，所得旋转体的体积为36π C ．以AC 所在直线为轴，将此三角形旋转一周，所得旋转体的侧面积为25πD ．以AC 所在直线为轴，将此三角形旋转一周，所得旋转体的体积为16π解析：选AD.以BC 所在直线为轴旋转时，所得旋转体为底面半径为3，母线长为5，高为4的圆锥，所以侧面积为π×3×5＝15π，体积为13 ×π×32×4＝12π，所以A 正确，B 错误；以AC 所在直线为轴旋转时，所得旋转体为底面半径为4，母线长为5，高为3的圆锥，侧面积为π×4×5＝20π，体积为13×π×42×3＝16π，所以C 错误；D 正确．故选AD.14．在长方体ABCD -A 1B 1C 1D 1中，AB ＝BC ＝2，过A 1，C 1，B 三点的平面截去长方体的一个角后，得到如图所示的几何体ABCD -A 1C 1D 1，这个几何体的体积为403.(1)求棱AA 1的长；(2)求经过A 1，C 1，B ，D 四点的球的表面积和体积．解：(1)设AA 1＝x ，依题意可得403 ＝2×2·x －13 ×12 ×2×2·x ，解得x ＝4，故棱AA 1的长为4.(2)依题意可知， 经过A 1，C 1，B ，D 四点的球就是长方体ABCD -A 1B 1C 1D 1的外接球，这个球的直径就是长方体的体对角线，所以球的直径2R ＝22＋22＋42 ＝26 ，解得R ＝6 .故所求球的表面积为4πR 2＝24π，体积为43·πR 3＝86 π.[C 拓展探究]15．如图，用一边长为2 的正方形硬纸，按各边中点垂直折起4个小三角形，做成一个“底座”，将体积为4π3 的球放入其中，“底座”形状保持不变，则球的最高点与“底座”底面的距离为( )A ．62 ＋32 B ．32C ．22 ＋32D ．32 ＋32解析：选D.由题意，可得“底座”的底面是边长为1的正方形，则经过4个小三角形的顶点截球所得的截面圆的直径为1.因为球的体积为4π3 ，所以球的半径为1，所以球心到截面圆的距离为1－⎝⎛⎭⎫122 ＝32 ，因为垂直折起的4个小直角三角形斜边上的高为12，所以球的最高点与“底座”底面的距离为32 ＋1＋12 ＝32 ＋32.故选D. 16.如图，四边形ABCD 是正方形，BD ︵是以 A 为圆心、AB 为半径的弧，将正方形 ABCD 以 AB 为轴旋转一周，求图中 Ⅰ，Ⅱ，Ⅲ 三部分经旋转所得几何体的体积之比．解：Ⅰ生成圆锥，Ⅱ生成的是半球去掉Ⅰ生成的圆锥，Ⅲ生成的是圆柱去掉扇形 ABD 生成的半球.设正方形的边长为 a ，则Ⅰ，Ⅱ，Ⅲ 三部分经旋转所得几何体的体积分别为 V Ⅰ，V Ⅱ，V Ⅲ，则 V Ⅰ＝13 πa 3，V Ⅱ＝12 ×43 πa 3－13 πa 3＝13 πa 3，V Ⅲ＝πa 3－12 ×43 πa 3＝13πa 3.所以三部分经旋转所得几何体的体积之比为1∶1∶1.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
柱、锥、台、球的表面积和体积
考纲要求：了解柱、锥、台、球的表面积和体积的计算公式（不要求记忆公式）；会求一些简单几何体的
表面积和体积，体会积分思想在计算表面积和体积的运用．
重难点：了解柱、锥、台、球的表面积和体积的计算公式，会求一些简单几何体的表面积和体积，体会
积分思想在计算表面积和体积的运用．
经典例题：在三棱柱ABC—DEF中，已知AD到面BCFE的距离为h，平行四边形BCFE的面积为S．
求：三棱柱的体积V．
当堂练习：
1．长方体ABCD-A1B1C1D1的AB=3，AD=2，CC1=1，一条绳子从A沿着表面拉到点C1，绳子的最短
长度是（ ）
A．+1 B． C． D．
2．若球的半径为R，则这个球的内接正方体的全面积等于（ ）
A．8R2 B． 9R2 C．10R2 D．12R2
3．边长为5cm的正方形EFGH是圆柱的轴截面, 则从E点沿圆柱的侧面到相对顶点G的最短距离是（ ）
A． 10cm B． 5cm C． 5cm D．cm
4．球的大圆面积扩大为原大圆面积的4倍，则球的表面积扩大成原球面积的（ ）
A．2倍 B． 4倍 C． 8倍 D．16倍
5．三个球的半径之比为1：2：3，那么最大球的表面积是其余两个球的表面积之和的（ ）
A．1倍 B．2倍 C．1倍 D．1倍
6．正方体的全面积是a2,它的顶点都在球面上，这个球的表面积是（ ）
A． B． C． D．
7．两个球的表面积之差为48,它们的大圆周长之和为12,这两个球的半径之差为（ ）
A．4 B． 3 C． 2 D． 1
8．已知正方体的棱长为a，过有公共顶点的三条棱的中点的截面分别截去8个角，则剩余部分的体积是
（ ）
A．a3 B．a3 C．a3 D．a3
9.正方形ABCD的边长为1，E、F分别为BC、CD的中点，沿AE，EF，AF折成一个三棱锥，使B，C，
D三点重合，那么这个三棱锥的体积为（ ）
A． B． C． D．
10.棱锥V-ABC的中截面是A1B1C1，则三棱锥V-A1B1C1与三棱锥A-A1BC的体积之比是（ ）
A．1：2 B． 1：4 C．1：6 D．1：8
11. 两个球的表面积之比是1：16，这两个球的体积之比为（ ）
A．1：32 B．1：24 C．1：64 D． 1：256
12．两个球的体积之比为8：27，那么，这两个球的表面积之比为（ ）
A．2：3 B．4：9 C． D．
13．棱长为a的正方体内有一个球，与这个正方体的12条棱都相切，则这个球的体积应为（ ）
A． 43 B． C． D．
14．半径为R的球的外切圆柱的表面积是______________．
15．E是边长为2的正方形ABCD边AD的中点，将图形沿EB、EC折成三棱锥A-BCE（A，D重合）， 则
此三棱锥的体积为____________．
16.直三棱柱的体积是V，D、E分别在、上，线段DE经过矩形的中心，
则四棱锥C-ABED的体积是________________．
17．一个直角三角形的两条直角边的长分别为3cm和4cm, 将这个直角三角形以斜边为轴旋转一周,所得旋
转体的体积是________________．
18．圆锥的底面半径为5cm, 高为12cm, 当它的内接圆柱的底面半径为何值时, 圆锥的内接圆柱的全面积
有最大值?最大值是多少?
19．A、B、C是球面上三点，已知弦AB=18cm，BC=24cm，AC=30cm，平面ABC与球心O的距离恰好
为球半径的一半，求球的面积．
20．圆锥轴截面为顶角等于1200的等腰三角形, 且过顶点的最大截面面积为8, 求这圆锥的全面积S和体
积V．
21．已知ABCD-A1B1C1D1是棱长为a的正方体， E、F分别为棱AA1与CC1的中点，求四棱锥A1-EBFD1
的体积．
参考答案：
经典例题： 解法一：把三棱柱补成一平行六面体EFDG—BCAH，可看成以s为底，以h为高，则体积
为sh． VABC-DEF= 这就是用补的方法求体积．
解法二：连DB、DC、BF，把三棱柱分割成三个等体积的三棱锥，如D—BEF就是以s为底，高为h
的三棱锥，则VD-BEF= 则VABC-DEF=3 VD-BEF=．
当堂练习：
1.C; 2.A; 3.D; 4.B; 5.C; 6.B; 7.C; 8.C; 9.B; 10.B; 11.C; 12.B; 13.C; 14. 6R2; 15. ; 16. ; 17.
;
18. 如图 ,SAB是圆锥的轴截面, 其中SO=12, OB=5.设圆锥内接圆柱底面半径为O1C=x , 由与
相似, 则
OO1=SO-SO1=12-,则圆柱的全面积S=S侧+2S底=2则当
时,S取到最大值．
19. 解：AB2+BC2=AC2， ABC为直角三角形， ABC的外接圆O1的半径r=15cm，
因圆O1即为平面ABC截球O所得的圆面，因此有R2=（）2+152，
R2=300，S球=4R2=1200（cm2）.
20. 解:设母线长为, 当截面的两条母线互相垂直时, 有最大的截面面积. 此时,
底面半径,高则S全=
21. 解：四棱锥A1-EBFD1的底面是菱形，连接EF，则
，平面ABB1A1，
三棱锥F-EBA1的高是CC1到平面AB1的距离，即棱长a，
S
佳艺幼儿园值班记录表
时间： 年 月 日 带班领导：
值班人员签名 值班情况（来电、来访、接收、偶发事件、巡查监测等情况）
上
午
下
午
晚
上
处理
结果
时间： 年 月 日 带班领导：
值班人员签名 值班情况（来电、来访、接收、偶发事件、巡查监测等情况）
上
午
下
午
晚
上
处理
结果
值班职责：
1.做好值班记录、来电记录、接待群众上级来访，传达有关通知。2.不迟到、不早
退，并做好值班登记手续，无故不来值班或马虎失职，出现事故，追究责任。若遇事不能到位
值班，应事先向学校请假，学校派人顶替。3.发生不安全事故，要保护好现场，报告有关领导或
报警。4.夜间值班，临睡前应巡视校门是否上锁，观察校园四周是否有异常现象。及时制止外人
进入校园干扰、破坏。5.要加强汛期巡查监测，发现有山体滑坡、塌方等地质灾害的险情，应及
时上报。6、此表由值班人员记录，学校收存备查。学校值班电话：2828181、2828183