圆轴扭转时的变形与刚度计算
合集下载
第4章圆轴扭转时的强度与刚度计算
圆轴扭转后横截面保持平面
第一个结论
圆轴扭转时，横截 面保持平面，平面上 各点只能在平面内转 动
圆轴扭转后横截面保持平面
假设平面不是刚性转动， 直径将变成曲线，A端观察 者看到的情形。
圆轴扭转后横截面保持平面
假设平面不是刚性转动， 直径将变成曲线，B端观察 者看到的情形。
圆轴扭转后横截面保持平面
最终结论
圆轴扭转时，横 截面 保持平面，并且 只能发生刚性转动。
圆轴扭转后横截面保持平面
变形协调方程
圆轴扭转时的变形协调方程
若将圆轴用同轴柱面分割成许多半径不等的圆柱，根据上述结论，在dx长度 上，虽然所有圆柱的两端面均转过相同的角度d，但半径不等的圆柱上产生的剪 应变各不相同，半径越小者剪应变越小。
其中P为功率，单位为千瓦（kW）； n为轴的转速，单位为转/分（r/min）。
4.1外加扭力矩、扭矩与 扭矩图
P[马力]
Me
7024 n[r / min]
[N m]
若P为功率，单位为马力 （1马力=735.5 N•m/s ）
n为轴的转速，单位为转/分（r/min）
4.1外加扭力矩、扭矩与 扭矩图
max
M x,max Wp
[ ]
[ ]为许用剪应力；是指圆轴所有横截面
上最大剪应力中的最大者，
钢 [ ] (0.5 ~ 0.6)[ ] 铸铁 [ ] (0.8 ~ 1)[ ]
例题1
已知：P＝7.5kW, n=100r/min,最大剪应力不得超过40MPa,空心圆轴的内外直 径之比 = 0.5。二轴长度相同。
圆轴扭转时横截面上的剪应力表达式
圆轴扭转时横截面上的剪应力表达式
圆轴扭转时横截面上的最大剪应力
杆在扭转时的变形 · 刚度条件
2
πd A实 1749 mm 2 4 2 2 π(76 71 ) A空 577mm 2 4
两轴材料、长度均相同, 故两轴重量比等于两轴的横截面积比，
A2 577 0.329 A1 1749
在最大切应力相等的情况下空心圆轴比实心圆轴轻, 即节省材料.
例题7 两端固定的圆截面杆AB, 在截面C 处受一个扭转力偶矩
Me 的作用, 如图所示.已知杆的抗扭刚度 GIp, 试求杆两端的支反 力偶矩. Me
A a
C
B b
l
解:去掉约束,代之以约束反力偶矩
Mx 0
M eA M eB M e 0
这是一次超静定问题,
Me
A
a
须建立一个补充方程
杆的变形相容条件是 C 截面相对于两固定端 A和B的相对扭转角相等.
'
Mt Ip
M tl GI p
max
• The strengh condition • The rigidity condition
Mt Wp
180
Mp GI p
o
例题5 图示等直杆, 已知直径d = 40mm, a = 400mm, 材料的剪切
弹性模量G = 80GPa，DB =1°. 试求：
（1） AD杆的最大切应力; （2）扭转角 CA 解：画扭矩图 Me D a C a 2Me B 2a 3Me Me +
3Me
A
Tmax= 3Me 计算外力偶矩Me
材料的许用切应力 [ ] = 100MPa, 切变模量为 G = 80GPa, 轴的许可扭角[′ ] = 2/m . 试校核轴的强度和刚度.
πd A实 1749 mm 2 4 2 2 π(76 71 ) A空 577mm 2 4
两轴材料、长度均相同, 故两轴重量比等于两轴的横截面积比，
A2 577 0.329 A1 1749
在最大切应力相等的情况下空心圆轴比实心圆轴轻, 即节省材料.
例题7 两端固定的圆截面杆AB, 在截面C 处受一个扭转力偶矩
Me 的作用, 如图所示.已知杆的抗扭刚度 GIp, 试求杆两端的支反 力偶矩. Me
A a
C
B b
l
解:去掉约束,代之以约束反力偶矩
Mx 0
M eA M eB M e 0
这是一次超静定问题,
Me
A
a
须建立一个补充方程
杆的变形相容条件是 C 截面相对于两固定端 A和B的相对扭转角相等.
'
Mt Ip
M tl GI p
max
• The strengh condition • The rigidity condition
Mt Wp
180
Mp GI p
o
例题5 图示等直杆, 已知直径d = 40mm, a = 400mm, 材料的剪切
弹性模量G = 80GPa，DB =1°. 试求：
（1） AD杆的最大切应力; （2）扭转角 CA 解：画扭矩图 Me D a C a 2Me B 2a 3Me Me +
3Me
A
Tmax= 3Me 计算外力偶矩Me
材料的许用切应力 [ ] = 100MPa, 切变模量为 G = 80GPa, 轴的许可扭角[′ ] = 2/m . 试校核轴的强度和刚度.
18圆轴扭转的强度和刚度计算
T
max
WP
[ ]
此时 T max 作用截面即为轴的危险截面；而对于变 截面圆轴，则要求：
max
T W P
[ ] max
此时，由于圆轴各段的抗扭截面系数不同，最大扭 矩作用截面不一定是危险截面。需要综合考虑扭矩和抗 扭截面系数的大小，判断可产生最大切应力的各横截面。 上面两式称为圆轴扭转强度条件。 11
17
巩固练习
18
巩固练习
【练习1】在例1中，若将该传动轴设计为空心轴，已
＝ 知：
di 0.9 ，试设计圆轴直径，并比较重量。 D
19
巩固练习
20
归纳总结 在在工程实际中，空心轴得到了广泛的应用，这主要是由 扭转切应力的分布规律决定的。 实心圆轴横截面上的扭转切应力分布如图(a)所示，当截面 周边处的切应力达到许用切应力时，圆心附近各点处的切应力 仍很小，这部分材料就没有充分发挥作用。所以，为了合理利 用材料，宜将材料放置在离圆心较远的部位，作成空心轴，此 时切应力分布规律如图(b)所示，其切应力和内力的力臂都将增 大，轴的抗扭能力将大大增强。
WP
D 3
16
d/D
IP 单位：mm4, WP单位：mm3
实例分析
扭转实验结果
4
任务十八 圆轴扭转时的强度和 刚度计算
教学目标
教学目标： （1）掌握基本概念； （ 2）掌握扭转变形时强度和刚度计算方法。 重点： （1）扭转变形时强度条件和刚度条件理解。 难点： （1）强度和刚度的计算方法应用。
扭转极限应力
由此可见，对于受扭 轴，塑性材料失效的标志 是屈服，试件屈服时横截 面上的最大切应力，即为 材料的扭转屈服应力，可 用 s 表示；脆性材料失效 的标志是断裂，试件断裂 时横截面上的最大切应力 即为材料的扭转强度极限， 用来 b 表示。
杆件的刚度计算汇总.
5
第一节
圆轴扭转时的变形及刚度计算
刚度计算的三方面：
① 校核刚度： ② 设计截面尺寸： ③ 计算许可载荷：
max
T max Ip G[ ]
T
max
GI p[ ]
有时，还可依据此条件进行选材。
6
第一节
[例]
圆轴扭转时的变形及刚度计算
图示阶梯圆轴，受力如图。已知该轴大端直径为
有足够的刚度。如果变形过大，将造成梁不能正常工作，进而
引起梁的破坏。如：高精度车床轴；桥梁；变速箱传动轴等。 绕曲线——梁在载荷作用下发生弯曲变形，梁轴线由直线 弯曲成一条光滑连续曲线。 梁曲线上任一点在垂直于梁变形前轴线方向的线位移 称为该点的挠度 。 梁任一横截面绕其中性轴转动的角度称为该截面的转角。
③ 轴上的绝对值最大的扭矩越小越合理，所以，1轮和
2轮应该换位。换位后,轴的扭矩如图所示,此时,轴的最 大直径才为 75mm。 T (kNm) 2.814 x – 4.21
13
第一节
圆轴扭转时的变形及刚度计算
课堂练习
14
第二节
梁的变形及刚度计算
一、弯曲变形的概念
为了确保梁的正常工作，梁除了满足强度条件外，还要求
D=60mm，小端直径为
d=30mm，已知G=80GPa，
1
0
/m 。试求：
1)．校核该轴刚度； 2)．A截面相对于C 截 面的扭转角。
解：1．内力分析：
画扭矩图如图所。
7
第一节
圆轴扭转时的变形及刚度计算
2．变形分析及刚度条件：
3.14 604 1012 I P1 1.27 106 (m 4 ) 32 32 d 4 3.14 304 1012 I P2 0.08 106 (m 4 ) 32 32 180 T1 180 2.5 103 0 1 1 . 4 ( /m) 9 6 GI P1 3.14 80 10 1.27 10 180 T2 180 1.5 103 0 2 1 . 35 ( /m) 9 6 GI P 2 3.14 80 10 0.08 10 故 max 1.4( 0 /m)
第一节
圆轴扭转时的变形及刚度计算
刚度计算的三方面：
① 校核刚度： ② 设计截面尺寸： ③ 计算许可载荷：
max
T max Ip G[ ]
T
max
GI p[ ]
有时，还可依据此条件进行选材。
6
第一节
[例]
圆轴扭转时的变形及刚度计算
图示阶梯圆轴，受力如图。已知该轴大端直径为
有足够的刚度。如果变形过大，将造成梁不能正常工作，进而
引起梁的破坏。如：高精度车床轴；桥梁；变速箱传动轴等。 绕曲线——梁在载荷作用下发生弯曲变形，梁轴线由直线 弯曲成一条光滑连续曲线。 梁曲线上任一点在垂直于梁变形前轴线方向的线位移 称为该点的挠度 。 梁任一横截面绕其中性轴转动的角度称为该截面的转角。
③ 轴上的绝对值最大的扭矩越小越合理，所以，1轮和
2轮应该换位。换位后,轴的扭矩如图所示,此时,轴的最 大直径才为 75mm。 T (kNm) 2.814 x – 4.21
13
第一节
圆轴扭转时的变形及刚度计算
课堂练习
14
第二节
梁的变形及刚度计算
一、弯曲变形的概念
为了确保梁的正常工作，梁除了满足强度条件外，还要求
D=60mm，小端直径为
d=30mm，已知G=80GPa，
1
0
/m 。试求：
1)．校核该轴刚度； 2)．A截面相对于C 截 面的扭转角。
解：1．内力分析：
画扭矩图如图所。
7
第一节
圆轴扭转时的变形及刚度计算
2．变形分析及刚度条件：
3.14 604 1012 I P1 1.27 106 (m 4 ) 32 32 d 4 3.14 304 1012 I P2 0.08 106 (m 4 ) 32 32 180 T1 180 2.5 103 0 1 1 . 4 ( /m) 9 6 GI P1 3.14 80 10 1.27 10 180 T2 180 1.5 103 0 2 1 . 35 ( /m) 9 6 GI P 2 3.14 80 10 0.08 10 故 max 1.4( 0 /m)
11圆轴扭转变形与刚度计算
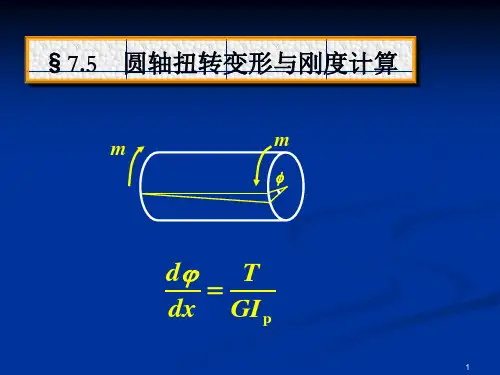
§7.5
圆轴扭转变形与刚度计算
m m
d T dx GI p
1
一、圆轴扭转变形公式
由
m
m
T ( x )dx 满足平面假设的圆轴： GI p ( x ) l Tl T=Const，等截面圆轴： GI p
GIp－抗扭刚度
d T dx GI p
Ti l i Ti，Ipi在各段内为常数的轴： i 1 GI pi
6
2. 用截面法求 各段内的扭矩
mB+T1=0
T1 350N m
mB+ mC+ T2=0 T2 700N m
-mD+ T3=0 T3 446N m 3. 作扭矩图
7
4. 确定最大扭矩
T max T2 700N m
5. 强度设计
max
d0
T
max
m d2 x l
10
d1
解：设距左端为 x 的任 意横截面的直径为 d(x) ， 按比例关系可得 d2
d1 d 2 x d d2 1 d2 l
x
l
m
d1
此横截面的极惯性矩为
d1 d 2 x Ip 1 32 32 d2 l
d
4
d2
or
T 180 [ ] GI p max
/ m
等截面圆轴扭转的刚度条件为：
Tmax [ ] (rad/m) GI p
or
Tmax 180 [ ] GI p
/ m
4
【例题1】
传动轴图所示。主动轮A输入功率 PA=36kw ， 从 动 轮 B 、 C 、 D 输 出 功 率 分 别 为 PB=PC=11kW ， PD=14kW ，轴的转速为 n=300r/min ， 许用切应力为[]=50MPa，切变模量为G=80GPa，单 位长度许用扭转角为[]=0.5()/m。试确定： 实心圆截面轴的直径d0；
圆轴扭转变形与刚度计算
m m
d T dx GI p
1
一、圆轴扭转变形公式
由
m
m
T ( x )dx 满足平面假设的圆轴： GI p ( x ) l Tl T=Const，等截面圆轴： GI p
GIp－抗扭刚度
d T dx GI p
Ti l i Ti，Ipi在各段内为常数的轴： i 1 GI pi
6
2. 用截面法求 各段内的扭矩
mB+T1=0
T1 350N m
mB+ mC+ T2=0 T2 700N m
-mD+ T3=0 T3 446N m 3. 作扭矩图
7
4. 确定最大扭矩
T max T2 700N m
5. 强度设计
max
d0
T
max
m d2 x l
10
d1
解：设距左端为 x 的任 意横截面的直径为 d(x) ， 按比例关系可得 d2
d1 d 2 x d d2 1 d2 l
x
l
m
d1
此横截面的极惯性矩为
d1 d 2 x Ip 1 32 32 d2 l
d
4
d2
or
T 180 [ ] GI p max
/ m
等截面圆轴扭转的刚度条件为：
Tmax [ ] (rad/m) GI p
or
Tmax 180 [ ] GI p
/ m
4
【例题1】
传动轴图所示。主动轮A输入功率 PA=36kw ， 从 动 轮 B 、 C 、 D 输 出 功 率 分 别 为 PB=PC=11kW ， PD=14kW ，轴的转速为 n=300r/min ， 许用切应力为[]=50MPa，切变模量为G=80GPa，单 位长度许用扭转角为[]=0.5()/m。试确定： 实心圆截面轴的直径d0；
材料力学-第4章圆轴扭转时的强度与刚度计算
B
I
C
A
II
D
III
I
II
III
M
x
0
确定各段圆轴内的扭 矩。
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
3 ． 建立 Mx － x 坐 标系，画出扭矩图 建 立 Mx － x 坐 标 系，其中x轴平行于 圆轴的轴线，Mx轴垂 直于圆轴的轴线。将 所求得的各段的扭矩 值，标在 Mx － x 坐标 系中，得到相应的点 ，过这些点作x轴的 平行线，即得到所需 要的扭矩图。
P M e 9549 [N m] n
其中P为功率，单位为千瓦（kW）；n为轴的转速，单位为转/ 分（r/min）。 如果功率P的单位用马力（1马力=735.5 N•m/s），则
P[马力] M e 7024 [N m] n[r / min]
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴 外加扭力矩、扭矩与扭矩图 剪应力互等定理 剪切胡克定律
圆轴扭转时横截面上的剪应力分析 与强度设计 圆杆扭转时的变形及刚度条件 结论与讨论
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
第4章 圆轴扭转时的强度与刚度计算
绘出扭矩图：
第4章 圆轴扭转时的强度与刚度计算
B C
I
外加扭力矩、扭矩与扭矩图 A III D II
I 扭矩Mn-图
II
III
159.2
（+）
（-）
63.7 159.2
M n,max 159.2( N m)
（在CA段和AD段）
I
C
A
II
D
III
I
II
III
M
x
0
确定各段圆轴内的扭 矩。
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
3 ． 建立 Mx － x 坐 标系，画出扭矩图 建 立 Mx － x 坐 标 系，其中x轴平行于 圆轴的轴线，Mx轴垂 直于圆轴的轴线。将 所求得的各段的扭矩 值，标在 Mx － x 坐标 系中，得到相应的点 ，过这些点作x轴的 平行线，即得到所需 要的扭矩图。
P M e 9549 [N m] n
其中P为功率，单位为千瓦（kW）；n为轴的转速，单位为转/ 分（r/min）。 如果功率P的单位用马力（1马力=735.5 N•m/s），则
P[马力] M e 7024 [N m] n[r / min]
第4章 圆轴扭转时的强度与刚度计算
外加扭力矩、扭矩与扭矩图
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴 外加扭力矩、扭矩与扭矩图 剪应力互等定理 剪切胡克定律
圆轴扭转时横截面上的剪应力分析 与强度设计 圆杆扭转时的变形及刚度条件 结论与讨论
第4章 圆轴扭转时的强度与刚度计算
工程中承受扭转的圆轴
第4章 圆轴扭转时的强度与刚度计算
绘出扭矩图：
第4章 圆轴扭转时的强度与刚度计算
B C
I
外加扭力矩、扭矩与扭矩图 A III D II
I 扭矩Mn-图
II
III
159.2
（+）
（-）
63.7 159.2
M n,max 159.2( N m)
（在CA段和AD段）
《工程力学：第七章+圆轴扭转时的应力变形分析与强度和刚度设计》
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
背 景
材
料
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计
背 景
材
料
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计 一、扭转的概念 复习 Me
mA
阻抗力 偶
主动力 偶
me
受力特点：杆两端作用着大小相等、方向相反的力偶，且力 偶作用面垂直于杆的轴线。 变形特点：杆任意两截面绕轴线发生相对转动。 主要发生扭转变形的杆——轴。
Mx 16M x 16 1.5kN m 103 max＝ ＝ 3 ＝ ＝50.9MPa 3 4 -3 4 WP πD 1 π 90mm 10 1 0.9传动轴的强度是安全的。
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计 2．确定实心轴的直径 根据实心轴与空心轴具有同样数值的最大剪应力的要求， 实心轴横截面上的最大剪应力也必须等于 50.9MPa 。若设实 心轴直径为d1，则有
b b
工程力学 第7章 圆轴扭转时的应力变形分析以及强度和刚度设计 T 一、 扭转强度计算 变截面圆轴: max W [ ] 1、强度条件： p
max
max
对脆性材料 [ ] 对韧性材料 [ ]
b
nb
工程力学第8章 变形及刚度计算
第8章 变形及刚度计算
结构构件在满足强度要求条件下，若其变形过大， 会影响正常使用。本章将学习杆件的变 形及刚度计算。
1
8.1 轴向拉压杆的变形
杆件在发生轴向拉伸或轴向压缩变形时，其纵向尺 寸和横向尺寸一般都会发生改变，现分别予以讨论。 8.1.1 轴向变形 图8.1所示一等直圆杆，变形前原长为l，横向直径 为d；变形后长度为l′，横向直径为d′，则称
8.8 题8.8图所示一直径为d的圆轴，长度为l，A端 固定，B端自由，在长度方向受分布力偶m 作用发生扭 转变形。已知材料的切变模量为G，试求B端的转角。
56
8.9 某传动轴，转速 n=150 r/min，传递的功率 P =60 kW，材料的切变模量为 G =80GPa，轴的单位长度 许用扭转角［θ］=0.5（°）/m，试设计轴的直径。
30
例 8.9 简支梁受力如图 8.11所示
31
8.4 简单超静定问题
8.4.1 超静定问题的概念 前面几章所研究的杆或杆系结构，其支座反力和内 力仅仅用静力平衡条件即可全部求解出来，这类问题称 为静定问题（staticallydeterminateproblem）。例如，图 8.12所示各结构皆为静定问题。在工程实际中，有时为 了提高强度或控制位移，常常采取增加约束的方式，使 静定问题变成了超静定问题或静不定问题 （staticallyindeterminateproblem）。超静定问题的特点 是，独立未知力的数目大于有效静力平衡方程式的数目， 仅仅利用静力平衡条件不能求出全部的支座反力和内力。
52
8.5 高为l的圆截面锥形杆直立于地面上，如题8.5图 所示。已知材料的重度γ和弹性模量E，试求杆在自重作 用下的轴向变形Δl。
53
54
结构构件在满足强度要求条件下，若其变形过大， 会影响正常使用。本章将学习杆件的变 形及刚度计算。
1
8.1 轴向拉压杆的变形
杆件在发生轴向拉伸或轴向压缩变形时，其纵向尺 寸和横向尺寸一般都会发生改变，现分别予以讨论。 8.1.1 轴向变形 图8.1所示一等直圆杆，变形前原长为l，横向直径 为d；变形后长度为l′，横向直径为d′，则称
8.8 题8.8图所示一直径为d的圆轴，长度为l，A端 固定，B端自由，在长度方向受分布力偶m 作用发生扭 转变形。已知材料的切变模量为G，试求B端的转角。
56
8.9 某传动轴，转速 n=150 r/min，传递的功率 P =60 kW，材料的切变模量为 G =80GPa，轴的单位长度 许用扭转角［θ］=0.5（°）/m，试设计轴的直径。
30
例 8.9 简支梁受力如图 8.11所示
31
8.4 简单超静定问题
8.4.1 超静定问题的概念 前面几章所研究的杆或杆系结构，其支座反力和内 力仅仅用静力平衡条件即可全部求解出来，这类问题称 为静定问题（staticallydeterminateproblem）。例如，图 8.12所示各结构皆为静定问题。在工程实际中，有时为 了提高强度或控制位移，常常采取增加约束的方式，使 静定问题变成了超静定问题或静不定问题 （staticallyindeterminateproblem）。超静定问题的特点 是，独立未知力的数目大于有效静力平衡方程式的数目， 仅仅利用静力平衡条件不能求出全部的支座反力和内力。
52
8.5 高为l的圆截面锥形杆直立于地面上，如题8.5图 所示。已知材料的重度γ和弹性模量E，试求杆在自重作 用下的轴向变形Δl。
53
54
09圆轴扭转时的变形、应变能
位置是?（其中ab∥AB∥ce）
B
b
e
A
a
c
d
ae. 因各条纵向纤维的应变相等，所以上边纤维长，伸长量也大。
2、图示直杆，其抗拉刚度为EA，试 求杆件的轴向变形△L，B点的位移
δB和C点的位移δC
A L
F
F
δB
=
∆LAB
=
FL EA
B
C
L
δC
=
δB
=
FL EA
3、塑性材料冷作硬化后，材料的力学性能 发生了变化。试判断以下结论哪一个是正确 的： （A）屈服应力提高，弹性模量降低； （B）屈服应力提高，塑性降低； （C）屈服应力不变，弹性模量不变； （D）屈服应力不变，塑性不变。 正确答案是（ B ）
lAB
A
lAC
ϕCA C
纯剪切应力状态下的应变能密度( τ ≤ τ p )
y
τ
dz γ dτ'
aτ
τ
dy
τp
O
b
τ' c
x
z
dx
O
γ
dW = 1 (τ d y d z)(γ d x)= 1τγ (d x d y d z)
vε
=
dVε dV2 = dWdV=1τγ2
(d
x
d
y
d
z
2
)
=
1
τγ
dxd ydz 2
例题4-4
例题4-5
传动轴的转速为n=500r/min，主动轮A 输入功率 P1=400kW，从动轮C，B 分别输出功率P2=160kW，P3=240kW。 已知[τ]=70MPa，[φˊ]=1°/m，G=80GPa。
B
b
e
A
a
c
d
ae. 因各条纵向纤维的应变相等，所以上边纤维长，伸长量也大。
2、图示直杆，其抗拉刚度为EA，试 求杆件的轴向变形△L，B点的位移
δB和C点的位移δC
A L
F
F
δB
=
∆LAB
=
FL EA
B
C
L
δC
=
δB
=
FL EA
3、塑性材料冷作硬化后，材料的力学性能 发生了变化。试判断以下结论哪一个是正确 的： （A）屈服应力提高，弹性模量降低； （B）屈服应力提高，塑性降低； （C）屈服应力不变，弹性模量不变； （D）屈服应力不变，塑性不变。 正确答案是（ B ）
lAB
A
lAC
ϕCA C
纯剪切应力状态下的应变能密度( τ ≤ τ p )
y
τ
dz γ dτ'
aτ
τ
dy
τp
O
b
τ' c
x
z
dx
O
γ
dW = 1 (τ d y d z)(γ d x)= 1τγ (d x d y d z)
vε
=
dVε dV2 = dWdV=1τγ2
(d
x
d
y
d
z
2
)
=
1
τγ
dxd ydz 2
例题4-4
例题4-5
传动轴的转速为n=500r/min，主动轮A 输入功率 P1=400kW，从动轮C，B 分别输出功率P2=160kW，P3=240kW。 已知[τ]=70MPa，[φˊ]=1°/m，G=80GPa。
圆轴扭转时的变形和刚度计算
=6.44×10-4m4
轴的最大切应力为 τmax=Tma /Wp=2.86×103N·m/1.43×104m
=20×106Pa=20MPa<［τ］=60MPa 可见强度满足要求。
4） 刚度校核。轴的单位长度最大扭转角为 θmax=Tmax/GIp×180/π
=2.86×103N·m/8.0×1010Pa×6.44×106m4×180/3.14 =0.318°/m＜［θ］=1.1°/m 可见刚度也满足要求。材Βιβλιοθήκη 力学圆轴扭转时的变形和刚度计算
1.1圆轴扭转时的变形 圆轴扭转时的变形通常是用两个横截面绕轴线转动的相对扭转角 φ来度量的。在上节中已得到式（3-5），即 dφ/dx=T/GIp
式中：dφ——相距为dx的两横截面间的扭转角。 上式也可写成 dφ=T/GIpdx
因此，相距为l的两横截面间的扭转角为 φ=∫ l dφ=∫(T l /GIp)dx （3-12 若该段轴为同一材料制成的等直圆轴，并且各横截面上扭矩T的 数值相同，则上式中的T、G、Ip均为常量，积分后得
得 D≥（16T/π［τ］）1/3
=（16×39.6×103/π×88.2×106）1/3m
=0.131m=131mm
2） 按刚度条件设计轴的直径。由刚度条件式（3-16），即 θmax=Tmax/GIp×180/π
=32×180Tmax/Gπ2D4≤ ［θ 得
D=（32×180T/Gπ2［θ］）1/4 =（32×180×39.6×103/79×109×π2×0.5）1/4m =0.156m=156mm 故取D＝160mm，显然轴能同时满足强度条件和刚度条件。
【例3-6】一钢制传动圆轴。材料的切变模量G=79×103MPa， 许用切应力［τ］=88.2MPa，单位长度许用扭转角［θ］ =0.5°/m，承受的扭矩为T=39.6kN·m。试根据强度条件和 刚度条件设计圆轴的直径D。
轴的最大切应力为 τmax=Tma /Wp=2.86×103N·m/1.43×104m
=20×106Pa=20MPa<［τ］=60MPa 可见强度满足要求。
4） 刚度校核。轴的单位长度最大扭转角为 θmax=Tmax/GIp×180/π
=2.86×103N·m/8.0×1010Pa×6.44×106m4×180/3.14 =0.318°/m＜［θ］=1.1°/m 可见刚度也满足要求。材Βιβλιοθήκη 力学圆轴扭转时的变形和刚度计算
1.1圆轴扭转时的变形 圆轴扭转时的变形通常是用两个横截面绕轴线转动的相对扭转角 φ来度量的。在上节中已得到式（3-5），即 dφ/dx=T/GIp
式中：dφ——相距为dx的两横截面间的扭转角。 上式也可写成 dφ=T/GIpdx
因此，相距为l的两横截面间的扭转角为 φ=∫ l dφ=∫(T l /GIp)dx （3-12 若该段轴为同一材料制成的等直圆轴，并且各横截面上扭矩T的 数值相同，则上式中的T、G、Ip均为常量，积分后得
得 D≥（16T/π［τ］）1/3
=（16×39.6×103/π×88.2×106）1/3m
=0.131m=131mm
2） 按刚度条件设计轴的直径。由刚度条件式（3-16），即 θmax=Tmax/GIp×180/π
=32×180Tmax/Gπ2D4≤ ［θ 得
D=（32×180T/Gπ2［θ］）1/4 =（32×180×39.6×103/79×109×π2×0.5）1/4m =0.156m=156mm 故取D＝160mm，显然轴能同时满足强度条件和刚度条件。
【例3-6】一钢制传动圆轴。材料的切变模量G=79×103MPa， 许用切应力［τ］=88.2MPa，单位长度许用扭转角［θ］ =0.5°/m，承受的扭矩为T=39.6kN·m。试根据强度条件和 刚度条件设计圆轴的直径D。
扭转刚度
ቤተ መጻሕፍቲ ባይዱ
T
D
D 2
FD 扭矩： 扭矩： T = 2
簧丝横截面上的应力： 簧丝横截面上的应力：
FS
1、剪力 F 引起的 τ1 近似 、 S 认为是均匀分布 2、扭矩 T 引起的 τ 2 按照 、 圆轴扭转计算
τ1
τ 2max
簧丝横截面上的应力： 簧丝横截面上的应力：
τ1 =
π
F d2
4F = πd 2
τ1
A d
簧丝横截面上的应力： 簧丝横截面上的应力：
τ max
8FD d = +1 A 3 πd 2D
τ1
τ 2max
A
对于簧丝的直径 d 远小 于弹簧的中径D的情况 的情况， 于弹簧的中径 的情况，
d
τ max
8FD ≅ πd 3
在考虑簧丝的曲率和
τ1 分布不均匀时： 分布不均匀时：
二、圆轴扭转刚度的计算 ϕ ′= ϕ 单位长度扭转角
l
T 显然 ϕ′ = GIP
圆轴扭转刚度条件为： 圆轴扭转刚度条件为：
ϕ′ ≤ [ϕ′]
单位长度扭转角的许可值
[ϕ′] ( ) m
0
圆轴扭转刚度条件为： 圆轴扭转刚度条件为：
T 180 GI × π ≤ [ϕ′] P m ax
Tmax =155 N ⋅ m
轴的强度条件为： 轴的强度条件为：
Tmax 16Tmax = = ≤ [τ ] 3 πD W t
16Tmax
MⅡ
T(N ⋅ m)
MⅢ
MⅣ
τ max
D≥3
π [τ ]
=3
16×155 π × 40×106
39.3
T
D
D 2
FD 扭矩： 扭矩： T = 2
簧丝横截面上的应力： 簧丝横截面上的应力：
FS
1、剪力 F 引起的 τ1 近似 、 S 认为是均匀分布 2、扭矩 T 引起的 τ 2 按照 、 圆轴扭转计算
τ1
τ 2max
簧丝横截面上的应力： 簧丝横截面上的应力：
τ1 =
π
F d2
4F = πd 2
τ1
A d
簧丝横截面上的应力： 簧丝横截面上的应力：
τ max
8FD d = +1 A 3 πd 2D
τ1
τ 2max
A
对于簧丝的直径 d 远小 于弹簧的中径D的情况 的情况， 于弹簧的中径 的情况，
d
τ max
8FD ≅ πd 3
在考虑簧丝的曲率和
τ1 分布不均匀时： 分布不均匀时：
二、圆轴扭转刚度的计算 ϕ ′= ϕ 单位长度扭转角
l
T 显然 ϕ′ = GIP
圆轴扭转刚度条件为： 圆轴扭转刚度条件为：
ϕ′ ≤ [ϕ′]
单位长度扭转角的许可值
[ϕ′] ( ) m
0
圆轴扭转刚度条件为： 圆轴扭转刚度条件为：
T 180 GI × π ≤ [ϕ′] P m ax
Tmax =155 N ⋅ m
轴的强度条件为： 轴的强度条件为：
Tmax 16Tmax = = ≤ [τ ] 3 πD W t
16Tmax
MⅡ
T(N ⋅ m)
MⅢ
MⅣ
τ max
D≥3
π [τ ]
=3
16×155 π × 40×106
39.3
圆轴扭转时的强度和刚度计算
A1 / A2 = [π (D 2 − d 2 ) / 4] /(πD 2 2 / 4) = (90 2 − 852 ) / 612 = 0.235
传动轴满足强度要求。 2)刚度校核 传动轴的极惯性矩为
I P = 0.1D 4 (1 − a 4 ) = {0.1 × 90 4 [1 − (85 / 90 ) 4 ]}mm 4 = 134 × 10 4 mm 4 θ max = 180 M n /(πGI P )
= (180 × 1500 × 10 3 / 80 × 10 3 × 134 × 10 4 π ) × 10 3 °/m
= 0.8°/m ＜ [θ ]
传动轴满足刚度要求。 (2)计算实心轴的直径
1)按强度条件设计(设直径为D1)。若实心轴与空心轴强 度相同，当材料相同时，它们的抗扭截面系数应相等，即
W n = πD 13 / 16 = πD 3 (1 Βιβλιοθήκη a 4 ) / 16由此得
D 1 = D3 1 − a 4 = [90 × 3 1 − (85 / 90) 4 ]mm = 53mm
根据扭转刚度条件，可以解决三类问题， 即校核刚度、 设计截面和确定许可载荷 。
例6-5 汽车传动轴AB由45号无缝钢管制成，外径D=90mm,
[ 内径d=85mm，许用切应力 [τ ]=60MPa，θ ] =1.0°/m，工作时最
大力偶矩M =1500N·m，G =80GPa。 (1)试校核其强度及刚度。 (2)若将AB轴改为实心轴，试求其直径。 (3)比较空心轴和实心轴的重量。 解 (1)试校核其强度及刚度。 1) 强度校核 传动轴各截面上的扭矩均为
θ max = 180M n /(πGI P ) ≤ [θ ]
(6-13)
圆轴扭转时的变形、刚度计算
功率分别为 剪切弹性模
N A =10 kW，N B G＝80GPa，若
=12 kW，N D=18
＝50MPa，
kW。材料的
＝0.3º/m，
试按强度条件和刚度条件设计此轴的直径。
解（1）求外力偶矩
MA MB
MC
d
M M
A B
9549 9549
NA
n NB
n
9549 10 318(N m) 300
工程力学
圆轴扭转时的变形、刚度计算
一、变形：（相对扭转角）
MT
GIP
d
dx
d
dx
MT GIP
d MT dx
GIP
MT dx L GIP —— T T (x) MT L
GIP —— T=常量
单位：弧度（rad）。 GIP——抗扭刚度。
MT L
GIP
——T=常量,且分段。
注意： “MT” 代入其“＋、－”号
AB
MT 3 M D 573（N·m)
(Nm) MT
d
MC
MD
(a)
C
D
573 N∙m
x
MT max 700N m
318 N∙m
(b)
（3）按强度条件设计轴的直径：由强度条件 700N∙m
max
MT ,max Wp
[ ]
Wp
d 3
16
得
d 3 16M n max
16 700103 3
9549 12 382(N m) 300
A
B
C
MC
9549
NC n
9549 40 300
1273(N m)
MD
第5节 圆轴扭转时的变形和刚度计算
第六章 圆轴的扭转
第五节 圆轴扭转时的变形和刚度计算
一、扭转变形 扭转角：圆轴扭转时，两横截 面相对转过的角度称为这两截 面的相对扭转角。 T d dx l l GI P
A M BO
M
若在圆轴的l长度内，T、G、IP 均为常数， Tl GI P 则圆轴两端截面的相对扭转角为：
A空 A实 4
(D d )
2 2
4
45
2
1245 0 . 61 2025
可见空心圆轴所用材料只占实心轴所用材料 的61%，节约了材料。
T2 M
B
A C D
M
468Nm
468 1168 700 N m
3-3截面的扭矩
T3 M
C
350 N m
绘出的扭矩图如图所示。显然AC段扭矩最大， 由于是等截面圆轴，故危险截面在AC段内。
第六章 圆轴的扭转
3） 强度校核
max
T 700 16 Pa 3 9 WP 45 10
第六章 圆轴的扭转
例6-3 传动轴如图所示，已知轴的直径d=45mm， 转速n =300r/min。主动轮A输入的功率PA=36.7KW； 从动轮B、C、D输出的功率分别为PB=14.7KW，PC= PD=11KW。轴材料的剪切弹性模量G=80GPa，许用切 应力[ ]=40MPa，单位长度的许用扭转角[ ]=1.5/m， 试校核轴的强度和刚度。
T 700 16 38 . 4 MPa 3 4 WP D (1 )
700 16
4 6
3
(1 0 . 7 ) 38 . 4 10
m 0 . 049 m 49 mm
第五节 圆轴扭转时的变形和刚度计算
一、扭转变形 扭转角：圆轴扭转时，两横截 面相对转过的角度称为这两截 面的相对扭转角。 T d dx l l GI P
A M BO
M
若在圆轴的l长度内，T、G、IP 均为常数， Tl GI P 则圆轴两端截面的相对扭转角为：
A空 A实 4
(D d )
2 2
4
45
2
1245 0 . 61 2025
可见空心圆轴所用材料只占实心轴所用材料 的61%，节约了材料。
T2 M
B
A C D
M
468Nm
468 1168 700 N m
3-3截面的扭矩
T3 M
C
350 N m
绘出的扭矩图如图所示。显然AC段扭矩最大， 由于是等截面圆轴，故危险截面在AC段内。
第六章 圆轴的扭转
3） 强度校核
max
T 700 16 Pa 3 9 WP 45 10
第六章 圆轴的扭转
例6-3 传动轴如图所示，已知轴的直径d=45mm， 转速n =300r/min。主动轮A输入的功率PA=36.7KW； 从动轮B、C、D输出的功率分别为PB=14.7KW，PC= PD=11KW。轴材料的剪切弹性模量G=80GPa，许用切 应力[ ]=40MPa，单位长度的许用扭转角[ ]=1.5/m， 试校核轴的强度和刚度。
T 700 16 38 . 4 MPa 3 4 WP D (1 )
700 16
4 6
3
(1 0 . 7 ) 38 . 4 10
m 0 . 049 m 49 mm
圆轴扭转时的强度与刚度计算材料力学
•
度条件为
max
Mn Wp
maxG MnIp •180
返回 下一张 上一张 小结
精品课件！
精品课件！
• （五）用强度，刚度条件解决实际部题的步骤
•
1）求出轴上外力偶矩；
•
2）计算扭矩和作出扭矩图；
•
3）分析危险截面；
•
4）列出危险截面的强度、刚度条件并进行计算。
返回 下一张 上一张 小结
返回 下一张 上一张 小结
• 二 剪应力计算：
• 1 几何关系： • • 2 物理关系：
P G
• • 3 静力关系：
Mnl d
G Ip
Mn d GIp d
• 扭转剪应力公式：
p
M n Ip
max
Mn Wp
返回 下一张 上一张 小结
•三
• •
截面极惯性矩 ；抗扭截面模量
ax
•
故求得直径为
4010
D3
16Mnmax3
1
6
628.467
0 .03 m 332 .2 3 mm
返回 下一张 上一张 小结
• （4）由刚度条件，得
maxM G nm pIax180G M nm D a4x 18 G n m 2a•x 18038 2 0 216 80 . 46 7 21 180
m ax0 .5 WM Pn 0 .6
0 .8 1 .0
• 2 强度计算的三个方面：
•
a 强度校核
•
b 截面选择
•
c 许可荷载确定
返回 下一张 上一张 小结
• 例1 如图为一钢圆轴，两端受外力偶m的作用，已知m=2.5
• KN.m,直径d=60m，许用应力为60MPa。试校核该轴的强度。
材料力学课件：第3章 圆轴扭转时的应力变形分析与强度刚度计算计算
韧性材料:不耐剪,最大剪应力所处截面是”最短木板”! 破坏方式是被剪断!
脆性材料:不耐拉,最大拉应力所处截面是”最短木板”! 破坏方式是被拉断!
承受扭转时圆轴的强度设计 与刚度设计
扭转强度设计
承受扭转时圆轴的强度设计 与刚度设计
扭转强度设计
与拉伸强度设计相类似，扭转强度设计时，首先需要根 据扭矩图和横截面的尺寸判断可能的危险截面；然后根据 危险截面上的应力分布确定危险点（即最大剪应力作用 点）；最后利用试验结果直接建立扭转时的强度设计准则。
承受扭转时圆轴的强度设计 与刚度设计
扭转实验与扭转破坏现象
韧性材料与脆性材料扭 转破坏时，其试样断口有着 明显的区别。韧性材料试样 最后沿横截面剪断，断口比 较光滑、平整。
铸铁试样扭转破坏时沿 45°螺旋面断开，断口呈细 小颗粒状。
经济学术语中的“木桶效应”，是说对于一个沿口 不齐的木桶而言，它盛水的多少并不在于木桶上那 块最长的木板，而在于木桶上最短的那块木板。
已知：钢制空心圆轴的外直径D＝100 mm，内直径d＝50 mm。若要求轴在2 m长度内的最大相对扭转角不超过1.5()，材 料的切变模量G＝80.4 GPa。
试： 1． 求该轴所能承受的最大扭矩； 2． 确定此时轴内最大剪应力。
解： 1．确定轴所能承受的最大扭矩 根据刚度设计准则，有
承受扭转时圆轴的强度设计 与刚度设计
＝
max
Mx WP
＝16M x πd13
＝16
1.5kN πd13
m
103
＝50.9
106
Pa
据此，实心轴的直径
d1＝3
16 1.5kN m 103＝53.1103 m＝53.1mm π 50.9 106 Pa
脆性材料:不耐拉,最大拉应力所处截面是”最短木板”! 破坏方式是被拉断!
承受扭转时圆轴的强度设计 与刚度设计
扭转强度设计
承受扭转时圆轴的强度设计 与刚度设计
扭转强度设计
与拉伸强度设计相类似，扭转强度设计时，首先需要根 据扭矩图和横截面的尺寸判断可能的危险截面；然后根据 危险截面上的应力分布确定危险点（即最大剪应力作用 点）；最后利用试验结果直接建立扭转时的强度设计准则。
承受扭转时圆轴的强度设计 与刚度设计
扭转实验与扭转破坏现象
韧性材料与脆性材料扭 转破坏时，其试样断口有着 明显的区别。韧性材料试样 最后沿横截面剪断，断口比 较光滑、平整。
铸铁试样扭转破坏时沿 45°螺旋面断开，断口呈细 小颗粒状。
经济学术语中的“木桶效应”，是说对于一个沿口 不齐的木桶而言，它盛水的多少并不在于木桶上那 块最长的木板，而在于木桶上最短的那块木板。
已知：钢制空心圆轴的外直径D＝100 mm，内直径d＝50 mm。若要求轴在2 m长度内的最大相对扭转角不超过1.5()，材 料的切变模量G＝80.4 GPa。
试： 1． 求该轴所能承受的最大扭矩； 2． 确定此时轴内最大剪应力。
解： 1．确定轴所能承受的最大扭矩 根据刚度设计准则，有
承受扭转时圆轴的强度设计 与刚度设计
＝
max
Mx WP
＝16M x πd13
＝16
1.5kN πd13
m
103
＝50.9
106
Pa
据此，实心轴的直径
d1＝3
16 1.5kN m 103＝53.1103 m＝53.1mm π 50.9 106 Pa
圆轴扭转时的变形与刚度计算
圆轴扭转时的变形与刚度计算圆轴扭转时的变形与刚度计算是机械工程中的一项重要内容。
圆轴扭转是指轴材受到扭矩作用产生的变形现象。
在圆轴扭转中，轴材会经历弹性变形和塑性变形。
弹性变形是指轴材在扭矩作用下恢复原状的变形，而塑性变形则是指超过轴材弹性限度后产生的永久变形。
圆轴扭转可通过弹性力学原理进行分析。
根据胡克定律，弹性体的应力与应变之间有线性关系。
对圆轴来说，变形主要体现为轴材的剪切变形。
剪切形变角度φ与应力τ之间的关系为：τ=G*φ其中，G是剪切模量，表示材料抵抗剪切变形的能力。
φ是单位长度的圆周上小弧δs扭转对应的形变角。
通过积分可得到实际的扭转角θ与应力之间的关系：τ=G*θ/L其中，L是轴材的长度。
对于圆轴来说，扭转力矩T与应力分布之间的关系为：T=τ*A其中，A是轴材的横截面积。
将τ带入等式可得到扭转角与扭转力矩之间的关系：T=G*θ*A/L从上述公式可知，轴材扭转角度与扭转力矩之间存在一线性关系，即扭转刚度k。
k=G*A/L通过上述公式，可以得到轴材的扭转刚度。
扭转刚度越大，则轴材对于扭转力矩的抵抗能力越强。
此外，圆轴扭转时的变形也与材料的断裂强度有关。
当扭转力矩超过材料的断裂强度时，轴材会发生塑性变形，产生永久变形。
在实际应用中，通常会根据所需要的刚度和工作条件来选择合适的轴材及其横截面积。
在计算中需要考虑到轴材的材料特性、几何形状和所受的载荷等因素。
此外，还可以通过模拟实验或数值计算的方法对扭转变形和刚度进行验证和评估。
总之，圆轴扭转时的变形与刚度计算是机械工程中的一项重要内容。
通过弹性力学原理，可以分析轴材在扭转力矩作用下的变形情况，并计算出轴材的扭转刚度。
这对于轴类零件的设计和工程应用具有重要意义。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§6-1 圆轴扭转时的应力和强度计算
目的要求：掌握扭转横截面上的应力分 布规律和强度条件的应用。
教学重点：强度条件及其应用。 教学难点：切应力互等定理和剪切胡克
定律。
延安大学西安创新学院建筑工程系
一、 切应力互等定理和剪切胡克定律 １、 切应力互等定理 相互垂直两个平面上的切应力必然成 对存 在，且大小相等、方向都垂直指向 或背离两平面的交线。
本章结束
延安大学西安创新学院建筑工程系
为研究对象， 受力图如图（c) 由（c）图可得：T1- MB =0 所以 T1=636.6N.m 2、用一截面从2-2处将轴切开，取右部分为研
究对象，受力图如图（d) 由（d）图可得：T2+MC=0 所以 T2= -954.9N.m 3、作扭矩图 如图(b)
延安大学西安创新学院建筑工程系
延安大学西安创新学院建筑工程系
解：1、求外力偶矩
2、求各段的扭矩 T1=M1=1591.7N.m T2=M1-M2=3183.3N.m
延安大学西安创新学院建筑工程系
4、设计直径 由
延安大学西安创新学院建筑工程系
5、按刚度条件设计D
由强度计算和刚度计算可知 D≥69.4mm
延安大学西安创新学院建筑工程系
第6章 圆轴的扭转
延安大学西安创新学院建筑工程系
圆轴的扭转 扭矩与扭矩图 圆轴扭转时的应力和强度计算 圆轴扭转时的变形与刚度计算
延安大学西安创新学院建筑工程系
圆轴的扭转 扭矩与扭矩图 目的要求：掌握圆轴扭转内力图的绘制。 教学重点：扭矩图的绘制。 教学难点：指定截面扭矩的计算。
延安大学西安创新学院建筑工程系
２、 横截面上任一点的切应力计算公式
其中：T---截面上的扭矩 ρ---要求应力的点到圆心O点的距离
延安大学西安创新学院建筑工程系
３、 横截面上最大切应力发生在周边上， 计算公式为
延安大学西安创新学院建筑工程系
4、实心和空心圆截的惯性矩Ip和抗扭截 面系数Wp
转变形。
3、圆轴扭转的变形特点：各横截面绕杆
轴线发生相对错动。
轴：以扭转变形为主的杆件称为轴
延安大学西安创新学院建筑工程系
4、实例
延安大学西安创新学院建筑工程系
发生扭转变形的水轮机轴
延安大学西安创新学院建筑工程系
二、 扭矩与扭矩图
１、 外力偶矩的计算 已知轴传递的功率，轴的转速，力
偶矩的计算公式为：
其中： Nk---功率（kW)
Me---外力偶矩(N.m)
n---轴的转速r/min)
延安大学西安创新学院建筑工程系
２、 扭矩：
（１）截面法分析扭转的内力——扭矩 (T)
当杆件受到外力偶矩作用发生扭转变形 时其横截面上的内力偶矩。
（用T表示；单位：N.m或kN.m)
教学重点：圆轴扭转的刚度Байду номын сангаас件。
教学难点：对圆轴扭转的刚度条件的理解和应 用。
延安大学西安创新学院建筑工程系
一、 圆轴扭转时的变形计算 1、扭转角(φ)：圆轴扭转时两横截面相对转过的角
度。
2、单位扭转角(θ)：单位长度上的扭转角。 (rad/m)
其中：T---截面上的扭矩 Iρ---截面对圆心O点的极惯性矩 L---两截面之间的距离 G---剪切弹性模量
延安大学西安创新学院建筑工程系
（２） 扭矩的正负号规定右手螺旋法则。
延安大学西安创新学院建筑工程系
（３） 指定截面扭矩的计算方法。
延安大学西安创新学院建筑工程系
用一假想的截从要求内力处将 杆件切开 分成两段，取其中的任意一段为研究对 象，画出其受力图，利用平衡方程，求 出 内力（扭矩）
注意：在受力图中，扭矩最好假设成正 方向，如上图。
由力偶平衡得： Me-T=0 即：T=Me
延安大学西安创新学院建筑工程系
3、 扭矩图： 用一个图形来表示截面上的扭矩随其截
面位置变化关系。
延安大学西安创新学院建筑工程系
例 M扭A1矩=：1图5图9。1示.5圆N轴.m的，外M力C=偶95矩4.M9NB=.m6。36试.6N作.m出，其 解：1、用一截面从1-1处将轴切开，取左部分
(1) 实心圆截面
（2）空心圆截面
延安大学西安创新学院建筑工程系
三、 圆轴扭转时的强度计算 １、 强度条件
延安大学西安创新学院建筑工程系
２、 例题 例1：如图所示，一钢制圆轴两端受外
力偶m作用，已知m=2.5KN，直径d=6cm， 许用应力[τ]=60MPa，试校核该轴的强度。
延安大学西安创新学院建筑工程系
二、 圆轴扭转时的刚度计算 １、 刚度条件
其中：[θ]---许用单位扭转角 （rad/m或°/m)
延安大学西安创新学院建筑工程系
三、刚度计算举例
例2：如图所示的实心传动轴，Nk1=50KW， Nk2=150KW，Nk3=100KW， n=300r/min，许 用应力[τ]=100MPa，[θ]=1°/m，G=80GPa， 试设计此轴的直径D。
延安大学西安创新学院建筑工程系
§6-1 圆轴扭转 扭矩与扭矩图
一、 圆轴扭转的概念与实例
1、扭转的概念
杆件的两端受到大小相等、转向相反且作
用平面直垂于杆轴线的力偶的作用，致使杆件
各横截面都绕杆轴线发生相对转动，杆件表面
的纵向线将变成螺旋线。
2、扭转的受力特点：受一对等值、反向、
作用面在横截面内的力偶作用时，圆轴产生扭
延安大学西安创新学院建筑工程系
２、 剪切胡克定律
τ＝τ’ （１）、 切应变：切应力只产生角应变，
单元体的直角的改变量称为切应变。
（２）、 剪切胡克定律
在剪切比例极限的范围内，切应力和切
应变成正比。比例常数为材料的切变模 量（G）。
τ＝Gγ
延安大学西安创新学院建筑工程系
二、 圆轴扭转时横截面上的应力 １、 切应力及其分布规律
延安大学西安创新学院建筑工程系
解： 1、计算轴的扭矩T
将轴在离左端任一距离处用截面切开， 取左段为脱离体，画出其受 力图如下图， 由平衡条件可得：T=M
2、校核强度
此轴满足强度要求
延安大学西安创新学院建筑工程系
§6-3 圆轴扭转时的变形与刚度计算
目的要求：掌握圆轴扭转的变形计算和刚度条 件。