微分方程数值解欧拉法
微分方程的数值解法

微分方程的数值解法微分方程是自然科学和现代技术领域中一种最基本的数学描述工具,它可以描述物理世界中的各种现象。
微分方程的解析解往往很难求出,因此数值解法成为解决微分方程问题的主要手段之一。
本文将介绍几种常见的微分方程的数值解法。
一、欧拉法欧拉法是微分方程初值问题的最简单的数值方法之一,它是由欧拉提出的。
考虑一阶常微分方程:$y'=f(t,y),y(t_0)=y_0$其中,$f(t,y)$表示$y$对$t$的导数,则$y(t_{i+1})=y(t_i)+hf(t_i,y_i)$其中,$h$为步长,$t_i=t_0+ih$,$y_i$是$y(t_i)$的近似值。
欧拉法的精度较低,误差随着步长的增加而增大,因此不适用于求解精度要求较高的问题。
二、改进欧拉法改进欧拉法又称为Heun方法,它是由Heun提出的。
改进欧拉法是在欧拉法的基础上进行的改进,它在每个步长内提高求解精度。
改进欧拉法的步骤如下:1. 根据当前$t_i$和$y_i$估算$y_{i+1}$:$y^*=y_i+hf(t_i,y_i),t^*=t_i+h$2. 利用$y^*$和$t^*$估算$f(t^*,y^*)$:$f^*=f(t^*,y^*)$3. 利用$y_i$、$f(t_i,y_i)$和$f^*$估算$y_{i+1}$:$y_{i+1}=y_i+\frac{h}{2}(f(t_i,y_i)+f^*)$改进欧拉法具有比欧拉法更高的精度,但是相较于其他更高精度的数值方法,它的精度仍然较低。
三、龙格-库塔法龙格-库塔法是一种广泛使用的高精度数值方法,它不仅能够求解一阶和二阶常微分方程,还能够求解高阶常微分方程和偏微分方程。
其中,经典的四阶龙格-库塔法是最常用的数值方法之一。
四阶龙格-库塔法的步骤如下:1. 根据当前$t_i$和$y_i$估算$k_1$:$k_1=f(t_i,y_i)$2. 根据$k_1$和$y_i$估算$k_2$:$k_2=f(t_i+\frac{h}{2},y_i+\frac{h}{2}k_1)$3. 根据$k_2$和$y_i$估算$k_3$:$k_3=f(t_i+\frac{h}{2},y_i+\frac{h}{2}k_2)$4. 根据$k_3$和$y_i$估算$k_4$:$k_4=f(t_i+h,y_i+hk_3)$5. 根据$k_1$、$k_2$、$k_3$和$k_4$计算$y_{i+1}$:$y_{i+1}=y_i+\frac{h}{6}(k_1+2k_2+2k_3+k_4)$龙格-库塔法的精度较高,在求解一些对精度要求较高的问题时,龙格-库塔法是一个比较好的选择。
第五章:常微分方程数值解法第一节欧拉法

常微分方程数值解法-欧拉法、改进欧拉法与四阶龙格库塔法常微分方程数值解法

y( xn1)
y( xn
Байду номын сангаас
h)
y(xn )
hy'( xn )
h2 2!
y''( )
进一步: 令
h2 y( xn ) hy'( xn ) 2! y''( xn )
常微分方 yn1 y( xn1 ) , yn y( xn )
程数值解
法-欧拉法 yn1 yn hf ( xn , yn ) h2
、改进欧 y( xn1 ) yn1
2
max y''( x)
a xb
拉法和四
三、Euler方法
已 知 初 值 问 题 的 一 般 形式 为:
dy
dx
f (x, y)
a xb
(1)
y( x0 ) y0
常微分方 用差商近似导数 程数值解 问题转化为
yn1 yn dy
h
dx
法-欧拉法 yn1 yn hf ( xn , yn )
法-欧 y(拉0) 法1
、改进欧
拉法和四
四、几何意义
由 x0 , y0 出发取解曲线 y yx 的切线(存在!),则斜率
dy
f x0, y0
dx x y
,
0
0
常微分方 由于 f x0, y0 及 x0, y0 已知,必有切线方程。
由点斜式写出切程线方数程:值解
法、-改欧进拉欧法 ddxy y y0 x x0
常微分方 程数值解 能用解析方法求出精确解的微分方程为数不多,
而且有的方程即使有解析解,也可能由于解的表达
法-欧拉法 式非常复杂而不易计算,因此有必要研究微分方程
分别利用欧拉法和改进欧拉法求解微分方程组的数值解

分别利用欧拉法和改进欧拉法求解微分方程组的数值解欧拉法(Euler’s Method)和改进欧拉法(Improved Euler’s Method),是求解常微分方程数值解的两种常用方法。
它们都属于一阶精度的显式迭代算法。
首先,我们来介绍一下欧拉法。
欧拉法是一种简单的数值求解算法,它基于微分方程的定义,将微分方程转化为差分方程。
考虑一个一阶常微分方程 dy/dx = f(x, y),并给定初始条件 y(x0)= y0,我们希望求解在给定区间 [x0, xn] 上方程的数值解。
首先,我们将区间 [x0, xn] 平均分成 N 个小区间,每个小区间的长度为 h = (xn - x0) / N。
然后,我们可以使用以下的欧拉迭代公式计算数值解:y[i+1] = y[i] + h * f(x[i], y[i])其中,x[i] = x0 + i * h,y[i] 是在点 x[i] 处的数值解。
通过不断迭代上述公式,我们可以获得[x0, xn] 上微分方程的数值解。
欧拉法的优点在于简单易懂,计算速度较快。
然而,欧拉法的缺点是精度较低,误差随着步长h 的增大而增大。
为了提高精度,我们可以使用改进欧拉法。
改进欧拉法,也称为龙格–库塔算法(Runge-Kutta Method)或四阶龙格–库塔方法,是一种基于欧拉法的改进算法。
改进欧拉法使用了更多的近似取值,以减小误差。
与欧拉法类似,我们将区间 [x0, xn] 平均分成 N 个小区间,每个小区间的长度为 h = (xn - x0) / N。
然后,我们可以使用以下的公式计算数值解:k1 = h * f(x[i], y[i])k2 = h * f(x[i] + h/2, y[i] + k1/2)y[i+1] = y[i] + k2其中,k1 和 k2 是计算过程中的辅助变量。
通过不断迭代上述公式,我们可以获得 [x0, xn] 上微分方程的数值解。
改进欧拉法相对于欧拉法而言,计算精度更高。
常微分方程数值解法欧拉法

)
f ( xn1, yn1)
hL
y(k ) n 1
yn1
L
hL
k 1
y(0) n 1
yn1
Q
hL 1,
y (k 1) n 1
yn1 (k
)
在迭代公式中取极限,有
yn1 yn h f ( xn1, yn1 ) 因此yn(k1)的极限就是隐式方程的解
几何意义
y
设已知曲线上一点 Pn (xn , yn ),过该 点作弦线,斜率为(xn+1 , yn +1 ) 点的 方向场f(x,y)方向,若步长h充分小, 可用弦线和垂线x=xn+1的交点近似 曲线与垂线的交点。
式。隐式公式不能直接求解,一般需要用Euler显式公式
得到初值,然后用Euler隐式公式迭代求解。因此隐式公
式较显式公式计算复杂,但稳定性好
y0 n1
yn
h
y(k 1) n1
yn
h
f (xn , yn )
f
( xn1 ,
y(k) n1
)
收敛性
y (k 1) n 1
yn1
h
f
( xn1,
y(k ) n 1
如何求解
解析解法:(常微分方程理论)
只能求解极少一类常微分方程;实际中给定的问题不一 定是解析表达式,而是函数表,无法用解析解法。
数值解法: 求解所有的常微分方程
计算解函数 y(x) 在一系列节点 a = x0< x1<…< xn= b
处的近似值 yi y( xi ) (i 1, ... , n)
y(xn1) y(xn ) hy(xn ) y(xn ) yn
y(xn1) yn1 yn h f (xn , yn )
微分方程的数值解法与近似求解技巧

微分方程的数值解法与近似求解技巧微分方程是数学中的重要概念,广泛应用于物理、工程、经济等领域。
在实际问题中,我们常常遇到无法直接求解的微分方程,这时候就需要借助数值解法和近似求解技巧来解决。
本文将介绍微分方程的数值解法和近似求解技巧,帮助读者更好地理解和应用这些方法。
一、数值解法1. 欧拉法欧拉法是最基础的数值解法之一,通过离散化微分方程,将其转化为差分方程,从而得到近似解。
欧拉法的基本思想是将微分方程中的导数用差商代替,然后通过迭代逼近真实解。
以一阶常微分方程为例,欧拉法的迭代公式如下:\[y_{n+1} = y_n + hf(x_n, y_n)\]其中,\(y_n\)表示第n个点的近似解,\(x_n\)表示对应的自变量的取值,h为步长,\(f(x_n, y_n)\)表示微分方程中的导数。
2. 改进的欧拉法改进的欧拉法是对欧拉法的改进,通过使用两个近似解的平均值来计算下一个点的近似解,从而提高了数值解的精度。
改进的欧拉法的迭代公式如下:\[y_{n+1} = y_n + \frac{h}{2}(f(x_n, y_n) + f(x_{n+1}, y_n + hf(x_n, y_n)))\]3. 二阶龙格-库塔法龙格-库塔法是一种常用的数值解法,通过计算多个近似解的加权平均值来提高数值解的精度。
其中,二阶龙格-库塔法是最简单的一种。
二阶龙格-库塔法的迭代公式如下:\[k_1 = hf(x_n, y_n)\]\[k_2 = hf(x_n + \frac{h}{2}, y_n + \frac{k_1}{2})\]\[y_{n+1} = y_n + k_2\]二、近似求解技巧1. 线性化方法线性化方法是一种常用的近似求解技巧,通过将非线性微分方程线性化,然后使用线性方程的求解方法来得到近似解。
以二阶线性微分方程为例,线性化方法的基本思想是将非线性项进行线性化处理,然后使用线性微分方程的求解方法来得到近似解。
常微分方程的数值解法(欧拉法、改进欧拉法、泰勒方法和龙格库塔法)
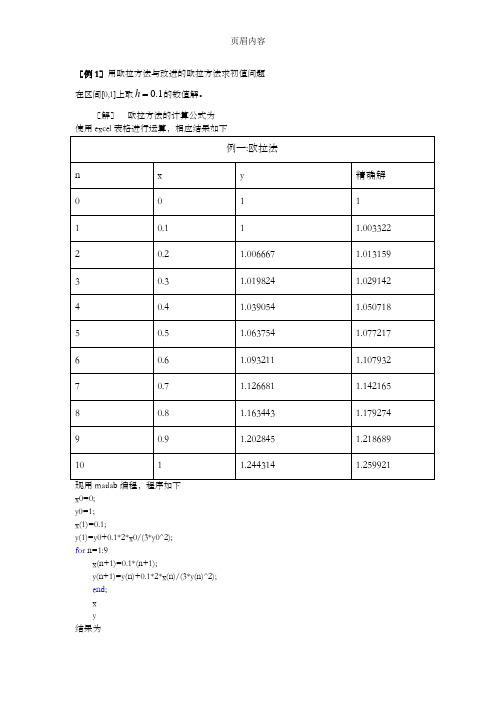
[例1]用欧拉方法与改进的欧拉方法求初值问题h 的数值解。
在区间[0,1]上取0.1[解]欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600[例2]用泰勒方法解x=0.1, 0.2, …, 1.0处的数值解,并与精确解进行比较。
微分方程的数值解法与稳定性分析

微分方程的数值解法与稳定性分析微分方程是研究自然现象和物理问题的重要数学工具。
在实际问题中,许多微分方程往往难以解析求解,因此需要借助计算机进行数值求解。
本文将介绍微分方程的数值解法以及稳定性分析。
一、欧拉法欧拉法是最简单、最基础的数值解法之一。
基本思想是将微分方程中的导数用差商逼近,得到差分方程,再求解差分方程以获得离散的数值解。
考虑一阶常微分方程 dy/dx = f(x, y),将自变量 x 分割为若干小区间,步长为 h。
欧拉法的迭代公式为 y_{i+1} = y_i + h * f(x_i, y_i),其中 y_i 和 x_i 是第 i 个点的数值解和自变量值。
欧拉法的简单易懂,但存在局限性。
当步长过大时,数值解的稳定性较差,可能出现数值误差增大、解发散等问题。
二、改进的欧拉法(改进欧拉法)为克服欧拉法的局限性,改进的欧拉法在迭代过程中增加了更高阶的差商项,提高了数值解的精度和稳定性。
举例说明,考虑一阶常微分方程 dy/dx = f(x, y),改进的欧拉法的迭代公式为 y_{i+1} = y_i + h * (f(x_i, y_i) + f(x_{i+1}, y_i + h * f(x_i, y_i))) / 2。
改进的欧拉法相比于欧拉法具有更好的数值稳定性和精度,但复杂度略高。
三、龙格-库塔法(RK方法)龙格-库塔法是一类常用的高精度数值解法,其思想是通过多个对函数 f(x, y) 的估计来提高数值解的准确性。
最常见的四阶龙格-库塔法(RK4)是利用四个不同的斜率估计来计算数值解。
其迭代公式为:k_1 = h * f(x_i, y_i)k_2 = h * f(x_i + h/2, y_i + k_1/2)k_3 = h * f(x_i + h/2, y_i + k_2/2)k_4 = h * f(x_i + h, y_i + k_3)y_{i+1} = y_i + (k_1 + 2k_2 + 2k_3 + k_4) / 6龙格-库塔法具有较高的精度和数值稳定性,适用于各种类型的微分方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1、求解初值问题()⎪⎩⎪⎨⎧=-=-10y yxe dx dyx ,已知精确解为()()x x x x y -+=2212当h=0.1时,解为:n xn y()n x y()nn y x y -0 1 1 00.1 0.900000 0.909362 9.3616E-03 0.2 0.819048 0.835105 1.6057E-02 0.3 0.753518 0.774155 2.0637E-02 0.4 0.700391 0.723946 2.3555E-02 0.5 0.657165 0.682347 2.5182E-02 0.6 0.621775 0.647598 2.5823E-02 0.7 0.592526 0.618249 2.5723E-02 0.8 0.568034 0.593114 2.5080E-02 0.9 0.547177 0.571230 2.4053E-02 1.00.529051 0.551819 2.2768E-020.10.20.30.40.50.60.70.80.91当h=0.05时,解为:n xn y()n x y()nn y x y -0 1 1 00.05 0.950000 0.952418 2.4185E-03 0.10 0.904878 0.909362 4.4835E-03 0.15 0.864158 0.870391 6.2326E-03 0.20 0.827406 0.835105 7.6996E-03 0.25 0.794223 0.803138 8.9155E-03 0.30 0.764247 0.774155 9.9084E-03 0.35 0.737147 0.747850 1.0704E-02 0.40 0.712621 0.723946 1.1324E-02 0.45 0.690397 0.702188 1.1791E-02 0.50 0.670223 0.682347 1.2124E-02 0.55 0.651876 0.664213 1.2338E-02 0.60 0.635148 0.647598 1.2450E-02 0.65 0.619855 0.632328 1.2473E-02 0.70 0.605829 0.618249 1.2420E-02 0.75 0.592918 0.605220 1.2302E-02 0.80 0.580985 0.593114 1.2129E-02 0.85 0.569909 0.581819 1.1909E-02 0.90 0.559579 0.571230 1.1651E-02 0.95 0.549896 0.561258 1.1362E-02 1.000.5407710.5518191.1048E-020.10.20.30.40.50.60.70.80.91h=50时,解为:n xn y()n x y()n n y x y -0 1 1 00.02 0.980000 0.980395 3.9471E-04 0.04 0.960792 0.961558 7.6599E-04 0.06 0.942345 0.943460 1.1148E-03 0.08 0.924628 0.926070 1.4422E-03 0.10 0.907613 0.909362 1.7491E-03 0.12 0.891270 0.893306 2.0363E-03 0.14 0.875573 0.877878 2.3048E-03 0.16 0.860496 0.863051 2.5553E-03 0.18 0.846013 0.848802 2.7888E-03 0.20 0.832100 0.835105 3.0058E-03 0.22 0.818732 0.821940 3.2073E-03 0.24 0.805889 0.809283 3.3938E-03 0.26 0.793547 0.797113 3.5662E-03 0.28 0.781685 0.785410 3.7250E-03 0.30 0.770284 0.774155 3.8709E-03 0.32 0.759323 0.763328 4.0045E-03 0.34 0.748784 0.752911 4.1264E-03 0.36 0.738649 0.742886 4.2371E-03 0.38 0.728899 0.733236 4.3373E-03 0.40 0.719518 0.723946 4.4274E-03 0.42 0.710490 0.714998 4.5079E-03 0.44 0.701800 0.706379 4.5793E-03 0.46 0.693431 0.698073 4.6421E-03 0.48 0.685371 0.690067 4.6967E-03 0.50 0.677603 0.682347 4.7435E-03 0.52 0.670117 0.674900 4.7830E-03 0.54 0.662897 0.667713 4.8156E-03 0.56 0.655933 0.660775 4.8415E-03 0.58 0.649212 0.654073 4.8613E-03 0.60 0.642723 0.647598 4.8751E-03 0.62 0.636454 0.641337 4.8835E-03 0.64 0.630395 0.635282 4.8866E-03 0.66 0.624537 0.629422 4.8848E-03 0.68 0.618868 0.623747 4.8784E-03 0.70 0.613381 0.618249 4.8676E-03 0.72 0.608066 0.612918 4.8528E-03 0.74 0.602914 0.607748 4.8341E-03 0.760.5979170.6027284.8119E-030.78 0.593067 0.597853 4.7863E-03 0.80 0.588357 0.593114 4.7577E-03 0.82 0.583779 0.588505 4.7261E-03 0.84 0.579326 0.584018 4.6918E-03 0.86 0.574992 0.579647 4.6550E-03 0.88 0.570771 0.575387 4.6159E-03 0.90 0.566656 0.571230 4.5746E-03 0.92 0.562641 0.567172 4.5314E-03 0.94 0.558721 0.563207 4.4864E-03 0.96 0.554890 0.559330 4.4397E-03 0.98 0.551144 0.555535 4.3916E-03 1.000.547477 0.551819 4.3420E-030.10.20.30.40.50.60.70.80.91有图像看出,当步长越小,计算得到的解越逼近精确解。
1.2、求解初值问题⎪⎩⎪⎨⎧=++-==110x y x y dx dy,已知精确解为:x e x y -+=,h=0.1欧拉法图像:改进欧拉法图像:预测-校正法图像:附录:源代码1.1、clearclcX0=0;X1=1;n=10;%更改分点数h=1/n;%步长y(1)=1;x(1)=X0;for i=1:nx(i+1)=x(i)+h;y(i+1)=y(i)+h*(x(i)*exp(-x(i))-y(i)); endx=vpa(x',6)y=vpa(y',6)X=(X0:0.001:X1);n=1/0.001;for(i=1:n+1)Y(i)=0.5*(X(i)^2+2)*exp(-X(i));endplot(x,y,'*')hold onplot(X,Y)X=X0:h:X1;Y=0.5.*(X.^2+2).*exp(-X);Y=vpa(Y',6)yy=abs(y-Y)1.2、欧拉法:clearclcX0=0;X1=1;n=10;h=1/n;y(1)=1;x(1)=X0;X=X0:h:X1;Y=X+exp(-X);Y=vpa(Y',9);%精确解XX=X0:0.0001:X1;YY=XX+exp(-XX);for i=1:nx(i+1)=x(i)+h;y(i+1)=y(i)+h*(-y(i)+x(i)+1); endy=vpa(y',9)plot(x,y,'*')hold onplot(XX,YY)改进的欧拉法:clearclcX0=0;X1=1;n=10;h=1/n;y(1)=1;x(1)=X0;X=X0:h:X1;Y=X+exp(-X);Y=vpa(Y',9);%精确解XX=X0:0.0001:X1;YY=XX+exp(-XX);for i=1:nx(i+1)=x(i)+h;y(i+1)=y(i)+h*(-y(i)+x(i)+1);endfor i=1:ny(i+1)=y(i)+0.5*h*((-y(i)+x(i)+1)+(-y(i+1)+x(i+1)+1));endy=vpa(y',9)plot(x,y,'*')hold onplot(XX,YY)预报-校正格式:clearclcX0=0;X1=1;n=10;h=1/n;y(1)=1;x(1)=X0;X=X0:h:X1;Y=X+exp(-X);Y=vpa(Y',9);%精确解XX=X0:0.0001:X1;YY=XX+exp(-XX);for i=1:nx(i+1)=x(i)+h;y(i+1)=y(i)+h*(-y(i)+x(i)+1);endfor i=1:nfor count=1:10 %预报-校正格式,迭代十次y(i+1)=y(i)+0.5*h*((-y(i)+x(i)+1)+(-y(i+1)+x(i+1)+1));endendy=vpa(y',9)plot(x,y,'*')hold onplot(XX,YY)。
