电磁感应定律(双语)
电磁感应 电磁场英文名词

4
物理学
第五版
物理学
第五版
物理学名词中英文对照
磁介质 磁化强度 磁化率 分子电流 分子磁矩 顺磁质 抗磁性
magnetic medium magnetization susceptibility molecular current molecular magnetic moment paramagnetism diamagnetism
附 录
3
物理学
第五版
物理学
第五版
物理学名词中英文对照
亨利 磁场能量 磁能密度
henry magnetic field energy magnetic energy density 位移电流 displacement current 电磁场 electromagnetic field 麦克斯韦 Maxwell,James Clerk 麦克斯韦方程组 Maxwell equations
附
录
6
物理学
第五版
物理学
第五版
物理学名词中英文对照
铁磁质 磁场强度
相对磁导率 传导电流 磁化电流 磁畴
ferromagnetic material magnetic field intensity Relative permeability conduction current magnetization current magnetic domain
物理学
第五版
物理学名词中英文对照
楞次 楞次定律 动生电动势 感生电动势 有旋电场 涡流
Lenz Lenz law motional electromotive force induced electromotive force curl electric field eddy current
12.1 电磁感应定律

产生 阻碍
磁通量变化
1313-1
电磁感应定律
判断感应电流的方向: 判断感应电流的方向:
1、判明穿过闭合回路内原磁场 、 的方向; 的方向; 2、根据原磁通量的变化 ∆ Φm , 、 按照楞次定律的要求确定感 应电流的磁场的方向; 应电流的磁场的方向; 3、按右手法则由感应电流磁场的 、 方向来确定感应电流的方向。 方向来确定感应电流的方向。
1313-1 例: 无限长直导线 i = i0 sinωt 共面矩形线圈 abcd 已知: 已知 l1
电磁感应定律
h
l2
b
c
l1
l2 h
求:
h+l2
εi
i
r r 解: Φm = ∫ B⋅ dS =
∫
h
µ0i l1dx 2πx
µ0i0l1 h + l2 ln sinωt = 2 π h
a x
d
dx
dΦm µ0i0l1 h+ l2 εi = − ln cosωt =− 2 π h dt
1313-1
电磁感应定律
法拉第简介
(Michael Faraday,1791-1867)
1.生平 1.生平 法拉第于1791年出生在英国伦敦附近的一个小村里, 法拉第于1791年出生在英国伦敦附近的一个小村里, 1791年出生在英国伦敦附近的一个小村里 父亲是铁匠,自幼家境贫寒,无钱上学读书。13岁时到 父亲是铁匠,自幼家境贫寒,无钱上学读书。13岁时到 一家书店里当报童,次年转为装订学徒工。 一家书店里当报童,次年转为装订学徒工。在学徒工期 间,法拉第除工作外,利用书店的条件,在业余时间贪 法拉第除工作外,利用书店的条件, 婪地阅读了许多科学著作,例如《化学对话》 婪地阅读了许多科学著作,例如《化学对话》、《大英 百科全书》 电学》条目等, 百科全书》的《电学》条目等,这些著作开拓了他的视 激发了他对科学的浓厚兴趣。 野,激发了他对科学的浓厚兴趣。
8-1电磁感应定律1PPT课件
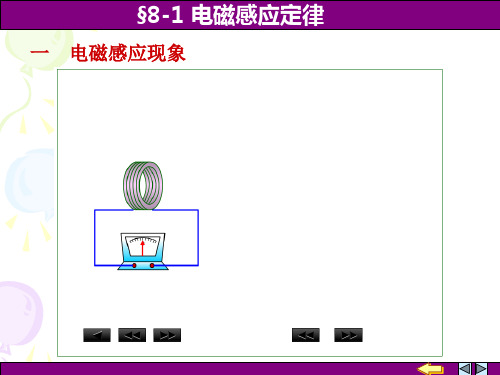
例2 如图所示,在通有电流为I=I0+kt(I0、k皆为正的恒 量,t为时间)的长直导线近旁有一等腰直角三角形线框
MNP,两者共面,MN与直导线平行,且相距为a,三角
形的直角边的长也是a。求线框中感应电动势的大小和方
向。
解 沿线框选定回路的顺时针 y
N
绕向,建立坐标如图所示的直
角坐标系Oxy
则则N通P过边面满积足元的d方S的程磁为通y=量2为a-x。O
结束语
当你尽了自己的最大努力时,失败 也是伟大的,所以不要放弃,坚持 就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End
感谢聆听
不足之处请大家批评指导
Please Criticize And Guide The Shortcomings
d
B dS
0I
(2a
x)dx
2x
xM a
y dx
Px
a
§8-1 电磁感应定律
穿过直角三角形所包围面积的总磁通量为
2a
d
0 I (2a x)dx
s
2 2x
y
N
0aI (2 ln 2 1) 2
0a(I0 kt) (2 ln 2 1) O 2
xM a
y dx
Px
a
由法拉第电磁感应定律得线框内的感应电动势为
磁通匝数(磁链) NΦ
i
d
dt
2)若闭合回路的电阻为 R ,感应电流为
Ii
1 R
dΦ dt
t t2 t1 时间内,流过回路的电荷
q
《法拉第电磁感应定律》的主要内容

《法拉第电磁感应定律》的主要内容法拉第电磁感应定律(FaradayLawofElectromagneticInduction)是现代物理学和电子学的基础,也是目前工业上最基本、使用最广泛的一个定律。
英国科学家麦可法拉第1831年首先提出了这个定律。
它揭示了当一个电磁场的磁感应强度发生变化时,在固定的形状的一个介质内的电流会自动产生。
它提供了非常重要的理论基础,这个理论基础为发电机、变频器、感应加热装置等主要的电子产品的应用提供了技术依据。
此外,法拉第电磁感应定律也必不可少地用于测量磁壁的分布,以及电磁波,太阳能、激光等空间时间分布的研究。
法拉第电磁感应定律由法拉第定律和麦克斯韦定律构成,它也被称为Meylor-Faraday定律,它概括地表述如下:当一个电磁场的磁感应强度发生变化时,在一个固定的形状的介质内(一个电线或磁环内),会自动产生一个相反方向的电流。
此外,它还提出了“磁感应强度改变量与电动势改变量之间的简单线性关系”,即:电动势改变量=磁感应强度改变量×电路面积法拉第电磁感应定律是由实验提出的,实验原理如下:将一个变阻器(也称为电阻箱)位于一个磁环内,当一个外部电磁场的磁感应强度发生变化时,就会在电阻箱内产生一个相反的电动势差,从而在电阻箱之间产生一个电流,而这个电流的大小则取决于外部磁场的强度及时间改变的速度,也就是说,电流的大小与外部磁场的磁感应强度的变化量成正比。
法拉第电磁感应定律就像一段美丽的音乐,它使磁电学具有生机活力,开启了电子这一领域的发展。
它为电磁场理论及其应用研究,为电动机、发电机、变频器、感应加热等产品的机理和应用研究提供了重要的理论基础,在工业科学发展史上占有重要的地位。
有研究表明,法拉第电磁感应定律也与所谓的“相对论”存在相互关联性。
1905年阿尔伯特爱因斯坦提出的“相对论”(以及普朗克的量子力学)在后续的发展中形成了物理学的基石,而这一理论根据法拉第电磁感应定律来推导,表明了磁和电现象是由相同的电磁场来解释。
电磁感应现象和法拉第定律

Ii
1 R
dΦ dt
t t2 t1 时间内,流过回路的电荷
q
t2 Idt 1
t1
R
Φ2 dΦ
Φ1
1 R
(Φ1
Φ2 )
5
楞次定律
闭合的导线回路中所 出现的感应电流,总是力 图阻止穿过导体回路的磁 通量的改变,亦即使它自 己所激发的磁场反抗任何 引发电磁感应的原因(反 抗相对运动、磁场变化或 线圈变形等).
o
iR
19
有效值
P 1 T I 2(t)Rdt P 1 T U 2 (t) / Rdt
T0
T0
P
I
2 有效
R
P
U
2 有效
/
R
20
发电机输出的瞬时功率为
P(t)
I
2
R
RI
2 m
sin
2
t
平均输出功率就是一个周期内输出的瞬时功率之平均值:
P 1 T
T 0
P(t)dt
1 2
I
2 m
R
P
I
2 有效
35
感生电场和静电场的对比
E静 和 Ek 均对电荷有力的作用.
静电场是保守场 L E静 dl 0
感生电场是非保守场
L
Ek
dl
dΦ dt
0
静电场由电荷产生;感生电场是由变化的磁 场产生 .
36
半径为 R 的圆柱形空间内充满与轴平行的磁场 B, B 随时间 t 变化 B = kt,圆柱形之外 B = 0,求圆 柱形空间外的电场分布。
13
例2 一导线矩形框的平面与磁感强度为 B 的均
匀磁场相垂直.在此矩形框上,有一质量为 m长为 l 的
法拉第电磁感应定律 - 维基百科,自由的百科全书

迈克尔·法拉第肖像画
其中:
是电动势,单位为伏特。 ΦB是通过电路的磁通量,单位为韦伯。
电动势的方向(公式中的负号)由楞次定律提供。“通过电路的磁通量”的意义会由下面的例子阐述。
传统上有两种改变通过电路的磁通量的方式。至于感应电动势时,改变的是自身的电场,例如改变生成场的电流(就像变压器那样)。而至于动生电动 势时,改变的是磁场中的整个或部份电路的运动,例如像在同极发电机中那样。
一个直觉上很吸引但错误的通量定则使用法是,将通过电流的通量当成只是ΦB = Bwℓ,其中w为移动环路的宽度。这数目与时间没有关系,所以这方法会 不正确地预测出无生成电动势。这套论述的缺陷在于它并没有考虑到整个电路,而整个电路是闭合的环路。
使用通量定则时,我们必须顾及整个电路,其中包括通过上下碟片边沿的路径。我们可以选择一通过两道边沿及移动环路的任意闭合路径,而通量定则会 找出该路径的电动势。任何有一部分连接移动环路的路径,都会表达到电路移动部分的相对运动。
作为一个路径例子,选择在上碟片按照转动方向,并下碟片按照转动反方向穿过电路(由图四的箭号表示)。在这情况下,对与回路成角θ的移动环路而 言,圆柱体的一部分面积A = rℓθ为电路的一部分。这面积与磁场垂直,所以造成了这个大小的通量:
其中式子为负,这是因为右手定则指出,电流环路所产生的磁场,与外加的磁场方向相反的缘故。由于这是通量中唯一一个跟随时间转变的部分,所以通 量定则预测的电动势为
N为线圈圈数; ΦB为通过一圈的磁通量,单位为韦伯。
图二:于空间内有定义的一矢量
场F(r,t),及以曲线∂Σ为边界的一 表面Σ,在场的积分范围内以速度v移
动。
在选择路径∂Σ(t)求电动势时,路径须满足两个基本条件:(一)路径闭合;(二)路径必需能描述到电路各部 分的相对运动(这就是∂Σ(t)中变量为时间的原因)。路径并不一定要跟随电流的流动路线,但用通量定律求出 的电动势,理所当然地会是通过所选路径的电动势。假若路径并不跟随电流的话,那么那电动势可能不是驱动着电流的那一电动势。
第12章 电磁感应(法拉第电磁感应定律)
(v B) 与 dl 同向
L
v l
d (v Байду номын сангаасB) dl v Bdl Bldl
1 2 B L d Bldl 2 o
o dl v B
L
B dΦ m d Ek dl B dS dS l t dt dt
B l Ek dl t dS
涡旋电场是非保守场 不能引入电势概念!
变化的均匀磁场
B B(t )
b a
Ek外
B Ek dl dS t L
dΦ m 其数学表达式为: ε dt
dΦ m ε dt
式中“-”
d m 0, 则<0 如图 (a) dt d m 0, 则 0 如图 (b) dt
若线圈是N 匝串联而成 , 则 :
d m d m N dt dt m=N m 单位:韦伯
m : 穿过整个线圈的磁通匝
Ek Ek
c
Ek外
dB (t ) 2 Ek 内 2π r π r dt dB (t ) Ek外 2π r π R2 dt
例:同一时刻 b、c 两点间 感生电场沿不同的路径的积 分值不同。
1 dB (t ) Ek 内 r 2 dt 1 dB(t ) 2 1 Ek外 R 2 dt r
o
交变的 电动势
x
i
0 r NI 0l
2π
π
da cos t ln d
取两个特殊的时间点来讨论
t
t
i 0
i i
L
电磁感应法拉第定律
电磁感应法拉第定律电磁感应法拉第定律(Faraday's Law of Electromagnetic Induction)是物理学中的一个基本定律,描述了磁场变化所引发的电场现象。
该定律是由英国物理学家迈克尔·法拉第于19世纪初提出的,被认为是电动势产生的原理之一。
根据法拉第定律,当一个导体(如电线)被放置在一个变化的磁场中,导体两端将产生电势差,即产生一个电动势。
这个电动势的大小与磁场变化的速率成正比,与导体的长度和磁场的强度密切相关。
具体来说,当磁通量发生变化时,即磁力线穿过导体的数量或导体与磁场之间的相对运动发生变化时,导体两端将产生一个与磁场变化速率成正比的电动势。
法拉第定律可以通过以下公式来表示:ε = -dΦ/dt其中,ε表示导体两端的电动势,dΦ/dt表示磁通量的变化率。
负号表示导体两端的电动势的方向与磁场变化的方向相反。
这个公式说明了电动势的大小与磁通量变化的速率成正比。
根据法拉第定律,我们可以解释一些日常生活中的现象。
例如,当我们将导线放置在一个变化的磁场中并形成电路后,通过电路就会有电流流动。
这个现象可以用法拉第定律来解释:磁场的变化导致导线两端的电动势产生,进而驱动电荷在导线中运动形成电流。
电磁感应法拉第定律在实际应用中有许多重要的应用。
最常见的应用之一就是发电机的工作原理。
发电机利用法拉第定律来将机械能转换为电能。
当发电机的转子旋转时,通过导线环路与磁场的相互作用,产生电动势,最终产生电流。
这就是发电机产生电能的原理。
除了发电机,变压器也是另一个常见的应用例子。
变压器利用法拉第定律来改变交流电的电压。
通过改变磁场的变化速率,可以在次级线圈上产生不同电动势,从而改变电压的大小。
这样,我们可以将高电压的交流电转化为低电压的交流电,或者相反。
此外,电磁感应法拉第定律在电磁感应加热、感应传感器、电磁铁等领域也有广泛的应用。
尽管电磁感应法拉第定律已经有一百多年的历史,但它仍然是研究电磁学和电磁现象的重要基础。
电磁感应定律表达式
电磁感应定律表达式
电磁感应定律是由法拉第提出的,它描述了磁场变化引起的电场感应和电场变化引起的磁场感应。
电磁感应定律的数学表达式可以分为两种情况。
1. 磁场变化引起的电场感应:
当磁场的磁通量ΦB随时间的变化率dΦB/dt不为零时,将在闭合线路上产生感应电动势ε。
根据电磁感应定律,感应电动势ε的大小等于磁通量变化率的负值乘以线路周围的导线数目n:
ε = -dΦB/dt * n
2. 电场变化引起的磁场感应:
当电场的电通量ΦE随时间的变化率dΦE/dt不为零时,将在闭合线路上产生感应磁场磁感应强度B。
根据电磁感应定律,感应磁场磁感应强度B的大小等于电通量变化率的负值乘以线路周围的导线数目n:
B = -dΦE/dt * n
其中,感应电动势ε的单位是伏特(V),磁通量ΦB的单位是韦伯(Wb),时间t的单位是秒(s),线路周围的导线数目n是无量纲的。
感应磁场磁感应强度B的单位是特斯拉(T),电通量ΦE的单位是库仑(C),时间t的单位是秒(s),线路周围的导线数目n是无量纲的。
电磁感应定律_1
d d i NBS cos w t dt dt NBS w sin w t
εi=εmsinωt
令εm=NBω,则
εi 为时间的正弦函数,称正弦交流电,简称交流电。
四、楞次定律(Lenz law)
楞次(Lenz,Heinrich Friedrich Emil)
否则只需一点力开始使 导线移动,若洛仑兹力 不去阻挠它的运动,将 有无限大的电能出现, 显然,这是不符合能量 守恒定律的。
V FL B S I
FL
I
F外
B
五、涡电流
1、涡电流
大块导体处在变化磁场中,或者相对于磁场运动 时,在导体内部也会产生感应电流。这些感应电流在大
块导体内的电流流线呈闭合的涡旋状,被称为涡电流或
涡流。
2、涡流的热效应
电阻小,电流大,能够产生大量的热量。
3、应用
高频感应炉
真空无接触加热 电磁率工作频率:20-30kH 热效率:80%
加热
4、涡流的阻尼作用
当铝片摆动时,穿过运动铝片
的磁通量是变化的,铝片内将产生涡流。 根据楞次定律感应电流的效果总是反抗 引起感应电流的原因。因此铝片的摆动 会受到阻滞而停止,这就是电磁阻尼。
法拉第(Michael Faraday 1791—1867)
伟大的英国物理学家和化学家。法拉第 主要从事电学、磁学、磁光学、电化学 方面的研究,并在这些领域取得了一系 列重大发现。他创造性地提出场的思想。 他是电磁理论的创始人之一,于1831年 发现电磁感应现象,后又相继发现电解 定律,物质的抗磁性和顺磁性,以及光 的偏振面在磁场中的旋转。电动机、发 电机都是他发明的,他为人类进入电气 化时代奠定了基础.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
When the induced electromotive force is generated in the coil, there is an electric field to push the charges to move in the coil, and this induced electric field is denoted as E.
The law of electromagnetic induction is one of basic laws for time-varying electromagnetic fields, and it is also one of Maxwell’s equations.
2. Inductances
1. Law of Electromagnetic Induction
From physics we know that when the magnetic flux through a
closed coil is changing, an induced electromotive force e will be
Considering SB dS , we have
lE
dl
t
SB
dS
eI
Which is called the law of electromagnetic induction, and it shows that when the magnetic field through a closed coil is changing, an induced electric field will be generated in the coil.
If the magnetic flux is increased with time, the direction of the induced electromotive force and that of the magnetic flux obey the left hand rule. if the magnetic flux is decreased with time, they will obey the right hand rule.
In a linear medium, the magnetic flux through the closed circuit is also proportional to the current I.
The magnetic flux linked with the current I is called the magnetic
eI
The induced magnetic flux caused by the induced current in the coil always resists the change of the original magnetic flux. The induced magnetic flux is called the reaction magnetic flux, and the induced electromotive force is called the back electromotive force.
generated in the coil, with the relation
e
d dt
eI
where the positive direction of the electromotive force e and that of the magnetic flux comply with the left hand rule.
The line integral of the induced electric field intensity around
the closed coil is equal to the induced electromotive force in the coil
e, i.e.
lE
dl
e
d dt
flux linkage with the current I, and it is denoted as . The ratio of
The law of electromagnetic induction shows that a time-varying magnetic field can produce a time-variable electric field.
Based on Stokes’ theorem, from the above equation we have
Chapter 6 Electromagnetic Induction
Law of Electromagnetic Induction Inductances
Energy and Force
1. Law of Electromagnetic Induction 2. Inductances 3. Energy in Steady Magnetic Fields 4. Magnetic Forces
S
(
E)
B t
dS
0
Since the equation holds for any area S, the integrand must be zero, so
that
E
B tcalled the differential form of law of electromagnetic induction, and it means that the negative time rate of change of the magnetic flux density at a point is equal to the curl of the timevariable electric field intensity at that point.
