全等三角形重难点题型讲练(无答案)
专题06三角形全等的判定之SAS重难点专练(原卷版)

学校:___________姓名:___________班级:___________考号:___________一、单选题1.(2021·浙江九年级专题练习)如图,在△ABC 中,AB =AC ,BD =CF ,BE =CD ,若∠A =40°,则∠EDF 的度数为()A .75°B .70°C .65°D .60°2.(2021·浙江八年级期末)如图,已知,AB DC ABC DCB =∠=∠.能直接判断ABC DCB △≌△的方法是()A .SASB .AASC .SSSD .ASA3.(2021·浙江宁波市·八年级期末)如图,在平面直角坐标系中,点A 的坐标为()1,0,以线段OA 为边在第四象限内作等边ABO ,点C 为x 轴正半轴上一动点(1OC >),设点C 的坐标为(),0x ,连结BC ,以线段BC 为边的第四象限内作等边CBD ,直线DA 交y 轴于点E ,点E 的坐标是()A .(B .0,2x ⎛⎫⎪⎝⎭C .()0,3D .x ⎛⎫ ⎪ ⎪⎝⎭四边形EFGH 的面积最大值为()A .4a b +B .2()4a b +C .2()8a b +D .2ab b -5.(2021·浙江九年级二模)如图,PA 和PB 是O 的两条切线,A ,B 为切点,点D 在AB 上,点E ,F 分别在线段PA 和PB 上,且AD BF =,BD AE =.若P α∠=,则EDF ∠的度数为()A .90α︒-B .32αC .1902α︒-D .2α6.(2021·浙江九年级一模)如图,四边形ABCD 和DEFG 均为正方形,点E 在对角线AC 上,点F 在边BC 上,连结CG 和EG .若知道正方形ABCD 和DEFG 的面积,则一定能求出()A .四边形ABFE 的周长B .四边形ECGD 的周长C .四边形AEGD 的周长D .四边形ACGD 的周长7.(2021·浙江八年级期末)如图,在ABCD 中,E F 、分别是AD BC 、边的中点,G H 、是对角线BD 上的两点,且BG DH =.有下列结论:①GF BD ⊥;②GF EH =;③四边形EGFH 是平行四边形;④EG FH =.则正确的个数为()A .1个B .2个C .3个D .4个8.(2021·浙江八年级期末)如图,四边形ABCD 是菱形,点E 、F 分别在边BC 、CD 上,且BE =DF ,AB =AE ,若∠EAF =75°,则∠C 的度数为()A .85°B .90°C .95°D .105°9.(2021·浙江湖州市·八年级期末)如图,已知ABCD ,以点A 为圆心,AD 长为半径画弧,交AB 于点E ;再分别以点D 、E 为圆心,大于12DE 长为半径画弧,两弧交于点F ,画射线AF ,与DC 交于点G .若90AGB ∠=︒,10CG =,则AB 的长为()A .2532B .123C .20D .1510.(【新东方】初中数学1228初二上)如图,在ABC 中,AB AC =,54BAC ∠=︒,BAC ∠平分线与AB 的垂直平分线交于点O ,将C ∠沿EF (E 在BC 上,F 在AC 上)折叠,点C 与点O 恰好重合,有如下五个结论:①AO BC ⊥;②OD OE =;③OEF 是等边三角形;④OEF CEF ≌;⑤54OEF ∠=︒.则上列说法中正确的个数是()11.(【新东方】初中数学1242初二上)如图,等腰Rt ABC 中,90BAC AD BC ∠=︒⊥,于D ,ABC ∠的平分线分别交AC AD 、于E F 、两点,M 为EF 的中点,延长AM 交BC 于点N ,连接DM MC 、下列结论:①DF DN =;②ABE MBN ≌;③ CMN 是等腰三角形;④AE CN =,其中正确的是()A .①②B .①④C .①③D .②③12.(【新东方】初中数学1223初三上)如图,在菱形ABCD 中,6,60,AB DAB AE =∠=︒分别交于BC 、BD 于点,2E F CE =、,连接CF ,以下结论:①ABF CBF ≌;②点E到AB 的距离是an t DCF ∠=;④ABF 的有几个()A .①B .①②C .①②③D .①②③④13.(2021·浙江八年级期末)如图,在正方形ABCD 中,点E ,F 分别是BC ,CD 上的点,AE 与BF 相交于点G ,连接AC 交BF 于点H .若CE =DF ,BG =GH ,AB =2,则△CFH 的面积为()A .4B .3﹣C .53D .6二、填空题15.(2021·浙江八年级期中)如图,在正方形ABCD 中,4AB =,点E ,F 分别在CD ,AD 上,CE DF =,BE ,CF 相交于点G ,若图中阴影部分的面积与正方形ABCD 的面积之比为3:4,则BCG 的周长为________.16.(2021·浙江杭州市·八年级期中)如图,在正方形ABCD 中,3AB =,点E ,F 分别在,CD AD 上,CE DF =,BE ,CE 相交于点G .若图中阴影部分的面积与正方形ABCD 的面积之比为2:3,则四边形GEDF 的面积为_______;BCG 的周长为______.17.(【新东方】初中数学20210625-006【初二上】)如图,在ABC 中,,100AB AC BAC =∠=︒,点D 在BC 边上,ABD AFD 、关于直线,AD 对称,FAC ∠的角平分线交BC 边于点G 、连接FG BAD θ∠=、,当θ的值等于_______时,DFG 为等腰三角形.点D ,E 为BC 边上的两点,且45DAE ∠=︒,连接EF ,BF ,则下列结论正确的是________.①AED AEF ≌△△;②AED 为等腰三角形;③BE DC DE +>;④222BE DC DE +=.19.(【新东方】初中数学1234初二上)如图,在等边ABC 中,点D ,E 分别在边BC ,AB 上,且BD AE =,AD 与CE 交于点F ,作CM AD ⊥,垂足为M ,下列结论正确的有________.①AD CE =;②BEC CDA ∠=∠;③120AFC ∠=︒;④12MF CF =;⑤AM CM =.20.(2021·台州市书生中学八年级月考)如图,正方形ABCD 的边长为2,M 是BC 的中点,N 是AM 上的动点,过点N 作EF ⊥AM 分别交AB ,CD 于点E ,F .(1)AM 的长为_____;(2)EM +AF 的最小值为_____.21.(【新东方】【2021.5.19】【JH 】【初二下】【数学】【JH0027】)如图,四边形ABCD 是M 为对角线BD (不含B 点)上任意一点.(1)AM CM +的最小值是______.(2)AM BM CM ++的最小值是________.三、解答题22.(2021·杭州市采荷中学九年级三模)如图,已知:在ABC ∆中,90BAC ︒∠=,延长BA 到点D ,使12AD AB =,点E ,F 分别是边BC ,AC 的中点.求证:DF BE =.23.(2020·重庆八年级月考)如图,AB =AC ,AD =AE ,∠BAC =∠DAE .(1)求证:△ABD ≌△ACE ;(2)若∠1=25°,∠2=30°,求∠3的度数.24.(2021·浙江九年级月考)图1,图2都是由边长为1的小等边三角形构成的网格,△ABC 为格点三角形.请仅用无刻度直尺在网格中完成下列画图.(1)在图1中,画出△ABC 中AB 边上的中线CM ;(2)在图2中,画出∠APC ,使∠APC =∠ABC ,且点P 是格点(画出一个即可).25.(2021·浙江)已知:如图,E F 、是平行四边形ABCD 的对角线AC 上的两点,AE CF =.求证:(1)ADF CBE △≌△;(2)//EB DF .26.(2021·浙江九年级期中)如图,点M ,N 分别在正方形ABCD 的边BC ,CD 上,且45MAN ∠=︒,把ADN △绕点A 顺时针旋转90︒得到ABE △.(1)求证:AEM △≌ANM .(2)若3BM =,2DN =,求正方形ABCD 的边长.27.(2021·浙江九年级期末)[教材呈现]如图是华师版八年级上册数学教材第69页的部分内容.[方法运用]在 ABC 中,AB =4,AC =2,点D 在边AC 上.(1)如图①,当点D 是边BC 中点时,AD 的取值范围是.(2)如图②,若BD :DC =1:2,求AD 的取值范围.[拓展提升](3)如图③,在 ABC 中,点D 、F 分别在边BC 、AB 上,线段AD 、CF 相交于点E ,且BD :DC =1:2,AE :ED =3:5.若 ACF 的面积为2,则 ABC 的面积为.28.(2021·浙江杭州市·八年级期末)如图,在△ABC 中,AB=AC ,∠BAC=90°,BC=12厘米.过点C 作直线l BC ⊥,动点P 从点C 开始沿射线CB 方向以2厘米/秒的速度运动,动点Q 也同时从点C 出发在直线l 上以1厘米/秒的速度向上或向下运动.连接AP 、AQ ,设运动时间为t 秒.(1)请写出CP 、CQ 的长度(用含t 的代数式表示):CP=厘米,CQ=厘米;(2)当点P 在边BC 上时,若△ABP 的面积为24厘米2,求t 的值;(3)当t 为多少时,△ABP 与△ACQ 全等?29.(2021·浙江杭州市·九年级二模)如图,AB 是O 的直径,C 是O 上的一点,过点B 作O 的切线BF ,过圆心O 作AC 的平行线交直线BF 于点F ,交O 于点E ,交BC 于点D ,连接CF .(1)判断CF 与O 的位置关系,并证明结论;(2)若四边形ACFO 是平行四边形,求DEOD 的值;(3)若ACB △运动后能与OFB △重合,则DEOD=______,请说明图形的运动过程.30.(2021·浙江湖州市·八年级期末)如图,已知在Rt ABC ∆中,90,ACB CD ∠=︒是斜边(1)求证:AD CE =.(2)若5,6AD AC ==,求BDE ∆的面积.31.(2021·浙江杭州市·八年级期中)如图,点A ,D ,B ,E 依次在同一条直线上,BC DF =,AD BE =,ABC EDF ∠=∠,求证:A E ∠=∠.32.(2021·浙江杭州市·八年级期末)如图,在AOB 和COD △中,OA OB =,OC OD =,若60AOB COD ∠=∠=︒,(1)求证:AC BD =.(2)求APB ∠的度数.33.(2021·浙江宁波市·八年级期末)如图1,ABC 是等边三角形,,D E 为AC 上两点,且AD CE =,延长BC 至点F ,使CF CD =,连结BD EF ,.(1)如图2,当,D E 两点重合时,求证:BD DF =.(2)如图3,延长FE 交线段BD 于点G .①求证:BD EF =.②求DGE ∠的度数.34.(2021·浙江八年级期末)如图,在ABC 中,AB AC =,点D 、E 、F 分别在AB 、BC 、AC 边上,且BE CF =,BD CE =.(1)求证:DEF 是等腰三角形;(2)当40A ∠=︒时,求DEF ∠的度数.35.(2021·浙江八年级期末)如图,AB AC =,AD AE =,BAD CAE ∠=∠,求证:D E ∠=∠.36.(2021·杭州育才中学九年级二模)如图,点O 为正方形ABCD 的中心.DE =AG ,连结EG ,过点O 作OF 丄EG 交AD 于点F .(1)连结E F ,△EDF '的周长与AD 的长有怎样的数量关系,并证明;(2)连结OE ,求∠EOF 的度数;(3)若AF :CE =m ,OF :OE =n ,求证:m =n 2.(1)判断BD 与CE 的数量关系,并证明你的结论;(2)若AB =AD =4,∠BAC =120°,∠CAD =30°.求BD 的长.38.(【新东方】【2021.4.21】【绍兴】【初二下】【数学】【00026】)平面上有ACD △与,BCE AD 与BE 相交于点,P AC 与BE 相交于点,M AD 与CE 相交于点N ,若,,AC BC CD CE ECD ACB ==∠=∠.(1)求证:≌ACD BCE V V ;(2)55,145ACE BCD ∠=︒∠=︒,求BPD ∠的度数.39.(2021·浙江九年级其他模拟)如图,在ABC 中,AB AC =,点D ,E 在BC 上()BD BE <,BD CE =.(1)求证:ABD △≌ACE .(2)若2ADE B ∠=∠,2BD =,求AE 的长.40.(【新东方】【2021.5.19】【JH 】【初二下】【数学】【JH0026】)如图,在一正方形ABCD 中,E 为对角线AC 上一点,连接EB 、ED .△≌△.(1)求证:BEC DEC(2)延长BE交AD于点F,若FD FE∠的度数.=.求AFE41.(2021·浙江温州市·九年级三模)如图,在五边形ABCDE中,AB=CD,∠ABC=∠BCD,BE,CE分别是∠ABC,∠BCD的角平分线.(1)求证:△ABE≌△DCE;(2)当∠A=80°,∠ABC=140°时,求∠AED的度数.42.(2021·浙江八年级期末)如图,在▱ABCD中,点E、F为对角线BD的三等分点,连结AE,CF,AF,CE.(1)求证:四边形AECF为平行四边形;(2)若四边形AECF为菱形,且AE=BE,求∠BAD的度数.43.(2021·浙江八年级期末)如图1,在正方形ABCD中,点P是对角线BD上的一点,连结CP.△≌△;(1)求证:ADP CDP(2)如图2,延长AP交线段DC于点Q,交BC的延长线于点G,点M是GQ的中点,⊥;连结CM.求证:PC MC(3)如图3,延长AP交射线DC于点Q,交BC于点G,点M是GQ的中点,连结CM.若PM=,302∠=︒.求AB的长.BAP44.(【新东方】初中数学1234初二上)如图,在ABC 中,5cm AB AC ==,6cm BC =,BD AC ⊥交AC 于点D .动点P 从点C 出发,按C A B C →→→的路径运动,且速度为2cm/s ,设出发时间为t 秒.(1)求BD 和AD 的长;(2)当 3.2t =秒时,求证:CP AB ⊥;(3)当点P 在BC 边上运动时,若CDP 是以CP 为腰的等腰三角形,请你求出所有满足条件的t 的值.45.(【新东方】初中数学1305【初二上】)如图1,ACB △和ECD 都是等腰直角三角形,,,CA CB CE CD ACB == 的顶点A 在ECD 的斜边DE 上.(1)证明ECA DAB ∠=∠;(2)猜想,,AE AB AD 之间的数量关系,并证明;(3)如图2,若4,80AE AC ==,点F 是AD 的中点,求CF 的长.46.(2021·浙江九年级专题练习)如图1,等边△ABC 边长为8,AD 是△ABC 的中线,P 为线段AD (不包括端点A 、D )上一动点,以CP 为一边且在CP 下方作如图所示的等边△CPE ,连结BE .(1)点P 在运动过程中,线段BE 与AP 始终相等吗?说说你的理由(2)若延长BE 至F ,使得CF=CE=5,如图2,①求出此时AP 的长;②当点P 在线段AD 的延长线上,点F 在射线BE 上时,判断EF 的长是否为定值,若是请直接写出EF 的长;若不是请简单说明理由.47.(【新东方】【2021.5.19】【JH 】【初二下】【数学】【JH0029】)如图1,在ABCD 中,BAD ∠的平分线交BC 于点E ,交DC 的延长线于点F ,以EC ,CF 为邻边作ECFG .(1)求证:ECFG 是菱形.(2)如图2,若90ABC ∠=︒,8AB =,12AD =,M 是EF 的中点,求DM 的长.(3)如图3,若120ABC ∠=︒,连接BD ,BG ,CG ,DG ,求BDG ∠的度数.48.(2021·浙江九年级一模)如图,在四边形ABCD 中,//AD BC ,2BA AD DC ===,45ABC ∠=︒,E 是BC 边上一动点,连结AE ,将AE 绕点A 逆时针旋转135°到AF ,连结EF 与AD 交于点G ,连结DE ,DF ,设BE 的长为x .(1)求证:ABE ADF ≌.(2)若DEF 的面积为y ,求y 关于x 的函数表达式,并求y 的最大值.(3)当FGD 是等腰三角形时,求x 的值.49.(【新东方】初中数学20210625-002【初二上】)如图,ACB △和DCE 均为等腰三角形,点A ,D ,E 在同一直线上,连接,BE CM 为DCE 中DE 边上的高,BN 为ABE △中AE 边上的高,若120ACB DCE ∠=∠=︒,且1CM =,2BN =.(1)求证:≌ACD BCE V V .(2)求AEB ∠的度数.(3)求AE 的长.50.(2020·浙江绍兴市·八年级其他模拟)如图1,ABC 是边长为4cm 的等边三角形,边AB 在射线OM 上,6cm OA =,另一个等边CDE △的顶点D 从O 点出发,沿OM 的方向以1cm/s 的速度运动,在运动过程中CDE △的形状始终保持不变,且点D 不与点A 重合.设运动时间为()s t .(1)求证:CDA CEB ≌;(2)如图2,当610t <<时,BDE 的周长是否存在最小值?若存在,求出BDE 的最小周长:若不存在,请说明理由;(3)如图3,当点D 在射线OM 上运动时,是否存在以D 、E 、B 为顶点的三角形是直角三角形?若存在,求出此时t 的值:若不存在,请说明理由.51.(2021·浙江八年级期末)在正方形ABCD 中,点E 、F 分别是边AD 和DC 上一点,且DE =DF ,连结CE 和AF ,点G 是射线CB 上一点,连结EG ,满足EG =EC ,AF 交EG 于点M ,交EC 于点N .(3)是否存在实数m,当AM=mAF时,BC=3BG?若存在,请求出m的值;若不存在,请说明理由.。
专题02 全等三角形重难点题型(解析版)-初中数学七年级上学期重难点题型分类高分必刷题(人教版)

专题02高分必刷题-全等三角形重难点题型分类(解析版)题型1:全等三角形的性质1.下列说法正确的是()A.两个等边三角形一定全等B.形状相同的两个三角形全等C.面积相等的两个三角形全等D.全等三角形的面积一定相等【解答】解:A、两个边长不相等的等边三角形不全等,故本选项错误;B、形状相同,边长不对应相等的两个三角形不全等,故本选项错误;C、面积相等的两个三角形不一定全等,故本选项错误;D、全等三角形的面积一定相等,故本选项正确.故选:D.2.如图,△ABC≌△DCB,△A=80°,△DBC=40°,则△DCA的度数为()A.20°B.25°C.30°D.35°【解答】解:△△ABC≌△DCB,∴∠D=△A=80°,△ACB=DBC=40°,∴∠DCB=180°﹣∠D﹣∠DBC=60°,∴∠DCA=△DCB﹣∠ACB=20°,故选:A.3.如图,△ABC≌△DEF,BE=7,AD=3,则AB=.【解答】解:△△ABC≌△DEF,∴AB=DE,∴AB﹣AD=DE﹣AD,即BD=AE,∵BE=7,AD=3,∴BD=AE==2∴AB=AD+DB=3+2=5.故答案为:5.题型2:添加一个条件,是两三角形全等4.如图,已知MB=ND,△MBA=△NDC,下列条件中不能判定△ABM≌△CDN的是()A.△M=△N B.AM∥CN C.AB=CD D.AM=CN【解答】解:A、△M=△N,符合ASA,能判定△ABM≌△CDN,故A选项不符合题意;B、AM∥CN,得出△MAB=△NCD,符合AAS,能判定△ABM≌△CDN,故B选项不符合题意.C、AB=CD,符合SAS,能判定△ABM≌△CDN,故C选项不符合题意;D、根据条件AM=CN,MB=ND,△MBA=△NDC,不能判定△ABM≌△CDN,故D选项符合题意;故选:D.5.如图,已知△ADB=△CBD,下列所给条件不能证明△ABD≌△CDB的是()A.△A=△C B.AD=BC C.△ABD=△CDB D.AB=CD【解答】解:在△ABD和△CDB中,,∴△ABD≌△CDB(AAS)∴选项A能证明;在△ABD和△CDB中,,∴△ABD≌△CDB(SAS),∴选项B能证明;在△ABD和△CDB中,,∴△ABD≌△CDB(ASA),∴选项C能证明;选项D不能证明△ABD≌△CDB;故选:D.6.如图,已知△1=△2,要使△ABC≌△CDA,还需要补充的条件不能是()A.AB=CD B.BC=DA C.△B=△D D.△BAC=△DCA 【解答】解:A、根据AB=CD和已知不能推出两三角形全等,错误,故本选项正确;B、△在△ABC和△CDA中∴△ABC≌△CDA(SAS),正确,故本选项错误;C、△在△ABC和△CDA中∴△ABC≌△CDA(AAS),正确,故本选项错误;D、△在△ABC和△CDA中∴△ABC≌△CDA(AAS),正确,故本选项错误;故选:A.题型三:尺规作图的依据7.如图,是用直尺和圆规作一个角等于已知角的示意图,则说明△A′O′B′=△AOB的依据是()A.SSS B.SAS C.AAS D.ASA【解答】解:由作法易得OD=O′D′,OC=O′C′,CD=C′D′,依据SSS可判定△COD≌△C'O'D',故选:A.8.工人师傅常用角尺平分一个任意角.做法如下:如图,△AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C作射线OC.由此作法便可得△MOC≌△NOC,其依据是()A.SSS B.SAS C.ASA D.AAS【解答】解:∵在△ONC和△OMC中,∴△MOC≌△NOC(SSS),∴∠BOC=∠AOC,故选:A.9.如图,红红书上的三角形被墨迹污染了一部分,她根据所学的知识很快就画了一个与书上完全一样的三角形,那么红红画图的依据是()A.SSS B.SAS C.ASA D.AAS【解答】解:根据题意,三角形的两角和它们的夹边是完整的,所以可以利用“角边角”定理作出完全一样的三角形.故选:C.题型4:角平分线的性质10.如图,在△ABC中,△C=90°,AC=BC,AD平分△CAB交BC于D,DE⊥AB于E,若AB=6cm,则△DBE的周长是()A.6 cm B.7 cm C.8 cm D.9 cm【解答】解:△AD平分△CAB,DE⊥AB,△C=90°,∴DE=CD,又△AC=BC,AC=AE,∴AC=BC=AE,∴△DBE的周长=DE+BD+EB=CD+BD+EB=BC+EB=AE+EB=AB,∵AB =6cm,∴△DBE的周长=6cm.故选:A.11.如图,△ABC中,△C=90°,AD是角平分线,AB=14,S△ABD=28,则CD的长为.【解答】解:如图,过D作DE⊥AB于E,∵∠C=90°,AD是角平分线,∴由角平分线的性质,得DE=CD.∵AB=14,S△ABD=28,∴×AB×DE=28,即×14×DE=28,解得DE=4,∴CD=4,故答案为:4.12.如图,BD是△ABC的平分线,DE⊥AB于E,S△ABC=36cm2,AB=18cm,BC=12cm,则DE=cm.【解答】解:过点D作DF⊥BC于点F,∵BD是△ABC的平分线,DE⊥AB,∴DE=DF,∵AB=18cm,BC=12cm,∴S△ABC=S△ABD+S△BCD=AB•DE+BC•DF=DE•(AB+BC)=36cm2,∴DE=2.4(cm).故答案为:2.4.题型五:全等三角形中档证明题考向1:重叠边技巧①短边相等+重叠边=长边相等②长边相等-重叠边=短边相等13.如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,△A=△D,AF=DC.求证:(1)△ABC≌△DEF;(2)BC∥EF.【解答】证明:(1)△AF=DC,∴AF+CF=DC+CF,∴AC=DF,∵在△ABC和△DEF中,∴△ABC≌△DEF(SAS);(2)△由(1)知△ABC≌△DEF,∴∠BCA=△EFD,∴BC∥EF.14.已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,求证:AB∥DE.【解答】证明:△AF=DC,∴AF﹣FC=DC﹣CF,即AC=DF.在△ACB和△DFE中,∴△ACB≌△DFE(SSS),∴∠A=△D,∴AB∥DE.考向2:重叠角技巧重叠角技巧:①小角相等+重叠角=大角相等②大角相等-重叠角=小角相等15.如图,AB=AD,△C=△E,△1=△2,求证:△ABC≌△ADE.【解答】证明:△△1=△2,∴∠1+∠EAC=△2+∠EAC,即△BAC=△DAE,在△ABC和△ADE中,,∴△ABC≌△ADE(AAS).16.如图,△ABC和△ADE都是等腰三角形,且△BAC=90°,△DAE=90°,B,C,D在同一条直线上.求证:BD=CE.【解答】证明:△△ABC和△ADE都是等腰直角三角形,∴AD=AE,AB=AC,又△△EAC =90°+∠CAD,△DAB=90°+∠CAD,∴∠DAB=△EAC,∵在△ADB和△AEC中,∴△ADB≌△AEC(SAS),∴BD=CE.考向三:等角的余角相等技巧:∠1+∠2=90,∠2+∠3=90, ∠1=∠3技巧:把全等三角形中一个三角形的两个锐角分别随意标上∠1、∠2,再从第二个三角形的两个锐角中挑一个和∠1或∠2互余的角标上∠3。
专题1-8 HL判定三角形全等-重难点题型(举一反三)(苏科版)(解析版)

专题1.8 HL判定三角形全等-重难点题型【苏科版】【题型1 HL判定三角形全等的条件】【例1】(2020秋•秦淮区期末)结合图,用符号语言表达定理“斜边和一条直角边分别相等的两个直角三角形全等”的推理形式:在Rt△ABC和Rt△DEF中,∠C=∠F=90°,AC=DF∴Rt△ABC≌Rt△DEF.【分析】根据条件可知,少一组斜边,所以可添加为:AB=DE.【解答】解:∵∠C=∠F=90°,∴在Rt△ABC和Rt△DEF中,{AC=DFAB=DE,∴Rt△ABC≌Rt△DEF(HL),故答案为:AB=DE.【点评】本题考查了直角三角形全等的判定定理,【变式1-1】(2020秋•金乡县期中)如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,若利用“HL”证明Rt△ABC≌Rt△DCB,你添加的条件是.(不添加字母和辅助线)【分析】根据:斜边与直角边对应相等的两个直角三角形全等,使Rt△ABC≌Rt△DCB,添加的条件是:AB=DC.【解答】解:∵斜边与直角边对应相等的两个直角三角形全等,∴在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,使Rt△ABC≌Rt△DCB,添加的条件是:AB=DC.故答案为:AB=DC(答案不唯一)【点评】此题主要考查了全等三角形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①判定定理1:SSS﹣﹣三条边分别对应相等的两个三角形全等.②判定定理2:SAS﹣﹣两边及其夹角分别对应相等的两个三角形全等.③判定定理3:ASA﹣﹣两角及其夹边分别对应相等的两个三角形全等.④判定定理4:AAS﹣﹣两角及其中一个角的对边对应相等的两个三角形全等.⑤判定定理5:HL﹣﹣斜边与直角边对应相等的两个直角三角形全等.【变式1-2】(2021春•宝安区期中)如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件的个数是()A.0B.1C.2D.3【分析】根据直角三角形的全等的条件进行判断,即可得出结论.【解答】解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);②当∠ABC=∠ABD时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);③当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);故选:D.【点评】本题主要考查了直角三角形全等的判定,直角三角形首先是三角形,所以一般三角形全等的判定方法都适合它,同时直角三角形又是特殊的三角形,作为“HL”公理就是直角三角形独有的判定方法.【变式1-3】(2021春•金水区校级月考)下列说法正确的有()①两个锐角分别相等的的两个直角三角形全等;②一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等;③两边分别相等的两个直角三角形全等;④一个锐角和一条边分别相等的两个直角三角形全等.A.1B.2C.3D.4【分析】根据直角三角形全等的判定方法逐条判定即可得到结论,【解答】解:①两个锐角分别相等的的两个直角三角形不一定全等,故该说法错误;②如图,已知:∠B=∠E=90°,BC=EF,AM=BM,DN=EN,CM=FN,求证:△ABC≌△DEF,证明:∵∠B=∠E=90°,BC=EF,CM=FN,∴Rt△BCM≌Rt△EFN(HL),∴BM=EN∵AM=BM,DN=EN,∴AB=DE,∴Rt△ABC≌Rt△EFN(SAS),故一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等的说法正确;③两对应边分别相等的两个直角三角形全等,如果是一个直角三角形的两条直角边和另一个直角三角形的一条直角边和一条斜边分别相等,这两个直角三角形不全等,故该说法错误;④一个锐角和一条边分别对应相等的两个直角三角形不一定全等,如果一个直角三角形的一条直角边和另一个直角三角形的一条斜边相等,这两个直角三角形不全等,故该说法错误;故选:A.【点评】本题主要考查了直角三角形全等的判定,熟练掌握全等三角形判定方法是解决问题的关键.【题型2 直角三角形全等的判定与性质(求角的度数)】【例2】(2020秋•昌平区期末)如图,Rt△ABC中,∠ACB=90°,∠B=50°,D,F分别是BC,AC上的点,DE⊥AB,垂足为E,CF=BE,DF=DB,则∠ADE的度数为()A.40°B.50°C.70°D.71°【分析】根据已知条件得出△CDF≌△EDB,从而得出CD=DE,从而得出△ACD≌△AED,从而得出∠DAE=20°,即可得出答案.【解答】解:根据题意:在Rt△CDF和Rt△EDB中,{FC=BEDF=DB,∴Rt△CDF≌Rt△EDB(HL),∴CD=DE,∵在Rt△ACD和Rt△AED中{CD=DEAD=AD,∴Rt△ACD≌Rt△AED(HL),∴∠DAE=20°,∴∠ADE=70°.故选:C.【点评】本题主要考查了全等三角形的判定及全等三角形的性质,难度适中.【变式2-1】(2021春•娄底月考)如图,已知∠C=∠F=90°,AC=DF,AE=DB,BC与EF交于点O.(1)求证:Rt△ABC≌Rt△DEF;(2)若∠A=51°,求∠BOF的度数.【分析】(1)根据HL证明两个三角形全等;(2)根据三角形全等的性质和三角形外角的性质可得结论.【解答】(1)证明:∵AE=DB,∴AE+EB=DB+EB,即AB=DE,在Rt△ACB和Rt△DFE中,{AC=DFAB=DE,∴Rt△ABC≌Rt△DEF(HL);(2)解:∵∠C=90°,∠A=51°,∴∠ABC=∠C﹣∠A=90°﹣51°=39°,由(1)知Rt△ABC≌Rt△DEF,∴∠ABC=∠DEF.∴∠DEF=39°,∴∠BOF=∠ABC+∠BEF=39°+39°=78°.【点评】本题考查了全等三角形的性质和判定,尤其是掌握直角三角形特殊的全等判定:HL,在判定三角形全等时,关键是选择恰当的判定条件.【变式2-2】(2021春•姑苏区期末)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:Rt△ABE≌Rt△CBF;(2)若∠CAE=30°,∠BAC=45°,求∠ACF的度数.【分析】(1)由AB =CB ,∠ABC =90°,AE =CF ,即可利用HL 证得Rt △ABE ≌Rt △CBF ;(2)由AB =CB ,∠ABC =90°,即可求得∠ACB 的度数,即可得∠BAE 的度数,又由Rt △ABE ≌Rt △CBF ,即可求得∠BCF 的度数,则由∠ACF =∠BCF +∠ACB 即可求得答案.【解答】(1)证明:∵∠ABC =90°,∴∠CBF =∠ABE =90°,在Rt △ABE 和Rt △CBF 中,{AE =CF AB =BC, ∴Rt △ABE ≌Rt △CBF (HL );(2)解:∵∠ABC =90°,∠BAC =45°,∴∠ACB =45°,又∵∠BAE =∠CAB ﹣∠CAE =45°﹣30°=15°,由(1)知:Rt △ABE ≌Rt △CBF ,∴∠BCF =∠BAE =15°,∴∠ACF =∠BCF +∠ACB =45°+15°=60°.【点评】此题考查了直角三角形全等的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用.【变式2-3】(2020秋•鹿城区校级月考)如图,已知BC =ED ,∠B =∠E =Rt ∠,∠ACD =∠ADC .(1)求证:△ABC ≌△AED ;(2)当∠BAE =140°时,求∠BCD 的度数.【分析】(1)由∠ACD =∠ADC 知AC =AD ,再利用“HL ”即可证明△ABC ≌△AED ;(2)由Rt △ABC ≌Rt △AED 可设∠BAC =∠EAD =x ,∠CAD =y ,根据∠BAE =140°知2x +y =140°,由∠B =90°得∠ACB =90°﹣x 、AC =AD 知∠ACD =∠ADC =90°−12y ,再根据∠BCD =∠ACB +∠ACD 求解可得.【解答】证明:(1)∵∠ACD =∠ADC ,∴AC =AD ,在Rt △ABC 和Rt △AED 中,∵{BC =ED AC =AD, ∴Rt △ABC ≌Rt △AED (HL );(2)∵Rt △ABC ≌Rt △AED ,∴可设∠BAC =∠EAD =x ,∠CAD =y ,∵∠BAE =140°,∴2x +y =140°,∵∠B =90°,∴∠ACB =90°﹣x ,又∵AC =AD ,∴∠ACD =∠ADC =180°−∠CAD 2=90°−12y , 则∠BCD =∠ACB +∠ACD=90°﹣x +90°−12y=180°−12(2x +y )=180°﹣70°=110°.【点评】本题主要考查全等三角形的判定与性质,解题的关键是掌握直角三角形全等的判定与性质、等腰三角形的性质.【题型3 直角三角形全等的判定与性质(求线段长度)】【例3】(2020秋•西城区校级期中)如图,已知Rt △ABC 中,∠ACB =90°,CA =CB ,D 是AC 上一点,E 在BC 的延长线上,且AE =BD ,BD 的延长线与AE 交于点F .若CD =3,则求CE 的长.【分析】证明△BDC≌△AEC得出:CD=CE.【解答】(1)解:∵∠ACB=90°,∴∠ACE=∠BCD=90°.在Rt△BDC与Rt△AEC中,{BC=ACBD=AE,∴Rt△BDC≌Rt△AEC(HL).∴CD=CE=3;【点评】本题考查了直角三角形全等的判定及性质的运用,解答时证明三角形全等是关键.【变式3-1】(2020秋•承德校级期中)在Rt△ABC中,∠ACB=90°,E是AB上一点,且BE=BC,过E 作DE⊥AB交AC于D,如果AC=5cm,则AD+DE等于()A.3 cm B.4 cm C.5 cm D.6 cm【分析】根据HL证Rt△BED≌Rt△BCD,推出DE=DC,得出AD+DE=AD+DC=AC,代入求出即可.【解答】解:∵DE⊥AB,∴∠DEB=90°=∠C,在Rt△BED和Rt△BCD中{BD=BDBE=BC,∴Rt△BED≌Rt△BCD(HL),∴DE=DC,∴AD+DE=AD+CD=AC=5cm,故选:C.【点评】本题考查了直角三角形全等的性质和判定,注意:全等三角形的对应边相等,判断直角三角形全等的方法有SAS,ASA,AAS,SSS,HL.【变式3-2】(2020秋•平谷区期末)如图,在Rt△ABC中,∠C=90°,D为BC上一点,连接AD,过D 点作DE⊥AB,且DE=DC.若AB=5,AC=3,则EB=.【分析】由“HL”可证Rt△ADE≌Rt△ADC,可得AC=AE=3,即可求BE.【解答】解:在Rt△ADE和Rt△ADC中,{AD=ADDE=DC,∴Rt△ADE≌Rt△ADC(HL),∴AC=AE=3,∴BE=AB﹣AE=2,故答案为2.【点评】本题考查了全等三角形的判定和性质,掌握全等三角形的判定定理是本题的关键.【变式3-3】(2020秋•兰山区期末)在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P、Q两点分别在边AC和射线AX上移动.当PQ=AB,AP=时,△ABC和△APQ全等.【分析】分情况讨论:①AP=BC=8cm时,Rt△ABC≌Rt△QP A(HL);②当P运动到与C点重合时,Rt△ABC≌Rt△PQA(HL),此时AP=AC=15cm.【解答】解:①当P运动到AP=BC时,如图1所示:在Rt △ABC 和Rt △QP A 中,{AB =QP BC =PA, ∴Rt △ABC ≌Rt △QP A (HL ),即AP =B =8cm ;②当P 运动到与C 点重合时,如图2所示:在Rt △ABC 和Rt △PQA 中,{AB =PQ AC =PA, ∴Rt △ABC ≌Rt △PQA (HL ),即AP =AC =15cm .综上所述,AP 的长度是8cm 或15cm .故答案为:8cm 或15cm .【点评】本题考查了三角形全等的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键,注意分类讨论,以免漏解.【题型4 直角三角形全等的判定与性质(证垂直)】【例4】(2021春•万柏林区校级月考)如图,AC ∥BD ,∠C =90°,AC =BE ,AB =DE ,求证:DE ⊥AB .【分析】先根据平行线的性质求出∠DBE=∠C=90°,再由HL定理可判定△ACB≌△EBD,由全等三角形的性质解答即可.【解答】证明:设AB与DE相交于点M,∵AC∥BD,∴∠C+∠DBE=180°,∵∠C=90°,∴∠DBE=90°,在Rt△ACB与Rt△EBD中,{AC=BE,AB=DE∴Rt△ACB≌Rt△EBD(HL),∴∠ABC=∠D,∵∠D+∠MEB=90°,∴∠ABC+∠MEB=90°,∴∠EMB=180°﹣∠ABC﹣∠MEB=90°,∴DE⊥AB.【点评】此题考查了全等三角形的判定与性质,根据HL判定Rt△ACB≌Rt△EBD是解题的关键.【变式4-1】(2021•三水区一模)如图,AB=AC,直线l过点A,BM⊥直线l,CN⊥直线l,垂足分别为M、N,且BM=AN.(1)求证△AMB≌△CNA;(2)求证∠BAC=90°.【分析】(1)由HL证明△AMB≌△CNA即可;(2)先由全等三角形的性质得∠BAM=∠ACN,再由∠CAN+∠ACN=90°,得∠CAN+∠BAM=90°,即可得出结论.【解答】证明:(1)∵BM⊥直线l,CN⊥直线l,∴∠AMB=∠CNA=90°,在Rt△AMB和Rt△CNA中,{AB=CABM=AN,∴Rt△AMB≌Rt△CNA(HL);(2)由(1)得:Rt△AMB≌Rt△CNA,∴∠BAM=∠ACN,∵∠CAN+∠ACN=90°,∴∠CAN+∠BAM=90°,∴∠BAC=180°﹣90°=90°.【点评】本题考查的是全等三角形的判定和性质以及直角三角形的性质,掌握全等三角形的判定定理和性质定理是解题的关键.【变式4-2】(2020秋•西湖区校级月考)如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.(1)Rt△ADE与Rt△BEC全等吗?并说明理由;(2)试判断CE和DE的关系,并说明理由.【分析】(1)由∠1=∠2,可得DE=CE,根据证明直角三角形全等的“HL”定理,证明即可;(2)由∠1=∠2,可得DE=CE,再根据题意,∠AED+∠ADE=90°,∠BEC+∠BCE=90°,又∠AED =∠BCE,∠ADE=∠BEC,所以,∠AED+∠BEC=90°,即可证得∠DEC=90°,即可得出.【解答】解:(1)结论:Rt△ADE≌Rt△BEC;理由如下:∵∠1=∠2,∴DE=CE,而∠A=∠B=90°,AE=BC∴在Rt△ADE和Rt△BEC中,DE=CE,AE=BC,∴Rt△ADE≌Rt△BEC(HL);(2)结论:DE=CE且DE⊥CE,理由如下:∵∠1=∠2∴DE=CE,∵Rt△ADE≌Rt△BEC,∴∠AED=∠BCE,∠ADE=∠BEC,又∵∠AED+∠ADE=90°,∠BEC+∠BCE=90°,∴2(∠AED+∠BEC)=180°,∴∠AED+∠BEC=90°,∴∠DEC=90°,∴DE⊥CE.【点评】本题主要考查了直角三角形的判定与性质,证明三角形全等时,关键是根据题意选取适当的条件.【变式4-3】(2020秋•城北区校级月考)如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.【分析】猜想:BF⊥AE,先证明△BDC≌△AEC得出∠CBD=∠CAE,从而得出∠BFE=90°,即BF⊥AE.【解答】解:猜想:BF⊥AE.理由:∵∠ACB=90°,∴∠ACE=∠BCD=90°.∴在Rt△BDC与Rt△AEC中{BC=ACBD=AE,∴Rt△BDC≌Rt△AEC(HL).∴∠CBD=∠CAE.又∴∠CAE+∠E=90°.∴∠EBF+∠E=90°.∴∠BFE=90°,即BF⊥AE.【点评】主要考查全等三角形的判定方法,以及全等三角形的性质.猜想问题一定要认真观察图形,根据图形先猜后证.。
专题1-3 全等三角形-重难点题型(举一反三)(苏科版)(解析版)

专题1.3 全等三角形-重难点题型【苏科版】【题型1 全等三角形的对应元素判断】【例1】(2020秋•潍城区期中)如图,△ABC≌△DEF,点E、C、F、B在同一条直线上.下列结论正确的是()A.∠B=∠D B.∠ACB=∠DEF C.AC=EF D.BF=CE【分析】根据全等三角形的对应边相等、对应角相等解答.【解答】解:∵△ABC≌△DEF,∴∠B=∠E,但∠B与∠D不一定相等,A选项结论错误,不符合题意;∵△ABC≌△DEF,∴∠ACB=∠EFD,当∠ACB与∠DEF不一定相等,B选项结论错误,不符合题意;∵△ABC≌△DEF,∴AC=DF,当AC与EF不一定相等,C选项结论错误,不符合题意;∵△ABC≌△DEF,∴BC=EF,∴BC﹣CF=EF﹣CF,即BF=CE,D选项结论正确,符合题意;故选:D.【点评】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、对应角相等是解题的关键.【变式1-1】(2020秋•合江县月考)如图,已知△ABC≌△CDA,下面四个结论中,不正确的是()A.△ABC和△CDA的面积相等B.△ABC和△CDA的周长相等C.∠B+∠ACB=∠D+∠ACD D.AD∥BC,且AD=CB【分析】由全等三角形的性质可得S△ABC=S△CDA,△ABC和△CDA的周长相等,AD=CB,∠B=∠D,∠ACB=∠DAC,进而可得AD∥BC,即可求解.【解答】解:∵△ABC≌△CDA,∴S△ABC=S△CDA,△ABC和△CDA的周长相等,AD=CB,∠B=∠D,∠ACB=∠DAC,∴AD∥BC,故选项A、B、D都不符合题意,∵∠ACB不一定等于∠ACD,∴∠B+∠ACB不一定等于∠D+∠ACD,故选项C符合题意,故选:C.【点评】本题考查了全等三角形的性质,掌握全等三角形的性质是本题的关键.【变式1-2】(2020秋•海珠区校级期中)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于下列结论:①AC=AF;②∠F AB=∠EAB;③EF=BC;④∠EAB=∠F AC.其中正确结论的个数是()A.1个B.2个C.3个D.4个【分析】利用全等三角形的性质可得答案.【解答】解:∵△ABC≌△AEF,∴AF=AC,EF=CB,∠F AE=∠BAC,∴∠F AE﹣∠F AB=∠BAC﹣∠BAF,即∠BAE=∠F AC,∴正确的结论是①③④,共3个,故选:C.【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形,对应边相等,对应角相等.【变式1-3】(2020秋•北碚区期中)如图所示,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上.下列结论:①BD是∠ABE的平分线;②AB⊥AC;③∠C=30°;④线段DE是△BDC的中线;⑤AD+BD=AC其中正确的有()个.A.2B.3C.4D.5【分析】根据全等三角形的对应角相等得出∠ABD=∠EBD,即可判断①;先由全等三角形的对应边相等得出BD=CD,BE=CE,再根据等腰三角形三线合一的性质得出DE⊥BC,则∠BED=90°,再根据全等三角形的对应角相等得出∠A=∠BED=90°,即可判断②;根据全等三角形的对应角相等得出∠ABD=∠EBD,∠EBD=∠C,从而可判断∠C,即可判断③;根据全等三角形的对应边相等得出BE=CE,再根据三角形中线的定义即可判断④;根据全等三角形的对应边相等得出BD=CD,但A、D、C 可能不在同一直线上,所以AD+CD可能不等于AC.【解答】解:①∵△ADB≌△EDB,∴∠ABD=∠EBD,∴BD是∠ABE的平分线,故①正确;②∵△BDE≌△CDE,∴BD=CD,BE=CE,∴DE⊥BC,∴∠BED=90°,∵△ADB≌△EDB,∴∠A=∠BED=90°,∴AB⊥AD,∵A、D、C可能不在同一直线上∴AB可能不垂直于AC,故②不正确;③∵△ADB≌△EDB,△BDE≌△CDE,∴∠ABD=∠EBD,∠EBD=∠C,∵∠A=90°若A、D、C不在同一直线上,则∠ABD+∠EBD+∠C≠90°,∴∠C≠30°,故③不正确;④∵△BDE≌△CDE,∴BE=CE,∴线段DE是△BDC的中线,故④正确;⑤∵△BDE≌△CDE,∴BD=CD,若A、D、C不在同一直线上,则AD+CD>AC,∴AD+BD>AC,故⑤不正确.故选:A.【点评】本题考查了全等三角形的性质:全等三角形的对应边相等,全等三角形的对应角相等.也考查了等腰三角形三线合一的性质,直角三角形两锐角互余的性质,难度适中.【题型2 利用全等三角形的性质求角度】【例2】(2020秋•兰山区期末)如图,已知△ABC≌△DEF,CD平分∠BCA,若∠A=30°,∠CGF=88°,则∠E的度数是()A.30°B.50°C.44°D.34°【分析】根据角平分线的性质得到∠ACD=∠BCD=12∠BCA,根据全等三角形的性质得到∠D=∠A=30°,根据三角形的外角性质、全等三角形的性质解答即可.【解答】解:∵CD平分∠BCA,∴∠ACD=∠BCD=12∠BCA,∵△ABC≌△DEF,∴∠D=∠A=30°,∵∠CGF=∠D+∠BCD,∴∠BCD=∠CGF﹣∠D=58°,∴∠BCA=116°,∴∠B=180°﹣30°﹣116°=34°,∵△ABC≌△DEF,∴∠E=∠B=34°,故选:D.【点评】本题考查的是全等三角形的性质、三角形内角和定理,掌握全等三角形的对应角相等是解题的关键.【变式2-1】(2020春•沙坪坝区校级期末)如图,△ABC≌△ADE,且AE∥BD,∠BAD=130°,则∠BAC 度数的值为.【分析】根据全等三角形的性质,可以得到AB=AD,∠BAC=∠DAE,从而可以得到∠ABD=∠ADB,再根据AE∥BD,∠BAD=130°,即可得到∠DAE的度数,从而可以得到∠BAC的度数.【解答】解:∵△ABC≌△ADE,∴AB=AD,∠BAC=∠DAE,∴∠ABD=∠ADB,∵∠BAD=130°,∴∠ABD=∠ADB=25°,∵AE∥BD,∴∠DAE=∠ADB,∴∠DAE=25°,∴∠BAC=25°,故答案为:25°.【点评】本题考查全等三角形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.【变式2-2】(2020秋•覃塘区期中)如图,已知△AEF≌△ABC,点E在BC边上,EF与AC交于点D.若∠B=64°,∠C=30°,求∠CDF的度数.【分析】根据全等三角形的性质和三角形外角性质解答即可.【解答】解:∵△AEF≌△ABC,∴AE=AB,∠AEF=∠B=64°,∵点E在BC边上,∴∠AEB=∠B=64°,∴∠DEC=180°﹣∠AEB﹣∠AEF=180°﹣64°﹣64°=52°,又∵∠C=30°,且∠CDF是△CDE的外角,∴∠CDF=∠DEC+∠C=52°+30°=82°.【点评】此题考查全等三角形的性质,关键是根据全等三角形的对应角相等解答.【变式2-3】(2020秋•西湖区校级月考)如图,△ABC≌△ADE,BC的延长线分别交AD,DE于点F,G,且∠DAC=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.【分析】先根据全等三角形的性质得∠BAC=∠DAE,由于∠DAE+∠CAD+∠BAC=120°,则可计算出∠BAC=55°,所以∠BAF=∠BAC+∠CAD=65°,根据三角形外角性质可得∠DFB=∠BAF+∠B=90°,∠DGB=65°.【解答】解:∵△ABC≌△ADE,∴∠BAC=∠DAE,∵∠EAB=120°,∴∠DAE+∠CAD+∠BAC=120°,∵∠CAD=10°,∴∠BAC=12(120°﹣10°)=55°,∴∠BAF=∠BAC+∠CAD=65°,∴∠DFB=∠BAF+∠B=65°+25°=90°;∵∠DFB=∠D+∠DGB,∴∠DGB=90°﹣25°=65°.【点评】本题考查了全等三角形的性质:全等三角形的性质是证明线段和角相等的理论依据,应用时要会找对应角和对应边.【题型3 利用全等三角形的性质求线段长度】【例3】(2020秋•永吉县期中)如图,△EFG≌△NMH,E,H,G,N在同一条直线上,EF和NM,FG 和MH是对应边,若EH=1.1cm,NH=3.3cm.求线段HG的长.【分析】由△EFG≌△NMH,EF和NM,FG和MH是对应边,得到EG和NH是对应边,根据全等三角形的性质得到EG=NH,根据线段的和差计算即可得到结果.【解答】解:∵△EFG≌△NMH,EF和NM,FG和MH是对应边,∴EG和NH是对应边,∴EG=NH,∴EH+HG=HG+NG,∴EH=NG,∵EH=1.1,∴NG=1.1∵NH=3.3cm,∴HG=NH﹣NG=3.3﹣1.1=2.2(cm).【点评】本题主要考查了全等三角形全等的性质,熟练找出两个全等三角形的对应边是解此题的关键.【变式3-1】(2020秋•永定区期中)如图,△ADE≌△BCF,AD=8cm,CD=6cm,则BD的长为cm.【分析】根据全等三角形的性质得出AD=BC=8cm,进而即可求得BD=BC﹣CD=2cm.【解答】解:∵△ADE≌△BCF,∴AD=BC=8cm,∵BD=BC﹣CD,CD=6cm,∴BD=8﹣6=2(cm).故答案为:2.【点评】本题考查了全等三角形的性质,熟记性质是解题的关键.【变式3-2】(2020秋•东莞市校级月考)如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,已知△AEH≌△CEB,EB=5,AE=7,则CH的长是.【分析】根据全等三角形的性质分别求出EC、EH,结合图形计算,得到答案.【解答】解:∵△AEH≌△CEB,∴EC=AE=7,EH=EB=5,∴CH=EC﹣EH=7﹣5=2,故答案为:2.【点评】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.【变式3-3】(2020秋•中山市期中)一个三角形的三条边的长分别是3,5,7,另一个三角形的三条边的长分别是3,3x ﹣2y ,x +2y ,若这两个三角形全等,则x +y 的值是 .【分析】根据全等三角形的性质可得方程组{3x −2y =5x +2y =7,或{x +2y =53x −2y =7,解方程组可得答案. 【解答】解:由题意得{3x −2y =5x +2y =7,或{x +2y =53x −2y =7, 解得:{x =3y =2或{x =3y =1, x +y =5或x +y =4,故答案为:5或4【点评】此题主要考查了全等三角形的性质,关键是掌握全等三角形对应边相等.【题型4 与全等三角形性质有关的证明】【例4】(2020秋•安徽月考)如图,△ABC ≌△ADE ,点E 在边BC 上,求证:∠BED =∠BAD .【分析】根据全等三角形的性质和三角形的外角的性质即可得到结论.【解答】证明:∵△ABC ≌△ADE ,∴∠C =∠AED ,∠BAC =∠DAE ,∴∠BAC ﹣∠BAE =∠DAE ﹣∠BAE ,即∠CAE =∠BAD ,∵∠AEB =∠AED +∠DEB =∠CAE +∠C ,∴∠CAE =∠BED ,∴∠BED =∠BAD .【点评】本题考查了三角形全等的性质,三角形的外角的性质,关键是熟练掌握全等三角形的性质.【变式4-1】(2020秋•大安市校级期中)已知△ABF ≌△DCE ,E 与F 是对应顶点.证明AF ∥DE .【分析】根据全等三角形的性质得出∠B =∠C ,∠BAF =∠CDE ,根据三角形外角性质求出∠AFE =∠DEF ,根据平行线的判定得出即可.【解答】证明:∵△ABF≌△DCE,∴∠B=∠C,∠BAF=∠CDE,∴∠B+∠BAF=∠C+∠CDE,∴∠AFE=∠DEF,∴AF∥DE.【点评】本题考查了全等三角形的性质,三角形外角性质,平行线的判定等知识点,能灵活运用定理机芯推理是解此题的关键.【变式4-2】(2020春•成都期中)如图,△ABC中,点E是AB边上一点,△BCE≌△ACE,ED∥AC,DF ⊥AB.(1)判断CE与AB是否垂直,并说明理由;(2)证明:∠EDF=∠BDF.【分析】(1)根据全等三角形的性质即可得到结论;(2)根据全等三角形的性质和平行线的判定和性质即可得到结论.【解答】解:(1)CE⊥AB,理由:∵△BCE≌△ACE,∴BEC=∠AEC=12×180°=90°,∴CE⊥AB;(2)∵ED∥AC,∴∠DEC=∠ACE,∵△BCE≌△ACE,∴∠BCE=∠ACE,∴∠CED=∠DCE,∵DF⊥AB,∴DF∥CE,∴∠BDF=∠DCE,∠EDF=∠CED,∴∠EDF=∠BDF.【点评】本题考查了全等三角形的性质,平行线的性质,正确的识别图形是解题的关键.【变式4-3】(2020秋•定远县月考)如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.(1)求证:BC=DE+CE;(2)当△ABC满足什么条件时,BC∥DE?【分析】(1)根据全等三角形的性质得出AE=BC,AC=DE,再求出答案即可;(2)根据平行线的性质得出∠BCE=∠E,根据全等三角形的性质得出∠ACB=∠E,求出∠ACB=∠BCE,再求出答案即可.【解答】(1)证明:∵△ABC≌△DAE,∴AE=BC,AC=DE,又∵AE=AC+CE,∴BC=DE+CE;(2)解:∵BC∥DE,∴∠BCE=∠E,又∵△ABC≌△DAE,∴∠ACB=∠E,∴∠ACB=∠BCE,又∵∠ACB+∠BCE=180°,∴∠ACB=90°,即当△ABC满足∠ACB为直角时,BC∥DE.【点评】本题考查了全等三角形的判定定理和平行线的性质和判定,能灵活运用定理进行推理是解此题的关键,注意:全等三角形的对应边相等,对应角相等.【题型5 与全等三角形性质有关的综合】【例5】(2020秋•朔州月考)如图,△ACF≌△DBE,其中点A、B、C、D在同一条直线上.(1)若BE⊥AD,∠F=63°,求∠A的大小.(2)若AD=11cm,BC=5cm,求AB的长.【分析】(1)根据全等三角形的性质得到∠FCA=∠EBD=90°,根据直角三角形的性质计算即可;(2)根据全等三角形的性质得到CA=BD,结合图形得到AB=CD,计算即可.【解答】解:(1)∵BE⊥AD,∴∠EBD=90°,∵△ACF≌△DBE,∴∠FCA=∠EBD=90°,∴∠A=90°﹣∠F=27°;(2)∵△ACF≌△DBE,∴CA=BD,∴CA﹣CB=BD﹣BC,即AB=CD,∵AD=11cm,BC=5cm,∴AB+CD=11﹣5=6cm,∴AB=3cm.【点评】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、对应角相等是解题的关键.【变式5-1】(2020秋•新罗区校级月考)如图,点A、B、C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2cm,BC=3cm.(1)求DE的长;(2)判断AC与BD的位置关系,并说明理由.(3)判断直线AD与直线CE的位置关系,并说明理由.【分析】(1)根据全等三角形的对应边相等得到BD=BC=5cm,BE=AB=2cm,计算即可;(2)根据全等三角形的对应角相等和平角的定义解答;(3)根据全等三角形的对应角相等和三角形内角和定理进行解答.【解答】解:(1)∵△ABD≌△EBC,∴BD=BC=3cm,BE=AB=2cm,∴DE=BD﹣BE=1cm;(2)DB与AC垂直,理由:∵△ABD≌△EBC,∴∠ABD=∠EBC,又A、B、C在一条直线上,∴∠EBC=90°,∴DB与AC垂直.(3)直线AD与直线CE垂直.理由:如图,延长CE交AD于F,∵△ABD≌△EBC,∴∠D=∠C,∵Rt△ABD中,∠A+∠D=90°,∴∠A+∠C=90°,∴∠AFC=90°,即CE⊥AD.【点评】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等、全等三角形的对应角相等是解题的关键.【变式5-2】(2018春•德化县期末)如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,(1)当DE=8,BC=5时,线段AE的长为;(2)已知∠D=35°,∠C=60°,①求∠DBC的度数;②求∠AFD的度数.【分析】(1)根据全等三角形的性质得出AB=DE=8,BE=BC=5,即可求出答案;(2)①根据全等三角形的性质得出∠A=∠D=35°,∠DBE=∠C=60°,根据三角形内角和定理求出∠ABC,即可得出答案;②根据三角形外角性质求出∠AEF,根据三角形外角性质求出∠AFD即可.【解答】解:(1)∵△ABC≌△DEB,DE=8,BC=5,∴AB=DE=8,BE=BC=5,∴AE=AB﹣BE=8﹣5=3,故答案为:3;(2)①∵△ABC≌△DEB∴∠A=∠D=35°,∠DBE=∠C=60°,∵∠A+∠ABC+∠C=180°,∴∠ABC=180°﹣∠A﹣∠C=85°,∴∠DBC=∠ABC﹣∠DBE=85°﹣60°=25°;②∵∠AEF是△DBE的外角,∴∠AEF=∠D+∠DBE=35°+60°=95°,∵∠AFD是△AEF的外角,∴∠AFD=∠A+∠AEF=35°+95°=130°.【点评】本题考查了全等三角形的性质,三角形内角和定理,三角形外角性质的应用,能熟记全等三角形的性质是解此题的关键,注意:全等三角形的对应边相等,对应角相等.【变式5-3】(2020春•铁西区期中)如图,点A、B、C、D在同一条直线上,点E、F是直线.AD上方的点,连接AE、CE、BF、DF,若△ACE≌△FDB,FD=3,AD=8.(1)判断直线CE与DF是否平行?并说明理由;(2)求CD的长;(3)若∠E=26°,∠F=53°,求∠ACE的度数.【分析】(1)根据全等三角形的性质和平行线的判定定理即可得到结论;(2)根据全等三角形的性质即可得到结论;(3)根据全等三角形的性质和三角形的内角和即可得到结论.【解答】解:(1)CE∥DF,理由:∵△ACE≌△FDB,∴∠ACE=∠D,∴CE∥DF;(2)∵△ACE≌△FDB,∴AC=DF=3,∵AD=8,∴CD=AD﹣AC=8﹣3=5;(3)∵△ACE≌△FDB,∴∠DBF=∠E=26°,∵CE∥DF,∴∠1=∠F=53°,∴∠ACE=180°﹣26°﹣53°=101°.【点评】本题考查了全等三角形的性质,平行线的判定,三角形的内角和,正确的识别图形是解题的关键.【题型6 与全等三角形性质有关的动点问题】【例6】(2020秋•丹徒区校级月考)如图,已知AB=3,AC=2,点D、E分别为线段BA、CA延长线上的动点,如果△ABC与△ADE全等,则AD为.【分析】分△ABC≌△ADE和△ABC≌△ADE两种情况,根据全等三角形的性质解答即可.【解答】解:当△ABC≌△ADE时,AD=AB=3,当△ABC≌△AED时,AD=AC=2,故答案为:2或3.【点评】本题考查的是全等三角形的性质,掌握全等三角形的对应边相等是解题的关键.【变式6-1】(2020秋•滨湖区期中)如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为s.【分析】由条件分两种情况,当△BPE≌△CQP时,则有BE=PC,由条件可得到关于t的方程,当△BPE≌△CPQ,则有BP=PC,同样可得出t的方程,可求出t的值.【解答】解:∵AB=20cm,AE=6cm,BC=16cm,∴BE=14cm,BP=2tcm,PC=(16﹣2t)cm,当△BPE≌△CQP时,则有BE=PC,即14=16﹣2t,解得t=1,当△BPE≌△CPQ时,则有BP=PC,即2t=16﹣2t,解得t=4,故答案为:1或4.【点评】本题主要考查全等三角形的性质,由条件分两种情况得到关于t的方程是解题的关键.【变式6-2】如图,∠C=∠CAM=90°,AC=8cm,BC=4cm,点P在线段AC上,以2cm/s速度从点A 出发向点C运动,到点C停止运动.点Q在射线AM上运动,且PQ=AB.若△ABC与△PQA全等,则点P运动的时间为()A.4s B.2s C.2s或3s或4s D.2s或4s【分析】分△ABC≌△PQA和△ABC≌△QP A两种情况,根据全等三角形的性质解答即可.【解答】解:当△ABC≌△PQA时,AP=AC=8,∵点P的速度为2cm/s,∴8÷2=4(s);当△ABC≌△QP A时,当AP=BC=4,∵点P的速度为2cm/s,∴4÷2=2(s)故选:D.【点评】此题考查的是全等三角形的性质,掌握全等三角形的对应边相等,全等三角形的对应角相等是解题的关键,注意分情况讨论思想的应用.【变式6-3】(2020春•广饶县期末)如图①,在Rt △ABC 中,∠C =90°,BC =9cm ,AC =12cm ,AB =15cm ,现有一动点P ,从点A 出发,沿着三角形的边AC →CB →BA 运动,回到点A 停止,速度为3cm /s ,设运动时间为ts .(1)如图(1),当t = 时,△APC 的面积等于△ABC 面积的一半;(2)如图(2),在△DEF 中,∠E =90°,DE =4cm ,DF =5cm ,∠D =∠A .在△ABC 的边上,若另外有一个动点Q ,与点P 同时从点A 出发,沿着边AB →BC →CA 运动,回到点A 停止.在两点运动过程中的某一时刻,恰好△APQ ≌△DEF ,求点Q 的运动速度.【分析】(1)分两种情况进行解答,①当点P 在BC 上时,②当点P 在BA 上时,分别画出图形,利用三角形的面积之间的关系,求出点P 移动的距离,从而求出时间即可;(2)由△APQ ≌△DEF ,可得对应顶点为A 与D ,P 与E ,Q 与F ;于是分两种情况进行解答,①当点P 在AC 上,AP =4,AQ =5,②当点P 在AB 上,AP =4,AQ =5,分别求出P 移动的距离和时间,进而求出Q 的移动速度.【解答】解:(1)①当点P 在BC 上时,如图①﹣1,若△APC 的面积等于△ABC 面积的一半;则CP =12BC =92cm ,此时,点P 移动的距离为AC +CP =12+92=332,移动的时间为:332÷3=112秒, ②当点P 在BA 上时,如图①﹣2若△APC 的面积等于△ABC 面积的一半;则PD =12BC ,即点P 为BA 中点,此时,点P 移动的距离为AC +CB +BP =12+9+152=572cm ,移动的时间为:572÷3=192秒, 故答案为:112或192;(2)△APQ ≌△DEF ,即,对应顶点为A 与D ,P 与E ,Q 与F ;①当点P 在AC 上,如图②﹣1所示:此时,AP =4,AQ =5,∴点Q 移动的速度为5÷(4÷3)=154cm /s ,②当点P 在AB 上,如图②﹣2所示:此时,AP =4,AQ =5,即,点P 移动的距离为9+12+15﹣4=32cm ,点Q 移动的距离为9+12+15﹣5=31cm ,∴点Q 移动的速度为31÷(32÷3)=9332cm /s , 综上所述,两点运动过程中的某一时刻,恰好△APQ ≌△DEF ,点Q 的运动速为154cm /s 或9332cm /s .【点评】考查直角三角形的性质,全等三角形的判定,画出相应图形,求出各点移动的距离是正确解答的关键.。
初二全等三角形难题压轴题

全等三角形难题易错点剖析一、错用三角对应相等说明全等例1如图,∠CAB=∠DBA,∠C=∠D,E为AC和BD的交点.△ADB与△BCA全等吗?说说理由.错解:△ADB≌△BCA.因为∠C=∠D,∠CAB=∠DBA,∠DAB=CBA,所以△CBE≌△DAE(AAA).分析:两个三角形全等是对的,但说明的理由不正确.三个角对应相等不能作为三角形全等的识别方法.因为三个角对应相等的两个三角形不一定全等.正解:△CBE≌△DAE.因为∠CAB=∠DBA,∠C=∠D,AB=BA(公共边),所以△CAB≌△DBA(AAS).二、错用两边及一角对应相等说明全等例2如图,已知△ABC中,AB=AC,D,E分别是AB,AC的中点,且CD=BE,△ADC与△AEB全等吗?说说理由.错解:△ADC≌△AEB.因为AB=AC,BE=CD,∠BAE=∠CAD,所以△ADC≌△AEB(SSA).分析:错解在把SSA作为三角形全等的识别方法,实际上,SSA不能作为三角形全等的识别条件.因为两边及一边对角相等的两个三角形不一定全等.正解:△ADC≌△AEB.因为AB=AC,D,E为AB,AC的中点,所以AD=AE.在△ADC和△AEB中,因为AB=AC,AD=AE,CD=BE,所以△ADC≌△AEB(SSS).三、错用部分当整体说明全等例3如图,已知AB=AC,BD=CE,试说明△ABE与△ACD全等的理由.错解:因为AB=AC,所以∠B=∠C,在△ABE和△ACD中,因为AB=AC,∠B=∠C,AD=CE,所以△ABE≌△ACD(SAS).分析:错解在把三角形边上的一部分当作说明的条件,这不符合三角形全等的识别方法.正解:△ABE与△ACD全等.因为AB=AC,所以∠B=∠C,因为BD=CE,所以BD+DE=CE+DE,即BE=CD.在△ABE和△ACD中,因为AB=AC,B=C,BE=CD,所以△ABC≌△ACF(SAS).四、错用减法运算说明全等例4如图,已知AC,BD相交于点O,∠A=∠B,∠1=∠2,AD=BC.试说明△AOD≌△BOC.错解:在△ADC和△BCD中,因为∠A=∠B,∠2=∠1,DC=CD,所以△ADC≌△BCD(AAS),所以△ADC-△DEC=△BCD-△DEC,即△A0D≌△B0C.分析:错解在将等式的性质盲目地用到三角形全等中,实际上,三角形全等是不能根据等式的性质说明的.正解:在△ADO和△BCD中,∠A=∠B,∠AOD=∠BOC,AD=BC,所以△AOD≌△BOC(AAS).。
全等三角形重要题型(手拉手模型、截长补短、中线倍长)
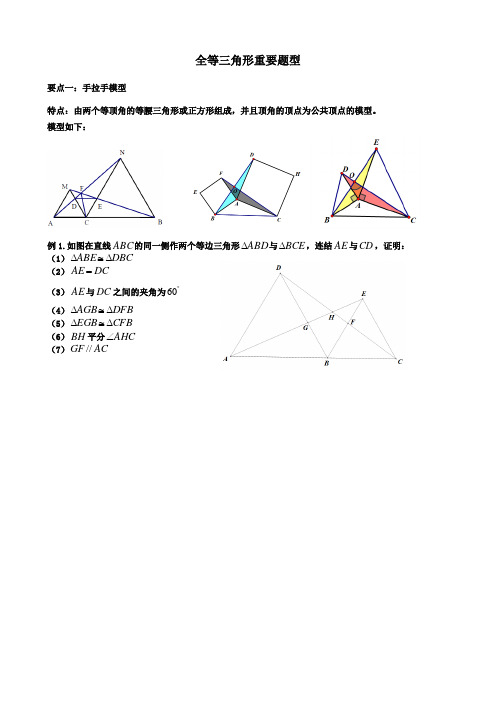
全等三角形重要题型要点一:手拉手模型特点:由两个等顶角的等腰三角形或正方形组成,并且顶角的顶点为公共顶点的模型。
模型如下:例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明: (1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,问:(1)DBC ABE ∆≅∆是否成立? (2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度? (4)HB 是否平分AHC ∠?要点二:截长补短法若遇到证明线段的和差倍分关系时,通常考虑截长补短法,构造全等三角形。
天津市和平区八年级数学上册第05课《全等三角形》全等三角形性质与判定同步提高讲义+练习一(pdf,无答案)
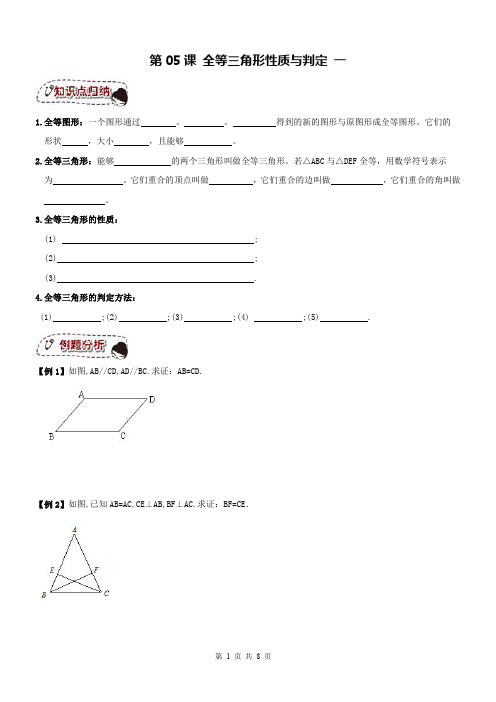
15.如图,OE=OF,OC=OD,CF 与 DE 交于点 A.求证:①∠E=∠F; ②AC=AD。
16.如图,在△ABC 中,AB=CB,∠ABC=90º,D 为 AB 延长线上一点,点 E 在 BC 上,且 BE=BD,连结 AE、DE、DC. (1)求证:△ABE≌△CBD; (2)若∠CAE=30º,求∠BCD 的度数.
第5页共8页
1.如图,在不等边△ABC 中,PM⊥AB 于点 M,PN⊥AC 于点 N,且 PM=PN,Q 在 AC 上,PQ=QA,MP=3,△AMP 的面积是 6,下
列结论:①AM<PQ+QN;②QP∥AM;③△BMP≌△PQC;④∠QPC+∠MPB=900;⑤△PQN 的周长是 7.其中正确的有
(
)个
A.1
B.2
C.3
D.4
第 1 题图
第 2 题图
2.将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角
形,……如此继续下去,结果如表:则 an=
(用含 n 的代数式表示).
3.如图,△ABC 中,∠BAC=900,AB=AC,BD 是∠ABC 的平分线,BD 的延长线垂直于过 C 点的直线于 E,直线 CE 交 BA
第 6 题图
7.如果△ABC≌△A/B/C/,若 AB=A/B/,∠B=500,∠C=700,则∠A/=
°
8.如图,△ABC≌△DEB,AB=DE,∠E=∠ABC,则∠C 的对应角为
,BD 的对应边为
.
第 8 题图
第 9 题图
第 10 题图
9.如图,已知 AB=DC,AD=BC,E,F 是 BD 上的两点,且 BE=DF,若∠AEB=1000,∠ADB=300,则∠BCF=________
(完整版)全等三角形难题超级好题汇总

1. 如图,已知等边△ ABC,P在AC延长线上一点,以PA为边作等边△ APE,EC延长线交BP于M,连接AM,求证:(1)BP=CE;(2)试证明:EM-PM=AM.3.已知,如图①所示,在△ABC和△ ADE中,AB AC,AD AE,BAC DAE ,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:① BE CD ;② AM AN ;2)在图①的基础上,将△ADE 绕点 A 按顺时针方向旋转180o,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立4、如图1,以△ ABC的边AB 、AC为边分别向外作正方形ABDE和正方形ACFG ,连结EG ,试判断△ABC与△AEG 面积之间的关系,并说明理由.2、点 C 为线段AB 上一点,△ ACM, △ CBN 都是等边三角形,线段AN,MC 交于点E,BM,CN交于点F。
求证:1)AN=MB. (2)将△ ACM 绕点 C 按逆时针方向旋转一定角度,如图②所示,其他条件不变,1)中的结论是否依然成立?(3)AN 与BM 相交所夹锐角是否发生变化。
B图①CB图1)F7、已知 Rt △ ABC 中, AC BC ,∠C 90,D 为AB 边的中点, EDF 90°,EDF 绕 D 点旋转,它的两边分别交 AC 、 CB (或它们的延长线)于 E 、 F.1 当 EDF 绕 D 点旋转到 DE AC 于E时(如图1),易证S △DEF S △CEF S △ ABC .DEF CEF 2 ABC当 EDF 绕 D 点旋转到 DE 和 AC 不垂直时, 在图 2 和图 3 这两种情况下, 上述结论是否成立?若成立, 请给予证明;8. 已知 AC//BD, ∠CAB 和∠ DBA 的平分线 EA 、EB 与 CD 相交于点 E. 求证 :AB=AC+BD.5、如图所示,已知△ ABC 和△ BDE 都是等边三角形,且 A 、 HB 平分∠ AHD ;④∠ AHC=60 °,⑤△ BFG 是等边三角形;⑥ A .3个 B .4 个 C .5个 D .6 个B 、D 三点共线.下列结论:① AE=CD ;② BF=BG ;③ FG ∥AD .其中正确的有()6. 如图所示,△ ABC 是等腰直角三角形,∠ ACB =90°,AD 交 AD 于点 F ,求证:∠ ADC =∠ BDE .是 BC 边上的中线,过 C 作 AD 的垂线,交 AB 于点 E , 、 S △CEF 、 S △ABC 又有怎样的数量关系?请写出你的猜想,不需证明.图1若不成立,S △ DEF 图2图210、已知,如图1,在四边形ABCD 中,BC>AB,AD=DC,BD 平分∠ ABC 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形重难点题型讲练
※题型讲练
【例1】已知:如图,AB∥CD,E是AB的中点,CE=DE.
求证:AC=BD.
变式训练1:
1.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.
【例2】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
(1)求证:∠FMC=∠FCM;
(2)AD与MC垂直吗?并说明理由.
变式训练2:
1.如图,在R t△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.
【例3】已知:如图,△ABC中,∠A=60°,BD、CE分别平分∠ABC和∠ACB,BD、CE交于点O.
(1)求∠BOC的度数;(2)求证:BE+CD=BC.
变式训练3:
1.如图,△ABC中,BD=AC,∠ADC=∠CAD,E是DC的中点,求证:AD平分∠BAE.
【例4】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
※课后练习
1.如图1,在△ABC 中AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E ,AD 、CE 交于点H ,EH =EB =3,AE =4,则CH 的长是( ) A .1 B .2 C .3 D .4
2.如图2,AD 是△ABC 的角平分线,DF ⊥AB 于F ,DE =DG ,△ADG 和△AED 的面积分别为50和39,则△EDF 的面积为( )
A .11
B .5.5
C .7
D .3.5
图1 图2
3
4.如图4,已知△ABC 中,∠ABC =45°,AC =4,H 是高AD 和BE 的交点,则线段BH 的长度为 .
图3 图4
5.如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,连接EF ,交AD 于G ,求证:AD ⊥EF
6.已知:点O 到△ABC
的两边
AB ,
AC 所在直线的距离相等,且OB =OC .
(1)如图1,若点O 在边BC 上,求证:AB =
AC
;
(2)如图2,若点O 在△ABC 的内部,求证:AB =AC ;
(3)若点O 在△ABC 的外部,AB =AC 成立吗?请画出图表示.
B
7.已知:△ADE中,AE=AD,∠EAD=90°.
(1)如图(1),若EC、DB分别平分∠AED、∠ADE,交AD、AE于点C、B,连接BC.求证:AB=AC;
(2)△ADE的位置保持不变,将(1)中的△ABC绕点A逆时针旋转至图(2)的位置,CD、BE相交于O,请你判断线段BE与CD的位置关系及数量关系,并说明理由;
8.如图,AD是△ABC的中线,E、F分别在AB、AC上,且DE⊥DF 求证:BE+CF>EF.
9.如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?。
