自动控制原理课件17 5-3对数频率特性
自动控制原理第5章(3)
故对数幅频特性为 L (ω ) = 20 lg
1 (Tω ) 2 + 1
= −20 lg (Tω ) 2 + 1
在时间常数T已知时,可以在ω从0变化到∞的范围内,逐点求出L(ω) 值,从而绘制出精确的对数幅频特性曲线,但十分费时。在工程中,一 般采用渐近线近似的方法,这已经满足大多数情况下的要求。
1.低频段 在Tω<<1(或ω<<1/T)的区段,可以近似地认为Tω≈0, 从而有 L (ω ) = −20 lg (T ω ) 2 + 1 ≈ −20 lg1 = 0 故在频率很低时,对数幅频特性可以近似用零分贝线表示, 这称为低频渐近线。
对数相频特性为ϕ(ω) = -arctanTω。 为了近似绘制相频特性,选择确定以下几个点。
同时,由于惯性环节的 相位与频率呈反正切函数 关系,所以,对数相频特 性曲线将对应于ω=1/T及 ϕ (ω)=-45° 这 一 点 对 称,可以清楚地看出在整 个频率范围内,ϕ(ω)呈滞 后持续增加的趋势,极限 为-90°。
L(ω ) = 20 lg A(ω ) = 20 lg (τω ) 2 + 1
对数相频特性为
ϕ(ω)=arctan(τω)
按照与惯性环节相似的作图方法画图。
L(ω ) = 20 lg A(ω ) = 20 lg (τω ) 2 + 1
1. 低频段 在Tω<<1(或ω<<1/T) 的区段,对数幅频特性可以近 似用零分贝线表示,为低频渐 近线。 2.高频段 在Tω>>1(或 ω >>1/T) 的区段,可以近似地认为高频 渐近线是一条斜线, 斜率为 20dB/dec, 当 频 率 变 化 10倍频时,L(ω)变化20dB。 转折频率为ωT=1/T。
自动控制原理3第三节典型环节的频率特性

左图是不同阻尼系数情况下的 对数幅频特性和对数相频特性 图。上图是不同阻尼系数情况 下的对数幅频特性实际曲线与 渐近线之间的误差曲线。
1 2T 1 T 2 T 5 T 10 T
1 5T
Saturday, November 05, 2016
15
微分环节的频率特性
⒌ 微分环节的频率特性: 微分环节有三种:纯微分、一阶微分和二阶微分。传递函 数分别为: G( s) s
05, 2016
12
振荡环节的波德图
2 T ( ) tg 相频特性: 1 T 2 2
1
几个特征点: 0, ( ) 0;
1 , ( ) ; , ( ) 。 T 2
由图可见:
K 10, T 1, 0.3 10 G ( j ) 2 s 0.6s 1 1 o T
1
幅频特性为: 相频特性为:
A( )
(1 T 2 2 )2 (2T )2 2 T ( ) tg 1 1 T 2 2
L( ) 20 log A( ) 20 log (1 T 2 2 ) 2 (2 T ) 2 对数幅频特性为:
低频段渐近线: T 1时,L( ) 0 高频段渐近线: T 1时, L( ) 20 log (T 2 2 ) 2 40 log T 1 两渐进线的交点 o 称为转折频率。斜率为-40dB/Dec。 T Saturday, November
1 2
T
时,无谐振峰值。当
M p A( p )
1 2
1 0.707时, p 0 。 2
时,有谐振峰值。
1 2 1 2
1 当 0 , A(0 ) , 。 L ( ) 20 lg 2 0 2
自动控制原理第5章频率特性

自动控制原理第5章频率特性频率特性是指系统对输入信号频率的响应特点。
在自动控制系统设计中,了解和分析系统的频率特性是非常重要的,因为它可以帮助工程师评估系统的稳定性,性能和稳定裕度。
本章主要介绍频率特性的相关概念和分析方法,包括频率响应函数、频率幅频特性、相频特性、对数坐标图等。
1.频率响应函数频率响应函数是描述系统在不同频率下的输出和输入之间的关系的函数。
在连续时间系统中,频率响应函数可以表示为H(jω),其中j是虚数单位,ω是频率。
频率响应函数通常是复数形式,它包含了系统的振幅和相位信息。
2.频率幅频特性频率幅频特性是频率响应函数的模的图形表示,通常用于表示系统的增益特性。
频率幅频特性通常用对数坐标图绘制,以便更好地显示系统在不同频率下的增益特性。
对数坐标图上,增益通常以分贝(dB)为单位表示。
3.相频特性相频特性是频率响应函数的相角的图形表示,通常用于表示系统的相位特性。
相频特性可以让我们了解系统对输入信号的相位延迟或提前情况。
在相频特性图上,频率通常是以对数坐标表示的。
4. Bode图Bode图是频率幅频特性和相频特性的综合图形表示。
它将频率幅频特性和相频特性分别绘制在纵轴和横轴上,因此可以直观地了解系统在不同频率下的增益和相位特性。
5.系统的稳定性分析频率特性可以帮助工程师判断系统的稳定性。
在Bode图上,当系统的相位角趋近于-180度,且增益在此处为0dB时,系统即将变得不稳定。
对于闭环控制系统,我们希望系统在特定频率范围内保持稳定,以便实现良好的控制性能。
6.频率特性的设计频率特性的设计是自动控制系统设计中的一个重要任务。
工程师需要根据系统对不同频率下的增益和相位的要求,设计出合适的控制器。
常见的设计方法包括校正器设计、分频补偿、频率域设计等。
总结:本章重点介绍了自动控制系统的频率特性,包括频率响应函数、频率幅频特性、相频特性和Bode图。
频率特性的分析和设计对于掌握自动控制系统的稳定性、性能和稳定裕度非常重要。
自动控制原理-频率特性与系统性能的关系课件
第四节 频率特性与系统性能的关 系
(2) ωc、γ与ts 之间的关系
根据:
ts=
3 ζωn
ts·ωc=3
4ζ4+1 -2ζ2 ζ
整理得
ts·ωc=
6 tgγ
调节时间 ts 与ωc以及γ有关。γ不变 时,穿越频率ωc 越大,调节时间越短。
第四节 频率特性与系统性能的关 系
例 采用频率法分析随动系统的性能,求 出系统的频域指标ωc、γ和时域指标 σ%、 ts。
系
闭环幅频特性曲线
系统的闭环频率 指标主要有:
1 零频幅值Mo
M(ω)
Mm
M0
0.707M(0)
432ω幅M程M=频o度0=o谐的带=谐谐最1闭上M时振幅闭宽振振大环反(,峰ω频环频频峰值峰映)输值=值幅率率值与了值M出反降值ωMωM零系出(与0映br到γr频)=统现输了0幅的时M.M7入系0值Mm快的o7相统(M之0速频ω等的0比b性率时),相=。。。的ω0没对.r在7频有稳0ω一率7误b定M定。差性0 的。ω
第四节 频率特性与系统性能的关 系
低频段的对数频率特性为:
L(ω)=20lgA(ω)=20lg
K ωv
=20lgK-v·20lgω
对数幅频特性曲线
对数幅频特性曲
L(ω)/dB
线的位置越高,开
ν=0 ν=1 -20ν ν=2 0 νK K
环增益K 越大,斜
率越负,积分环节
K
ω 数越多。系统稳态 性能越好。
1)=τ9=00o-.0712.38o+3.6o
L(ω)/dB
系统=2开1.环22传o 递函数 ξ=γ/100=0.21
ωGn=(s)=4ζ2S04(ω(+001c..05-12SζS+2+1=1)6).59
自动控制原理-5.3 控制系统的频率特性

-2.67k
Im
→
0
Re
=0
16
5.3.2 开环伯德图
开环对数幅频特性和开环对数相频特性分别为
n
n
n
Lk () 20 lg A() 20 lg Ai () 20 lg Ai () Li ()
i 1
i 1
i 1
n
( ) i ( ) i 1
与实轴的交点:
令 Im() = 0 求出 x 代入 Re(x)
(4) 由起点出发,绘制曲线大致形状。
6
m
k (is 1)
= 设开环传递函数G(s)H(s)
i1
s n (Tjs 1)
相频特性:
j1
φ(ω)=-υ×90o+Σim=a1 rtan(ωτi)-jΣn=-1aυ rtan(ωTj )
例5-3 已知系统开环传函为 k
Gk (s) (T1s 1)(T2s 1) 试绘制系统的开环幅相曲线。 解:系统开环频率特性
Gk
(
j
)
T1T2
(
j
k 1 T1
)(
j
1 T2
)
-1/T2
-1/T1
j (1)Gk (j0) = k0
(2)Gk (j) = 0180
() = 90 arctanT
2
A() T 1
() = 90 arctanT
1 (T )2
T
0 0.1 0.3 1.0 2.0 5.0 ∞
A() 0 0.0995 0.288 0.707 0.895 0.982 1
()(°) 90 84.3 73.3 45 30 11.3 0
自动控制原理 第五章第一节频率特性的基本概念

《自动控制原理》第五章线性系统的频域分析与校正西北工业大学自动化学院1.频率特性的基本概念2. 幅相频率特性(Nyquist图)3. 对数频率特性(Bode图)4.频域稳定判据5. 稳定裕度6. 利用开环频率特性分析系统的性能7.利用闭环频率特性分析系统的性能8.频率法串联校正频域分析法特点(1)研究稳态正弦响应的幅值和相角随输入信号频率的变化规律(2)由开环频率特性研究闭环系统的性能(3)图解分析法(4)有一定的近似性5.1 频率特性的基本概念RC 电路如图所示,u r (t )=A sin ωt , 求u c (t )=?建模[]r c=+CR 1U s U ()1()()CR 1c r U s G s ==U s s +例1 r c=+R u i u c=C i u r c c=+CR u u u 频率响应()()()c r s s =====+++T CR 111T CR 1T 11TU G s U s s s 0122222()c +=⋅=+++++1T 1T 1T C A ωC s C U s s s s s ωω02222lim →−==++1T T T 1T s A A C s ωωωω222=+1T A C ωω122-=+T 1T A C ωω222222222222()c ⎡⎤=⋅+⋅−⋅⎢⎥+++++++⎣⎦T 11T 1T 1T 1T 1T 1T A A s U s s s s ωωωωωωωωωRC 电路如图所示,u r (t )=A sin ωt , 求u c (t )=?例1 []T 2222T ()sin cos cos sin 1T 1Tt c A A u t e t t ωωαωαωω−=+⋅−⋅++22−=++T T 1Tt A e ωω频率响应:线性系统稳态正弦响应的幅值、相角随输入频率的变化规律。
22()sin(-arctan T)1T s A c t t ωωω=+()sin r t A tω=RC 电路频率特性G (j ω)的定义:()()()=∠j j j G G G ωωω()sin r t A t ω=22()sin(-arctan T)1T s A c t t ωωω=+22()()()==+s 1j 1T c t G r t ωωs ()()()arctan ∠=∠−∠=−j T G c t r t ωω幅频特性相频特性频率特性的获取方法:()()==j j s G G s ωω=−221arctan T 1T ωω∠+=∠++111j T 1j T ωω1=1+j T ωj 1T 1s ωs =+()sin r t A t ω=22()sin(-arctan T)1T s A c t t ωωω=+系统模型间的关系总结()()()=∠j j j G G G ωωωs 22()()()==+1j 1T c t G r t ωωs ()()()∠=∠−∠=−j arctan T G c t r t ωωG(j ω)的定义:G(j ω)的获取方法:()()==j j s G G s ωω感谢聆听,下节再见。
自动控制原理频率特性及其表示法ppt课件

实际系统具有“低通”滤波器特性 实际系统的输出量都随频率的升高而出现失真,
幅值衰减。
频率特性可应用到某些非线性系统的分析中去
自动控制原理
13
1 频率特性的基本概念
频率特性的求取
根据定义求取 对已知系统的微分方程,把正弦输入函数代
入,求出其稳态解,取输出稳态分量与输入正弦 量的复数比即可得到。
系统频率特性能间接地揭示系统的动态特性和 稳态特性,可简单迅速地判断某些环节或参数对系 统性能的影响,指出系统改进方向。
频率特性可以由实验确定,这对于难以建立动 态模型的系统来说,很有用处。
自动控制原理
2
5.1 频率特性及其表示法
1 频率特性的基本概念 2 频率特性的表示
自动控制原理
3
5.1 频率特性及其表示法
5.1 频率特性及其表示法 5.2 典型环节的频率特性 5.3 系统开环频率特性的绘制 5.4 用频率特性分析控制系统的稳定性 5.5 系统瞬态特性和开环频率特性的关系 5.6 闭环系统频率特性 5.7 系统瞬态特性和闭环频率特性的关系
自动控制原理
1
第5章 频域分析法
频率特性是控制系统在频域中的一种数学模 型,是研究自动控制系统的一种工程方法。
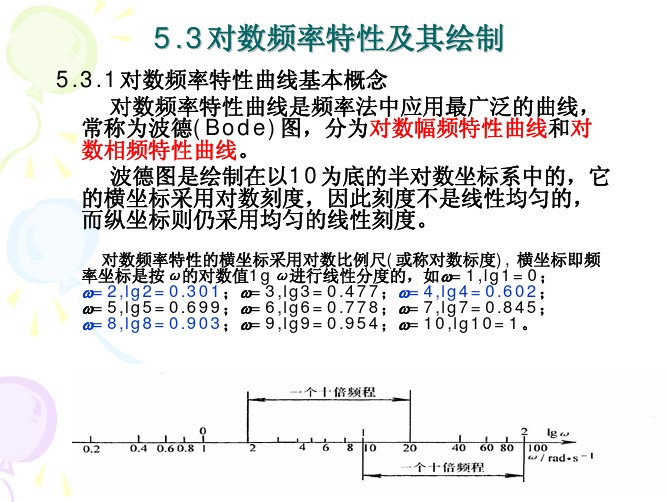
这个单位长度代表10倍频的距离,称之为 “十倍频”或“十倍频程”。
❖ 纵坐标用普通比例尺标度。
自动控制原理
21
A()
100
A
增 10
加
10 1
倍
0.1 0.01
自动控制原理
对数频率特性
L()
40
20 L 增加 20 dB
0
_20
_ 40 0.1
自动控制原理

幅频特性和相频特性分别为
G( j )H ( j ) K
1
1
T12 2 1 T22 2 1
G(
j )H (
j )
arctgT1
arctgT2
arctg
(T1 T2 ) 1 T1T2 2
34
1 极坐标图
当 0 时,G( j)H ( j) K,G( j)H ( j) 00
当 1
时,G( j )H ( j ) K T1T2 ,G( j )H ( j ) 900
对数相频特性
ω
tg1
2ζ Tω 1 T2ω2
低频段,即ωT<<1时
Lω 20lg1=0 dB
——低频渐近线为一条0dB的水平直线。
22
Lω 20lg 1 T2ω2 2 2ζ Tω 2
高频段,即ωT>>1时
L( ) 20 lg( 2T 2 ) 40 lg(T )
当ω增加10倍
部和虚部,求出渐近线;
5. 最后在G(jω)H(jω)平面上绘制出系统开环频率特性的
极坐标图。
2
绘制系统开环频率特性的极坐标图,需把系统所包含 的各个环节对应频率的幅值相乘,相角相加。
例5.2 :求如下传递函数的极坐标图。
Gjω ejω T
1 jω T 解: G(jω)可写为:
Gjω e jω T 1
0.1
0.2 0.3
0.7 1
0.1
0.2 0.3 0.7
1
0.2
0.4 0.6 0.8 1
/n
2
4 6 8 10
24
可见:当频率接近 ω ωn 时,将产生谐振峰
值。阻尼比的大小决定了谐振峰值的幅值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
系统开环对数频率特性的特点(2)
• 2)开环对数幅频特性经过一个转折频率,其斜率要发生 变化,其高频段最终的斜率为-20*(n-m)dB/dec,开环对 数相频特性最终相角为-(n-m)*900。 3)开环对数幅频特性曲线与横坐标轴的交点频率,称为 截止频率或穿越频率,用wc表示。 即在该频率下,L(w)=0
L1 ( )
0
0.1 0.2
0.5 1
10
1
-1 -0.7
2 3
-0.3 0
L4 () L3 ()
1
L2 ()
L() L1()L2 ()L3()L4 ()L5 ()
L1() 20lg 6.25
L2
(
)
20
lg
1 s
6.25 Wk (s) s(5s 1)(2s 1)(s 1)
L3
(
)
20
lg
1 5s
§ 5-3对数频率特性
二.典型环节的对数频率特性
(一)比例环节 W ( j) K Ke j0 L() 20lg K,() 0
0.1 1 Ψ(ω)
10 ω ω
L(w是) 一条等高度等于 的20直lg线k
K>1时 L() ;0 K<1时, L(;) 0
K=1时 L() 0
相频特性是一条 () 直0线0 。
L(2 ) L(1) 20lg 2T (20lg 1T ) 20(lg2T lg 1T )
20 lg
2 1
20lg10
20dB dec
为一斜率为-20dB/dec的直线。
这样其对数幅频特性可用两条渐近线近似表示
一条是低频渐近线
0
1零分贝线,
T
一条是高频渐近线
1 T
斜 率 为-20dB/dec
幅频特性和相频特性曲线合成的图为频率特性的 对数坐标图或波特图(Bode)。
2 伯德图 (Bode图,由两幅图组成)
一幅是对数幅频特性图,横坐标是对数频率,纵坐标是幅值的分贝值,即
20lg G( j) 。另一幅是对数相频率特性图,横坐标是对数频率,纵坐标是相角
20 lg G( j) 。
幅频特性
20 lg G( j)
§ 5-3对数频率特性
例5 绘制 特性。
6.25
Wk (s) (5s 1)(2s 1对)(s数1幅) 相频率
W(k j)
(5
j
6.25
1)(2 j 1)(
j
1)
解:
①各交接频率为 1 0.2 2 0.5 3 1
② 在 处 1,
20lg K 20lg 6.25 15.9dB
③系统属零型系统,过 A( 1, L() 15.9dB) 做斜率为0的渐近线。
§ 5-3对数频率特性
§ 5-3对数频率特性
一 .对数频率特性
为了便于计算和绘图,可将幅相频率特性分成幅 频特性和相频特性两部分。幅频特性采用对数表 示形式,而相频特性仍采用线性刻度。则原来的 幅值相乘(除)运算便转化为相加(减)运算。 从而给计算和作图带来极大的方便。
1.表示方法 设系统开环频率特性
如 ,则1 低频渐近1 线1的延长线经过A点。
§ 5-3对数频率特性
(3) 在⑴⑵基础上之后每遇到一个交换频率斜 率改变一次,
1
当遇到 jTi 环1 节时,斜率增加 当遇到 jTi 1环节时,斜率增加
20dB dec 20dB dec
当遇到振荡环节时,斜率增加 40dB dec
当遇到一重基本环节时,斜率增加k倍(k为重数)
• 0dB/dec------0
• -20dB/dec-----I
• ..............
系统开环对数频率特性的特点(1)
• 1)开环对数频率特性在低频段的形状(对于最小相位系 统而言),只与系统的开环增益K和积分环节的个数有关。
• 0dB/dec------0型,相角从-900开始 • -20dB/dec-----I型,相角从-2*900开始 • .......... • 开环对数幅频特性在低频段的高度由开环增益K决定
分别如图 ,写出对应的传递函数;
作业1
• 画出传递函数的对数频率特性曲线
G(s)
50
s 2 (s 2 s 1)(6s 1)
例5.19(作业)
• 某最小相位系统开环对数频率特性如图所示,要求: • 1)写出系统开环传递函数
• 2)求得截止频率(穿越频率)c
0
-20
ω=1
ω
(1) 理想微分
90° Ψ(ω)
0
ω
W ( j)
jT
Te
j
2,L(
)
20
lg
T
,
(
)
2
幅频是一斜率为20dB/dec的直线,与0dB线交于
1 T
相频特性是90度的水平线。
(2) 比例微分环节 W ( j) 1 jT 1 2T 2 e jarctanT
L() 20lg 1 2T 2 () arctanT
§ 5-3对数频率特性
(二)非周期环节 (惯性环节)
W ( j) 1
1
e j arctanT
1 jT 1 2T 2
(1) L() 20lg 12T 2 T 1 时即 时1T
L() 0dB
T 1 时即
(2)
令
1
1
当T
程有
时1T
时 即2 与101
L() 20lg T
相差10倍2 频1
§ 5-3对数频率特性
§ 5-3对数频率特性
*与非周期环节幅频关于odB线 相频关于0度
线镜向对称。
L(w)
20dB/del
低频渐近线 odB
1/T 0
高频渐近线 过
1 T
90°
Ψ
斜率为 20dB/dec.
ω ω
45°
(五) 振荡环节 (1)
0°
W ( j)
1
1
e j arctan122TT2
T 2 2 2T j 1 (1 2T 2 )2 (2T )2
1. 绘制开环对数频率特性的步骤 (1)将开环传函写成各基本环节的乘积,确定交接频 率ω1,ω2,…,ωn,标在频率轴上。 (2)低频段过点 A( 1, L() 20lg K() K为开环放大 系数)
(3)通过A点过一条斜率为 20 N dB dec 的直线, 其中N为系统的类型,直到遇到第一个交接频率 ,
• 穿越频率(截止频率)Wc求法 •例
48( s 1)
G(s) s(
s
10 1)(
s
1)
20 100
20 20
lg lg
48 1
48 10
10 10
20
L(
)
20
lg
48
10
20 100
20
20
lg
48 10
20
100
100
• 求得L(w)=1的解即为所求 96
m
n
L() 20 lg K 20 N lg 20 lg 1 (Ti )2 20 lg 1 (Tj )2
i 1
j 1
低频段 Ti 1 Tj 1 L() 20lg K 20N lg
所以低频段过点 A( 1, L() 20lg K)
或 ( N K , L() 0)
例 最小相角系统传递函数的近似对数幅频特性曲线
2
§ 5-3对数频率特性
(2)若n个积分环节串联则
W ( j)
1
( j)n
1
n
jn
e2
L() 20n lg
() n
2
L() 与0dB线交于 n 1 1 。 L() 是斜率为-20ndB/dec的直线。
() 是 90的n水平直线。
§ 5-3对数频率特性
L(w)
20dB/del
(四) 微分环节
§ 5-3对数频率特性
(4)相频特性
0 时,渐近于0度
Lm
时,渐近于-180度。
1 T
n时
(n ) 90 0
整个相频特性斜对称于-90度。 -90°
(六)延迟环节
-180°
W ( j) e j L() 0,()
0.1
00..53 0.7 ξ=1
§ 5-3对数频率特性
三.开环系统的对数频率特性
⑤相频特性:() arctan5 arctan2 arctan。
0 0.2 0.5 1
() 0 78.5 139.8 187.1 270
§ 5-3对数频率特性
2、系统类型与开环对数频率特性
m
K (Ti j 1)
Wk ( j)
i 1 nN
( j)N (Tj j 1)
j 1
对数幅频特性:
G( j)
G( j)
G( j)
相频特性
§ 5-3对数频率特性
3.对数频率特性的优点 (1) 简化了频率特性的绘制工作
(乘除运算化为加减运算) 可用分段渐近线代替精确曲线绘制对数幅频特性 和相频特性,稍加修正就可达到足够的精度。 (2) 缩小了频率比例尺,便于研究频率较宽范围的系 统频率特性。 (3) 最小相位系统的频率特性与传函之间存在一一对 应的关系,便于用实验方法确定系统的传函。 (4) 可以迅速直观的判断出环节或参数对系统瞬态性 能指标和稳态特性的影响。(时域法不能) 因此频率特性法是工程上最常用的系统分析和设计方 法。
L() 20lg (1 2T 2 )2 (2T )2
(
)
arc
tan 1
