机械原理第一次作业
《机械原理》课后习题附答案
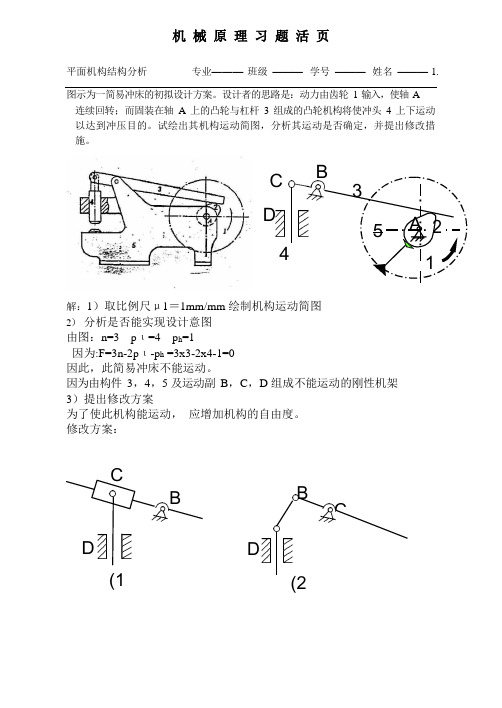
CB D BC平面机构结构分析专业———班级———学号———姓名——— 1.图示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1 输入,使轴A连续回转;而固装在轴A 上的凸轮与杠杆3 组成的凸轮机构将使冲头4 上下运动以达到冲压目的。
试绘出其机构运动简图,分析其运动是否确定,并提出修改措施。
C B 35 A 24 1解:1)取比例尺μ1=1mm/mm 绘制机构运动简图2)分析是否能实现设计意图由图:n=3 pι=4 p h=1因为:F=3n-2pι-p h =3x3-2x4-1=0因此,此简易冲床不能运动。
因为由构件3,4,5 及运动副B,C,D 组成不能运动的刚性机架3)提出修改方案为了使此机构能运动,应增加机构的自由度。
修改方案:D(1 (2DG7D 64C EF9 38B 2 A122如图所示为一小型压力机。
图中齿轮 1与偏心轮 1’为同一构件,绕固定轴心 o 连续转动。
在齿轮 5上开有凸轮凹槽,摆杆 4上的滚子 6嵌在凹槽中,从而使摆杆 4 绕 C 轴上下摆动。
同时,又通过偏心轮 1’、连杆 2、滑杆 3使 C 轴上下移动。
最后通过在摆杆 4的叉槽中的滑块 7和铰链 G 使冲头 8实现冲压运动。
试绘制其机构运动简图,并计算自由度。
b)解:计算该机构的自由度n=7, p ι=9, p h =2 F=3n-2p e -p h =3x7-2x8-2=13. 试计算下列二图所示齿轮连杆组合机构的自由度。
图中相切的圆周表示一对齿轮传动的节圆;凡局部自由度、复合铰链和虚约束均需明确指出。
解:a )解n=4 P ι=5 Ph=1F=3x4-2x5-1=134 C A复合铰链1a)BD 5b)解:n=6 Pι=7 Ph=3F=3×6-2×7-3=14.试计算下列二图所示压榨机的自由度。
图a 中,左右两半完全对称;图b 中,CD = FI = KL = KM = FJ = CE,LI =KF = MJ = JE = FC = ID。
机械原理大作业范文

机械原理大作业范文摘要:机械传动是机械学中的基础内容之一,广泛应用于各个行业和领域。
本文将对机械传动的原理、类型以及应用进行系统的介绍和探讨。
首先介绍了机械传动的定义和作用,然后详细介绍了各种常见的机械传动类型,包括齿轮传动、皮带传动、链传动等,并分别对其工作原理进行了分析。
最后列举了一些机械传动的应用案例,证明了机械传动在现实生活中的重要性和广泛性。
一、引言机械传动是将动力从一个地方传递到另一个地方的机械装置。
它作为机械工程学的基础内容,广泛应用于工业、农业、建筑等各个领域。
机械传动具有传递力量的功能,并能实现运动的改变、平衡、变速等目的。
本文将对机械传动的类型、原理以及应用进行详细介绍。
二、机械传动的类型机械传动可以分为多种类型,常见的有齿轮传动、皮带传动、链传动等。
齿轮传动是利用齿轮间的啮合来传递扭矩和运动的一种传动方式,具有传动效率高、传动比稳定等优点。
皮带传动则是通过绕在两个轮子上的带子来传递力量,常用于需要减速的场合。
链传动与皮带传动类似,但是链传动的传动效率更高,扭矩传递更稳定。
三、机械传动的工作原理1.齿轮传动:齿轮传动采用齿轮之间的啮合来实现传动的目的。
主要通过齿轮的大小、齿数来调整传递的速度和扭矩。
其中,齿轮的齿数比称为传动比,可以实现速度的改变。
齿轮传动通常包括齿轮轴、轴承、齿轮齿廓等组成部分。
2.皮带传动:皮带传动通过绕在轮子上的带子来传递力量。
常见的皮带传动有平行轴带传动和交叉轴带传动。
通过调整轮子的直径和材料来改变传递效果。
皮带传动具有传递动力平稳、减震效果好的特点。
3.链传动:链传动与皮带传动类似,也是通过绕在轮子上的链条来传递力量。
链传动具有噪音低、传动效率高等优点,广泛应用于自行车、摩托车等交通工具中。
四、机械传动的应用1.工业应用:机械传动在工业制造中有广泛的应用。
例如,齿轮传动被广泛应用于机床、起重机械、输送设备等,实现力量的传递和工作的协调。
皮带传动常用于风机、泵等需要平稳传递动力的设备中。
机械原理题库(含答案)---3[修改版]
![机械原理题库(含答案)---3[修改版]](https://img.taocdn.com/s3/m/66b56bec10a6f524cdbf8556.png)
第一篇:机械原理题库(含答案)---3机械原理---3(共63 题)1、铰链四杆机构的压力角是指在不计算摩擦情况下连杆作用于B 上的力与该力作用点速度所夹的锐角。
A.主动件B.从动件C.机架D.连架杆2、平面四杆机构中,是否存在死点,取决于B 是否与连杆共线。
A.主动件B.从动件C.机架D.摇杆3、一个K大于1的铰链四杆机构与K=1的对心曲柄滑块机构串联组合,该串联组合而成的机构的行程变化系数K A 。
A.大于1B.小于1C.等于1D.等于24、在设计铰链四杆机构时,应使最小传动角γmin B 。
A.尽可能小一些B.尽可能大一些C.为0°D.45°5、与连杆机构相比,凸轮机构最大的缺点是B 。
A.惯性力难以平衡B.点、线接触,易磨损C.设计较为复杂D.不能实现间歇运动6、与其他机构相比,凸轮机构最大的优点是A 。
A.可实现各种预期的运动规律B.便于润滑C.制造方便,易获得较高的精度D.从动件的行程可较大7、C 盘形凸轮机构的压力角恒等于常数。
A.摆动尖顶推杆B.直动滚子推杆C.摆动平底推杆D.摆动滚子推杆8、对于直动推杆盘形凸轮机构来讲,在其他条件相同的情况下,偏置直动推杆与对心直动推杆相比,两者在推程段最大压力角的关系为 D 。
A.偏置比对心大B.对心比偏置大C.一样大D.不一定9、下述几种运动规律中,B 既不会产生柔性冲击也不会产生刚性冲击,可用于高速场合。
A.等速运动规律B.摆线运动规律(正弦加速度运动规律)C.等加速等减速运动规律D.简谐运动规律(余弦加速度运动规律)10、对心直动尖顶推杆盘形凸轮机构的推程压力角超过许用值时,可采用A 措施来解决。
A.增大基圆半径B.改用滚子推杆C.改变凸轮转向D.改为偏置直动尖顶推杆11、渐开线上某点的压力角是指该点所受压力的方向与该点A 方向线之间所夹的锐角。
A.绝对速度B.相对速度C.滑动速度D.牵连速度12、渐开线在基圆上的压力角为B 。
朱理版--机械原理课后作业全部答案.

习题解答
2.1 试求图示各机构在图示位置时全部瞬心。
2.2 在图示机构中,已知各构件尺寸为lAB =180mm , lBC =180mm , lBD =180mm , lCD =180mm , lAE =120mm , φ=30º, 构件AB上点E的速度为 vE =150 mm /s ,试求该位置时C、D 两点的速度及连杆2的角速度ω2 。
a5 aD4 a pd4 0.2214.94 3.287rad / s2
aC aB aCnB aCt B
大小
? ω12lAB ω22lBC ?
方向 水平 B→A C→B ⊥CB
aB 12 lAB 102 0.05 5m / s2
a
5/
作业
作业
1.2 1.3(高副低代,拆杆组) 1.4 (a) (b) (c) (d) 1.5
a) F=3x4-2x5-1=1 b) F=3x5-2x6-2=1
F=3x7-2x8-2-2=1 c) F=3x9-2x13=1
d) F=3x6-2x8-1=1 e) F=3x6-2x8=2
作业 2-1 2-2 2-3 2-4
本章考点
①.绘制平面连杆机构运动简图,并确定该机构类型;
②.根据机构中给定的各杆长度(或尺寸范围)来确定属于何种 铰链四杆机构;
③.根据机构中给定的各杆长度判定机构有无急回特性和死点 位置,确定行程速比系数K和最小传动角;
④.已知活动铰链中心的位置设计四杆机构,以实现二个(或 三个)预定的连杆位置;
解:C点速度vC 0 ( P24即C点为绝对瞬心)
vD vp13 1lAp13
vE lAE
l Ap13
西南交通大学机械原理B基础作业及答案

机械原理B线下作业第一次作业一、判断题(判断正误,共2道小题)1. 机构是具有确定运动的运动链正确答案:说法正确2. 平面四杆机构的曲柄存在条件为最长杆与最短杆的杆长之和不大于其余两杆长之和正确答案:说法错误二、主观题(共7道小题)3. 齿轮的定传动比传动条件是什么?答:不论两齿廓在何位置接触,过接触点所作的齿廓公法线必须与两齿轮的连心线相交于一固定点。
4. 计算图7-2所示大减速比减速器的传动比。
答:将轮系分为两个周转轮系①齿轮A、B、E和系杆C组成的行星轮系;②齿轮A、E、F、G和系杆C组成的差动轮系。
因为,所以将代入上式,最后得5. 图7-4中,,为轮系的输入运动,C为轮系的运动输出构件。
已知确定转速的大小和转向。
答:该轮系是由定轴轮系(1-2)和周转轮系(2-3-4-4’-5)组成的混合轮系。
对定轴轮系(1-2),有即对周转轮系(2-3-4-4’-5),有将,,代入上式,最后得,其中“-”表示齿轮5的转向与相同,方向“↓”,如下图所示。
6. 在图8-3中凸轮为半径为R的圆盘,凸轮为主动件。
(1)写出机构的压力角α与凸轮从图示位置转过的角度δ之间的关系;(2)讨论如果a ≥[a],应采用什么改进设计的措施?答:当凸轮转动任意角时,其压力角a如下图所示。
由图中几何关系有所以机构的压力角 a与凸轮转角之间的关系为(1)如果,则应减小偏距e,增大圆盘半径R和滚子半径r r。
(2)7. 机械系统的等效驱动力矩和等效阻力矩的变化如图9-2所示。
等效构件的平均角速度为。
求该系统的最大盈亏功。
答:由下图中的几何关系可以求出各个盈、亏功的值如下其中“+”表示盈功,“—”表示亏功。
画出示功图,如下图(b),先画出一条水平线,从点a开始,盈功向上画,亏功向下画。
示功图中的最低点对应,最高点对应。
图 (b)可以看出,点b最高,则在该点系统的角速度最大;点c最低,系统的角速度最小。
则的积分下限和上限应为下图(a)中的点b和点c。
机械原理作业总结报告

机械原理作业总结报告
在本次机械原理作业中,我通过学习和实践,对机械原理的基本概念和应用有了更深入的理解。
以下是我对作业内容的总结报告。
首先,在机械原理的学习过程中,我深入了解了机械的基本原理和运动规律。
我熟悉了平衡条件、力的作用规律、杠杆原理、滑动摩擦和动态平衡等概念。
通过分析实际问题,我能够应用这些知识解决机械的平衡和运动问题。
其次,我在实践中掌握了机械原理的应用方法。
作为机械原理作业的一部分,我需要对给定的机械系统进行分析和设计。
通过计算和模拟,我能够确定系统的力和力矩平衡,并预测系统的运动趋势。
这让我对机械设计有了更深入的认识,并学会了如何应用机械原理解决实际问题。
此外,通过作业的完成,我进一步提高了解决问题的能力和团队合作意识。
在完成作业过程中,我主动与同学们进行讨论和交流,分享我们对问题的分析和解决方法。
这不仅加深了对机械原理的理解,还培养了我们的团队合作能力和沟通技巧。
在未来,我会继续加强对机械原理的学习和实践。
我会深入研究机械原理的更高级内容,并应用到实际的机械设计和问题求解中。
我也计划通过参与机械工程项目和竞赛等实践活动,进一步提升自己的能力和专业技术水平。
总而言之,通过本次机械原理作业的学习和实践,我对机械原
理的基本概念和应用有了更深入的理解。
通过分析和解决实际问题,我提高了解决问题的能力和团队合作意识。
我将继续深入学习和应用机械原理,以进一步发展自己的机械工程能力。
(完整word)用matlab分析曲柄摇杆机构

机械原理第一次作业(matlab7。
0):求:r1旋转360°时,θ2,θ3,ω2,ω3,α2,α3和C点的加速度。
设r1=400,r2=1000,r3=700,r4=12001、角位移的M函数:function y=jweiyi(x)% Input parameters% x(1)=theta—1% x(2)=theta—2 guess value% x(3)=theta-3 guess value% x(4)=r1% x(5)=r2% x(6)=r3% x(7)=r4% Output parameters% y(1)=theta-2% y(2)=theta—3theta2=x(2);theta3=x(3);%epsilon=1.0E—6;%f=[x(4)*cos(x(1))+x(5)*cos(theta2)—x(7)—x(6)*cos(theta3);x(4)*sin(x(1))+x(5)*sin(theta2)—x(6)*sin(theta3)];%while norm(f)〉epsilonJ=[—x(5)*sin(theta2) x(6)*sin(theta3);x(5)*cos(theta2) —x(6)*cos(theta3)]; dth=inv(J)*(-1.0*f);theta2=theta2+dth(1);theta3=theta3+dth(2);f=[x(4)*cos(x(1))+x(5)*cos(theta2)-x(7)—x(6)*cos(theta3);x(4)*sin(x(1))+x(5)*sin(theta2)—x(6)*sin(theta3)];norm(f);end;y(1)=theta2;y(2)=theta3;r1旋转360°时,θ2,θ3的M文件程序:r(1)=400;r(2)=1000;r(3)=700;r(4)=1200;dr=pi/180;th(1)=0;th(2)=44。
机械原理部分试题及解答

第一章机构的组成和结构1-1 试画出图示平面机构的运动简图,并计算其自由度。
F=3×3-2×4=1 F=3×3-2×4=1F=3×3-2×4=1 F=3×3-2×4=11-2 计算图示平面机构的自由度。
将其中高副化为低副。
确定机构所含杆组的数目和级别,以及机构的级别。
(机构中的原动件用圆弧箭头表示。
)F=3×7-2×10=1 F=3×7-2×10=1 含3个Ⅱ级杆组:6-7,4-5,2-3。
含3个Ⅱ级杆组:6-7,4-5,2-3。
该机构为Ⅱ级机构构件2、3、4连接处为复合铰链。
该机构为Ⅱ级机构F=3×4-2×5-1=1 F=3×3-2×3-2=1F=3×5-2×7=1(高副低代后)F=3×5-2×7=1(高副低代后)含1个Ⅲ级杆组:2-3-4-5。
含2个Ⅱ级杆组:4-5,2-3。
该机构为Ⅲ级机构构件2、3、4连接处为复合铰链。
该机构为Ⅱ级机构F=3×8-2×11-1=1 F=3×6-2×8-1=1F=3×9-2×13=1(高副低代后)F=3×7-2×10=1(高副低代后)含4个Ⅱ级杆组:8-6,5-7,4-3,2-11。
含1个Ⅱ级杆组6-7。
该机构为Ⅱ级机构含1个Ⅲ级杆组2-3-4-5。
第二章 连 杆 机 构2-1 在左下图所示凸轮机构中,已知r = 50mm ,l OA =22mm ,l AC =80mm,︒=901ϕ,凸轮1的等角速度ω1=10rad/s ,逆时针方向转动。
试用瞬心法求从动件2的角速度ω2。
解:如右图,先观察得出瞬心P 13和P 23为两个铰链中心。
再求瞬心P 12:根据三心定理,P 12应在P 13与P 23的连线上,另外根据瞬心法,P 12应在过B 点垂直于构件2的直线上,过B 点和凸轮中心O 作直线并延长,与P 13、P 23连线的交点即为P 12。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理大作业一、题目(平面机构的运动分析)已知:r AE=70mm,r AB=40mm,r EF=60mm,r DE=35mm,r CD=75mm,r BC=50mm,原动件以等角速度w1=10rad/s回转。
试以图解法求在θ1=50°时C点的速度VC 和加速度二、对机构进行位置分析由封闭形ABCDEA与AEFA有:r 1+r 2=r 6+r 3+r 4 r 7=r 6+r 8即r 2-r 3-r 4=-r 1+r 6 -r 8+r 7=r 6(1)位置方程r 2cos θ2-r 3cos θ3-r 4cos(θ4+180°)=-r 1cos(θ1+180°)+r 6 r 2sin θ2-r 3sin θ3-r 4sin(θ4+180°)=-r 1sin(θ1+180°)-r 8cos θ4+ r 7cos θ1=r 6 - r 8sin θ4+ r 7sin θ1=0 X c =r 1cos(θ1+180°)+r 2cos θ2 Yc= r 1sin(θ1+180°) +r 2 sin θ2(2)速度方程-r 2sin θ 2 r 3sin θ 3 r 4cos(θ4+180°) 0 w 2 r 2cos θ2-r 3cos θ 3-r 4cos(θ4+180°) 0w 3 0 0 r 8sin θ4 cos θ 1w 4 0 0 -r 8cos θ 4 sin θ 1r 7r 1sin(θ1+180°)=1 -r 1cos(θ1+180°) r 7 sin θ1-r 7cos θ1V cx = -r 1w 1sin(θ1+180°)-w 2 r 2sin θ2V cy=r w2cos(θ1+180°)+ w2 r2cosθ 2(3)加速度方程-r2sinθ2r3sinθ 3 - r4sinθ 4 0 a2r2cosθ 2 -r3cosθ 3 r4cosθ 4 0 a30 0 r8sinθ 4 cosθ 1 a40 0 -r8cosθ 4 sinθ 1 r’7- w2r2cosθ 2 w3r3cosθ 3 -w4r4cosθ 4 0= - -w2r2sinθ 2 - w3 r3sinθ 3 -w4r4sinθ 4 00 0 w4r8cosθ 4 -w1sinθ10 0 w4r8sinθ 4 -w1cosθ 1w2 w1r1cosθ1w3 w1r1 sinθ1w4+ w1w1r7cosθ1+v sinθ1r7w1r7sinθ1+v cosθ1a= w12r1cosθ1 - w22r2cosθ 2 - a2r2sinθ 2cxa= w12r1 sinθ1 - w22r2 sinθ 2 +a2r2cosθ 2cy三、编写程序%-------------------连杆机构运动分析------------------------------%设定各连杆的长度Lab=40;Lbc=50;Lcd=75;Lde=35;Lef=60;Lae=70;w1=10; %角速度syms w2w3w4r2r3r4laf1laf2%定义角速度和角加速度fai1=-1;%初始化输入角T1=2/w1;%------------计算各个杆的角速度,角加速度并存储------------------------for i=1:50Laf=Lae*cos(fai1)+sqrt((Lef^2-(Lae^2)*(sin(fai1)).^2));fai4=acos((Lef^2+Laf.^2-Lae^2)/(2*Lef*Laf))-fai1;%定义常量m、km=Lae+Lab*cos(fai1)-Lde*cos(fai4);k=Lab*sin(fai1)-Lde*sin(fai4);r=acos((m.^2+k.^2-Lbc^2-Lcd^2)/(2*Lbc*Lcd));%定义常量S、TS=(Lbc+Lcd)*cos(r/2);T=(Lbc-Lcd)*sin(r/2);fai2=acos((m*S'+k*T')./(T.^2+S.^2))+(acos((m.^2+k.^2-Lbc^2-Lcd^2) /(2*Lbc*Lcd)))/2;fai3=acos((m*S'+k*T')./(T.^2+S.^2))-(acos((m.^2+k.^2-Lbc^2-Lcd^2) /(2*Lbc*Lcd)))/2;%---将角位移存入矩阵f1中---f1(i,:)=[fai1,fai2,fai3,fai4];%------计算角速度------a1=[Lbc*sin(fai2) Lcd*sin(fai3) Lde*sin(fai4) 0];a2=[Lbc*cos(fai2) Lcd*cos(fai3) Lde*sin(fai4) 0];a3=[0 0 Lef*sin(fai4) cos(fai1)];a4=[0 0 Lef*cos(fai4) sin(fai1)];A=[a1;a2;a3;a4];W=[w2;w3;w4;laf1];W1=w1*[-Lab*sin(fai1) Lab*cos(fai1) Laf.*sin(fai1) Laf.*cos(fai1)]';W=inv(A)*W1;%---将角速度值存入f2中---f2(i,:)=[i,W(1),W(2),W(3),W(4)];%------计算角加速度-----b1=[Lbc*sin(fai2) Lcd*sin(fai3) Lde*sin(fai4) 0];b2=[Lbc*cos(fai2) Lcd*cos(fai3) Lde*cos(fai4) 0];b3=[0 0 Lef*sin(fai4) cos(fai1)];b4=[0 0 Lef*cos(fai4) sin(fai1)];B=[b1;b2;b3;b4];R=[r2;r3;r4;laf2];m1=[W(1)*Lbc*cos(fai2) W(2)*Lcd*cos(fai3) W(3)*Lde*cos(fai4) 0];m2=[-W(1)*Lbc*sin(fai2) -W(2)*Lcd*sin(fai3) -W(3)*Lde*sin(fai4) 0];m3=[0 0 W(3)*Lef*cos(fai4) -w1*sin(fai1)];m4=[0 0 W(3)*Lef*sin(fai4) w1*cos(fai1)];M=-[m1;m2;m3;m4];P=w1*[-Lab*w1*cos(fai1);Lab*w1*sin(fai1);Laf*w1*cos(fai1)+W(3)*sin(fai1);W(3)*cos(fai1)-Laf*w1*sin(fai1)];R=inv(B)*(M*W+P);%---将角加速度存入f3中---f3(i,:)=subs([i,R(1),R(2),R(3),R(4)]);t(i)=(i-25)*T1/50;%(fai1从-1.029按步长0.04增加到1.029)fai1=-1+0.04*i;end%-------------------绘制线图--------------------------------------figure %做出角位移线图plot(f1(:,1),f1(:,2),'o',f1(:,1),f1(:,3),'*r',f1(:,1),f1(:,4),'x')grid ontitle('角位移线图')xlabel('输入角度rad/s')ylabel('输出角度rad/s')text(0.6,1.5,'杆件BC角位移')text(-0.4,-0.5,'杆件CD角位移')text(0.4,0,'杆件DF角位移')figure %做出角速度线图plot(t,f2(:,2),t,f2(:,3),'r',t,f2(:,4),'g',t,f2(:,5),'--')axis([-0.1,0.1,-100,100])grid onxlabel('时间t/s')ylabel('角速度rad/s')title('角速度线图')text(0,-10,'杆件BC角速度')text(0.09,5,'杆件CD角速度')text(-0.01,18,'杆件DF角速度')text(0.01,60,'AE长度变化率')figure %做出角加速度线图plot(t,f3(:,2),t,f3(:,3),'r',t,f3(:,4),'m',t,f3(:,5),'b-.')grid ontext(-0.08,-10000,'杆BC')text(-0.08,12000,'杆CD角加速度')text(0,5000,'杆DE角加速度')text(0.06,20000,'杆EF长度变化')xlabel('时间t/s')ylabel('角加速度rad/s^2')title('角加速度线图')%----------------输出结果---------------------------------------disp ' fai1 fai2 fai3 fai4 'con1=[f1(:,1),f1(:,2),f1(:,3),f1(:,4)];disp(con1)disp 'W(2) W(3) W(4) W(5) 'con2=([f2(:,2),f2(:,3),f2(:,4),f2(:,5)])disp(con2)disp 'R(1) R(2) R(3) R(5)'con3=[f3(:,2),f3(:,3),f3(:,4),f3(:,5)];disp(con3)四、输出结果1、角位移随角的变化1fai1 fai2 fai3 fai4-1.0000 0.4593 + 0.3583i 0.4593 - 0.2417i 2.3793 -0.9600 0.4856 + 0.3224i 0.4856 - 0.2170i 2.2321 -0.9200 0.5039 + 0.2721i 0.5039 - 0.1827i 2.1096 -0.8800 0.5180 + 0.1951i 0.5180 - 0.1305i 1.9979 -0.8400 0.5717 0.4647 1.8927-0.8000 0.6891 0.3080 1.7916-0.7600 0.7585 0.2158 1.6936-0.7200 0.8142 0.1369 1.5977-0.6800 0.8614 0.0634 1.5036-0.6400 0.9019 -0.0079 1.4108-0.6000 0.9364 -0.0785 1.3192-0.5600 0.9652 -0.1495 1.2284-0.5200 0.9882 -0.2213 1.1384-0.4400 1.0163 -0.3694 0.9601 -0.4000 1.0207 -0.4461 0.8716 -0.3600 1.0182 -0.5246 0.7835 -0.3200 1.0086 -0.6050 0.6958 -0.2800 0.9915 -0.6869 0.6083 -0.2400 0.9668 -0.7698 0.5210 -0.2000 0.9346 -0.8531 0.4339 -0.1600 0.9356 -0.8951 0.3470 -0.1200 1.0161 -0.8490 0.2601 -0.0800 1.0933 -0.7969 0.1734 -0.0400 1.1654 -0.7401 0.08672、角速度变化W(2) W(3) W(4) W(5)1.0e+003 *0.0352 -0.0167 -0.0028 -0.6137 0.0110 -0.0017 -0.0007 -0.7793 0.0068 0.0000 0.0012 -0.9225 0.0041 0.0007 0.0031 -1.0447 0.0020 0.0010 0.0049 -1.1460 0.0003 0.0011 0.0066 -1.2264 -0.0012 0.0011 0.0083 -1.2857 -0.0024 0.0011 0.0098 -1.3237 -0.0034 0.0011 0.0114 -1.3404 -0.0042 0.0011 0.0128 -1.3358 -0.0048 0.0012 0.0141 -1.3105 -0.0050 0.0013 0.0154 -1.2649 -0.0050 0.0015 0.0165 -1.2001 -0.0046 0.0017 0.0176 -1.1170 -0.0039 0.0021 0.0185 -1.0171 -0.0028 0.0024 0.0193 -0.9018 -0.0014 0.0028 0.0200 -0.7731 0.0001 0.0031 0.0206 -0.6328 0.0013 0.0035 0.0211 -0.4830 0.0026 0.0040 0.0214 -0.3261 0.0040 0.0046 0.0216 -0.1643 0.0053 0.0053 0.0217 0 0.0048 0.0054 0.0216 0.0433 0.0042 0.0054 0.0214 0.0866 0.0037 0.0054 0.0211 0.1298 0.0031 0.0054 0.0206 0.1729 0.0025 0.0054 0.0200 0.2158 0.0020 0.0054 0.0193 0.25850.0009 0.0053 0.0176 0.3432 0.0003 0.0052 0.0165 0.3852 -0.0002 0.0051 0.0154 0.4269 -0.0007 0.0049 0.0141 0.4684 -0.0012 0.0048 0.0128 0.5096 -0.0016 0.0047 0.0114 0.5507 -0.0021 0.0045 0.0098 0.5916 -0.0025 0.0044 0.0083 0.6327 -0.0028 0.0042 0.0066 0.6740 -0.0031 0.0041 0.0049 0.7159 -0.0033 0.0039 0.0031 0.7590 -0.0035 0.0038 0.0012 0.8040 -0.0036 0.0037 -0.0007 0.8522 -0.0036 0.0037 -0.0028 0.9060 -0.0033 0.0038 -0.0051 0.9697 -0.0028 0.0041 -0.0077 1.0535 -0.0016 0.0048 -0.0112 1.18553、角加速度变化R(1) R(2) R(3) R(5)1.0e+004 *-1.8608 1.2344 0.0456 -2.4143-0.1321 0.0780 0.0485 -2.4569-0.0836 0.0428 0.0499 -2.3550-0.0658 0.0288 0.0497 -2.1388-0.0557 0.0207 0.0481 -1.8399-0.0486 0.0156 0.0452 -1.4913-0.0430 0.0124 0.0413 -1.1262-0.0380 0.0106 0.0365 -0.7763-0.0336 0.0099 0.0311 -0.4695-0.0295 0.0102 0.0255 -0.2283-0.0258 0.0111 0.0198 -0.0686-0.0225 0.0125 0.0143 0.0016-0.0196 0.0140 0.0094 -0.0178-0.0173 0.0156 0.0051 -0.1192-0.0156 0.0171 0.0017 -0.2880-0.0145 0.0185 -0.0008 -0.5046-0.0141 0.0197 -0.0024 -0.7457-0.0155 0.0202 -0.0031 -0.9863-0.0206 0.0189 -0.0030 -1.2025-0.0263 0.0167 -0.0023 -1.3730-0.0321 0.0138 -0.0011 -1.4812-0.0374 0.0105 0.0004 -1.5167-0.0372 0.0103 -0.0005 -1.5001 -0.0367 0.0101 -0.0015 -1.4522 -0.0357 0.0099 -0.0025 -1.3735 -0.0343 0.0097 -0.0037 -1.2651 -0.0325 0.0096 -0.0050 -1.1285 -0.0303 0.0097 -0.0066 -0.9656 -0.0277 0.0099 -0.0083 -0.7785 -0.0248 0.0103 -0.0103 -0.5697 -0.0216 0.0108 -0.0126 -0.3422 -0.0181 0.0117 -0.0151 -0.0987 -0.0144 0.0127 -0.0178 0.1574 -0.0107 0.0140 -0.0208 0.4229 -0.0068 0.0155 -0.0240 0.6945 -0.0030 0.0172 -0.0274 0.96890.0007 0.0191 -0.0310 1.24300.0043 0.0212 -0.0347 1.51370.0078 0.0235 -0.0386 1.77860.0110 0.0259 -0.0425 2.03550.0139 0.0284 -0.0466 2.28290.0166 0.0310 -0.0507 2.52050.0189 0.0337 -0.0551 2.74870.0210 0.0366 -0.0599 2.96870.0227 0.0398 -0.0654 3.17700.0234 0.0436 -0.0720 3.3176五、函数曲线1、各杆角位移与输入角的函数线图12、各杆角速度随时间变化函数线图2、各杆角加速度随时间变化函数线图附:参考资料1、《机械原理》(第七版)孙桓陈作模葛文杰主编高等教育出版社2、《机械原理同步辅导及习题全解》(第七版)唐亚楠主编中国矿业大学出版社3,《数学实验初步》(MATLAB)肖海军编科学出版社二、题目(平面机构的力分析)在图示的正弦机构中,已知l AB =100 mm,h1=120 mm,h2 =80 mm,W1 =10 rad/s(常数),滑块2和构件3的重量分别为G2 =40 N和G3 =100 N,质心S2 和S3 的位置如图所示,加于构件3上的生产阻力Fr=400 N,构件1的重力和惯性力略去不计。
