数模第四次作业
《数学建模》期末考试试卷四与参考答案

《数学建模》期末考试试卷 班级 姓名 学号一、(15分)某厂利用甲、乙、丙三种原料生产A 、B 、C 、D 、E 五种产品,单位产品(万件)对原材料的消耗(吨)、原材料的限量(吨)以及单位问五种产品各生产多少才能使总利润达到最大? (1)建立线性规划问题数学模型。
(2)写出用LINGO 软件求解的程序。
二、(15分)用单纯形方法求如下线性规划问题的最优解。
123123123123max 614134248..2460,,0S x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎨⎪≥⎩三、(15分)某厂生产甲、乙、丙三种产品,消耗两种主要原材料A 与B 。
每单位产品生产过程中需要消耗两种资源A 与B 的数量、可供使用的原材料数量以及单位产品利润如下表:设生产甲、乙、丙产品的数量分别为123,,x x x 单位,可以建立线性规划问题的数学模型:123123123123max 4003005006030504500..3040503000,,0S x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎨⎪≥⎩利用LINGO10.0软件进行求解,得求解结果如下:Objective value: 35000.00 Total solver iterations: 2 Variable Value Reduced CostX1 50.00000 0.000000 X2 0.000000 66.66667 X3 30.00000 0.000000 Row Slack or Surplus Dual Price 1 35000.00 1.000000 2 0.000000 3.333333 3 0.000000 6.666667(1)指出问题的最优解并给出原应用问题的答案;(2)写出该线性规划问题的对偶线性规划问题,并指出对偶问题的最优解;(3)灵敏度分析结果如下:Objective Coefficient RangesCurrent Allowable Allowable Variable Coefficient Increase DecreaseX1 400.0000 200.0000 100.0000X2 300.0000 66.66667 INFINITYX3 500.0000 166.6667 66.66667Righthand Side RangesRow Current Allowable AllowableRHS Increase Decrease2 4500.000 1500.000 1500.0003 3000.000 1500.000 750.0000对灵敏度分析结果进行分析四、(10分)一个公司要分派4个推销员去4个地区推销某种产品,4个推销员在各个地区推销这种产品的预期利润(万元)如下表。
创界学校高三数学第四次模拟测试试题 文含解析 试题

智才艺州攀枝花市创界学校宁夏六盘山高级2021届高三数学第四次模拟测试试题文〔含解析〕本卷须知: 12.选择题答案使需要用2B 铅笔填涂,非选择题答案使用毫米的黑色中性〔签字〕笔或者碳素笔书写,字体工整,笔迹清楚.3.做答时,必须将答案写在答题卡上,写在本试题上、超出答题区域或者非题号对应区域之答案一律无效.一、选择题:〔本大题一一共12个小题,每一小题5分,一共60分〕 1.集合2{|21},{|30}A x x B x x x =-<<=-≤,那么A B =〔〕A.(0,1)B.(2,3]-C.[0,1)D.(1,3]【答案】C 【解析】 【分析】先求出集合B ,再进展交集运算即可. 【详解】集合{}2{|30}03B x x x x x =-≤=≤≤,所以{01}[0,1)A B x x ⋂=≤<=应选C.【点睛】此题考察一元二次不等式的解法,集合的交集运算,属根底题. 2.“2,0x x R e x ∀∈->〞的否认是〔〕A.0200,0x x R e x ∃∈-> B.0200,0x x R e x ∃∈-≤ C.0200,0x x R e x ∃∈-≥D.0200,0x x R ex ∃∈-<【答案】B 【解析】 【分析】. 【详解】2,0x x R e x ∀∈->〞的否认是:“0200,0x x R e x ∃∈-≤〞所以B 选项符合. 应选:B 【点睛】.3.0a>,2log (0)()1(0)xxx f x a x >⎧=⎨-≤⎩,且(2)3f -=,那么1(())4f f =〔〕A.3B.3-C.4-D.34-【答案】A 【解析】 【分析】 求出1()4f 的值,根据(2)3f -=,即得答案. 【详解】211log 244f ⎛⎫==- ⎪⎝⎭,又()23f -=,()1234f f f ⎛⎫⎛⎫∴=-=⎪ ⎪⎝⎭⎝⎭. 应选:A .【点睛】此题考察分段函数求值,属于根底题. 4.等比数列{}n a 中,22a =,68a =,那么4a =〔〕A.4B.4±C.4-D.5【答案】A 【解析】 【分析】由等比数列知识可知4624a qa ==,进而求出2q 的值,再由242a a q =⋅进展计算即可得解. 【详解】设等比数列{}n a 的首项为1a ,公比为q ,所以462842a q a ===,所以22q =,所以242224a a q =⋅=⋅=.应选:A .【点睛】此题考察等比数列通项公式的应用,侧重考察对根底知识的理解和掌握,考察计算才能,属于常考题.5.由“半径为R 的圆内接矩形中,正方形的面积最大〞,推理出“半径为R 的球的内接长方体中,正方体的体积最大〞是 A.类比推理 B.归纳推理C.演绎推理D.以上都不是 【答案】A 【解析】试题分析:从推理形式上看,由特殊到特殊的推理是类比推理,由局部到整体,个别到一般的推理是归纳推理,由一般到特殊的推理是演绎推理. 考点:逻辑推理.6.以以下图来自古希腊数学家希波克拉底所研究的几何图形,此图由一个半圆和一个四分之一圆构成,两个阴影局局部别标记为A 和M .在此图内任取一点,此点取自A 区域的概率记为()P A ,取自M 区域的概率记为()P M ,那么〔〕A.()()P A P M >B.()()P A P M <C.()()PA P M =D.()PA 与()P M 的大小关系与半径长度有关 【答案】C 【解析】 【分析】利用圆的面积公式和扇形的面积公式,分别求得阴影局部的面积,得到阴影局部A 的面积=阴影局部M 的面积,即可求解.【详解】由题意,设四分之一圆的半径为R R , 阴影局部A 的面积为212R ,空白局部的面积为221142R R π-,阴影局部M 的面积为:2222111122422R R R R ππ⎛⎫⎛⎫⨯⨯--= ⎪ ⎪ ⎪⎝⎭⎝⎭, 阴影局部A 的面积=阴影局部M 的面积,所以PA P M ()=(),应选C. 【点睛】此题主要考察了几何概型的应用,其中解答中认真审题,正确求解阴影局部的面积是解答的关键,着重考察了推理与运算才能,属于根底题. 7.某圆锥的侧面展开图是圆心角为23π,面积为3π的扇形,那么该圆锥的底面半径为〔〕 A.4 B.3C.2D.1【答案】D 【解析】 【分析】根据扇形的面积计算出扇形的半径,即圆锥的母线长,由此可计算出扇形的弧长,即为圆锥的底面圆周长,进而可计算出该圆锥的底面半径.【详解】设圆锥的母线长为l ,底面半径为r ,那么212323l ππ⨯⨯=,解得3l =,所以,圆锥的底面圆周长为2223r l πππ==,解得1r =. 应选:D.【点睛】此题考察圆锥底面半径的计算,考察了圆锥侧面积的计算,考察计算才能,属于根底题. 8.以下函数中,最小正周期为π且图象关于原点对称的函数是〔〕A.cos 22y x π⎛⎫=+ ⎪⎝⎭B.sin 22y x π⎛⎫=+ ⎪⎝⎭C.sin2cos2y x x =+D.sin cos y x x =+【答案】A 【解析】 【分析】求出函数的周期,函数的奇偶性,判断求解即可. 【详解】解:y =cos 〔2x 2π+〕=﹣sin2x ,是奇函数,函数的周期为:π,满足题意,所以A 正确y =sin 〔2x 2π+〕=cos2x ,函数是偶函数,周期为:π,不满足题意,所以B 不正确;y =sin2x +cos2x =〔2x 4π+〕,函数是非奇非偶函数,周期为π,所以C 不正确;y =sin x +cosx =〔x 4π+〕,函数是非奇非偶函数,周期为2π,所以D 不正确;应选A .考点:三角函数的性质.9.最早发现勾股定理的人是我国西周数学家商高,商高比毕达哥拉斯早500多年发现勾股定理,如以下图,ABC 满足“勾三股四弦五〞,其中股4AB =,D 为弦BC 上一点〔不含端点〕,且ABD △满足勾股定理,那么cos ,AB AD <>=〔〕A.35 B.45C.34D.512【答案】A 【解析】 【分析】首先根据直角三角形等面积公式计算斜边的高AD的长,再根据向量数量积公式转化,并计算cos ,AB AD <>的值.【详解】由题意可知AD BC ⊥,所以根据等面积转化可知435BA AC BC AD AD ⨯=⨯⇔⨯=⨯,解得:125AD =()2AB AD AD DB AD AD⋅=+⋅=,23cos ,454AD AB AD ADAB AD AB ADAD⋅<>====. 应选:A【点睛】此题考察向量数量积,向量夹角的余弦值,重点考察转化与化归的思想,计算才能,属于根底题型. 10.在ABC 中,设,,a b c 分别是角,,A B C 所对的边长,且直线cos cos 0ax y A B +-=与cos cos 0x B by A -+=垂直,那么ABC 一定是〔〕A.等边三角形B.直角三角形C.等腰三角形D.等腰直角三角形 【答案】C 【解析】【分析】 此题首先可以结合角,,A B C 是ABC 的内角排除两条直线一条平行于x 轴、一条平行于y 轴的情况,然后根据两直线垂直得出cos cos 0a B b A ,最后结合正弦定理边角互化以及两角差的正弦公式即可得出结果.【详解】当cos 0A =,cos 0B =时,两直线方程为0x =、0y =,互相垂直,因为角,,A B C 是ABC 的内角,所以cos A 与cos B 不可能同时为0,故排除这种情况,因为直线cos cos 0ax y A B +-=与cos cos 0x B by A -+=垂直, 所以cos cos 0a Bb A ,即sin cos cos sin 0A B A B -=,()sin 0A B -=,A B =,故ABC 一定是等腰三角形,应选:C.【点睛】此题考察两直线垂直的相关性质,假设两直线0Ax By C ++=与0Dx Ey F ++=垂直,那么满足一条直线平行于x 轴、一条直线平行于y 轴或者0A D B E ,考察计算才能,考察化归与转化思想,是中档题.11.12,F F 是双曲线C 的左右焦点,点P 在双曲线C 上,126F PF π∠=,且2121()0F F F P F P +⋅=,那么双曲线C 的离心率为〔〕1B.121【答案】D 【解析】【分析】设N 为1PF 的中点,由2121()0F F F P F P +⋅=,可得12F F P 为等腰三角形,由双曲线的定义可得122PF a c =+,在直角三角2PNF中,122cos 2PN a c F PF PF c +∠===可求出答案. 【详解】如图,设N 为1PF 的中点,那么21222F F F P F N +=, 由2121()0F F F P F P +⋅=,即210F N F P ⋅=,所以21F N F P ⊥所以12F F P 为等腰三角形,1222F F F P c ==由双曲线的定义有:122PF F P a -=,所以122PF a c =+那么PN a c =+在直角三角2PNF 中,126F PF π∠=,所以122cos 2PN a c F PF PF c +∠===所以1a c +=e =应选:D【点睛】此题考察向量在平面解析几何中的应用,求双曲线的离心率,关键是向量条件的转化处理,属于中档题. 12.函数()(),x x f x x e e -=-且313(log )(log )2(1),+≤f x f x f 那么x 的取值范围是〔〕A.1[,1]3B.[1,3]C.1[,3]3D.1(,][3,)3-∞+∞ 【答案】C 【解析】 【分析】首先判断函数的奇偶性,再利用导数判断函数的单调性,利用函数是偶函数,不等式等价于()()3log 1f x f ≤,再利用函数的奇偶性和单调性,解抽象不等式.【详解】由题意可知x ∈R ,()()()x x f x x e e f x --=--=()f x ∴是偶函数,且当0x>时,()()()0x x x xf x e e x e e --'=-++>,∴在区间()0,∞+上,函数()f x 单调递增,133log log x x =-,()()1333log log log f x f x f x ⎛⎫∴=-= ⎪⎝⎭∴原不等式等价于()()32log 21f x f ≤⇔()()3log 1f x f ≤,即3log 1x ≤,即31log 1x -≤≤,解得:133x ≤≤,即不等式的解集是1,33⎡⎤⎢⎥⎣⎦. 应选:C【点睛】此题考察函数的奇偶性和单调性,以及利用函数性质解抽象不等式,对数不等式,重点考察转化与化归的思想,计算才能,属于中档题型.二、填空题:〔此题一共4小题,每一小题5分,一共20分.〕 13.假设复数()211z m m i =--+是纯虚数,那么实数m =____________.【答案】1 【解析】 【分析】根据复数z 为纯虚数得出复数z 的实部为零,虚部不为零,由此可解得实数m 的值.【详解】由于复数()211z m m i =--+为纯虚数,那么21010m m ⎧-=⎨+≠⎩,解得1m =.故答案为:1.【点睛】此题考察利用复数的概念求参数,考察计算才能,属于根底题. 14.等差数列{}n a 中,14730a a a ++=,36924a a a ++=,那么其前9项和9S =____________.【答案】81 【解析】 【分析】由等差数列的性质:假设m n p q +=+,那么m n p q a a a a +=+可得14743a a a a ++=,即可求出4a 的值,同理可求得6a ,根据求和公式及等差的性质可得,194699()9()22a a a a S ++==,代入数据即可求解.【详解】在等差数列中1474330a a a a ++==,所以410a =,同理3696324a a a a ++==,所以68a =,所以194699()9()9(108)81222a a a a S ++⨯+====. 故答案为81.【点睛】此题主要考察等差数列的性质及前n 项和的计算,注意灵敏应用此性质,可大大降低计算难度,属根底题. 15.曲线()cos x f x e x x =+在点(0,(0))f 处的切线方程为____________. 【答案】21y x =+【解析】 【分析】求出导函数,得(0)2f '=,即切线斜率,然后可得切线方程. 【详解】由()cos x f x e x x =+,那么(0)1f =由题意()cos sin 1x x f x e x e x '=-+,那么(0)2f '=所以曲线()cos x f x e x x =+在点(0,(0))f 处的切线的斜率为(0)2k f '==所以所求切线方程为:()120y x -=-,即21y x =+故答案为:21y x =+【点睛】此题考察导数的几何意义,函数()f x 在点00(,())x f x 处的切线方程是()000()()y f x f x x x '-=-.属于根底题.16.正三棱柱111ABC A B C -的所有棱长都相等,M 是棱11A B 的中点,那么异面直线AM 与BC 所成角的余弦值为__________.【答案】10【解析】 【分析】将正三棱柱补成如以下图的四棱柱,那么MAD ∠为异面直线AM 与BC 所成角,解三角形即可. 【详解】解:将正三棱柱补成如以下图的四棱柱1111ABCD A B C D -,其中//AB CD ,//AD BC ,连接MD ,1MD , 因为//AD BC ,所以MAD ∠为异面直线AM 与BC 所成角〔或者其补角〕,设12AB BC AA x ===,那么1A M x =,AM =,∵111A B C ∆为正三角形,∴111=120B A D ∠︒,由余弦定理得2221111D M A D A M =+1112cos120A D A M -⋅︒2214222x x x x =++⋅⋅⋅,∴1D M=,那么DM =,∴222cos2AM AD DM MAD AM AD +-∠=⋅22210==-,∴异面直线AM 与BC 所成角的余弦值为【点睛】此题主要考察异面直线所成的角,考察计算才能,属于根底题.三、解答题:〔一共70分,解容许写出文字说明、证明过程或者演算步骤.第17~21题为必考题,每个试题考生都必须答题.第22、23为选考题,考生根据要求答题〕 〔一〕必考题:〔每道题12分,一共60分〕 17.ABC 的内角A ,B ,C 所对的边长分别为a ,b ,c ,ABC 的面积为S ,且BA BC S ⋅=.〔1〕求tan B 的值; 〔2〕假设3cos 5A =,2c =,求b . 【答案】〔1〕tan 2B =;〔2〕2. 【解析】 【分析】〔1〕由BA BC S⋅=得12cos sin ac ac BB =,即可求出tan B 的值; 〔2〕由tan 2B =和22sin cos 1B B +=,易得sin B 和cos B 的值,再由3cos 5A =可得出sin A 的值,进一步可得sin sin()sin CA B B =+=,进而得出B C =,最后得出2b c ==. 【详解】〔1〕由BA BCS⋅=得12cos sin ac ac BB =,即12cos sin B B =,∴sin tan 2cos BBB==; 〔2〕∵tan 2B =,∴sin 2cos BB=,即sin 2cos B B =,①又∵22sin cos 1B B +=,②又(0,)B π∈,由①②可得sin B =cos B =,又3cos 5A =,(0,)A π∈,4sin 5A ∴==, sinB =,∴B C =或者B C π+=〔舍去〕,故ABC 为等腰三角形,所以2b c ==.【点睛】此题主要考察三角形的面积公式,考察同角三角函数的根本关系,考察简单三角恒等变换,考察逻辑思维才能和运算求解才能,属于常考题.18.在贯彻精准扶贫的过程中,某单位在某定点帮扶甲、乙两村各50户贫困户,工作组对这100户村民的年收入、劳动才能、子女受教育等情况等进展调查,并把调查结果转换为贫困指标x ,再将指标x 分成[)0,0.2、[)0.2,0.4、[)0.4,0.6、[)0.6,0.8、[]0.8,1.0五组,得到如以以下图所示的频率分布直方图.假设规定00.6x ≤<,那么认定该户为“绝对贫困户〞,否那么认定该户为“相对贫困户〞,且当0.8 1.0x ≤≤时,认定该户为“低收入户〞,当00.2x ≤<时,认定该户为“亟待帮助户〞.此次调查中甲村的“绝对贫困户〞占甲村贫困户的24%.〔1〕完成以以下联表,并判断是否有90%的把握认为“绝对贫困户〞数与村落有关; 〔2〕某HY 决定在这两村贫困指标在[)0,0.2、[)0.2,0.4内的贫困户中,利用分层抽样抽取6户,现从这6户中再随机选取2户进展帮扶,求所选2户中至少有一户是“亟待帮助户〞的概率.附:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.【答案】〔1〕列联表见解析,没有90%的把握认为绝对贫困户数与村落有关;〔2〕5. 【解析】 【分析】〔1〕计算出甲村中“绝对贫困户〞的户数,计算出甲、乙两村的“绝对贫困户〞户数之和,可得出22⨯列联表,可计算出2K 的观测值,结合临界值表可得出结论;〔2〕计算出所抽取的6户中,抽到的“亟待帮助户〞户数为2,分别记为a 、b ,抽到不是“亟待帮助户〞户数为4,分别记为A 、B 、C 、D ,列举出所有的根本领件,并确定事件“所选2户中至少有一户是“亟待帮助户〞〞所包含的根本领件,利用古典概型的概率公式可求得所求事件的概率. 【详解】〔1〕由题意可知,甲村中“绝对贫困户〞有500.2412⨯=〔户〕, 甲、乙两村的“绝对贫困户〞有()0.250.500.750.210030++⨯⨯=〔户〕, 可得出下表:所以2K的观测值()210012321838122.706307050507k ⨯⨯-⨯==<⨯⨯⨯, 查表可知,没有90%的把握认为“绝对贫困户〞数与村落有关; 〔2〕贫困指标在[)00.4,内的贫困户一共有()0.250.50.210015+⨯⨯=〔户〕, 亟待帮助户一共有0.250.21005⨯⨯=〔户〕,所以利用分层抽样抽取6户,抽到的“亟待帮助户〞户数为56215⨯=〔户〕,分别记为a 、b , 抽到不是“亟待帮助户〞户数为624-=〔户〕,分别记为A 、B 、C 、D ,所有的根本领件有:(),a b 、(),a A 、(),a B 、(),a C 、(),a D 、(),b A 、(),b B 、(),b C 、(),b D 、(),A B 、(),A C 、(),A D 、(),B C 、(),B D 、(),C D ,一共15个,其中,事件“所选2户中至少有一户是“亟待帮助户〞〞所包含的根本领件有:(),a b 、(),a A 、(),a B 、(),a C 、(),a D 、(),b A 、(),b B 、(),b C 、(),b D ,一共9个.因此,事件“所选2户中至少有一户是“亟待帮助户〞〞的概率为93155P==. 【点睛】此题考察利用HY 性检验解决实际问题,同时也考察了古典概型概率的计算,考察数据处理才能与计算才能,属于中等题.19.如图,AB 为圆O 的直径,点E ,F 在圆O 上,//AB EF ,矩形ABCD 所在平面和圆O 所在平面互相垂直,2AB =,1EF =, 〔1〕求证:平面ADF ⊥平面BCF〔2〕假设几何体F BCE -和几何体F ABCD -的体积分别为1V 和2V ,求12:V V . 【答案】〔1〕证明见解析;〔2〕12:1:4V V =.【解析】 【分析】〔1〕由面面垂直可得AD ⊥平面ABEF ,从而得到AD BF ⊥,由圆的直径的性质得BF AF ⊥,故得出BF⊥平面ADF ,从而得出平面DAF ⊥平面CBF ;〔2〕F BCEC BEF V V --=,设AD BC a ==,那么可用a 表示出1V ,2V ,从而得出体积比.【详解】〔1〕∵平面ABCD ⊥平面ABEF ,平面ABCD 平面ABEF AB =,AD AB ⊥,AD ⊂平面ABCD ,∴AD ⊥平面ABEF ,∵BF ⊂平面ABE ,∴AD BF ⊥,∵AB 是圆O 的直径, ∴BF AF ⊥,又AD ⊂平面ADF ,AF ⊂平面ADF ,AD AF A =,∴BF⊥平面ADF ,∵BF ⊂平面BCF ,∴平面DAF ⊥平面CBF ;〔2〕如图,连结OE 、OF ,那么1OE OF EF ===,∴AOF ,OEF ,BOE △是等边三角形,过F 作FM AB ⊥于M ,那么2FM =,FM ⊥平面ABCD ,设AD BC a ==,那么11111332F BCE C BEF BEFVV V S BC a --===⋅=⨯⨯=△,21123323F ABCD ABCD V V S FM a -==⋅=⨯⨯=矩形.∴121:4123:VV ==:. 【点睛】此题考察平面与平面垂直的断定,考察棱锥体积的求法,考察空间想象才能和计算才能,属于常考题.20.双曲线2213x y -=的左右焦点分别为12,F F ,12PF F △的周长为12.〔1〕求点P 的轨迹C 的方程.〔2〕点(8,0)Q ,是否存在过点Q 的直线l 与曲线C 交于不同的两点,M N ,使得22||||MF NF =,假设存在,求出直线l 的方程,假设不存在,请说明理由.【答案】〔1〕221(0)1612x y y +=≠;〔2〕不存在,答案见解析. 【解析】 【分析】〔1〕依题意根据椭圆的定义可知点P 的轨迹为椭圆,〔除去与x 轴的交点〕,设方程为22221(0,0)x y y a b a b+-≠>>,由4a =,2c =,求出b 即可得到椭圆方程; 〔2显然直线l 的斜率不存在时,直线与椭圆无交点;当直线l 的斜率存在时,设方程为(8)y k x =-,联立直线与椭圆方程,消元,由>0∆求出k 的取值范围,设点()()1122,,,M x y N x y ,MN 的中点()00,T x y ,列出韦达定理,表示出00,x y ,由又22MF NF =,得到2F TMN⊥,得到方程判断方程的解即可;【详解】解:〔1〕由题意可得()12,0F -,()22,0F ,∴124F F =,又∵12F F Р的周长为12,∴12128F P F P F F +=>,∴点P 的轨迹是椭圆〔除去与x 轴的交点〕,设方程为22221(0,0)x y y a b a b+-≠>>, ∴2824a c =⎧⎨=⎩,∴42a c =⎧⎨=⎩,∴216412b =-=,∴点P 的轨迹C 的方程为221(0)1612x y y +=≠.〔2〕①当直线l 的斜率不存在时,直线与椭圆无交点; ②当直线l 的斜率存在时,设直线l 的斜率为k , 那么:(8)l y k x =-,联立22(8)1(0)1612y k x x y y =-⎧⎪⎨+=≠⎪⎩, 得2222(43)6416(163)0k x k x k +-+-=,由()()()222264443161630k k k ∆=--+⨯->, 解得1122k -<<,且0k ≠. 设点()()1122,,,Mx y N x y ,MN 的中点()00,T x y∵21226443k x x k +=+,∴2023243x k k =+ 又∵22MF NF =,∴2F T MN⊥,∵22441F Tkk k -=- ∴2224141F Tk K k k -⨯==--,此方程无解.综上所述,不存在直线l 使得22MF NF =.【点睛】此题考察椭圆的定义的应用,直线与椭圆的综合应用,属于中档题.21.函数()()1x f x ax x R e=-∈. 〔1〕当2a =-时,求函数()f x 的单调区间;〔2〕假设0a>且1x ≥时,()ln f x x ≤,求a 的取值范围.【答案】〔1〕单调递减区间为(),ln 2-∞-,单调递增区间为()ln 2,-+∞;〔2〕1,e ⎡⎫+∞⎪⎢⎣⎭. 【解析】 【分析】〔1〕将2a =-代入函数()y f x =的解析式,求得该函数的导数,求出该函数的极值点,并分析导数的符号变化,由此可得出函数()y f x =的单调递增区间和递减区间; 〔2〕由题意得出不等式1n 0l x x ex a -+≥对任意的1x ≥恒成立,构造函数()()1ln 0xg x x ax a e =-+>,可得出()min0g x ≥,利用导数分析函数()y g x =在区间[)1,+∞上的单调性,求得函数()y g x =的最小值,由此可解得实数a 的取值范围.【详解】〔1〕当2a =-时,()12x f x x e =+,()12xf x e '∴=-+. 令()12120x x xe f x e e -'=-+==,得1ln ln 22x ==-. 当ln2x <-时,()0f x '<;当ln 2x >-时,()0f x '>.∴函数()y f x =的单调递减区间为(),ln 2-∞-,单调递增区间为()ln 2,-+∞;〔2〕()()ln 1f x x x ≤≥等价于1ln x ax x e -≤,即1n 0l xx ex a -+≥. 令()()1ln 0x gx x ax a e =-+>,那么()110xg x a x e '=++>, ∴函数()y g x =在[)1,+∞上单调递增,()()min 110g x g a e∴==-≥,解得1a e≥,因此,实数a 的取值范围是1,e ⎡⎫+∞⎪⎢⎣⎭. 【点睛】此题考察利用导数求解函数的单调区间,同时也考察了利用函数不等式恒成立求参数,考察分析问题和解决问题的才能,属于中等题.〔二〕选考题:〔一共10分.请考生在第22、23题中任选一题答题.假设多做,那么按所做的第一题计分〕22.在平面直角坐标系xOy 中,曲线C 的参数方程为sin x y θθ⎧=⎪⎨=⎪⎩〔θ为参数〕,在以原点O 为极点,x 的非负半轴为极轴建立的极坐标系中,直线l 的极坐标方程为cos()4πρθ+=〔1〕求曲线C 的普通方程和直线l 的直角坐标方程;〔2〕设直线l 与x 轴,y 轴分别交于A ,B 两点,点P 是曲线C 上任意一点,求PAB △面积的最大值.【答案】〔1〕2213x y +=,20x y -+=;〔2〕4. 【解析】 【分析】 〔1〕利用22sin cos 1θθ+=消去曲线C 参数方程中的参数θ得到C 的普通方程,利用两角和的余弦公式和cos sin x y ρθρθ=⎧⎨=⎩将直线l 的极坐标方程化为直角坐标方程;〔2〕设点P 的坐标为,sin )θθ,可求出点P 到直线l 的间隔d ≤||AB =,进而求出面积的最大值.【详解】〔1〕由sin x y θθ⎧=⎪⎨=⎪⎩〔θ为参数〕消去参数θ,得2213x y +=,所以曲线C 的普通方程为:2213x y +=,由cos()4πρθ+=cos sin 2ρθρθ-=-, 可得直线l 的直角坐标方程为:20x y -+=;〔2〕设点P 的坐标为,sin )θθ,那么点P 到直线l 的间隔为:2sin 23cos sin 232222d πθθθ⎛⎫-+ ⎪-+⎝⎭==≤, 又直线l 与x 轴,y 轴的交点分别为()2,0A -,()0,2B ,所以||22AB =,所以PAB △面积的最大值为1222242⨯⨯=. 【点睛】此题考察参数方程与普通方程的互化,考察极坐标方程与直角坐标方程的互化,考察参数法解决三角形面积的最值问题,考察逻辑思维才能和运算求解才能,考察转化才能,属于常考题. 23.函数f (x )=|2x -a |+|2x -1|(a ∈R ). (1)当a =-1时,求f (x )≤2的解集;(2)假设f (x )≤|2x +1|的解集包含集合1,12⎡⎤⎢⎥⎣⎦,务实数a 的取值范围. 【答案】〔1〕;〔2〕51,2⎡⎤-⎢⎥⎣⎦. 【解析】 试题分析: 〔1〕代入1a =-,由()2f x ≥,根据绝对值的几何意义,求出满足条件的x 的值即可;〔2〕根据题意,把()21f x x ≤+,转化为22121x a x x -+-≤+在1[,1]2x ∈上恒成立,求解max min (22)(22)x a x -≤≤+,即可求解实数a 的取值范围.试题解析:(1)当a =-1时,f(x)=|2x +1|+|2x -1|,f(x)≤2⇒+≤1,上述不等式的几何意义为数轴上点x 到两点-,间隔之和小于或者等于1,那么-≤x≤, 即原不等式的解集为.(2)∵f(x)≤|2x+1|的解集包含,∴当x∈时,不等式f(x)≤|2x+1|恒成立, ∴当x∈时,|2x -a|+2x -1≤2x+1恒成立,∴2x-2≤a≤2x+2在x∈上恒成立,∴(2x-2)max≤a≤(2x+2)min,∴0≤a≤3.。
数学建模y04下料问题B题

aij :第 j 种下料方式中第 i 种零件的切割数量, i = 1, , m, j = 1, , p 。 x j :第 j 种下料方式使用的次数, j = 1, , p 。
∑ q :所需原材料的数量, q = p x j 。 j =1
五.问题分析
一个好的下料方案首先应该使原材料的利用率最大,从而减少损失,降低成本,提高经 济效益。其次要求所采用的不同的下料方式尽可能少,即希望用最少的下料方式来完成任务。 因为在生产中转换下料方式需要费用和时间,既提高成本,又降低效率。此外,每种零件有 各自的交货时间,每天下料的数量受到企业生产能力的限制。因此实用下料问题的目标是在 生产能力容许的条件下,以最少数量的原材料,尽可能按时完成需求任务,同时下料方式数 也尽量得少。
802~850 之间,且已找到 q = 850 的可行解。
表 2 不同废料长度下的下料方案
下料方案
T p
0 20" 40882
x = ( x1 , , x p )T , x j :第 j 种下料方式使用的次数,且 j = 1, , p 。
可行的下料方案应满足零件个数的约束,设下料方式集为 Am× p ,则有:
Am×p x ≥ n
其中 n = ( n1 ,…,nm ),且 x j 为整数,满足 x j ≥ 0, j = 1, , p 。
上取整值,由 A 、 x 中各分量的非负性,可以证明 A ⎡⎢ x⎤⎥ ≥ n 。
因此,若 x 为线性规划范畴下的可行解, ⎡⎢ x⎤⎥ 即为可行的下料方案,同理,若 x 为线性
规划范畴下的最优解, ⎡⎢ x⎤⎥ 即为较优的下料方案,对比同一下料方式集下最优的下料方案,
其原材料使用数量之差不大于 x 中非零分量的个数,例如在下料方式集 A0 下,线性规划结
江苏省南通市2019-2020学年高考数学仿真第四次备考试题含解析

江苏省南通市2019-2020学年高考数学仿真第四次备考试题一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知F 为抛物线24y x =的焦点,点A 在抛物线上,且5AF =,过点F 的动直线l 与抛物线,B C 交于两点,O 为坐标原点,抛物线的准线与x 轴的交点为M .给出下列四个命题: ①在抛物线上满足条件的点A 仅有一个;②若P 是抛物线准线上一动点,则PA PO +的最小值为 ③无论过点F 的直线l 在什么位置,总有OMB OMC ∠=∠;④若点C 在抛物线准线上的射影为D ,则三点B O D 、、在同一条直线上. 其中所有正确命题的个数为( ) A .1 B .2C .3D .4【答案】C 【解析】 【分析】①:由抛物线的定义可知15AF a =+=,从而可求A 的坐标;②:做A 关于准线1x =-的对称点为'A ,通过分析可知当',,A P O 三点共线时PA PO +取最小值,由两点间的距离公式,可求此时最小值'A O ;③:设出直线l 方程,联立直线与抛物线方程,结合韦达定理,可知焦点坐标的关系,进而可求0MB MC k k +=,从而可判断出,OMB OMC ∠∠的关系;④:计算直线,OD OB 的斜率之差,可得两直线斜率相等,进而可判断三点B O D 、、在同一条直线上. 【详解】解:对于①,设(),A a b ,由抛物线的方程得()1,0F ,则15AF a =+=, 故4a =, 所以()4,4A 或()4,4-,所以满足条件的点A 有二个,故①不正确; 对于②,不妨设()4,4A ,则A 关于准线1x =-的对称点为()'6,4A -,故''PA OP PA OP A O +=+≥==, 当且仅当',,A P O 三点共线时等号成立,故②正确;对于③,由题意知,()1,0M - ,且l 的斜率不为0,则设l 方程为:()10x my m =+≠, 设l 与抛物线的交点坐标为()()1122,,,B x y C x y ,联立直线与抛物线的方程为,214x my y x=+⎧⎨=⎩ ,整理得2440y my --=,则12124,4y y m y y +==-,所以21242x x m +=+,()()221212114411x x my my m m =++=-++=则()()()()1221121212121212121122211111MB MCy x y x y y y y my y k k x x x x x x x x ++++++=+==+++++++ 2242404211m m m ⨯-⨯==+++.故,MB MC 的倾斜角互补,所以OMB OMC ∠=∠,故③正确. 对于④,由题意知()21,D y - ,由③知,12124,4y y m y y +==- 则12114,OB OD y k k y x y ===- ,由12211440OB OD y y k k y y y +-=+==, 知OB OD k k =,即三点B O D 、、在同一条直线上,故④正确. 故选:C. 【点睛】本题考查了抛物线的定义,考查了直线与抛物线的位置关系,考查了抛物线的性质,考查了直线方程,考查了两点的斜率公式.本题的难点在于第二个命题,结合初中的“饮马问题”分析出何时取最小值. 2.已知排球发球考试规则:每位考生最多可发球三次,若发球成功,则停止发球,否则一直发到3次结束为止.某考生一次发球成功的概率为()01p p <<,发球次数为X ,若X 的数学期望() 1.75E X >,则p 的取值范围为( )A .10,2⎛⎫⎪⎝⎭B .70,12⎛⎫ ⎪⎝⎭C .1,12⎛⎫ ⎪⎝⎭D .7,112⎛⎫ ⎪⎝⎭【答案】A 【解析】 【分析】根据题意,分别求出()()()123P X P X P X ===,,,再根据离散型随机变量期望公式进行求解即可 【详解】由题可知()1P X p ==,()()21P X p p ==-,()()()()2323111P X p p p p ==-+-=-,则()()()()()()21232131 1.75E X P X P X P X p p p p =====+-+->+2+3解得5122p p ><或,由()0,1p ∈可得10,2p ⎛∈⎫⎪⎝⎭, 答案选A 【点睛】本题考查离散型随机变量期望的求解,易错点为第三次发球分为两种情况:三次都不成功、第三次成功 3.已知数列{}n a 满足:12125 1,6n n n a a a a n -≤⎧=⎨-⎩L …()*n N ∈)若正整数()5k k ≥使得2221212k k a a a a a a ++⋯+=⋯成立,则k =( )A .16B .17C .18D .19【答案】B 【解析】 【分析】计算2226716...5n n a a a a a n ++++=-+-,故2221211...161k k k a a a a k a +++++=+-=+,解得答案.【详解】当6n ≥时,()1211111n n n n n a a a a a a a +--==+-L ,即211n n n a a a +=-+,且631a =.故()()()222677687116......55n n n n a a a a a a a a a n a a n +++++=-+-++-+-=-+-,2221211...161k k k a a a a k a +++++=+-=+,故17k =.故选:B . 【点睛】本题考查了数列的相关计算,意在考查学生的计算能力和对于数列公式方法的综合应用.4.已知抛物线22(0)y px p =>,F 为抛物线的焦点且MN 为过焦点的弦,若||1OF =,||8MN =,则OMN V 的面积为( )A .B .C .D .2【答案】A 【解析】 【分析】根据||1OF =可知24y x =,再利用抛物线的焦半径公式以及三角形面积公式求解即可. 【详解】由题意可知抛物线方程为24y x =,设点()11,M x y 点()22,N x y ,则由抛物线定义知,12|||||2MN MF NF x x =+=++,||8MN =则126x x +=.由24y x =得2114y x =,2224y x =则221224y y +=.又MN 为过焦点的弦,所以124y y =-,则21y y -==所以211||2OMN S OF y y =⋅-=V . 故选:A【点睛】本题考查抛物线的方程应用,同时也考查了焦半径公式等.属于中档题.5.若数列{}n a 为等差数列,且满足5383a a a ++=,n S 为数列{}n a 的前n 项和,则11S =( ) A .27 B .33C .39D .44【答案】B 【解析】 【分析】利用等差数列性质,若m n p q ++=,则m n p q a a a a ++= 求出63a =,再利用等差数列前n 项和公式得111116+)11(11332a a S a ===【详解】解:因为 5383a a a ++=,由等差数列性质,若m n p q ++=,则m n p q a a a a ++=得,63a ∴=.n S 为数列{}n a 的前n 项和,则111116+)11(11332a a S a ===.故选:B . 【点睛】本题考查等差数列性质与等差数列前n 项和.(1)如果{}n a 为等差数列,若m n p q ++=,则m n p q a a a a ++= ()*m n p q N ∈,,,. (2)要注意等差数列前n 项和公式的灵活应用,如21(21)n n S n a -=-.6.已知抛物线24x y =上一点A 的纵坐标为4,则点A 到抛物线焦点的距离为( ) A .2 B .3 C .4 D .5【答案】D 【解析】试题分析:抛物线24x y =焦点在y 轴上,开口向上,所以焦点坐标为(0,1),准线方程为1y =-,因为点A 的纵坐标为4,所以点A 到抛物线准线的距离为415+=,因为抛物线上的点到焦点的距离等于到准线的距离,所以点A 与抛物线焦点的距离为5.考点:本小题主要考查应用抛物线定义和抛物线上点的性质抛物线上的点到焦点的距离,考查学生的运算求解能力.点评:抛物线上的点到焦点的距离等于到准线的距离,这条性质在解题时经常用到,可以简化运算. 7.用数学归纳法证明,则当时,左端应在的基础上加上( )A .B .C .D .【答案】C 【解析】 【分析】首先分析题目求用数学归纳法证明1+1+3+…+n 1=时,当n=k+1时左端应在n=k 的基础上加上的式子,可以分别使得n=k ,和n=k+1代入等式,然后把n=k+1时等式的左端减去n=k 时等式的左端,即可得到答案. 【详解】当n=k 时,等式左端=1+1+…+k 1,当n=k+1时,等式左端=1+1+…+k 1+k 1+1+k 1+1+…+(k+1)1,增加了项(k 1+1)+(k 1+1)+(k 1+3)+…+(k+1)1. 故选:C . 【点睛】本题主要考查数学归纳法,属于中档题./8.函数22()2cos (sin cos )2f x x x x =++-的一个单调递增区间是( ) A .,44ππ⎡⎤-⎢⎥⎣⎦ B .3,88ππ⎡⎤-⎢⎥⎣⎦ C .5,88ππ⎡⎤⎢⎥⎣⎦D .59,88ππ⎡⎤⎢⎥⎣⎦【答案】D 【解析】 【分析】利用同角三角函数的基本关系式、二倍角公式和辅助角公式化简()f x 表达式,再根据三角函数单调区间的求法,求得()f x 的单调区间,由此确定正确选项. 【详解】因为22()2cos (sin cos )2f x x x x =++-1cos 21sin 22224x x x π⎛⎫=+++-=+ ⎪⎝⎭,由()f x 单调递增,则222242k x k πππππ-≤+≤+(k ∈Z ),解得388k x k ππππ-≤≤+(k ∈Z ),当1k =时,D 选项正确.C 选项是递减区间,A ,B 选项中有部分增区间部分减区间. 故选:D 【点睛】本小题考查三角函数的恒等变换,三角函数的图象与性质等基础知识;考查运算求解能力,推理论证能力,数形结合思想,应用意识.9.在ABC ∆中,“tan tan 1B C >”是“ABC ∆为钝角三角形”的( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既不充分也不必要条件【答案】C 【解析】分析:从两个方向去判断,先看tan tan 1A B >能推出三角形的形状是锐角三角形,而非钝角三角形,从而得到充分性不成立,再看当三角形是钝角三角形时,也推不出tan tan 1A B >成立,从而必要性也不满足,从而选出正确的结果.详解:由题意可得,在ABC ∆中,因为tan tan 1A B >, 所以sin sin 1cos cos A BA B>,因为0,0A B ππ<<<<,所以sin sin 0A B >,cos cos 0A B >,结合三角形内角的条件,故A,B 同为锐角,因为sin sin cos cos A B A B >, 所以cos cos sin sin 0A B A B -<,即cos()0A B +<,所以2A B ππ<+<,因此02C <<π,所以ABC ∆是锐角三角形,不是钝角三角形,所以充分性不满足,反之,若ABC ∆是钝角三角形,也推不出“tan tan 1B C >,故必要性不成立, 所以为既不充分也不必要条件,故选D.点睛:该题考查的是有关充分必要条件的判断问题,在解题的过程中,需要用到不等式的等价转化,余弦的和角公式,诱导公式等,需要明确对应此类问题的解题步骤,以及三角形形状对应的特征. 10.数列{}n a 满足:21n n n a a a +++=,11a =,22a =,n S 为其前n 项和,则2019S =( ) A .0 B .1C .3D .4【答案】D 【解析】 【分析】用1n +去换21n n n a a a +++=中的n ,得312n n n a a a ++++=,相加即可找到数列{}n a 的周期,再利用2019S =6123336S a a a +++计算.【详解】由已知,21n n n a a a +++=①,所以312n n n a a a ++++=②,①+②,得3n n a a +=-,从而6n n a a +=,数列是以6为周期的周期数列,且前6项分别为1,2,1,-1,-2,-1,所以60S =,2019126123336()01214S a a a a a a =++++++=+++=L .故选:D. 【点睛】本题考查周期数列的应用,在求2019S 时,先算出一个周期的和即6S ,再将2019S 表示成6123336S a a a +++即可,本题是一道中档题.11.某四棱锥的三视图如图所示,该几何体的体积是( )A .8B .83C .4D .43【答案】D 【解析】 【分析】根据三视图知,该几何体是一条垂直于底面的侧棱为2的四棱锥,画出图形,结合图形求出底面积代入体积公式求它的体积. 【详解】根据三视图知,该几何体是侧棱PA ⊥底面ABCD 的四棱锥,如图所示:结合图中数据知,该四棱锥底面为对角线为2的正方形, 高为PA=2,∴四棱锥的体积为21242323V =⋅⋅=.故选:D. 【点睛】本题考查由三视图求几何体体积,由三视图正确复原几何体是解题的关键,考查空间想象能力.属于中等题.12.一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为( )A .18B .17C .16D .15【答案】D 【解析】 【分析】 【详解】试题分析:如图所示,截去部分是正方体的一个角,其体积是正方体体积的16,剩余部分体积是正方体体积的56,所以截去部分体积与剩余部分体积的比值为,故选D. 考点:本题主要考查三视图及几何体体积的计算. 二、填空题:本题共4小题,每小题5分,共20分。
数学建模第4章作业

第8题解:假设每月初开始流入水,从题中可知,未用来发电的水可直接排出设XA1,XA2为本月和下月A水库供应A发电站的水量XB1,XB2为本月和下月B水库供应B发电站的水量YA1,YA2为本月和下月从A水库直接排出的水量YB1,YB2为本月和下月从B水库直接排出的水量ZA1,ZA2为本月和下月结束时A水库所剩的水量ZB1,ZB2为本月和下月结束时B水库所剩的水量M1,M2为本月和下月200元/千度售出的电量,N1,N2为本月和下月140元/千度售出的电量目标函数:Max 200(M1+M2)+140(N1+N2)约束条件:1,水的约束(本月) XA1+YA1+ZA1=1900+200XB1+YB1+ZB1=850+40+XA1+Y A1(下月)XA2+YA2+ZA2=ZA1+130XB2+YB1+ZB2=15+ZB2+XA2+YA22,发电量(本月)400XA1+200XB1=M1+N1(下月)400XA2+200XB2=M2+N23,发电能力A电站400XA1≦60000400XA2≦60000B电站200XB1≦35000200XB2≦350004,水库蓄水量A水库1200≦ZA1≦20001200≦ZA2≦2000B水库800≦ZB1≦1500800≦ZB2≦15005,高价电M1≦50000,M2≦50000用LINGO求解model:max=200*M1+200*M2+140*N1+140*N2;XA1+Y A1+ZA1-1900-200=0;XA2+Y A2+ZA2-ZA1-130=0;XB1+YB1+ZB1-850-40-XA1-YA1=0;XB2+YB1+ZB2-15-ZB2-XA2-YA2=0;400*XA1+200*XB1-M1-N1=0;400*XA2+200*XB2-M-+N2=0;400*XA1<60000;400*XA2<60000;200*XB1<35000;200*XB2<35000;1200<ZA1;ZA1<2000;1200<ZA2;ZA2<2000;800<ZB1;ZB1<1500;800<ZB2;ZB2<1500;M1<50000;M2<50000;end运行结果Global optimal solution found.Objective value: 0.3960000E+08Total solver iterations: 8Variable Value Reduced Cost M1 50000.00 0.000000 M2 50000.00 0.000000 N1 45000.00 0.000000 N2 95000.00 0.000000 XA1 150.0000 0.000000 YA1 0.000000 0.000000 ZA1 1950.000 0.000000 XA2 150.0000 0.000000 YA2 10.00000 0.000000 ZA2 1920.000 0.000000 XB1 175.0000 0.000000 YB1 0.000000 0.000000 ZB1 865.0000 0.000000 XB2 175.0000 0.000000 ZB2 800.0000 0.000000 M 0.000000 140.0000Row Slack or Surplus Dual Price1 0.3960000E+08 1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 -140.00007 0.000000 -140.00008 0.000000 140.00009 0.000000 140.000010 0.000000 140.000011 0.000000 140.000012 750.0000 0.00000013 50.00000 0.00000014 720.0000 0.00000015 80.00000 0.00000016 65.00000 0.00000017 635.0000 0.00000018 0.000000 0.00000019 700.0000 0.00000020 0.000000 60.0000021 0.000000 200.0000结果:A水库供应A电站发电的水量本月和下月都为150万立方米,B水库供应B电站发电的水量本月和下月都为175万立方米本月和下月高价卖出电量都为50000千度,低价卖出量分别为45000千度和95000千度总收入为396*10^5元。
北京工业大学数学建模作业汇总

第一次作业数学建模入门1.冷却定律与破案按照Newton冷却定律,温度为T的物体在温度为To (To<T)的环境中冷却的速度与温差T-To成正比。
你能用该定律确定张某是否是下面案件中的犯罪嫌疑人。
某公安局于晚上7时30分发现一具女尸,当晚8时20分法医测得尸体温度为32.6℃,一小时后,尸体被抬走时又测得尸体温度为31.4℃,,已知室温在几个小时内均为21.1℃,由案情分析得知张某是此案的主要犯罪嫌疑人,但张某矢口否认,并有证人说:“下午张某一直在办公室,下午5时打一个电话后才离开办公室”。
从办公室到案发现场步行需要5分钟,问张某是否能被排除在犯罪嫌疑人之外?解答:首先,牛顿冷却定律为温度为T(t)的物体在温度的环境中冷却的速度与温度差成正比。
所以,得出微分方程 ( ,K为比例常数。
任意时刻t,物体的温度为 ,C为常数根据已知条件,记晚上8时20分为t=0时刻,T(0)=32.6℃,T(1)=31.4℃,=21.1℃:求解函数得,k=-0.11,C=11.5,即假定人的正常体温为37℃,代入公式得t-2.95小时, 即遇害时间为8.33-2.95=5.38≈5时23分。
张某在5时离开办公室,步行需要5分钟到达案发地点,所以张某不能排除作案嫌疑。
2.锻炼想象力、洞察力和判断力的问题(1)某人早8时从山下旅店出发沿一条山路上山,下午5时到达山顶并留宿,次日8时沿同一条路径下山,下午5时回到旅店。
该人必在两天中的同一是可经过路径中的同一地点,为什么?解答:令:A(t)表示此人第一天上山时t时刻离山脚的路程;B(t)表示此人第二天下山时t时刻离山脚的路程。
假设山顶到山下的总路程为S,由已知条件可知:A(8)=0,A(17)= SB(8)= S,B(17)=0令:C(t)= A(t)- B(t);则C(8)=-S,C(17)= S;由于C(t)为连续函数,由零点定理推出结论:在t=[8,17]中间,至少存在一点 t 使C(t)= A(t)- B(t)=0;即A(t)= B(t),可证明这人必在两天中的同一时刻经过路径中的同一地点。
陕西省榆林市2021届高三下学期第四次模拟考试理科数学答案

陕西省榆林市2021届高三下学期第四次模拟考试理科数学试题参考答案1.B 【思路点拨】求出集合,A B 中的元素后,由交集定义求得交集后可得元素个数. 【解析】因为{2,1,0,1,2,3,4}A =--,{4,2,0,2,4,6,8}B =--,所以{2,0,2,4}A B ⋂=-.元素个数是4. 故选:B .2.C 【思路点拨】利用数量积的定义和运算律可求题设中的数量积.【解析】23()||||||cos 11545AB AB AC AB AB AC A ⋅+=+⋅=+⨯⨯=, 故选:C.3.B 【思路点拨】作出可行域,平移直线z x y =-,找出使得该直线在x 轴上的截距最大时对应的最优解,代入目标函数即可得解.【解析】作出不等式组23326x x y x y ≤⎧⎪+≤⎨⎪+≥⎩所表示的可行域如下图所示:联立2326x x y =⎧⎨+=⎩,解得20x y =⎧⎨=⎩,即点()2,0C ,平移直线z x y =-,当该直线经过可行域的顶点C 时,直线z x y =-在x 轴上的截距最大,此时z 取最大值,即max 202z =-=. 故选:B.【名师指导】思路点睛:本题主要考查线性规划中,利用可行域求目标函数的最值,属于简单题.求目标函数最值的一般步骤是“一画、二移、三求”: (1)作出可行域(一定要注意是实线还是虚线);(2)找到目标函数对应的最优解对应点(在可行域内平移变形后的目标函数,最先通过或最后通过的顶点就是最优解);(3)将最优解坐标代入目标函数求出最值.4.D 【思路点拨】结合偶函数图像关于y 轴对称可求解. 【解析】解:当0x ≥时,由()lg(31)10f x x =+->,得3x >.又因为函数()f x 为偶函数,所以不等式()0f x >的解集为(,3)(3,)-∞-⋃+∞. 故选:D.5.D 【思路点拨】利用赋值法得到n 的值,由二项式定理即可得结果.【解析】因为展开式中所有项的系数和为64,令1x =,可得()264n-=,所以6n =. 因为通项公式为316(3)rrrr T C x -+=-,所以2236(3)135T C x x =-=.故选:D.6.D 【思路点拨】利用对数的运算性质,由香农公式分别计算信噪比为1000和16000时C 的比值即可求解. 【解析】解:由题意221.1log 16000lg1600034lg 21 1.11 1.110.54log 1000lg10003W W +-=⨯-=⨯-=,所以C 大约增加了54%. 故选:D.7.C 【思路点拨】根据框图,模拟程序运行即可求解. 【解析】第一次执行程序11011a =+=,5i =; 第二次执行程序52227a =+=,10i =; 第三次执行程序215475a =+=,15i =;第四次执行程序69150100a =+>,20i =,跳出循环输出i , 故输出的20i =. 故选:C8.B 【思路点拨】先把()y f x =化简,利用周期求出1ω=,根据()y f x =的图像关于直线8x π=对称,求得7242k ππϕ=+,求出ϕ的最小值. 【解析】()cos cos cos sin 66266f x x x x x πππππωϕωϕωϕωϕ⎛⎫⎛⎫⎛⎫⎛⎫=+-+-+=-+-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭1sin 2223x πωϕ⎛⎫=-+- ⎪⎝⎭.因为()f x 的最小正周期为π,所以22ππω=,得1ω=. 依题意得22832k πππϕπ⨯+-=+,k ∈Z ,所以7242k ππϕ=+,当1k =-时,||ϕ取得最小值524π. 故选:B【名师指导】三角函数问题通常需要把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题.9.A 【思路点拨】设正五边形数构成数列{}n a ,根据题中条件,得到递推关系,再由累加法,即可得出通项公式,从而可求出结果.【解析】设正五边形数构成数列{}n a ,则11a =,25a =,且当3n ≥时,15(1)n n a a n -=+-, 于是()()()2324315(1)552535(1)2n n n n n a a a a a a a a n --=+-+-+⋅⋅⋅+-=+⨯+⨯+⋅⋅⋅+-=, 故20215202120205101020212a ⨯⨯==⨯⨯.故选:A.10.B 【思路点拨】作出图形,找出与BD 共面的棱,利用组合计数原理以及古典概型的概率公式可求得结果.【解析】如图,这九条棱中,与BD 共面的是BC 、1BB 、1CC 、11B C 、AB ,共五条,故所求概率252913118C P C =-=.故选:B.11.A 【思路点拨】过A 作AE l ⊥于E ,过B 作BC l ⊥于C ,利用抛物线定义及PCB PHF 可求解.【解析】解:如图,设准线为l ,l 与x 轴交点为H ,过A 作AE l ⊥于E ,过B 作BC l ⊥于C .2AP AF =,F ∴是PA 的中点,所以12AE AF PF PA ===. 在RT PEA 中,1sin 2AE EPA AP∠==, 30EPA ∴∠=,即30HPF ∠=.在RT PHF 中,HF p =,2PF p ∴=,PCB PHF ,且2BC BF ==,BC PB HFPF∴=,即2222p p p-=,解得3p =. 故选:A.【名师指导】关键点点睛:涉及抛物线上的点到焦点的距离,常结合抛物线的定义与简单几何性质求解.12.C 【思路点拨】根据“凹函数”的定义转化为22x t x e x ⎛⎫>-- ⎪⎝⎭在()0,2上恒成立,再构造函数求出最大值即可得解.【解析】因为221()1x x x x e x e e e tf x t t x x x x x ⋅-⎛⎫'=-+=--- ⎪⎝⎭, 所以22423222221()x x x x x e x e e x e x t t f x e x x x x x x x⋅-⋅-⋅⎛⎫''=-+=-++ ⎪⎝⎭. 因为()f x 在()0,2上为“凹函数”,所以在()0,2上322221()0x tf x e x xx x ⎛⎫''=-++>⎪⎝⎭,即22x t x e x ⎛⎫>-- ⎪⎝⎭恒成立,令2()2x g x x e x ⎛⎫=-- ⎪⎝⎭,()0,2x ∈, 则()22222()(1)(2(1)2)x x x g x e x e x x x x e x'=-++---=, 当01x <<时,()0g x '>,当12x <<时,()0g x '<,所以()g x 在()0,1上单调递增,在()1,2上单调递减,所以()max ()1g x g e ==-, 所以t e >-. 故选:C【名师指导】结论点睛:本题考查不等式的恒成立与有解问题,可按如下规则转化: ①若()k f x ≥在[,]a b 上恒成立,则max ()k f x ≥; ②若()k f x ≤在[,]a b 上恒成立,则min ()k f x ≤;③若()k f x ≥在[,]a b 上有解,则min ()k f x ≥; ④若()k f x ≤在[,]a b 上有解,则max ()k f x ≤.13.9-【思路点拨】利用复数的乘法化简复数z ,由此可得出复数z 的实部. 【解析】()()21215171097z i i i i i =--=-+=--,因此,复数z 的实部为9-.故答案为:9-.14.6【思路点拨】根据双曲线的方程求出,a b ,再由222c a b =+可求出c ,再根据离心率ce a=求解即可.【解析】由双曲线22135y x -=可得1a =,b =6c =,所以离心率6ce a==. 故答案为:615.2nn 【思路点拨】根据题中条件,得到{}n na 是等比数列,求出其通项公式,进而可得n a .【解析】依题意可得数列{}n na 是首项为2,公比为2的等比数列,则2nn na =,所以2nn a n=. 故答案为:2nn. 16.36π【思路点拨】作出图形,计算出木球的最大半径,利用球体的表面积公式可求得结果.【解析】如图,球O 与铁桶盖的切点为铁桶盖所在圆的圆心1O ,设球O 与铁桶上底面圆的切点为B ,连接1O B ,则1O B 为球O 的一条直径,且11O B O A ⊥, 点B 到铁盖中心1O 的距离恰好是球最大的直径,因为AB =160O AB ∠=,则1sin606O B AB ==,即球最大的半径为3, 此时木球的表面积为24336ππ⨯=.故答案为:36π.【名师指导】关键点点睛:本题求解球体表面积的计算,解题的关键在于分析出球与铁桶以及铁桶盖相切的位置,结合球体的结构特征列等式求解球的半径.17.【思路点拨】(1)利用正弦定理求得sin B 的值,由此求得cos 2B 的值.(2)利用余弦定理求得cos A ,结合基本不等式求得A 的最大值,由此求得此时ABC 的面积.【解析】(1)由正弦定理sin sin a b A B =32sin 2B =,解得3sin B = 所以21cos 212sin 3B B =-=. (2)由余弦定理得22221cos 24b c a c A bc c +-+==. 因为2121442c c c c +≥=,当且仅当1c =时,等号成立,所以1cos 2A ≥,则03A π<≤,则A 的最大值为3π.此时,ABC 的面积113sin 21sin 2232S bc A π==⨯⨯⨯=. 18.(1)平均车速为70.5千米/时;(2)635辆;(3)0.499.【思路点拨】(1)根据频率分布直方图,利用平均数公式求解;(2)根据Z 服从正态分布()2,N μσ,利用3σ原则求解;(3)根据(2)得到行车速度低于84.8千米/时的概率为10.158650.84135-=,再根据~(4,0.84135)B ξ求解.【解析】(1)由题意知所以(4595)0.1(5585)0.15650.2750.370.5x =+⨯++⨯+⨯+⨯=, 所以这4000辆机动车的平均车速为70.5千米/时.(2)依题意,Z 服从正态分布()2,N μσ,其中70.5x μ==,22204.75s σ==,所以14.3σ=. 因为()(56.284.8)0.6827P Z P Z μσμσ-<≤+=<≤≈,所以10.6827(84.8)0.158652P Z -≥==, 所以车速不低于84.8千米/时的车辆估计有0.158654000634.6635⨯=≈辆. (3)行车速度低于84.8千米/时的概率为10.158650.84135-=,而~(4,0.84135)B ξ,所以4(3)1(4)10.841350.499P P ξξ≤=-==-=.【名师指导】方法点睛:关于正态曲线在某个区间内取值的概率求法:①熟记P (μ-σ<X ≤μ+σ),P (μ-2σ<X ≤μ+2σ),P (μ-3σ<X ≤μ+3σ)的值;②充分利用正态曲线的对称性和曲线与x 轴之间面积为1.19.【思路点拨】(1)先证AB ⊥平面PAC ,得AB AM ⊥,AM CD ⊥,结合AM PC ⊥得AM ⊥平面PCD ,然后可证得面面垂直;(2)建立如图所示的空间直角坐标系,用空间向量法求二面角的余弦值. 【解析】(1)证明:由题意知点A 为圆O 上一点,则AB AC ⊥. 由PA ⊥底面ABCD ,AB ⊂平面ABCD ,知PA AB ⊥.又PAAC A =,,PA AC ⊂平面PAC .因此AB ⊥平面PAC ,AM ⊂平面PAC ,则AB AM ⊥,又//AB CD ,则AM CD ⊥.因为AC AP =,M 为PC 的中点,所以AM PC ⊥.又CD PC C =,,CD PC ⊂平面PCD ,所以AM ⊥平面PCD .因为AM ⊂平面OAM ,所以平面OAM ⊥平面PCD .(2)解:如图,以A 为原点,AB 的方向为x 轴的正方向建立空间直角坐标系A xyz -, 则(0,2,0)C ,()23,2,0D -,(0,1,1)M,()3,1,0O,()3,0,1OM =-,()33,1,0OD =-.设(,,)n x y z =为平面OMD 的法向量,则0,0,n ON n OD ⎧⋅=⎨⋅=⎩即30,330.x z x y ⎧-+=⎪⎨-+=⎪⎩ 令1x =,得()1,33,3n =.由(1)可知,AM ⊥平面PCD ,则平面CDM 的一个法向量(0,1,1)m =,所以2186cos ,31||||m n m n m n ⋅〈〉==. 由图可知二面角O MD C --为锐角,故二面角O MD C --的余弦值为218631.【名师指导】方法点睛:本题考查证明面面垂直,考查求二面角.求二面角的方法: (1)几何法(定义法):根据定义作出二面角的平面角并证明,然后解三角形得出结论; (2)空间向量法:建立空间直角坐标系,写出各点为坐标,求出二面角两个面的法向量,由两个平面法向量的夹角得二面角(它们相等或互补).20.【思路点拨】(1)求出函数导数,令()0f x '=,分析导数在零点分割定义域所得区间上的符号,即可的出函数的单调性;(2)原函数零点可转化为()f x a =方程根的个数,利用函数的单调性求出函数()f x 的极值,即可讨论出答案.【解析】(1)3258()e (38)(1)e 333x x xf x x x x x x ⎛⎫'=+-=+- ⎪⎝⎭, 因为[1,)x ∈-+∞,所以()'f x 的零点为0和1.令()0f x '<,得01x <<;令()0f x '>,得1x >或10x -≤<. 所以()f x 的单调递减区间为(0,1),单调递增区间为[1,0)-,(1,)+∞. (2)由(1)知,()f x 在[]1,2-上的极大值为(0)0f =,极小值为e (1)3f =-, 因为7(1)3ef -=-,22(1)771(1)e 2.7f f -=<<,所以(1)(1)0f f <-<. 28e (2)3f =,由()0g x =,得()f x a =. 当e 3a <-或28e 3a >时,()g x 的零点个数为0;当e 3a =-或28e 03a <≤时,()g x 的零点个数为1;当e 733e a -<<-或0a =时,()g x 的零点个数为2; 当703ea -≤<时,()g x 的零点个数为3. 【名师指导】关键点点睛:函数()()g x f x a =-在[]1,2-上的零点个数可转化为()f x a =在[]1,2-上根的个数,需要结合函数()f x 的极值,讨论a 的范围得出方程根的个数,属于中档题.21.【思路点拨】(1)根据定义求出a 、b 、c ,即可写出椭圆的标准方程;(2)设直线MN 的方程为1x my =+,用“设而不求法”表示出AN ,AG ,证明出//AN AG ,即可得到A ,N ,G 三点共线.【解析】(1)解:由椭圆的定义知122PF PF a +=,则22PF a =-由光学性质可知PQ 是12F PF ∠的角平分线,所以1212PF PF FQ F Q=.因为1c =2=,得2a =,从而2223b a c =-=,故椭圆C 的方程为22143x y +=.(2)证明:设直线MN 的方程为1x my =+,()11,M x y ,()22,N x y联立方程组221,1,43x my x y =+⎧⎪⎨+=⎪⎩得()2234690m y my ++-=,则122634m y y m +=-+,122934y y m =-+ 因为直线MB 的方程为11(2)2y y x x =--, 所以令4x =,得1124,2y G x ⎛⎫⎪-⎝⎭, 因为()222,AN x y =+,1126,2y AG x ⎛⎫= ⎪-⎝⎭, 又()()()()21121212122111612346262211y my y my my y y y y y x x my my --+-+-+⨯==--- 2219646343401m m m m my ⎛⎫⎛⎫--- ⎪ ⎪++⎝⎭⎝⎭==-.所以//AN AG . 因为ANAG A =,所以A ,N ,G 三点共线.【名师指导】(1)待定系数法、代入法可以求二次曲线的标准方程;(2)“设而不求法”是一种在解析几何中常见的解题方法,可以解决直线与二次曲线相交的问题.22.【思路点拨】(1)结合圆的参数方程求得曲线C 的一个参数方程.(2)设出P 点的坐标,求得2PA PB OA OP ⋅+⋅的表达式,进而求得2PA PB OA OP ⋅+⋅的取值范围.【解析】(1)由x =,得2223x y y =-++,整理得22(1)4x y +-=,又0x =≥,所以曲线C 的一个参数方程为2cos ,12sin x y θθ=⎧⎨=+⎩(θ为参数,且22ππθ-≤≤).(2)由(1)可设点P 的坐标为(2cos ,12sin )θθ+,22ππθ-≤≤.因为(12cos ,12sin )PA θθ=---,(12cos ,12sin )PB θθ=----, 所以2(12cos )(12cos )(12sin )44sin PA PB θθθθ⋅=---+--=+. 又2cos OA OP θ⋅=,所以244(sin cos )44PA PB OA OP πθθθ⎛⎫⋅+⋅=++=++ ⎪⎝⎭.因为22ππθ-≤≤,3444πππθ-≤+≤,所以sin 14πθ⎛⎫≤+≤ ⎪⎝⎭,4πθ⎛⎫⎡+∈- ⎪⎣⎝⎭,故2PA PB OA OP ⋅+⋅的取值范围是0,4⎡+⎣.【名师指导】由曲线的直角坐标方程求其参数方程,要注意参数的取值范围.23.【思路点拨】(1)利用绝对值三角形不等式得到()||f x a b ≥-,再根据232a b b =++,得到22||22(1)11a b b b b -=++=++≥证明;(2)根据不等式()7f x 的解集为[6,1]-,得到(6)(1)7f f -==,不妨取0a =,则5b =,再证明|||5|7x x ++≤的解集为[6,1]-即可.【解析】(1)证明:()|||||()|||f x x a x b x a x b a b =+++≥+-+=-. 因为232a b b =++,所以22||22(1)11a b b b b -=++=++≥,当1b =-时,||-a b 取得最小值1, 故x ∀∈R ,b ∈R ,()1f x ≥. (2)依题意可得(6)(1)7f f -==, 即|6||6||1||1|7a b a b -+-=+++=, 不妨取0a =,则5b =.下面证明|||5|7x x ++≤的解集为[6,1]-.证明:当5x ≤-时,257x --≤,则6x ≥-,又5x ≤-, 所以65x -≤≤-.当5x 0-<<时,57≤显然成立,所以5x 0-<<.当0 x ≥时,257x +≤,则1x ≤,又0x ≥,所以01x ≤≤. 所以|||5|7x x ++≤的解集为[6,1]-, 故a ,b 的一组值为0,5.【名师指导】关键点点睛:本题第一问关键是绝对值三角不等式的应用和232a b b =++的变形的巧妙结合.。
数学模型第四版课后习题4—1答案
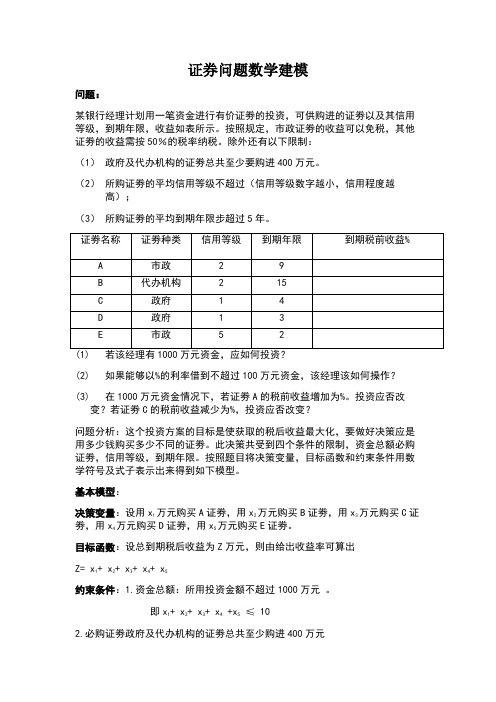
证券问题数学建模问题:某银行经理计划用一笔资金进行有价证劵的投资,可供购进的证劵以及其信用等级,到期年限,收益如表所示。
按照规定,市政证劵的收益可以免税,其他证劵的收益需按50%的税率纳税。
除外还有以下限制:(1)政府及代办机构的证劵总共至少要购进400万元。
(2)所购证劵的平均信用等级不超过(信用等级数字越小,信用程度越高);(3)所购证劵的平均到期年限步超过5年。
证劵名称证劵种类信用等级到期年限到期税前收益%A市政29B代办机构215C政府14D政府13E市政52(2)如果能够以%的利率借到不超过100万元资金,该经理该如何操作?(3)在1000万元资金情况下,若证劵A的税前收益增加为%。
投资应否改变?若证劵C的税前收益减少为%,投资应否改变?问题分析:这个投资方案的目标是使获取的税后收益最大化,要做好决策应是用多少钱购买多少不同的证劵。
此决策共受到四个条件的限制,资金总额必购证劵,信用等级,到期年限。
按照题目将决策变量,目标函数和约束条件用数学符号及式子表示出来得到如下模型。
基本模型:决策变量:设用x1万元购买A证劵,用x2万元购买B证劵,用x3万元购买C证劵,用x4万元购买D证劵,用x5万元购买E证劵。
目标函数:设总到期税后收益为Z万元,则由给出收益率可算出Z= x1+ x2+ x3+ x4+ x5约束条件:1.资金总额:所用投资金额不超过1000万元。
即x1+ x2+ x3+ x4+x5102.必购证劵政府及代办机构的证劵总共至少购进400万元即x2+ x3+ x443.信用等级:所购证劵的平均信用等级都不超过,即4.到期年限:所购证劵的平均到期年限步超过5年,即5.非负约束x1 x2x3x4x5为输入方便,将(3)(4)化简可得到该问题的基本模型Max Z= x1+ x2+ x3+ x4+ x5(1)x 1 +x2+ x3+ x4+x510(2)x 2+ x3+ x44(3)6x1+ 6x2-4x3-4x4+36x510(4)4x1+10 x2- x3-2x4-3x510(5)x 1x2x3x4 x5模型求解:用LINGO软件求解输入:model:max= *x1+* x2+* x3+* x4+* x5;[money] x1+ x2+ x3+ x4+x510;[must] x2+ x3+ x44;[credit] 6*x1+ 6*x2-4*x3-4*x4+36*x50;[time] 4*x1+10*x2-x3-2*x4-3*x50 ;end得到如下输出:Global optimal solution found.Objective value:Infeasibilities:Total solver iterations: 5Variable Value Reduced CostX1X2X3X4X5Row Slack or Surplus Dual Price1MONEYMUSTCREDITTIMERanges in which the basis is unchanged:Objective Coefficient RangesCurrent Allowable Allowable Variable Coefficient Increase Decrease X1X2 INFINITYX3X4 INFINITYX5Righthand Side RangesRow Current Allowable Allowable RHS Increase Decrease MONEY INFINITYMUST INFINITYCREDITTIME最优解为x1=,x2=0,x3=,x4=,x5=0;最优值为Z=;即证劵A,C,E分别投资百万元,百万元,百万元,最大税后收益为百万元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
f=sym('-0.2*x+120*exp(-0.6*t)');
a=0; b=20; h=0.4;
n=(b-a)/h+1; % n=(b-a)/h;
t=0; x=0;
szj=[t,x];
for i=1:n-1 % i=1:n
l1=subs(f,{'t','x'},{t,x});
l2=subs(f,{'t','x'},{t+h/2,x+l1*h/2});
l3=subs(f,{'t','x'},{t+h/2,x+l2*h/2});
l4=subs(f,{'t','x'},{t+h,x+l3*h});
x=x+h*(l1+2*l2+2*l3+l4)/6;
t=t+h;
szj=[szj;t,x];
End
szj
plot(szj(:,1),szj(:,2), 'dg-')
szj =
0 0
0.4000 40.9465
0.8000 70.0080
1.2000 89.9626
1.6000 10
2.9767
2.0000 110.7376
2.4000 114.5566
2.8000 115.4504
3.2000 11
4.2055
3.6000 111.4280
4.0000 107.5832
4.4000 103.0264
4.8000 98.0273
5.2000 92.7892
5.6000 87.4633
6.0000 82.1611
6.4000 76.9630
6.8000 71.9259
7.2000 67.0883
7.6000 62.4749
8.0000 58.1000
8.4000 53.9700
8.8000 50.0857
9.2000 46.4434
9.6000 43.0367
10.0000 39.8569 10.4000 36.8941
10.8000 34.1374
11.2000 31.5756
11.6000 29.1973
12.0000 26.9914 12.4000 24.9468
12.8000 23.0528
13.2000 21.2994
13.6000 19.6767
14.0000 18.1756 14.4000 16.7874
14.8000 15.5039
15.2000 14.3176
15.6000 13.2213
16.0000 12.2083 16.4000 11.2725
16.8000 10.4080
17.2000 9.6095
17.6000 8.8721
18.0000 8.1910 18.4000 7.5621
18.8000 6.9813
19.2000 6.4451
19.6000 5.9500
20.0000 5.4928
=
17
v/
m
s
(3)如图所示
(4)MATLAB程序
a=8;
dogxa=[];rabbitxa=[];dogya=[];rabbitya=[];
d=1;
dogx=-100*sqrt(2);dogy=-100*sqrt(2);rabbitx=0;rabbity=0;
t=0;
dt=0.01;
for b=8:0.5:40
dogx=-100*sqrt(2);dogy=-100*sqrt(2);rabbitx=0;rabbity=0;
t=0;
c=b;
a=8;
while(sqrt((dogx-rabbitx)^2+(dogy-
rabbity)^2)>d&rabbity<60*sqrt(2))
%while cabbity<60*sqrt(2)
if(sqrt((dogx-rabbitx)^2+(dogy-rabbity)^2)<=30)
b=b*1.1^dt;
a=a*0.5^dt;
end
t=t+dt;
d ogx=dogx+b*dt*(rabbitx-dogx)/sqrt((dogx-rabbitx)^2+(dogy-rabbity)^2);
d ogy=dogy+b*dt*(rabbity-dogy)/sqrt((dogx-rabbitx)^2+(dogy-rabbity)^2);
r abbitx=rabbitx-a*dt*cos(pi/4);
r abbity=rabbity+a*sin(pi/4)*dt;
end
if (rabbity<=60*sqrt(2))
b=c;
b reak
end
end
fprintf('the minspeed of dog is:%2f',b);
a=8;
b=15.5;
dogxb=[];rabbitxb=[];dogyb=[];rabbityb=[];
dogx=-100*sqrt(2);dogy=-100*sqrt(2);rabbitx=0;rabbity=0; t=0;
dt=0.01;
s=0;
while(sqrt((dogx-rabbitx)^2+(dogy-rabbity)^2)>d)
t=t+dt;
if(sqrt((dogx-rabbitx)^2+(dogy-rabbity)^2)<=30)
b=b*1.1^dt;
a=a*0.5^dt
end
dogx0=dogx;
dogy0=dogy;
dogx=dogx+b*dt*(rabbitx-dogx)/sqrt((rabbitx-dogx)^2+(rabbity-dogy)^2);
dogxb=[dogxb,dogx];
dogy=dogy+b*dt*(rabbity-dogy)/sqrt((rabbitx-dogx)^2+(rabbity-dogy)^2);
dogyb=[dogyb,dogy];
rabbitx=rabbitx-a*dt*cos(pi/4);
rabbity=rabbity+a*sin(pi/4)*dt;
rabbitxb=[rabbitxb,rabbitx];
cabbityb=[cabbityb,cabbity];
s=s+sqrt((dogx0-dogx)^2+(dogy0-dogy)^2);
end
fprintf('the length dog run is:%.1f',s);
plot(dogxb,dogyb,rabbitxb,rabbityb,'*')。
