信号与系统 刘树棠 第二版 中文答案 第6章
信号与系统(第二版)电子工业出版社【参考答案】

第一章1.8 系统的数学模型如下,试判断其线性、时不变性和因果性。
其中X (0-)为系统的初始状态。
(2)()()2f t y t e = (5)()()cos2y t f t t = (8)()()2y t f t = 解:(2)()()2f t y t e = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()122212,f t f t y t ey t e==那么 ()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==,显然,()()()1122y t a y t a y t ≠+,所以是非线性的。
② 时不变性设()()11,f t y t →则 ()()()()10122110,f t t f t y t e y t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t e y t t -==-,所以是时不变的。
③ 因果性因为对任意时刻 t 1,()()121f t y t e =,即输出由当前时刻的输入决定,所以系统是因果的。
(5)()()cos2y t f t t = ① 线性: 设 ()()()()1122,f t y t f t y t →→,则 ()()()()1122cos2,cos2y t f t t y t f t t ==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t +→=+=+⎡⎤⎣⎦, 显然()()()1122y t a y t a y t =+,所以系统是线性的。
② 时不变性设()()11,f t y t →则 ()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-,所以是时变的。
信号与系统第六章习题答案

z z −3 = z −1 z −1
, ε [n − 8] ↔ z
−8
z z −7 = z −1 z −1
再根据 z 变换的线性,则有:
Z [ε [n] − 2ε [n − 4] + ε [n − 8]] =
n
z 2 z −3 z − 7 z − 2 z −3 + z −7 − + = z −1 z −1 z −1 z −1
z z ,有 F1 ( z ) = z−a z +1
n
(4)令 f 1 [n] = (− 1) ε [n] ⋅ ,则根据 a nε [n ] ↔ 所以 根据 z 变换的微分性质,有:
f [n] = (− 1) nε [n]⋅ = nf 1 [n]
F (z ) = − z
(5) nε [n] ↔
d z F1 (z ) = − dz ( z + 1)2
F (z) F (z) 为有理分式,则可将 展开成部分分式,再乘以 z ,再利用常 z z
j π 4 −j π 4
n
n
对该级数,当 e
z
−1
< 1且 e
z
−1
< 1 ,即 z > 1 时,级数收敛,并有
1 F (z ) = × 2
1 1 − e 4 z −1
j π
1 + × 2
1 1− e
−j π 4
z −1
1 z z = + π π j −j 2 z−e 4 z−e 4
n ∞ ∞ 1 n ∞ 1 n 1 −1 n n −n F ( z ) = Z + 3 ε [n] = ∑ + 3 ε [n ]z = ∑ z + ∑ 3 z −1 n= 0 n= 0 2 2 2 n=0
信号与系统 奥本海姆 第二版(刘树棠译)

四. 信号与系统分析的主要应用领域 信号与系统分析的一个目的是研究系统对 给定输入信号所产生的输出响应. 给定输入信号所产生的输出响应.
另一个目的是研究为了使给定输入信号经 过系统后其输出响应符合人们的希望或要求, 过系统后其输出响应符合人们的希望或要求, 系统应该具有什么样的特性, 系统应该具有什么样的特性,进而设计出该 系统. 系统. 通信,电路设计,生物工程,远程医疗等; 通信,电路设计,生物工程,远程医疗等; 信号处理,图象恢复与增强,噪声抑制等; 信号处理,图象恢复与增强,噪声抑制等;
总计:授课54学时 习题课8学时 复习2学时 学时, 学时, 总计:授课 学时,习题课 学时,复习 学时
参考书目录
A.V.Oppenheim, A.S.Willsky with I.T.Young. Signals and Systems. Prentice-Hall. Inc. 1997. . 吴湘淇. 信号,系统与信号处理》 吴湘淇 《信号,系统与信号处理》 北京:电子工业出版社, 北京:电子工业出版社,1996. 郑君里,杨为理 信号与系统》 郑君里,杨为理. 《信号与系统》 清华大学出版社, 清华大学出版社 1999. 管致中,夏恭恪 信号与线性系统》 管致中,夏恭恪. 《信号与线性系统》 人民教育出版社,1983. 人民教育出版社, 阎鸿森,王新凤,田惠生 信号与线性系统》 阎鸿森,王新凤,田惠生. 《信号与线性系统》 西安交通大学出版社, 西安交通大学出版社,1999.
因此,系统的概念是非常广泛的. 因此,系统的概念是非常广泛的.系统分析 的理论与方法当然也是极其重要的. 的理论与方法当然也是极其重要的. 二. 本课程所涉及的内容 两大模块:信号分析, 两大模块:信号分析,系统分析 研究对象: 研究对象:确知信号与线性时不变系统 (Linear Time- Invariant System )
信号与系统课后答案第六章作业答案
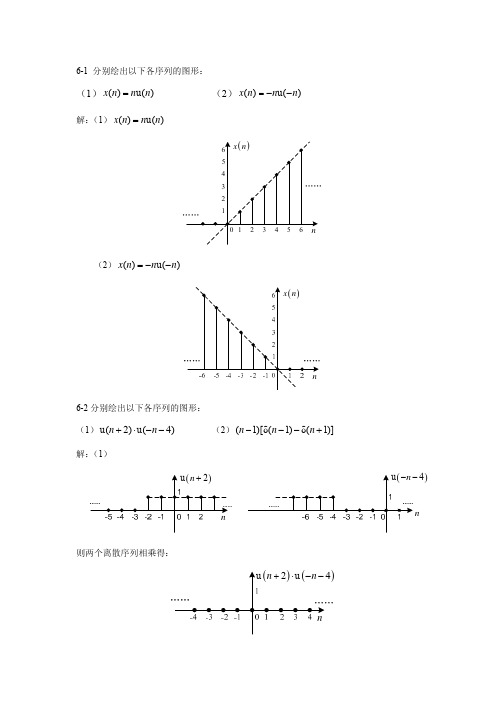
⋅
2⎤⎥⎦
⋅
u
(n
−
3)
=
2⋅
( −1)n
⎡2 ⎢⎣ k =0
( −1)− k
⎤ ⎥⎦
⋅
u
(n
−
3)
∑ y
f
(3)
=
2
⋅
(
−1)3
⎡ ⎢⎣
k
2 =0
(
−1)−k
⎤ ⎥⎦
=
2
⋅
( −1)
⋅
(1
−1
+
1)
=
−2
∑ y
f
(4)
=
2
⋅
(
−1)4
⎡ ⎢⎣
k
2 =0
(
−1)−k⎤ ⎥⎦=2⋅(1)
⋅
(1
−1
+
1)
-1
对应时刻点相乘后累加得 y(1) = 4 。 由于 f1(n) 和 f2 (n) 为有限序列,故该题可采用数乘法进行计算:
11112 2 2 2 ↑ 1 1 1 1 −1 −1 −1 ↑
−1 −1 −1 −1 − 2 − 2 −2 −2 −1 −1 −1 −1 − 2 − 2 −2 −2 −1 −1 −1 −1 − 2 − 2 −2 −2
u
(
n
+
4)
(4)利用卷积的性质( f (n) *δ(n − m) = f (n − m) )可得:
nu(n) * δ(n + 3) = nu(n) n=n+3 = (n + 3) u(n + 3)
6-7 如题图 6-4 所示,如果 y(n) = f1(n) * f2 (n) ,则试求 y(−2)、y(0)、y(1) 的值。
信号与系统刘树棠课后答案

信号与系统刘树棠课后答案【篇一:信号与系统复习指导】>本课程是电子信息与电气类专业本科生的一门重要的专业基础课程。
它主要讨论信号、线性时不变系统的分析方法,并通过实例分析,向学生介绍工程应用中的重要方法。
通过这门课程的学习,提高学生的分析问题和解决问题的能力,为学生今后进一步学习信号处理、网络分析综合、通信理论、控制理论等课程打下良好的基础。
本课程需要较强的数学基础,其主要任务是运用相关数学方法进行信号与线性时不变系统分析。
注重结合工程实际。
先修课程:“高等数学”、“大学物理”、“电路分析”等。
□ 课程的主要内容和基本要求1. 信号与系统的基本概念(1) 掌握信号的基本描述方法、分类及其基本运算。
(2) 掌握系统的基本概念和描述方法,掌握线性时不变系统的概念。
2. 信号与系统的时域分析(1) 掌握卷积积分的概念及其性质。
(2) 掌握卷积和的概念及计算。
(3) 掌握连续信号的理想取样模型及取样定理。
3. 连续时间信号与系统的频域分析 (1) 掌握周期信号的傅里叶级数展开。
(2) 掌握傅里叶变换及其基本性质。
(3) 掌握信号的频谱的概念及其特性。
(4) 掌握系统对信号响应的频域分析方法。
(5) 掌握系统的频域传输函数的概念。
(6) 掌握理想低通滤波器特性,了解系统延时、失真、因果等概念。
(7) 掌握线性系统的不失真传输条件。
4.离散时间信号与系统的频域分析 (1) 理解周期信号的傅里叶级数展开。
(2) 掌握傅里叶变换及其基本性质。
(4) 掌握系统的频率响应。
(5) 掌握系统对信号响应的频域分析方法。
5. 连续时间信号与系统的复频域分析(1) 掌握单边拉普拉斯变换的定义和性质。
(2) 掌握拉普拉斯反变换的计算方法(部分分式分解法)。
(3) 掌握系统的拉普拉斯变换分析方法。
(4) 掌握系统函数的概念。
(5) 掌握系统极零点的概念及其应用。
(6) 掌握系统稳定性概念。
(7) 掌握系统的框图与信号流图描述。
信号与系统分析(第2版)第6章_5-7

6.1 引言
6.2 离散时间傅里叶变换
6.3 离散时间系统的频域分析
6.4 离散傅里叶变换 6.5 信号频谱的数值计算 6.6 离散傅里叶变换的性质 6.7 快速傅里叶变换简介
信号与系统分析(第2版)电子教案
1
6.5 信号频谱的数值计算
6.5 信号频谱的数值计算
O
t
O
R( )
r (t )
1
O
t
O
只 要 对 带 限 信 号 进 行 DFT 计算,就必须先截断 xt ,这样 一来,频谱泄露就无法避免。
x1 (t )
X 1 ( )
O
t
O
所以时域混叠与频谱泄露是一对矛盾。
信号与系统分析(第2版)电子教案
15
6.5 信号频谱的数值计算
3. 数据截断问题
信号与系统分析(第2版)电子教案
12
6.5 信号频谱的数值计算
3. 数据截断问题
(1) 时限信号抽样及频谱的混叠现象 ① 计算机只能处理时限信号,对非时限信号应先 截短; ② 时限信号的频带无限,抽样定理 s M无法实 现,所以频率混叠不可避免。 ③ 减少混频的措施: a、 s 应尽量取大,这需要大储存空间和快速计 算设备; b、先经过低通滤波器,滤掉信号中大于 M 的频 率分量。
2 j kn e 16 j4 2 k 16
DFT: X [k ]
n 0
3
1 e
2 j k 1 e 16
j k 1 e 2 j k 1 e 8
O
5
10
15
n
《信号与系统(第2版》【附录+习题答案】
附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦:e e sh 2x xx --=双曲余弦:e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =,C 为常数(下同)d()d d u v u v ±=±,u 、v 为t 的函数(下同) d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式(1)等比数列123,,,,N a a a a 的通项为11n n a a q -=,q 为公比,前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑(2)等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-,d 为公差,前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰, 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰,1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭,B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰,0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑,0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑,0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤,附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤,B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1(a)确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
信号与系统(刘树棠译)第六章
2 0lgH (j) 1 0lg2 3d B
41
相频特性:
H(j)tg1()
1 时,
1 时,
1 时,
H(j)0
H( j)
2
H( j)
4
将其折线化可得相位特性的直线型渐近线:
42
0 ,
H( j)
lg 1,
4
, 2
0.1/
0.1 10
10/
43
二. 二阶系统:
模型: d2 dy t2 (t)2ndy d(tt)n2y(t)n2x(t)
如:对RLC串联谐振电路,可列出电路方程
n2 1/ LC
y(t)Ry(t)1y(t)1x(t) L L C L C
R 2
C L
44
由二阶系统的方程可得系统的频率响应:
H (j)(j)22 n n 2 (j)n2(j n)22 1 (j n)1
45
1.时域特性:
由 H (j)(jc 1)(n2 jc2)j M c1j M c2
c1,2nn 21
M n 2 2 1
h(t)M ec1tec2t u(t) h ( t )
12?sinsaccjt?cccthted?tt????????????23如果理想低通滤波器具有线性相位特性e则??sinsacccthtttt?????????????????hj???j??c???0?c??24理想低通滤波器的单位阶跃响应sthtut?sin??1sincttcctxdtdxtxx?????ct??????????25001sin1sinctxxdxdxxx?????????0sinsixd?x????令si
由于
x ,Si(x);
x ,Si(x)
信号与系统-答案(刘树棠,第二版) _第1-10章
输入x(t)单位冲激响应h(t)
(a)x(t)=2xo(t)h(t)=ho(t)
(b)x(t)=xo(t)-xo(t-2)h(t)=ho(t)
1.22
一离散时间信号x[n]如图original所示,请画出下列信号并给予标注。
a)x[n-4]
b)x[3-n]
c)x[3n]
e)x[n]u[3-n]
f)x[n-2]δ[n-2]
1.23
确定并画出图original信号的奇部和偶部,并给予标注。
1.25
判定下列连续时间信号的周期性,若是周期的,确定它的基波周期。
Charpt 1
1.21—(a),(b),(c)
一连续时间信号x(t)如图original所示,请画出下列信号并给予标注:
a)x(t-1)
b)x(2-t)
c)x(2t+1)
d)x(4-t/2)
e)[x(t)=x(-t)]u(t)
f)x(t)[δ(t+3/2)-δ(t-3/2)]
(d),(e),(f)
只有奇次谐波
(b) 奇谐信号,
如下图所示。
,(k为奇数)
,(k为偶数)
3.44解:
由T=6,可得
由条件4可知,
即, ,所以k为奇数
由于当k=0和k>2时,有
所以当k=2时, 且
因此,
又由 为实信号可知,
由条件5,6可知
所以
则,
3.48解:
(a)
(b)
c).
(d)
2023年大学_信号与系统第二版(陈生潭著)课后答案下载
2023年信号与系统第二版(陈生潭著)课后答案下载2023年信号与系统第二版(陈生潭著)课后答案下载第1章信号与系统的基本概念1.0 信号与系统1.1 信号的描述和分类1.1.1 信号的描述1.1.2 信号的分类1.2 信号的基本特性1.3 信号的基本运算1.3.1 相加和相乘1.3.2 翻转、平移和展缩1.3.3 信号的导数和积分1.3.4 信号的差分和迭分1.4 阶跃信号和冲激信号1.4.1 连续时间阶跃信号1.4.2 连续时间冲激信号1.4.3 广义函数和艿函数性质1.4.4 阶跃序列和脉冲序列1.5 系统的描述1.5.1 系统模型1.5.2 系统的输入输出描述1.5.3 系统的状态空间描述1.5.4 系统的框图表示1.6 系统的特性和分类1.6.1 线性特性1.6.2 时不变特性1.6.3 因果性1.6.4 稳定性1.6.5 系统的分类1.7 信号与系统的分析方法习题一第2章连续信号与系统的`时域分析 2.0 引言2.1 连续时间基本信号2.1.1 奇异信号2.1.2 正弦信号2.1.3 指数信号2.2 卷积积分2.2.1 卷积的定义2.2.2 卷积的图解机理2.2.3 卷积性质2.2.4 常用信号的卷积公式2.3 系统的微分算子方程2.3.1 微分算子和积分算子2.3.2 LTI系统的微分算子方程2.3.3 电路系统算子方程的建立2.4 连续系统的零输入响应2.4.1 系统初始条件2.4.2 零输入响应算子方程2.4.3 简单系统的零输入响应2.4.4 一般系统的零输入响应2.5 连续系统的零状态响应2.5.1 连续信号的艿(£)分解2.5.2 基本信号d(£)激励下的零状态响应 2.5.3 一般信号厂(£)激励下的零状态响应2.5.4 零状态响应的另一个计算公式2.6 系统微分方程的经典解法2.6.1 齐次解和特解2.6.2 响应的完全解习题二第3章连续信号与系统的频域分析3.0 引言3.1 信号的正交分解3.1.1 矢量的正交分解3.1.2 信号的正交分解3.2 周期信号的连续时间傅里叶级数3.2.1 三角形式的傅里叶级数3.2.2 指数形式的傅里叶级数3.3 周期信号的频谱3.3.1 周期信号的频谱3.3.2周期信号频谱的特点3.3.3周期信号的功率3.4 非周期信号的连续时IⅫ傅里叶变换 3.4.1 傅里叶变换3.4.2 非周期信号的频谱函数3.4.3 典型信号的傅里叶变换3.5 傅里叶变换的性质3.6 周期信号的傅里叶变换3.7 连续信号的抽样定理3.7.1 信号的时域抽样定理3.7.2 周期脉冲抽样……第4章连续信号与系统的S域分析第5章离散信号与系统的时域分析第6章离散信号与系统的频域分析第7章离散信号与系统的Z域分析第8章系统的状态空间分析第9章随机信号通过线性系统分析第10章 MATLAB在信号与系统分析中的应用附录各章习题参考答案信号与系统第二版(陈生潭著):内容提要本书可作为高等学校电子信息工程、通信工程、计算机科学与技术、测控技术与仪器、光信息科学与技术、电气工程及自动化等专业“信号与系统”课程的教材,也可供相关专业科技工作人员参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 6&7 4/26/2022
6.22
一个称为低通微分器的连续时间滤波器的频率响应如图所示,试对以下每个输入信号 x(t)求输出信号y(t)
(a))2cos()(θπ+=t t x (b))4cos()(θπ+=t t x
解: (a))(2
1)(221θπθπω--++=t j t j e e j X
∴在通过如图所示的系统时
频谱为在πω20=和πω20-=处的两个冲击,且在滤波器通过的范围之内。
所以振幅加权为)(320ωj H ,相位在πω20=处为提前2π在πω20-=处滞后2π。
所以
输出信号为)2sin(32)](2[32)]**(21[32)(222222θπθπθπθπθπππ+-=-=+=--+---+t e e j e e e e t y t j t j j t j j t j (b)此时信号的频谱为在πω40=和πω40-=的冲击,落在滤波器的通带范围之外所以y(t)=0
6.28 画出下列频率响应的波特图
(3)4)2(16
+ωj (7)ωωj j +-11
)10/(
解:
(3)
(7)
Chapter 7
7.21
一信号x(t),其傅立叶变换为)(ωj X ,对x(t)进行冲击串采样,产生)(t x p 为
∑∞
-∞=-=
n p nT t nT x t x )()()(δ 其中T=410-.关于x(t)或)(ωj X 所作的假设采用抽样定理能保证x(t)从)(t x p 完全恢复吗?
(a)πωω5000||,0)(>=j X (b)πωω1500||,0)(>=j X (f)πωωω1500,0)(*)(>=j X j X
解:
∵T =410-s ∴πππω2000010
1224===-s s f 又∵由抽样定理有当h s ωω2≥时可以恢复原信号
∴
(a)πππω20000100005000*22<==h
∴可以恢复
(b) πππω200003000015000*22>==h
∴不能恢复
(f)由条件可知在ππω7500215000=>
h 时0)(=ωj X ∴πππω20000150007500*22<=≤h ∴可以恢复原信号
7.22
信号y(t)由两个均为带限信号)(1t x 和)(2t x 卷积而成,即
)(*)()(21t x t x t y =
其中
πωω1000,0)(1>=j X πωω2000,0)(2>=j X
现对y(t)作冲击串采样,以得到
请给出y(t)保证能从)(t y p 中恢复出来的采样周期T 的范围。
解:
由条件知πππωω300020001000,0)(=+>=j Y ∴抽样周期应满足 T<
s 410313000*22-⨯=ππ
∑∞-∞=-=
n p nT t nT y t y )()()(δ。
