最新结构力学复习公式
结构力学常用公式

结构力学常用公式
1.应力公式:σ=F/A,其中 F 为作用力,A 为作用面积,σ为应力。
2. 应变公式:ε = ΔL/L0,其中ΔL 为变形量,L0 为原始长度,ε为应变。
3. 弹性模量公式:E = σ/ε,其中 E 为弹性模量。
4. 餘弦定理:c = a + b - 2abcosC,其中 a,b 为两边的长度,
C 为两边之间的夹角,c 为斜边的长度。
5. 正弦定理:a/sinA = b/sinB = c/sinC,其中 a,b,c 为三角形三条边的长度,A,B,C 为三角形对应的内角。
6. 面积公式:A = 1/2bh,其中 b 为底边的长度,h 为高度。
7. 矩形截面抵消矩阵算式:I = bh/12,其中 I 为矩形截面的抵消矩阵,b 为宽度,h 为高度。
8. 圆形截面抵消矩阵算式:I = πr/4,其中 I 为圆形截面的抵消矩阵,r 为半径。
9. 计算杆件最大承受力公式:Fmax = σmaxA,其中 Fmax 为杆件最大承受力,σmax 为材料的最大允许应力,A 为杆件横截面积。
10. 悬索线的张力公式:T = (Wl)/(8d),其中 T 为悬索线的张力,W 为悬挂物的重量,l 为悬挂物的长度,d 为悬索线的跨度。
- 1 -。
《结构力学2》公式小汇

《结构力学2》公式小汇第9章矩阵位移法
1、单元转换矩阵
2、局部坐标系下单元刚度方程
3、整体坐标下单元刚度方程公式
4、等效节点荷载公式
5、单元杆端力计算公式
第16章结构的极限荷载
1、屈服弯矩、极限弯矩
2、上限定理(极小定理)、下限定理(极大定理)
第10章结构的动力计算
单自由度体系
1、无阻尼简谐荷载作用下过渡阶段位移
2、无阻尼强迫振动杜哈梅积分位移
3、短时突加荷载(F P(t)=F P0 (0≤t≤u))作用下位移、动力系数t≤u时,
t>u时,
4、有阻尼自由振动位移及阻尼比计算公式
ξ<1,
ξ=1,
5、有阻尼强迫振动杜哈梅积分位移
6、有阻尼简谐荷载作用下平稳阶段位移
多自由度体系
7、双层刚架刚度矩阵[K]
8、刚度法运动方程、频率方程
9、刚度法的第一、二频率解
10、刚度法第一、二主振型
11、柔度法的第一、二频率解
12、柔度法第一、二主振型
13、柔度法运动方程、频率方程
14、主振型第一、二正交关系
15、正则坐标运动方程
其中,16、强迫振动的主振型叠加法正则坐标计算公式
17、能量法求第一频率(瑞利法)公式。
二级建造师建筑工程考试 重要公式复习

二级建造师建筑工程考试重要公式复习在二级建造师的考试中,掌握和熟练运用各种重要公式是非常重要的。
这些公式在建设工程中起着关键的作用,能够帮助工程师解决实际问题,确保建筑工程的质量和安全。
本文将介绍一些在二级建造师建筑工程考试中常见的重要公式,帮助考生进行复习。
一、土木工程测量公式1. 斜距公式:斜距 = 平距/余弦α其中,平距指两点之间的水平距离,α为斜线与水平线之间的夹角。
2. 高差公式:高差 = 斜距 ×正弦α其中,α为斜线与水平线之间的夹角。
3. 边角求边长公式:b² = a² + c² - 2ac × cosB其中,a、b、c为三角形的边长,B为两边所夹角的角度。
二、结构力学公式1. 弯矩公式:M = F × d其中,M为弯矩,F为作用力,d为力臂的长度。
2. 重力公式:F = mg其中,F为重力,m为物体的质量,g为重力加速度。
3. 悬臂梁最大弯矩公式:Mmax = W × L² / 8其中,Mmax为悬臂梁的最大弯矩,W为均布荷载,L为悬臂梁的长度。
三、钢筋混凝土结构设计公式1. 刚度折减系数公式:ε = (d - x) / ε₀其中,ε为刚度折减系数,d为钢筋混凝土截面的有效深度,x为受压区高度离截面底边的距离,ε₀为钢筋混凝土的弹性模量。
2. 钢筋混凝土截面抗弯承载力公式:M = As × fyd × (d - x) + A' × fcd × a × (d - x')²其中,M为截面抗弯矩,As为受拉钢筋的面积,fyd为受拉钢筋的抗拉强度,d为截面的有效深度,x为受压区高度离截面底边的距离,A'为受压区域的面积,fcd为混凝土的抗压强度,a为受压区域内应力分布的高度系数,x'为受压纵筋合力点至截面底边的距离。
四、建筑经济学公式1. 单位面积造价公式:C = T / A其中,C为单位面积造价,T为总造价,A为建筑面积。
结构力学公式大全

结构力学公式大全之蔡仲巾千创作1、经常使用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它暗示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边沿到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全(完整资料).doc
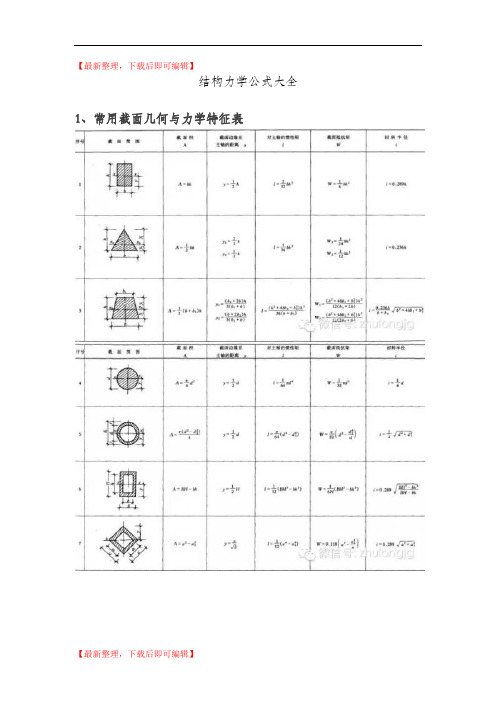
【最新整理,下载后即可编辑】结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全

结构力学公式大全1、常用截面几何与力学特征表注:1.I称为截面对主轴(形心轴)的截面惯性矩(mm4)。
基本计算公式如下:2.W称为截面抵抗矩(mm3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:3.i称截面回转半径(mm),其基本计算公式如下:4.上列各式中,A为截面面积(mm2),y为截面边缘到主轴(形心轴)的距离(mm),I为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2、单跨梁的内力及变形表2.1 简支梁的反力、剪力、弯矩、挠度2.2 悬臂梁的反力、剪力、弯矩和挠度2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度2.4 两端固定梁的反力、剪力、弯矩和挠度2.5 外伸梁的反力、剪力、弯矩和挠度3.等截面连续梁的内力及变形表3.1 二跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F;。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
[解] MB支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN·mVB左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l=6m,均布荷载q=11.76kN/m,求边跨最大跨中弯矩。
[解] M1=0.080×11.76×62=33.87kN·m。
3.2 三跨等跨梁的内力和挠度系数注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql;。
结构力学公式大全
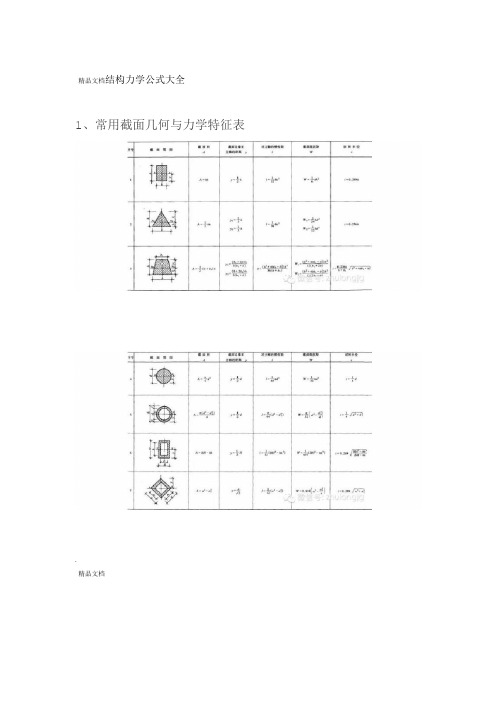
精品文档结构力学公式大全1、常用截面几何与力学特征表.精品文档.精品文档.精品文档)。
基本计算公式如mm4.I称为截面对主轴(形心轴)的截面惯性矩(1注:下:),它表示截面抵抗弯曲变形能力的大小,基本mm3W称为截面抵抗矩(2.计算公式如下:mm),其基本计算公式如下:3.i称截面回转半径(为截面边缘到主轴(形心轴)的距y为截面面积(mm2),.上列各式中,4A I为对主轴(形心轴)的惯性矩。
mm离(),.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
52、单跨梁的内力及变形表简支梁的反力、剪力、弯矩、挠度2.1 .精品文档.精品文档.精品文档2.2 悬臂梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.3 一端简支另一端固定梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.4 两端固定梁的反力、剪力、弯矩和挠度.精品文档.精品文档2.5 外伸梁的反力、剪力、弯矩和挠度.精品文档.精品文档.精品文档.等截面连续梁的内力及变形表3 3.1 二跨等跨梁的内力和挠度系数.精品文档;。
qlql2;V=表中系数×注:1.在均布荷载作用下:M=表中系数×;。
;V =表中系数×F 2.在集中荷载作用下:M=表中系数×Fl,每跨各有一集11.76kN/m,均布荷载q=例1] 已知二跨等跨梁l=5m [ =29.4kN,求中间支座的最大弯矩和剪力。
中荷载F 5))+(-0.188×29.4××解[] MB 支=(-0.125×11.7652m64.39kN·36.75)+(-27.64)=-=(-29.40.688×)0.625 VB左=(-×11.76×5)+(-56.98kN)+(-20.23)=-=(-36.75,求边跨最大跨中11.76kN/m6m,均布荷载q==2] [例已知三跨等跨梁l 弯矩。
最新结构力学重点公式

(3)优惠多荷载频率θ=2πn/60
阻尼比ζ=(1/20π)*ln
动力系数β=1/
最大弯矩 Mmax=(G*βFp)*l*0.25
最大正应力σmax=(G+βFp)*l/4Wz
标题:大学生究竟难在哪?—创业要迈五道坎2004年3月23日最大竖向位移Ymax=(G+βFp)δ
=-
Beadwrks公司还组织各国的“芝自制饰品店”定期进行作品交流,体现东方女性聪慧的作品曾在其他国家大受欢迎;同样,自各国作品也曾无数次启发过中国姑娘们的灵感,这里更是创作的源泉。W= =
400-500元1326%Y2max=y02+( )2
V0=w*
(五)DIY手工艺品的“价格弹性化”柔度系数б=L3/48EI
据统计,上海国民经济持续快速增长。03全年就实现国内生产总值(GDP)6250.81亿元,按可比价格计算,比上年增长11.8%。第三产业的增速受非典影响而有所减缓,全年实现增加值3027.11亿元,增长8%,增幅比上年下降2个百分点。=(б11m1- )(22m2- )-б12m2б21m1=0
主振型 =-
主振型 =-
=-
W= =
Y2max=y02+( )2
V0=w*
柔度系数б=L3/48EI
自振频率w=
荷载频率θ=2πn/60
阻尼比ζ=(1/20π)*ln
动力系数β=1/
最大弯矩 Mmax=(G*βFp)*l*0.25
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
平面体系的计算自由度 W 的求法
2
(1)刚片法:体系看作由刚片组成,铰结、刚结、链杆为约束。
3
刚片数 m ;
4
约束数:单铰数 h ,简单刚结数 g ,单链杆数 b 。
5
W = 6
3m - 2h - 3g -b
7
(2)节点法:体系由结点组成,链杆为约束。
8
结点数 j ;
9
约束数:链杆(含支杆)数 b 。
10
W = 2j 11
– b
12
(3)组合算法
13
约束对象:刚片数 m ,结点数 j
14
约束条件:单铰数 h ,简单刚结数 g ,单链杆(含支杆)数 b
15
W = (3m + 2j)16
-(3+2h+ b)
17
比较可得:三铰拱与简支梁的竖向支反力完全相同。
注意到水平支反力式中18
的分子就是简支梁上截面C的弯矩,则水平支反力可写作:
19
20
综上所述,三铰拱在竖向荷载作用下,任一截面上的弯矩、剪力荷轴力的计21
算公式如下:
22
23
4.4.1 各种结构位移计算公式
24
25
:虚设单位荷载P=1作用下的结构的内力;
26
:实际荷载作用下的结构的内力
27
28
29
30
图乘法
31
位移公式:
32
4.5.2 常见图形的面积和形心
33
常见图形的形心和面积(图4.10)。
34
35
36
图4.10
37
以上图形的抛物线均为标准抛物线:抛物线的顶点处的切线都是与基线平行38
4.5.3 应用图乘法时的几个具体问题
39
(2) 如果有一个图形为折线,则应分段考虑(图4.12)
40
41
图4.12
42
43
(3) 如果图形比较复杂,应根据弯矩图的叠加原理将图形分解为几个简单图44
形,分项计算后再进行叠加图4.13
45
46
图4.13
47
(图4.13b中A1与y1的乘积为负值;图4.13c中抛物线为非48
标准曲线)。
49
例5:试求出图4.16刚架结点B 的水平位移和转角,EI 为常数
50
51
图4.16
52
解: (1)虚设单位荷载,作实际状态和虚设单位荷载的弯矩图(图4.17a、b、53
c)
54
55
图4.17
56
(2)代入公式,图乘。
57
B 点竖向位移:
58
59
B 点转角位移:
60
61
力法的基本概念
62
Δ11=δ11X1 力法典型方程:δ11X1+ Δ1P =0
63
a)做基本结构在荷载作用下的荷载弯矩M P和单位未知力X1=1的作用64
下的单位弯矩图M1应用叠加公式得到结构的弯矩图M。
65
b)
66
力法的基本方程:二次超静定结构
67
68
69
位移互等定理:δij=δji
70
δij表示单位力X j =1在基本结构沿X i 方向产生的位移,称柔度系数。
71
ΔiP表示在基本结构实际荷载沿X i方向产生的位移。
72
力法解超静定结构
73
:绘图
74
5.10a超
75
静定刚
76
架的弯
77
矩图。
78
图5.10
79
解:
80
(1)基
81
本体系
82
(图
83
5.10b)
84
(2)力法方程
85
基本体系应满足B 点无水平位移的变形条件。
力法方程为
86
δ11X1+ Δ1P =0
87
(3)计算系数和自由项
88
分别画出实际荷载及单位未知力X1 =1的作用的弯矩图(图5.10c、d),利89
用图乘法计算系数。
90
91
92
(4)求多余的未知力
93
94
(5)作弯矩图(图5.10e)
95
96
97。
